-
Общие сведения
-
Постановка задачи безусловной оптимизации функции многих переменных
-
Постановка
задачи поиска минимума функции содержит:
-
целевую
функцию
 где
где ,
,
определенную наn-мерном
евклидовом пространстве .
. -
множество
допустимых решений
 ,
,
среди элементов которого осуществляется
поиск.
Требуется
найти такой вектор
![]() из множества допустимых решений, которому
из множества допустимых решений, которому
соответствует минимальное значение
целевой функции на этом множестве:
![]()
Если
множество допустимых решений
![]() задается ограничениями, накладываемыми
задается ограничениями, накладываемыми
на вектор![]() ,
,
то решается задач условного экстремума.
Если![]() ,
,
т.е. ограничения на вектор![]() отсутствуют, то решается задача поиска
отсутствуют, то решается задача поиска
безусловного экстремума.
Введем
обозначения:
-
вектор-градиент
функции

![]()
-
симметричная
матрица вторых частных производных
(Гессиан)

-
Глобальный оптимум функции
Точка
![]() называется точкой глобального минимума
называется точкой глобального минимума
функции![]() на множестве
на множестве![]() ,
,
если функция достигает в этой точке
своего наименьшего значения, т.е.:
![]() ,
,
![]()
-
Локальный оптимум функции
Точка
![]() называется точкой локального минимума
называется точкой локального минимума
функции![]() на множестве
на множестве![]() ,
,
если существует![]() ,
,
такое, что если![]() и
и![]() ,
,
то![]() .
.
-
Выпуклость множеств и функций
Множество
![]() называется выпуклым, если оно содержит
называется выпуклым, если оно содержит
всякий отрезок, концы которого принадлежат![]() ,
,
т.е. если для любых![]() ,
,![]()
![]() и
и![]() справедливо
справедливо![]() .
.
Функция
![]() ,
,
определенная на выпуклом множестве![]() ,
,
называется выпуклой, если![]() ,
,![]() ,
,![]() .
.
Функция
![]() ,
,
определенная на выпуклом множестве![]() ,
,
называется строго выпуклой, если![]() ,
,![]() ,
,![]() .
.
Функцию
![]() называют выпуклой (строго выпуклой),
называют выпуклой (строго выпуклой),
если она целиком лежит не выше (ниже)
отрезка, соединяющего две ее произвольные
точки.
Если
![]() выпуклая функция на выпуклом множестве
выпуклая функция на выпуклом множестве![]() ,
,
то всякая точка локального минимума
является точкой ее глобального минимума
на![]() .
.
Если выпуклая функция достигает своего
минимума в двух различных точках, то
она достигает минимума во всех точках
отрезка, соединяющего эти две точки.
-
Методы прямого поиска безусловного оптимума функции многих переменных
Методы
прямого поиска являются методами, в
которых используются только значения
функции.
Методы
прямого поиска наиболее эффективно
используются если функция
![]() и/или ее градиент разрывны в точке
и/или ее градиент разрывны в точке
оптимума, аналитическое выражение
градиента невозможно или затруднено,
а численное дифференцирование требует
больших вычислительных ресурсов.
С
общих позиций их можно разделить на
эвристические (метод покоординатного
спуска, метод Нелдера-Мида) и теоретические
(метод сопряженных направлений).
Эвристические методы реализуют процедуру
поиска с помощью интуитивных геометрических
представлений. Теоретические методы –
с помощью фундаментальных математических
теорем.
-
Эвристические методы
-
Метод Хука-Дживса (метод прямого поиска)
-
Хук
и Дживс предложили логически простую
стратегию поиска, использующую априорные
сведения и в то же время отвергающую
устаревшую информацию относительно
характера топологии целевой функции в
![]() .
.
Этот алгоритм включает два основных
этапа: «исследующий поиск» вокруг
базисной точки и «поиск по образцу»,
т.е. в направлении, выбранном для
минимизации. На рис. 1 представлена
упрощенная информационная блок-схема
этого алгоритма.
Рассматриваемый
алгоритм состоит из следующих операций.
Прежде всего задаются начальные значения
элементов x, а также
начальное приращение![]() .
.
Чтобы начать «исследующий поиск»,
следует вычислить значение функции![]() в базисной точке (базисная точка
в базисной точке (базисная точка
представляет собой начальный вектор
предполагаемых искомых значений
независимых переменных на первом цикле).
Затем в циклическом порядке изменяется
каждая переменная (каждый раз только
одна) на выбранные величины приращений,
пока все параметры не будут таким образом
изменены. В частности,![]() изменяется на величину
изменяется на величину![]() ,
,
так что![]() .
.
Если приращение не улучшает целевую
функцию,![]() изменяется на
изменяется на![]() и значение
и значение![]() проверяется как и ранее. Если значение
проверяется как и ранее. Если значение![]() не улучшают ни
не улучшают ни![]() ,
,
ни![]() ,
,
то![]() оставляют без изменений. Затем
оставляют без изменений. Затем![]() изменяют на величину
изменяют на величину![]() и т.д., пока не будут изменены все
и т.д., пока не будут изменены все
независимые переменные, что завершает
один исследующий поиск. На каждом шаге
или сдвиге по независимой переменной
значение целевой функции сравнивается
с ее значением в предыдущей точке. Если
целевая функция улучшается на данном
шаге, то ее старое значение заменяется
на новое при последующих сравнениях.
Однако если произведенное возмущение
поxнеудачно, то сохраняется
прежнее значение![]() .
.
После
проведения одного (или более) исследующего
поиска применяется стратегия поиска
по образцу. Удачные изменения переменных
в исследующим поиске (т.е. те изменения
переменных, которые уменьшили
![]() )
)
определяют вектор![]() ,
,
указывающий некоторое направление
минимизации, которое может привести к
успеху. Серия ускоряющихся шагов, или
поиск по образцу, проводится вдоль этого
вектора до тех пор, пока![]() уменьшается при каждом таком поиске.
уменьшается при каждом таком поиске.
Длина шага при поиске по образцу в данном
координатном направлении приблизительно
пропорциональна числу удачных шагов,
имевших место ранее в этом координатном
направлении во время исследующих поисков
за несколько предыдущих циклов. Для
ускорения процесса оптимизации изменение
размера шага![]()
в поиске по образцу осуществляется
путем введения некоторого множителя
при величине![]() ,
,
используемой в исследующих поисках.
Исследующий поиск, проводимый после
поиска по образцу, называется исследующим
поиском типа II; успех или неудачу по
данному образцу нельзя установить до
завершения исследующего поиска типаII.![]()
Если
![]() не уменьшается в процессе исследующего
не уменьшается в процессе исследующего
поиска типаII, то говорят,
что данный поиск по образцу неудачен,
и проводится новый исследующий поиск
типаIдля определения
нового удачного направления. Если
исследующий поиск типаIне дает нового удачного направления,
то последовательно уменьшают![]() ,
,
пока либо можно будет определить новое
удачное направление, либо![]() не станет меньше, чем некоторая заранее
не станет меньше, чем некоторая заранее
заданная величина. Невозможность
уменьшить![]() ,
,
когда![]() достаточно мала, указывает на то, что
достаточно мала, указывает на то, что
достигнут локальный оптимум. Описанная
последовательность поисков заканчивается,
если оказываются удовлетворенными
условия трех основных тестов. Первый
тест проводится после каждого исследующего
поиска и поиска по образцу: изменение
целевой функции сравнивается с заранее
малой величиной. Если значение целевой
функции не отличается на величину,
большую, чем это число, от предыдущего
основного значения целевой функции,
исследующий поиск или поиск по образцу
считается неудачным. В противном случае
проводится тест для определения,
увеличилась ли целевая функция (неудача)
или уменьшилась (удачный поиск) этот
второй тест нужен для того, чтобы быть
уверенным, что значение целевой функции
все время улучшается. Третий тест
проводится после неудачи в исследующем
поиске на стадии уменьшения изменения![]() .
.
Поиск может быть закончен, если на данном
шаге изменение каждой переменной![]() оказывается меньше, чем некоторое
оказывается меньше, чем некоторое
заранее определенное число.
Р ис.
ис.
1. Информационная блок-схема минимизации
прямым поиском
Соседние файлы в папке Лекции
- #
- #
- #
- #
- #
- #
Эвристические алгоритмы формирования портфеля инвестиций
Время на прочтение
10 мин
Количество просмотров 11K
Предположим, что у нас есть 100 млн. долларов, которые нужно вложить в несколько возможных инвестиций. Каждое из этих вложений имеет различную стоимость и различный ожидаемый доход. Мы должны решить, как потратить деньги, чтобы получить максимальную прибыль.
Задачи такого типа называются задачами формирования портфеля. У нас есть несколько позиций (инвестиций), которые должны поместиться в портфель фиксированного размера (100 млн. долларов). Каждая позиция имеет свою прибыльность. Необходимо найти набор позиций, которые помещаются в портфель и дают максимальную прибыль.
Многие из вас скажут, что никакие эвристики тут не нужны, и что вполне можно обойтись полным перебором. Другие заявят, что и полный перебор не нужен, ведь существует метод ветвей и границ. Но как быть, если количество возможных инвестиций 65? Полное дерево решений содержит более 7*10^19 узлов. Предположим, что метод ветвей и границ перебирает десятую часть процента этих узлов, а компьютер проверяет миллион узлов в секунду. В этих условиях для решения задачи потребовалось бы более 2 млн. лет. Именно для таких сложных задач и используются эвристики. Если вам интересно, милости прошу под кат.
Восхождение на холм
Эвристический метод восхождения на холм вносит изменения в текущее решение, продвигая его максимально близко к цели. Этот процесс называется восхождением на холм, потому что похож на то, как заблудившийся путешественник пытается ночью добраться до вершины горы. Даже если уже слишком темно, чтобы разглядеть что-то вдали, он может попробовать достигнуть вершины горы, постоянно двигаясь вверх.
Конечно, существует вероятность, что путник остановится на вершине меньшего холма и не достигнет пика. Эта проблема существует и при использовании данного эвристического метода. Алгоритм может найти решение, которое будет локально-оптимальным, но не будет лучшим возможным решением.
В задаче формирования портфеля инвестиций цель состоит в том, чтобы выбрать набор позиций с общей стоимостью не более допустимого предела, а общая прибыль при этом должна быть как можно больше. Эвристика восхождения на холм для этой задачи выбирает позицию, которая даёт максимальную прибыль на каждом шаге. При этом решение будет всё лучше соответствовать цели – получению максимальной прибыли.
Алгоритм сначала добавляет к решению позицию с максимальной прибылью, затем добавляется следующая позиция с максимальной прибылью (при условии, что полная цена остаётся в допустимых пределах). Присоединение позиций с максимальной прибылью будет продолжаться, пока не будет исчерпан лимит стоимости.
Для списка инвестиций, приведённого ниже, программа сначала выберет сделку A, потому что она имеет самую большую прибыль (9 млн. долларов). Затем выбирается сделка C, потому что она имеет самую большую прибыль из оставшихся (8 млн. долларов). В этот момент времени из допустимых 100 млн. потрачено уже 93 млн., и алгоритм больше не сможет выбирать какие-либо сделки. Решение, вычисленное с помощью этой эвристики, включает элементы A и C, стоит 93 млн. и даёт прибыль в 17 млн.

Эвристика восхождения на холм заполняет портфель очень быстро. Если элементы изначально упорядочены в порядке уменьшения прибыли, то сложность алгоритма составляет порядка O(N). Программа просто перемещается по списку, добавляя позиции с максимальной прибылью, пока не будет исчерпан лимит средств. Если список не отсортирован, то сложность этого алгоритма составляет N*log(N). Это много лучше, чем O(2^N) шагов, необходимых для полного перебора всех узлов дерева. Для 20 позиций эта эвристика использует около 400 шагов, метод ветвей и границ – несколько тысяч, а полный перебор – более чем 2 млн.
Метод наименьшей стоимости
Стратегия, которая в некотором смысле является противоположностью методу восхождения на холм, называется методом наименьшей стоимости. Вместо того, чтобы на каждом шаге приближать решение максимально близко к цели, можно попробовать уменьшить стоимость решения. В примере с формированием портфеля инвестиций на каждом шаге к решению добавляется позиция с минимальной стоимостью.
Данная стратегия будет помещать в решение максимально возможное число позиций. Это хорошо работает в случае, если все позиции имеют примерно одинаковую стоимость. Но если дорогая сделка приносит большую прибыль, эта стратегия может пропустить выпавший шанс, давая не лучший из возможных результатов.
Для инвестиций, приведённых выше, стратегия минимальной стоимости начинает с того, что сначала добавляет к решению сделку E стоимостью 23 млн. Затем она выбирает позицию D стоимостью 27 млн. и C стоимостью 30 млн. В этой точке алгоритм уже потратил 80 млн. из 100 млн. долларов и не может больше сделать ни одного вложения.
Полученное решение стоит 80 млн. и даёт прибыль 18 млн. Это на миллион лучше, чем решение, которое даёт нам эвристика восхождения на холм, но алгоритм минимальной стоимости далеко не всегда работает эффективнее, чем алгоритм восхождения на холм. Какой из методов даст лучшее решение зависит от конкретных данных.
Структура программ, реализующих эвристики минимальной стоимости и эвристики восхождения на холм, почти идентична. Единственная разница заключается в выборе следующей позиции, которая добавляется к имеющемуся решению. Метод минимальной стоимости вместо позиции с максимальной прибылью выбирает позицию, которая имеет самую низкую стоимость. Поскольку эти два метода очень похожи, сложность их одинаковы. Если позиции должным образом отсортированы, оба алгоритма имеют сложность порядка O(N). При случайном расположении позиций их сложность составит порядка O(N*log(N)).
Сбалансированная прибыль
Стратегия восхождения на холм не учитывает стоимости добавляемых позиций. Она выбирает позиции с максимальной прибылью, даже если они имеют большую стоимость. Стратегия минимальной стоимости не берёт в расчёт приносимую позицией прибыль. Она выбирает элементы с небольшими затратами, даже если они имеют маленькую прибыль.
Эвристика сбалансированной прибыли сравнивает как прибыль, так и стоимость позиций, чтобы определить, какие позиции необходимо выбрать. На каждом шаге эвристика выбирает элемент с самым большим отношением прибыли к стоимости (при условии, что после включения инвестиции в портфель, суммарная цена останется в допустимых пределах).
Включим в таблицу новый столбец – отношение прибыль/стоимость. При таком подходе сначала выбирается позиция C, потому что она имеет самое высокое отношение – 0.27. Затем добавляется D с отношением 0.26 и B с отношением 0.20. В этой точке потрачено 92 млн. из 100 млн., и в решение нельзя добавить ни одной позиции.
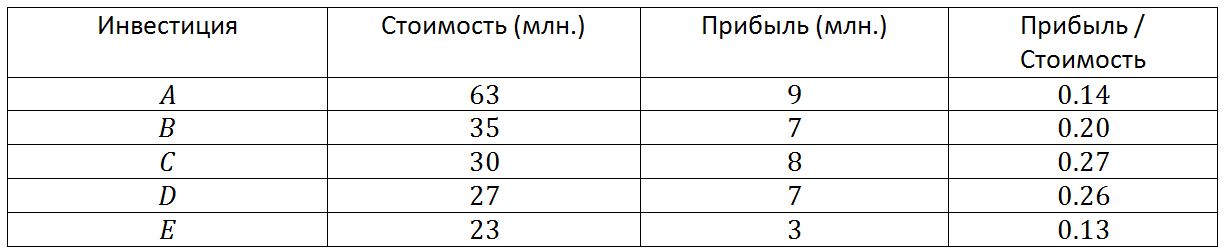
Это решение имеет стоимость 92 млн. и даёт прибыль в 22 млн. Это на 4 млн. лучше, чем решение, найденное с помощью метода минимальной стоимости и на 5 млн. лучше, чем решение найденное эвристикой восхождения на холм. Более того, найденное решение вообще будет наилучшим из всех возможных, что подтвердят результаты поиска полным перебором или методом ветвей и границ. Но важно понимать, что сбалансированная прибыль – это всё-таки эвристика, поэтому с помощью этого не всегда отыскивается лучшее возможное решение. Очень часто этот метод находит лучшие решения, чем решения, найденные методами восхождения на холм и минимальной стоимости, но это случается не всегда. Структура программы, реализующей эвристику сбалансированной прибыли, почти идентична структуре программ восхождения на холм и минимальной стоимости. Единственная разница заключается в способе выбора следующей позиции, которая добавляется к решению. Сложность этой эвристики пропорциональна O(N), при условии предварительной сортировки. В случае, если позиции расположены произвольно, сложность алгоритма составит O(N*log(N)).
Случайные методы
Случайный поиск
Случайный поиск выполняется в соответствии со своим названием. На каждом шаге алгоритм добавляет случайно выбранную позицию, которая удовлетворяет границам стоимости. Этот вид перебора называется методом Монте-Карло.
Поскольку случайно выбранное решение вряд ли окажется наилучшим, то для получения приемлемого результата необходимо повторить поиск несколько раз. Хотя на первый взгляд кажется, что вероятность нахождения хорошего решения очень мала, использование этого метода иногда приносит удивительно хорошие результаты. В зависимости от исходных данных и числа проверенных случайных решений, эта эвристика часто работает лучше, чем методы восхождения на холм и минимальной стоимости.
Преимущество случайного поиска состоит в том, что этот метод лёгок для понимания и реализации. Иногда трудно представить, как реализовать для конкретной задачи метод восхождения на холм, минимальной стоимости или приведённой прибыли, но всегда легко генерировать решения наугад. Даже для решения крайне сложных задач случайный поиск является наиболее простым методом.
Последовательное приближение
Другая стратегия состоит в том, чтобы начать со случайного решения, а затем производить последовательное приближение. Начав с произвольно сгенерированного решения, программа делает случайный выбор. Если новое решение является улучшением предыдущего, программа закрепляет изменение и продолжает проверку других позиций. Если изменение не улучшает решение, программа отказывается от него и делает новую попытку.
Особенно просто реализовать метод последовательного приближения для задачи формирования портфеля инвестиций. Программа всего-навсего выбирает случайную позицию из пробного решения и удаляет её из текущего. Затем она случайным образом добавляет в решение позиции до тех пор, пока не будет исчерпан лимит средств. Если удалённая позиция имела очень высокую стоимость, то не её место программа может добавить несколько позиций.
Как и случайный поиск, эта эвристика проста для понимания и реализации. Для решения сложной задачи бывает нелегко создать алгоритмы восхождения на холм, минимальной стоимости и приведённой прибыли, но довольно просто написать эвристический алгоритм последовательного приближения.
Момент остановки
Существует несколько хороших способов определить момент, когда необходимо прекратить случайные изменения. Например, допускается выполнить фиксированное число изменений. Для задачи из N элементов можно выполнить N или N^2 случайных изменений и затем остановить выполнение программы.
Другая стратегия состоит в том, чтобы делать изменения до тех пор, пока последовательных изменения будут приносить улучшения. Как только несколько подряд идущих изменений не дают улучшений, программу можно остановить.
Локальный оптимум
Если программа заменяет случайно выбранную позицию в пробном решении, она может найти решение, которое уже нельзя улучшать, но оно всё же не будет лучшим возможным решением. В качестве примера рассмотрим следующий набор возможных инвестиций.

Предположим, что алгоритм случайно выбирает позиции A и B в качестве начального решения. Его стоимость будет равна 90 млн., оно принесёт прибыль в 17 млн.
Если программа удаляет или A, или B, то решение будет иметь достаточно большую стоимость, поэтому программа сможет добавить только одну новую позицию. Поскольку позиции A и B имеют самую большую прибыль, замена их другой позицией уменьшит полную прибыль. Случайное удаление одной позиции из этого решения никогда не приведёт к улучшению.
Лучшее решение содержит позиции C, D, E. Его полная стоимость равна 98 млн., полная прибыль – 18 млн. Чтобы найти это решение, алгоритм должен удалить из решения сразу обе позиции A и B и добавить на их место новые.
Такие решения, когда небольшие изменения не могут улучшить решения, называются локальным оптимумом. Есть два способа, при применении которых, программа не остановится в локальном оптимуме, а будет искать глобальный оптимум.
Во-первых, программу можно изменить так, чтобы она удаляла из решения несколько позиций. Если программа удалит две случайно выбранные позиции, она сможет найти правильное решение для данного примера. Однако для задач большего размера удалить две позиции обычно недостаточно. Программе надо будет удалить три, четыре, а может большее количество позиций.
Более простой способ состоит в том, чтобы выполнить большее количество испытаний с различными исходными решениями. Некоторые из начальных решений могут привести к локальным оптимумам, но одно из них позволит достичь глобального оптимума.
Метод отжига
Метод отжига заимствован из термодинамики. При отжиге металл нагревается до высокой температуры. Молекулы в горячем металле совершают быстрые колебания. Если металл медленно охлаждать, то молекулы начинают выстраиваться в линии, образуя кристаллы. При этом молекулы постепенно переходят в состояние с минимальной энергией.
Когда металл остывает, соседние кристаллы сливаются друг с другом. Молекулы одного кристалла временно покидают свои позиции с минимальной энергией и соединяются с молекулами другого кристалла. Энергия получившегося кристалла большего размера будет меньше, чем сумма энергий двух исходных кристаллов. Если металл охлаждать достаточно медленно, кристаллы станут просто огромными. Конечное расположение молекул будет иметь очень низкую суммарную энергию, поэтому металл будет очень прочным.
Начиная с состояния с высокой энергией, молекулы в конечном счёте достигают состояния с низкой энергией. На пути к окончательному положению они проходят через множество локальных минимумов энергии. Каждая комбинация кристаллов представляет локальный минимум. Довести кристалл до минимального энергетического состояния можно только временным разрешением структуры меньших кристаллов, увеличивая тем самым энергию системы, в результате чего кристаллы могут объединяться.
Метод отжига использует аналогичный способ поиска лучшего решения задачи. Когда программа ищет путь решения, она может «застрять» в локальном оптимуме. Чтобы избежать этого, она время от времени вносит в решение случайные изменения, даже если очередной вариант не приводит к мгновенному улучшению результата. Это позволяет программе выйти из локального оптимума и отыскать лучшее решение.
Чтобы программа не зацикливалась на этих модификациях, алгоритм через какое-то время изменяет вероятность внесения случайных изменений. Вероятность внесения одного изменения равна P=1/e^(E/(k*T)), где E — количество «энергии», добавленной системе, k — константа, выбранная в зависимости от рода задачи и T – переменная, соответствующая «температуре».
Сначала величина T должна быть довольно высокой, поэтому вероятность изменений тоже будет довольно высокой. Через какое-то время значение величины T снижается, и вероятность случайных изменений тоже уменьшается. Как только процесс достиг точки, в которой никакие изменения не смогут улучшить решение и значение T станет настолько мало, что случайные изменения будут очень редкими, алгоритм закончит работу.
Для задачи формирования портфеля инвестиций E — величина, на которую сокращается прибыль в результате изменения. Например, если мы удаляем позицию, прибыль которой равна 10 млн. долларов, и заменяем её позицией, имеющей прибыль в 7 млн. долларов, добавленная к системе энергия будет равна 3. Если величина E велика, то вероятность изменений небольшая, поэтому вероятность больших изменений ниже.
Сравнение эвристических методов
Различные эвристические методы ведут себя по-разному в различных задачах. Для решения задачи о формировании портфеля инвестиций эвристика сбалансированной прибыли достаточно хороша, учитывая её простоту. Стратегия последовательного приближения тоже работает достаточно хорошо, но требует гораздо большего времени. Для других задач наилучшей может быть какая-нибудь другая эвристика, в том числе и не рассмотренная в этой главе.
Эвристики работают гораздо быстрее, чем методы полного перебора и ветвей и границ. Некоторые эвристические подходы (восхождение на холм, минимальная стоимость, сбалансированная прибыль и т.д.) работают чрезвычайно быстро, потому что рассматривают только одно возможное решение. Эти методы работают настолько быстро, что порой имеет смысл выполнить их все по очереди, а затем выбрать наилучшее из трёх полученных решений. Конечно, невозможно гарантировать, что это решение будет наилучшем, но оно точно будет достаточно хорошим.
Локальный и глобальный оптимумы
Почему решатель не находит наименьший минимум
В общем случае решатели возвращают локальный минимум (или оптимум). Результатом может быть глобальный минимум (или оптимум), но этот результат не гарантируется.
-
Минимум local функции является точкой, где значение функции меньше, чем в соседних точках, но возможно больше, чем в удаленной точке.
-
Минимум global является точкой, где значение функции меньше, чем во всех других допустимых точках.
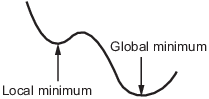
Решатели Optimization Toolbox™ обычно находят локальный минимум. (Этот локальный минимум может быть глобальным минимумом.) Они находят минимум в basin of attraction начальной точки. Для получения дополнительной информации об областях притяжения, смотрите Области притяжения.
Следующее является исключениями к этому общему правилу.
-
Задачи линейного программирования и положительные определенные проблемы квадратичного программирования выпуклы с выпуклыми выполнимыми областями, таким образом, у них есть только одна область притяжения. В зависимости от заданных опций,
linprogигнорирует любую предоставленную пользователями начальную точку, иquadprogне требует один, даже при том, что можно иногда ускорять минимизацию путем предоставления начальной точки. -
Функции Global Optimization Toolbox, такой как
simulannealbnd, попытайтесь искать больше чем одну область притяжения.
Поиск меньшего минимума
Если вам нужен глобальный минимум, необходимо найти начальное значение для решателя в области притяжения глобального минимума.
Можно установить начальные значения, чтобы искать глобальный минимум этими способами:
-
Используйте регулярную сетку начальных точек.
-
Используйте случайные точки, полученные из равномерного распределения, если все координаты задачи ограничены. Используйте точки, полученные из нормальных, экспоненциальных, или других случайных распределений, если некоторые компоненты неограниченны. Чем меньше вы знаете о местоположении глобального минимума, тем более распространено ваше случайное распределение должно быть. Например, нормальные распределения редко производят больше чем три стандартных отклонения далеко от их средних значений, но распределение Коши (плотность 1 / (π (1 + x 2))) делает значительно разрозненные выборки.
-
Используйте идентичные начальные точки с добавленными случайными возмущениями на каждой координате — ограниченный, нормальный, экспоненциальный, или другой.
-
Если у вас есть лицензия Global Optimization Toolbox, используйте
GlobalSearch(Global Optimization Toolbox) илиMultiStart(Global Optimization Toolbox) решатели. Эти решатели автоматически генерируют случайные стартовые точки внутри границ.
Чем больше вы знаете о возможных начальных точках, тем более сфокусирован и успешен ваш поиск будет.
Области притяжения
Если целевая функция, которой f (x) является гладким, вектор – ∇f (x), указывает в направлении, где f (x) уменьшается наиболее быстро. Уравнение наискорейшего спуска, а именно,
дает путь x (t), который приводит к локальному минимуму, когда t увеличивается. Обычно x начальных значений (0), которые находятся друг около друга, дает наикратчайшие пути, которые стремятся к той же минимальной точке. basin of attraction для наискорейшего спуска является набором начальных значений, которые приводят к тому же локальному минимуму.
Этот рисунок показывает два одномерных минимума. Рисунок показывает различные области притяжения с различными стилями линии и указывает на направления наискорейшего спуска стрелками. Для этого и последующих фигур, черные точки представляют локальные минимумы. Каждый наикратчайший путь, x начинающийся в точке (0), идет к черной точке в области, содержащей x (0).
Одномерные области
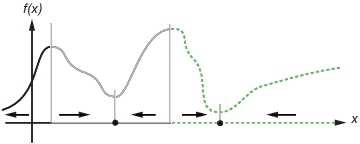
Следующий рисунок показывают, как пути наискорейшего спуска могут быть более сложными для больших размерностей.
Одна область притяжения, показывая наикратчайшие пути от различных начальных точек
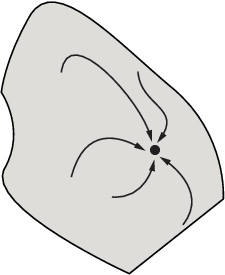
Этот рисунок показывает еще более сложные пути и области притяжения.
Несколько областей притяжения

Ограничения могут разбить одну область притяжения в несколько частей. Например, рассмотрите минимизацию y, удовлетворяющий:
y ≥ |x |
y ≥ 5 – 4 (x –2) 2.
Этот рисунок показывает две области притяжения с конечными точками.
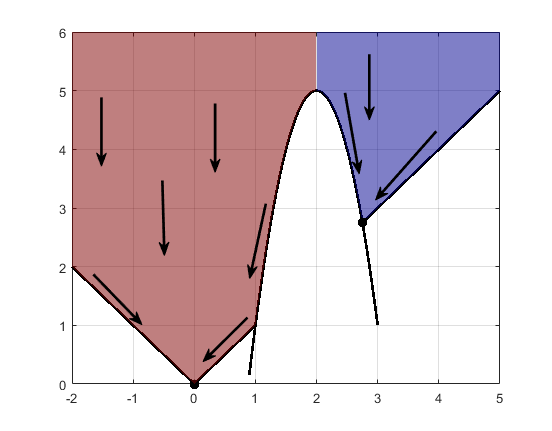
 Код для генерации фигуры
Код для генерации фигуры
Наикратчайшие пути являются прямыми линиями вниз к границам ограничений. От границ ограничений наикратчайшие пути перемещаются вниз вдоль контуров. Конечная точка или (0,0) или (11/4,11/4), в зависимости от того, является ли начальный x – значение выше или ниже 2.
Похожие темы
- Улучшите результаты
Глобальный оптимум
Cтраница 1
Глобальный оптимум можно получить, осуществляя перебор табулированных значений zn на всех этапах поиска. На каждом этапе путем сравнительной оценки отбираются наилучшие значения Дгп.
[1]
Глобальный оптимум можно найти, повторив поиск, что требует большого числа экспериментов.
[2]
Глобальный оптимум можно получить, осуществляя перебор табулированных значений г на всех этапах поиска. На каждом этапе путем сравнительной оценки отбираются наилучшие значения Дгп.
[3]
Глобальный оптимум функционирования системы, как правило, не совпадает с оптимумом отдельных элементов, составляющих систему.
[4]
Локальный или глобальный оптимум. Если известно, что с определенной вероятностью на поверхности отклика существует множество локальных оптимумов, то естественно возникает вопрос: насколько необходима локализация глобального оптимума. Можно утверждать, что очень часто нахождение локального оптимума явится приемлемым результатом. Это утверждение справедливо, в частности, в тех случаях, когда различия ( по величине отклика) между глобальным и неким локальным оптимумами незначительны. Иногда локальный оптимум по косвенным соображениям может оказаться предпочтительнее глобального. Например, истинно оптимальным разрешением, возможно, придется пожертвовать ради снижения температуры, применения более дешевого или менее токсичного растворителя или нахождения менее критических условий. В силу последнего соображения более широкий локальный оптимум может оказаться предпочтительнее более высокого и острого глобального оптимума.
[5]
Можно пропустить глобальный оптимум, если остаются неисследованными большие области.
[6]
Можно пропустить глобальный оптимум, если остаются неисследованными большие области.
[7]
Пытаться найти истинный глобальный оптимум имеет смысл по трем следующим причинам. Во-первых, если анализ должен выполняться многократно ( например, наблюдение за процессом, контроль качества), то целесообразно затратить время и усилия на его оптимизацию с тем, чтобы анализ проводился быстро и стоил дешево.
[8]
Для нахождения глобального оптимума в задаче (12.16) может быть применен метод ветвей и границ, а также его модификации.
[9]
Во-вторых, выявить глобальный оптимум необходимо потому, что мы не можем сказать, является ли данная частная хро-матограмма приемлемым результатом процесса оптимизации. Только если образец содержит небольшое число известных соединений и если заведомо известно, что он не содержит никаких других компонентов ( например, примесей, продуктов разложения, метаболитов), способных помешать нормальному анализу, мы можем судить, представляет ли данная хромато-грамма окончательный результат. Существует опасность того, что мы примем за такой результат хроматограмму, содержащую пять хорошо разрешенных пиков, в то время как образец содержит шесть или более компонентов. Такая опасность особенно велика, если в процессе оптимизации не была получена полная картина поверхности отклика. В общем случае мы не можем решить, приемлем ли локальный оптимум, если глобальный оптимум не известен.
[10]
При наличии ограничений глобальный оптимум может вообще оказаться не в точке экстремума, а на определяемой этими ограничениями границе n – мерной области независимых переменных.
[11]
Таким образом, глобальный оптимум проекта оболочки, вообще говоря, может достигаться только в случае общей постановки задачи s ( ф, 6), реализация которой осуществляется методом ОСП.
[13]
Во-первых, отыскание глобального оптимума в редуцированной задаче возможно лишь в исключительных случаях. Ясно, что тогда в расширенной задаче ( J E) мы получаем в определенном смысле локальные решения задачи, или экстремали относительно некоторого класса вариаций.
[14]
Вероятность того, что глобальный оптимум не будет обнаружен, возрастает если 1) увеличивается кривизна линий удерживания; 2) значительные части параметрического пространства остаются не исследованными; 3) между различными оптимума-ми ( предсказанными) наблюдаются лишь небольшие различия.
[15]
Страницы:
1
2
3
4
С точки зрения конечной цели поиска первый подход более естествен и предпочтителен, так как не требует избыточной информации о локальных оптимумах. Однако известно, что методы поиска глобального оптимума (методы перебора и динамического программирования) имеют на практике ограниченное применение из-за большого машиносчетного времени. Поэтому при решении практических задач часто более эффективными оказываются алгоритмы, включающие в себя поиск локальных оптимумов. Обобщения по использованию методов локального поиска для решения задач глобальной оптимизации даны в [71]. [c.133]
Блок формирования задачи по своему содержанию аналогичен соответствующему блоку для алгоритмов локального поиска (рис. 5.7,а). Блок выбора начальных точек включает методы перебора (обычно метод Монте-Карло). Число перебираемых точек N фиксируется заранее. Выше указывалось, что с ростом М увеличивается вероятность отыскания глобального оптимума. Однако реализация соответствующего количества локальных поисков может оказаться очень трудоемкой даже для мощных современных ЭВМ. В таких случаях из N начальных точек производится отбор приемлемого числа точек, что требует включения в рассматриваемый блок также правил отбора. [c.134]
Кроме алгоритмов направленного поиска в блок поиска локальных оптимумов можно включать также алгоритмы вероятностной аппроксимации целевой функции. Применяя идеи сглаживания и фильтрации путем усреднения результатов случайных испытаний, эти алгоритмы позволяют строить такие аппроксимирующие функции, которые унимодальны и имеют оптимум, совпадающий с глобальным оптимумом Hq [64]. Тогда поиск глобального оптимума Но сводится к поиску локального оптимума аппроксимирующей функции. [c.135]
В блоке оценки глобальности оптимума (рис. 5.7,6) производится сравнительный анализ найденных ранее локальных оптимумов, выбор оптимального решения, подозреваемого на глобальность, и оценка его удовлетворительности. При неудовлетворительной оценке выбранного решения производится смена алгоритмов или параметров в блоках выбора начальных точек и поиска локальных оптимумов, что указано соответствующими обратными связями на рис. 5.7, б. [c.135]
Необходимость оценки наилучшего из локальных оптимумов на глобальность вызвана вероятностным характером процессов поиска и, следовательно, асимптотической сходимостью к глобальному оптимуму. Поэтому необязательно, чтобы наилучший из найденных локальных оптимумов совпадал бы с искомым глобальным оптимумом. Для повышения вероятности этого совпадения (уверенности в глобальной оптимальности полученного решения) требуется дополнительная информация, получаемая либо за счет дополнительных вычислений, либо за счет априорных предположений. [c.135]
Простейшим априорным допущением может служить задание нижней грани глобального оптимума. Величина нижней грани устанавливается априори на основе обобщения имеющегося опыта проектирования тех или иных конструкций. Как только нижняя грань будет достигнута или превзойдена, полученное решение считается удовлетворительным и поиск прекращается. Однако такой [c.135]
По чувствительности и времени поиска аналогичны упорядоченному перебору время поиска уменьшается лишь при специальных предположениях или стремлении к локальному оптимуму Требуют поворота координатных осей для отыскания оптимума в овражных ситуациях Основаны на использовании необходимых и достаточных (особенно в окрестности оптимума) условий экстремума Применяются при ограничениях в виде гиперплоскостей Время поиска резко увеличивается с уменьшением е, при определенных условиях возможен поиск глобального оптимума [c.146]
В общем случае достаточно эффективным оказывается применение алгоритмов с комбинацией методов статистических испытаний (Монте-Карло) и покоординатного поиска. Для ограничений достаточно общего вида (7.22) путем введения соответствующих масштабов строится многомерный куб. В этом кубе путем статистических испытаний с определенной вероятностью находится аппроксимирующая управляющая функция, которая принимается за начальное приближение к глобальному оптимуму. Принимая полученное решение за начальное, методом покоординатного поиска находится ближайший локальный оптимум. Если начальное решение находится в сфере притяжения глобального оптимума, то полученное после покоординатного поиска решение можно считать окончательным. При наличии овражных ситуаций можно использовать специальные приемы, например поворот координатных осей. [c.217]
Глобальный оптимум можно получить, осуществляя перебор табулированных [c.255]
Такой же результат получается и при поиске методом упорядоченного перебора, если число дискретных значений переменных одинаково. Следовательно, время поиска глобального оптимума методами динамического программирования и упорядоченного перебора можно считать практически одинаковым. В этом смысле динамическое программирование так же, как и прямой перебор, применимо лишь при малом числе переменных и может рассматриваться в качестве одного из способов организации упорядоченного перебора. [c.255]
Следовательно, в перспективных энергетических балансах предприятий должны определяться все плановые показатели по ВЭР, используемые для разработки сводных планов по экономии топлива в промышленности на более высоких звеньях управления. Поскольку топливно-энергетическое хозяйство предприятия имеет многочисленные связи с энергетической системой района, вопросы разработки рационального энергетического баланса предприятия и использования ВЭР не могут решаться изолированно без учета оптимальных тенденций в развитии энергетики района и всей страны. На данном этапе разработки оптимальных планов развития энергохозяйства объектов промышленности средством увязки локальных решений по оптимизации энергетического баланса предприятия с глобальным оптимумом топливно- [c.231]
Первое обстоятельство заключается в повышении достоверности результата проектирования — вероятность того, что будет найден глобальный оптимум, будет выше — ив возможности сокращения времени счета. Действительно, при использовании случайного поиска значений выбираемых параметров достоверность результата при общих равных условиях тем выше, чем для большего числа сочетаний случайных чисел Xj произведено исследование. Поэтому, если по ходу расчетов еще до их завершения имеется возможность установить, что данное сочетание случайных чисел Xj должно быть исключено из дальнейшего рассмотрения, то при использовании этой возможности будет увеличено при данном времени счета число рассмотренных сочетаний чисел Xj и, следовательно, увеличена достоверность результата. Если же число вариантов, которое должно исследоваться, предписано заранее, то указанный выше подход позволяет сократить потребное время счета. [c.139]
Для математической оптимизации может быть использован метод динамического программирования, который сводится к рекуррентным соотношениям [например, распределение припуска по технологическим переходам, см. формулу (10)]. Динамическое программирование является вычислительным методом, приводящим к глобальному оптимуму. [c.221]
После нахождения глобального оптимума по локальным решение можно считать завершенным. [c.136]
Найденная в результате численной реализации модели М характеристика ее глобального оптимума Е в силу (4.49) совпадает [c.185]
Гиперболические уравнения в частных производных 124 Гиперповерхность 138 Глобальный оптимум 141 Градиентные методы 168 [c.231]
При решении задачи оптимизации направленного ФК использовались способы анализа и параметризации функции коэффициента связи такие же, как и в предыдущей задаче. Характерной особенностью направленных ФГ, функция коэффициента связи которого обращается в О на концах области связи, является полубесконечный рабочий интервал частот, т. е. ФГ на основе НЛП позволяет заградить все высшие гармонические составляющие сигнала, поступающего на его вход, начиная со второй гармоники. Интересным свойством ФГ является также наличие для значений Со< <20 дБ двух оптимальных решений К(г), соответствующих локальному и глобальному минимумам минимаксной оптимизационной задачи [279, 291]. На рис. 10.14 показаны функции коэффициента связи и переходного ослабления направленных ФГ для двух типов решений задачи оптимизации. Решения получены для п=5 Со Ш Сз=30. Характерно наличие провала в центре функции коэффициента связи направленного ФГ, соответствующего локально оптимальному решению задачи оптимизации (кривые 2). С увеличением Со оба решения для К (г) сближаются. Для значений Со, больших некоторого критического, они сливаются в одно. Отмеченное свойство направленных ФГ имеет место и при использовании других способов параметризации функции коэффициента связи [291], отличных от способа параметризации с помощью сплайн-функций. Поэтому можно считать, что его наличие не связано с конкретным выбором способа параметризации. Отмеченное свойство ФГ на НЛП может использоваться для разработки направленных ФГ с малыми значениями переходного ослабления в полосе пропускания. Результаты оптимизации направленных ФГ с решениями, отвечающими глобальному оптимуму, даны в [25]. [c.257]
Цели в ограничениях целевое программирование. Все глобальные оптимумы являются в более широком контексте локальными оптимумами. Мы знаем, что решения оптимальны только в ограниченном контексте. Оптимальное решение — это не та стратегия, которой нужно следовать, это дополнительная информация, которую следует учесть в контексте большой системы, для которой данная задача является компонентой. В большинстве случаев наша цель — максимизация прибыли всего производства. Это создает впечатление, что у нас только одна цель — прибыль. Но предположим, что принята более широкая точка зрения, включающая несколько отдельных целей, которые нельзя легко объединить в одну оптимизируемую функцию. Например, можно рассмотреть уровни производства для двух разных изделий, для которых получены наибольшие чистая и общая прибыль, а также состояние денежных средств при некоторых ограничениях на ресурсы. [c.260]
Время поиска существенно уменьшается при стремлении к локальному оптимуму. В этом случае соотношение (П.43) принципиально сохраняет свою силу, однако значения N существенно уменьшаются и не являются постоянными. Количество расчетов Но на каждом этапе определяется принятым методом одномерной оптимизации и начальной точкой, с которой начинается поиск на данном этапе. Поэтому N изменяется при повторной оптимизации на данном этапе. На основе стратегии динамического программирования построены алгоритмы локальной оптимизации, обеспечивающие значительно меньшее время поиска по сравнению с глобальной оптимизацией [4, 8]. [c.255]
Поскольку при высокой размерности пространства количество стационарных точек велико, а их исследование и классификация бывают практически невозможны, то найденный вышеописанным способом оптимум может не соответствовать поставленным требованиям задачи синтеза. В таких случаях возникает необходимость прощупывания или зондирования многомерного пространства для выявления более подходящих оптимумов, из которых можно отобрать подходящий, который часто называют глобальным в отличие от общего количества оптимумов, которые называют локальными. [c.115]
| Рис. 3. Схематическая карта распределения осадков, главным образом в летнее время, в эпоху климатического оптимума (5000—8000 лет назад, когда глобальная температура воздуха была на несколько градусов выше). | 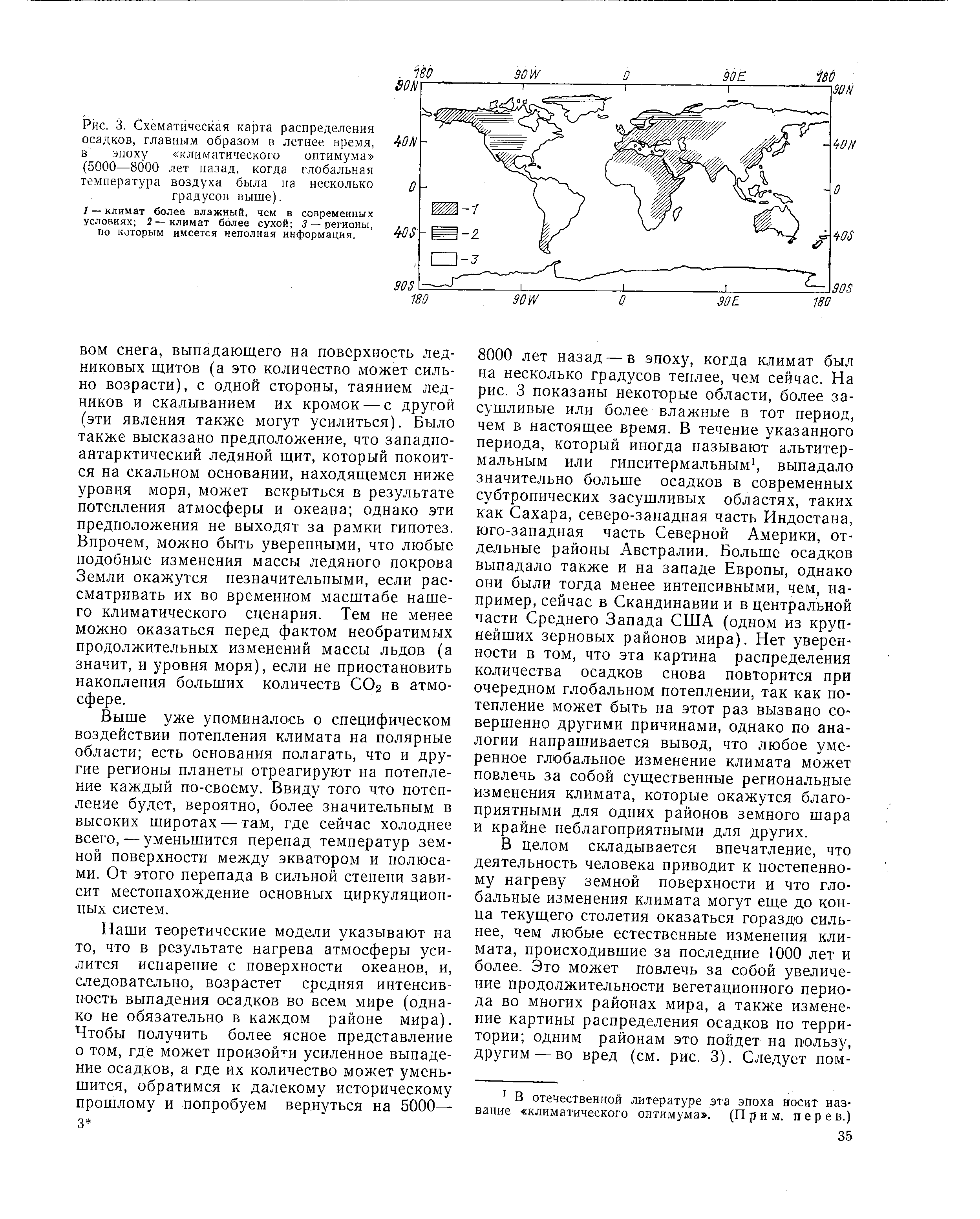 |
Результаты оптимизации водогрейных котлов на ЭВМ показывают, что влияние каждой переменной различно. В допустимой области изменения оптимизируемых переменных расчетные затраты монотонно убывают при росте одних параметров (п, гг) и увеличиваются при росте других (da, Si, S2). Кроме того, совокупность частных оптимумов каждого параметра не совпадает с глобальным. [c.61]
А, является принципиальным при оптимальном проектировании конструкций из композитов, с практической точки зрения его принципиальный характер обусловлен органической связью с технологической реализацией оптимума конкретного проекта, а с позиций теории — с проблемами существования и достижимости глобальных решений соответствующих оптимизационных задач. Для многослойных композитов понятия направление армирования и угол укладки монослоя являются синонимичными. Следовательно, вопрос о минимальном необходимом числе направлений армирования для многослойного композита есть вопрос о минимальном необходимом числе М различных типов структурных элементов, позволяющих получить любую возможную реализацию А. [c.200]
На рис. 6.3 приведен пример геометрической интерпретации многоэкстремальной задачи оптимального проектирования. На рисунке показаны линии равного уровня целевой функции F(X) (аз>а2>а >ао) и видны три локальных оптимума, которые находятся в областях, определяемых общим направляющим принципом (точки Х Л0К> ХглОКг Хзлок являются точками локальных оптимумов, причем точка Хзлок совпадает с глобальным оптимумом). [c.279]
Заметим, что для выпуклой программы (3)—(4) локальный оптимум является необходимо глобальным оптимумом. Это замечание существенно, так как проект, который может быть более легким лишь по сравнению с удовлетворяющими ограничениям смежными проектами, имеет небольшое практическое значение. Заметим также, что в общем случае оптимум не будет соответствовать точке пространства проектов, лежащей на грани или совпадающей с вершиной допустимой области. Это замечание показывает, что интуитивно привлекательная концепция конкурируюш,их ограничений выполняется не обязательно. Допустим, например, что найден проект s,, S2, S3, для которого щ<и2<и1 = б. Если обозначить через As достаточно малое изменение жесткости, то можно ожидать, что проект Si + As, Sj — As, S3, имеющий тот же вес, будет иметь прогибы . 2, йз, удовлетворяющие условиям з < 2, 2 < з < М] = 6, и все три жесткости можно пропорционально уменьшать до тех пор, пока прогиб в первом шарнире не достигнет вновь значения 6. [c.89]
При наличии в допустимой области нескольких локальных оп-тимумов требуется выбрать наилучший из них, т. е. найти глобальный оптимум. Процесс поиска в этом случае организуется с помощью двух основных подходов. Первый подход использует непосредственное стремление к глобальному оптимуму второй подход, наоборот, сначала предполагает поиск локальных оптимумов, а затем путем их сравнения выбор глобального оптимума. [c.133]
К алгоритмам оптимального проектирования ЭМП целесообразно предъявлять следующие общие требования 1) небольшая погрешность и большая вероятность получения глобального оптимума как для целевой функции, так и для параметров оптимизации, особенно при проектировании серий 2) невысокая чувствительность к функциональным свойствам задачи из-за сложности их изучения 3) малое количество шагов в процессе поиска, обеспечивающее удовлетворительное машиносчетное время при больших вычислительных объемах поверочных расчетов электромеханических преобразователей 4) малый объем вычислений, простота и наглядность, обеспечивающие быстрое усвоение и реализацию алгорит- [c.144]
Из методов динамического программирования для решения дискретной задачи в общем случае применима вычислительная схема, основанная на полной системе функциональных уравнений, предназначенная для отыскания глобального оптимума. Так же, как и при прямом шереборе, дискретные значения переменных на каждом этапе задаются условиями (П.58), что обеспечивает сходимость к точному решению [32, 48]. [c.262]
Использование нелинейных математических моделей и методов математического моделирования а ЭВМ позволяет решить задачу оптимизации для реальных сложных схем турбоустановок с учетом технических ограничений типа неравенств. В то же время наличие ступеней проточной части турбины при определении места отборов пара приводит к дискретности переменных, что вызывает серьезные трудности в реализации поиска глобального оптимума даже на ЭВМ с высоким быстродействием. Поэтому при оптимизации сложных схем прибегают к идеализации проточной части, не рассматривая ее дискретности. Тем самым большинство дискретных оптимизируемых переменных становится непрерывным, и это появоляет применять наиболее эффективные градиентные методы направленного поиска. [c.59]
Так, например, поиск оптимального параметра диаметра труб конвективной части при фиксированном значении остальных переменных приводит к наименьшему граничному значению диаметра труб, равному 25X3 мм, глобальный оптимум соответствует диаметру 28X3 мм. Необходимо отметить, что локальные оптимумы при варьировании всех переменных оказались практически на границах допустимой области изменений. Таким образом, имеют место локальные условные экстремумы. [c.61]
Неизбежность принятия тех или иных волевых решений при оптимизации параметров теплоэнергетических установок в условиях неопределенности требует уточнения цели оптимизации. Такой целью является не определение единственного глобального оптимума (поскольку в условиях неопределенности это невозможно), а всестороннее исследование зоны неопределенности решения задачи и сьедение к минимуму состава тех совокупностей параметров, среди которых в конечном итоге придется делать выбор с привлечением интуитивных соображений. Здесь оптимизация рассматривается не как средство принятия окончательного решения, а как способ выявления и экономической оценки вероятных вариантов теплоэнергетической установки, позволяющий получить информацию для принятия окончательного решения с учетом его преимуществ и недостатков по сравнению с другими, в том или ином смысле также оптимальными решениями. [c.182]
Для решения многоэкстремальных задач в математике наиболее часто рекомендуется следующая процедура случайным образом берутся начальные приближения, далее от каждого приближения производится спуск к локальному оптимуму и затем на основе сравнения локальных о птимумов определяется наилучший (глобальный) оптимум [Л. 30]. При этом вероятность нахождения наилучшего из локальных оптимумов будет тем выше, чем большее число локальных оптимумов будет просмотрено. [c.54]
Синтез – это теоретическое соединение по установленным правилам друг с другом лучших частей средств восстановления деталей, выделенных при анализе, с добавлением перспективных и прогрессивных элементов и последующим образованием новой, более эффективной системы средств восстановления. Синтез включает образование многоуровневых структур создаваемой системы, формализацию этих структур и их оптимизацию за счет нахождения области глобальных оптимумов целевь[х функций. Синтез – основной и заключительный этап проектирования. [c.48]
Поскольку на основании (4.90) Пв является включением О, то из общих соображений очевидно, что оптимум модели М, вообще говоря, предпочтительнее оптимума модели Ме, так как показатели эффективности оптимального проекта оболочки, найденные в постановке задачи 5 = 0, не могут быть лучще соответствующих показателей оптимального проекта оболочки, полученного из решения задачи, сформулированной в общей постановке 5=(ф,0). Геометрически это означает, что точка 5 модели М может принадлежать 5 5е, т. е. не принадлежать 5е. Таким образом, глобальный оптимум проекта оболочки, вообще говоря, может достигаться только в случае общей постановки задачи 5= (ф, 0), реализация которой осуществляется методом ОСП. Если в конкретной задаче оптимизации имеет место указанная ситуация, то очевидно (см. рис. 4.5), что решение такой задачи в постановке 5 = 0 будет принадлежать одной из двух границ 5е, определяемых уравнениями [c.199]
Численная реализация задач. Как указывалось в разделе 4.3.7, для моделей слоистого композита рассматриваемого класса П. -° глобальный оптимум проекта конструкции в постановке задачи оптимизации по 5 вида (5.4) достигается уже при М = 2 (см. (4.93)). Следовательно, минимальная размерность моделей (5.13) гп1п = 1+3 = 4. Однако численное решение рассматриваемых задач затруднено многоэкстремальностью М,- по параметрам ф и ф2. Поэтому оптимизацию рассматриваемых проектов оболочки целесообразно провести по методу ОСП. Это значит, что в соответ- [c.220]
Глобальный оптимум — это оптимальное решение для всего пространства проектирования. Око лучше всех других решений, соответствующих локальны.м опти.му.ма.м, и именно его ищет конструктор. Возлюжен случай нескольки.х разных глобальных оптимулюв, расположенных в разных частях пространства проектнровання. Как ставится задача опти. и зации, лучше всего показать на примере. [c.141]
Возможность существования особых точек (седловых, типа гребней и оврагов и т. д.), разрывности функционала и изменений переменных условных экстремумов на границах допустимых областей, многосвязности, многоэкстремальности функционала, ограничений типа неравенств, дискретность переменных и т. д. — все это приводит к практической непригодности аналитических методов оптимизации теплоэнергетических установок. Применение ЭВМ. и численных методов нелинейного программирования позволяет в основном преодолеть эти затруднения. При малом числе оптимизируемых переменных и при узких пределах их изменения отыскание глобального экстремума практически обеспечивает метод сплошного перебора на ЭВМ вариантов путем обхода в определенном порядке узлов многомерной сетки в пространстве независимых переменных и вычисление в каждой точке значений функций ограничений и функционала. При этом отбрасываются те точки, в которых ограничения не выполняются, а среди точек, для которых ограничения справедливы, выбирается точка с наименьшим (или наибольшим) значением функционала. При оптимизации по большому числу параметров применяются методы направленного поиска оптимума градиентные, наискорейшего спуска, покоординатного спуска (Л. 21]. [c.57]
