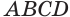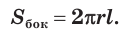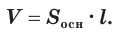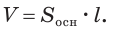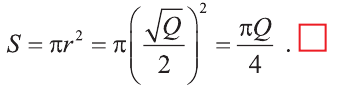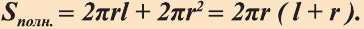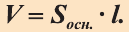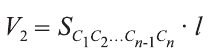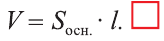Решение обратной задачи гравиразведки для кругового горизонтального цилиндра. Гравитационное поле над горизонтальным круговым цилиндром
Страницы работы
Содержание работы
Практическая
работа №3
Решение
обратной задачи гравиразведки
Обратная
задача гравиразведки заключается в вычислении по заданному распределению поля
ускорения силы тяжести параметров анамалеобразующего тела, т. е. его размеров
R, V, глубины залегания h.
Исходные данные:
Вариант №14
Таблица 1 – исходные данные
|
Δx, м |
δ, г/см3 |
δ, кг/м3 |
Аномалеобразующее тело |
|
20 |
0,7 |
700 |
Горизонтальный круговой цилиндр |
Решение
обратной задачи гравиразведки для кругового горизонтального цилиндра
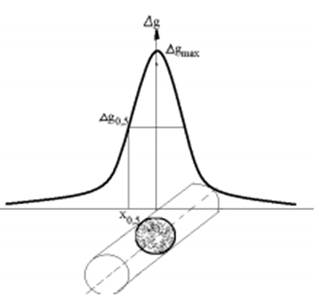
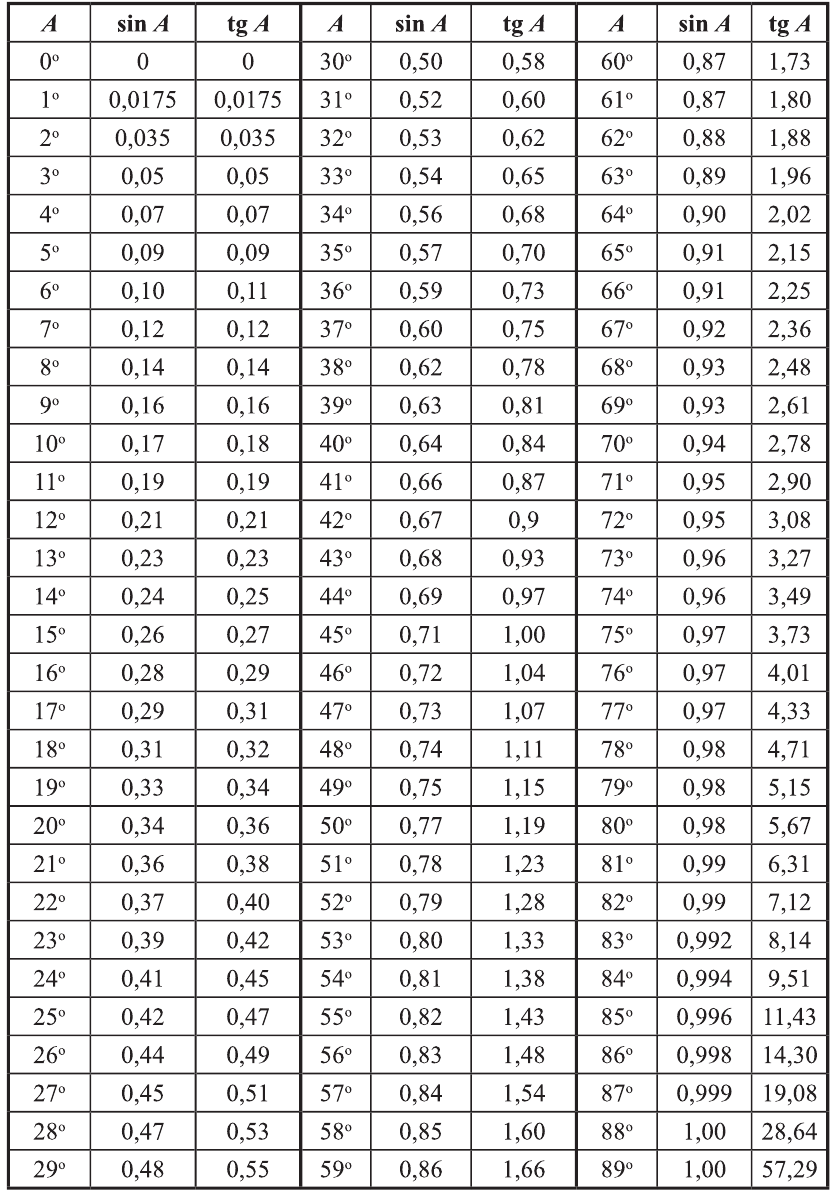
Из анализа решения прямой задачи
кривая всюду положительна и симметрична относительно максимума, который
находится над центром горизонтального цилиндра. Следовательно начало координат
совпадает с максимумом кривой т.е.при x=0. Для точки, удаленной от максимума на
расстояние x0,5 формула для вычисления глубины залегания центра шара
будет иметь вид:
x0,5=h; (1)
где h – глубина залегания аномалеобразующего
тела. Величины х0,5 и ∆gmax снимают с графика (рисунок 1).
Рисунок
1 – Гравитационное поле над горизонтальным круговым цилиндром
Если известна избыточная плотность,
то можно найти радиус цилиндра:
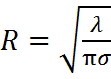
где, R – радиус цилиндра
(м); – линейная
плотность (избыточная масса) цилиндра (кг/см) и –
избыточная плотность (г/см3).
Проведем
качественную интерпретацию гравитационной аномалии полученной в ходе выполнения
практической работы №2.
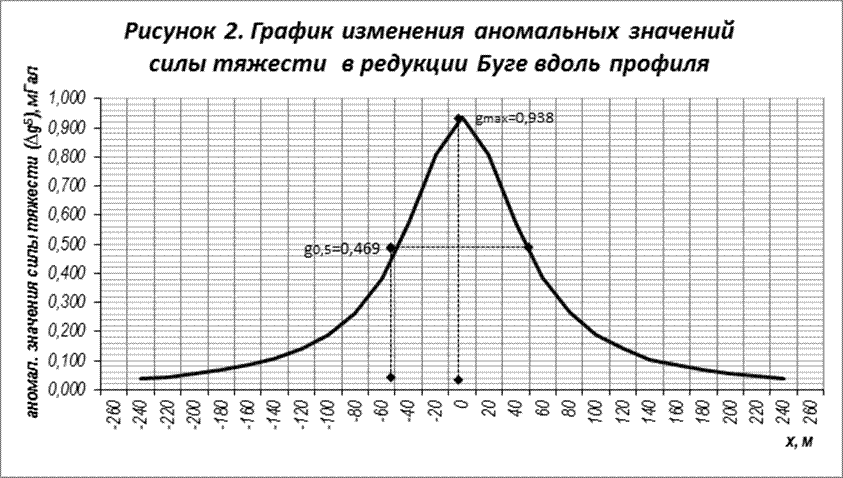
Исходя из того, что кривая аномалии
силы тяжести везде положительна и симметрична относительно максимума, который
будет находиться над центром горизонтального цилиндра, то начало координат
совпадет с максимумом кривой, то есть х=0 (рисунок 2). Максимум кривой имеет
значение Δgmax =0,938 мГал.
Для определения глубины залегания
цилиндра возьмем на оси абсцисс точку удаленную от максимума на расстояние – х0,5,
в которой значение аномалии равнялось бы Δg0,5
(рисунок 2).
Δg0,5=
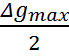
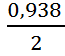
мГал.
Опустив
перпендикуляр из данной точки на кривой на ось абсцисс, определим значение x0,5,
которое будет равняться x0,5=50 м (рисунок 2).
По формуле 1 определим глубину
залегания горизонтального цилиндра.
Так
как у нас имеется значение избыточной плотности, можно определить радиус
цилиндра по формуле 2, но первоначально необходимо определить значение линейной
плотности (избыточной массы) цилиндра (x0,5=h=50 м) по формуле:
=
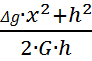
Подставив известные значения получим:
=
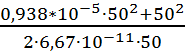
(кг/см);
Теперь, подставив значение линейной
плотности, определим радиус цилиндра R:
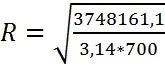
(м).
Все
определенные параметры представлены в таблице 2.
Таблица 2 – определенные параметры
для задания 1
|
Определенные параметры |
||||
|
Δgmax, мГал |
Δg0,5,мГал |
h, м |
λ, кг/см |
R, м |
|
0,938 |
0,469 |
50 |
3748161,1 |
41,3 |
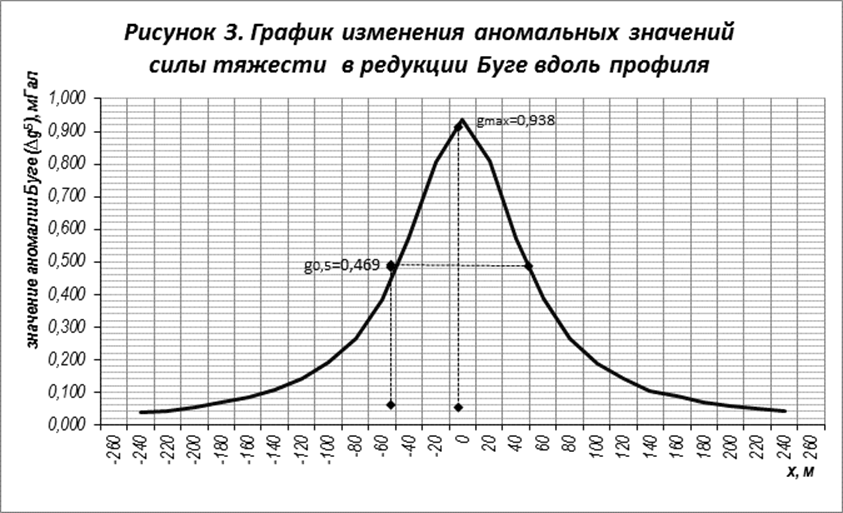
Аналогично поступим и с заданием 2. Аномалия силы
тяжести представлена на рисунке 3.
Максимальное
значение аномалии наблюдается, так же как и в первом случае, на 0 пикете, и
имеет значение Δgmax =0,938 мГал.
Для определения глубины залегания
цилиндра возьмем на оси абсцисс точку удаленную от максимума на расстояние – х0,5,
в которой значение аномалии равнялось бы Δg0,5
(рисунок 3).
Δg0,5=
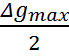
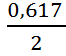
мГал.
Глубина
залегания аномалеобразующего тела – x0,5=h=55 м.
Определяем
значение линейной плотности цилиндра по формуле:
=
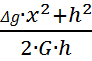
=
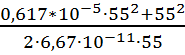
(кг/см);
Теперь, подставив значение линейной
плотности, определим радиус цилиндра R:
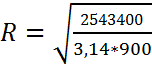
(м).
Всеопределенные параметры представлены в таблице 3.
Таблица 3 – определенные параметры
для задания 2
|
Определенные параметры |
||||
|
Δgmax, мГал |
Δg0,5,мГал |
h, м |
λ, кг/см |
R, м |
|
0,617 |
0,309 |
55 |
2543400 |
30 |
Выводы:
Похожие материалы
- Геодезическое обеспечение геолого-разведочных работ. Топографическая основа геологоразведочных работ. Маркшейдерско-геодезические работы при геофизических методах разведки
- Геометризация объема массивной залежи посредством интерполяции значений мощностей в скважинах
- Геометризация объема массивной залежи посредством переоцифровки изолиний структурной карты по кровле коллектора
Информация о работе
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание – внизу страницы.
Расчет объема цилиндра в м3 онлайн сегодня не проблема. Для тех, кому надо срочно сделать подобные исчисления, разработаны специальные сервисы. Рассчитать объем цилиндра в онлайн-калькуляторе очень просто. Для этого потребуется лишь знать его величины.
Как происходит расчет
Пользователь должен знать:
- высоту цилиндра;
- радиус его основания;
- площадь основания.
Программа выдаст детальное описание примера, его пошаговое решение и вы сможете понять, по какому алгоритму решалась задача. Это позволяет закрепить выученные сведения. При этом используется формула объема цилиндра, и вы можете узнать величину в литрах.
Чтобы рассчитать объем, нужно внести в строку известные вам величины, ввести все цифровые данные и нажать кнопку «рассчитать объем». Через несколько секунд программа выдаст вам не только решение, но и его объяснение!
По высоте и радиусу
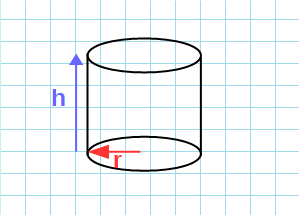
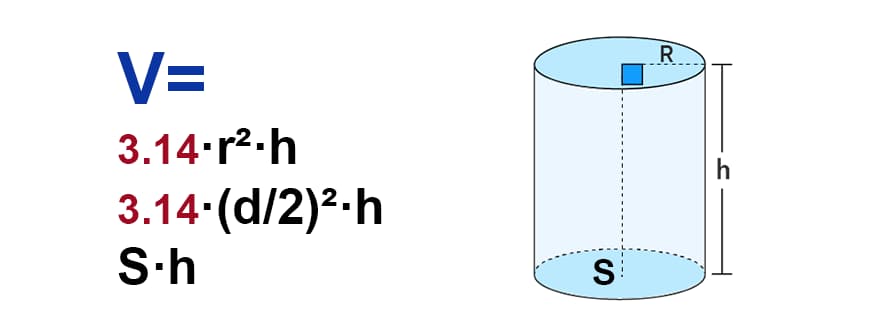
Формула объема цилиндра через высоту и радиус:
V=π·r²·h
π – константа равная (3.14); r – радиус основания; h – высота цилиндра.
Через площадь основания и высоту
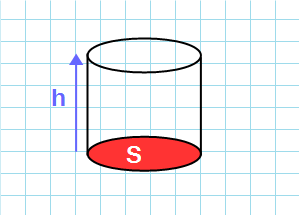
Ответы:
Формула объема цилиндра через высоту и площадь основания:
V=S·h
S – площадь основания цилиндра; h – высота цилиндра.

Калькулятор для расчета объема цилиндра
C помощью нашего Онлайн-калькулятора для расчета объема цилиндра Вы можете быстро и точно рассчитать объем цилиндра. Для того, чтобы вычислить объем цилиндра, сначала выберите формулу, по которой Вы собираетесь произвести расчет. Объем цилиндра (в зависимости от исходных данных) можно вычислить двумя способами: 1. через высоту и радиус основания; 2. через высоту и площадь основания. Затем введите значения исходных данных для расчета (значение высоты цилиндра, значение радиуса основания цилиндра (или значение площади основания цилиндра) и нажмите кнопку “Рассчитать”. Также Вы можете указать точность полученного результата, т.е. количество знаков после запятой, до которого будет округлен рассчитанный объем цилиндра.
Формула нахождения объема цилиндра:
через высоту и радиус основания
через высоту и площадь основания
Округлить результат до
знаков после запятой
Рассчитать
Цилиндр – это геометрическое тело, которое ограничено двумя параллельными поверхностями, пересекающими цилиндрическую поверхность. Цилиндрическая поверхность называется боковой поверхностью цилиндра. Две параллельные поверхности называются основаниями цилиндра.
Объем цилиндра можно вычислить по двум формулам:
- через высоту цилиндра и радиус основания;
- через высоту цилиндра и площадь основания.
Калькулятор объема цилиндра
Рассчитайте онлайн объем любого цилиндрического объекта: трубы, бочки, банки.
Что известно
Размерность
Радиус основания
см
Диаметр основания
см
Площадь основания
см2
Высота
см
Раcсчитать
Оглавление:
- 📝 Как это работает?
- 🤔 Частые вопросы и ответы
- 📋 Похожие материалы
- 📢 Поделиться и комментировать
🛢️ Когда требуется знать объем цилиндра?
Знание объема цилиндра может потребоваться в различных ситуациях, к примеру:
- Расчет объема бака или резервуара: если вы планируете хранить жидкость или газ в баке или резервуаре, то может быть важно знать его объем, чтобы знать, сколько материала вы можете в него поместить.
- Расчет объема емкости для транспортировки: если вы занимаетесь перевозкой жидкостей или газов, то может потребоваться знать объем емкости, чтобы убедиться, что вы можете перевезти нужное количество материала.
- Расчет объема цилиндрических труб: если вы занимаетесь установкой трубопроводов или работой с другими цилиндрическими объектами, то может быть полезно знать их объем, чтобы правильно рассчитать количество материала, необходимого для работы.
- Расчет объема бутылки или бочки: если вы хотите знать, сколько жидкости вы можете вместить в определенную бутылку или бочку, то калькулятор объема цилиндра может помочь рассчитать объем емкости.
- Определение объема цилиндрических объектов, используемых в декоративных целях, например, колонн, скульптур и других элементов архитектуры и дизайна.
Также умение рассчитывать объем цилиндра пригодится в строительстве, химии и фармацевтике, механике и технике, производстве, учебе и творчестве.
📏 Как рассчитывается объем цилиндра?
Объем цилиндра можно рассчитать по формуле:
V = πr²h
где V – объем цилиндра, r – радиус основания цилиндра, h – высота цилиндра, π (пи) – математическая константа, приблизительно равная 3,14.
Чтобы использовать эту формулу, необходимо знать значения радиуса основания и высоты цилиндра. Радиус основания – это расстояние от центра основания до края, высота цилиндра – это расстояние между основаниями цилиндра.
Например, если радиус основания цилиндра равен 5 см, а высота цилиндра составляет 10 см, то объем цилиндра можно рассчитать следующим образом:
V = 3,14 x 5² x 10 = 785 см3
Обратите внимание, что единицы измерения должны быть одинаковыми, чтобы получить правильный ответ. Если радиус основания и высота цилиндра измеряются в сантиметрах, то и объем цилиндра должен быть выражен в кубических сантиметрах.
🧮 Что такое калькулятор объема цилиндра?
Калькулятор объема цилиндра – это инструмент, который позволяет автоматически рассчитывать объем цилиндра по его размерам. Обычно калькулятор объема цилиндра предоставляет пользователю простую форму, где нужно ввести значение радиуса основания и высоты цилиндра, а затем нажать кнопку «Рассчитать». Калькулятор объема цилиндра может быть представлен в виде программы на компьютере или мобильном устройстве, а также в виде онлайн-сервиса на веб-сайте, как у нас.
Использование калькулятора объема цилиндра упрощает и ускоряет процесс расчета объема цилиндра, особенно если нужно рассчитать объем нескольких цилиндров или если значения радиуса и высоты цилиндра имеют сложные числовые значения. Калькулятор объема цилиндра может быть полезен в различных областях, включая науку, технику, строительство, производство, учебу и домашнее хозяйство.
📏 Как работает калькулятор объема цилиндра?
Калькулятор объема цилиндра работает на основе математической формулы для расчета объема цилиндра, рассмотренной выше.
Чтобы рассчитать объем цилиндра, пользователь должен ввести значения радиуса основания и высоты цилиндра в соответствующие поля калькулятора и нажать кнопку «Рассчитать». Калькулятор использует введенные значения, выполняет математическую операцию по формуле и выводит результат в соответствующем поле на экране.
Некоторые калькуляторы объема цилиндра могут иметь дополнительные функции, такие как выбор единиц измерения (например, сантиметры или дюймы) и возможность рассчитать объем цилиндра, используя диаметр основания вместо радиуса.
🛢 Как использовать калькулятор объема цилиндра?
Для использования калькулятора объема цилиндра следуйте этим простым шагам:
- Откройте калькулятор объема цилиндра, который находится на компьютере, мобильном устройстве или на веб-сайте.
- Введите значение радиуса основания цилиндра в соответствующее поле калькулятора. Если вы используете калькулятор, который принимает во внимание диаметр, убедитесь, что вы выбрали правильную единицу измерения.
- Введите значение высоты цилиндра в соответствующее поле калькулятора. Убедитесь, что вы выбрали правильную единицу измерения.
- Нажмите кнопку «Рассчитать» или «Получить результат». Калькулятор выполнит расчеты и выведет объем цилиндра в соответствующем поле.
- Проверьте результаты и убедитесь, что все значения введены правильно и выбраны правильные единицы измерения.
- Если нужно рассчитать объем нескольких цилиндров, повторите шаги 2-5 для каждого цилиндра.
- Сохраните результаты или скопируйте их в буфер обмена, если нужно использовать их в другой программе или приложении.
В зависимости от функционала калькулятор может иметь дополнительные функции, такие как выбор единиц измерения, возможность использовать диаметр вместо радиуса, а также возможность сохранения результатов в файл или их отправки по электронной почте.
В чем измеряется объем цилиндра?
Объем цилиндра измеряется в кубических единицах длины. Например, если размеры цилиндра измеряются в метрах, то его объем будет выражаться в кубических метрах (м³). Если размеры измеряются в сантиметрах, то объем будет выражаться в кубических сантиметрах (см³). Также можно использовать другие единицы измерения, такие как литры или галлоны, которые также выражают объем жидкости или газа, но они не являются кубическими единицами длины.
Несколько лайфхаков
Если вы хотите упростить расчет объема цилиндра, есть несколько лайфхаков, которые могут пригодиться:
- Используйте формулу площади основания цилиндра. Объем цилиндра можно вычислить, умножив площадь основания на высоту. Если вы знаете формулу площади основания цилиндра, то можете сначала вычислить ее, а затем умножить на высоту, чтобы найти объем.
- Используйте приближенное значение числа Пи. Число Пи является бесконечной десятичной дробью, но для большинства расчетов достаточно использовать его приближенное значение. Например, можно использовать значение 3,14 или 22/7 вместо точного значения числа Пи, которое равно примерно 3,14159265359.
- Используйте онлайн калькулятор. Наш онлайн калькулятор объема цилиндра поможет быстро выполнить расчеты за вас. Просто введите значения радиуса и высоты, и калькулятор автоматически вычислит объем.
- Используйте замены единиц измерения. Если вы хотите перевести объем из одной единицы измерения в другую, например, из кубических сантиметров в литры, можете также воспользоваться калькулятором на нашем сайте.
❓ Вопросы и ответы
Сейчас мы представим ответы на вопросы, которые часто возникают по данной теме.
Что такое цилиндр?
Цилиндр — это геометрическая фигура, которая имеет два плоских основания, обычно круглой формы, и боковую поверхность, которая состоит из параллельных прямых линий.
Как вычислить объем цилиндра?
Объем цилиндра можно вычислить, используя формулу:
V = πr²h
где V – объем цилиндра, π – число Пи (приблизительно равно 3.14), r – радиус основания цилиндра и h – высота цилиндра.
Можно ли использовать формулу объема цилиндра для вычисления объема других фигур?
Нет, формула объема цилиндра может использоваться только для вычисления объема цилиндра. Для других фигур существуют свои собственные формулы для расчета объема.
Как найти радиус или диаметр цилиндра, если они неизвестны?
Если известна площадь основания цилиндра, можно найти радиус, используя формулу:
r = √(A/π)
где A – площадь основания цилиндра.
Если известен объем цилиндра, можно найти радиус, используя формулу:
r = √(V/πh)
где V – объем цилиндра, h – высота цилиндра.
Диаметр можно найти, удваивая радиус.
Как найти объем трубы или канала?
Для трубы или канала формула для вычисления объема имеет немного другой вид:
V = πr²h
где V – объем, r – радиус, h – длина (высота) трубы или канала.
Например, если радиус трубы равен 10 см, а длина трубы составляет 2 м, то объем трубы будет:
V = 3.14 * 10² * 200 = 62,800 см³, что равно 62.8 литрам.
Как узнать, сколько литров вмещает бочка?
Чтобы узнать, сколько литров вмещает бочка, нужно знать ее объем. Если известны диаметр и высота бочки, то можно использовать формулу для объема цилиндра. Например, если диаметр бочки составляет 1 метр, а высота – 1,5 метра, то ее объем будет:
V = πr²h = 3.14 * (1/2)² * 1.5 = 1.18 кубических метров, что равно 1180 литрам. Таким образом, бочка вмещает 1180 литров жидкости.
Как узнать, сколько литров вмещает труба?
Для расчета объема трубы нужно знать ее длину и радиус. Если известны диаметр и длина трубы, то радиус можно найти, разделив диаметр на 2. Например, если диаметр трубы составляет 10 см, а длина трубы – 2 метра, то радиус будет 5 см. Тогда объем трубы можно найти, используя формулу:
V = πr²h = 3.14 * (5/100)² * 200 = 15.7 литров. Таким образом, труба вмещает 15.7 литров жидкости.
Какой тип калькулятора нужен для расчета объема цилиндра?
Для расчета объема цилиндра нужен специальный калькулятор, который может выполнить математические операции с использованием формулы для объема цилиндра.
Какие значения нужно ввести в калькулятор объема цилиндра?
Для расчета объема цилиндра необходимо ввести значение радиуса основания цилиндра и высоты цилиндра.
Какие единицы измерения могут использоваться при вводе значений в калькулятор объема цилиндра?
Единицы измерения, которые могут использоваться при вводе значений в калькулятор объема цилиндра, это сантиметры, метры, дюймы и т.д.
Какие дополнительные функции могут быть включены в калькулятор объема цилиндра?
Некоторые калькуляторы объема цилиндра могут иметь дополнительные функции, такие как выбор единиц измерения, возможность использовать диаметр вместо радиуса, а также возможность сохранения результатов в файл или их отправки по электронной почте.
Где можно найти калькулятор объема цилиндра?
Калькулятор объема цилиндра можно найти в Интернете на специализированных сайтах, в приложениях для мобильных устройств и на компьютерах, а также в других программных приложениях, связанных с инженерными и научными расчетами.
Похожие калькуляторы
Возможно вам пригодятся ещё несколько калькуляторов по данной теме:
- Калькулятор масштабов. Переведите онлайн именованный масштаб на чертеже в реальный и наоборот.
- Калькулятор числа Пи. Узнайте, чему равно число Пи с точностью до нужного количества знаков после запятой.
- Калькулятор объема параллелепипеда. Рассчитайте онлайн объем любого параллелепипеда по длинам его ребер и не только.
- Калькулятор объема куба. Рассчитайте онлайн объем любого кубического предмета по длине стороны или диагоналям.
- Калькулятор объема бака. Посчитайте объем цилиндрического, прямоугольного или автомобильного бака по габаритам (по расходу и пройденному расстоянию).
- Калькулятор объема помещения. Посчитайте объем комнаты или любого помещения в кв.метра или литрах.
- Калькулятор длины дуги. Рассчитайте онлайн длину дуги окружности по радиусу и углу или по формуле Гюйгенса.
- Калькулятор объема трубы. Рассчитайте онлайн объем трубы в куб. м. или литрах в зависимости от диаметра и длины трубопровода.
- Калькулятор объема пирамиды. Рассчитайте объем пирамиды по высоте, площади основания или стороне основания. Основание может быть любой формы.
- Калькулятор объема и площади усеченного конуса. Рассчитайте онлайн объем и площадь поверхности усеченного конуса по его радиусам и высоте.
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Показать комментарии
Содержание:
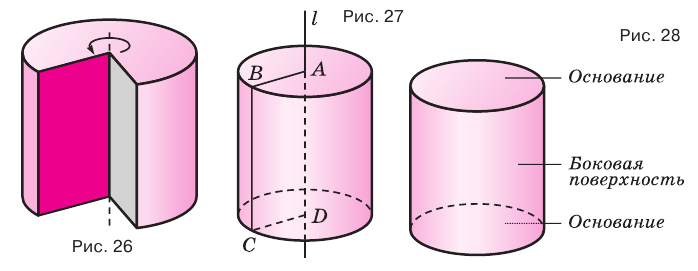
Цилиндром называется тело, полученное вращением прямоугольника вокруг оси, проходящей через его сторону (рис. 26). На рисунке 27 показано образование цилиндра при вращении прямоугольника
Образующая цилиндра является его высотой.
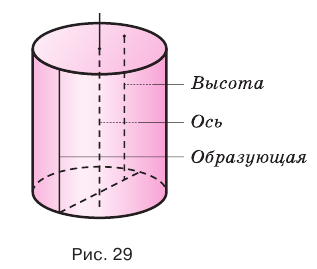
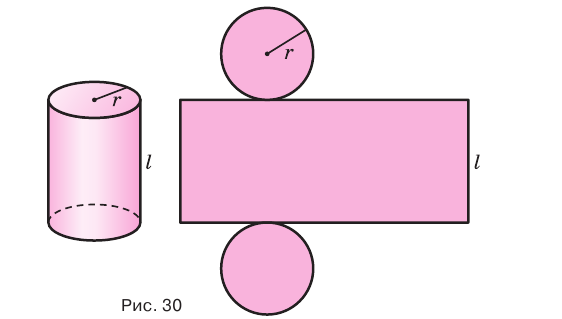
Поверхность цилиндра можно развернуть на плоскость, в результате получится прямоугольник, представляющий боковую поверхность цилиндра, и два круга, представляющих его основания. На рисунке 30 показан цилиндр и его развертка.
Теорема 4.
Боковая поверхность цилиндра равна произведению длины окружности основания и образующей:
На плоскости важной конфигурацией, которая часто встречается в задачах, является сочетание окружности с прямой. Подобной пространственной конфигурацией является сочетание цилиндра с плоскостью.
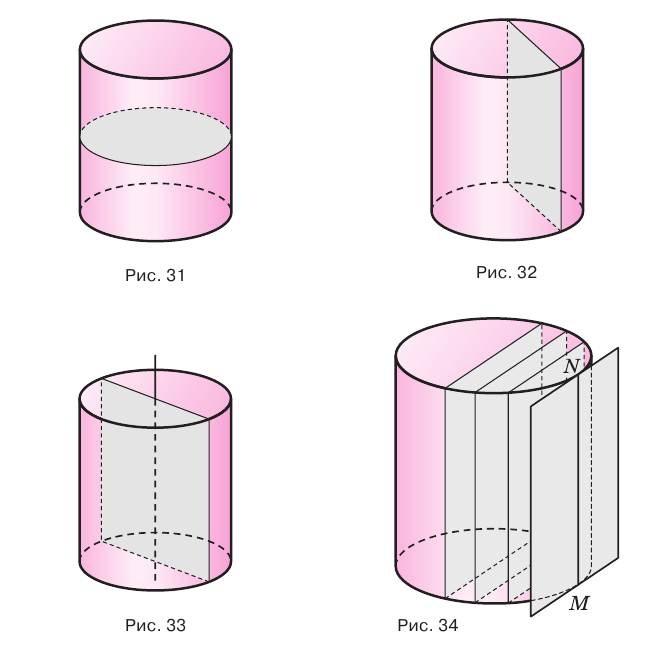
Если цилиндр пересечь плоскостью, параллельной основанию, то получится круг, равный основанию (рис. 31), а если плоскостью, перпендикулярной основанию, то — прямоугольник, одна сторона которого равна высоте цилиндра (рис. 32). Осевое сечение цилиндра, т. е. сечение плоскостью, проходящей через ось цилиндра, является прямоугольником, стороны которого равны высоте цилиндра и диаметру его основания (рис. 33).
Будем двигать плоскость, проходящую через ось цилиндра, параллельно самой себе (рис. 34). При этом две противолежащие стороны прямоугольника-сечения цилиндра, являющиеся хордами оснований, будут уменьшаться, а две другие стороны, которые являются образующими цилиндра, — сближаться до того момента, пока не совпадут. Получим плоскость, содержащую образующую 
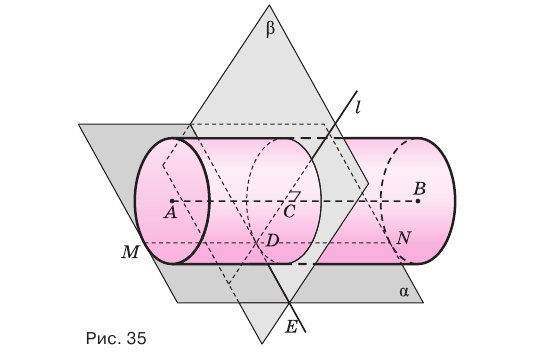
Теорема 5.
Если плоскость касается цилиндра по некоторой образующей, то ей перпендикулярна плоскость, проходящая через эту образующую и ось цилиндра.
Доказательство:
Пусть плоскость 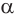
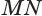
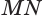
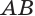
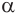
Проведем прямую 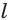
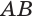
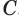
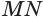
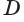
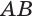
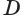
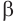
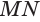
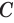
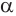
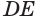
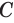
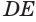
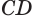
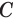
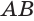
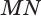
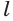
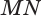
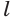
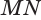
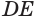
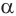
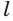
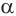
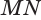
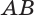
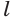
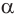
Теорема 5 выражает свойство касательной плоскости цилиндра.
Теорема 6.
Плоскость касается цилиндра, если она проходит через его образующую и перпендикулярна плоскости, содержащей эту образующую и ось цилиндра.
Доказательство:
Пусть плоскость 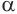
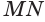
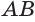
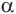
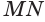
Пусть 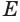
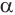
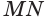
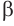
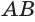
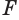
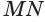
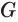
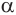
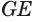
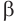
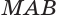
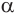
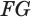
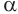
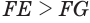
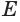
Теорема 6 выражает признак касательной плоскости цилиндра.
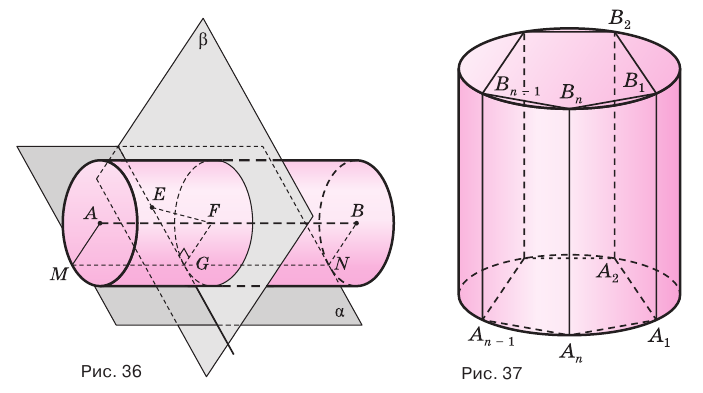
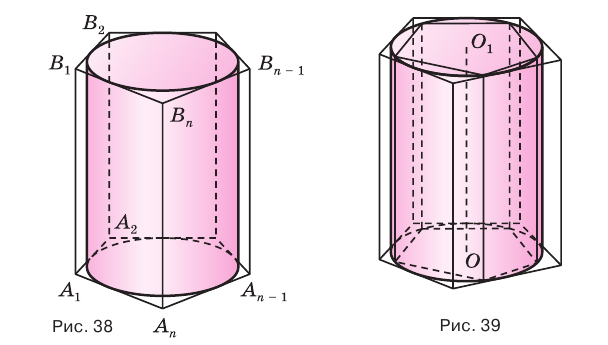
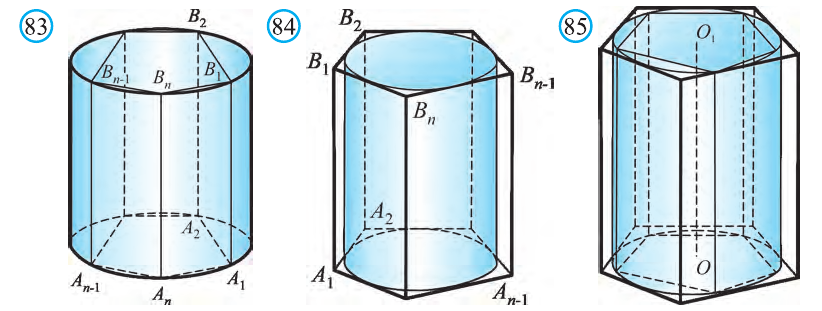
Пусть имеется цилиндр (рис. 37). Впишем в одно из оснований цилиндра многоугольник 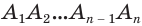
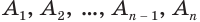
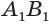
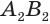
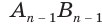
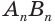
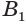
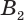
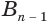
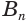
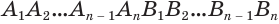
Если цилиндр описан около призмы, то основания цилиндра описаны около оснований призмы, а боковая поверхность цилиндра содержит боковые ребра призмы.
Подобным образом вводится понятие призмы, описанной около цилиндра, и цилиндра, вписанного в призму (рис. 38). Если призма описана около цилиндра, то ее основания описаны около оснований цилиндра, а боковые грани касаются боковой поверхности цилиндра.
Теорема 7.
Объем цилиндра равен произведению площади его основания и образующей:
Доказательство:
Пусть имеется цилиндр с осью 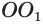
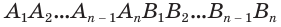
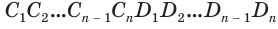
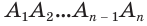
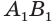
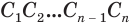
Будем количество 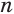
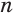
В описанном процессе высота 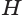
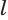
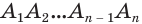
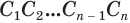
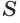
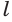
Поверхность цилиндра
Ещё один важный класс пространственных фигур – тела вращения. Цилиндр является одним из них, мы познакомимся с ним глубже. Свойства цилиндра похожи на свойства призм, мы последовательно изучим их.
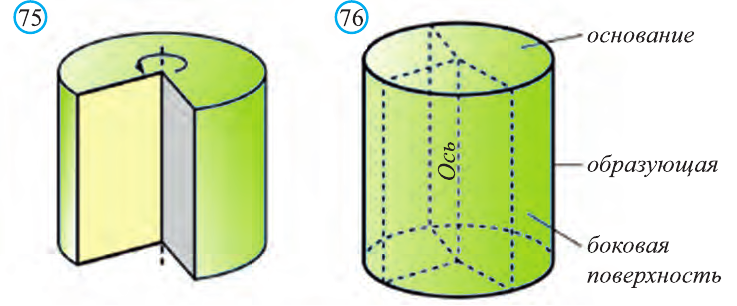
Тело, полученное вращением прямоугольника вокруг одной из его сторон называют цилиндром (точнее, прямой круговой цилиндр) (рис. 75). При вращении прямоугольника одна его сторона остаётся неподвижной. Её называют осью цилиндра. Поверхность, образованную при вращении противоположной стороны прямоугольника называют цилиндрической поверхностью, а саму сторону образующей цилиндра. Две другие стороны прямоугольника при этом вращении образуют два равных круга, которые называют основаниями цилиндра (рис. 76).
Замечание. Тело, полученное вращением прямоугольника вокруг одной из его сторон называют прямым круговым цилиндром. Более широкое понятие цилиндра вводят следующим образом.
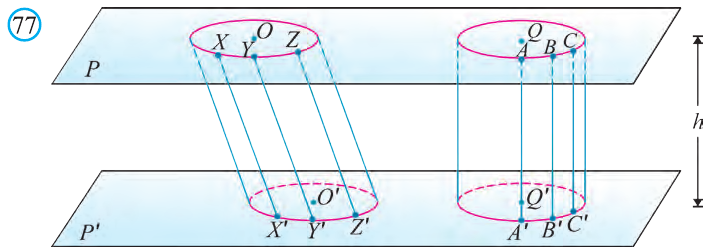
Пусть в пространстве параллельный перенос переводит плоскую фигуру F1, в фигуру F2. Тело, состоящее из этих фигур и отрезков, соединяющих их соответствующие точки, называют цилиндром (рис. 77).
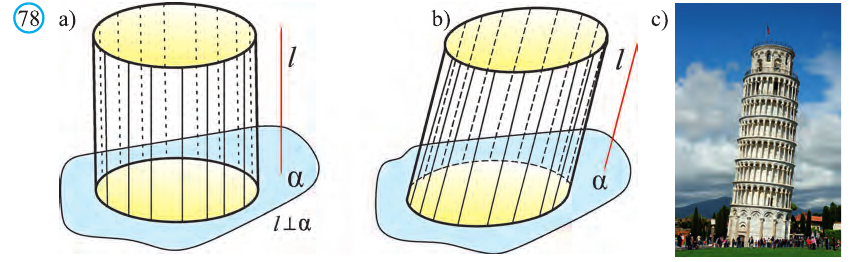
Если при параллельном переносе образующая перпендикулярна плоскости фигуры F1 , цилиндр называют прямым (рис. 78.а), в противном случае наклонным цилиндром (рис. 78.b). На рисунке 78.с изображена Пизанская башня, имеющая вид наклонного цилиндра.
Если фигура F1 является кругом, то цилиндр называют круговым цилиндром.
Только прямой круговой цилиндр является телом вращения. В дальнейшем мы будем рассматривать прямые круговые цилиндры, которые для краткости будем называть цилиндрами.
Основания цилиндра являясь равными кругами, лежат на параллельных плоскостях. Перпендикуляр, опущенный из некоторой точки одного основания на другое, называют его высотой.
Расстояние между параллельными плоскостями равно высоте цилиндра. Ось цилиндра также является его высотой.
Образующие цилиндра параллельны и равны. Точно также, длины высоты, оси и образующих цилиндра будут равны между собой.
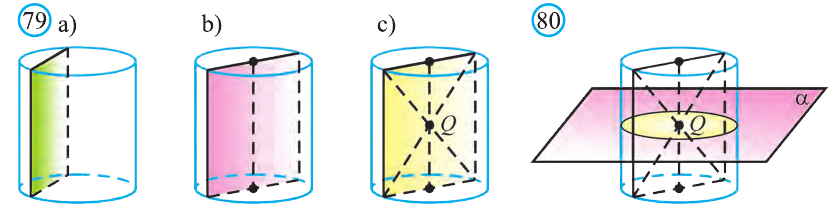
Сечением цилиндра плоскостью параллельной его оси является прямоугольник (рис.79.а). Две противоположные его стороны – это образующие цилиндра, а две другие стороны – соответствующие параллельные хорды оснований цилиндра.
В частности, осевое сечение также прямоугольник, образованный сечением цилиндра плоскостью, проходящей через его ось (рис. 79.b).
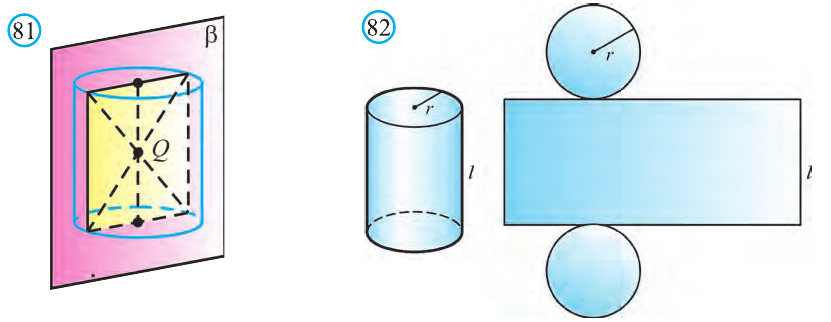
Диагонали осевого сечения цилиндра проходят через точку являющуюся серединой отрезка, соединяющего центры оснований цилиндра. Следовательно, эта точка Q есть центр симметрии цилиндра (рис. 79.с).
Плоскость, проходящая через точку Q перпендикулярно оси цилиндра является его плоскостью симметрии (рис. 80). Любая плоскость, проходящая через ось цилиндра также будет ось симметрии цилиндра (рис. 81).
Пример:
Осевое сечение цилиндра – квадрат, площадь которого Q. Найдите площадь основания цилиндра.
Решение:
Сторона квадрата равна 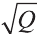
основания. Поэтому его площадь равна
Докажите самостоятельно эту теорему пользуясь рисунком 82.
Следствие. Полная поверхность цилиндра равна сумме его боковой поверхности и площадей двух его оснований:
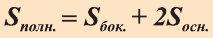
Пусть дан произвольный цилиндр. Впишем в одно из его оснований многоугольник 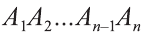
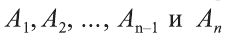
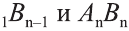
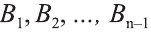
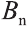
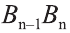
Ясно, что если вокруг основания призмы можно описать окружность, то вокруг призмы можно описать цилиндр.
Аналогично вводятся понятия призмы, описанной вокруг цилиндра и цилиндра, вписанного в призму (рис. 84). Если призма описана вокруг цилиндра, то основание призмы будет описано вокруг основания цилиндра и боковые грани призмы будут касаться боковой поверхности цилиндра.
Ясно, что если в основание призмы можно вписать окружность, то вокруг цилиндра можно описать призму.
Объём цилиндра
Теорема. Объём цилиндра равен произведению площади его основания и образующей цилиндра:
Доказательство. Пусть дан цилиндр с осью ОО1 (рис. 85). Впишем в него призму 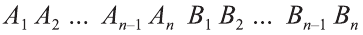
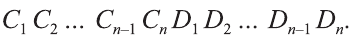
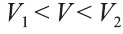
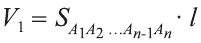
Будем всё больше и больше увеличивать число n сторон оснований призм. Тогда объём вписанной призмы будет увеличиваться, а объём описанной призмы уменьшаться. Если число n сторон увеличивать неограниченно, то разность между объёмами будет стремится к нулю. Число, к которому приближаются объёмы вписанной и описанной призм, принимают за объём данной призмы. При этом площади многогранников 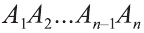
Исторические сведения:
В произведении Абу Райхна Беруни «Книга о началах искусства астрономии» («Астрономия») как введение в стереометрию в разделе о геометрии приводятся следующие определения фигур:
Куб – физическая фигура, похожая на кубик для игры в нарды, ограниченная с шести сторон квадратами.
Призма – представляет собой фигуру, ограниченную по бокам плоскостями в форме квадрата или прямоугольника, а сверху и снизу -двумя треугольниками. В этом определении Беруни приведено описание частного вида призмы, а именно треугольной призмы.
Книга Беруни «Канон Масьуда» написана в 1037 году. В ней приведены правила нахождения объёмов параллелепипеда и призмы: «Если тело не четырёхугольное или другого вида, то его расчёт таков: найди площадь, умножь его на глубину, в итоге получишь объём». В произведении Абу Али ибн Сино «Книга знания» в разделе «Основы изучения геометрических тел» дано описание тела и треугольной призмы. А также описаны условия взаимного равенства двух призм. Ибн Сино даёт следующее определение призмы: «Призма – тело, ограниченное двумя плоскими треугольными сторонами.»
В произведении Аль Каши «Книга счёта» приведёт много примеров расчета площадей поверхностей и объёмов тел. Благодаря своим глубоким знаниям в математике, геометрии, тригонометрии, механике и астрономии он пользовался вниманием и уважением Улугбека. Аль Каши наряду с многоугольниками изучачл призмы, пирамиды, цилиндры, конусы, усечённые конусы.
Таблица приближенных значений тригонометрических функций:
- Пирамида в геометрии
- Конус в геометрии
- Сфера в геометрии
- Шар в геометрии
- Возникновение геометрии
- Призма в геометрии
- Планиметрия – формулы, определение и вычисление
- Стереометрия – формулы, определение и вычисление