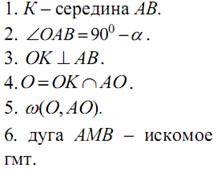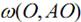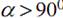Геометрические места точек
Геометрическим местом точек называют множество точек, заданное условием, являющимся и свойством, и признаком.
Другими словами, все точки из рассматриваемого геометрического места точек, и только они, удовлетворяют заданному условию.
Примеры геометрических мест точек (сокращённо ГМТ ) на плоскости представлены в следующей таблице, причём геометрические места точек изображаются в таблице красным цветом .
Метод геометрических мест точек
Одним из методов решения задач на построение является метод геометрических мест. Понятие геометрического места является одним из важнейших в геометрии. Термин «геометрическое место точек» был введен еще древнегреческим ученым и философом Аристотелем (384-222 гг. до новой эры), который представлял себе линию, как некоторое «место», где могут быть размещены точки. Понятие линии как следа движущей точки или совокупность точек, возникли значительно позже.
Геометрическим местом точек (сокращенно ГМТ), обладающих определенным свойством, называется множество всех точек, которые обладают этим свойством.
Сущность метода состоит в следующем. Пусть, решая задачу на построение, нам надо найти точку X , удовлетворяющую двум условиям. ГМТ, удовлетворяющих первому условию, есть некоторая фигура A, а ГМТ, удовлетворяющих второму условию, есть некоторая фигура B. Искомая точка X принадлежит A и B, т.е. является их точкой пересечения.
При решении задач этим методом надо знать основные геометрические места точек на плоскости:
1. ГМТ, равноудаленных от двух данных точек.
2. ГМТ, находящихся на данном расстоянии oт данной точки.
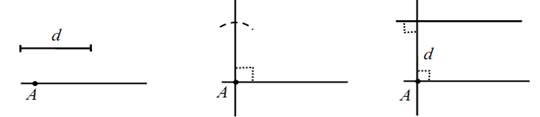
3. ГМТ, удаленных на расстояние d oт данной прямой.
4. ГМТ, равноудаленных от двух данных параллельных прямых.
5. ГМТ, равноудаленных от сторон угла.
6. ГМТ, из которых данный отрезок виден под данным углом.
Некоторые геометрические места точек, часто используемые
Рассмотрим построение основных ГМТ, перечисленных в предыдущем пункте.
1. Геометрическим местом точек, равноудаленных от двух данных
точек, является серединный перпендикуляр к отрезку с концами в этих
2. Геометрическим местом точек, находящихся на данном расстоянии
oт данной точки, является окружность с центром в данной точке и радиусом, равном данному отрезку.
3. Геометрическим местом точек, удаленных на расстояние d oт
данной прямой в выбранной полуплоскости, является прямая
параллельная данной и находящаяся на расстоянии d от нее.
А выбираем произвольно.
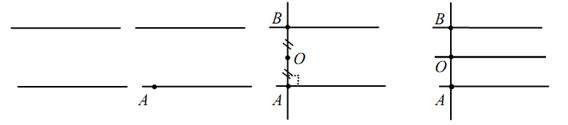
4. Геометрическим местом точек, равноудаленных от двух данных
параллельных прямых, является прямая, находящаяся на одинаковом
расстоянии от данных прямых (ось симметрии этих прямых).
5. Геометрическим местом точек, равноудаленных от сторон угла,
является биссектриса этого угла. (См. построение 4).
6. Геометрическим местом точек, из которых данный отрезок виден под
данным углом, является дуга окружности, опирающейся на этот отрезок.
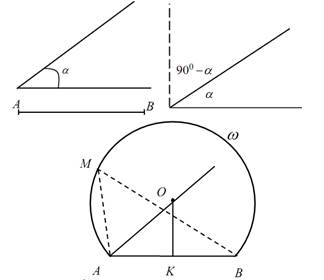
АВ – данный отрезок.
Действительно, ∟АМВ, как угол, вписанный в окружность, измеряется
половиной малой дуги АВ, так как центральный угол ∟АОВ = 2α, то
При этом заметим, что центр окружности О и вершина М угла лежат по
одну сторону от данного отрезка
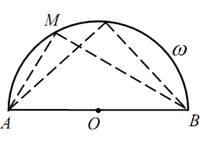
1. О – середина АВ.
Полуокружность
(Любой угол, опирающийся на диаметр –
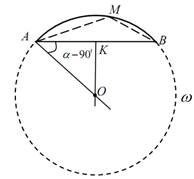
III случай:
Действительно, ∟АОВ = 2( 90 0 – (α – 90 0 )) = 2(180 0 – α). Тогда большая дуга
АВ равна 360 0 – 2(180 0 – α) = 2α и угол АМВ, опирающийся на большую дугу АВ, измеряется половиной этой дуги, т.е. равен α.
Как найти гмт от окружности
Геометрические места точек
Геометрическим местом точек называют множество точек, заданное условием, являющимся и свойством, и признаком.
Другими словами, все точки из рассматриваемого геометрического места точек, и только они, удовлетворяют заданному условию.
Примеры геометрических мест точек (сокращённо ГМТ ) на плоскости представлены в следующей таблице, причём геометрические места точек изображаются в таблице красным цветом .
Геометрическое место точек
Геометрическое место точек (ГМТ) — это фигура, состоящая из всех точек плоскости, удовлетворяющих определённому условию.
Чтобы выяснить, что собой представляет некоторая фигура F — геометрическое место точек, удовлетворяющих заданному условию P, нужно доказать:
1) если определённая точка принадлежит фигуре F, то она удовлетворяет заданному условию P;
2) если определённая точка удовлетворяет заданному условию P, то она принадлежит фигуре F.
(то есть требуется доказать прямую теорему — свойство P точек, принадлежащих фигуре F, и обратную теорему — признак фигуры F: если точка удовлетворяет условию P, то она принадлежит F).
Геометрическое место точек, равноудалённых от данной точки — окружность.
Это следует непосредственно из определения окружности.
Некоторые теоремы о ГМТ
1) Геометрическим местом точек, равноудалённых от двух данных точек, является серединный перпендикуляр к отрезку, соединяющему эти точки.
2) Геометрическим местом точек, равноудалённых от сторон неразвёрнутого угла, является биссектриса этого угла.
3) Геометрическим местом точек, удалённых от данной прямой на расстояние h, состоит из двух прямых, параллельных данной прямой и отстоящих от неё на h.
4) Геометрическим местом точек, равноудалённых от двух параллельных прямых, является прямая, параллельная этим прямым и проходящая через середину их общего перпендикуляра.
Понятие ГМТ часто используют при решении задач на построение.
Как найти гмт от окружности
| Учебный курс | Решаем задачи по геометрии |
Геометрическое место точек. Метод геометрических мест
Определение: Геометрическим местом точек называется геометрическая фигура на плоскости, каждая точка которой обладает одним и тем же определенным свойством.
Метод геометрических мест применяется чаще всего при построениях. Например, серединный перпендикуляр к отрезку можно определить как геометрическое место точек, равноудаленных от точек концов отрезков; окружность можно определить как геометрическое место точек, равноудаленных от данной точки.
Теорема (о геометрическом месте точек). Геометрическое место точек, равноудаленных от двух данных точек, есть прямая, перпендикулярная отрезку, соединяющему эти точки, и проходящая через его середину.
Доказательство. Пусть даны точки А и В, а точка С – середина отрезка АВ. Нужно найти геометрическое место точек, равноудаленных от точек А и В.
Доказательство основано на свойстве серединного перпендикуляра к отрезку.
Серединный перпендикуляр СК, принадлежащий прямой а, как и любая точка этой прямой, — есть геометрическое место точек, равноудаленных от А и В, так как СКꓕАВ.
Допустим, что есть еще точка К1, расстояние до которой от А и В одинаково.
Рассмотрим ∆АК1В, он разбит отрезком К1С на два треугольника: ∆АК1С и ∆К1СВ. Если эти треугольники равны, то точка К1 тоже удалена на одинаковое расстояние от А и В.
Через точку С проходят две прямые СК и СК1. На основании теоремы 16 (о единственности перпендикуляра из точки к прямой), если СКꓕАВ по построению, то СК1 не может быть перпендикулярна АВ.
Метод геометрических мест
Построить точку Х, равноудаленную от А и В и находящуюся на расстоянии h от точки С.
1.Построим геометрическое место точек, удовлетворяющее первому условию: это будет серединный перпендикуляр к отрезку АВ. Прямая а, которая содержит серединный перпендикуляр к отрезку АВ, удовлетворяет полностью первому условию.
2.На перпендикуляре (прямая а) должна находится точка Х, которая удовлетворяла бы второму условию (расстояние от нее до С должно составлять h).
Если из точки С радиусом h провести окружность, то все точки окружности будут расположены от С на одинаковом расстоянии h (построили второе геометрическое место точек, равноудаленных от С).
3.Пересечение первого геометрического места точек (прямая а) и второго (окружности с центром в точке С) будет удовлетворять обоим условиям задачи. Точки пересечения окружности и прямой (Х1 и Х) и будут теми искомыми точками, которые равноудалены от точек А и В и находятся от С на расстоянии h.
[spoiler title=”источники:”]
http://poisk-ru.ru/s5189t3.html
http://b4.cooksy.ru/articles/kak-nayti-gmt-ot-okruzhnosti
[/spoiler]
Здравствуйте , уважаемая МаШа !
,, Геометрическое место точек равноудаленых от двух прямых ,,
Что Вы должны вообще представляете себе о этом термине ,, ГМТ ,,
– Это есть уравнение некоторой линии , обладающей указанными свойствами !
В данном случае этим свойством является : ,, геометрическое место точек равноудаленых
от двух прямых ,,
– Для установления этого уравнения необходимо :
– Изобразить две заданные прямые в одной системе координат , при этом рассмотрев
два случая ( параллельных прямых и пересекающихся прямых )
– Выбрать во внутренней области этх прямых произвольную точку
– Из этой точки опустить перпендикуляры на данные прямые
– Составить уравнение полученных перпендикуляров ( через две точки Y1 и Y , Y2 и Y )
– Так как эти отрезки перпендикуляров по условию задачи раны , то приравнять I YY1 I = I YY2 I
– Преобразовать полученное уравнение к общепринятому виду .
Это и будет искомое уравнекние вида : Y = X + c – уравнение бисектрисы угла между двумя пересекающимися прямыми !
Желаю Вам успешно грызть гранит науки !
С массой наилучших пожеланий и счастья в личной жизни !
Добавлено согласно Вашего добавления к вопросу !
тоочная формулировка: уравнение геометрическогоо места точек плоскости, равноудаленых от двух прямых y=2x+16 и y=2x-4, имеет вид??
– Из заданных уравнений прямых следует что они параллельны , а значит и угловой
коэффициент искомой прямой будет также равен 2 : k =2
– Остаётся определить величину ,, с ,,
– X = ( X1 + X2 ) : 2 или Y = ( Y1 + Y2 ) : 2 – как координата середины отрезка , тогда
( 16 + ( – 4 ) ) : 2 = 6,
значит
Y = 2X + 6 – есть искомое ураснение ГМТ !
Ещё раз : Успеха и счастья во всём !!!
Определение
Геометрическое место точек (ГМТ) — это фигура, состоящая из всех точек плоскости, удовлетворяющих определённому условию.
Чтобы выяснить, что собой представляет некоторая фигура F — геометрическое место точек, удовлетворяющих заданному условию P, нужно доказать:
1) если определённая точка принадлежит фигуре F, то она удовлетворяет заданному условию P;
2) если определённая точка удовлетворяет заданному условию P, то она принадлежит фигуре F.
(то есть требуется доказать прямую теорему — свойство P точек, принадлежащих фигуре F, и обратную теорему — признак фигуры F: если точка удовлетворяет условию P, то она принадлежит F).
Геометрическое место точек, равноудалённых от данной точки — окружность.
Это следует непосредственно из определения окружности.
Некоторые теоремы о ГМТ
1) Геометрическим местом точек, равноудалённых от двух данных точек, является серединный перпендикуляр к отрезку, соединяющему эти точки.
2) Геометрическим местом точек, равноудалённых от сторон неразвёрнутого угла, является биссектриса этого угла.
3) Геометрическим местом точек, удалённых от данной прямой на расстояние h, состоит из двух прямых, параллельных данной прямой и отстоящих от неё на h.
4) Геометрическим местом точек, равноудалённых от двух параллельных прямых, является прямая, параллельная этим прямым и проходящая через середину их общего перпендикуляра.
Теорема 1 — свойство серединного перпендикуляра.
Теорема 2 — свойство биссектрисы угла.
Понятие ГМТ часто используют при решении задач на построение.
В математике это выражение употребляется для описания множества точек, обладающих некоторым свойством.
Пожалуй, самым первым приходящим на ум геометрическим местом точек (ГМТ) является окружность. Каждая точка окружности удалена от некоторой точки, называемой центром на расстояние R. Вспомните, какие действия мы производим при попытке начертить ровную окружность. Разводим ножки циркуля на выбранное расстояние, обязательно при этом фиксируем это расстояния, насколько позволяет инструмент. Это важный пункт, ибо если в процессе изображения окружности собьётся расстояние, то никакой окружности не получится. Далее, устанавливаем иглу в выбранный центр и оставляем грифелем след во всех местах, где это возможно.
Казалось бы, какие очевидные вещи сейчас обсуждаются, но не это ли свойство ГМТ используется, например, при поиске пропавших туристов или даже воздушных судов? Если со времени последнего известного положения интересующего объекта X прошло время t, то при максимальной скорости объекта V он мог преодолеть расстояние R=Vt. Важно что, после потери контакта с объектом направление его движения может быть самым непредсказуемым. Именно поэтому говорят о зоне поиска в окружности, радиусом R.
ГМТ на практике
Вспомним трагические события 2014 года, когда бесследно исчез пассажирский самолет рейса 370. До сих пор кроме предположений нет никакой информации о судьбе всех его пассажиров. Сейчас нас будет интересовать то, каким образом поисковый штаб ограничил часть земной поверхности, в которой предположительно мог находиться потерянный самолет.
Поскольку известна последняя точка, где самолет был зафиксирован радиолокатором и после этого не выходил на связь, то в самом пессимистичном случае он не мог преодолеть расстояние, более чем ему бы позволил остаток топлива. А так как дальнейший маршрут полета неизвестен, то, опять же, в самом пессимистичном случае необходимо применить это самое свойство ГМТ.
Количество этих самых ГМТ довольно внушительно и можно только представить сколько полезной работы человек доверил этим математическим понятиям.
Если рассматривать вышеуказанную задачу не на плоскости, а трехмерном пространстве, то получим сферу. Более строгое определение этого – ГМТ равноудаленных от одной точки в пространстве, есть сфера с центром в данной точке. Это математическое свойство несомненно учитывается при определении координат в спутниковых системах навигации. Поскольку спутники находятся довольно далеко от поверхности планеты, то принимается модель сферического распространения радиоволн от точечного источника.
Более подробно об этом способе можно узнать из статьи про особенности работы глобальной системы позиционирования GPS.
Более сложный случай ГМТ
Это всего пара примеров, где выполняющееся для точек условием было предельно простым. Это всего лишь равенство. Конкретно равенство расстояний. Но что будет, если в качестве условия будет поставлено более сложное выражение. Тут как из рога изобилия будут высыпаться еще более интересные случаи.
Что мы видим на рисунке выше? Да это всем известная гипербола. Вот же ее фокусы в точках (-с,0) и (с,0). А знаете ли вы, что это не менее удивительное ГМТ? Для всех точек гиперболы верно условие d2 – d1 = 2a. Простыми словами – разность между расстояниями от фокусов до любой точки гиперболы постоянна. “И что?” – это самый желанный вопрос, потому что на этом принципе работают другие системы навигации, важность которых в деятельности человека недооценить невозможно. Их еще называют системами гиперболического типа и красота математики этих решении просто запредельная. Об этом вы лучше узнаете из этой статьи.
А какие геометрические места точек и области их применения знаете вы?
*****************************************************************************
Канал, которому посвящено мое сегодняшнее промо – канал моего друга – специалиста, обладающего широчайшим спектром знаний об IT-технологиях. На своем ДЗЕН-канале, а также на YouTube он простым языком объясняет не только многие моменты из мира компьютеров и электроники, но и ставит настоящие эксперименты!
*****************************************************************************
Геометрическое место точек. Метод геометрических мест
Определение: Геометрическим местом точек называется геометрическая фигура на плоскости, каждая точка которой обладает одним и тем же определенным свойством.
Метод геометрических мест применяется чаще всего при построениях. Например, серединный перпендикуляр к отрезку можно определить как геометрическое место точек, равноудаленных от точек концов отрезков; окружность можно определить как геометрическое место точек, равноудаленных от данной точки.
Теорема (о геометрическом месте точек). Геометрическое место точек, равноудаленных от двух данных точек, есть прямая, перпендикулярная отрезку, соединяющему эти точки, и проходящая через его середину.
Доказательство. Пусть даны точки А и В, а точка С
– середина отрезка АВ. Нужно найти геометрическое место точек, равноудаленных от точек А и В.
Доказательство основано на свойстве серединного перпендикуляра к отрезку.
Серединный перпендикуляр СК, принадлежащий прямой а, как и любая точка этой прямой, – есть геометрическое место точек, равноудаленных от А и В, так как СКꓕАВ.
Допустим, что есть еще точка К1, расстояние до которой от А и В одинаково.
Рассмотрим ∆АК1В, он разбит отрезком К1С
на два треугольника: ∆АК1С и ∆К1СВ. Если эти треугольники равны, то точка К1
тоже удалена на одинаковое расстояние от А и В.
Через точку С проходят две прямые СК
и СК1. На основании теоремы 16 (о единственности перпендикуляра из точки к прямой), если СКꓕАВ
по построению, то СК1 не может быть перпендикулярна АВ.
Так как из двух смежных углов (∟К1СА и ∟К1СВ) один должен быть острый, а второй – тупой, то ∆К1СА≠∆К1СВ, следовательно, К1А≠К1В (есть две равные стороны, АС=ВС
и К1С
– общая, но нет равных углов между ними), значит, К1С – наклонная к АВ и АК1≠ВК1.
Метод геометрических мест
Определение: Сущность метода геометрических мест в том, что при наличии не одного, а нескольких условий для построения геометрической фигуры, нужно построить несколько геометрических фигур, которые по очереди будут удовлетворять каждому из условий, а потом найти такое геометрическое место точек, которое при пересечении или совмещении этих фигур будет удовлетворять всем условиям построения.
Например: Даны три точки: А, В, С.
Построить точку Х, равноудаленную от А и В и находящуюся на расстоянии h от точки С.
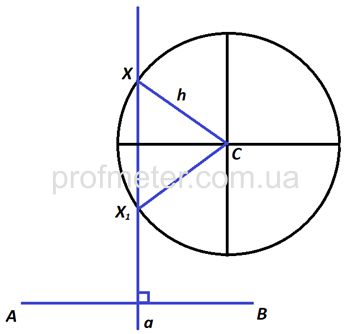
Порядок построения:
1.Построим геометрическое место точек, удовлетворяющее первому условию: это будет серединный перпендикуляр к отрезку АВ. Прямая а, которая содержит серединный перпендикуляр к отрезку АВ, удовлетворяет полностью первому условию.
2.На перпендикуляре (прямая а) должна находится точка Х, которая удовлетворяла бы второму условию (расстояние от нее до С должно составлять h).
Если из точки С
радиусом h провести окружность, то все точки окружности будут расположены от С на одинаковом расстоянии h (построили второе геометрическое место точек, равноудаленных от С).
3.Пересечение первого геометрического места точек (прямая а) и второго (окружности с центром в точке С) будет удовлетворять обоим условиям задачи. Точки пересечения окружности и прямой (Х1
и Х) и будут теми искомыми точками, которые равноудалены от точек А
и В
и находятся от С на расстоянии h.
0
Точки, отрезки и прямые |
Описание курса
| Отрезки в координатной плоскости