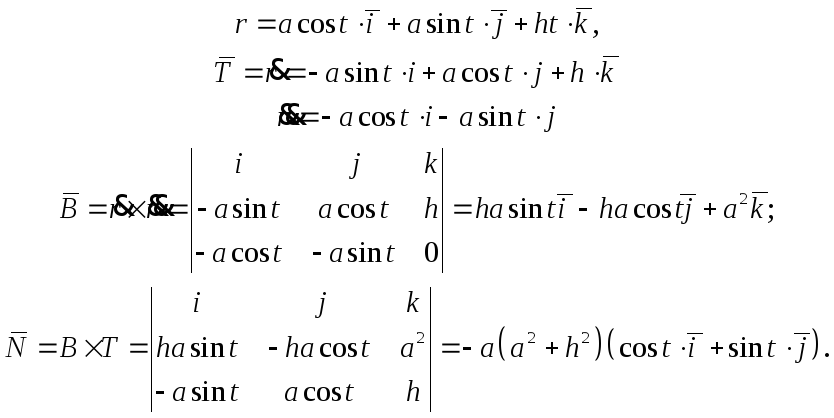Как найти годограф вектор функции

1 Найти годограф вектор-функции

.

Решение. Параметрические уравнения годографа есть

, , .

Из первых двух уравнений исключаем параметр :

.

Следовательно, годографом вектор-функции является окружность

, ,

Из которой исключена точка .

При изменении от до точка на годографе движется от точки против часовой стрелки (если наблюдать из точки, расположенной выше плоскости ). При этом

, .

2 Вычислить , если .

Решение. Согласно определению

.

3 Найти единичный касательный вектор годографа вектор-функции

При .

Решение. Параметрические уравнения годографа есть

, , .

Найдем координаты направляющего вектора касательной к кривой :

,

В частности в точке

.

Тогда единичный вектор годографа имеет вид

.

4 Найти производную скалярного произведения векторов

и .

Решение. Согласно свойствам дифференцируемых векторных функций, имеем

==.

5 Дано уравнение движения . Определить траекторию и скорость движения.

Решение. Параметрические уравнения годографа есть

, , .

Из первого уравнения исключим параметр

И подставим во второе

.

Отсюда уравнение траектории движения

, .

Вектор скорости движения есть

.

6 Написать уравнения касательной и нормальной плоскости к кривой

В точке .

Решение. Данной точке соответствует значение параметра .

Имеем

, , .

Подставляя значение , получаем

, , .

Тогда уравнение касательной:

,

Уравнение нормальной плоскости:

Или .

7 Найти скорость и ускорение материальной точки , движущейся с постоянной угловой скоростью по окружности

.

Решение. Пусть – произвольная точка окружности. Обозначим через угол между радиус-вектором точки и положительным направлением оси . По условию

,

Где – время движения.

Выразим координаты точки как функции времени (рисунок 9.8):

,

.

Следовательно, радиус-вектор точки

,

Скорость движения точки

,

Модуль скорости

.

Рисунок 9.8 – Геометрическая интерпретация задачи 7.

Скалярное произведение векторов и есть:

,

Т. е. векторы и перпендикулярны.

Отсюда следует, что вектор направлен по касательной к окружности, по которой движется точка .

Найдем ускорение :

.

Значит, векторы и имеют противоположные направления.

Таким образом, ускорение материальной точки, движущейся с постоянной угловой скоростью по окружности, в каждый момент времени направлено к центру этой окружности.

8 К годографу винтовой линии (рисунок 9.9)

А) найти уравнения касательной прямой и нормальной плоскости в точке ;

Б) доказать, что касательная к винтовой линии образует постоянный угол с осью ;

В) записать натуральное уравнение винтовой линии;

Г) найти дифференциал длины дуги.

Рисунок 9.9 – Годограф функции

Решение. а) координаты точки касания есть:

, , .

Координаты вектора :

, . .

Тогда уравнение касательной прямой имеет вид

,

А уравнение нормальной плоскости

;

Б) вектор касательный к годографу вектора :

.

Тогда

.

В) векторная функция является непрерывно дифференцируемой и

.

Тогда . Интегрируя обе части, получим . Из начального условия , имеем . При этом длина винтовой линии равна

.

Следовательно, .

Отсюда натуральное уравнение винтовой линии в координатной форме запишется в виде:

,

Где .

Г) дифференциал длины дуги равен

.

Для винтовой линии имеем

.

< Предыдущая		Следующая >

Переменные векторы. Вектор-функции и их дифференцирование

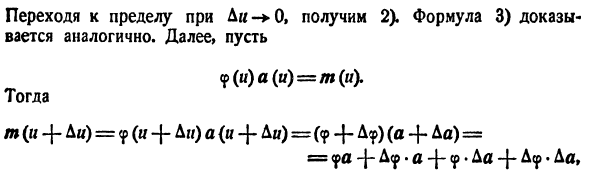
Переменные векторы. Вектор-функции и их дифференцирование

• Переменный вектор. Векторные функции и их различие № 1. Переменный вектор. Функция вектора Годограф. Представьте себе точку M (x, y, z) t, движущуюся в пространстве вдоль определенной кривой K (рис. 293). Выберите единицу времени и первый момент. И любой момент времени характеризуется числом т.

Непрерывность векторной функции. Их дифференциация № 3. Непрерывность векторной функции. Различать их. Дай мне а = а (и) Функция вектора и скалярного аргумента. Как и в случае обыкновенных дифференциальных вычислений, если бесконечно малое приращение аргумента соответствует бесконечно малому приращению функции, a (n) называется непрерывным. lirn [a (u + Lee) -a (//)] = 0. (7) к- * 0 Равенство (7) также может быть описано в следующем формате: lim a (u — — di) = a (u). Где u0, a, —

Поэтому гл. II, свойство непрерывности вектор-функции означает, что предел (и u0) этой функции равен значению из предела аргумента. Далее поясняется операция дифференцирования непрерывной вектор-функции. Дай мне а = а (и) -Такую функцию. Давайте сделаем пять вещей: 1) Исправьте значение аргумента и найдите соответствующее значение функции a (s). 2) Дайте аргументу приращение A и найдите новое значение функции a (u — <- Au); 3) Найдите приращение Da = a (u + A «)

a (u). .v да (s + Dy) -a (s) 4) Настройте отношение -m— = —1-! -r1, -;

б) (s) и обозначается одним из символов. , T, h da a, a ‘(s), g. Нахождение ‘(u) называется производной функции a (u). *) Конечно, этого может и не быть.

Поверните A на ноль и ищите пределы *) lim * Джим Ли 0 Ли Аа 0 Ли Это ограничение называется производной функции a Людмила Фирмаль

Легко найти геометрический смысл производной a ‘(u). Для этого представим годограф векторной функции. Если (см. Рисунок 295) a (u) -OM, a (n-dY) = ON, тогда A a = LSH Отношение-вектор в том же направлении А Ды]> 0 для ММ, Di 0 и о = МП, Вы можете видеть, что вектор MP направлен на годограф по секущей линии.

Если Да -О (из-за непрерывности вектор-функции), точка N стремится соответствовать точке М. Поэтому предельное положение вектора MP направлено на годограф по касательной MQ. Однако эта предельная позиция n является производной от o ‘(u). Следовательно, производная вектор-функции направлена ​​по касательной к годографу этой функции. Пример. Переместить точку М в пространстве, r = r (t)

Векторное уравнение для этого движения. Годограф радиус-вектора r (0 — траектория точки М. Производная / (t) называется скоростью точки М. Следовательно, скорость точки — это вектор, который касается траектории этой точки. Этот вектор является направлением движения. И характеризуем скорость: r ‘(0 — предел длины вектора г (/ + ac-g (0 ат Учитывая ясность,Однако (рис. 296) DO-g (01 — длина кода MN, Включает в себя минимальную дугу MN точечной траектории. Как вы знаете, эти коды и дуги эквивалентны друг другу Поэтому друзья if’wi-lim, x, 1 w / a rW / r (t + AtJ

• Другими словами, длина вектора скорости является пределом отношения пути, по которому течет ток через бесконечно короткие промежутки времени. 296.Время этого периода Gap. Это скалярное значение — скорость точки. Направление вектора / (t) указывает направление движения. № 4. Формулы и правила дифференцирования векторных функций. Правила дифференцирования векторных функций полностью аналогичны правилам обыкновенных дифференциальных вычислений.

Они использованы в следующей таблице. a = a (u), b = b (u) -: векторная функция скалярного аргумента и вектор c-константы? (O) -скалярная функция и k-константа, v-скалярный аргумент, связанный с выражением q = u (m>): 1) ду * 6) рфа-дурь 2) d (a — — b) du da | du 1 db du * 7) rfu и i

. -A * + e du db du ‘8) rf (ffl) du 4) dfoa) du rfa. du * 9) d [ab] du б) д (ка) __ ду ■ к да • * ду ’10) да дв ‘да ду ду дв’ Формула 1) понятна. Положите s-a — — b, чтобы доказать 2). Тогда s + bs = (a — — Да) + отсюда D $ = Да + Db и AL, AB Я Ли 1 Ли

Когда вы достигнете предела Di 0, вы получите 2). Формула 3) тоже доказана. Дальше давайте

0, *) получается уравнение 4). Формулы 5) и 6) являются частными случаями 4). Уравнение 7) доказывается так же, как 4). Частные случаи 8) -7) и 9) такие же, как 4). Наконец, 10) доказывается точно так же, как и скалярный анализ.

Пусть ax, ay> ar — проекция вектор-функции a = a (n). тогда a = axi — — ay] — — атака. Используя уравнения 2) и 6) da_dax. , День da2- «Du

du J ^ Ifa Da Da Однако, когда вектор разлагается на векторы единичных координат, коэффициент единичного вектора i является проекцией разрешимого вектора на ось * Ox. так дакс н да du — iip * du 9

То есть проекция векторной производной на ось равна производной этой проекции на эту ось. Людмила Фирмаль

Пример. r = r (0 — радиус-вектор движущейся точки) М (х, у, z). Введите u =. Как вы уже знаете, v это скорость Точка М. Как сказано, vx = ^

-t. Но Tx = х. о Следовательно, проекция векторов на другие оси одинакова. Вот так дз дт *

То есть спроецированная скорость движущейся точки (на оси координат) равна производной соответствующей координаты по времени. Например, если точка движется как x = 8t * -1, = = z = tz + 1, vx = 16 /, r> y = 4, vz = 3Отс Выше называется «скорость движения®» и равна г / — = Y * 2LY * — — 1 () -) — 9/4 В момент времени t = 1, y = 16,8. *) Поскольку предполагается, что функция a (s) непрерывна, litnAa = 6 для Ли 0.

Равен длине временного интервала, отделяющего этот момент от первого момента. В этом случае знак присваивается номеру t. Или это зависит от того, следует ли момент интереса или предшествует первому моменту. Радиус-вектор r = OM в каждый конкретный момент t имеет определенную длину и направление. Однако их длина и направление со временем изменятся *). Итак, здесь мы имеем дело с переменными векторами. Как правило, переменные векторы — это векторы, которые различаются по длине или направлению.

Однако мы рассматриваем постоянные векторы как частный случай переменных (аналогично использованию констант в скалярном анализе). Скалярный анализ различал индивидуальные постоянные значения при работе с переменными. Фактически, переменная задача состояла из задачи этого набора значений. Аналогичным образом определим переменную вектор а Вы определите набор постоянных векторов — индивидуальное значение. В процессе изменения a принимает одно из этих значений. Если a является переменным вектором, его проекция ayt ax также является (скалярной!) Переменной. Установка вектора a эквивалентна установке переменных ay и av.

Если a принимает одно из своих значений, ay ay1 также принимает соответствующее постоянное значение. Очень важным примером переменного вектора является скалярная функция-вектор аргумента. Они говорят, что переменная vector a является векторной функцией скалярных аргументов, и каждое значение связано с определенным значением a. В этом случае они пишут а = а (к). г » И м Рисунок 293.

Если a = a (u), проекционный топор и ar ag являются (скалярными!) Аргументными функциями, ax = ax (u), y = a y (u), ax = ax (u). *) Длина r не изменяется, если кривая K находится на поверхности шара с центром в начале координат. Точно так же, если K — луч, происхождение которого является источником, это может быть в определенном направлении r.

Пример вектор-функции показан для радиус-вектора r = OM в точке M перемещения, описанной выше. Здесь, поскольку аргумент — время U, g = g (0- (1) Это уравнение называется векторным уравнением движения для точки М. Поскольку координаты точки M (x, y, r) являются проекциями ее радиус-вектора r, уравнение (1) можно заменить тремя скалярными уравнениями движения. x = x (t), y = y (f), z = z (t). Например, равенство x = Py y = 7t + 2, z = s nt Движение точки происходит. Их можно заменить одним векторным уравнением r = t4 — — (7t-2) / + sin tk.

Годограф определенного вектора переменных — это геометрическое положение конечных точек всех значений, если каждое значение откладывается от общей начальной точки. Годограф вектор-функции a (u) представляет собой (как правило, пространственную) кривую. Если все значения a (u) установлены на что-то отличное от источника, уравнение x = ax (u), y = ay (u), z = az (u) Представляет параметрическое уравнение вышеуказанной линии. Если вектор a (u) постоянен, годограф — это линия на поверхности шара.

Постоянный векторный годограф — это точка. Годограф радиус-вектора r = OM движущейся точки M является ее точкой. n ° 2. Векторное ограничение. Рассмотрим переменный вектор a, который изменяется в соответствии с законом *).Определение 1. Переменный вектор a называется бесконечно малым, если он имеет тенденцию быть нулевым по длине. Определение 2. Постоянный вектор I называется пределом переменного вектора a.

Разница между ними — бесконечно малый вектор. •) Например, a является векторной функцией скалярного аргумента a = a (s) и имеет определенные ограничения. Или, в более простом случае, пронумерованная последовательность постоянных значений alt at) atl …

Запишите с любой формулой Лима = /, а- + Л (Рис. 294) Приведите векторы / и a к общему началу координат 0 и приведите их в соответствие с началом координат. Далее разность I-a представлена ​​вектором AL. Если длина этого вектора стремится к нулю, точка A стремится соответствовать точке L, поэтому X A XV Однако, в конце концов (поскольку 0 соответствует началу координат), xA и xL являются проекциями векторов a и / на ось Ox. Таким образом, предыдущие отношения Я, — * / *.

Эта ситуация аналогична проекции векторов на другие оси. 80М это правда Рисунок 294. Теорема 1. Связь (2) (3) 1g lim a = 1 Это предполагает тройные отношения. 1G a9 Покажем, что обратное также верно в соответствии с теоремой 2. (3) — (2). Фактически, переместите векторы a и / к общему началу координат 0. Это совпадает с происхождением. В то же время конечными точками векторов a и I являются точки A и ξ. a = OAt 1 = O b

В понятной нотации * «= * # Ay = ul ‘*» = * # (3) чк

+ ги Откуда Y (XA- + (YA-Y0 * + (* A- * jf- * ° — и Последнее соотношение можно записать как AL — + 0, Это означает, что по определению 2 (2) верно. Таким образом, векторное соотношение (2) эквивалентно скалярному отношению тройка (3). Эта эквивалентность позволяет легко переносить наиболее важные свойства скалярных переменных в вектор.

Например, теорема 3I верна. а * л * т (4) тогда a + a * a-a * -> l-l * t (5) м. е. Предел суммы (разности) ограниченных векторов равен сумме пределов (разности). Конечно, это из (4) * * *! * ….. AJ-WJ. тогда i * -faj + ^ -f>> / j, -f l> 9 + + (6) Для простоты Если a — — a * = b, 1 + 1 * = m, (6) можно переписать в следующем формате bx-> tx% by —► tu, bg- * mt> По теореме 2 Lim 6 = / I Это эквивалентно первому соотношению (5). Второе доказывается аналогично. Подобные рассуждения доказывают еще две теоремы. Теорема 4. С (4)

(A, a *) — * (/, / *), [a, a *) -> — [/, / *], / я. д. Предел скалярного (векторного) произведения двух векторов с ограничениями равен (соответствующему) произведению этих ограничений. Теорема б. если И это = /, l p скалярная переменная с конечными ограничениями q> then lim (pa) = 0 /.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Вектор-функции

Предел и непрерывность вектор-функции.

Понятие вектор-функции.

Если каждому значению (tin E), где (Esubsetmathbb), поставлен в соответствие вектор (r(t)) трехмерного пространства, то говорят, что на множестве (E) задана векторная функция (r(t)) скалярного аргумента (t).

Пусть в пространстве фиксирована прямоугольная система координат (Oxyz). Тогда задание вектор-функции (r(t), tin E), означает задание координат (x(t), y(t), z(t)) вектора (r(t), tin E). Если (i,j,k) — единичные векторы координатных осей, то
$$
r(t)=x(t)i+y(t)j+z(t)k,qquad tin E,nonumber
$$
или
$$
r(t)=(x(t),y(t),z(t)).nonumber
$$
Если (z(t)=0) при всех (tin E), то вектор-функцию (r(t)) называют двумерной.

В случае, когда начало каждого из векторов (r(t)) совпадает с началом координат (рис. 21.1), эти векторы называют радиус-векторами, а множество их концов — годографом вектор-функции (r(t)), (tin E), который можно рассматривать как траекторию точки (M(t)) конца вектора (r(t)), если считать, что (t) — время.

Предел вектор-функции.

Вектор (a) называют пределом вектор-функции (r(t)) в точке (t_0) и пишут (displaystyle lim_>r(t)=a) или (r(t)rightarrow a) при (trightarrow t_0), если
$$
lim_> |r(t)-a|=0,label
$$
то есть длина вектора (r(t)-a) стремится к нулю при (trightarrow t_0).

Рис. 20.1

Если заданы (r(t)=(x(t),y(t),z(t))) и (a=(a_<1>,a_<2>,a_<3>)), то
$$
lim_>r(t)=alabel
$$
тогда и только тогда, когда
$$
x(t)rightarrow a_1, y(t)rightarrow a_2, z(t)rightarrow a_3quad при trightarrow t_0.label
$$

Поэтому, если (r(t)rightarrow a) при (trightarrow t_0), то есть выполняется условие eqref, то выполняется условие eqref.

Обратно: если выполняются условия eqref, то из равенства eqref следует, что выполнено условие eqref. (bullet)

При доказательстве свойств предела вектор-функции удобно использовать следующее очевидное утверждение: условие eqref выполняется в том и только том случае, когда
$$
r(t)=a+alpha(t),nonumber
$$
где (alpha(t)) — бесконечно малая вектор-функция, то есть
$$
alpha(t)rightarrow 0quad mbox <при> trightarrow t_<0>.nonumber
$$

Свойства пределов вектор-функций.

(circ) Это свойство следует из неравенства
$$
||r(t)|-|a|| leq |r(t)-a|.qquad bulletnonumber
$$

Если (r(t)rightarrow a) при (trightarrow t_<0>), а скалярная функция (f(t)) такова, что (f(t)rightarrow A) при (trightarrow t_<0>), то (f(t)r(t)rightarrow Aa) при (trightarrow t_<0>), то есть
$$
lim_f(t)r(t)=lim_>f(t)lim_r(t).label
$$

(circ) Из определений пределов скалярной функции и вектор-функции следует, что (r(t)=a+alpha(t), f(t)=A+beta(t)), где (alpha(t)) — бесконечно малая вектор-функция, (beta(t)) — бесконечно малая функция при (trightarrow t_0). Поэтому (f(t)r(t)=Aa+gamma(t)), где (gamma(t)=Aalpha(t)+beta(t)a+beta(t)alpha(t)) — бесконечно малая вектор-функция при (trightarrow t_0), откуда получаем равенство eqref. (bullet)

(circ) По условию (r_(t)=a_+alpha_), где (a_i(t)rightarrow 0) при (trightarrow t_<0> (i=1,2)). Поэтому (r_1(t)+r_2(t)=a_1+a_2+beta(t)), где (beta(t)=alpha_<1>(t)+alpha_2(t)rightarrow 0) при (trightarrow t_<0>), откуда следует eqref. Докажем формулу eqref. В силу свойств скалярного произведения
$$
(r_<1>(t),r_2(t))-(a_1,a_2)=(alpha_<1>(t),a_<2>)+(alpha_<2>(t),a_1)+(alpha_1(t),alpha_2(t)),nonumber
$$
причем в правой части этого равенства — бесконечно малая функция, так как (alpha_<1>(t),alpha_<2>(t)) — бесконечно малые вектор-функции и (|(p,q)| leq |p|cdot|q|) для любых векторов (p) и (q).

Аналогично доказывается формула eqref, в этом случае следует воспользоваться неравенством (|[p,q]| leq |p|cdot|q|). (bullet)

Непрерывность вектор-функции.

Вектор-функцию (r(t)) называют непрерывной при (t=t_<0>), если
$$
lim_>r(t)=r(t_0).label
$$
Непрерывность вектор-функции (r(t)=(x(t),y(t),z(t))) при (t=t_<0>) в силу эквивалентности условий eqref и eqref означает, что ее координаты (x(t),y(t),z(t)) непрерывны в точке (t_<0>).

Назовем вектор-функцию (Delta r=r((t_0+Delta t)-r(t_0)) приращением вектор-функции (r(t)) в точке (t_<0>). Тогда условие eqref означает, что
$$
Delta rrightarrow 0quad приquad Delta trightarrow 0.label
$$

Из определения непрерывности вектор-функции и свойств пределов векторных функций следует, что сумма, векторное и скалярное произведения вектор-функций (r_1(t)) и (r_2(t)) являются непрерывными функциями при (t=t_<0>), если вектор-функции (r_1(t)) и (r_2(t)) непрерывны в точке (t_<0>).

Производная и дифференциал вектор-функции.

Производная вектор-функции.

Если существует (displaystyle lim_<Delta trightarrow 0>frac<Delta r><Delta t>) где (Delta r=r(t_0+Delta t)-r(t_0)), то этот предел называют производной вектор-функции (r(t)) в точке (t_0) и обозначают (r'(t_0)) или (dot(t_0)).

Таким образом,
$$
r'(t_<0>)=lim_<Delta trightarrow 0>frac+Delta t)-r(t_<0>)><Delta t>.label
$$
Аналогично вводится понятие второй производной
$$
r″(t_<0>)=lim_<Delta trightarrow 0>frac+Delta t)-r'(t_<0>)><Delta t>nonumber
$$
и производной порядка (n > 2) вектор-функции. Заметим, что если (r(t)=(x(t),y(t),z(t))), то
$$
r'(t_<0>)=(x'(t_0),y'(t_0),z'(t_0))label
$$
Утверждение eqref следует из определения eqref и свойств пределов вектор-функций.

Аналогично, если существует (r″(t_<0>)), то
$$
r″(t_<0>)=(x″(t_0),y″(t_0),z″(t_0)).nonumber
$$
Из определения производной следует, что (Delta r=r'(t_0)Delta t+alpha(Delta t)Delta t), где (alpha(Delta t)rightarrow 0) при (Delta trightarrow 0), и потому (Delta rrightarrow 0) при (Delta trightarrow 0). Таким образом, выполняется условие eqref, то есть вектор-функция (r(t)), имеющая производную в точке (t_<0>), непрерывна при (t=t_<0>).

(circ) Формулы eqref-eqref справедливы в точке (t), если в этой точке соответствующие функции имеют производные. Ограничимся доказательством формулы eqref. Пусть (Delta r_) — приращение вектор-функции (r_k(t)), соответствующее приращению аргумента (Delta t), то есть (Delta r_k=r_k(t+Delta t)-r_k(t), k=1,2). Тогда, используя свойства скалярного произведения и свойства пределов вектор-функций, получаем
$$
begin
(r_<1>,r_<2>)’=displaystylelim_<Delta trightarrow 0>frac<(r_<1>(t+Delta t),r_<2>(t+Delta t))-(r_<1>(t),r_<2>(t))><Delta t>=\
=lim_<Delta trightarrow 0>left[left(r_<1>(t),frac<Delta r_<2>(t)><Delta t>right)+left(frac<Delta r_<1>(t)><Delta t>,r_2(t)right)+left(frac<Delta r_<1>(t)><Delta t>,Delta r_2(t)right)right]=\
=(r_1,r_2′)+(r_1′,r_2),
endnonumber
$$
так как (displaystyle frac<triangle mathrm_><triangle t>rightarrow r_‘(t)) при (Delta trightarrow 0 (i=1,2)) и (Delta r_2rightarrow 0) при (Delta trightarrow 0). (bullet)

Пусть существует (r'(t)) для всех (tin(alpha,beta)) и пусть (|r(t)|=C=const) для всех (tin(alpha,beta)).

Доказать, что ((r(t),r'(t))=0), то есть векторы (r(t)) и (r'(t)) ортогональны.

(triangle) Используя формулу (|r(t)|^2=(r(t),r(t))), правило дифференцирования скалярного произведения (формула eqref) и условие (|r(t)|=C), получаем ((r(t),r(t))’=2(r'(t),r(t))=0), так как (|r(t)|^<2>)’=(C^<2>)’=0). Итак,
$$
|r(t)|=CRightarrow (r(t),r'(t))=0.quadblacktrianglenonumber
$$

Дифференциал вектор-функции.

Вектор-функцию (r(t)), определенную в некоторой окрестности точки (t_<0>), называют дифференцируемой при (t=t_<0>), если ее приращение (Delta r=r(t_<0>+Delta t)-r(t_<0>)) в точке (t_<0>) представляется в виде
$$
Delta r=aDelta t+Delta talpha(Delta t),label
$$
где вектор (a) не зависит от (Delta t), (alpha(Delta t)rightarrow 0) при (Delta trightarrow 0).

Полагая (dt=Delta t), запишем равенство eqref в виде
$$
dr=r’dt,nonumber
$$
где опущено обозначение аргумента функции (r’). Отсюда получаем
$$
r’=frac

.label (21)
$$

Замена переменного.

Если функция (t=t(s)) дифференцируема при (s=s_<0>, t(s_<0>)=t_<0>), а вектор-функция (r(t)) дифференцируема в точке (t_<0>), то вектор-функция (rho(s)=r(t(s))) дифференцируема в точке (s_<0>), а производная этой функции выражается формулой
$$
rho’ (s_0)=r_s'(t(s_0))=r_'(t_<0>)t_‘(s_<0>),label
$$

где индекс указывает, по какому переменному производится дифференцирование.

(circ) Функция (alpha(Delta(t))) в формуле eqref не определена при (Delta t=0). Доопределим ее при (Delta t=0), полагая (alpha(0)=0).

Так как (t=t(s)) — функция, дифференцируемая при (s=s_0), то (Delta t=t(s_<0>+Delta s)-t(s_<0>)rightarrow 0) при (Delta srightarrow 0). Разделив обе части равенства eqref на (Delta sneq 0), получим
$$
frac<Delta r><Delta s>=r'(t_0)frac<Delta t><Delta s>+alpha(Delta t)frac<Delta t><Delta s>.label
$$
Правая часть eqref имеет при (Delta srightarrow 0) предел, равный (r'(t_0)t'(s_0)), так как (Delta trightarrow 0) при (Delta srightarrow 0) и (alpha(Delta t)rightarrow 0) при (Delta trightarrow 0). Следовательно, существует предел в левом части eqref, и справедливо равенство eqref. Формулу eqref запишем кратко в виде равенства
$$
r_’=r_’t_’,label
$$
выражающего правило дифференцирования вектор-функции при замене переменного. (bullet)

Теорема Лагранжа и локальная формула Тейлора для вектор-функции.

Формула Лагранжа, то есть формула
$$
r(beta)-r(alpha)=r'(xi)(beta-alpha),quad xiin(alpha,beta),label
$$
для вектор-функции, вообще говоря, неверна.

(circ) В самом деле, пусть формула eqref верна, и пусть (r(t)=(cos t,sin t)), тогда (r'(t)=(-sin t,cos t), |r'(t)|=1). Полагая (alpha=0,beta=2pi), получим из равенства eqref (0=r(2pi)-r(0)=r'(xi)2pi), что невозможно, так как (|r'(xi)|=1). (bullet)

Если вектор-функция (r(t)) непрерывна на отрезке ([alpha,beta]) и дифференцируема на интервале ((alpha,beta)), то
$$
existsxiin(alpha,beta): |r(beta)-r(alpha)|leq|r'(xi)|(beta-alpha).label
$$

(circ) Рассмотрим скалярную функцию
$$
varphi(t)=(r(beta)-r(alpha),r(t)).nonumber
$$
эта функция непрерывна на отрезке ([alpha,beta]), так как вектор-функция (r(t)) непрерывна на этом отрезке. Кроме этого, функция (varphi(t)) дифференцируема на интервале ((alpha,beta)), так как функция (r(t)) дифференцируема этом интервале, причем в силу правила дифференцирования скалярного произведения
$$
varphi'(t)=(r(beta)-r(alpha),r'(t)).nonumber
$$
По теореме Лагранжа
$$
existsxiin(alpha,beta): varphi(beta)-varphi(alpha)=varphi'(xi)(beta-alpha)label
$$
Преобразуем левую часть неравенства eqref:
$$
begin
varphi(beta)-varphi(alpha)=(r(beta)-r(alpha),r(beta))-(r(beta)-r(alpha),r(alpha))=\
=(r(beta)-r(alpha),r(beta)-r(alpha))=|r(beta)-r(alpha)|^2
endnonumber
$$
Тогда равенство eqref примет вид
$$
|r(beta)-r(alpha)|^<2>=(r(beta)-r(alpha),r'(xi))(beta-alpha).label
$$
Если (r(beta)=r(alpha)), то неравенство eqref справедливо при любом (xiin in(alpha,beta)). Если (r(beta)neq r(alpha)), то (|r(beta)-r(alpha)| > 0). Тогда, используя неравенство (|(a,b)|leq|a|cdot|b|), из формулы eqref получим
$$
|r(beta)-r(alpha)|^<2>leq|r(beta)-r(alpha)|cdot |r'(xi)|(beta-alpha),nonumber
$$
откуда, разделив обе части неравенства на (|r(beta)-r(alpha)| > 0), получим неравенство eqref. (bullet)

Для вектор-функции (r(t)) справедлива локальная формула Тейлора
$$
r(t)=sum_^frac(t_<0>)>(t-t_<0>)^+varepsilon(t-t_<0>),label
$$
где (varepsilon(t-t_0)=o((t-t_<0>)^)) — вектор-функция такая, что (varepsilon(t-t_0)=(t-t_<0>)^varepsilon_<1>(t-t_<0>)), где (varepsilon_<1>(t-t_<0>)rightarrow 0) при (trightarrow t_<0>).Эта формула справедлива в предположении, что существует (r^<(n)>(t_0)). Для доказательства формулы eqref достаточно воспользоваться локальной формулой Тейлора для компонент вектор-функции (r(t)).

[spoiler title=”источники:”]

http://univerlib.com/mathematical_analysis/derivative/vector_functions/

[/spoiler]

Векторная функция скалярного аргумента

и
её дифференцирование.

Одним из наиболее
простых способов задания пространственной
кривой является задание векторного
уравнения:

1. ,

где
– радиус-вектор точки кривой, а– параметр, определяющий положение
точки.

Т.о.
переменный вектор
есть функция скаляра.
Такие функции в математическом анализе
называют векторными функциями скалярного
аргумента.

Разлагая
по ортам, уравнению (1) можно придать
вид:

1. 

Это разложение даёт
возможность перейти к параметрическому
уравнению кривой:

1. 

Другими
словами, задание векторной функции
равносильно заданию трёх скалярных.

По
отношению к векторной функции (1),
определяющему данную кривую, сама кривая
называется годографом этой функции.
Начало координат называют в этом случае
полюсом годографа.

Пусть
теперь
и– точки кривой, определяемой уравнением
(1). Причём,
аРадиус-векторы этих точек будут

и
.

Вектор
называют приращением векторной функции,
соответствующее приращениюеё аргумента, и обозначают через,

.

Векторная
функция
будет непрерывной функцией,
если

.

Для
нахождения производной от
поступим следующим образом –

.

Установим
теперь направление
.
Очевидно, чтоколлинеарен си принаправлен в ту же сторону, что иа при– в противоположную сторону. Но в первом
случаеа во второмТ.о. векторвсегда направлен по секущей годографав сторону возрастания.

Если
воспользоваться разложением
ипо ортам, то

(*) где

Отсюда
деля (*) на
и переходя к пределудляполучим

1. 

Опираясь на
(4), можно показать, что справедливы
следующие формулы:

(5)

(6) – скалярная функция.

1. 

2. 

Доказательство
(7).

Ч.Т.Д.

Исследуем
теперь некоторые свойства
.
Прежде всего найдём его модуль:

.

Далее

Т.к.
мы считаем дугу годографа спрямляемой,
то тогда
– есть длина хорды, а– длина дуги. Поэтому

Т.о. модуль производной
от векторной функции скалярного аргумента
равен производной от дуги годографа по
тому же аргументу.

Следствие
1. Если
– единичный вектор, направленный по
касательной к годографу в сторону
увеличения,
то

Следствие
2. Если за аргумент векторной функции
принята длина дуги годографа
,
то

(т.к.
)

Т.о. производная от
векторной функции по длине дуги годографа
равна единичному вектору касательной
к годографу, направленному в сторону
увеличения длины дуги.

Следствие
3. Если годограф векторной функции
рассматривать как траекторию движения
точки, а
– как время движения, отсчитываемое от
некоторого,
топо величине и направлению совпадает с
вектором скорости движения.

В
самом деле, скалярная величина скорости
равна производной от пути по времени:

Кроме
того, вектор
направлен по касательной к траектории
в сторону движения, что соответствует
направлению возрастания,
т.е. соответствует направлению.

Т.о.
.

Рассмотрим
теперь
,
длина которого постоянна,,
т.е.

(*) где

Дифференцируя
(*), найдём:

,
т.е.

В
частности, производный вектор от любого
переменного по направлению единичного
всегда.

Пусть
теперь
угол между радиусами единичной сферы,
проведёнными в точкиигодографа.
Тогда длина хордыиз треугольникабудет равна

Модуль производной
от единичного переменного вектора равен
угловой скорости вращения этого вектора.

Как
и для скалярных функций, дифференциал
векторной функции записывается в виде

Но
и тогда

Кривизна
пространственной кривой.

Сопровождающий
трёхгранник.

Согласно
следствию 2, для
можно записать формулу:

Изменение
направления
,
связанное с изменением касательной к
пространственной кривой, характеризует
кривизну кривой. За меру кривизны
пространственной кривой, как и для
плоской, принимают предел отношения
угла смежности к длине дуги, когда

кривизна,
угол
смежности,длина
дуги.

С
другой стороны,
единичный
вектор и производный к нему векторперпендикулярен к нему, а его модульДифференцируяпои
вводяединичный
вектор с направлением,
найдём:

Вектор
вектор
кривизны пространственной кривой. Его
направление, перпендикулярное к
направлению касательной, является
направлением нормали пространственной
кривой. Но пространственная кривая
имеет в любой точке бесчисленное
множество нормалей, которые все лежат
в плоскости,
проходящей
через данную точку кривой и перпендикулярно
к касательной в данной точке. Эту
плоскость называют нормальной плоскостью
пространственной кривой.

Определение.
Нормаль кривой, по которой направлен
вектор кривизны кривой в данной точке
– главная нормаль пространственной
кривой. Т.о.
единичный
вектор главной нормали.

Построим
теперь третий единичный вектор
равный векторному произведениюи

Вектор
,
как итакже перпендикулярент.е. лежит в нормальной плоскости. Его
направление называют направлением
бинормали пространственной кривой в
данной точке. Вектораисоставляют тройку взаимно перпендикулярных
единичных векторов, направление которых
зависит от положения точки на
пространственной кривой и изменяется
от точки к точке. Эти вектора образуют
т.н. сопровождающий трехгранник
(трехгранник Френе) пространственной
кривой. Вектораиобразуют правую тройку, так же как и
единичные ортыв правой системе координат.

Взятые
попарно
определяют три плоскости, проходящие
через одну и ту же точку на кривой и
образуют грани сопровождающего
трехгранника. При этомиопределяют соприкасающую плоскость
(б.м. дуга кривой в окрестности данной
точки есть дуга плоской кривой в
соприкасаемой плоскости с точностью
до б.м. высшего порядка);

и– спрямляющая плоскость;

и– нормальная плоскость.

Уравнения
касательной, нормали и бинормали.

Уравнения
плоскостей сопровождающего трехгранника.

Зная
и,
или любые коллинеарные им неединичные
вектораT,
N и B
выведем уравнения, поименованные в этом
параграфе.

Для
этого в каноническом уравнении прямой

и
в уравнении плоскости, проходящей через
данную точку

принять
за
координаты
выбранной на кривой точки, заили соответственно запринять координаты того из векторовили,
который определяет направление искомой
прямой или нормали к искомой плоскости:

или– для касательной или нормальной
плоскости,

или– для главной нормали и спрямляющей
плоскости,

или– для бинормали и соприкасающейся
плоскости.

Если
кривая задана векторным уравнением
илито за векторнаправленный
по касательной можно принять

1. 

Для
нахождения
инайдём сначала разложениепо векторамРанее (следствие 1) мы нашли, чтоДифференцируя по,
получим:

Но,
т.к.

Перемножим
теперь векторно
и

(*)

На
основании (*) за вектор
,
имеющий направление бинормали, можнл
взять вектор

Но
тогда, за
можно принять векторное произведение
этих последних:

Т.о. в любой точке
произвольной кривой мы можем определить
все элементы сопроводдающего трехгранника.

Пример.
Уравнение касательной, нормали и
бинормали к правой винтовой линии в
любой точке.

Касательная

Главнвя
нормаль

Бинормаль

Соседние файлы в папке Мат_Анализ

• #
• #
• #
• #
• #

Годографом вектора являющегося функцией скаляра называется геометрическое место точек, которое онисывает конец этого вектора при изменении скаляра когда начало вектора помещено в фиксированную точку О пространства (рис. 80).

Рис. 79.

Рис. 80.

Годографом радиуса-вектора движущейся точки будет сама траектория этой точки. Годографом же скорости будет некоторая новая линия (рис. 81).

Пример. Построим годограф вектора Это построение можно вести по точкам, составляя таблицу

(см. скан)

Но можно поступить и так: обозначив проекции вектора на коордипатные оси через мы получим

Исключив из этих трех уравнений параметр мы получим уравнения двух параболических цилиндров:

Эти цилиндры и пересекаются по нашему годографу (рис. 82).

Рис. 81.

Рис. 82.

Рис. 83.