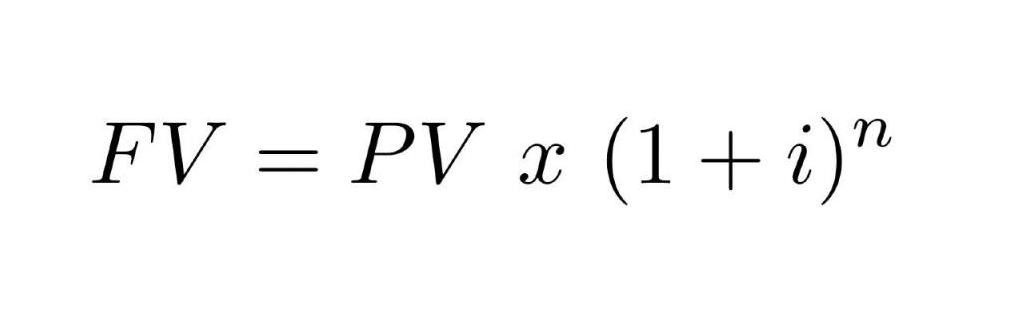Это слайд-шоу требует JavaScript.
ФОРМУЛА ПРОСТЫХ ПРОЦЕНТОВ
Формула простых процентов для срока, который не кратен году, т.е. не составляет целое число лет, выглядит следующим образом:
S=P(1+t/K*i), где
S — сумма в конце срока
P — первоначальная сумма
i — годовая процентная ставка
t — число дней кредита
K — число дней в году, или временная база начисления процентов
При вычислении показателя по формуле простых процентов подразумевается, что процент, в отличие от расчетов по формуле сложных процентов, начисляется только на первоначальную сумму долга независимо от срока пользования заемными средствами. Например, если в кредит была получена сумма в размере 1 000 000 рублей на срок 5 лет под 20% годовых, то в первый год и последующие годы, ежегодные выплаты по кредиту составят 200 000 рублей.
Также следует учитывать, что данная формула верна, если в расчетах указана именно годовая процентная ставка.
ВЫЧИСЛЕНИЕ ГОДОВОЙ ПРОЦЕНТНОЙ СТАВКИ
Формула для вычисления годовой процентной ставки по формуле простых процентов
i=(S/P-1)*K/t
Всего можно выделить четыре наиболее часто встречающихся варианта расчета простых процентов в зависимости точности срока кредита и количества дней в году.
1. Точное число в месяцах, точное число дней в году
Например, для периода с 01.01.2012 по 31.06.2012 включительно срок в виде дроби выглядит как 182/366. Всего 182 дня, так как январь (31) +февраль (29) + март (31)+апрель (30)+май (31)+июль (30)=182. В году 366 дней, так как год високосный.
2. Точное число дней в месяцах, число дней в году равно 360
Для периода с 01.01.2012 по 31.06.2012, срок равен 182 дням и записывается дробью как 182/360.
3. 12 месяцев по 30 дней в каждом
Срок в виде дроби для периода с 01.01.2012 по 31.06.2012 будет выглядеть как 180/360, 6 месяцев*30 дней=180.
4. Точное число дней в месяцах, число дней в году принимается за 365
Срок в виде дроби для периода с 01.01.2012 по 31.06.2012 будет выглядеть как 182/365
Практикум
ПРИМЕР РАСЧЕТА ГОДОВОЙ ПРОЦЕНТНОЙ СТАВКИ
Банк выдал клиенту кредит в размере 1 000 000 рублей на период с 01.01.2012 г. по 30.06.2012 г. включительно. В качестве платы за пользование кредитом банк ежемесячно начисляет клиенту по 20 000 рублей. По условию кредита клиент обязался погасить всю сумму в конце срока. Требуется определить годовую процентную ставку по формуле простых процентов, применив четыре метода.
Расчет годовой процентной ставки по формуле простых процентов
Предварительно рассчитаем сумму к погашению, точное и приближенное число дней.
Точное число дней 182.
Приближенное число дней 180.
Сумма к погашению = 6 месяцев * 20 000 рублей + 1 000 000 рублей= 1 120 000 рублей
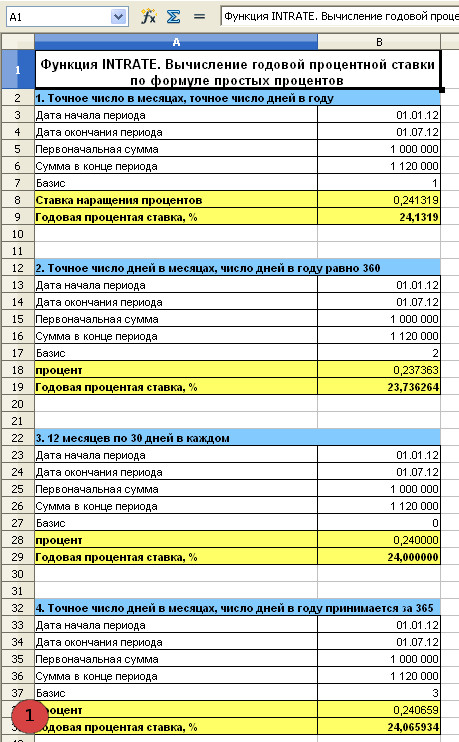
1. Точное число дней в месяцах, точное число дней в году
i=(S/P-1)*K/t=(1 120 000/1 000 000-1)*366/182=0,2413 или 24,13%
2. Точное число дней в месяцах, число дней в году равно 360.
i=(S/P-1)*K/t=(1 120 000/1 000 000-1)*360/182=0,23736 или 23,73%
3. 12 месяцев, по 30 дней в каждом
i=(S/P-1)*K/t=(1 120 000/1 000 000-1)*360/180=0,24 или 24,00%
4. Точное число дней в месяцах, число дней в году принимается за 365
i=(S/P-1)*K/t=(1 120 000/1 000 000-1)*365/182=0,24065 или 24,07%
Анализ динамики процентной ставки
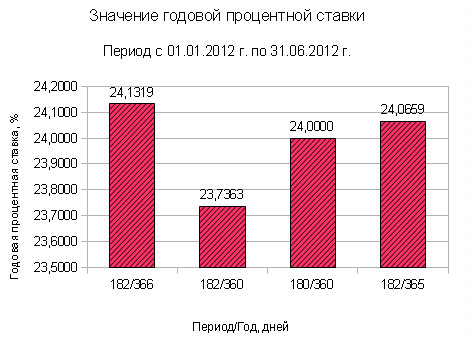
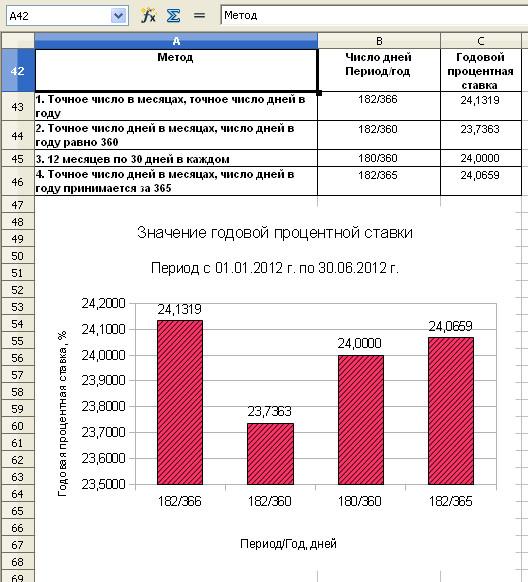
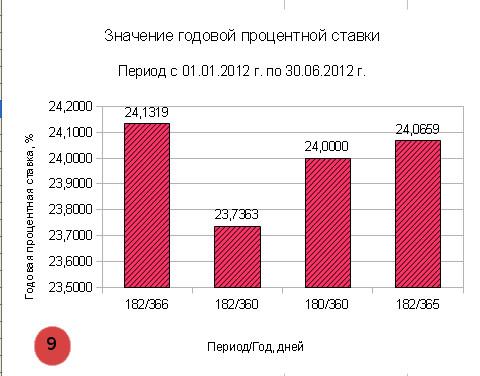
Проанализируем с помощью гистограммы значения годовой процентной ставки в зависимости от выбранного метода расчета.
Годовая процентная ставка за кредит за период с 01.01.2012 г. по 30.06.2012 г. по формуле простых процентов
|
Описание |
Число дней Период/год |
Годовой процент |
| 1. Точное число дней в месяцах, точное число дней в году |
182/366 |
0,2413 или 24,13% |
| 2. Точное число дней в месяцах, число дней в году равно 360 |
182/360 |
0,23736 или 23,73% |
| 3. 12 месяцев по 30 дней в каждом |
180/360 |
0,24 или 24,00% |
| 4. Точное число дней в месяцах, число дней в году принимается за 365 |
182/365 |
0,24065 или 24,07% |
Openoffice Calc. Пример применения функции INTRATE для расчет годовой процентной ставки по формуле простых процентов
В OpenOffice Calc для расчета годовой процентной ставки по формуле простых процентов применяется функция INTRATE.
Синтаксис функции INTRATE
INTRATE(дата начала периода; дата окончания периода; первоначальная сумма; сумма в конце периода; Базис)
| Базис – это метод вычисления года. | ||
|
Базис |
Метод |
Вычисление |
|
0 или отсутствует |
1 |
Американский метод (NASD): 12 месяцев по 30 дней в каждом |
|
1 |
2 |
Точное число дней в месяцах, точное число дней в году |
|
2 |
3 |
Точное число дней в месяцах, число дней в году принимается за 360 |
|
3 |
4 |
Точное число дней в месяцах, число дней в году принимается за 365 |
1. Таблица с расчетами годовой процентной ставки по формуле простых процентов 4-мя методами
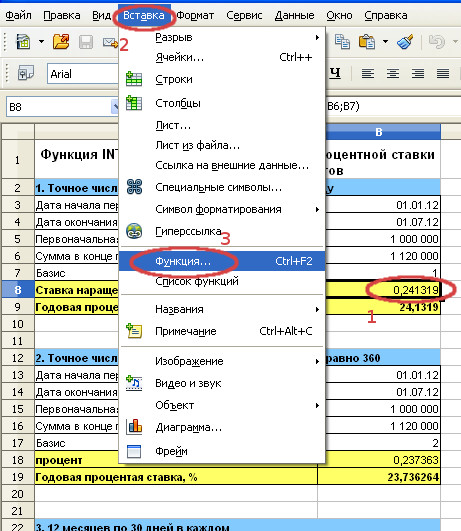
2. Вызов мастера функций
Вызовем Мастер функций, чтобы лучше понять, как применять функцию INTRATE. Для этого выделим ячейку с формулой (для первого примера это B8) и затем последовательно выберем Вставка/Функция…
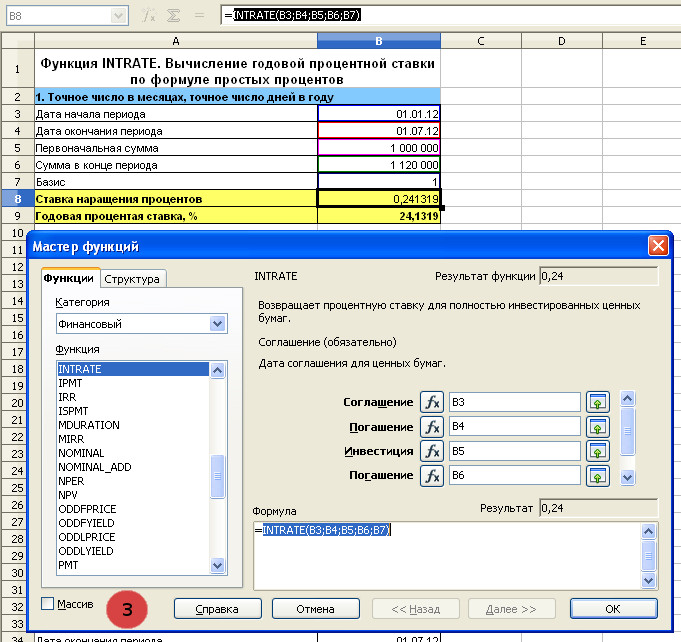
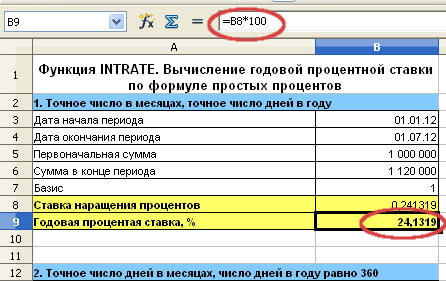
3. Базис 1. Функция INTRATE. Вычисление годовой процентной ставки по формуле простых процентов
Мастер функций с заполненными полями. Формула в ячейке B8. Необходимо нажать ОК, чтобы вернуться к исходной таблице.
Переведём полученный результат в проценты умножив его на 100.
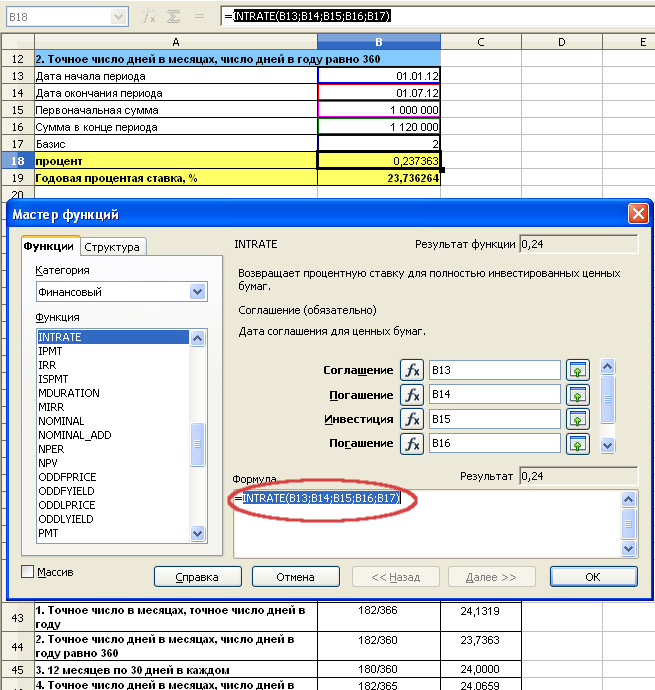
4. Базис 2. Функция INTRATE. Вычисление годовой процентной ставки по формуле простых процентов
Мастер функций с заполненными полями. Формула в ячейке B18. Необходимо нажать ОК, чтобы вернуться к исходной таблице.
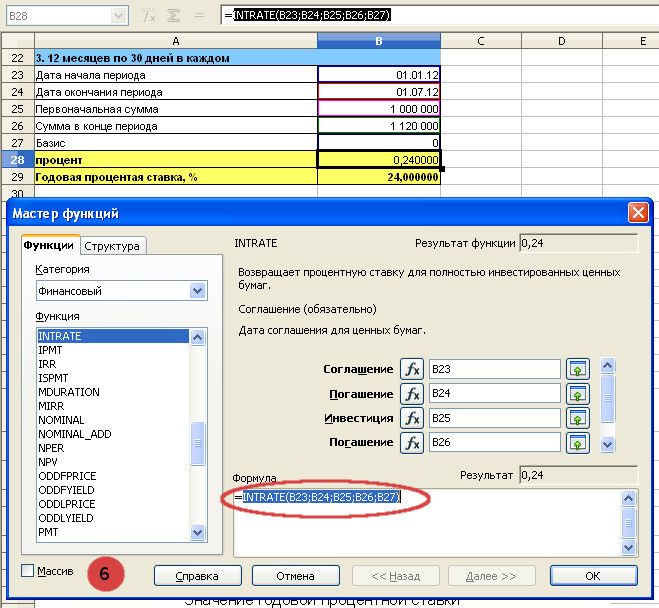
5. Базис 0. Функция INTRATE. Вычисление годовой процентной ставки по формуле простых процентов
Мастер функций с заполненными полями. Формула в ячейке B28. Необходимо нажать ОК, чтобы вернуться к исходной таблице.
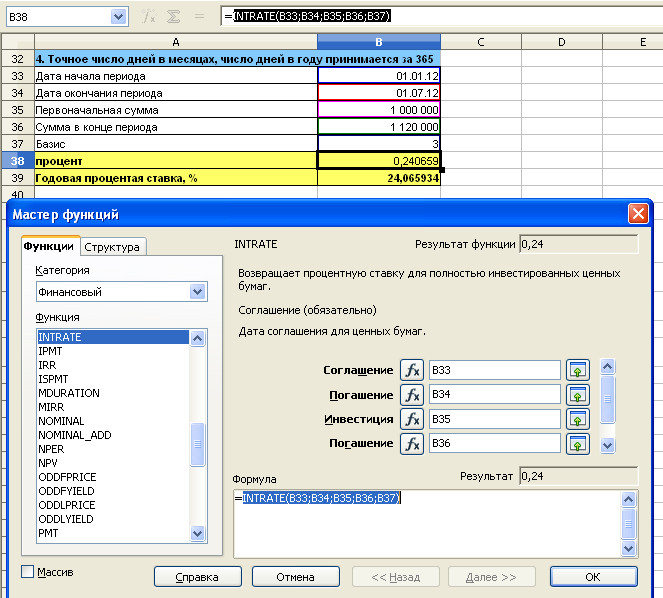
6. Базис 3. Функция INTRATE. Вычисление годовой процентной ставки по формуле простых процентов
Мастер функций с заполненными полями. Формула в ячейке B38. Необходимо нажать ОК, чтобы вернуться к исходной таблице.
7. Гистограмма значений годовых процентных ставок по формуле простого процента рассчитанных 4-мя методами
Расчет годовых процентов: формула, правила расчета и примеры расчетов

- 9 Декабря, 2020
- Бухгалтерия
Расчет годовых процентов производится для выяснения размера вознаграждения как по депозиту, так и по кредиту. Техника подсчета используется в целом во всех сферах финансового сектора.
Если вы решили приумножить свои сбережения, то лучше провести анализ кредитных организаций и выбрать наиболее подходящий вариант. Для этого нужно знать критерий выделения прибыльного предложения. В этом поможет оценка ставки.
Как рассчитать процентную ставку: годовую или месячную
Зачастую на сайтах организаций есть специальный калькулятор, с помощью которого можно узнать доходность вклада. Что же делать, если такой функции на сайте не представлено? Да и в договоре вряд ли будет стоять ссылка на результаты подсчета, сделанные калькулятором. Его можно изменить или вообще убрать. Лучше всего производить вычисления самому.
Расчет процентов по годовой ставке включает в себя формулу простого и сложного процента. Она указывается в документах и может быть фиксированной и плавающей. С последней иметь дело сложнее, так как она трудно прогнозируется. В этом случае базой для плавающей ставки может быть какой-нибудь ключевой параметр, например, ставка рефинансирования ЦБ. При ее изменении с определенным лагом меняется и плавающая ставка. Фиксированная же ставка привносит больше легкости в сравнительный анализ и общее понимание.
Способ расчета простого процента
Простой процент – это процент по вкладу или кредиту, имеющий указанные в договоре периодичность и срок выплат, но без включения начисленных процентов в предыдущем периоде. Расчет годового процента по кредиту аналогичен подсчетам, проводимым по депозиту. На картинке ниже представлена формула, где Р – это тело кредита, а S – начисленные проценты. В обычной практике приравнивают количество дней в году к 365 или 366 (редко к 360), а в месяце к 30 дням.
Исходя из формулы, можно заметить, что сумма простого процента находится в зависимости от процентной ставки и срока вклада. Однако фактор периодичности начисления совершенно не имеет влияния на конечную доходность. Это объясняется тем, что проценты не присоединяются к основной сумме вклада.
В свою очередь, если в условиях договора указано, что проценты выплачиваются с определенной периодичностью, а не по завершении срока, то итоговая доходность равна сумме процентов. Примером служит ежемесячное начисление.
Пример использования простых процентов
Условие задачи № 1
Клиент обратился в банк с просьбой о размещении вклада со сроком на полгода. Для 6 месяцев депозита предусмотрена ставка 8,7 % годовых с ежемесячным начислением. Минимальная сумма для совершения сделки: 30 000 рублей.
Итак, взаимодействуя с банком на предъявленных условиях, получаем:
Сумма процентов = 30 000 х 181 х 8,7 : (100 х 365) = 1294,3 руб. Надо отметить, что расчет годового процента по кредиту выглядел бы совершенно таким же образом.
Но в связи с тем, что в условии сказано о ежемесячной выплате процентов, полученная сумма будет осуществлена шестью платежами. Количество календарных дней влияет на размер этих самых выплат. Допустим клиент обратился в декабре, тогда:
- Проценты за декабрь, январь, март, май = 30 000 х 31 х 8,7 : (100 х 365) = 221,67 руб.
- Проценты за февраль = 30 000 х 28 х 8,76 : (100 х 365) = 200,22 руб.
- Проценты за апрель = 30 000 х 30 х 8,7 : (100 х 365) = 214,52 руб.
В итоге за 6 месяцев сумма депозита или кредита с начисленными процентами составит:
- Сумма с процентами = 30 000 х (1 + 181 х 8,7 : (100 х 365)) = 31 294,274 руб. Или просто 30 000 + 1294,3 = 31 294,3 руб.
Способ расчета сложного процента
Плата за пользование полученными деньгами (в случае кредита) и вознаграждение за передачу собственных средств на хранение (в случае депозита) в основном вычисляются с помощью второго вида доходности. Расчет годовых процентов сложного типа включает в себя процент, учитывающий как начисление на сумму вклада, так и сумму ранее начисленных по вкладу процентов. При этом периодичность и срок договора также входят в условия расчета капитализированного процента. Ниже представлена формула расчета суммы процентов. Годовые значения имеют наращенный характер. Далее представлено на примере, какой из методов начисления процентов является наиболее выгодным для потребителя.
Формула расчета годовых процентов показывает, что вклад или кредит с капитализацией обязательно должен иметь периодичное начисление процентов. Это приводит к тому, что разбитый на периоды срок банковского договора способствует начислению процента за каждый временной промежуток с последующей капитализацией. Месяц выступает в роли наиболее популярного периода причисления процента, доход которого определяется по календарным дням. Поэтому совокупная прибыльность вклада выводится по сумме процентов, начисленных по отдельным периодам.
Пример использования сложных процентов
Далее выведем прибыльность сберегательного вклада с тем же условием, как и в предыдущем примере. Исключение составляет применение метода капитализированного процента.
Задача № 2
Условия депозита:
- Вложение – от 30 000 рублей.
- Депозитный срок – 6 месяцев (декабрь-май).
- Периодичность начисления и выплаты процентов – ежемесячно с капитализацией.
- Ставка по вкладу – 8,7 % годовых.
Алгоритм расчета приведен в таблице ниже.
|
Месяц |
Сумма, рублей |
Количество дней |
Проценты |
Итог по месяцам, рублей |
|
1-й месяц |
30 000 |
31 |
8,7 : (100 х 365) |
221,67 |
|
2-й месяц |
30 000 + 221,67 |
31 |
8,7 : (100 х 365) |
223,31 |
|
3-й месяц |
30 221,67 + 223,31 |
28 |
8,7 : (100 х 365) |
203,19 |
|
4-й месяц |
30 444,98 + 203,19 |
31 |
8,7 : (100 х 365) |
226,46 |
|
5-й месяц |
30 648,17 + 226,46 |
30 |
8,7 : (100 х 365) |
220,77 |
|
6-й месяц |
30 874,63 + 220,77 |
31 |
8,7 : (100 х 365) |
229,77 |
В итоге спустя полгода сумма сложных процентов стала равной 1325,17 руб., итоговая сумма вклада с процентами – 31 325,17 руб. Таким образом, вклад с капитализацией процентов за 6 месяцев принес дополнительный доход в размере 30,87 руб.
Расчет годового процента по займу производился бы тем же путем. В ситуации взятия кредита или обращения в мелкие финансовые организации, такие как МФО, процентные начисления производятся таким же способом. Отличие заключается в формулировке названия. В случае депозита – это доходность, в случае кредита – это комиссии клиента или доходность самого банка.
Основные правила начисления вознаграждения
Финансовые вычисления включают в себя также анализ инвестиционного процесса. Ведь годовые проценты применяются не только для расчета традиционных методов сохранения средств, то есть для сберегательных вкладов, но и для оценки инвестиций на фондовом рынке. Ниже представлены основные принципы расчета, относящиеся ко всем типам приумножения капитала.
Если процент – это денежные поступления в качестве дохода, то простой и сложный процент – это ставки, по которым этот доход начисляется с определенной периодичностью на тело вклада или долга. При рассмотрении двух видов процента можно заметить, как индивид получает большую доходность, если банк используется сложные проценты. Это связано с постоянным реинвестированием накопленного дохода.
Изменение стоимости денег во времени
Как связаны временная денежная стоимость и расчет годовых процентов ? Дело в том, что процесс начисления процентов увеличивает первоначальную сумму свободных финансовых средств. Чтобы выбрать из нескольких вариантов инвестирования, нужно проводить анализ доходностей активов. Особенность заключается в разных периодах поступления дивидендов. Для сравнения их приводят к одному временному периоду. Ниже приведены примеры.
Пример будущей стоимости денег
Задача № 3
Найти будущую стоимость (БС) актива, если планируется вложение 5000 рублей, под 10,5 % годовых на 3 года.
В этой задаче текущей стоимостью (ТС) будет являться 5000 рублей, а БС этих же средств рассчитывается двумя способами. Первый без реинвестирования, а второй с учетом реинвестирования данных средств. Тогда данные расчеты выступают аналогом простых и сложных процентов.
Формула использования сложных процентов выглядит следующим образом:
Где:
- FV (англ. Future Value) – будущая стоимость денег.
- PV (англ. Present Value) – текущая или первоначальная стоимость.
Использование простых процентов выглядит так же, но записанная в скобки ставка процентов не возводится в степень, а умножается непосредственно на количество периодов.
Тогда в задаче, представленной выше, БС с применением простых процентов будет равна:
- FV = 5000 х (1 + 5 х (10,5 : 100)) = 5000 х 1,525 = 7625.
А с применением сложных процентов иначе:
- FV = 5000 х (1 + (10,5 : 100))^5 = 5000 х 1,647 = 8235.
Разница в доходности составит 610 рублей. Отсюда, взаимодействовать с финансовыми организациями, использующими сложные проценты для своих расчетов, намного выгоднее.
Чтобы сравнить денежные притоки по инвестициям, которые осуществляются в разные сроки, нужно привести их к одному моменту времени. Эта процедура называется дисконтированием, если финансовые поступления приводятся к начальному периоду, и наращением, если к будущему моменту времени. Однако в обоих случаях формула расчета процентов не изменяется. Меняется только расположение процентного множителя.
Использование Excel для подсчета
Использование компьютерной программы для произведения расчетов является более выгодной стратегией. Автоматизация вычисления позволяет быстро обработать большое количество материала.
Вбивание формул простых и сложных процентов упрощает процедуру калькуляции. Для этого не нужно каждый раз ее прописывать, достаточно вбить и протянуть формулу по ячейкам, чье количество равно числу периодов. Тем самым облегчается процесс анализа инвестиционных стратегий или выбор банковских предложений.
Рассчитываем проценты по вкладу: формула и примеры
Чтобы выяснить, какой доход принесет вклад, недостаточно знать годовую ставку. На прибыльность также методика начисления банком процентов. В финансовой системе существуют понятия простого и сложного процента, позволяющего получить при почти равных условиях разный доход по вкладам.
Рассчитать проценты по вкладу можно самостоятельно без помощи специалиста. В статье разбираем особенности каждой схемы и объясняем, как работать с формулами.
Простые проценты
Это вознаграждение, которое начисляется на начальную сумму вклада за определенный период. Простые проценты не прибавляются к телу депозита и выплачиваются либо по истечении срока договора, либо раз в месяц или год по выбору вкладчика. Если договор продлевается на новый срок, то прибыль за предыдущий период также не суммируется с вкладом.
Такая методика начисления применяется, как правило, для вкладов с возможностью пополнения и снятия средств. Процентная ставка в этом случае ниже, чем при начислении сложных процентов. Это объясняется тем, что ваш вклад — финансовый инструмент получения прибыли банком. И чем меньше уверенности, что вы не заберете деньги раньше срока, тем ниже вероятность долгосрочного инвестирования капиталов банком, а значит — и ниже доход.
Сложные проценты или капитализация
В этом случае доход за оговоренный срок прибавляется к сумме вклада. В последующий период вознаграждение начисляется уже на увеличенный размер депозита. Сумма вклада постепенно растет за счет накапливаемых процентов, итоговый доход становится выше.
Срок капитализации — периодичность, с которой процент суммируется с текущим телом вклада. Банки добавляют проценты раз в месяц, квартал или день. Вам могут предложить депозит с плавающими ставками, когда процент увеличивается с течением времени. Как правило, процент повышается при увеличении срока хранения денег на депозите при условии, что снятий не было.
Доходность вкладов с капитализацией выше за счет увеличения тела кредита, однако наибольший доход дает тот депозит, по которому ограничено движение средств: запрещены снятия и пополнения, или дополнительные взносы разрешены, но с ограничением. Например, сумма всех пополнений не может превышать сумму открытия более, чем в 10 раз.
Расчет простых процентов
Выяснив годовую ставку, периоды и виды начисления процентов, можно посчитать доход по вкладу.
Простые проценты начисляются по следующей формуле:
где:
S — выплаченные проценты,
P — первоначальная сумма вложений,
I — годовая ставка,
T — количество дней вклада,
K — количество дней в году — 365 или 366.
Если вкладчик открыл депозит на 350 000 руб. сроком на 9 месяцев под 4,7%, процентный доход по вкладу составит:
Расчет сложных процентов
Чаще всего банки предлагают программы с ежемесячной капитализацией. Выбирая условия по вкладу, помните об общей закономерности: чем реже проценты прибавляются к телу депозита, тем меньше доход.
Ежедневная капитализация
Рассчитать доход за каждый день действия вклада поможет следующая формула:
где
Дв — сумма на конец срока, включая сумму открытия и начисленный процент,
Р — первоначальный размер депозита,
N — годовая процентная ставка, разделенная на 100,
К — количество дней в году — 365 или 366,
Т — срок вложения в днях.
Если клиент внес 350 000 руб. под 4,7% на 9 месяцев или 273 дня, в конце срока он получит:
Возвести число в большую степень можно на инженерном калькуляторе, где есть функция x^y, воспользоваться онлайн-сервисами или калькуляторами на сайтах банков.
Зная Дв, легко вычислить сумму процентов по вкладу за весь период:
Ежемесячная капитализация
Когда банк суммирует доход по депозиту раз в месяц, расчет ведется по формуле:
где:
Дв — итоговый доход, то есть размер вклада на конец срока включая сумму открытия и начисленный процент,
P — начальный депозит,
N — годовая ставка, разделенная на 100,
T — срок договора в месяцах.
Рассчитаем итоговую сумму с теми же исходными данными:
Процентный доход составит 12 532,56 ₽
Ежеквартальная капитализация
При начислении вознаграждения каждый квартал, а не раз в месяц, понадобится формула:
в ней Т — количество кварталов в сроке, остальные обозначения прежние.
Рассчитаем тот же вклад в конце срока:
Доход в виде процентов составит 12 483 ₽.
Но следует помнить: чем дольше срок размещения депозита, тем выше ставка. Поэтому при внесении денег на депозит надо сравнить условия с фактической ставкой, применяемой по выбранными вами условиям.
Итоги
Из таблицы видна разница доходов по методу простых и сложных процентов при равных условиях.
| Проценты по вкладу | Доход, руб. |
|---|---|
|
Простые |
12 303 |
|
Сложные: |
|
|
ежедневные |
12 521 |
|
ежемесячные |
12 532 |
|
ежеквартальные |
12 483 |
Однако нельзя однозначно утверждать о предпочтительности сложных процентов для каждого клиента. Оптимальная схема, тип банковского депозита — накопительный счет или вклад — зависят от ваших планов и потребностей:
- желаемый срок действия вклада и вероятность досрочного снятия средств
- необходимость регулярно пополнять счет или снимать средства
- необходимость регулярно снимать проценты
Если закрыт вклад до срока, вне зависимости от того, срочный он или до востребования, банк может применить санкции:
- Пересчитать процент по простой ставке до востребования. Законодательно ее размер не установлен, но большинство банков выплачивают всего 0,1–0,01%.
- Оставить половину или даже треть начальной ставки и тоже сделать перерасчет процентов.
Поэтому перед открытием депозита четко определите его срок и назначение. Райффайзен Банк предлагает банковские вклады без ограничений по снятию и пополнению, где проценты можно получать ежемесячно или добавлять к сумме депозита.
Эта страница полезна?
99
% клиентов считают страницу полезной
Следите за нами в соцсетях и в блоге
Загрузить PDF
Загрузить PDF
Годовая процентная ставка определяет сумму, выплачиваемую получателем кредита за его использование в течение года, или сумму, получаемую инвестором (за год) с инвестиций. Однако многие кредиторы указывают ежемесячную или ежеквартальную, а не ежегодную процентную ставку, потому что ежемесячные ставки не кажутся очень высокими, что в свою очередь привлекает больше заемщиков. Имейте в виду, что реальная годовая процентная ставка зависит от частоты начисления сложных процентов. Если указывается ежемесячная процентная ставка, то сложные проценты могут начисляться как ежемесячно, так и ежегодно. Эта, казалось бы, незначительная разница приводит к большим различиям в конечном значении годовой процентной ставки. Вычислив точное значение годовой процентной ставки, по которой обслуживается кредит или возвращаются инвестиции, вы сможете принять правильное финансовое решение.
-
1
Определите, начисляется ли процентная ставка на ежегодной основе. Это указано в договоре займа или инвестиционных документах. Проценты могут начисляться ежеквартально (4 раза в год), ежемесячно или еженедельно. Если проценты начисляются ежегодно, нужно вычислить простую годовую процентную ставку.
- Например, в рекламе некоторых кредитных карт указывается ежемесячная процентная ставка (1-2%), а в кредитном договоре указывается годовая процентная ставка.[1]
- Например, в рекламе некоторых кредитных карт указывается ежемесячная процентная ставка (1-2%), а в кредитном договоре указывается годовая процентная ставка.[1]
-
2
Определите периодическую процентную ставку. Это сумма, выплачиваемая или получаемая за определенный период времени. Периодическая процентная ставка начисляется на еженедельной, ежемесячной или ежеквартальной основе. Например, если по кредитной карте выплачивается 1% в месяц, периодическая процентная ставка равна 1%.[2]
- Чтобы вычислить годовую процентную ставку, нужно знать периодическую процентную ставку, выраженную в виде десятичной дроби. Для этого разделите указанную периодическую процентную ставку на 100.
- Например: 1% = 1/100 = 0,01.
-
3
Определите число периодов в рассматриваемом году. Это количество периодов, в течение которых осуществляются процентные платежи. Например, если указана месячная процентная ставка, число периодов равно 12; если указана недельная процентная ставка, число периодов равно 52; если указана квартальная процентная ставка, число периодов равно 4.
- Выплата процентов по облигациям осуществляется на полугодовой основе. В этом случае число периодов равно 2.[3]
- Выплата процентов по облигациям осуществляется на полугодовой основе. В этом случае число периодов равно 2.[3]
-
4
Вычислите годовую процентную ставку. Это делается по формуле:
, где n – число периодов за рассматриваемый год, r – периодическая процентная ставка.
- Например, если месячная процентная ставка равна 1% (r = 0,01, n = 12), то годовая процентная ставка равна
(то есть 12%).
- Этот метод используется в том случае, когда сложные проценты начисляется на ежегодной, а не ежеквартальной, ежемесячной, еженедельной (и так далее) основе.
Реклама
- Например, если месячная процентная ставка равна 1% (r = 0,01, n = 12), то годовая процентная ставка равна
-
1
Выясните, как начисляется заявленная процентная ставка в течение года. Имейте в виду, что существует разница, когда проценты начисляются раз в год (то есть платежи осуществляются только один раз в год) и когда проценты начисляются раз в месяц (или с другой периодичностью). Если проценты начисляются на ежегодной основе, используйте метод, описанный в предыдущем разделе; в противном случае вычислите сложную годовую процентную ставку.[4]
-
2
Определите периодическую процентную ставку. Это сумма, выплачиваемая или получаемая за определенный период времени. Например, если по кредиту выплачивается 1% в месяц, периодическая процентная ставка равна 1%. Если в течение года периодическая процентная ставка не меняется, на ее основе можно вычислить годовую процентную ставку.
- Чтобы вычислить годовую процентную ставку, нужно знать периодическую процентную ставку, выраженную в виде десятичной дроби. Для этого разделите указанную периодическую процентную ставку на 100.
- Например: 1% = 1/100 = 0,01.[5]
-
3
Определите число периодов в рассматриваемом году. Это количество периодов (за один год), в течение которых начисляются сложные проценты. Например, если указана месячная процентная ставка, число периодов равно 12 (за один год).[6]
-
4
Подставьте известные значение в формулу. Сложная годовая процентная ставка вычисляется по формуле:
, где n – число периодов за рассматриваемый год, r – периодическая процентная ставка.
- Например, если месячная процентная ставка равна 1% (r = 0,01, n = 12), то сложная годовая процентная ставка равна
.[7]
- Например, если месячная процентная ставка равна 1% (r = 0,01, n = 12), то сложная годовая процентная ставка равна
-
5
Решите уравнение. Не забудьте про определенный порядок выполнения математических операций. Начните с выражения, которое заключено в скобки.
- Сложив (1 + 0,01), уравнение примет следующий вид:
- Вычислите степень. Возьмите научный калькулятор и введите основание степени (в нашем примере число 1,01), затем нажмите клавишу степени (обычно обозначается
), а потом введите показатель степени (в нашем примере число 12) и нажмите клавишу ввода. Теперь уравнение примет вид:
- Число 1,127 было округлено, чтобы упростить процесс вычисления. Но чем больше цифр после десятичной запятой, тем точнее конечный результат.
- Вычтите единицу. Вы получите:
. Преобразуйте это число в проценты, умножив его на 100: 0,127 * 100 = 12,7%.
- Таким образом, если месячная процентная ставка равна 1%, то сложная годовая процентная ставка равна 12,7%.[8]
Реклама
- Сложив (1 + 0,01), уравнение примет следующий вид:
-
1
Определите, когда использовать этот метод. В некоторых случаях, например, в случае инвестиций, доходность сложно посчитать на ежемесячной, ежеквартальной или еженедельной основе. В этом случае доходность вычисляется с начала года до текущей даты в годовом исчислении. Этот метод не применяется для вычисления простой или сложной годовой процентной ставки. Однако полученная доходность может свидетельствовать о рентабельности инвестиций в годовом исчислении; более того, эту доходность можно сравнить с доходностью по другим инвестициям.[9]
-
2
Найдите доходность с начала года до текущей даты. То есть выясните, сколько вы заработали (или потеряли) на инвестициях. Для этого вычтите стоимость инвестиций в начале года из стоимости инвестиций на текущий момент времени.
- Например, если в начале года стоимость инвестиций была равна 20000 рублей, а на текущую дату стоимость инвестиций равна 20800 рублей, то доходность с начала года до текущей даты равна 800 рублей (20800 – 20000).[10]
- Например, если в начале года стоимость инвестиций была равна 20000 рублей, а на текущую дату стоимость инвестиций равна 20800 рублей, то доходность с начала года до текущей даты равна 800 рублей (20800 – 20000).[10]
-
3
Полученное значение преобразуйте в проценты. Для этого найденную доходность разделите на стоимость инвестиций в начале года, а затем результат умножьте на 100.
- В нашем примере: 800 рублей (доходность с начала года до текущей даты) разделите на 20000 (стоимость инвестиций в начале года), и получите 0,04.
- Это число умножьте на 100, чтобы вычислить доходность, выраженную в процентах: 100 * 0,04 = 4%.[11]
-
4
Вычислите временной коэффициент. Он описывает время, прошедшее с начала года, и используется при определении процента доходности в годовом исчислении. Чтобы вычислить временной коэффициент, разделите количество месяцев, прошедшее с начала года, на 12.[12]
- Например, если рассматривается конец августа, то с начала года прошло 8 месяцев.
- В этом примере временной коэффициент равен: 12/8 = 1,5.
-
5
Вычислите доходность в годовом исчислении. Для этого умножьте процент доходности на временной коэффициент. Результат будет характеризовать рентабельность инвестиций в годовом исчислении; также полученную доходность можно сравнить с доходностью за другие периоды времени.[13]
- В нашем примере: 4% (процент доходности) * 1,5 (временной коэффициент) = 6%, то есть процент доходности в годовом исчислении равен 6%.
- Таким образом, если инвестиции в размере 20000 рублей в конце августа принесли 800 рублей дохода, то в годовом исчислении процент доходности будет равен 6%.
Реклама
Советы
- Если указывается годовая процентная ставка, кредит выдается на 365 дней. Если кредит погашается досрочно, то значение годовой процентной ставки уменьшается. Невозможно заранее предугадать точное значение процентной ставки, если неизвестна основная сумма кредита и дата ее выдачи.
Реклама
Об этой статье
Эту страницу просматривали 28 235 раз.
Была ли эта статья полезной?
Содержание
- Способ расчета простого процента
- Пример использования простых процентов
- 1. Простые проценты (срочный вклад)
- Пример 1. Срок 1 год, ставка 8% годовых
- 2. Вклады с капитализацией (управляемые вклады) — расчёт процентов
- 3. Налог на доход от вклада
- 4. Расчёт процентов по вкладу в високосные года
- 5. Онлайн калькулятор по расчёту процентов
- Как рассчитать годовые проценты по кредиту?
- Как самостоятельно рассчитать аннуитетный платеж
- Какие данные нужны для расчета платежа по кредиту
- Воспользуемся банковскими калькуляторами
- Виды ежемесячных выплат по кредитам
- Из чего состоит ежемесячный платеж
- Формула расчета процентов по кредиту
- Погашать долг можно по-разному
- Как составить график платежей
- Сложные проценты или капитализация
- Как различаются вклады
- Как рассчитать доходность вклада с простым начислением процентов?
- Как рассчитать вклад с капитализацией?
Зачастую на сайтах организаций есть специальный калькулятор, с помощью которого можно узнать доходность вклада. Что же делать, если такой функции на сайте не представлено? Да и в договоре вряд ли будет стоять ссылка на результаты подсчета, сделанные калькулятором. Его можно изменить или вообще убрать. Лучше всего производить вычисления самому.
Расчет процентов по годовой ставке включает в себя формулу простого и сложного процента. Она указывается в документах и может быть фиксированной и плавающей. С последней иметь дело сложнее, так как она трудно прогнозируется.
В этом случае базой для плавающей ставки может быть какой-нибудь ключевой параметр, например, ставка рефинансирования ЦБ. При ее изменении с определенным лагом меняется и плавающая ставка. Фиксированная же ставка привносит больше легкости в сравнительный анализ и общее понимание.
Способ расчета простого процента
Простой процент – это процент по вкладу или кредиту, имеющий указанные в договоре периодичность и срок выплат, но без включения начисленных процентов в предыдущем периоде. Расчет годового процента по кредиту аналогичен подсчетам, проводимым по депозиту. На картинке ниже представлена формула, где Р – это тело кредита, а S – начисленные проценты.
В обычной практике приравнивают количество дней в году к 365 или 366 (редко к 360), а в месяце к 30 дням.
Исходя из формулы, можно заметить, что сумма простого процента находится в зависимости от процентной ставки и срока вклада. Однако фактор периодичности начисления совершенно не имеет влияния на конечную доходность. Это объясняется тем, что проценты не присоединяются к основной сумме вклада.
В свою очередь, если в условиях договора указано, что проценты выплачиваются с определенной периодичностью, а не по завершении срока, то итоговая доходность равна сумме процентов. Примером служит ежемесячное начисление.
Пример использования простых процентов
Условие задачи № 1
Клиент обратился в банк с просьбой о размещении вклада со сроком на полгода. Для 6 месяцев депозита предусмотрена ставка 8,7 % годовых с ежемесячным начислением. Минимальная сумма для совершения сделки: 30 000 рублей.
Итак, взаимодействуя с банком на предъявленных условиях, получаем:
Сумма процентов = 30 000 х 181 х 8,7 : (100 х 365) = 1294,3 руб. Надо отметить, что расчет годового процента по кредиту выглядел бы совершенно таким же образом.
Но в связи с тем, что в условии сказано о ежемесячной выплате процентов, полученная сумма будет осуществлена шестью платежами. Количество календарных дней влияет на размер этих самых выплат. Допустим клиент обратился в декабре, тогда:
- Проценты за декабрь, январь, март, май = 30 000 х 31 х 8,7 : (100 х 365) = 221,67 руб.
- Проценты за февраль = 30 000 х 28 х 8,76 : (100 х 365) = 200,22 руб.
- Проценты за апрель = 30 000 х 30 х 8,7 : (100 х 365) = 214,52 руб.
В итоге за 6 месяцев сумма депозита или кредита с начисленными процентами составит:
- Сумма с процентами = 30 000 х (1 + 181 х 8,7 : (100 х 365)) = 31 294,274 руб. Или просто 30 000 + 1294,3 = 31 294,3 руб.
1. Простые проценты (срочный вклад)
Чаще всего банковские вклады относятся к виду «срочных». Данный тип вклада самый популярный среди населения за счёт самого большого процента из всей линейки банковских предложений.
Однако за такую щедрость от банка клиентам необходимо принять следующие условия:
- Отсутствие возможности снять средства частично на весь срок действия договора;
- Без пополнения;
- Проценты начисляются один раз в конце срока (без капитализации);
Пример 1. Срок 1 год, ставка 8% годовых
Вклад имеет ставку 8% годовых, без пополнения и открывается сроком на 1 год. В этом случае проценты по вкладу можно рассчитать на любом калькуляторе, умножив стартовую сумму на коэффициент 0,08 (8%).
Формула расчёта процентов по вкладу на 1 год:
Например, если сумма была 200 тыс. рублей, то прибыль за год составит 16 тыс. рублей, а итоговая сумма будет 216 тыс. рублей.
Естественно, в зависимости от ставки депозита умножать сумму необходимо на различные суммы.
2. Вклады с капитализацией (управляемые вклады) — расчёт процентов
Вклады с капитализацией имеют немного более низкие процентные ставки. Это связано с тем, что проценты начисляемые за месяц перечисляются на тот же счёт и тем самым сумма растёт быстрее. На следующий месяц прибыль будет больше, поскольку сумма на депозите стала больше.
Для таких вкладов есть важное понятие: «эффективная процентная ставка».
Эффективная процентная ставка (ЭПС) — это фактический годовой процент, который будет заработан на вкладе. Он будет больше, чем исходный процент, поскольку расчёт происходит по «сложным процентам».
Такое понятие имеет место только для вкладов с капитализацией.
Например, положили 100 тыс. рублей под 12% годовых с ежемесячной капитализацией. Через один месяц на счёте будет лежать сумма 101 тыс. рублей и уже она будет лежать под 12% годовых.
Через 2 месяца сумма будет уже 102,01 тыс. рублей (вместо 102 тыс. рублей). Поскольку на заработанную 1000 рублей в первый месяц также будут начисляться проценты под 12%.
Для расчёта сложных процентов лучше всего воспользоваться онлайн калькуляторами, поскольку рассчитывать их на листочке будет проблематично. Хотя это не так уж и сложно.
Для нашего примера надо просто умножить 100 на (1,01) 12 . Проще говоря умножить 1,01 сам на себя двенадцать раз. Чтобы упростить себе задачу можно воспользоваться функцией в калькуляторе возведение в произвольную степень: x y .
Пенсионные вклады в среднем дают немного больше, чем обычные.
3. Налог на доход от вклада
С 2021 г. появился налог на доходы от вклада превышающих 1 млн рублей. Также есть два условия, когда есть обязательный налог:
- Если ставка по вкладу выше, чем ключевая на 5 базисных пункта;
- На валютные вклады свыше 9% годовых;
Если выполняется одно из двух условий, то берётся налог только со сверхдохода. Ставка налога составляет 30% для резидентов РФ и 35% для нерезидентов.
Например, если ключевая ставка ЦБ составляет 8%, а банковский депозит 15%, то превышение составляет 2% (8%+5%=13% — максимально возможная ставка без налога). На доход с 2% будет браться налог.
Текущая ключевая ставка ЦБ 7,50% (обновлено 28 октября 2022 года).
4. Расчёт процентов по вкладу в високосные года
В високосный год на 1 рабочий день больше (366). Это накладывает некоторые нюансы на расчёт процентов. Рассмотрим два варианта.
1 Вклад открыт в високосный год и закрывается в этот же год. Тогда никаких сложностей нет. Нужно просто разделить число дней депозита на 366.
2 Если депозит лежит часть года в високосный и часть в невисокосный год. Например, вклад открывается 1 сентября 2016 года на 181 дней. Ставка 8%. Расчёт придется разделить на два этапа:
Необходимо посчитать число дней в високосный год и разделить на 366. Оставшиеся дни будут не в високосный год, поэтому делим на 365.
5. Онлайн калькулятор по расчёту процентов
В интернете можно найти множество сайтов, которые предлагают рассчитать проценты по вкладу. В каждом из них надо задать следующие параметры:
- Сумма (это понятно);
- Процент;
- Сроки;
- Капитализация (если проценты начисляются ежемесячно, то надо ставить галочку);
- Сумма дополнительных взносов;
- ; ; ; ;
После этого калькулятор даст подробную выписку по счёту, что заранее позволит прогнозировать семейный бюджет.
Как рассчитать годовые проценты по кредиту?
Для аннуитетного платежа достаточно умножить сумму всего взятого кредита на процентную ставку. Наглядно это выглядит так:
10000 * 12% = 1200 рублей составит сумма, которую необходимо выплатить за пользование процентами банку.
При дифференцированном платеже сумма годовых процентов рассчитывается немого сложнее, поскольку необходимо помножить остаток по кредиту на процентную ставку и поделить на 12.
То есть, если из наших 10000 выплачено 5000, то: 5000 * 12%/12 = 50 рублей ежемесячно придется отдавать банку за пользование кредитом. При этом, помножив это же число на 12, получим среднюю сумму для оплаты процентов за весь год.
При обращении в банк для получения кредита следует уточнить, какая система кредитования работает в данной организации. Если предлагается сделать выбор самостоятельно, то есть смысл остановиться на дифференцированном платеже. По такому платежу меньше переплата, да и само осознание того, что платить приходится за свои деньги, является немаловажным фактором при выборе способа кредитования.
Ипотечные кредиты также выгодно выплачивать дифференцированно, так как при растущей стоимости недвижимости невыгодно выплачивать кредит с переплатой значительной суммы средств.
Самым оптимальным решением при выборе выплаты по кредиту будет попросить банковского служащего распечатать примерные графики и суммы платежей по обоим кредитам и сравнить, какой из них наиболее выгодный.
Также полезно будет узнать, какой вид платежа предлагается по умолчанию в каком-либо банке.
Как самостоятельно рассчитать аннуитетный платеж
Для самостоятельного расчета понадобится срок кредита, сумма и процентная ставка.
Стандартная формула расчета аннуитетного платежа выглядит так:
Иногда формула может отличаться. Например, если банк предлагает направлять первые платежи только на погашение процентов. Но чаще всего считают по стандартной формуле.
А вот как рассчитывается коэффициент аннуитета:
Для примера возьмем 300 000 рублей, срок 18 месяцев и процентную ставку 15% годовых.
Месячная процентная ставка = 15% / 12 = 1,25%, то есть 0,0125.
Количество платежей равно количеству месяцев — 18.
Подставляем данные в формулу и считаем коэффициент аннуитета:
0,0125 × (1 + 0,0125) 18 / ((1 + 0,0125) 18 − 1) = 0,062385
Теперь подставляем коэффициент аннуитета в расчет платежа: 300 000 × 0,062385 = 18 715,44 Р — в точности как в кредитном калькуляторе.
Какие данные нужны для расчета платежа по кредиту
Ежемесячный платеж – важная характеристика для многих. Хочется найти золотую середину – платить посильный взнос с наименьшей переплатой.
Рассчитать его можно самостоятельно или через специальные сервисы. Для этого вам понадобятся:
- ставка,
- размер желаемого займа,
- срок, на который вы хотите занять деньги.
Воспользуемся банковскими калькуляторами
Банки побеспокоились о том, чтобы клиенты не морочили себе голову арифметикой, а сразу получали искомые параметры.
Составлено множество программ, которые названы «калькуляторами». Им стоит только задать основные величины, как они тут же произведут расчёт и покажут всё, что интересует заказчика, вплоть до помесячного графика платежей и суммы переплаты за кредит.
Виды ежемесячных выплат по кредитам
Ежемесячные платежи по кредитам, которые списывают в банках, бывают двух видов: аннуитетные и дифференцированные.
Аннуитетные — с должника на протяжении всего периода пользовании кредитом списывают равные суммы. По очередности списания приоритет у начисленных процентов. Проценты к оплате пересчитываются ежемесячно исходя из неоплаченной на текущий момент суммы долга.
Остальная сумма, которая остается после удержания процентов, идет на погашения основной задолженности.
В будущем периоде сумма основного долга становится меньше, и на него насчитывается меньше процентов. Значит, из очередного равного платежа сумма распределится по-другому: меньше уйдет на проценты и больше на основной долг. Чем длиннее срок кредитования, тем большая получается итоговая переплата, хотя сумма ежемесячного платежа будет одинаковой для заемщика с начала и до конца периода кредитования.
Дифференцированные выплаты в отличие от аннуитетных не равные. Вначале кредитования суммы выше, а затем они уменьшаются. Снижение ежемесячного платежа происходит постоянно. Пересчет процентов такой же, как и при аннуитетных выплатах. Но итоговая сумма процентов, уплаченных кредитору, получается меньше.
Банки самостоятельно решают, какой тип ежемесячного платежа установлен по кредиту. Хотя некоторые компании предоставляют заемщику право выбора. Но если выбора нет, то клиент может закрыть кредит досрочно, когда для этого появятся деньги. В этом случае, понадобится заранее уведомить банк о своем желании, чтобы задолженность была погашена правильно.
Особенно важно это сделать при полном досрочном погашении. Если это не отследить, можно столкнуться с неприятностями и испортить свою кредитную историю. Чтобы этого не произошло, после завершения выплат всегда запрашивайте документ, где указано, что ваши обязательства перед кредитором исполнены и долгов нет.
Из чего состоит ежемесячный платеж
Расплачиваться за взятые в долг деньги придется ежемесячно. Этот взнос складывается из основного долга и процентов, взятых в разном соотношении. В каком именно – зависит от типа платежей.
Вы можете заплатить меньше или больше установленной выплаты. Если заплатите меньше, вас накажут за просрочку штрафами и пени. Они могут прибавиться к следующей выплате. А если заплатите больше – поможете себе и снизите размер общей переплаты.
Формула расчета процентов по кредиту
- S = вычисляемые проценты;
- S3 = общая сумма кредита;
- i = процентная ставка по кредиту;
- Kk = кол-во дней по платежам;
- Kr = кол-во дней на календарный год.
Погашать долг можно по-разному
Видов платежей два. Они бывают аннуитетными или дифференцированными, и от того, какой вы изберёте, зависит картина выплат.
С точки зрения банка, ежемесячный платёж распадается на несколько частей. Главными в них является тело долга и проценты, но есть и прочие составляющие.
Банк в первую очередь заботится о выплатах процентов, поскольку это его доход. Поэтому в первых платежах, какой бы вид вы ни выбрали, основная часть отводится именно им. По мере продвижения к концу срока доля процентной части уменьшается, а доля основного долга, соответственно, увеличивается.
Если платёж аннуитетный, то его величина остаётся постоянной на всём протяжении погашения долга.
Дифференцированный платёж имеет переменный размер, но в нём тоже есть постоянная часть: это доля основного долга. Процентная часть плавающая, она от максимума в первом платеже постепенно уменьшается до нуля в последнем, поскольку рассчитывается от величины оставшейся части долга (ОстДолга).
, поскольку в этом случае переплата меньше. Банку, соответственно, интереснее аннуитетные, и в последнее время они решительно преобладают. Делается это, якобы, во благо заёмщика, ведь с постоянным платежом ему удобнее обращаться.
Если срок небольшой и проценты невелики, то и разница некритична. А вот на многолетних ипотеках, да ещё с высокими процентами, расхождение весьма ощутимо.
Как составить график платежей
Самый простой способ — воспользоваться кредитным калькулятором: график платежей составляется автоматически.
Еще мы написали калькулятор в экселе, в котором можно прикинуть график платежей и ежемесячные платежи при обоих способах погашения.
Если вы хотите рассчитать график платежей самостоятельно, давайте разберемся на примере ранее рассчитанного платежа: кредит на 300 000 рублей, 18 месяцев под 15% годовых.
При аннуитетном способе ежемесячный платеж неизменный из месяца в месяц. Как мы посчитали выше, в нашем случае он составит 18 715,44 Р .
В целом график платежей уже понятен, но мы дополнительно можем посчитать, каким будет соотношение основного долга и процентов в каждом месяце.
Сначала считаем проценты:
Остаток долга × Процентная ставка × Количество дней в месяце / Количество дней в году
Если год не високосный, а в месяце 30 дней, получится 3698,63 Р — это сумма процентов, которые мы заплатим в первом месяце. На погашение основного долга пойдет остаток от нашего ежемесячного платежа: 18 715,44 Р − 3698,63 Р = 15 016,81 Р .
Во втором месяце сумма процентов начислится на сумму кредита минус платеж по основному долгу в первом месяце: 300 000 Р − 15 015,81 Р = 284 983,19 Р .
Считаем проценты во втором месяце. Предположим, что во втором месяце 31 день: 284 983,19 × 15% × 31 / 365 = 3630,61 Р .
На погашение основного долга во втором месяце пойдет 15 084,83 Р (18 715,44 − 3630,61).
Таким образом можно посчитать соотношение процентов и основного долга в каждом месяце кредита.
Сложные проценты или капитализация
В этом случае доход за оговоренный срок прибавляется к сумме вклада. В последующий период вознаграждение начисляется уже на увеличенный размер депозита. Сумма вклада постепенно растет за счет накапливаемых процентов, итоговый доход становится выше.
Срок капитализации — периодичность, с которой процент суммируется с текущим телом вклада. Банки добавляют проценты раз в месяц, квартал или день. Вам могут предложить депозит с плавающими ставками, когда процент увеличивается с течением времени.
Как правило, процент повышается при увеличении срока хранения денег на депозите при условии, что снятий не было.
Доходность вкладов с капитализацией выше за счет увеличения тела кредита, однако наибольший доход дает тот депозит, по которому ограничено движение средств: запрещены снятия и пополнения, или дополнительные взносы разрешены, но с ограничением. Например, сумма всех пополнений не может превышать сумму открытия более, чем в 10 раз.
Как различаются вклады
Чтобы точно понимать разницу между депозитами в отношении расчета процентных ставок, напомним некоторые общие понятия:
- Под процентной ставкой по вкладу практически всегда понимается годовая процентная ставка. Даже если средства размещаются на 3 месяца, полгода или 5 лет.
- Расчет процентов может происходить через разные промежутки времени, в зависимости от условий договора. Но отправной точкой все равно будет годовая процентная ставка.
- Вклад может размещаться в банке на определенный срок или бессрочно. Это заранее оговаривается в депозитном договоре и влияет на ставку. Проценты по бессрочным договорам (до востребования и т.п.) обычно ниже.
Суммой, от которой ведется расчет, всегда бывает первоначальная величина вклада. Но к этой расчетной величине могут добавляться или не добавляться:
- уже начисленные проценты;
- позднейшие пополнения вклада.
Условия размещения депозита могут также разрешать или не разрешать снятие части основной суммы или начисленных процентов.
Из перечисленных условий большинство банковских вкладов можно классифицировать таким образом:
- вклады с простым начислением процентов; ;
- вклады с фиксированной суммой;
- пополняемые вклады.
Каждый из перечисленных типов банковского депозита имеет свои особенности расчета процентов. Другие условия банковского депозита на расчет процентов также влияют, но обычно в меньшей степени, и не прямо.
Как рассчитать доходность вклада с простым начислением процентов?
Простое начисление процентов – это расчет годовой процентной ставки только от величины первоначально вложенной суммы.
Самый простой и понятный способ. Расчетные периоды здесь могут различаться: можно начислять проценты раз в год или раз в месяц, но итоговая сумма будет одинаковой.
Рассмотрим это на примере размещения в банке 50 тысяч рублей под 8 процентов годовых, без капитализации, пополнения или досрочного снятия:
- При начислении процентов по окончании срока размещения вклада владелец средств получит 54 тысячи рублей.
Однако обычно начисление процентов происходит ежемесячно. Такой способ дает вкладчику больше уверенности, он знает, что его депозит уже вырос.
Расчет процентов происходит из общей ставки, в зависимости от количества дней в каждом месяце. Применительно к выбранной сумме расчет за январь будет таким:
- 50 000 * (0,08 / 365 * 31) = 340 рублей;
общая сумма, принадлежащая вкладчику – 50 тысяч 340 рублей.
Для февраля ситуация будет такой:
- 50 000 * (0,08 / 365 * 28) = 307 рублей;
общая сумма, принадлежащая вкладчику – 50 тысяч 647 рублей.
Расчетная таблица за год будет такой:
Основная сумма вклада, руб.
Начисленные проценты, руб.
Общая сумма вклада, руб.
Видно, что по итогам года вкладчик получит ровно столько, сколько вышло бы при начислении процентов по итогам года. То есть 54 тысячи рублей.
Сейчас большинство банков учитывают интересы вкладчиков и начисляют проценты ежемесячно. При досрочном снятии вклада делается перерасчет исходя из количества дней размещения вклада. Однако так происходит не всегда, условия расчета при разных вариантах снятия лучше уточнять при заключении депозитного договора.
Как рассчитать вклад с капитализацией?
Капитализация – это добавление процентов, начисленных на первоначальную сумму вложения к общей сумме, и дальнейший расчет по той же ставке, но уже от общей суммы.
Выгода капитализации, без точного расчета не очевидна. Рекламные предложения банков обычно делают упор на простые цифры: либо на высокую годовую ставку, либо на сумму приращения капитала. Кстати, последнее – более надежный показатель доходности вложения.
Чтобы выяснить, как работает капитализация, возьмем тот же пример с 50 тысячами рублей и 8%. Снова поместим средства на годовой депозит, но с ежемесячной капитализацией.
Формула расчета процентов по вкладу с капитализацией в первый месяц (январь) останется прежней:
- 50 000 * (0,08 / 365 * 31) = 340 рублей;
общая сумма, принадлежащая вкладчику – 50 тысяч 340 рублей.
Но для февраля исходные данные и результат поменяются:
- 50 340 * (0,08 / 365 * 28) = 318 рублей;
общая сумма, принадлежащая вкладчику – 50 тысяч 657 рублей.
Прибавка в 10 рублей покажется небольшой, однако в следующие периоды сумма будет расти:
Основная сумма вклада, руб.
Начисленные проценты, руб.
Общая сумма вклада, руб.
Разница между вариантами с капитализацией и без нее по итогам года составит 261 рубль. Это чуть более половины процента от общей суммы, как если бы вложение было сделано не под 8% годовых, а по ставке в 8,522%. Если рассчитать вклад с капитализацией, на тех же условиях, но на 3 года, то разница с простым начислением составит уже 1 тысячу 903 рубля.
И это на 50 тысячах, на 500 результат будет уже 19 тысяч 30 рублей.
«Хорошая прибавка к пенсии» и, что важно, совершенно законная и безопасная.
Эффект подобной капитализации дает возможность пополнения депозита с перерасчетом процентов на новую сумму. Расчет будет подобен приведенному выше, но с применением сумм конкретных пополнений. Еще лучший результат обеспечивает сочетание пополнения вклада и частой капитализации.