Размещённые в настоящем разделе сайта публикации носят исключительно ознакомительный характер, представленная в них информация не является гарантией и/или обещанием эффективности деятельности (доходности вложений) в будущем. Информация в статьях выражает лишь мнение автора (коллектива авторов) по тому или иному вопросу и не может рассматриваться как прямое руководство к действию или как официальная позиция/рекомендация АО «Открытие Брокер». АО «Открытие Брокер» не несёт ответственности за использование информации, содержащейся в публикациях, а также за возможные убытки от любых сделок с активами, совершённых на основании данных, содержащихся в публикациях. 18+
АО «Открытие Брокер» (бренд «Открытие Инвестиции»), лицензия профессионального участника рынка ценных бумаг на осуществление брокерской деятельности № 045-06097-100000, выдана ФКЦБ России 28.06.2002 (без ограничения срока действия).
ООО УК «ОТКРЫТИЕ». Лицензия № 21-000-1-00048 от 11 апреля 2001 г. на осуществление деятельности по управлению инвестиционными фондами, паевыми инвестиционными фондами и негосударственными пенсионными фондами, выданная ФКЦБ России, без ограничения срока действия. Лицензия профессионального участника рынка ценных бумаг №045-07524-001000 от 23 марта 2004 г. на осуществление деятельности по управлению ценными бумагами, выданная ФКЦБ России, без ограничения срока действия.
Задача 1
Определите,
какой из вариантов кредитования (по уровню доходности по ставке простых
процентов) наиболее выгоден для заемщика:
– сумма
первоначального долга 120000 рублей; срок кредитования 250 дней; наращенная
сумма долга 130000 рублей;
– сумма
первоначального долга 120000 рублей; срок кредитования 180 дней; наращенная
сумма долга 128000 рублей;
– сумма
первоначального долга 120000 рублей; срок кредитования 320 дней; наращенная
сумма долга 136000 рублей;
Задача 2
Клиент взял
в банке кредит на 180 дней по номинальной ставке 16% и в конце срока вернул всю
сумму долга с процентами, что составило 310 тыс. руб. Определить сумму
выданного кредита.
Задача 3
На какой
срок необходимо поместить имеющуюся денежную сумму под простую процентную
ставку 28% годовых, чтобы она увеличилась в 1,5 раза?
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 4
Определите
годовую ставку простых процентов, при которой сумма в 5 тыс. руб. за три
квартала возрастет до 6,5 тыс. руб.
Задача 5
5 июня клиент взял кредит 200 тыс. руб. При
погашении кредита единым платежом клиент заплатил 230 тыс. руб. Определить срок
операции и дату погашения кредита, если в операции использовалась простая
процентная ставка 18% годовых (точные проценты с фактическим сроком операции).
Задача 6
Через 120
дней с момента подписания кредитного договора заемщик должен вернуть банку 750
тыс. руб. Процентная ставка по кредиту равна 18% годовых. Чему равна
первоначальная сумма долга?
Задача 7
Банк
принимает депозиты на 3 месяца по ставке 50% годовых, на 6 месяцев по ставке
70% годовых и на год по ставке 90% годовых. Определить суммы, которые может
получить владелец депозита 4500 руб., выбрать наиболее выгодный вариант
размещения вклада.
Задача 8
Банк
объявил следующие условия выдачи ссуды на один год: за первый квартал ссудный
процент 50%; за второй квартал – 75%; за третий – 100%; за четвертый квартал –
125%. Определить сумму к возврату в банк, если ссуда составляет 200000 руб.
Задача 9
Найдите
простой процент, начисленный за четыре месяца по ставке 1% на сумму 10 тыс.
руб.
Задача 10
Ссуда в
размере 50 тыс. руб. была выдана на полгода при условии начисления на нее
простых процентов по ставке 20%. Определите сумму погашения.
Задача 11
Банк
начисляет 10 тыс. руб. за использование 800 руб. в течение 60 дней. Найдите
простую процентную ставку, если применяются обыкновенные проценты.
Задача 12
Какая
сумма необходима для того, чтобы накопить за пять лет 70 тыс. руб., если на эту
сумму будут начисляться простые проценты по ставке 8%?
Задача 13
За
сколько дней сумма 800 тыс. руб. увеличится до 900 тыс. руб., если на исходную
сумму начисляются обыкновенные простые проценты по ставке 9%?
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 14
Сумма 100
тыс. руб. была получена в долг 20 января с условием начисления на нее точных
простых процентов по ставке 25% и возвращения денег через год в сумме 120 тыс.
руб. Определите дату погашения долга, если год високосный.
Задача 15
В один и
тот же день в банк были вложены сумма 20 000 руб. под 4 % годовых и сумма 18
000 руб. под 5 % годовых. Вычислите, через сколько лет оба дохода будут
одинаковыми.
Задача 16
Ставка процентов банка по вкладам до
востребования, составлявшая в начале года 10% годовых, через полгода была
снижена до 8% годовых, а еще через 3 месяца до 6% годовых. Определите общую сумму, полученную клиентом банка
через год, если им был внесен вклад в размере 10 тыс. руб.
Задача 17
Банк
предлагает разместить вкладчику 700 000 руб. на срочный депозит в трех
вариантах: а) на 1 день под 6% годовых с последующим реинвестированием
ежедневно в течение месяца; б) на 10 дней под 10% годовых с последующим
реинвестированием каждую декаду в течение месяцев; в) на 1 месяц под 18%
годовых. Определить наиболее выгодный вариант вложения денежных средств.
Задача 18
Какая сумма была внесена на счет в
банке, если по истечении 5 лет на счета стало 5200 руб. Начисление процентов
осуществлялось по схеме простых процентов по ставке 10% за каждое полугодие?
Задача 19
Ссуда в
размере 10 тыс. руб. выдается по учетной ставке простых процентов 8% годовых.
Определить срок ссуды в годах, если заемщик хочет получить 9,5 тыс. руб.
Задача 20
Проценты
по ссуде размером 5 тыс. р., выданной на два месяца, составила 125 р. Какова
процентная ставка?
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 21
Кредит для покупки товара на сумму
50 тыс. руб. открыт с 12.02 до 02.10 включительно под 18% годовых. Какую сумму
заплатит должник в конце срока при начислении простых процентов? (временная база – ACT/360)
Задача 22
Найти простой процент для 7000 руб.
за пять месяцев при 3% годовых.
Задача 23
Какой капитал, будучи отдан в рост
под 7,5%, обратится через год вместе с процентными деньгами в 1343 рубля 75
копеек?
Задача 24
Ссуда
800000 руб. выдана на квартал по простой ставке процентов 20% годовых.
Определить наращенную сумму.
Задача 25
Какую сумму необходимо положить в
банк на 9 месяцев, чтобы накопить 900 руб., если он принимает вклады на
условиях 30% годовых?
Задача 26
Определите размер наращенной суммы
за один год, если первоначальная сумма равна 10 тыс. руб., первые полгода
годовая ставка простых процентов равна 18%, а вторые 21%.
Задача 27
Вклад в размере 250 000 руб.
помещен в банк по ставке 15% годовых. Спустя некоторое время получатель снял со
своего вклада 290 000 руб. Необходимо найти срок размещения вклада в
банке.
Задача 28
Через сколько лет сумма вклада
утроится, если банк работает по ставке 18% годовых.
Задача 29
Банк «Российский кредит» принимает
вклады до востребования по простой ставке 40% годовых. Определить сумму
начисленных процентов и сумму долга с начисленными процентами на вклад 2000 руб.,
размещенный на полгода.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 30
Вкладчик положил в банк 3000 руб.,
который выплачивает в год 6% (простых). Какая сумма будет на счету вкладчика
через 170 дней?
Задача 31
В банк было положено 150000 руб.
Сколько процентов (простых) выплачивает банк в год? Если через 2 года 9 месяцев
на счету было 270000 руб.
Задача 32
Найти
сумму начисленных простых процентов I и конечную сумму S, если
вклад P=1107.08 руб. размещен на t=10 месяцев при годовой
ставке i=70.7%.
Задача 33
Сколько
дней t понадобится, чтобы сумма в P=2228.23 рублей
«заработала» I=2.77 рублей, если она инвестируются при ставке i=23.7%
обыкновенного простого процента?
Задача 34
В банк положены на срочный
сберегательный счет 10000 руб. на 2 года по простой ставке 9% годовых с
дальнейшей пролонгацией на последующие 3 года по простой ставке 5% годовых:
а) Найдите наращенную сумму по
истечении 5 лет;
б) Найдите наращенную сумму по
истечении 5 лет, если через 2 года вклад изымается и кладется на новый счет на
3 года по простой ставке 5% годовых.
Укажите, какой вариант является
более предпочтительным а) или б)
Задача 35
Вами открыт вклад под 21% годовых.
На него начислен процентный платеж в сумме 21 тыс. руб. Найдите величину
вклада, если он был открыт на 21 год.
Задача 36
Ссуда в размере 30 000 руб. выдана
на полгода по простой ставке 100% годовых. Определить наращенную сумму.
Задача 37
Определите годовую ставку простых
процентов, при которой сумма в 5 тыс. руб. за три квартала возрастет до 6,5
тыс. руб.
Задача 38
В банк помещен капитал под 20%
годовых (обыкновенные проценты). По истечении 270 дней его величина составила
575 тыс. руб. Определить величину помещенного в банк капитала и сумму
начисленных процентов.
Задача 39
Банк
принимает депозиты на 3 месяца по ставке 15% годовых, на 8 месяцев по ставке
17% годовых и на год по ставке 19% годовых. Определить суммы, которые может
получить владелец депозита 14500 руб. Выбрать наиболее выгодный вариант
размещения вклада.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 40
Определить
срок в годах, при начислении простых процентов, по следующим данным:
Процентная
ставка 18%
Вклад –
2000 руб.
Вклад с
процентами – 10200 руб.
Задача 41
По
контракту кредитор предоставил в долг 60000 руб. Заемщик должен уплатить 70000
руб. через 90 дней. Определить доходность финансовой операции для кредитора в
виде процентной ставки i простых процентов.
Задача 42
Годовая ставка простых процентов в
банке составляет 12%. Через сколько лет вложенная сумма а) удвоится; б)
утроится?
Задача 43
В банк
положено 10000 руб., а через 2,5 года на счете было 120000 руб. Определить
ставку процентов банка.
Задача 44
За
сколько лет удвоится сумма долга, если применяется простая годовая ставка 17%?
Задача 45
При
открытии сберегательного счета при ставке 8% годовых 20 апреля на счет была
положена сумма 1 млн. рублей. Затем 5 июля этого же года было добавлено 500
тыс. руб. 10 сентября сняли сумму 750 тыс. рублей, а 20 ноября того же года
счет был закрыт.
Какую
сумму получил вкладчик при закрытии счета?
Задача 46
Какую
сумму надо положить в банк, выплачивающий 4% простых в год, чтобы получить 50
тыс. руб. а) через 4 месяца, б) через 1 год, в) через 2 года 9 месяцев?
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 47
Договор
предусматривает следующие ставки простых процентов: за первый квартал j1=20%, за второй квартал j2=18%, за третий квартал j3=16%, за четвертый квартал j4=14%. Определить
коэффициент наращения за год.
Задача 48
Определите
годовую ставку простых процентов, при которой сумма в 5 тыс. руб. за три
квартала возрастет до 6,5 тыс. руб.
Задача 49
На какой
срок необходимо поместить имеющуюся денежную сумму под простую процентную
ставку 28% годовых, чтобы она увеличилась в 1,5 раза?
Виды процентов по вкладам
Если вы приносите деньги в банк на хранение, а он ими пользуется, то вы получаете за это вознаграждение — определённый процент. Банковские проценты бывают двух видов: простые и сложные (их ещё называют капитализацией).
Простые проценты
Использовать формулу простых процентов целесообразно, если проценты вам начисляют в конце срока вклада или если они переводятся на отдельный счёт. Например, вы положили на счёт 10 000 рублей под 7% годовых, через год такой вклад принесёт вам 700 рублей прибыли.
Простые проценты не прибавляются к депозиту и выплачиваются либо по истечении срока договора, либо раз в месяц или год по выбору вкладчика. Если договор продлевается на новый срок, то прибыль за предыдущий период также не суммируется с вкладом.
Сложные проценты (капитализация)
Здесь всё намного интереснее — сложные проценты начисляются на первоначальную сумму депозита и на проценты от предыдущих периодов.
Сложные проценты — это проценты, рассчитанные как на сумму вложенных денег, так и на «набежавшую» по ним сумму. Другими словами — это проценты, которые вкладчик зарабатывает на процентах. Сумма вклада постепенно растёт за счёт накапливаемых процентов. В результате и итоговый доход становится выше.
10 000 рублей из предыдущего примера через год превращаются в 10 700, и проценты в следующем периоде будут начислять именно на эту сумму. И так будет каждый раз, пока не закроете вклад. Получается, что база, на которую начисляется процент, с каждым таким пополнением растёт. Соответственно, и ваш доход с каждым разом будет увеличиваться. Этот процесс называют капитализацией по вкладу.
Периодичность капитализации бывает нескольких видов: ежемесячная, ежегодная, реже встречается ежедневная и ежеквартальная.
Годовые проценты
Годовой процент по вкладам — это ставки, по которым рассчитывают процент вознаграждения вкладчиков за размещение денег в банке. Под словом «ставка» обычно имеют в виду именно годовую процентную ставку. Поэтому если срок вклада отличается от года (например, он составляет шесть месяцев или три года), то и доход нужно высчитывать в соответствии с календарём. Например, вклад на сумму 10 000 под 7%, открытый на год, даст 700 рублей прибыли. А если вы положите те же 10 000 рублей под 7% на полгода, то получите 350 рублей.
Но как узнать, какой вклад окажется более выгодным — простой под высокие проценты или с капитализацией за месяц? Для этого требуется рассчитать проценты по вкладу для каждого предложения и сравнить.
Для дальнейших расчётов мы предположим, что вы открыли депозит на 300 000 под 6,9% годовых на один год. Итак, вот как рассчитать процент по вкладу.
Расчёт простых процентов
Тут всё просто: так как проценты за простой вклад начисляются один раз в год, то номинальная ставка будет равна эффективной, то есть 6,9%.
Теперь нужно посчитать доходность от вклада, используя следующую формулу:
(S × G × D / V) / 100, где:
S — сумма вложений,
G — годовая ставка,
D — число дней вклада,
V — число дней в году — 365 или 366.
Подставляем в нашу формулу значения, вот что получается:
(300 000 × 6,9 × 365 / 365) / 100 = 20 700.
Именно столько денег за год удастся заработать на вкладе.
Расчёт сложных процентов
В этом разделе расчётов процентов будет несколько, так как банки предлагают разные периоды начисления.
Ежедневная капитализация по вкладу
Банк начисляет проценты на вклад каждый день. Вот эта формула поможет узнать, сколько насобирает вклад за год:
S × (1 + F / V)D, где
S — первоначальный депозит;
F — годовая ставка, поделённая на 100;
V — количество дней в году — 365 или 366;
D — срок вложения в днях.
Значит, через год после того, как мы откроем вклад с ежедневной капитализацией, мы получим: 300 000 × (1 + 0,069 / 365)365 = 321 428. То есть процентный доход составит 21 428 рублей.
Совет: чтобы возвести число в большую степень, проводите расчёты не на обычном, а на инженерном калькуляторе (тип можно выбрать в настройках как для ПК, так и в приложении на смартфоне).
Ежемесячная капитализация по вкладу
Банк начисляет проценты за месяц и прибавляет их к сумме депозита. Вот как рассчитать процент по вкладу:
S × (1 + F / 12)M, где:
S — депозит;
F — годовая ставка, разделённая на 100;
M — срок договора в месяцах.
Подставляем значения и получаем: 300 000 × (1 + 0,069 / 12)12 = 321 367. Процентный доход будет чуть меньше, чем с ежедневной капитализацией по вкладу, — 21 367 рублей.
Калькулятор доходности вкладов
Если расчёты кажутся вам сложными или вы хотите внести в формулу дополнительные условия, например указать частичное изъятие вклада или пополнение, то советуем воспользоваться специальными онлайн-калькуляторами.
Такие калькуляторы встречаются на сайтах банков, чтобы клиенты смогли сразу оценить выгоду от предложения. Калькуляторы показывают доход, который вы получите в конце срока
Какие вклады облагаются налогом
В марте 2022 года россиян освободили от уплаты налога на доходы от банковских вкладов, полученных в 2021 и 2022 годы. Впервые заплатить налог придётся только в 2024 году. Оплате подлежит только часть, которая превышает лимит, установленный Центробанком.
Содержание
- Способ расчета простого процента
- Пример использования простых процентов
- 1. Простые проценты (срочный вклад)
- Пример 1. Срок 1 год, ставка 8% годовых
- 2. Вклады с капитализацией (управляемые вклады) — расчёт процентов
- 3. Налог на доход от вклада
- 4. Расчёт процентов по вкладу в високосные года
- 5. Онлайн калькулятор по расчёту процентов
- Как рассчитать годовые проценты по кредиту?
- Как самостоятельно рассчитать аннуитетный платеж
- Какие данные нужны для расчета платежа по кредиту
- Воспользуемся банковскими калькуляторами
- Виды ежемесячных выплат по кредитам
- Из чего состоит ежемесячный платеж
- Формула расчета процентов по кредиту
- Погашать долг можно по-разному
- Как составить график платежей
- Сложные проценты или капитализация
- Как различаются вклады
- Как рассчитать доходность вклада с простым начислением процентов?
- Как рассчитать вклад с капитализацией?
Зачастую на сайтах организаций есть специальный калькулятор, с помощью которого можно узнать доходность вклада. Что же делать, если такой функции на сайте не представлено? Да и в договоре вряд ли будет стоять ссылка на результаты подсчета, сделанные калькулятором. Его можно изменить или вообще убрать. Лучше всего производить вычисления самому.
Расчет процентов по годовой ставке включает в себя формулу простого и сложного процента. Она указывается в документах и может быть фиксированной и плавающей. С последней иметь дело сложнее, так как она трудно прогнозируется.
В этом случае базой для плавающей ставки может быть какой-нибудь ключевой параметр, например, ставка рефинансирования ЦБ. При ее изменении с определенным лагом меняется и плавающая ставка. Фиксированная же ставка привносит больше легкости в сравнительный анализ и общее понимание.
Способ расчета простого процента
Простой процент – это процент по вкладу или кредиту, имеющий указанные в договоре периодичность и срок выплат, но без включения начисленных процентов в предыдущем периоде. Расчет годового процента по кредиту аналогичен подсчетам, проводимым по депозиту. На картинке ниже представлена формула, где Р – это тело кредита, а S – начисленные проценты.
В обычной практике приравнивают количество дней в году к 365 или 366 (редко к 360), а в месяце к 30 дням.
Исходя из формулы, можно заметить, что сумма простого процента находится в зависимости от процентной ставки и срока вклада. Однако фактор периодичности начисления совершенно не имеет влияния на конечную доходность. Это объясняется тем, что проценты не присоединяются к основной сумме вклада.
В свою очередь, если в условиях договора указано, что проценты выплачиваются с определенной периодичностью, а не по завершении срока, то итоговая доходность равна сумме процентов. Примером служит ежемесячное начисление.
Пример использования простых процентов
Условие задачи № 1
Клиент обратился в банк с просьбой о размещении вклада со сроком на полгода. Для 6 месяцев депозита предусмотрена ставка 8,7 % годовых с ежемесячным начислением. Минимальная сумма для совершения сделки: 30 000 рублей.
Итак, взаимодействуя с банком на предъявленных условиях, получаем:
Сумма процентов = 30 000 х 181 х 8,7 : (100 х 365) = 1294,3 руб. Надо отметить, что расчет годового процента по кредиту выглядел бы совершенно таким же образом.
Но в связи с тем, что в условии сказано о ежемесячной выплате процентов, полученная сумма будет осуществлена шестью платежами. Количество календарных дней влияет на размер этих самых выплат. Допустим клиент обратился в декабре, тогда:
- Проценты за декабрь, январь, март, май = 30 000 х 31 х 8,7 : (100 х 365) = 221,67 руб.
- Проценты за февраль = 30 000 х 28 х 8,76 : (100 х 365) = 200,22 руб.
- Проценты за апрель = 30 000 х 30 х 8,7 : (100 х 365) = 214,52 руб.
В итоге за 6 месяцев сумма депозита или кредита с начисленными процентами составит:
- Сумма с процентами = 30 000 х (1 + 181 х 8,7 : (100 х 365)) = 31 294,274 руб. Или просто 30 000 + 1294,3 = 31 294,3 руб.
1. Простые проценты (срочный вклад)
Чаще всего банковские вклады относятся к виду «срочных». Данный тип вклада самый популярный среди населения за счёт самого большого процента из всей линейки банковских предложений.
Однако за такую щедрость от банка клиентам необходимо принять следующие условия:
- Отсутствие возможности снять средства частично на весь срок действия договора;
- Без пополнения;
- Проценты начисляются один раз в конце срока (без капитализации);
Пример 1. Срок 1 год, ставка 8% годовых
Вклад имеет ставку 8% годовых, без пополнения и открывается сроком на 1 год. В этом случае проценты по вкладу можно рассчитать на любом калькуляторе, умножив стартовую сумму на коэффициент 0,08 (8%).
Формула расчёта процентов по вкладу на 1 год:
Например, если сумма была 200 тыс. рублей, то прибыль за год составит 16 тыс. рублей, а итоговая сумма будет 216 тыс. рублей.
Естественно, в зависимости от ставки депозита умножать сумму необходимо на различные суммы.
2. Вклады с капитализацией (управляемые вклады) — расчёт процентов
Вклады с капитализацией имеют немного более низкие процентные ставки. Это связано с тем, что проценты начисляемые за месяц перечисляются на тот же счёт и тем самым сумма растёт быстрее. На следующий месяц прибыль будет больше, поскольку сумма на депозите стала больше.
Для таких вкладов есть важное понятие: «эффективная процентная ставка».
Эффективная процентная ставка (ЭПС) — это фактический годовой процент, который будет заработан на вкладе. Он будет больше, чем исходный процент, поскольку расчёт происходит по «сложным процентам».
Такое понятие имеет место только для вкладов с капитализацией.
Например, положили 100 тыс. рублей под 12% годовых с ежемесячной капитализацией. Через один месяц на счёте будет лежать сумма 101 тыс. рублей и уже она будет лежать под 12% годовых.
Через 2 месяца сумма будет уже 102,01 тыс. рублей (вместо 102 тыс. рублей). Поскольку на заработанную 1000 рублей в первый месяц также будут начисляться проценты под 12%.
Для расчёта сложных процентов лучше всего воспользоваться онлайн калькуляторами, поскольку рассчитывать их на листочке будет проблематично. Хотя это не так уж и сложно.
Для нашего примера надо просто умножить 100 на (1,01) 12 . Проще говоря умножить 1,01 сам на себя двенадцать раз. Чтобы упростить себе задачу можно воспользоваться функцией в калькуляторе возведение в произвольную степень: x y .
Пенсионные вклады в среднем дают немного больше, чем обычные.
3. Налог на доход от вклада
С 2021 г. появился налог на доходы от вклада превышающих 1 млн рублей. Также есть два условия, когда есть обязательный налог:
- Если ставка по вкладу выше, чем ключевая на 5 базисных пункта;
- На валютные вклады свыше 9% годовых;
Если выполняется одно из двух условий, то берётся налог только со сверхдохода. Ставка налога составляет 30% для резидентов РФ и 35% для нерезидентов.
Например, если ключевая ставка ЦБ составляет 8%, а банковский депозит 15%, то превышение составляет 2% (8%+5%=13% — максимально возможная ставка без налога). На доход с 2% будет браться налог.
Текущая ключевая ставка ЦБ 7,50% (обновлено 28 октября 2022 года).
4. Расчёт процентов по вкладу в високосные года
В високосный год на 1 рабочий день больше (366). Это накладывает некоторые нюансы на расчёт процентов. Рассмотрим два варианта.
1 Вклад открыт в високосный год и закрывается в этот же год. Тогда никаких сложностей нет. Нужно просто разделить число дней депозита на 366.
2 Если депозит лежит часть года в високосный и часть в невисокосный год. Например, вклад открывается 1 сентября 2016 года на 181 дней. Ставка 8%. Расчёт придется разделить на два этапа:
Необходимо посчитать число дней в високосный год и разделить на 366. Оставшиеся дни будут не в високосный год, поэтому делим на 365.
5. Онлайн калькулятор по расчёту процентов
В интернете можно найти множество сайтов, которые предлагают рассчитать проценты по вкладу. В каждом из них надо задать следующие параметры:
- Сумма (это понятно);
- Процент;
- Сроки;
- Капитализация (если проценты начисляются ежемесячно, то надо ставить галочку);
- Сумма дополнительных взносов;
- ; ; ; ;
После этого калькулятор даст подробную выписку по счёту, что заранее позволит прогнозировать семейный бюджет.
Как рассчитать годовые проценты по кредиту?
Для аннуитетного платежа достаточно умножить сумму всего взятого кредита на процентную ставку. Наглядно это выглядит так:
10000 * 12% = 1200 рублей составит сумма, которую необходимо выплатить за пользование процентами банку.
При дифференцированном платеже сумма годовых процентов рассчитывается немого сложнее, поскольку необходимо помножить остаток по кредиту на процентную ставку и поделить на 12.
То есть, если из наших 10000 выплачено 5000, то: 5000 * 12%/12 = 50 рублей ежемесячно придется отдавать банку за пользование кредитом. При этом, помножив это же число на 12, получим среднюю сумму для оплаты процентов за весь год.
При обращении в банк для получения кредита следует уточнить, какая система кредитования работает в данной организации. Если предлагается сделать выбор самостоятельно, то есть смысл остановиться на дифференцированном платеже. По такому платежу меньше переплата, да и само осознание того, что платить приходится за свои деньги, является немаловажным фактором при выборе способа кредитования.
Ипотечные кредиты также выгодно выплачивать дифференцированно, так как при растущей стоимости недвижимости невыгодно выплачивать кредит с переплатой значительной суммы средств.
Самым оптимальным решением при выборе выплаты по кредиту будет попросить банковского служащего распечатать примерные графики и суммы платежей по обоим кредитам и сравнить, какой из них наиболее выгодный.
Также полезно будет узнать, какой вид платежа предлагается по умолчанию в каком-либо банке.
Как самостоятельно рассчитать аннуитетный платеж
Для самостоятельного расчета понадобится срок кредита, сумма и процентная ставка.
Стандартная формула расчета аннуитетного платежа выглядит так:
Иногда формула может отличаться. Например, если банк предлагает направлять первые платежи только на погашение процентов. Но чаще всего считают по стандартной формуле.
А вот как рассчитывается коэффициент аннуитета:
Для примера возьмем 300 000 рублей, срок 18 месяцев и процентную ставку 15% годовых.
Месячная процентная ставка = 15% / 12 = 1,25%, то есть 0,0125.
Количество платежей равно количеству месяцев — 18.
Подставляем данные в формулу и считаем коэффициент аннуитета:
0,0125 × (1 + 0,0125) 18 / ((1 + 0,0125) 18 − 1) = 0,062385
Теперь подставляем коэффициент аннуитета в расчет платежа: 300 000 × 0,062385 = 18 715,44 Р — в точности как в кредитном калькуляторе.
Какие данные нужны для расчета платежа по кредиту
Ежемесячный платеж – важная характеристика для многих. Хочется найти золотую середину – платить посильный взнос с наименьшей переплатой.
Рассчитать его можно самостоятельно или через специальные сервисы. Для этого вам понадобятся:
- ставка,
- размер желаемого займа,
- срок, на который вы хотите занять деньги.
Воспользуемся банковскими калькуляторами
Банки побеспокоились о том, чтобы клиенты не морочили себе голову арифметикой, а сразу получали искомые параметры.
Составлено множество программ, которые названы «калькуляторами». Им стоит только задать основные величины, как они тут же произведут расчёт и покажут всё, что интересует заказчика, вплоть до помесячного графика платежей и суммы переплаты за кредит.
Виды ежемесячных выплат по кредитам
Ежемесячные платежи по кредитам, которые списывают в банках, бывают двух видов: аннуитетные и дифференцированные.
Аннуитетные — с должника на протяжении всего периода пользовании кредитом списывают равные суммы. По очередности списания приоритет у начисленных процентов. Проценты к оплате пересчитываются ежемесячно исходя из неоплаченной на текущий момент суммы долга.
Остальная сумма, которая остается после удержания процентов, идет на погашения основной задолженности.
В будущем периоде сумма основного долга становится меньше, и на него насчитывается меньше процентов. Значит, из очередного равного платежа сумма распределится по-другому: меньше уйдет на проценты и больше на основной долг. Чем длиннее срок кредитования, тем большая получается итоговая переплата, хотя сумма ежемесячного платежа будет одинаковой для заемщика с начала и до конца периода кредитования.
Дифференцированные выплаты в отличие от аннуитетных не равные. Вначале кредитования суммы выше, а затем они уменьшаются. Снижение ежемесячного платежа происходит постоянно. Пересчет процентов такой же, как и при аннуитетных выплатах. Но итоговая сумма процентов, уплаченных кредитору, получается меньше.
Банки самостоятельно решают, какой тип ежемесячного платежа установлен по кредиту. Хотя некоторые компании предоставляют заемщику право выбора. Но если выбора нет, то клиент может закрыть кредит досрочно, когда для этого появятся деньги. В этом случае, понадобится заранее уведомить банк о своем желании, чтобы задолженность была погашена правильно.
Особенно важно это сделать при полном досрочном погашении. Если это не отследить, можно столкнуться с неприятностями и испортить свою кредитную историю. Чтобы этого не произошло, после завершения выплат всегда запрашивайте документ, где указано, что ваши обязательства перед кредитором исполнены и долгов нет.
Из чего состоит ежемесячный платеж
Расплачиваться за взятые в долг деньги придется ежемесячно. Этот взнос складывается из основного долга и процентов, взятых в разном соотношении. В каком именно – зависит от типа платежей.
Вы можете заплатить меньше или больше установленной выплаты. Если заплатите меньше, вас накажут за просрочку штрафами и пени. Они могут прибавиться к следующей выплате. А если заплатите больше – поможете себе и снизите размер общей переплаты.
Формула расчета процентов по кредиту
- S = вычисляемые проценты;
- S3 = общая сумма кредита;
- i = процентная ставка по кредиту;
- Kk = кол-во дней по платежам;
- Kr = кол-во дней на календарный год.
Погашать долг можно по-разному
Видов платежей два. Они бывают аннуитетными или дифференцированными, и от того, какой вы изберёте, зависит картина выплат.
С точки зрения банка, ежемесячный платёж распадается на несколько частей. Главными в них является тело долга и проценты, но есть и прочие составляющие.
Банк в первую очередь заботится о выплатах процентов, поскольку это его доход. Поэтому в первых платежах, какой бы вид вы ни выбрали, основная часть отводится именно им. По мере продвижения к концу срока доля процентной части уменьшается, а доля основного долга, соответственно, увеличивается.
Если платёж аннуитетный, то его величина остаётся постоянной на всём протяжении погашения долга.
Дифференцированный платёж имеет переменный размер, но в нём тоже есть постоянная часть: это доля основного долга. Процентная часть плавающая, она от максимума в первом платеже постепенно уменьшается до нуля в последнем, поскольку рассчитывается от величины оставшейся части долга (ОстДолга).
, поскольку в этом случае переплата меньше. Банку, соответственно, интереснее аннуитетные, и в последнее время они решительно преобладают. Делается это, якобы, во благо заёмщика, ведь с постоянным платежом ему удобнее обращаться.
Если срок небольшой и проценты невелики, то и разница некритична. А вот на многолетних ипотеках, да ещё с высокими процентами, расхождение весьма ощутимо.
Как составить график платежей
Самый простой способ — воспользоваться кредитным калькулятором: график платежей составляется автоматически.
Еще мы написали калькулятор в экселе, в котором можно прикинуть график платежей и ежемесячные платежи при обоих способах погашения.
Если вы хотите рассчитать график платежей самостоятельно, давайте разберемся на примере ранее рассчитанного платежа: кредит на 300 000 рублей, 18 месяцев под 15% годовых.
При аннуитетном способе ежемесячный платеж неизменный из месяца в месяц. Как мы посчитали выше, в нашем случае он составит 18 715,44 Р .
В целом график платежей уже понятен, но мы дополнительно можем посчитать, каким будет соотношение основного долга и процентов в каждом месяце.
Сначала считаем проценты:
Остаток долга × Процентная ставка × Количество дней в месяце / Количество дней в году
Если год не високосный, а в месяце 30 дней, получится 3698,63 Р — это сумма процентов, которые мы заплатим в первом месяце. На погашение основного долга пойдет остаток от нашего ежемесячного платежа: 18 715,44 Р − 3698,63 Р = 15 016,81 Р .
Во втором месяце сумма процентов начислится на сумму кредита минус платеж по основному долгу в первом месяце: 300 000 Р − 15 015,81 Р = 284 983,19 Р .
Считаем проценты во втором месяце. Предположим, что во втором месяце 31 день: 284 983,19 × 15% × 31 / 365 = 3630,61 Р .
На погашение основного долга во втором месяце пойдет 15 084,83 Р (18 715,44 − 3630,61).
Таким образом можно посчитать соотношение процентов и основного долга в каждом месяце кредита.
Сложные проценты или капитализация
В этом случае доход за оговоренный срок прибавляется к сумме вклада. В последующий период вознаграждение начисляется уже на увеличенный размер депозита. Сумма вклада постепенно растет за счет накапливаемых процентов, итоговый доход становится выше.
Срок капитализации — периодичность, с которой процент суммируется с текущим телом вклада. Банки добавляют проценты раз в месяц, квартал или день. Вам могут предложить депозит с плавающими ставками, когда процент увеличивается с течением времени.
Как правило, процент повышается при увеличении срока хранения денег на депозите при условии, что снятий не было.
Доходность вкладов с капитализацией выше за счет увеличения тела кредита, однако наибольший доход дает тот депозит, по которому ограничено движение средств: запрещены снятия и пополнения, или дополнительные взносы разрешены, но с ограничением. Например, сумма всех пополнений не может превышать сумму открытия более, чем в 10 раз.
Как различаются вклады
Чтобы точно понимать разницу между депозитами в отношении расчета процентных ставок, напомним некоторые общие понятия:
- Под процентной ставкой по вкладу практически всегда понимается годовая процентная ставка. Даже если средства размещаются на 3 месяца, полгода или 5 лет.
- Расчет процентов может происходить через разные промежутки времени, в зависимости от условий договора. Но отправной точкой все равно будет годовая процентная ставка.
- Вклад может размещаться в банке на определенный срок или бессрочно. Это заранее оговаривается в депозитном договоре и влияет на ставку. Проценты по бессрочным договорам (до востребования и т.п.) обычно ниже.
Суммой, от которой ведется расчет, всегда бывает первоначальная величина вклада. Но к этой расчетной величине могут добавляться или не добавляться:
- уже начисленные проценты;
- позднейшие пополнения вклада.
Условия размещения депозита могут также разрешать или не разрешать снятие части основной суммы или начисленных процентов.
Из перечисленных условий большинство банковских вкладов можно классифицировать таким образом:
- вклады с простым начислением процентов; ;
- вклады с фиксированной суммой;
- пополняемые вклады.
Каждый из перечисленных типов банковского депозита имеет свои особенности расчета процентов. Другие условия банковского депозита на расчет процентов также влияют, но обычно в меньшей степени, и не прямо.
Как рассчитать доходность вклада с простым начислением процентов?
Простое начисление процентов – это расчет годовой процентной ставки только от величины первоначально вложенной суммы.
Самый простой и понятный способ. Расчетные периоды здесь могут различаться: можно начислять проценты раз в год или раз в месяц, но итоговая сумма будет одинаковой.
Рассмотрим это на примере размещения в банке 50 тысяч рублей под 8 процентов годовых, без капитализации, пополнения или досрочного снятия:
- При начислении процентов по окончании срока размещения вклада владелец средств получит 54 тысячи рублей.
Однако обычно начисление процентов происходит ежемесячно. Такой способ дает вкладчику больше уверенности, он знает, что его депозит уже вырос.
Расчет процентов происходит из общей ставки, в зависимости от количества дней в каждом месяце. Применительно к выбранной сумме расчет за январь будет таким:
- 50 000 * (0,08 / 365 * 31) = 340 рублей;
общая сумма, принадлежащая вкладчику – 50 тысяч 340 рублей.
Для февраля ситуация будет такой:
- 50 000 * (0,08 / 365 * 28) = 307 рублей;
общая сумма, принадлежащая вкладчику – 50 тысяч 647 рублей.
Расчетная таблица за год будет такой:
Основная сумма вклада, руб.
Начисленные проценты, руб.
Общая сумма вклада, руб.
Видно, что по итогам года вкладчик получит ровно столько, сколько вышло бы при начислении процентов по итогам года. То есть 54 тысячи рублей.
Сейчас большинство банков учитывают интересы вкладчиков и начисляют проценты ежемесячно. При досрочном снятии вклада делается перерасчет исходя из количества дней размещения вклада. Однако так происходит не всегда, условия расчета при разных вариантах снятия лучше уточнять при заключении депозитного договора.
Как рассчитать вклад с капитализацией?
Капитализация – это добавление процентов, начисленных на первоначальную сумму вложения к общей сумме, и дальнейший расчет по той же ставке, но уже от общей суммы.
Выгода капитализации, без точного расчета не очевидна. Рекламные предложения банков обычно делают упор на простые цифры: либо на высокую годовую ставку, либо на сумму приращения капитала. Кстати, последнее – более надежный показатель доходности вложения.
Чтобы выяснить, как работает капитализация, возьмем тот же пример с 50 тысячами рублей и 8%. Снова поместим средства на годовой депозит, но с ежемесячной капитализацией.
Формула расчета процентов по вкладу с капитализацией в первый месяц (январь) останется прежней:
- 50 000 * (0,08 / 365 * 31) = 340 рублей;
общая сумма, принадлежащая вкладчику – 50 тысяч 340 рублей.
Но для февраля исходные данные и результат поменяются:
- 50 340 * (0,08 / 365 * 28) = 318 рублей;
общая сумма, принадлежащая вкладчику – 50 тысяч 657 рублей.
Прибавка в 10 рублей покажется небольшой, однако в следующие периоды сумма будет расти:
Основная сумма вклада, руб.
Начисленные проценты, руб.
Общая сумма вклада, руб.
Разница между вариантами с капитализацией и без нее по итогам года составит 261 рубль. Это чуть более половины процента от общей суммы, как если бы вложение было сделано не под 8% годовых, а по ставке в 8,522%. Если рассчитать вклад с капитализацией, на тех же условиях, но на 3 года, то разница с простым начислением составит уже 1 тысячу 903 рубля.
И это на 50 тысячах, на 500 результат будет уже 19 тысяч 30 рублей.
«Хорошая прибавка к пенсии» и, что важно, совершенно законная и безопасная.
Эффект подобной капитализации дает возможность пополнения депозита с перерасчетом процентов на новую сумму. Расчет будет подобен приведенному выше, но с применением сумм конкретных пополнений. Еще лучший результат обеспечивает сочетание пополнения вклада и частой капитализации.
Это слайд-шоу требует JavaScript.
ФОРМУЛА ПРОСТЫХ ПРОЦЕНТОВ
Формула простых процентов для срока, который не кратен году, т.е. не составляет целое число лет, выглядит следующим образом:
S=P(1+t/K*i), где
S — сумма в конце срока
P — первоначальная сумма
i — годовая процентная ставка
t — число дней кредита
K — число дней в году, или временная база начисления процентов
При вычислении показателя по формуле простых процентов подразумевается, что процент, в отличие от расчетов по формуле сложных процентов, начисляется только на первоначальную сумму долга независимо от срока пользования заемными средствами. Например, если в кредит была получена сумма в размере 1 000 000 рублей на срок 5 лет под 20% годовых, то в первый год и последующие годы, ежегодные выплаты по кредиту составят 200 000 рублей.
Также следует учитывать, что данная формула верна, если в расчетах указана именно годовая процентная ставка.
ВЫЧИСЛЕНИЕ ГОДОВОЙ ПРОЦЕНТНОЙ СТАВКИ
Формула для вычисления годовой процентной ставки по формуле простых процентов
i=(S/P-1)*K/t
Всего можно выделить четыре наиболее часто встречающихся варианта расчета простых процентов в зависимости точности срока кредита и количества дней в году.
1. Точное число в месяцах, точное число дней в году
Например, для периода с 01.01.2012 по 31.06.2012 включительно срок в виде дроби выглядит как 182/366. Всего 182 дня, так как январь (31) +февраль (29) + март (31)+апрель (30)+май (31)+июль (30)=182. В году 366 дней, так как год високосный.
2. Точное число дней в месяцах, число дней в году равно 360
Для периода с 01.01.2012 по 31.06.2012, срок равен 182 дням и записывается дробью как 182/360.
3. 12 месяцев по 30 дней в каждом
Срок в виде дроби для периода с 01.01.2012 по 31.06.2012 будет выглядеть как 180/360, 6 месяцев*30 дней=180.
4. Точное число дней в месяцах, число дней в году принимается за 365
Срок в виде дроби для периода с 01.01.2012 по 31.06.2012 будет выглядеть как 182/365
Практикум
ПРИМЕР РАСЧЕТА ГОДОВОЙ ПРОЦЕНТНОЙ СТАВКИ
Банк выдал клиенту кредит в размере 1 000 000 рублей на период с 01.01.2012 г. по 30.06.2012 г. включительно. В качестве платы за пользование кредитом банк ежемесячно начисляет клиенту по 20 000 рублей. По условию кредита клиент обязался погасить всю сумму в конце срока. Требуется определить годовую процентную ставку по формуле простых процентов, применив четыре метода.
Расчет годовой процентной ставки по формуле простых процентов
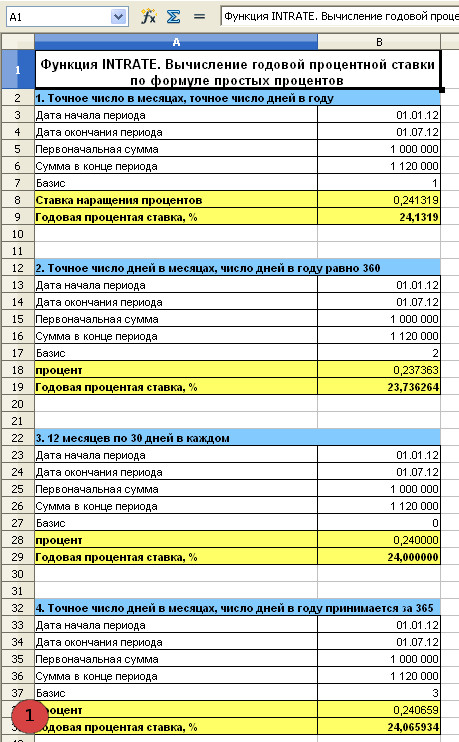
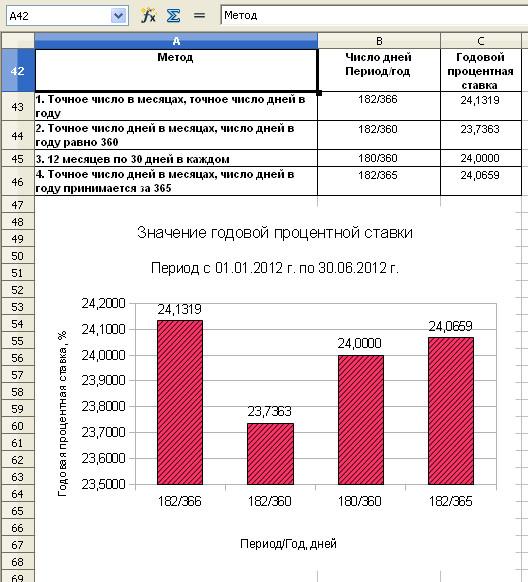
Предварительно рассчитаем сумму к погашению, точное и приближенное число дней.
Точное число дней 182.
Приближенное число дней 180.
Сумма к погашению = 6 месяцев * 20 000 рублей + 1 000 000 рублей= 1 120 000 рублей
1. Точное число дней в месяцах, точное число дней в году
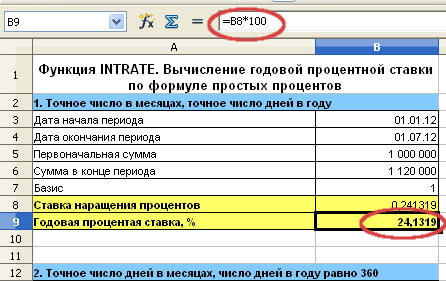
i=(S/P-1)*K/t=(1 120 000/1 000 000-1)*366/182=0,2413 или 24,13%
2. Точное число дней в месяцах, число дней в году равно 360.
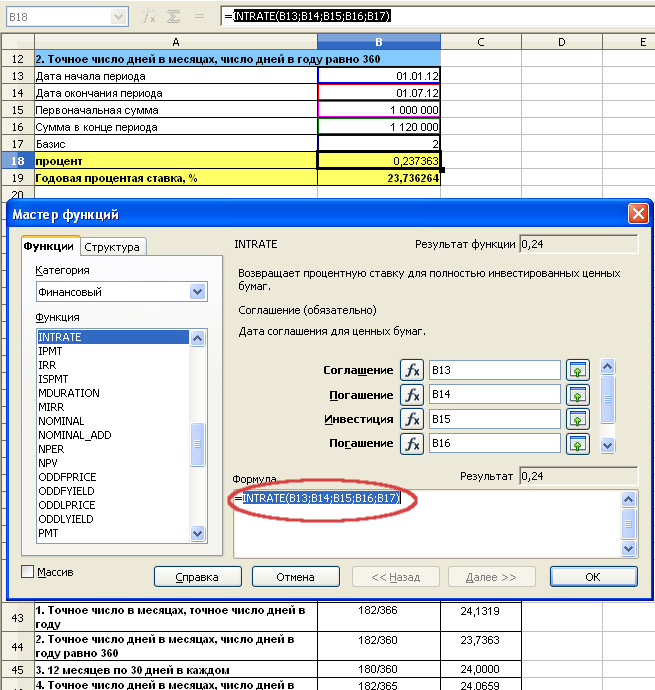
i=(S/P-1)*K/t=(1 120 000/1 000 000-1)*360/182=0,23736 или 23,73%
3. 12 месяцев, по 30 дней в каждом
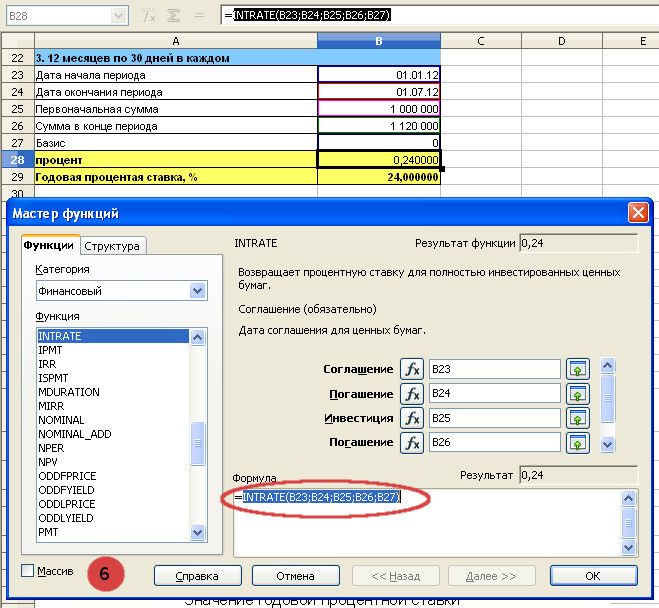
i=(S/P-1)*K/t=(1 120 000/1 000 000-1)*360/180=0,24 или 24,00%
4. Точное число дней в месяцах, число дней в году принимается за 365
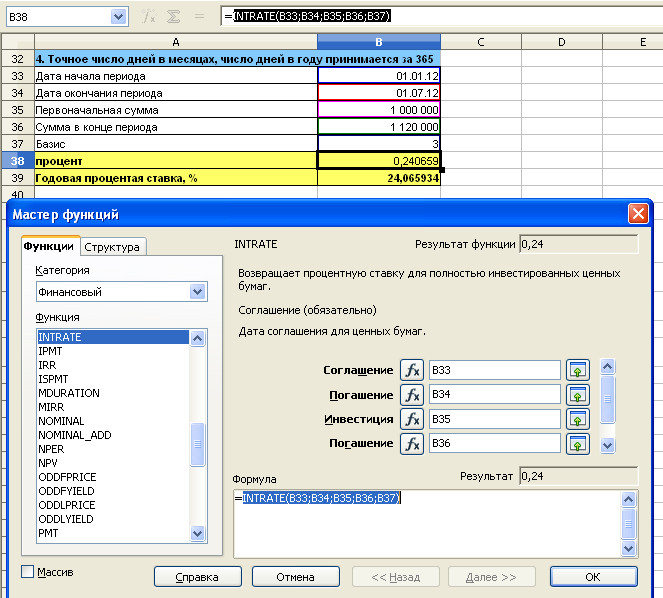
i=(S/P-1)*K/t=(1 120 000/1 000 000-1)*365/182=0,24065 или 24,07%
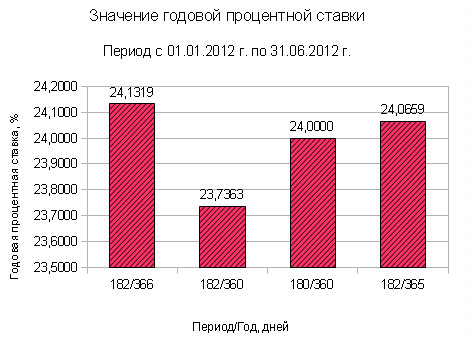
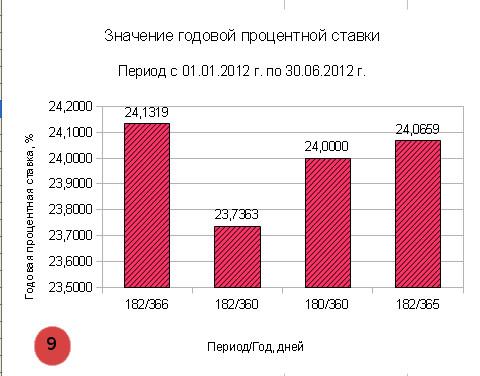
Анализ динамики процентной ставки
Проанализируем с помощью гистограммы значения годовой процентной ставки в зависимости от выбранного метода расчета.
Годовая процентная ставка за кредит за период с 01.01.2012 г. по 30.06.2012 г. по формуле простых процентов
|
Описание |
Число дней Период/год |
Годовой процент |
| 1. Точное число дней в месяцах, точное число дней в году |
182/366 |
0,2413 или 24,13% |
| 2. Точное число дней в месяцах, число дней в году равно 360 |
182/360 |
0,23736 или 23,73% |
| 3. 12 месяцев по 30 дней в каждом |
180/360 |
0,24 или 24,00% |
| 4. Точное число дней в месяцах, число дней в году принимается за 365 |
182/365 |
0,24065 или 24,07% |
Openoffice Calc. Пример применения функции INTRATE для расчет годовой процентной ставки по формуле простых процентов
В OpenOffice Calc для расчета годовой процентной ставки по формуле простых процентов применяется функция INTRATE.
Синтаксис функции INTRATE
INTRATE(дата начала периода; дата окончания периода; первоначальная сумма; сумма в конце периода; Базис)
| Базис – это метод вычисления года. | ||
|
Базис |
Метод |
Вычисление |
|
0 или отсутствует |
1 |
Американский метод (NASD): 12 месяцев по 30 дней в каждом |
|
1 |
2 |
Точное число дней в месяцах, точное число дней в году |
|
2 |
3 |
Точное число дней в месяцах, число дней в году принимается за 360 |
|
3 |
4 |
Точное число дней в месяцах, число дней в году принимается за 365 |
1. Таблица с расчетами годовой процентной ставки по формуле простых процентов 4-мя методами
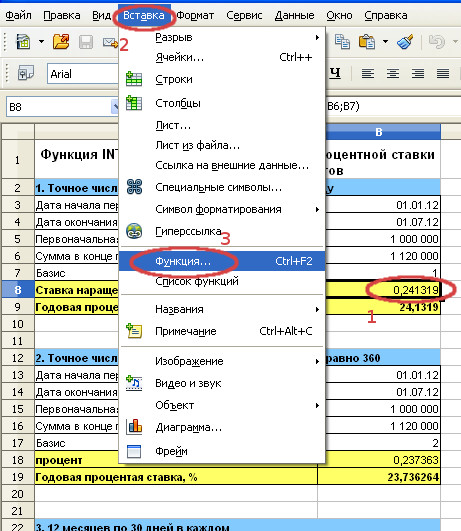
2. Вызов мастера функций
Вызовем Мастер функций, чтобы лучше понять, как применять функцию INTRATE. Для этого выделим ячейку с формулой (для первого примера это B8) и затем последовательно выберем Вставка/Функция…
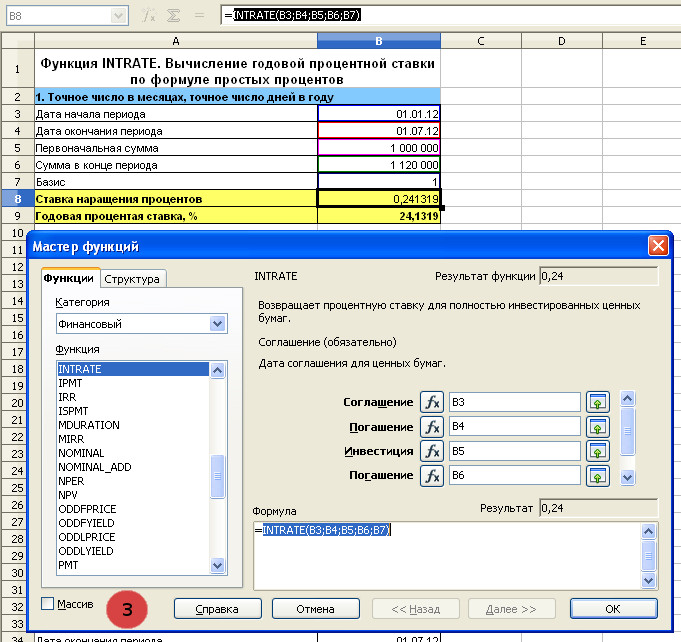
3. Базис 1. Функция INTRATE. Вычисление годовой процентной ставки по формуле простых процентов
Мастер функций с заполненными полями. Формула в ячейке B8. Необходимо нажать ОК, чтобы вернуться к исходной таблице.
Переведём полученный результат в проценты умножив его на 100.
4. Базис 2. Функция INTRATE. Вычисление годовой процентной ставки по формуле простых процентов
Мастер функций с заполненными полями. Формула в ячейке B18. Необходимо нажать ОК, чтобы вернуться к исходной таблице.
5. Базис 0. Функция INTRATE. Вычисление годовой процентной ставки по формуле простых процентов
Мастер функций с заполненными полями. Формула в ячейке B28. Необходимо нажать ОК, чтобы вернуться к исходной таблице.
6. Базис 3. Функция INTRATE. Вычисление годовой процентной ставки по формуле простых процентов
Мастер функций с заполненными полями. Формула в ячейке B38. Необходимо нажать ОК, чтобы вернуться к исходной таблице.
7. Гистограмма значений годовых процентных ставок по формуле простого процента рассчитанных 4-мя методами