Начертательная геометрия: конспект лекций.
4. Горизонтали и фронтали плоскости.
Среди прямых, которые лежат в некоторой плоскости, можно выделить два класса прямых, играющих большую роль при решении всевозможных задач. Это прямые, которые называют горизонталями и фронталями.
Горизонталь плоскости Р (рис. 41) – прямая, которая лежит в этой плоскости и параллельна горизонтальной плоскости. Горизонталь как прямая, параллельная горизонтальной плоскости, имеет фронтальную проекцию ѓ, параллельную оси х.
Три прямые – горизонталь Г, ее горизонтальная проекция г и горизонтальный след Рh плоскости Р – параллельны (рис. 42).
Действительно, горизонталь является прямой, параллельной горизонтальной плоскости, и поэтому не имеет горизонтального следа Рh, лежащего с ней в одной плоскости. При этом горизонталь Г не может пересечь свою горизонтальную проекцию г. В противном случае в этой точке пересечения она встречала бы горизонтальную плоскость, что противоречит определению, т. е. все три прямые Г, г и Рh параллельны.
Любая из плоскостей имеет множество горизонталей. Все горизонтали этой плоскости параллельны друг другу вследствие того, что все они параллельны прямой Рh.
Фронталь плоскости Р – прямая, которая лежит в этой плоскости и параллельна фронтальной плоскости (рис. 43).
Фронталь является прямой, параллельной фронтальной плоскости, и ее горизонтальная проекция ф параллельна оси х.
Фронталь Ф, ее фронтальная проекция ф́ и фронтальный след Рv взаимно параллельны. У каждой плоскости есть бесчисленное множество фронталей. Все фронтали данной плоскости параллельны, за исключением плоскости, параллельной фронтальной плоскости.
Горизонталь плоскости
Горизонталь плоскости – одна из главных линий плоскости.
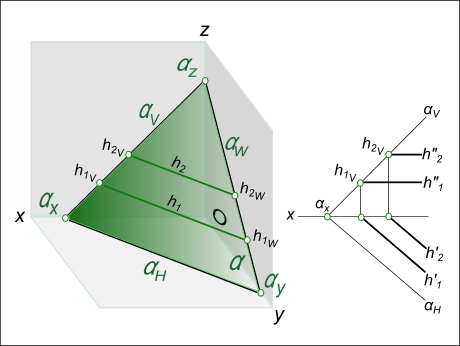
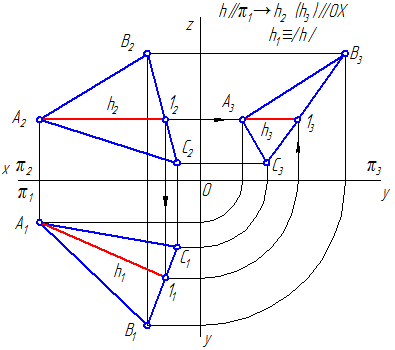
На рисунке показаны: горизонталь плоскости α – h, фронталь υ плоскости α, профильная прямая ω плоскости α, задание линий уровня на эпюре.
Главными линиями плоскости называют: 1. Прямые, принадлежащие плоскости и параллельные какой-либо плоскости проекции. 2. Прямые принадлежащие плоскости и перпендикулярные к какой-либо линии, отмеченной в пункте 1.
Прямые, параллельные плоскости проекции (1), принадлежат плоскости уровня, поэтому их называют также, прямыми (или линиями) уровня.
Линии уровня подразделяют на три вида: а) Если h⊂α ^ h║H , то прямая h представляет собой горизонталь плоскости α; б) В случае когда υ⊂α ^ υ║V, то прямую υ называют фронталь плоскости α; в) В случае когда ω⊂α ^ ω║W, то прямую ω называют профильная прямая плоскости α.
| Наименование линии | Горизонтальная проекция | Фронтальная проекция | Профильная проекция |
| Горизонталь | ║αH | ║оси x | ║оси y |
| Фронталь | ║оси x | ║αV | ║оси z |
| Профильная прямая | ║оси y | ║оси z | ║αW |
В плоскости можно провести множество горизонталей
и по горизонталям плоскости построить следы плоскости, то есть перейти от какого то способа задания плоскости к заданию следами. И наоборот, от задания плоскости следами, по горизонталям плоскости можно перейти к другим способам задания той же самой плоскости.
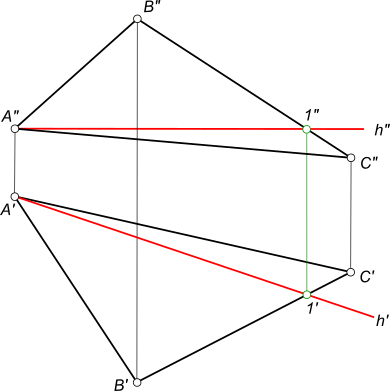
построить горизонталь треугольника ABC
чтобы построить горизонталь плоскости выраженной треугольником ABC необходимо: – построить фронтальную проекцию h” искомой горизонтали, причем h” ‖ x, проводим из вершины A треугольника, достигая этим цели наименьшим количеством построений; – в пересечении h” с B”C” противолежащей стороной треугольника отмечаем точку 1″; – находим 1` в пересечении ее линии проекционной связи со стороной B`C`; – находим h` искомой горизонтали, соединив прямой линией точки A` и 1`.
Лекция 3. Плоскость
3.1. Способы задания плоскости на ортогональных чертежах
Рисунок 3.1 – Способы задания плоскостей
Плоскость общего положения – это плоскость, которая не параллельна и не перпендикулярна ни одной из плоскостей проекций.
Следом плоскости называется прямая, полученная в результате пересечения заданной плоскости с одной из плоскостей проекций.
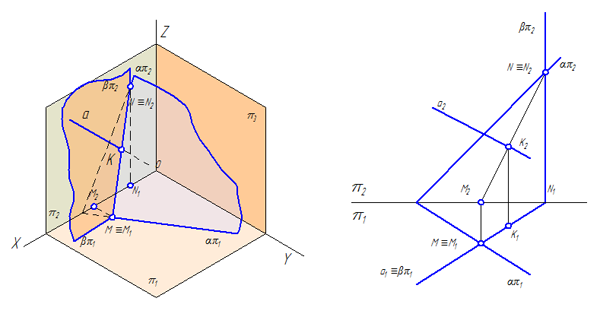
Плоскость общего положения может иметь три следа: горизонтальный – απ1, фронтальный – απ2 и профильный – απ3, которые она образует при пересечении с известными плоскостями проекций: горизонтальной π1, фронтальной π2 и профильной π3 (Рисунок 3.2).
Рисунок 3.2 – Следы плоскости общего положения
3.2. Плоскости частного положения
Плоскость частного положения – плоскость, перпендикулярная или параллельная плоскости проекций.
Плоскость, перпендикулярная плоскости проекций, называется проецирующей и на эту плоскость проекций она будет проецироваться в виде прямой линии.
Свойство проецирующей плоскости : все точки, линии, плоские фигуры, принадлежащие проецирующей плоскости, имеют проекции на наклонном следе плоскости (Рисунок 3.3).
Рисунок 3.3 – Фронтально-проецирующая плоскость, которой принадлежат: точки А, В, С; линии АС, АВ, ВС; плоскость треугольника АВС
Фронтально-проецирующая плоскость – плоскость, перпендикулярная фронтальной плоскости проекций (Рисунок 3.4, а).
Горизонтально-проецирующая плоскость – плоскость, перпендикулярная горизонтальной плоскости проекций (Рисунок 3.4, б).
Профильно-проецирующая плоскость – плоскость, перпендикулярная профильной плоскости проекций.
Плоскости, параллельные плоскостям проекций, называются плоскостями уровня или дважды проецирующими плоскостями.
Фронтальная плоскость уровня – плоскость, параллельная фронтальной плоскости проекций (Рисунок 3.4, в).
Горизонтальная плоскость уровня – плоскость, параллельная горизонтальной плоскости проекций (Рисунок 3.4, г).
Профильная плоскость уровня – плоскость, параллельная профильной плоскости проекций (Рисунок 3.4, д).
Рисунок 3.4 – Эпюры плоскостей частного положения
3.3. Точка и прямая в плоскости. Принадлежность точки и прямой плоскости
Точка принадлежит плоскости, если она принадлежит какой-либо прямой, лежащей в этой плоскости (Рисунок 3.5). Прямая принадлежит плоскости, если она имеет с плоскостью хотя бы две общие точки (Рисунок 3.6).
Рисунок 3.5 – Принадлежность точки плоскости
Рисунок 3.6 – Принадлежность прямой плоскости
left.beginalpha=mparallel n,\Dinalpha\Cinalpha\endright> Longrightarrow CDinalpha
Упражнение
Рисунок 3.7 – Решение задачи
Решение :
- ABCD – плоский четырехугольник, задающий плоскость.
- Проведём в нём диагонали AC и BD (Рисунок 3.7, б), которые являются пересекающимися прямыми, также задающими ту же плоскость.
- Согласно признаку пересекающихся прямых, построим фронтальную проекцию точки пересечения этих прямых — K: A2C2 ∩ B2D2=K2.
- Восстановим линию проекционной связи до пересечения с горизонтальной проекцией прямой BD: на проекции диагонали B1D1 строим К1.
- Через А1К1 проводим проекцию диагонали А1С1.
- Точку С1 получаем, посредством линии проекционной связи до пересечения её с горизонтальной проекцией продолженной диагонали А1К1.
3.4. Главные линии плоскости
В плоскости можно построить бесконечное множество прямых, но есть особые прямые, лежащие в плоскости, называемые главными линиями плоскости (Рисунок 3.8 – 3.11).
Прямой уровня или параллелью плоскости называется прямая, лежащая в данной плоскости и параллельная одной из плоскостей проекций.
Горизонталь или горизонтальная прямая уровня h (первая параллель) – это прямая, лежащая в данной плоскости и параллельная горизонтальной плоскости проекций (π1) (Рисунок 3.8, а; 3.9).
Фронталь или фронтальная прямая уровня f (вторая параллель) – это прямая лежащая в данной плоскости и параллельная фронтальной плоскости проекций (π2) (Рисунок 3.8, б; 3.10).
Профильная прямая уровня p (третья параллель) – это прямая лежащая в данной плоскости и параллельная профильной плоскости проекций (π3) (Рисунок 3.8, в; 3.11).
| Интерактивная модель Горизонталь плоскости |
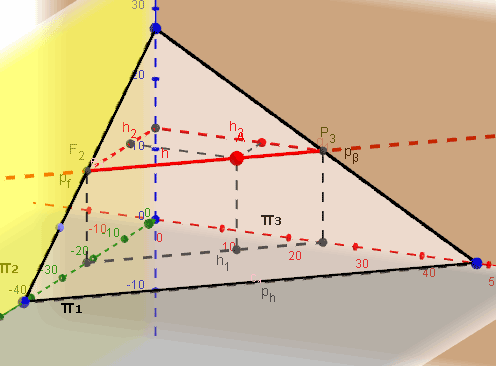 |
Рисунок 3.8 а – Горизонтальная прямая уровня в плоскости, заданной треугольником
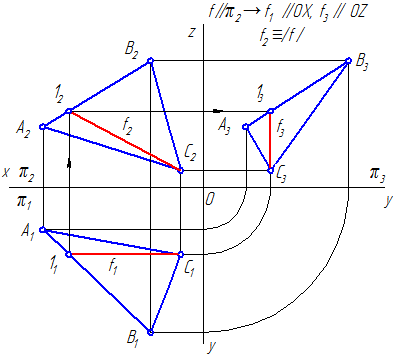
| Интерактивная модель Фронталь плоскости |
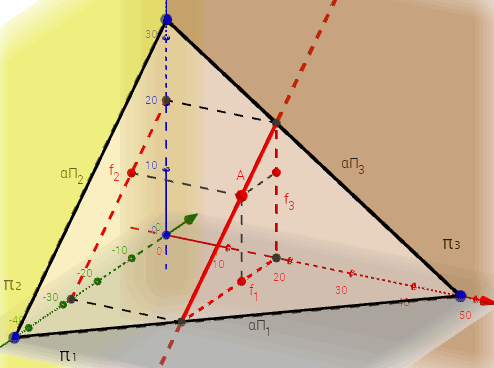 |
Рисунок 3.8 б – Фронтальная прямая уровня в плоскости, заданной треугольником

| Интерактивная модель Профильная прямая плоскости |
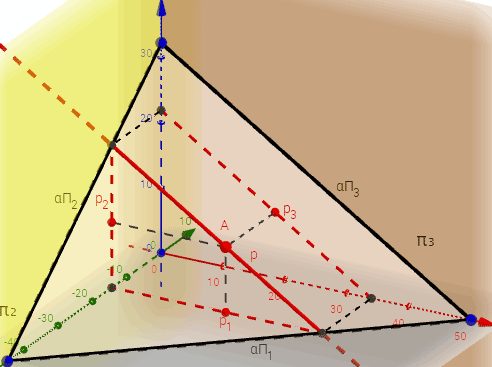 |
Рисунок 3.8 в – Профильная прямая уровня в плоскости, заданной треугольником
Рисунок 3.9 – Горизонтальная прямая уровня в плоскости, заданной следами
Рисунок 3.10 – Фронтальная прямая уровня в плоскости, заданной следами
Рисунок 3.11 – Профильная прямая уровня в плоскости, заданной следами
3.5. Взаимное положение прямой и плоскости
Прямая по отношению к заданной плоскости может быть параллельной и может с ней иметь общую точку, то есть пересекаться.
3.5.1. Параллельность прямой плоскости
Признак параллельности прямой плоскости : прямая параллельна плоскости, если она параллельна какой-либо прямой, принадлежащей этой плоскости (Рисунок 3.12).
alpha=mcap n\left.begina_2parallel m_2\a_1parallel m_1\endright> Rightarrow aparallelalpha
Рисунок 3.12 – Параллельность прямой плоскости
3.5.2. Пересечение прямой с плоскостью
Для построения точки пересечения прямой с плоскостью общего положения (Рисунок 3.13), необходимо:
- Заключить прямую а во вспомогательную плоскость β (в качестве вспомогательной плоскости следует выбирать плоскости частного положения);
- Найти линию пересечения вспомогательной плоскости β с заданной плоскостью α;
- Найти точку пересечения заданной прямой а с линией пересечения плоскостей MN.
Рисунок 3.13 – Построение точки встречи прямой с плоскостью
Упражнение
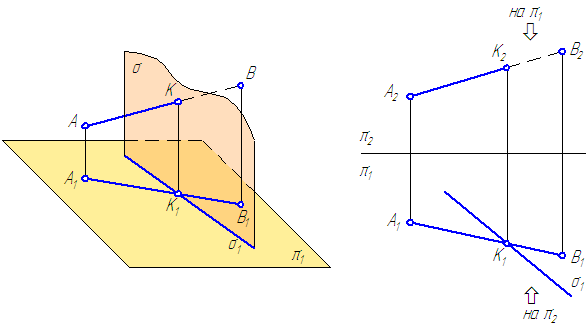
Заданы: прямая АВ общего положения, плоскость σ⊥π1. (Рисунок 3.14). Построить точку пересечения прямой АВ с плоскостью σ.
Решение :
-
- Точка К должна принадлежать прямой АВ ⇒ К1∈А1В и заданной плоскости σ ⇒ К1∈σ, следовательно, К1 находится в точке пересечения проекций А1В1 и σ1;
- Плоскость σ – горизонтально-проецирующая, следовательно, горизонтальной проекцией плоскости σ является прямая σ1 (горизонтальный след плоскости);
- Фронтальную проекцию точки К находим посредством линии проекционной связи: К2∈А2В2.
Рисунок 3.14 – Пересечение прямой общего положения с плоскостью частного положения
Упражнение
Заданы: плоскость σ = ΔАВС – общего положения, прямая EF (Рисунок 3.15).
Требуется построить точку пересечения прямой EF с плоскостью σ.
Рисунок 3.15 – Пересечение прямой с плоскостью
Решение:
- Заключим прямую EF во вспомогательную плоскость, в качестве которой воспользуемся горизонтально-проецирующей плоскостью α (Рисунок 3.15, а);
- Если α⊥π1, то на плоскость проекций π1 плоскость α проецируется в прямую (горизонтальный след плоскости απ1 или α1), совпадающую с E1F1;
- Найдём прямую пересечения (1-2) проецирующей плоскости α с плоскостью σ (решение подобной задачи будет рассмотрено ниже);
- Прямая (1-2) и заданная прямая EF лежат в одной плоскости α и пересекаются в точке K.
Алгоритм решения задачи (Рисунок 3.15, б): Через EF проведем вспомогательную плоскость α:
- left.beginalpha perp pi_1\alphain EF\endright> Longrightarrow alpha_1in E_1F_1
- alphacapsigma=(1-2)left.begin|alpha_1cap A_1C_1=1_1longrightarrow 1_2\|alpha_1cap A_1B_1=2_1longrightarrow 2_2\endright.
- (1_2-2_2)cap E_2F_2=K_2\left.beginKin EF\Kin (1-2)Rightarrow Kinsigma\endright>Longrightarrow K=EFcap (sigma =triangle ABC)
3.6. Определение видимости методом конкурирующих точек
При оценке положения данной прямой, необходимо определить – точка какого участка прямой расположена ближе (дальше) к нам, как к наблюдателям, при взгляде на плоскость проекций π1 или π2.
Точки, которые принадлежат разным объектам, а на одной из плоскостей проекций их проекции совпадают (то есть, две точки проецируются в одну), называются конкурирующими на этой плоскости проекций.
Необходимо отдельно определить видимость на каждой плоскости проекций.
Видимость на π2 (рис. 3.15)
Выберем точки, конкурирующие на π2 – точки 3 и 4. Пусть точка 3∈ВС∈σ, точка 4∈EF.
Чтобы определить видимость точек на плоскости проекций π2 надо определить расположение этих точек на горизонтальной плоскости проекций при взгляде на π2.
Направление взгляда на π2 показано стрелкой.
По горизонтальным проекциям точек 3 и 4, при взгляде на π2, видно, что точка 41 располагается ближе к наблюдателю, чем 31.
41∈E1F1 ⇒ 4∈EF ⇒ на π2 будет видима точка 4, лежащая на прямой EF, следовательно, прямая EF на участке рассматриваемых конкурирующих точек расположена перед плоскостью σ и будет видима до точки K – точки пересечения прямой с плоскостью σ.
Видимость на π1.
Для определения видимости выберем точки, конкурирующие на π1 – точки 2 и 5.
Чтобы определить видимость точек на плоскости проекций π1 надо определить расположение этих точек на фронтальной плоскости проекций при взгляде на π1.
Направление взгляда на π1 показано стрелкой.
По фронтальным проекциям точек 2 и 5, при взгляде на π1, видно, что точка 22 располагается ближе к наблюдателю, чем 52.
22∈А2В2 ⇒ 2∈АВ ⇒ на π1 будет видима точка 2, лежащая на прямой АВ, следовательно, прямая EF на участке рассматриваемых конкурирующих точек расположена под плоскостью σ и будет невидима до точки K – точки пересечения прямой с плоскостью σ.
Видимой из двух конкурирующих точек будет та, у которой координата «Z» или(и) «Y» больше.
3.7. Перпендикулярность прямой плоскости
Признак перпендикулярности прямой плоскости : прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости.
Рисунок 3.16 – Задание прямой, перпендикулярной плоскости
Теорема. Если прямая перпендикулярна плоскости, то на эпюре: горизонтальная проекции прямой перпендикулярна горизонтальной проекции горизонтали плоскости, а фронтальная проекция прямой перпендикулярна фронтальной проекции фронтали (Рисунок 3.16, б)
Теорема доказывается через теорему о проецировании прямого угла в частном случае.
Если плоскость задана следами, то проекции прямой перпендикулярной плоскости перпендикулярны соответствующим следам плоскости (Рисунок 3.16, а).
Пусть прямая p перпендикулярна плоскости σ=ΔАВС и проходит через точку K.
3.8. Взаимное положение двух плоскостей
3.8.1. Параллельность плоскостей
Две плоскости могут быть параллельными и пересекающимися между собой.
Признак параллельности двух плоскостей : две плоскости взаимно параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.
Упражнение
Задана плоскость общего положения α=ΔАВС и точка F∉α (Рисунок 3.17).
Через точку F провести плоскость β, параллельную плоскости α.
Рисунок 3.17 – Построение плоскости, параллельной заданной
Решение : В качестве пересекающихся прямых плоскости α возьмем, например, стороны треугольника АВ и ВС.
- Через точку F проводим прямую m, параллельную, например, АВ.
- Через точку F, или же через любую точку, принадлежащую m, проводим прямую n, параллельную, например, ВС, причём m∩n=F.
- β = m∩n и β//α по определению.
| Интерактивная модель Параллельность двух плоскостей |
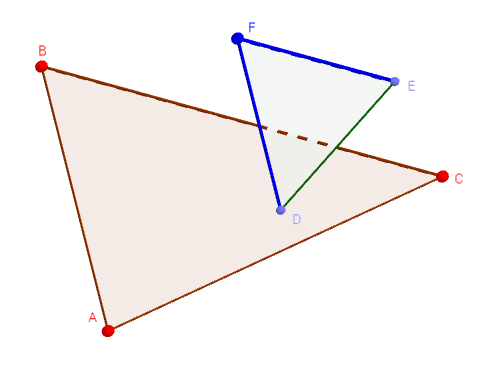 |
3.8.2. Пересечение плоскостей
Результатом пересечения 2-х плоскостей является прямая. Любая прямая на плоскости или в пространстве может быть однозначно задана двумя точками. Поэтому для того, чтобы построить линию пересечения двух плоскостей, следует найти две точки, общие для обеих плоскостей, после чего соединить их.
Рассмотрим примеры пересечения двух плоскостей при различных способах их задания: следами; тремя точками, не лежащими на одной прямой; параллельными прямыми; пересекающимися прямыми и др.
Упражнение
Рисунок 3.18 – Пересечение плоскостей общего положения, заданных следами
Порядок построения линии пересечения плоскостей:
- Найти точку пересечения горизонтальных следов — это точка М (её проекции М1 и М2, при этом М1=М, т.к. М – точка частного положения, принадлежащая плоскости π1).
- Найти точку пересечения фронтальных следов — это точка N (её проекции N1 и N2, при этом N2=N, т.к. N – точка частного положения, принадлежащая плоскости π2).
- Построить линию пересечения плоскостей, соединив одноименные проекции полученных точек: М1N1 и М2N2.
МN – линия пересечения плоскостей.
Упражнение
Решение:
Так как плоскость α пересекает стороны АВ и АС треугольника АВС, то точки пересечения K и L этих сторон с плоскостью α являются общими для обеих заданных плоскостей, что позволит, соединив их, найти искомую линию пересечения.
Точки могут быть найдены как точки пересечения прямых с проецирующей плоскостью: находим горизонтальные проекции точек K и L, то есть K1 и L1 , на пересечении горизонтального следа (α1) заданной плоскости α с горизонтальными проекциями сторон ΔАВС: А1В1 и A1C1. После чего посредством линий проекционной связи находим фронтальные проекции этих точек K2 и L2 на фронтальных проекциях прямых АВ и АС. Соединим одноимённые проекции: K1 и L1; K2 и L2. Линия пересечения заданных плоскостей построена.
Алгоритм решения задачи :
left.beginABcapsigma=K\ACcapsigma=L\endright> left.beginRightarrow A_1B_1capsigma_1=K_1 rightarrow K_2\Rightarrow A_1C_1cap sigma_1=L_1 rightarrow L_2\endright.
KL – линия пересечения ΔАВС и σ (α∩σ = KL).
Рисунок 3.19 – Пересечение плоскостей общего и частного положения
Упражнение
Рисунок 3.20 – Пересечение двух плоскостей общего положения (общий случай)
Алгоритм решения задачи :
left.beginalphacapsigma=(4-5)\betacapsigma=(3-2)\endright>\left.beginalphacaptau=(6-7)\betacaptau=(1-8)\endright>left.begin(4_1-5_1)cap(3_1-2_1)=M_1rightarrow M_2\(6_1-7_1)cap(1_1-8_1)=N_1rightarrow N_2\endright>rightarrow\left.beginM_1N_1\M_2N_2\endright>Rightarrowalphacapbeta=MN
Упражнение
Заданы плоскости α = ΔАВС и β = a//b. Построить линию пересечения заданных плоскостей (Рисунок 3.21).
Рисунок 3.21 Решение задачи на пересечение плоскостей
Решение: Воспользуемся вспомогательными секущими плоскостями частного положения. Введём их так, чтобы сократить количество построений. Например, введём плоскость σ⊥π2, заключив прямую a во вспомогательную плоскость σ (σ∈a). Плоскость σ пересекает плоскость α по прямой (1-2), а σ∩β=а. Следовательно (1-2)∩а=K. Точка К принадлежит обеим плоскостям α и β. Следовательно, точка K, является одной из искомых точек, через которые проходит прямая пересечения заданных плоскостей α и β. Для нахождения второй точки, принадлежащей прямой пересечения α и β, заключим прямую b во вспомогательную плоскость τ⊥π2 (τ∈b). Соединив точки K и L, получим прямую пересечения плоскостей α и β.
3.8.3. Взаимно перпендикулярные плоскости
Плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой.
Упражнение
Задана плоскость σ⊥π2 и прямая общего положения – DE (Рисунок 3.22)
Требуется построить через DE плоскость τ⊥σ.
Рисунок 3.22 – Построение плоскости, перпендикулярной к заданной плоскости
По теореме о проецировании прямого угла C1D1 должна быть параллельна оси проекций. Пересекающиеся прямые CD∩DE задают плоскость τ. Итак, τ⊥σ. Аналогичные рассуждения, в случае плоскости общего положения.
Упражнение
Рисунок 3.23 – Построение плоскости, перпендикулярной к заданной ΔАВС
3.9. Задачи для самостоятельного решения
1. Задана плоскость α = m//n (Рисунок 3.24). Известно, что K∈α.
Постройте фронтальную проекцию точки К.
2. Постройте следы прямой, заданной отрезком CB, и определите квадранты, через которые она проходит (Рисунок 3.25).
3. Постройте проекции квадрата, принадлежащего плоскости α⊥π2, если его диагональ MN //π2 (Рисунок 3.26).
4. Построить прямоугольник ABCD с большей стороной ВС на прямой m, исходя из условия, что отношение его сторон равно 2 (Рисунок 3.27).
5. Задана плоскость α=a//b (Рисунок 3.28). Построить плоскость β параллельную плоскости α и удаленную от нее на расстоянии 20 мм.
6. Задана плоскость α=∆АВС и точка D вне плоскости. Построить через точку D плоскость β⊥α и β⊥π1.
7. Задана плоскость α=∆АВС и точка D вне плоскости. Построить через точку D прямую DE//α и DE//π1.
[spoiler title=”источники:”]
http://ngeo.fxyz.ru/%D0%BE%D1%80%D1%82%D0%BE%D0%B3%D0%BE%D0%BD%D0%B0%D0%BB%D1%8C%D0%BD%D1%8B%D0%B5_%D0%BF%D1%80%D0%BE%D0%B5%D0%BA%D1%86%D0%B8%D0%B8/%D0%B3%D0%BE%D1%80%D0%B8%D0%B7%D0%BE%D0%BD%D1%82%D0%B0%D0%BB%D1%8C_%D0%BF%D0%BB%D0%BE%D1%81%D0%BA%D0%BE%D1%81%D1%82%D0%B8/
[/spoiler]
Задача 1
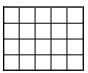
Суммарная длина перегородок в клетчатом прямоугольнике 4 × 5 на рисунке равна 31. Чему равна суммарная длина перегородок в прямоугольнике 12 × 50? (Задача из вступительных экзаменов в 5 класс ФМЛ 239 за 2017 г )
Решение
Несложно увидеть, что количество внутренних линий, идущих от края до края – как вертикальных, так и горизонтальных, на 1 меньше, чем число клеток по горизонтали и вертикали соответственно.
По вертикали в этом прямоугольнике 4 клетки и 3 внутренних горизонтальных линии, а по горизонтали 5 клеток и 4 внутренних вертикальных линии.
На каждой вертикальной линии 4 перегородки (т.к. 4 клетки по вертикали), на каждой горизонтальной линии 5 перегородок (т.к. 5 клеток по горизонтали)
число вертикальных перегородок: 4∙4 = 16
число горизонтальных перегородок: 3∙5 = 15
Таким образом, общее число горизонтальных и вертикальных перегородок = 16 + 15 = 31 – что как раз соответствует суммарной длине перегородок из условия задачи. Очевидно, в данном случае это обусловлено тем, что все клетки являются одинаковыми квадратами.
Для прямоугольника 12×50, равно как и для любого другого будет выполняться то же правило – количество внутренних линий, идущих от края до края – как вертикальных, так и горизонтальных, на 1 меньше, чем число клеток по горизонтали и вертикали соответственно.
Таким образом, в прямоугольнике 12×50 имеется 11 горизонтальных линий и 49 вертикальных.
число вертикальных перегородок: 49∙12 = 588
число горизонтальных перегородок: 11∙50 = 550
Общее число горизонтальных и вертикальных перегородок = 588+550 = 1138
Ответ: 1138
Задача 2
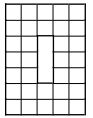
На рисунке изображена буква О ширины 5, высоты 7, толщины 2 клетки. Суммарная длина её внутренних перегородок равна 48. Чему равна суммарная длина внутренних перегородок буквы О, у которой толщина 4, высота 40, ширина 30 клеток? (Задача из вступительных экзаменов в 5 класс ФМЛ 239, 2018 г)
Решение
Эту задачу можно решить двумя способами:
1. Найти, как число внутренних перегородок зависит от размера «дырки» внутри буквы О, т.е. от толщины
2. Воспользовавшись методикой из предыдущей задачи, найти, сколько перегородок должно быть внутри буквы «О», если бы в ней не было дырки, и вычесть число внутренних перегородок внутри дырки, если бы они там были, а также вычесть внешние края буквы О, которые тоже не являются внутренними перегородками
Мы применим второй способ. Для начала проверим его на исходной букве «О» размером 5×7 и толщиной 2 клетки.
Число вертикальных линий – 4 (на 1 меньше, чем число клеток по горизонтали )
Число горизонтальных линий – 6 (на 1 меньше, чем число клеток по вертикали)
Если бы внутри буквы «О» не было бы дырки, то мы имели бы прямоугольник со следующим числом внутренних перегородок:
число вертикальных перегородок: 4∙7 = 28
число горизонтальных перегородок: 6∙5 = 30
Общее число внутренних перегородок: 28 + 30 = 58
Теперь рассмотрим дырку от буквы «О». Её размеры 3×1.
Посчитаем, сколько внутренних перегородок в ней было бы, если бы они были нарисованы
число вертикальных перегородок: 0
число горизонтальных перегородок: 2
Общее число внутренних перегородок: 2
Также нам надо учесть перегородки, составляющие внешние края дырки:
Всего таких перегородок: 2∙3 + 2∙1 = 8
Таким образом, общее число внутренних перегородок нашего исходного прямоугольника, которые пришлись на дырку, составляет 2 + 8 = 10
Таким образом, общее число внутренних перегородок внутри буквы О –
58 – 10 = 48
48 – это как раз то число, которое у нас в условии задачи, то есть мы посчитали верно.
Теперь перейдём к букве «О», у которой толщина 4, высота 40, ширина 30 клеток.
Найдём число внутренних перегородок у соответствующего прямоугольника 40×30, когда в нём нет дырки:
Число вертикальных линий – 29 (на 1 меньше, чем число клеток по горизонтали )
Число горизонтальных линий – 39 (на 1 меньше, чем число клеток по вертикали)
число вертикальных перегородок: 29∙40 = 1160
число горизонтальных перегородок: 39∙30 = 1170
Общее число внутренних перегородок – 2330
Найдём размеры дырки от буквы «О»
Чтобы найти ширину дырки, надо из общей ширины прямоугольника вычесть толщину левого и правого края, которая составляет, исходя из условия задачи, 4. Высота дырки находится аналогично, толщина верхнего и нижнего края в данном случае тоже равна 4.
Ширина дырки: 30 – 4 – 4 = 22
Высота дырки: 40 – 4 – 4 = 32
Найдём число внутренних перегородок у дырки, если бы они были нарисованы
число вертикальных перегородок: (22 – 1)∙32 = 672
число горизонтальных перегородок: (32 – 1)∙22 = 682
Общее число внутренних перегородок = 672 + 682 = 1354
Перегородки, составляющие внешние края дырки: 2∙22 + 2∙32 = 108
Общее число внутренних перегородок в букве «О»: 2330 – 1354 – 108 = 868
Ответ: 868
В этой статье мы разберем в подробностях, как найти каждую из сторон прямоугольника. Посмотрим, какие ситуации возможны в задачах и разберем самые трудные и интересные из задач.
Содержание
- Длины прямоугольника
- Примеры решения задач
- Задача 1
- Задача 2
- Задача 3
- Что мы узнали?
Длины прямоугольника
Очень часто понятия длины и ширины путаются. Некоторые источники утверждают, что вертикальные стороны прямоугольника – это ширина. Но это редкость, обычно длиной называется большая сторона прямоугольника, а шириной меньшая.
Для лучшего восприятия стоит располагать фигуру так, чтобы длина находилась в основании, а боковые стороны имели размеры ширины. Так будет проще решать задачи.
Перед тем, как перейти непосредственно к решению задач, нужно повторить несколько фактов, которые облегчат решение:
- Диагонали прямоугольника равны.
- Диагонали точкой пересечения делятся пополам.
- Диагонали прямоугольника делят прямоугольник на 4 равнобедренных треугольника, которые равны между собой.
Рис. 1. Прямоугольник
Примеры решения задач
Решим задачу, связанную с формулами вычисления сторон прямоугольника. Рассмотрим несколько вариантов нахождения длин сторон при различных известных параметрах.
Задача 1
- Известно, что площадь прямоугольника равна 21, а периметр 20. Найти стороны прямоугольника.
Такая задача содержит две неизвестных. Величины сторон a и b. Чтобы найти оба значения необходимо составить систему уравнений:
$(a+b)*2=P$ (уравнение нахождения периметра как суммы сторон фигуры)
$a*b=S$ (уравнение для нахождения площади)
При наличии двух неизвестных для решения системы необходимо наличие двух уравнений. Поэтому невозможно найти стороны прямоугольника, зная только площадь или только периметр.
Продолжим решение. Выразим значение a из первого выражения системы.
- $(а+b)*2=Р$
- $а+b={Рover{2}}$
- $а={Рover{2}}-b$
- Подставим значение периметра: $а={20over{2}}-b=10-b$
Подставим получившееся выражение в уравнение нахождения площади:
$a*b=S$
$(10-b)*b=21$
$b^2-10b-21=0$
Это квадратное уравнение. Решим его с помощью теоремы Виета. Такое уравнение будет иметь два корня. Сумма корней будет равна 10, а произведение 21. Такое возможно при значении корней 3 и 7, так как это единственные числа, подходящие под данные условия.
$а=10-b$
Значит, при $b=3$, $а=10-3=7$
При $b=7$, $a=10-7=3$. То есть в любом случае, стороны будут равны 7 и 3. Это и есть ответ задачи.
Задача 2
- Известно, что сторона прямоугольника равна 16, а диагональ 20. Найти другую сторону прямоугольника.
Рис. 2. Рисунок к задаче.
Задача решается теоремой Пифагора. Диагональ делит прямоугольник на два равных прямоугольных треугольника. В таком треугольнике нам известна гипотенуза (20) и катет (16).
Сумма квадратов катетов равняется квадрату гипотенузы. Искать будем сторону а, предположив, что известная нам сторона это сторона b.
$D^2=a^2+b^2$
$A^2=d^2-b^2$
$а^2=400-256=144$
Корень квадратный из 144 равен 12. Это и есть ответ к задаче.
Задача 3
- Известно, что прямоугольник представляет собой ромб. Площадь ромба равна 25, необходимо найти все стороны четырехугольника.
Рис. 3. Квадрат.
У прямоугольника все углы прямые, а у ромба все стороны между собой равны. Значит, четырехугольник, который одновременно является и ромбом, и прямоугольником это фигура с 4 прямыми углами и сторонами, равными между собой. Такой фигурой может быть только квадрат.
Стороны квадрата равны, значит нас интересует одно значение. Площадь квадрата это значение стороны, возведенное в квадрат.
$а^2=S$
$а^2=25$
$а=5$
Что мы узнали?
Мы узнали, как найти длины прямоугольника. Рассмотрели различные типовые ситуации и научились решать задачи, связанные с нахождением длин прямоугольника.
Предыдущая
МатематикаПорядок выполнения сложения и вычитания
Следующая
МатематикаГипотенуза треугольника – формула длины
Задача нахождения границ повернутого прямоугольника одинаково востребована, как в векторной, так и в растровой графике. При создании разного рода редакторов необходима область, описывающая фигуру, к которой применена трансформация. При обработке изображений, фото, для достижения каких-то художественных эффектов или решения сугубо технических проблем, например, для «выравнивания горизонта».
Возможно, Вы попали на эту страницу по запросу: «Поворот прямоугольника и нахождение вершин онлайн«. В этом случае имеет смысл посмотреть эту ссылку. Там прямой ответ на этот вопрос. Если требуется поворот вокруг центра прямоугольника, не забудьте установить переключатель «Вращать вокруг центра прямоугольника«.
Подобные задачи можно разделить на три группы:
- Нахождение описывающего прямоугольника для повернутого прямоугольника.
- Нахождение ширины и высоты повернутого прямоугольника, вписанного в некий прямоугольник.
- Нахождение вписанного прямоугольника в повернутый прямоугольник.
Повернуть прямоугольник
Чтобы повернуть прямоугольник необходимо воспользоваться аффинным преобразованием поворота, или просто применить формулы преобразования ко всем четырем вершинам прямоугольника.
Формулы преобразования поворота доказываются тут.
Давайте создадим прямоугольник и зададим угол поворота. Можно менять угол поворота зажав и перетаскивая оранжевую вершину.
Угол поворота:
Ширина:
Высота:
Get a better browser, bro…
Рис.1. Поворот прямоугольника. O(x,y) — координаты центра вращения. За оранжевую вершину можно тащить.
Чтобы посчитать координаты вершин повернутого прямоугольника, используются следующие формулы:
Если вращение происходит не вокруг центра координат, необходимо добавить координаты центра вращения, как на рисунке.1.
Немного кода:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
type T4PointF = array [0..3] of TPointF; //********************************************************************* // Посчитать координаты массива точек повернутых на Angle радиан //********************************************************************* function CalcAnglePoints(const APoints: T4PointF; const ACenter: TPointF; const Angle: single): T4PointF; var i: Integer; sn,cs: single; begin SinCos(Angle, sn, cs); for i := 0 to Length(APoints)–1 do begin Result[i].X := (APoints[i].X–ACenter.X) * cs – (APoints[i].Y–ACenter.Y) * sn + ACenter.X; Result[i].Y := (APoints[i].X–ACenter.X) * sn + (APoints[i].Y–ACenter.Y) * cs + ACenter.Y; end; end; |
Описывающий прямоугольник повернутого прямоугольника
Краткая формулировка задачи:
Есть некий прямоугольник (a b c d), с шириной w и высотой h. К нему применен поворот на α градусов. Необходимо найти ширину W и высоту H описывающего прямоугольника.
Get a better browser, bro…
Рис.2. Описывающий прямоугольник для повернутого прямоугольника. За оранжевую вершину можно тащить.
На рисунке синий цвет угла означает направление против часовой и положительный знак угла, красный — по часовой и отрицательный.
В качестве поворачиваемого прямоугольника может выступать, допустим, картинка. Чтобы получить на выходе «необрезанное» по краям изображение, необходимо посчитать размер будущей картинки, чтобы повернутое изображение полностью входило в область.
Можно решить задачу следующим образом: пройтись по вершинам, найти минимальные и максимальные значения координат:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
//************************************************************** // Получить описывающий прямоугольник массива вершин //************************************************************** function GetPointsRect(const APoints: T4PointF): TRect; var i: Integer; begin Result := Rect(MaxInt, MaxInt, –MaxInt, –MaxInt); for i := 0 to Length(APoints)–1 do begin if APoints[i].X < Result.Left then Result.Left := Trunc(APoints[i].X); if APoints[i].X > Result.Right then Result.Right := Round(APoints[i].X); if APoints[i].Y < Result.Top then Result.Top := Trunc(APoints[i].Y); if APoints[i].Y > Result.Bottom then Result.Bottom := Round(APoints[i].Y); end; end; |
Это способ хороший, не особо затратный и универсальный. Если у нас число таких вершин непредсказуемо большое и отличается таким же непредсказуемым многообразием, это пожалуй, единственный способ. Но для прямоугольника есть способ лучше и проще.
Вспомним свойства прямоугольника.
— Прямоугольник является параллелограммом — его противоположные стороны попарно параллельны.
— Стороны прямоугольника являются его высотами. Середины сторон прямоугольника образуют ромб.
— Квадрат диагонали прямоугольника равен сумме квадратов двух его смежных сторон (по теореме Пифагора).
— Около любого прямоугольника можно описать окружность, причём диагональ прямоугольника равна диаметру описанной окружности (радиус равен полудиагонали).
Википедия
По теме прямоугольника можно заглянуть сюда (не реклама, просто симпатично, кратко, емко).
Сейчас нас интересует попарная параллельность сторон и то, что все углы прямоугольника — прямые. На основании этого и будет строится дальнейшее рассуждение. Предполагается, что про углы у параллельных прямых все в курсе.
Get a better browser, bro…
Рис.4. Расчет ширины W и высоты H описывающего прямоугольника. За оранжевую вершину можно тащить.
Рассмотрим рисунок 4.
- Угол β — интересующая нас часть угла α, остаток от деления на π / 2.
- Угол γ — это дополнение угла β до π / 2, т.е. γ = π / 2 — β.
Цвет в данном случае означает попадание β в один из квадрантов. Синий — квадранты 1 и 3, красный — 2 и 4.
Внимание! Следующий текст генерируется автоматически в зависимости от угла на рисунках.
Поставив галочку ниже, в рисунках 2 и 4 будет отображаться решение. Не стал сразу выводить, ну чтоб не нарушать интригу.
Показать решение
В качестве итога. Чтобы найти высоту и ширину описывающего прямоугольника для повернутого прямоугольника всегда работают эти красивые формулы:
Где:
- W’ — ширина описывающего прямоугольника
- H’ — высота описывающего прямоугольника
- w — ширина исходного прямоугольника
- h — высота исходного прямоугольника
- α — угол поворота
Зная координаты центра трансформации, высоту и ширину границ, нетрудно рассчитать координаты описывающего прямоугольника.
Друзья, спасибо за внимание!
Подписывайтесь на телеграм-канал.
Жду ваших комментариев. Надо ли рассказывать, как вписать повернутый прямоугольник в заданный прямоугольник? Или может про «выравнивание горизонта»?
Горизонталь плоскости
Горизонталь плоскости – одна из главных линий плоскости.
Горизонталь плоскости
На рисунке показаны:
горизонталь плоскости α – h,
фронталь υ плоскости α,
профильная прямая ω плоскости α,
задание линий уровня на эпюре.
Главными линиями плоскости называют:
1. Прямые, принадлежащие плоскости и параллельные какой-либо плоскости проекции.
2. Прямые принадлежащие плоскости и перпендикулярные к какой-либо линии, отмеченной в пункте 1.
Прямые, параллельные плоскости проекции (1), принадлежат плоскости уровня, поэтому их называют также, прямыми (или линиями) уровня.
Линии уровня подразделяют на три вида:
а) Если h⊂α ^ h║H, то прямая h представляет собой горизонталь плоскости α;
б) В случае когда υ⊂α ^ υ║V, то прямую υ называют фронталь плоскости α;
в) В случае когда ω⊂α ^ ω║W, то прямую ω называют профильная прямая плоскости α.
| Наименование линии | Горизонтальная проекция | Фронтальная проекция | Профильная проекция |
| Горизонталь | ║αH | ║оси x | ║оси y |
| Фронталь | ║оси x | ║αV | ║оси z |
| Профильная прямая | ║оси y | ║оси z | ║αW |
В плоскости можно провести множество горизонталей
Горизонталь плоскости
и по горизонталям плоскости построить следы плоскости, то есть перейти от какого то способа задания плоскости к заданию следами.
И наоборот, от задания плоскости следами, по горизонталям плоскости можно перейти к другим способам задания той же самой плоскости.
построить горизонталь треугольника ABC
Горизонталь плоскости
чтобы построить горизонталь плоскости выраженной треугольником ABC необходимо:
– построить фронтальную проекцию h” искомой горизонтали, причем h” ‖ x, проводим из вершины A треугольника, достигая этим цели наименьшим количеством построений;
– в пересечении h” с B”C” противолежащей стороной треугольника отмечаем точку 1″;
– находим 1` в пересечении ее линии проекционной связи со стороной B`C`;
– находим h` искомой горизонтали, соединив прямой линией точки A` и 1`.
+