Содержание:
Развертки поверхностей:
Развертыванием поверхности называется такое преобразование, в результате которого поверхность всеми точками совмещается с плоскостью. Полученная при этом плоская фигура называется разверткой.
Поверхности делятся на развертываемые и неразвертываемые.
Разветываемые поверхности совмещаются с плоскостью без разрывов и складок. Признаком развертываемости является пересечение соседних образующих или их параллельность. К развертываемым поверхностям относятся многогранные, цилиндрические, конические, торсовые. Развертки многогранников строятся точно, учитываются лишь погрешности инструмента и графических построений. Развертки цилиндрических, конических и торсовых поверхностей получаются приближенно, так как эти поверхности заменяются вписанными в них или описанными около них многогранными поверхностями, которые и развертываются.
Неразвертываемые поверхности с плоскостью не совмещаются, т.е. теоретически они разверток не имеют, так как образующие их скрещиваются. К неразвертываемым относятся поверхности с плоскостью параллелизма (цилиндроид, коноид, косая плоскость), криволинейные (сфера, тор и т.п.) и графические.
В инженерной практике строятся условные развертки неразверты-ваемых поверхностей. Для этого неразвертываемая поверхность делится на части (доли), которые заменяются развертываемыми поверхностями.
Если рассматривать поверхность и ее развертку как множество точек, то между этими множествами устанавливается взаимооднозначное соответствие, т.е. каждой точке на поверхности соответствует единственная точка на развертке и наоборот.
Свойства развертки
1. Прямая на поверхности переходит в прямую на развертке.
2. Параллельные прямые на поверхности будут параллельными прямыми на развертке.
3. На развертке сохраняются:
- – длина линии, лежащей на поверхности;
- – величина угла между линиями поверхности;
- – величина площади фигуры на поверхности.
Развертки прямых круговых цилиндра и конуса
Развертка боковой поверхности прямого кругового цилиндра представляет собой прямоугольник, высота которого равна высоте цилиндра, а длина – длине окружности основания 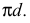
Развертка боковой поверхности прямого кругового конуса (рис. 241) представляет собой круговой сектор. Длина дуги 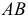
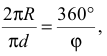
откуда
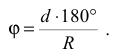
Отложив центральный угол 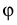 и проведя дугу из центра
и проведя дугу из центра 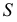 радиусом
радиусом 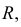 строят точную развертку прямого кругового конуса, не считая графических погрешностей.
строят точную развертку прямого кругового конуса, не считая графических погрешностей.
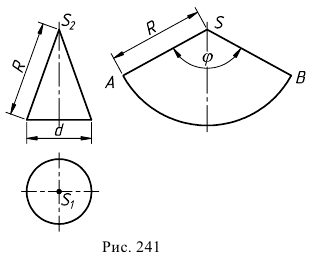
Развертки линейчатых поверхностей
Способ триангуляции
Способ триангуляции (треугольников) универсален, его можно применять для построения разверток любых поверхностей, в том числе и криволинейных (например, подвесные сферические своды). Однако способ триангуляции не всегда является рациональным. Для каждой группы поверхностей рекомендуется соответствующий графический способ построения разверток. Все линейчатые поверхности, включая и неразвертываемые (цилиндроид, коноид, косая плоскость), можно развернуть способом триангуляции.
Сущность способа заключается в следующем:
1. Криволинейная поверхность заменяется вписанной в нее многогранной поверхностью. Так, на рис. 242 в наклонный эллиптический конус (нормальное сечение – эллипс) с круговым основанием вписана двенадцатигранная пирамида. Для этого основание конуса разбивается па 12 равных частей.
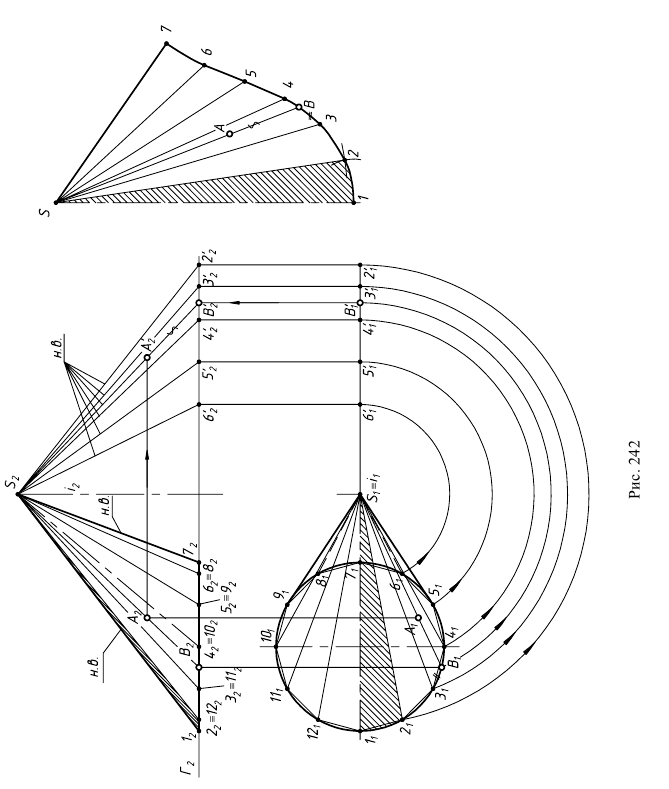
Исследование точности построения разверток показало, что оптимально деление окружности на 12 частей. При делении на 8 и менее частей длина кривой на развертке получается значительно короче длины окружности основания. При делении более чем на 12 частей, увеличивается величина графических неточностей. Полученные после деления окружности дуги заменяются стягивающими хордами. Затем проводятся образующие 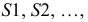 которые являются ребрами вписанной пирамиды.
которые являются ребрами вписанной пирамиды.
2. Определяются натуральные величины сторон каждого треугольника 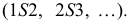 У данной поверхности образующие
У данной поверхности образующие 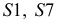 являются фронталями, их фронтальные проекции равны натуральной величине
являются фронталями, их фронтальные проекции равны натуральной величине 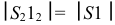 и
и 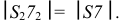 Все остальные образующие – прямые общего положения. Их натуральные величины удобно определять вращением вокруг оси
Все остальные образующие – прямые общего положения. Их натуральные величины удобно определять вращением вокруг оси 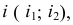 проходящей через вершину конуса
проходящей через вершину конуса 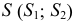 перпендикулярно горизонтальной плоскости проекции. Натуральные величины образующих равны соответственно отрезкам
перпендикулярно горизонтальной плоскости проекции. Натуральные величины образующих равны соответственно отрезкам 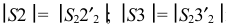 и т.д.
и т.д.
Третьей стороной у каждого треугольника являются хорды, которые на горизонтальную плоскость проекций проецируются без искажения. Натуральные величины хорд 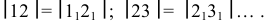
3. Развертка выполняется последовательным построением всех треугольников. Каждый треугольник строят по трем сторонам, натуральные величины которых известны. Если отсек поверхности симметричен, то развертку следует выполнять также симметричной и построение начинать с оси симметрии. Допускается строить половину развертки, которая с одной стороны должна быть ограничена осевой линией. Рекомендуется поверхность разрезать по самой короткой образующей, чтобы длина соединительных “швов” была наименьшей.
Осевая линия располагается на чертеже вертикально или горизонтально. На ней откладывается отрезок 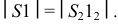 Из точки 1 проводится дуга радиусом
Из точки 1 проводится дуга радиусом 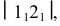 а из точки
а из точки 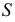 – вторая дуга радиусом
– вторая дуга радиусом 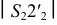 до пересечения с первой в точке 2: соединив тонкими линиями точки 1 и 2,
до пересечения с первой в точке 2: соединив тонкими линиями точки 1 и 2, 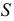 и 2, получаем
и 2, получаем 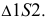 Аналогично пристраивается
Аналогично пристраивается 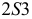 и т.д. Точки 1, 2, 3 соединяются плавной кривой. Контур развертки обводится основной линией до оси симметрии (см. рис. 242).
и т.д. Точки 1, 2, 3 соединяются плавной кривой. Контур развертки обводится основной линией до оси симметрии (см. рис. 242).
На развертках часто приходится строить линии, расположенные на поверхностях. К ним относятся линии пересечения двух поверхностей и сечения поверхности плоскостью.
Для построения на развертке точки выполняют следующее:
- через данную точку проводят линию, лежащую на поверхности и удобную для построения (чаще всего это прямая или окружность). На рис. 242 точка
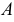 принадлежит образующей
принадлежит образующей 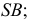
- определяют натуральную величину этой линии и на нее переносят рассматриваемую точку. На рис. 242
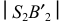 – натуральная величина образующей и точка
– натуральная величина образующей и точка 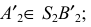
- на развертке строят соответствующую линию. Образующая
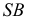 располагается между образующими
располагается между образующими 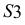 и
и 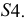 Отрезок
Отрезок 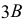 равен хорде, а расстояние
равен хорде, а расстояние 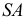 берется равным натуральной величине –
берется равным натуральной величине – 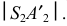
Способ нормального сечения
Способ применяется для построения разверток призматических и цилиндрических поверхностей.
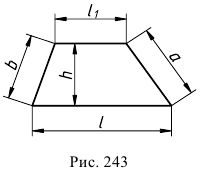
При построении развертки призматической поверхности необходимо все ее грани последовательно совместить с плоскостью. В общем случае (наклонная призма с непараллельными основаниями) боковые грани призмы – трапеции. Чтобы построить натуральные величины этих граней, необходимо определить натуральные величины ребер призмы, которые являются основаниями трапеций – отрезки 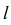 и
и 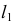 (рис. 243). Кроме того, нужно знать или расстояние между ребрами
(рис. 243). Кроме того, нужно знать или расстояние между ребрами 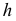 – высоты трапеций, или натуральные величины сторон основания призмы
– высоты трапеций, или натуральные величины сторон основания призмы 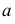 и
и 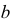 – боковые стороны трапеций.
– боковые стороны трапеций.
В зависимости от того, высота или боковые стороны применяются при построении разверток, различают два способа: нормального сечения и раскатки. В первом способе расстояние между образующими определяется при помощи нормального сечения. В способе раскатки используются натуральные величины сторон основания призмы.
Развертка призматической поверхности строится точно, не считая графических погрешностей. При построении развертки цилиндрической поверхности необходимо сначала вписать в нее призматическую поверхность, которую затем развернуть. Следовательно, развертка цилиндрической поверхности является приближенной.
На рис. 244 показано построение развертки наклонной призмы способом нормального сечения. При помощи нормального сечения, перпендикулярного к образующим, определяют расстояния между ними. Способ целесообразно применять в тех случаях, когда основания призмы или цилиндра заданы в общем положении.
Последовательность построений:
1) определяются натуральные величины образующих, если они заданы в общем положении (см. рис. 244). Натуральные величины ребер определяются проецированием на дополнительную плоскость проекций  параллельную ребрам:
параллельную ребрам: 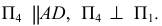 Тогда
Тогда 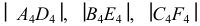 -натуральные величины ребер;
-натуральные величины ребер;
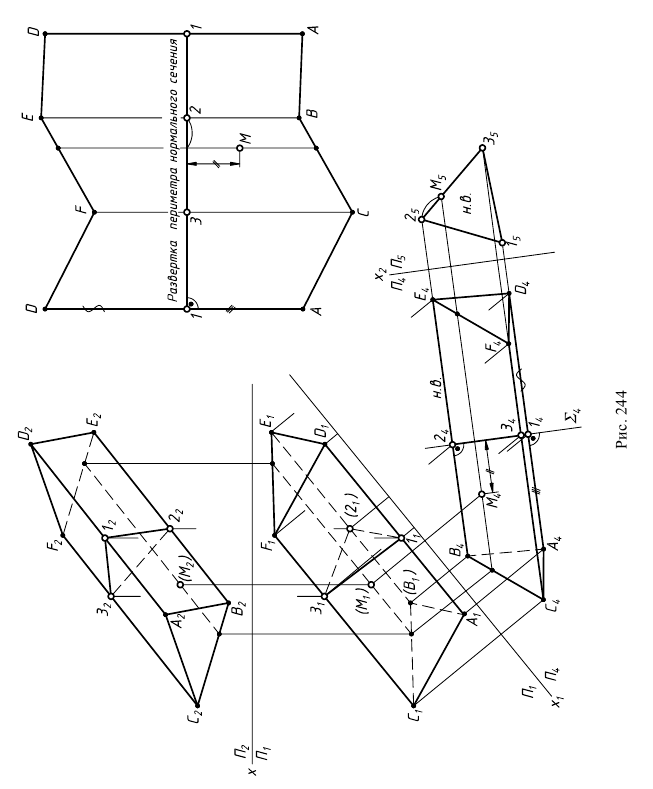
2) строится нормальное сечение перпендикулярно ребрам призмы. Так как ребра параллельны плоскости 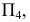 то сечение
то сечение 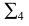 вырождается в прямую линию
вырождается в прямую линию 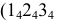 – прямая) и является проецирующим относительно
– прямая) и является проецирующим относительно 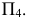 Относительно плоскостей
Относительно плоскостей 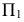 и
и 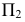 это сечение занимает общее положение;
это сечение занимает общее положение;
3) определяется натуральная величина нормального сечения любым способом. В данном примере она определена проецированием на плоскость 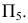 Проекция
Проекция 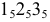 – натуральная величина;
– натуральная величина;
4) строится развертка следующим образом:
а) периметр нормального сечения “развертывается” в прямую линию, на которой 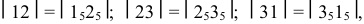 то есть эти отрезки равны расстояниям между образующими (ребрами):
то есть эти отрезки равны расстояниям между образующими (ребрами):
б) через точки 1, 2, 3 проводятся образующие, перпендикулярные развертке нормального сечения;
в) на этих линиях откладываются натуральные величины образующих: 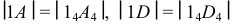 и т.д.;
и т.д.;
г) полученные точки соединяются ломаной линией.
На рис. 244 показано построение на развертке точки 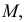 принадлежащей поверхности призмы. Точка
принадлежащей поверхности призмы. Точка 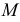 принадлежит образующей, параллельной ребрам.
принадлежит образующей, параллельной ребрам.
Развертки криволинейных поверхностей вращения
Криволинейные поверхности вращения (сфера, тор и др.) относятся к неразвертываемым, их нельзя совместить с плоскостью без разрывов и складок, поэтому при выполнении их из листового материала строятся условные развертки.
Последовательность построений:
- поверхность разрезается по меридианам или параллелям на ряд частей;
- каждая такая часть заменяется вписанной или описанной развертываемой поверхностью (цилиндрической или конической);
- строятся развертки отдельных частей, из которых затем собирается заданная поверхность.
При разрезании по меридианам каждая доля заменяется описанной цилиндрической поверхностью. Такой прием называется способом вспомогательных цилиндров.
При разрезании по параллелям поверхность разбивается на ряд поясов, которые заменяются вписанными коническими поверхностями. Этот прием называется способом вспомогательных конусов.
Способ вспомогательных цилиндров
Построение развертки сферы способом вспомогательных цилиндров показано на рис. 245:
- поверхность сферы меридиональными плоскостями
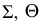 и
и 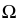 разрезают на равные части (доли). Рекомендуется разбивать ее не менее чем на 12 частей. В примере принято 6 долей для того, чтобы отрезки были крупнее и чертеж более четким;
разрезают на равные части (доли). Рекомендуется разбивать ее не менее чем на 12 частей. В примере принято 6 долей для того, чтобы отрезки были крупнее и чертеж более четким; - каждую такую долю заменяют описанной цилиндрической поверхностью, касающейся ее по линии симметрии доли.
Цилиндрическая поверхность касается доли I по главному меридиану. Разделив его на 6 равных частей, через точки 2, 3, 4, 5, 6 проводят параллели – окружности. Затем строят образующие цилиндра, касающиеся параллелей в точках 2, 3, 6. Образующие 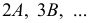 являются фронтально-проецирующими. Таким образом, цилиндрическая поверхность, касательная к доле I, является фронтально-проецирующей и фронтальная проекция ее совпадает с главным меридианом
являются фронтально-проецирующими. Таким образом, цилиндрическая поверхность, касательная к доле I, является фронтально-проецирующей и фронтальная проекция ее совпадает с главным меридианом 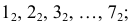
3) строят развертку каждого описанного цилиндра способом нормального сечения:
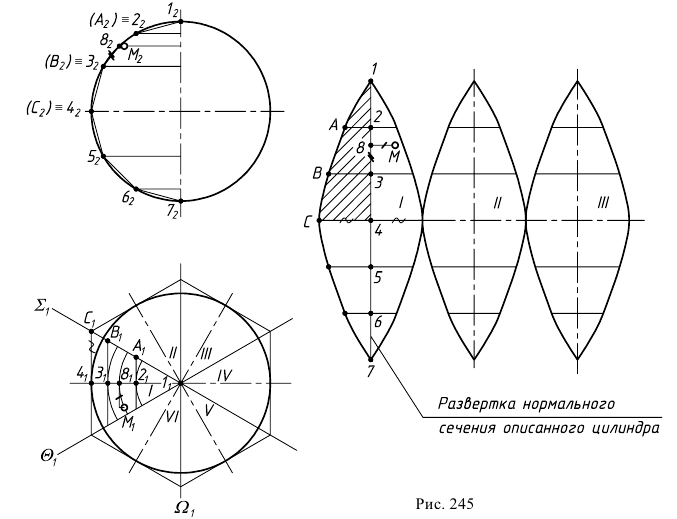
а) нормальным сечением доли 1 является главный меридиан, который развертывается в отрезок 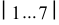 вертикальной прямой. На ней откладывают отрезки, равные фронтальным проекциям хорд:
вертикальной прямой. На ней откладывают отрезки, равные фронтальным проекциям хорд: 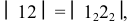
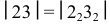 и т.д.;
и т.д.;
б) через полученные точки 2, 3, 4, 5, 6 проводят образующие цилиндра перпендикулярно ”развертке” нормального сечения. Размеры образующих берут с горизонтальной проекции 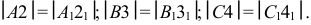 Через полученные точки
Через полученные точки 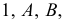 и
и 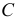 проводят плавную кривую. Развертка каждой доли имеет вертикальную и горизонтальную оси симметрии, поэтому, построив 1/4 часть развертки, аналогично строят остальные 3/4. Полная развертка сферы будет состоять из шести (двенадцати) таких долей. На практике подобные развертки удобно делать по шаблону. На рис. 245 такой шаблон заштрихован.
проводят плавную кривую. Развертка каждой доли имеет вертикальную и горизонтальную оси симметрии, поэтому, построив 1/4 часть развертки, аналогично строят остальные 3/4. Полная развертка сферы будет состоять из шести (двенадцати) таких долей. На практике подобные развертки удобно делать по шаблону. На рис. 245 такой шаблон заштрихован.
Местоположение точки 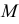 на развертке, как и любой точки на плоскости, определяется двумя координатами – вертикальной и горизонтальной. Вертикальная координата – расстояние от точки соседней параллели, горизонтальная – от оси симметрии. Вертикальная координата
на развертке, как и любой точки на плоскости, определяется двумя координатами – вертикальной и горизонтальной. Вертикальная координата – расстояние от точки соседней параллели, горизонтальная – от оси симметрии. Вертикальная координата 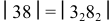 берется с фронтальной проекции, горизонтальная
берется с фронтальной проекции, горизонтальная 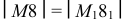 – c горизонтальной плоскости проекций.
– c горизонтальной плоскости проекций.
Способ вспомогательных конусов
Построение развертки сферы этим способом показано на рис. 246:
1) поверхность сферы разрезается по параллелям горизонтальными плоскостями на ряд поясов и два сегмента;
2) в полученные шаровые пояса и сегменты вписываются поверхности вращения, оси которых совпадают с осью 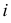 сферы, а основания – с соответствующими параллелями.
сферы, а основания – с соответствующими параллелями.
В шаровой сегмент IV вписывается полный конус вращения, вершина которого совпадает с точкой 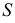 пересечения оси вращения
пересечения оси вращения 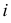 с главным меридианом сферы.
с главным меридианом сферы.
В шаровые пояса III и II вписываются усеченные конусы вращения. Образующие конусов совпадают с хордами 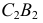 и
и 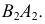 Вершины конусов
Вершины конусов 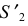 и
и 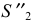 получаются на пересечении этих образующих с осью вращения.
получаются на пересечении этих образующих с осью вращения.
В экваториальный пояс I вписывается цилиндр вращения;
3) строятся развертки вписанных поверхностей.
Разверткой конуса является сектор, радиус которого равен образующей конуса. Для пояса II – образующая 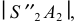 для III –
для III – 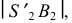 для IV –
для IV – 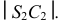 Центры секторов рекомендуется размещать на одной линии, принимаемой за ось симметрии разверток. Длины дуг секторов равны длинам параллелей окружностей соответствующих поясов. Их размеры берутся с горизонтальной плоскости проекций, для этого окружности делятся на 12 частей. Так, длина дуги
Центры секторов рекомендуется размещать на одной линии, принимаемой за ось симметрии разверток. Длины дуг секторов равны длинам параллелей окружностей соответствующих поясов. Их размеры берутся с горизонтальной плоскости проекций, для этого окружности делятся на 12 частей. Так, длина дуги 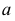 на развертке равна длине горизонтальной проекции параллели
на развертке равна длине горизонтальной проекции параллели 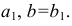
Построенные части I и II соединяются между собой по линиям 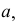 II и III – по линиям
II и III – по линиям 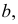 III и IV – по линиям
III и IV – по линиям 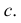
Примеры построения разверток некоторых поверхностей
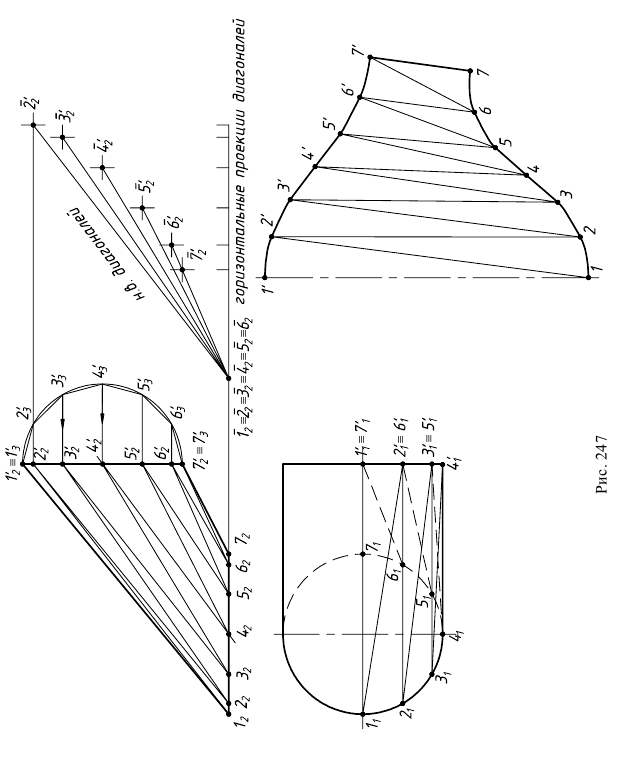
Задача 1 (рис. 247). Дано: поверхность цилиндроида, плоскостью параллелизма которой является плоскость проекций 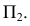
Требуется: построить развертку способом триангуляции.
Решение:
1. В заданную поверхность вписывается многогранная поверхность. Окружность нижнего основания разбивается на 12 равных частей. Окружность верхнего основания лежит в профильной плоскости уровня, поэтому дополнительно строится полуокружность, соответствующая его профильной проекции. Полуокружность разбивается на 6 равных частей. Полученные дуги заменяются стягивающими хордами, точки деления переносят на фронтальную и горизонтальную проекции верхнего основания. Затем проводятся образующие 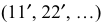 и диагонали
и диагонали 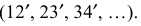
В результате получается многогранная поверхность, ограниченная треугольниками 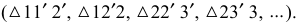
2. Определяются натуральные величины диагоналей (способом плоскопараллельного перемещения). У образующих натуральными величинами являются их фронтальные проекции, т.к. все они параллельны 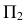 – плоскости параллелизма данного цилиндроида.
– плоскости параллелизма данного цилиндроида.
3. Строится развертка. Заданная поверхность имеет плоскость симметрии, поэтому развертка будет симметричной и достаточно построить ее половину.
Поверхность разрезается по наименьшей образующей 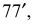 тогда образующая
тогда образующая 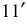 совпадает с осью симметрии развертки, которая на чертеже занимает вертикальное положение. К ней пристраивается треугольник
совпадает с осью симметрии развертки, которая на чертеже занимает вертикальное положение. К ней пристраивается треугольник 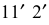 со сторонами:
со сторонами: 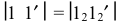 – фронтальная проекция образующей,
– фронтальная проекция образующей, 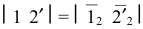 – натуральная величина диагонали,
– натуральная величина диагонали, 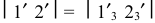 — профильная проекция хорды, стягивающей 1/12 часть окружности верхнего основания.
— профильная проекция хорды, стягивающей 1/12 часть окружности верхнего основания.
На стороне 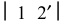 строится второй треугольник
строится второй треугольник 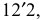 у которого
у которого 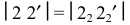 – натуральная величина образующей,
– натуральная величина образующей, 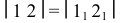 – горизонтальная проекция хорды, стягивающей 1/12 часть нижнего основания.
– горизонтальная проекция хорды, стягивающей 1/12 часть нижнего основания.
Аналогично продолжается построение следующих треугольников. Полученные точки нижнего основания (1, 2, 3,…, 7) и верхнего основания 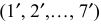 соединяются по лекалу плавной линией.
соединяются по лекалу плавной линией.
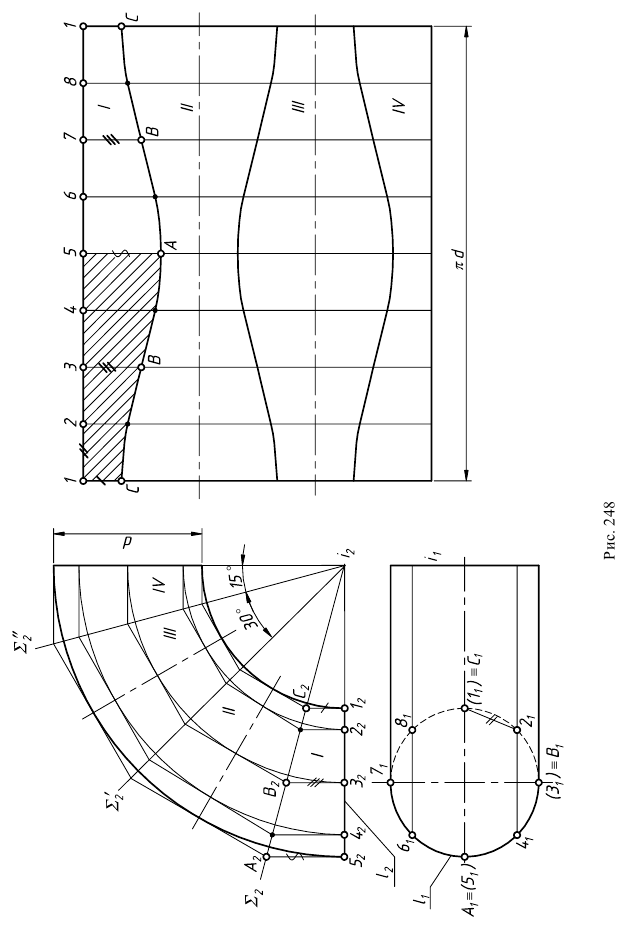
Задача 2 (рис. 248). Дано: отвод под углом 90° (1/4 часть тора).
Требуется: построить развертку поверхности тора способом описанных цилиндров.
Решение:
1. Поверхность тора проецирующими меридиональными плоскостями 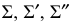 делится на четыре части. Деление надо произвести так, чтобы у крайних звеньев с торца получались окружности, к которым присоединяются трубопроводы круглого сечения. С этой целью торцевые звенья делаются равными половине средних. Торцевые звенья равняются 1/6 части отвода и их центральный угол равен 15°, а средние равны 2/6 частям каждый, центральный угол которых 30°.
делится на четыре части. Деление надо произвести так, чтобы у крайних звеньев с торца получались окружности, к которым присоединяются трубопроводы круглого сечения. С этой целью торцевые звенья делаются равными половине средних. Торцевые звенья равняются 1/6 части отвода и их центральный угол равен 15°, а средние равны 2/6 частям каждый, центральный угол которых 30°.
2. Все звенья кругового кольца заменяются описанными цилиндрами. Нормальным сечением этих цилиндров является окружность /, образующая тор. Эта окружность делится на 8 (или 12) частей. Через точки деления 2, 3…8 проводятся параллели (на фронтальной проекции это четверти окружностей радиусами 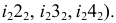 Затем строятся образующие цилиндров, касательные к параллелям. У крайних звеньев точки касания расположены на торцевых окружностях, а у средних – на линии симметрии.
Затем строятся образующие цилиндров, касательные к параллелям. У крайних звеньев точки касания расположены на торцевых окружностях, а у средних – на линии симметрии.
3. Строятся развертки описанных цилиндров способом нормального сечения. Нормальное сечение каждой части (сечение, перпендикулярное образующим цилиндров) есть окружность 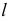 заданного диаметра
заданного диаметра 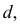 которая разворачивается в прямую линию. На рис. 248 ”развертка” нормального сечения изображается отрезком 1, 2, 3, 8, 1 горизонтальной прямой. Перпендикулярно к этой линии через точки 1, 2, 3 и т.д. проводятся образующие цилиндров, размеры которых берут с фронтальной проекции. Для торцевых звеньев образующие
которая разворачивается в прямую линию. На рис. 248 ”развертка” нормального сечения изображается отрезком 1, 2, 3, 8, 1 горизонтальной прямой. Перпендикулярно к этой линии через точки 1, 2, 3 и т.д. проводятся образующие цилиндров, размеры которых берут с фронтальной проекции. Для торцевых звеньев образующие 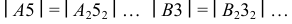 Полученные точки
Полученные точки 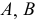 и
и 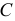 соединяют плавной кривой линией. Развертка звена симметрична относительно образующей
соединяют плавной кривой линией. Развертка звена симметрична относительно образующей 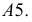 На практике обычно строится шаблон половины развертки торцевого звена (на рис. 248 заштрихованная часть). Повернув его вокруг образующей
На практике обычно строится шаблон половины развертки торцевого звена (на рис. 248 заштрихованная часть). Повернув его вокруг образующей 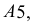 очерчивается вторая половина развертки. На развертке среднего звена укладываются 4 таких шаблона.
очерчивается вторая половина развертки. На развертке среднего звена укладываются 4 таких шаблона.
Весь тор можно раскроить из единого листа без обрезков. Для этого развертки звеньев надо разместить на листе так, как показано на рис. 248. Из чертежа видно, что звенья разрезаются попеременно, то по образующей 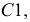 то по образующей
то по образующей 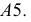 Таким образом, при сборке тора швы на звеньях получаются прерывистыми.
Таким образом, при сборке тора швы на звеньях получаются прерывистыми.
В практике при раскрое даются припуски на швы в соответствии с типом соединения.
Развертка поверхностей
Разверткой поверхности называется плоская фигура, полученная путем совмещения элементов поверхности с плоскостью.
Если для поверхности можно построить её развертку точно без складок и разрывов, то поверхность называется развертываемой, в противном случае – неразвертываемой.
К развертываемым поверхностям относятся все гранные, а из линейчатых только -цилиндрические, конические и поверхности е ребром возврата.
Построение разверток развертываемых поверхностей
Существуют следующие способы построения разверток развертываемых поверхностей:
- Способ триангуляции (треугольников);
- Способ раскатки;
- Способ нормального сечения.
Способ триангуляции (треугольников) применяется для построения разверток пирамидальных и конических поверхностей. Они выполняются по одному принципу. Каждая грань пирамиды представляет треугольник и для построения развертки необходимо определить натуральные величины всех сторон треугольника. По найденным натуральным величинам сторон вычерчиваются последовательно треугольные грани. Коническая поверхность, заменяется вписанной в нее, пирамидальной и решение задачи ведется аналогично пирамиде.
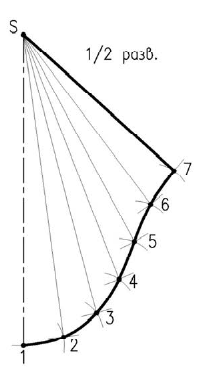
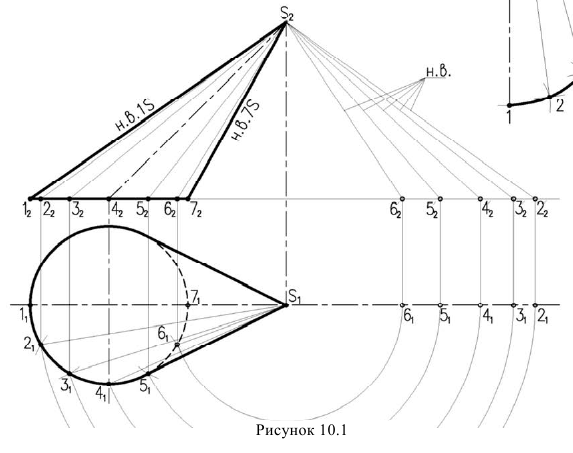
Рассмотрим пример, построения развертки, конической поверхности (рисунок 10.1)
Для построения развертки в конус вписываем двенадцатигранную пирамиду. Т.к. по условию конус расположен симметрично относительно оси, построим половину развертки.
Образующие конуса имеют разную длину, поэтому натуральную величину определяем вращением до положения параллельного фронтальной плоскости проекций. Только образующие 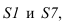 проецируются в натуральную величину. По полученным натуральным величинам образующих и размерам хорд окружности основания, между образующими, строим половину развертки, состоящую из шести треугольников вписанной в конус пирамиды. Точки основания соединяем плавной кривой линией.
проецируются в натуральную величину. По полученным натуральным величинам образующих и размерам хорд окружности основания, между образующими, строим половину развертки, состоящую из шести треугольников вписанной в конус пирамиды. Точки основания соединяем плавной кривой линией.
Способ раскатки применяется для построения разверток призматической и цилиндрической поверхности. И если поверхность цилиндрическая, то в нее вписывается призматическая поверхность. Поэтому принцип построения этих разверток одинаков.
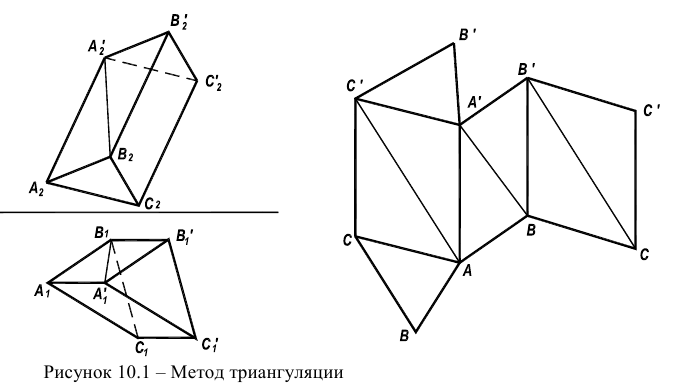
Рассмотрим пример построения развертки наклонной треугольной призмы
Развертку можно выполнять только в том случае, если боковые ребра призмы параллельны плоскости проекций, как на рисунке 10.2. В противном случае, сначала выполняется преобразование (методом замены строится новая проекция на плоскость параллельную ребрам). При выполнении развертки методом раскатки точки 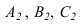 перемещаются по перпендикулярам к боковым ребрам призмы. А натуральные величины отрезков
перемещаются по перпендикулярам к боковым ребрам призмы. А натуральные величины отрезков 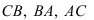 берутся из горизонтальной проекции, т.к. основание призмы параллельно плоскости
берутся из горизонтальной проекции, т.к. основание призмы параллельно плоскости 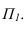 Боковые ребра остаются на развертке параллельными, т.к. каждая грань призмы является параллелограммом.
Боковые ребра остаются на развертке параллельными, т.к. каждая грань призмы является параллелограммом.
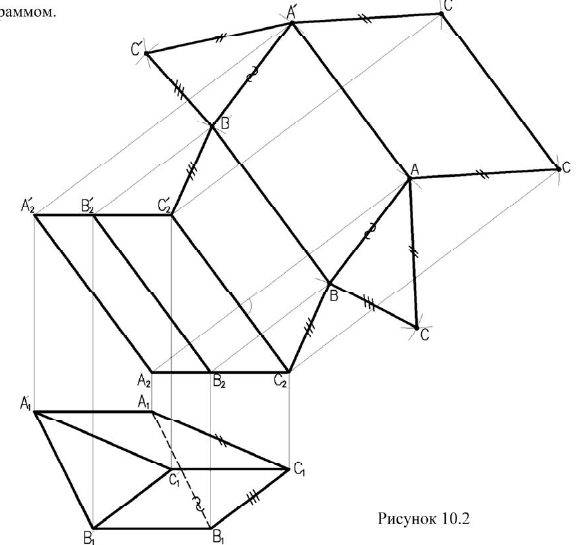
Способ нормального сечения используется также для построения разверток призматической и цилиндрической поверхностей.
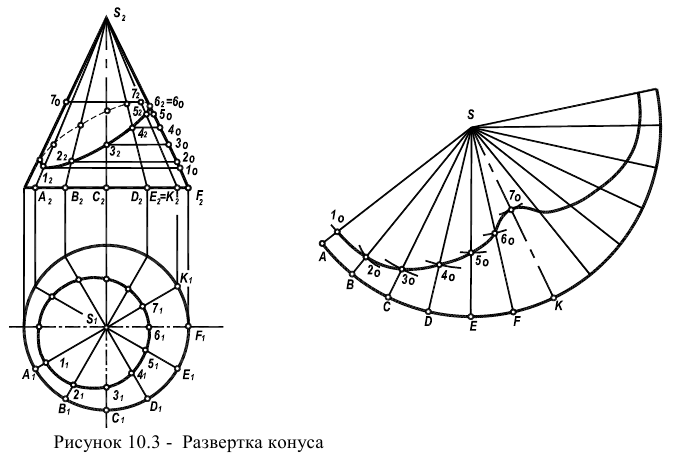
Рассмотрим построение развертки призмы изображенной на рисунке 10.3а. Для этого построим нормальное сечение – сечение перпендикулярное боковым ребрам призмы  Определим натуральную величину этого сечения, расположив его параллельно плоскости проекций
Определим натуральную величину этого сечения, расположив его параллельно плоскости проекций 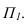 Для построения развертки боковой поверхности призмы, строим периметр треугольника нормального сечения (рисунок 10.36). Через точки сечения 1,2,3,1 проводим боковые ребра перпендикулярно сечению и откладываем на них натуральную величину, которая берется из фронтальной проекции рисунка 10.3а.
Для построения развертки боковой поверхности призмы, строим периметр треугольника нормального сечения (рисунок 10.36). Через точки сечения 1,2,3,1 проводим боковые ребра перпендикулярно сечению и откладываем на них натуральную величину, которая берется из фронтальной проекции рисунка 10.3а.
Соединив построенные точки, получим развертку боковой поверхности данной призмы (рисунок 10.36).
Построение приближенной развертки неразвёртываемых поверхностей
Когда надо развернуть неразвертывающуюся поверхность ее заменяют развертывающейся (цилиндрической, конической, одной или несколькими), имеющей общие линии е данной.
Такая замена называется аппроксимацией, а полученная развертка – условной или приближенной.
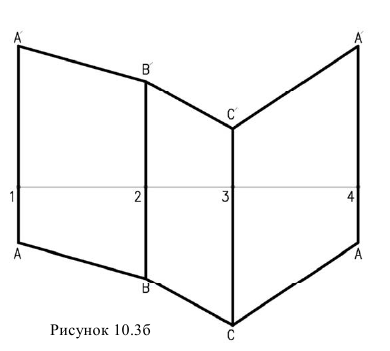
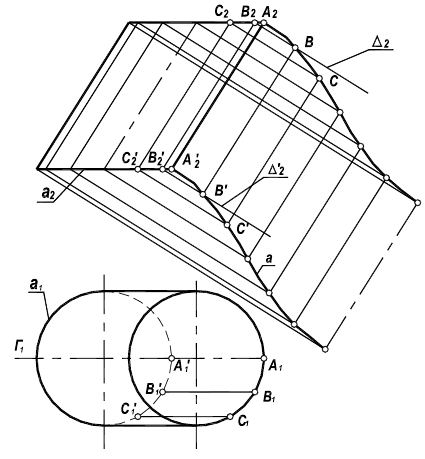
Рассмотрим построение такой развертки на примере полусферы (рисунок 10.4).
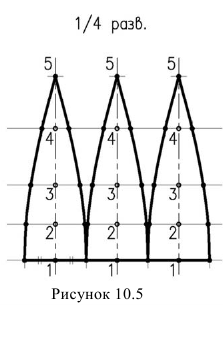
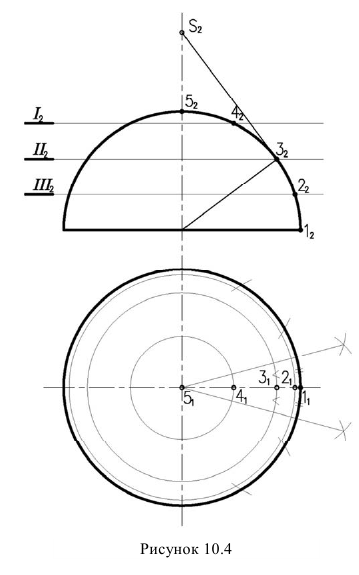
Полусферическую поверхность разделим меридиональными плоскостями на дольки (на 12 частей). По высоте сферу делим на несколько частей параллелями. Возьмем одну дольку, ось которой параллельна фронтальной проекции и развернем ее в плоскую фигуру, ось которой будет равна 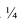 длины окружности (рисунок 10.5).
длины окружности (рисунок 10.5).
Через точки 1,2,3,4 проводим перпендикуляры к оси дольки и на них откладываем от оси в обе стороны половину ширины каждой дольки измеренную на горизонтальной проекции. Полная развертка составит двенадцать таких долек.
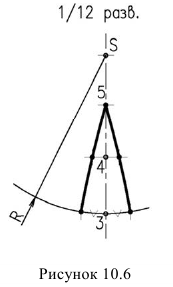
Если развертывающаяся долька начинается с экватора, то на развертке линия экватора изобразится прямой (рисунок 10.5). Если же долька начинается какой-то параллелью, то на развертке эта параллель изобразится окружностью. Например, параллель, проходящая через точку 3. Для нахождения радиуса этой окружности на фронтальной проекции необходимо провести касательную прямую в точке 5, к окружности до пересечения с осью сферы 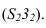 . И при построении дольки через точку 3 проводим дугу радиуса
. И при построении дольки через точку 3 проводим дугу радиуса 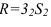 (рисунок 10.6).
(рисунок 10.6).
Решение задач
Задача 1. Построить развертку усеченного прямого кругового цилиндра (рисунок 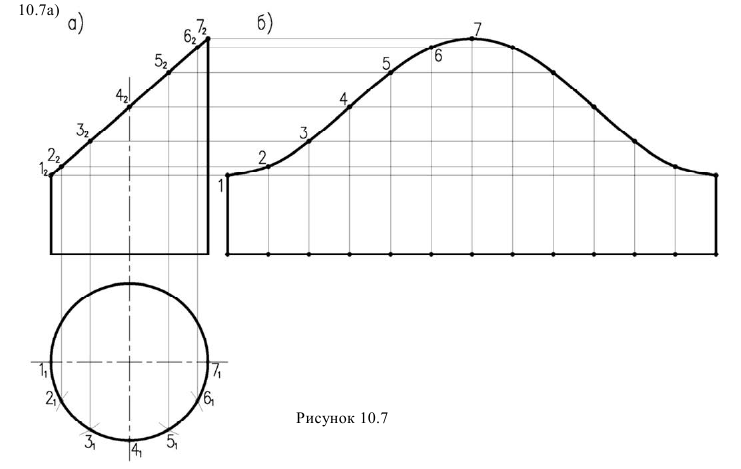
Развертка боковой поверхности цилиндра строится фактически методом нормального сечения, т.к. основание цилиндра перпендикулярно оси. Окружность основания развертывается в прямую линию равную длине окружности 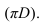 Можно ее построить, отложив размер хорд, соединяющих точки основания. Конечно, длина будет тем точнее, чем на большее число частей разбита окружность. Кривая сечения на развертке изобразится синусоидой (рисунок 10.7,б) Для построения полной развертки необходимо к развертке боковой поверхности добавить основание и натуральную величину сечения.
Можно ее построить, отложив размер хорд, соединяющих точки основания. Конечно, длина будет тем точнее, чем на большее число частей разбита окружность. Кривая сечения на развертке изобразится синусоидой (рисунок 10.7,б) Для построения полной развертки необходимо к развертке боковой поверхности добавить основание и натуральную величину сечения.
Задача 2. Построить развертку усеченного прямого кругового конуса (рисунок
10.8а).
Так как в прямом круговом конусе все образующие одинаковой длины, развертка представляет собой сектор окружности с радиусом равным длине образующей конуса 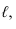 а длина дуги равная длине окружности основания конуса (рисунок 10.86). Поэтому, разделив окружность основания на 12 частей и затем, отложив на дуге сектора таких же 12 частей, получим развертку.
а длина дуги равная длине окружности основания конуса (рисунок 10.86). Поэтому, разделив окружность основания на 12 частей и затем, отложив на дуге сектора таких же 12 частей, получим развертку.
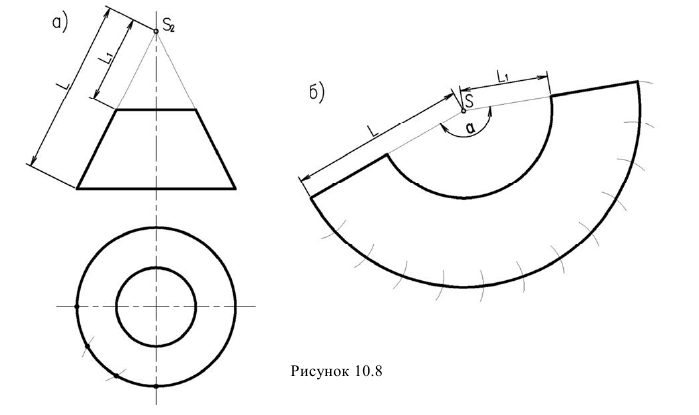
Угол а также можно определить по формуле:
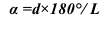 где d – диаметр основания.
где d – диаметр основания.
Что такое развертка поверхности
Разверткой называется плоская фигура, полученная при совмещении поверхности геометрического тела с одной плоскостью (без наложения граней или иных элементов поверхности друг на друга).
Приступая к изучению развертки поверхности, последнюю целесообразно рассматривать как гибкую, нерастяжимую пленку. Некоторые из представленных таким образом поверхностей можно путем изгибания совместить с плоскостью.
Если отсек поверхности может быть совмещен с плоскостью без разрывов и склеивания, то такую поверхность называют развертывающейся, а полученную плоскую фигуру – ее разверткой.
Свойства развёртки
Длины двух соответствующих линий поверхности и ее развертки равны между собой;
Угол между линиями на поверхности равен углу между соответствующими им линиями на развертке;
Прямой на поверхности соответствует также прямая на развертке;
Параллельным прямым на поверхности соответствуют также параллельные прямые на развертке;
Если линии, принадлежащей поверхности и соединяющей две точки поверхности, соответствует прямая на развертке, то эта линия является геодезической.
Способы построения развёртки
Существует три способа построения развертки многогранных поверхностей:
- Способ треугольника
- Способ нормального сечения
- Способ раскатки
К развертывающим поверхностям относятся все поверхности гранные, то есть поверхности, состоящие из отсеков плоскостей. Из кривых поверхностей к ним относятся только те линейчатые поверхности. У которых касательная плоскость касается поверхности о всех точках ее прямолинейной образующей. Этому условию удовлетворяют три типа линейчатых поверхностей: цилиндрическая, коническая, торсовая [1].
Все остальные поверхности относятся к неразвёртывающимся или косым.
Развертки могут быть точными. Это развертки прямого кругового цилиндра и конуса. Если пренебречь графическими ошибками, то к точным развёрткам можно отнести развертки многогранников.
Развертки всех других поверхностей как развертывающихся, так и неразвёртывающихся, которые, как правило, строятся графически, являются приближенными.
Любая конструкция рассматривается как комбинация простейших геометрических поверхностей.
Рассмотрим наиболее простую гранную поверхность.
Развертки гранных поверхностей
Разверткой многогранной поверхности называется плоская фигура, получаемая последовательным совмещением всех граней поверхности с плоскостью.
Так как все грани многогранной поверхности изображаются на развертке в натуральную величину, построение ее сводится к определению величины истинных размеров и формы отдельных граней поверхности – плоских многоугольников и вычерчиванию их в том порядке, в каком они следуют друг за другом на самой поверхности.
Рассмотрим на примере решение задачи
Развертка поверхности прямой призмы
Представим, что поверхности призмы разрезана по ребру АА1.
Развернем ее боковую поверхность и совместим се грани с плоскостью чертежа (рис.10.1) [1].
Так как призма прямая, то ее основание развернется в прямую линию. Поэтому на свободном поле чертежа проведем прямую линию, на которой произвольно выберем точку А. От этой точки развернем основание призмы. Поскольку основание данной призмы проецируется на горизонтальную плоскость проекций в натуральную величину, на прямой от точки А последовательно отложим отрезки, равные соответствующим сторонам основания.
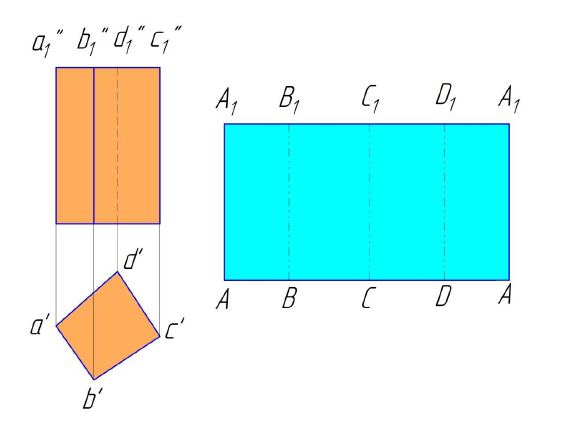
Рисунок 10.1- Развертка поверхности прямой призмы
Учитывая, что призма прямая и ее ребра проецируются на фронтальную плоскость проекций в натуральную величину, к прямой – развёртке основания в точках 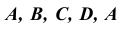 – проведем перпендикуляры, на которых отложим величину ребра. Соединив точки
– проведем перпендикуляры, на которых отложим величину ребра. Соединив точки 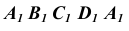 , получим развертку боковой поверхности призмы.
, получим развертку боковой поверхности призмы.
Полная развертка призмы состоит из развертки ее боковой поверхности и двух оснований – верхнего и нижнего.
Так как призма прямая, и ее основание проецируется на горизонтальную плоскость проекций в натуральную величину, к боковой развертке в любом месте пристраиваем два четырехугольника 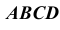 , перенося их адекватно с горизонтальной проекции призмы.
, перенося их адекватно с горизонтальной проекции призмы.
Развертка поверхности наклонной призмы
Построение развёртки может быть выполнено способом нормального (перпендикулярного) сечения. Способом раскатки и способом треугольников (триангуляция). Рассмотрим каждый способ в раздельности [1].
Построение развертки способом нормального сечения (рис.10.2).
Рисунок 10.2 – Построение развертки призмы способом нормального сечения
Если разрезать боковую поверхность наклонной призмы по любому ребру и совместить с плоскостью чертежа, то очевидно, что основание такой призмы развернется не в прямую, а в ломаную линию.
Если же призму пересечь плоскостью, перпендикулярной рёбрам, то полученное при этом сечение при развертывании даст прямую линию. Поэтому для решения задачи необходимо:
- Пересечь призму плоскостью, перпендикулярной ее ребрам;
- Найти проекции сечения вспомогательной плоскости с призмой;
- Определить истинную величину нормального сечения;
- Развернуть полученный четырехугольник сечения прямую линию;
- Отложить вверх и вниз от этой линии истинные величины отрезков ребер относительно сечения призмы.
Проведем плоскость Р, перпендикулярную ребрам призмы (рис.10.2 а).
Эта плоскость Р – фронтально проецирующая и следы ее будут перпенди-кулярны соответствующим проекциям ребер.
Найдем проекции сечения призмы плоскостью Р. Фронтальные проекции 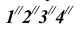 точек пересечения ребер с плоскостью лежат на ее фронтальном следе
точек пересечения ребер с плоскостью лежат на ее фронтальном следе  , горизонтальные проекции
, горизонтальные проекции 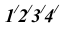 определяются по линиям связи. Соединив проекции точек прямыми, получим проекции сечения.
определяются по линиям связи. Соединив проекции точек прямыми, получим проекции сечения.
Истинную величину фигуры (четырёхугольника) сечения определяем любым способом, например. Способом замены плоскостей проекций.
На свободном поле чертежа (рис.10.2 б) проведём горизонтальную прямую, на которой последовательно отложим от точки 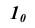 истинные величины сторон четырехугольного сечения. Через точки
истинные величины сторон четырехугольного сечения. Через точки 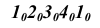 проведем перпендикуляры к прямой, на которых откладываем истинные величины отрезков боковых ребер вверх и вниз от прямой
проведем перпендикуляры к прямой, на которых откладываем истинные величины отрезков боковых ребер вверх и вниз от прямой 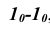 , перенося соответствующие отрезки с фронтальной проекции призмы (так как ребра призмы параллельны плоскости проекций V). Соединив концы сложенных отрезков, получим развертку боковой поверхности призмы.
, перенося соответствующие отрезки с фронтальной проекции призмы (так как ребра призмы параллельны плоскости проекций V). Соединив концы сложенных отрезков, получим развертку боковой поверхности призмы.
Развертка призмы способом раскатки
Так как основание призмы на горизонтальной плоскости проекций изображается в натуральную величину, ее развертку можно построить более удобным способом, чем способ нормального сечения.
Построения развертки призмы способом раскатки показано на рис 10.3.
Поскольку ребра призмы параллельны фронтальной плоскости проек-ций, то каждую грань можно повернуть вокруг бокового ребра (как вокруг фронтали) до положения, при котором грань будет параллельна плоскости V и спроецируется на эту плоскость без искажения. Разворачивая таким образом одну грань за другой по порядку, получим развертку боковой поверхности.
Практически такое построение выполняется следующим образом [1] .
Так как при повороте грани 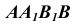 вокруг ребра
вокруг ребра 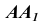 точка В будет перемещаться по окружности, фронтальная проекция которой изображается прямой, перпендикулярной
точка В будет перемещаться по окружности, фронтальная проекция которой изображается прямой, перпендикулярной 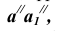 , через точку
, через точку 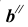 проведем прямую, перпен-дикулярную
проведем прямую, перпен-дикулярную 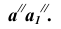 Радиусом
Радиусом 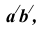 равным истинной величине стороны основания призмы
равным истинной величине стороны основания призмы 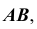 из точки
из точки 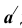 делаем засечку на перпендикуляре.
делаем засечку на перпендикуляре.
Таким образом, находим точку 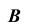 развертки. Через точку
развертки. Через точку 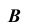 проведем прямую, параллельную
проведем прямую, параллельную 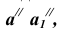 на которой откладываем истинную величину ребра призмы, т.е. величину его фронтальной проекции, получим точку
на которой откладываем истинную величину ребра призмы, т.е. величину его фронтальной проекции, получим точку 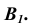
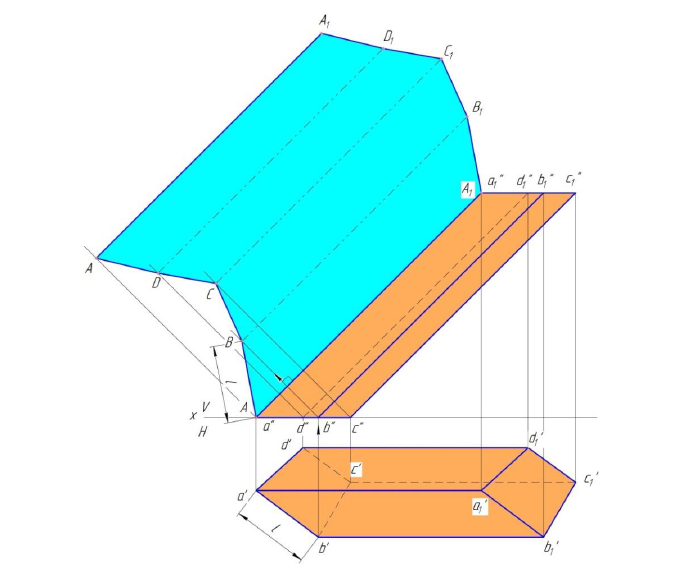
Рисунок 10.3 – Построение развертки призмы способом раскатки
Из точки 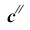 проведем перпендикуляр к
проведем перпендикуляр к 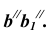 Сделав в нем засечку радиусом
Сделав в нем засечку радиусом 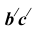 из точки
из точки 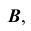 найдем точку
найдем точку 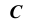 развертки. Через
развертки. Через 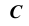 проведем прямую, параллельную
проведем прямую, параллельную 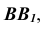 и отложим на ней величину ребра призмы. Получим точку
и отложим на ней величину ребра призмы. Получим точку 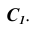 Аналогичным способом определяются точки
Аналогичным способом определяются точки 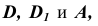
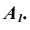 Соединив их прямыми, соответствующими сторонам оснований, получим развертку боковой поверхности призмы.
Соединив их прямыми, соответствующими сторонам оснований, получим развертку боковой поверхности призмы.
Следует отметить, что если ребра призмы не параллельны плоскости проекций, а развертку необходимо выполнить раскаткой, то предварительно меняют плоскости проекций новой системой, в которой ребра окажутся параллельными одной из плоскостей проекций.
Построение развертки пирамиды (способ треугольника)
Так как боковые грани наклонной призмы являются парраллелограммами, для построение их истиной величины недостаточно иметь только истинные значения ребер и сторон основания призмы. Для этого необходима еще одна величина – диагонали, что и положено в основу построения развертки боковой поверхности призмы способом треугольника [1].
При построении развертки следует:
- Разбить каждую из граней призмы диагоналями на треугольники;
- Определить длину неизвестных сторон треугольника (например, методом плоскопараллельного перемещения);
- Построить треугольники в плоскости чертежа в той последователь-ности, в которой они расположены в многограннике.
Задача. Построить развертку поверхности пирамиды SABC (рис.10.4).
Развернутая поверхность пирамиды состоит из треугольника – ее боковых граней, расположенных в определенной последовательности, и основания.
Для построения боковых граней – треугольника развертки, необходимо определить истинные длины боковых ребер с учетом того, что основание пирамиды на горизонтальной проекции изображается в натуральную величину. Используем наиболее простой способ – способ вращения. Выберем ось вращения I, перпендикулярную плоскости H и проходящую через вершину пирамиды S. Поворачивая вокруг оси горизонтальные проекции ребер до положения, параллельного оси X, получим на фронтальной проекции отрезки 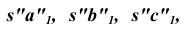 представляющие собой истинные длины ребер пирамиды.
представляющие собой истинные длины ребер пирамиды.
Каждая боковая грань строится как треугольник по трем известным сторонам, и развертка получается в виде примыкающих друг к другу в соответствующем порядке треугольников с общей вершиной S.
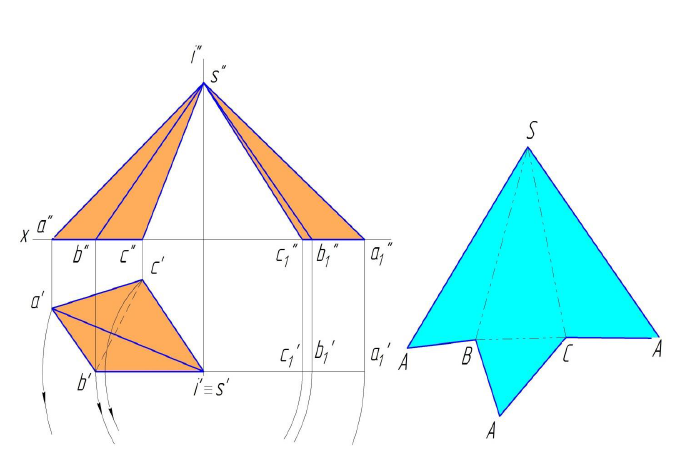
Рисунок 10.4 – Построение развертки пирамиды
Развертывание поверхностей вращения
Как было упомянуто ранее, развертки кривых поверхностей, как правило, строятся приближенные. Даже для таких развертывающихся поверхностей как цилиндрическая и коническая, которые имеют теоретические точные развертки, на практике строят их приближенными, заменяя (аппроксимируя) эти поверхности гранными, вписывая или описывая их вокруг заданной поверхности.
Надо иметь в виду, что если развертываемый элемент имеет плоскость симметрии, то линию разреза поверхности лучше выбирать так, чтобы развертка получалась в виде симметричной фигуры. При этом предпочтительнее выбирать наиболее короткую линию разреза.
Развёртка цилиндрической поверхности
Развертка цилиндрической поверхности выполняется аналогично развертке призмы. Предварительно в заданный цилиндр вписывают n-угольную призму. Чем больше углов в призме, тем точнее развертка ( при n → ∞ призма преобразуется в цилиндр).
На рис. 10.6. приведено построение полной развёртки усечённого цилиндра (см. условия задания рис. 8.2) стр. 61.
Для построения развертки боковой поверхности на горизонтальной прямой откладывают длину окружности основания πd и делят ее на 12 равных частей (с определенной степенью точности вместо 1/12 длины окружности можно откладывать длину соответствующей хорды) [5]. Из точек деления проводят перпендикуляры к отрезку πd и на них откладывают длины образующих от основания до секущих плоскостей α , β, χ. Для построения точек А, В, С, D на развертке использовано расположение этих точек на горизонтальной проекции цилиндра (от точек деления откладывают длины дуг 2А и 12В) Точки 1, А, С и 1, В, D соединены прямыми линиями.
Точки С, 3…11, D соединяют плавной линией.
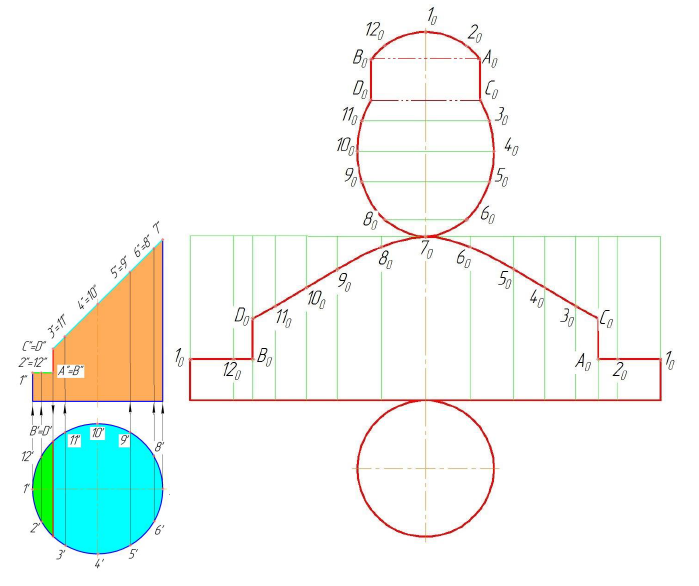
Рисунок 10.6 – Полная развёртка поверхности усечённого цилиндра.
К прямой линии πd (развертка нижнего основания цилиндра) присоединяют окружность основания, а к верхней части боковой развертки натуральные фигуры сечения плоскостями (часть эллипса, прямоугольник, сегмент окружности).
Развертка поверхности конуса
Развертка боковой поверхности прямого кругового конуса с радиусом снованием r представляет собой круговой сектор, радиус которого равен длине образующей конуса L, а центральный угол φ=Пr/L.
Чтобы избежать вычислений, связанных с определением длины дуги сектора или угла, вначале в основанием конуса вписывают правильный 12-угольник. Затем на свободном поле чертежа из точки S проводят дугу радиусом l. От произвольно выбранной начальной точки по дуге последо-вательно засекают 12 дуг, хорды которых равны стороне 12-угольника.
Таким образом, построение развертки боковой поверхности конуса заменяют построением развертки, вписанной в него правильной 12-гранной пирамиды [1] (рис. 10.7).
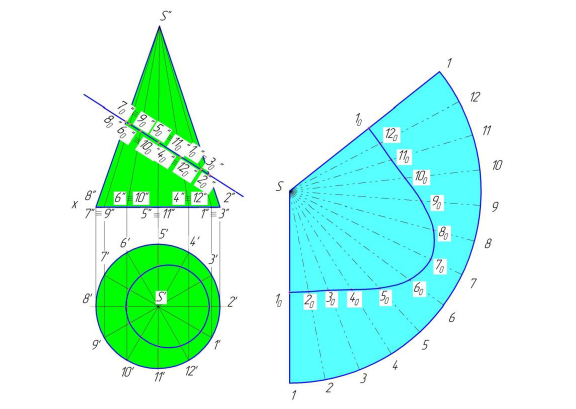
Рисунок 10.7 – Построение развертки боковой поверхности конуса
На рисунке 10.7 построена развертка боковой поверхности конуса и нанесена ней линия сечения плоскостью P.
В конус впишем правильную 12-гранную пирамиду. Для этого основание конуса разбиваем на 12 равных частей (рис. 7 а). На фронтальной плоскости проекций получим фронтальные проекции (на оси X) точек деления 1″, 2″ ,3″ и т.д. и соединим их с точкой S′ (1″s″, 2″s″, 3″s″, 4″s″ и т.д. – фронтальные проекции образующих конуса, т.е. ребер вписанной пирамиды).
На свободном поле чертежа из произвольно выбранной точки S, проведем угу радиусом L и отложим на ней 12 дуг, хорды которых равны сторонам основания пирамиды (рис. 10.7). Полученные точки соединим с вершиной S, в результате чего образуется развертка боковой поверхности конуса.
Затем на ней строим линию сечения. Для этого найдем истинные величины отрезков образующих, или ребер пирамиды, от вершины до плоскости сечения. Истинные величины можно найти любым способом. Найденные отрезки отложим на соответствующих образующих на развертке. Полученные точки соединим плавной кривой. Последняя и будет линией сечения.
Развертка наклонных тел вращения
Развертки наклонных тел вращения строятся аналогично предыдущим задачам, т.е. поверхность вращения аппроксимируется гранной ( пирамидой или призмой) соответственно с максимально возможным числом граней, а затем используются все те же методы решения, что и при развертке гранных поверхностей.
На рис.10.8 приведено построение полной равертки наклонного конуса [1].
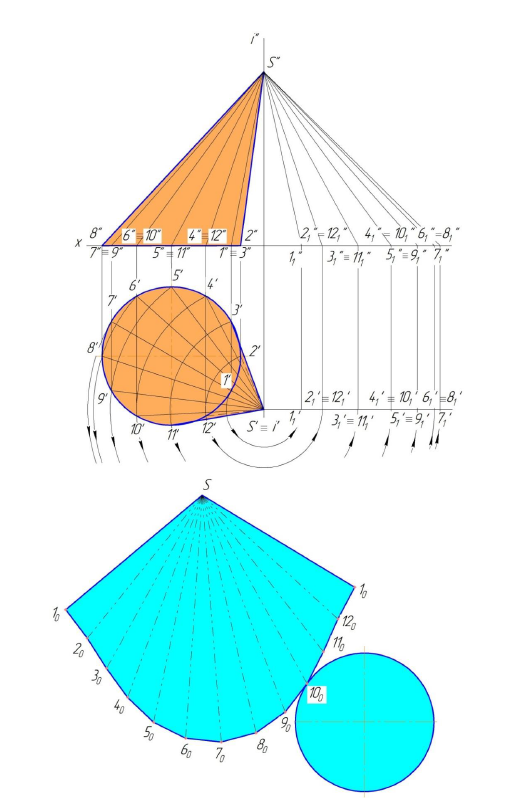
Рисунок 10.8 – Построение полной развертки наклонного конуса
Построение условной развертки сферы
На рисунке 10.9 показано построение условной развертки сферы [5].
Так как сферическая поверхность принадлежит к числу не развертывающихся, то возможна лишь ее приближенная (условная) развертка. Способ построения состоит в том, что сферу разбивают с помощью меридианов на узкие равные между собой доли (клинья). Каждую такую долю заменяют описанной цилиндрической поверхностью, которая касается сферы по среднему меридиану доли. Этот средний меридиан будет нормальным сечением цилиндрической поверхности. Границами цилиндрической поверхности будут плоскости меридианов, ограничивающих рассматриваемую долю.
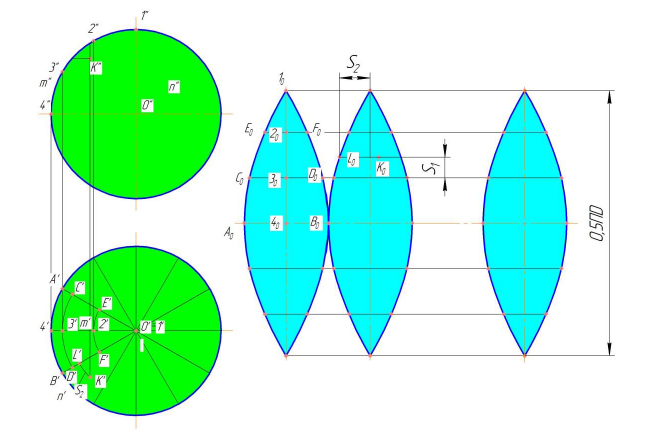
Рисунок 10.9 – Построение условной развертки сферы.
Горизонтальную проекцию n’ экватора n разбиваем на 12 равных частей и через полученные точки проводим горизонтальные проекции меридианов ( рис. 10.9 а).
Рассмотрим построение приближенной развертки 1/12 части (доли) сферы, средним меридианом которой является меридиан 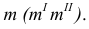
Заменим часть сферы цилиндрической поверхностью. Описанной около нее. Образующие этой поверхности будут фронтально-проецирующими прямыми. Для построения развертки элемента цилиндрической поверхности половину фронтального меридиана разбиваем на 6 равных частей (отмечены точками 1, 2, 3, 4 только половина симметричной части). На горизонтальной прямой (рис. 8.14,б) откладываем отрезок 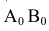 равный 1/12 окружности диаметра D. Через середину
равный 1/12 окружности диаметра D. Через середину 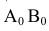 проводим перпендикуляр и откладываем на нем отрезки
проводим перпендикуляр и откладываем на нем отрезки 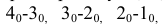 равные длине дуг меридиана m. Через полученные точки проводим горизонтальные прямые, на которых откладываем отрезки
равные длине дуг меридиана m. Через полученные точки проводим горизонтальные прямые, на которых откладываем отрезки 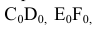 соответственно равные длине образующим цилиндрической поверхности C-D, E-F. Отрезки A-B, C-D, E-F представляют собой спрямленные дуги соответствующих параллелей сферической доли. Соединив найденные точки лекальной кривой. Получим плоскую фигуру, являющейся приближенной разверткой 1/12 части сферы.
соответственно равные длине образующим цилиндрической поверхности C-D, E-F. Отрезки A-B, C-D, E-F представляют собой спрямленные дуги соответствующих параллелей сферической доли. Соединив найденные точки лекальной кривой. Получим плоскую фигуру, являющейся приближенной разверткой 1/12 части сферы.
Для придания каждой доли развертки сферической поверхности кроме изгибания проводят растяжение и сжатие материала.
Положение произвольной точки К принадлежащей поверхности сферы, может быть определено на развертке с помощью двух «координат» – длин дуг 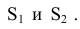 Дуга
Дуга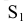 определяет смещение точки Л от одной из параллелей по меридиану, а дуга
определяет смещение точки Л от одной из параллелей по меридиану, а дуга 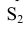 – смещение ее от одного из меридианов по параллели сферы.
– смещение ее от одного из меридианов по параллели сферы.
Построение развёрток поверхностей
Развёрткой называется плоская фигура, полученная при совмещении поверхности геометрического тела с одной плоскостью (без наложения граней или иных элементов поверхности друг на друга.)
Развертка усеченной призмы
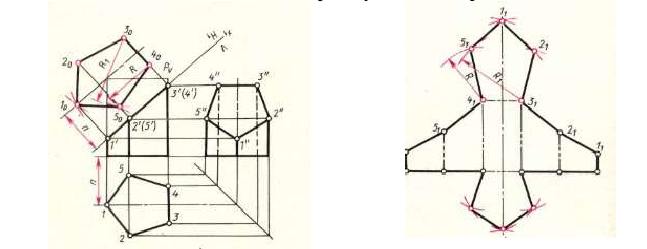
Развертку боковой поверхности с основанием и фигурой сечения призмы строят следующим образом. Проводят прямую, на которой откладывают пять отрезков, равных длинам сторон пятиугольника, лежащего в основании призмы. Из полученных точек проводят перпендикуляры, на которых откладывают действительные длины ребер усеченной призмы, беря их с фронтальной или профильной проекции, получают развертку боковой поверхности призмы.
К развертке боковой поверхности пристраивают фигуру нижнего основания — пятиугольник и фигуру сечения. При этом используют метод триангуляции (метод засечек). На рисунке показано построение вершины 5 методом триангуляции. Линии сгиба по ГОСТ 2.303—68 показывают на развертке штрих-пунктирной линией с двумя точками.
- Заказать чертежи
Развертка усеченного цилиндра
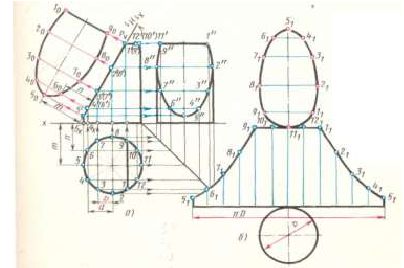
Для построения развертки на горизонтальной прямой откладывают длину окружности основания, равную 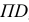 и делят ее на 12 равных частей. Из точек деления восставляют перпендикуляры к отрезку
и делят ее на 12 равных частей. Из точек деления восставляют перпендикуляры к отрезку 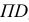 , на них откладывают действительные длины образующих цилиндра от основания до секущей плоскости Р, которые взяты с фронтальной или профильной проекции цилиндра. Полученные точки
, на них откладывают действительные длины образующих цилиндра от основания до секущей плоскости Р, которые взяты с фронтальной или профильной проекции цилиндра. Полученные точки 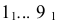 соединяют по лекалу плавной кривой. Затем фигуру сечения соединяют с частью верхнего основания цилиндра, ограниченного хордой
соединяют по лекалу плавной кривой. Затем фигуру сечения соединяют с частью верхнего основания цилиндра, ограниченного хордой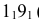 (сегмент), а фигуру нижнего основания цилиндра (окружность) соединяют с нижней частью развертки.
(сегмент), а фигуру нижнего основания цилиндра (окружность) соединяют с нижней частью развертки.
Развертка усеченной пирамиды
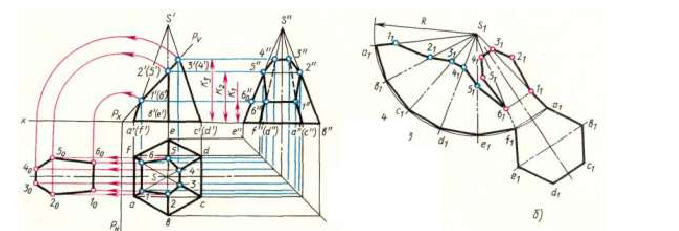
Сначала строят развертку неусеченной пирамиды, все грани которой, имеющие форму треугольника, одинаковы. На плоскости намечают точку 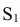 (вершину пирамиды) и из нее, как из центра, проводят дугу окружности радиусом R, равным действительной длине бокового ребра пирамиды. Действительную длину ребра можно определить по профильной проекции пирамиды, например отрезки s”e” или s”b’, так как эти ребра параллельны плоскости W и изображаются на ней действительной длиной. Далее по дуге окружности от любой точки, например
(вершину пирамиды) и из нее, как из центра, проводят дугу окружности радиусом R, равным действительной длине бокового ребра пирамиды. Действительную длину ребра можно определить по профильной проекции пирамиды, например отрезки s”e” или s”b’, так как эти ребра параллельны плоскости W и изображаются на ней действительной длиной. Далее по дуге окружности от любой точки, например 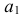 откладывают шесть одинаковых отрезков, равных действительной длине стороны шестиугольника — основания пирамиды. Действительную длину стороны основания пирамиды получаем на горизонтальной проекции (отрезок ab). Точки
откладывают шесть одинаковых отрезков, равных действительной длине стороны шестиугольника — основания пирамиды. Действительную длину стороны основания пирамиды получаем на горизонтальной проекции (отрезок ab). Точки 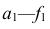 соединяют прямыми с вершиной .
соединяют прямыми с вершиной .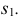 .Затем от вершины
.Затем от вершины 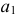 на этих прямых откладывают действительные длины отрезков ребер до секущей плоскости.
на этих прямых откладывают действительные длины отрезков ребер до секущей плоскости.
На профильной проекции усеченной пирамиды имеются действительные длины только двух отрезков — 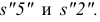 Действительные длины остальных отрезков определяют способом вращения их вокруг оси, перпендикулярной к плоскости Н и проходящей через вершину
Действительные длины остальных отрезков определяют способом вращения их вокруг оси, перпендикулярной к плоскости Н и проходящей через вершину 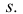 Например, повернув отрезок s”6″ около оси до положения, параллельного плоскости W, получим на этой плоскости его действительную длину. Для этого достаточно через точку 6” провести горизонтальную прямую до пересечения с действительной длиной ребра SE (или SB). Отрезок
Например, повернув отрезок s”6″ около оси до положения, параллельного плоскости W, получим на этой плоскости его действительную длину. Для этого достаточно через точку 6” провести горизонтальную прямую до пересечения с действительной длиной ребра SE (или SB). Отрезок 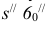 представляет собой действительную длину отрезка S6 .
представляет собой действительную длину отрезка S6 .
Полученные точки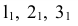 и т. д. соединяют прямыми и пристраивают фигуры основания и сечения, пользуясь методом триангуляции. Линии сгиба на развертке проводят штрихпунктирной линией с двумя точками.
и т. д. соединяют прямыми и пристраивают фигуры основания и сечения, пользуясь методом триангуляции. Линии сгиба на развертке проводят штрихпунктирной линией с двумя точками.
Развертка усеченного конуса
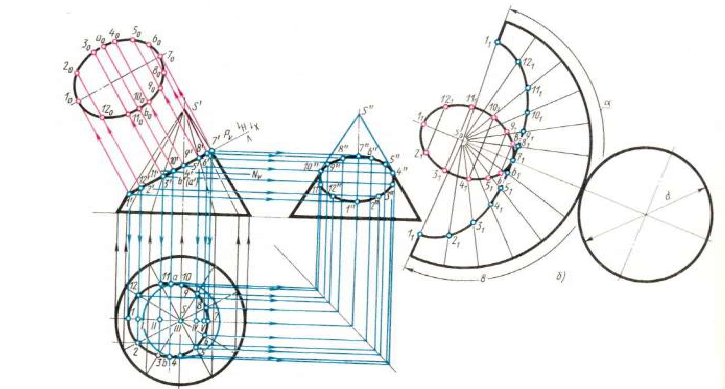
Построение развертки поверхности конуса начинают с проведения дуги окружности радиусом, равным длине образующей конуса из точки л». Длина дуги определяется углом а:
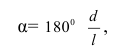
где d — диаметр окружности основания конуса в мм;
l — длина образующей конуса в мм.
Дугу делят на 12 частей и полученные точки соединяют с вершиной л>. От вершины 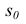 откладывают действительные длины отрезков образующих от вершины конуса до секущей плоскости Р.
откладывают действительные длины отрезков образующих от вершины конуса до секущей плоскости Р.
Действительные длины этих отрезков находят, как и в примере с пирамидой, способом вращения около вертикальной оси, проходящей через вершину конуса. Так, например, чтобы получить действительную длину отрезка S2, надо из 2′ провести горизонтальную прямую до пересечения в точке 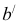 с контурной образующей конуса, являющейся действительной ее длиной.
с контурной образующей конуса, являющейся действительной ее длиной.
К развертке конической поверхности пристраивают фигуры сечения и основания конуса.
Развертки поверхностей
Фигура, получающаяся при совмещении всех точек поверхности с плоскостью (без складок и разрывов), получила название развертки. Поверхности же, допускающие такую операцию, называют развертывающимися.
Построение разверток является важной практической задачей, что связано с изготовлением множества изделий из листового материала (резервуары и трубы, изделия швейной и кожевенной промышленности и т.п.).
Из физической модели процесса развертывания поверхности на плоскость следует, что площадь отсека поверхности должна быть равна площади отсека плоскости на развертке.
Свойство сохранения площади влечет за собой справедливость следующих двух утверждений: длины соответственных линий поверхности и ее развертки равны, углы, образованные линиями поверхности, равны углам, составленным их образами на развертке. Углом между двумя линиями поверхности в их точке пересечения называют угол, составленный касательными, проведенными к кривым в точке.
Это в свою очередь приводит к следующему: прямая поверхности отображается на прямую развертки; параллельные прямые поверхности, отображаются на параллельные прямые развертки.
На этих свойствах и базируются графические и машинные алгоритмы построения разверток.
Из дифференциальной геометрии известно, что к развертывающимся поверхностям относятся только поверхности нулевой кривизны (состоящие только из параболических точек). У этих (линейчатых) поверхностей касательные плоскости, проведенные во всех точках одной образующей, совпадают.
Изо всего множества линейчатых поверхностей развернуты на плоскость могут быть только цилиндрические, конические и торсовые. Развертки для них строятся приближенно. В процессе построения развертки эти поверхности аппроксимируются (заменяются) многогранными поверхностями. Последнее вызвано тем, что спрямление кривых линий базируется на замене их ломаными. Точные развертки аппроксимирующих многогранных поверхностей принимают за приближенные развертки развертываемых поверхностей.
Развертки гранных поверхностен
Процесс получения развертки гранной поверхности сводится к совмещению с плоскостью ее граней. Для гранной поверхности всегда можно построить развертку.
К наиболее распространенным многогранным поверхностям следует отнести призмы и пирамиды.
Развертка поверхности призмы строится в основном двумя способами, с помощью треугольников (триангуляции) и нормальных сечений.
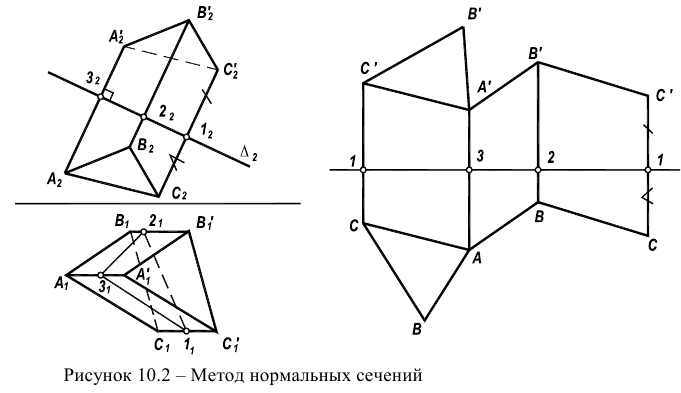
первом способе каждая грань призмы разбивается на два треугольника, для которых определяются натуральные длины сторон. Затем на плоскости последовательно строят треугольники в натуральную величину. Способ основан на свойстве «жесткости» треугольника — три отрезка определяют единственный треугольник.
По способу нормальных сечений призма пересекается плоскостью 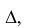 перпендикулярной ее боковым ребрам. Затем определяются длины сторон ломаной линии (сечения), и она (ломаная) развертывается в отрезок прямой.
перпендикулярной ее боковым ребрам. Затем определяются длины сторон ломаной линии (сечения), и она (ломаная) развертывается в отрезок прямой.
Через точки, соответствующие положению вершин, проводятся прямые, перпендикулярные к развертке ломаной. На построенных перпендикулярах откладываются натуральные длины соответствующих отрезков ребер. Концы ребер последовательно соединяются отрезками прямых.
При необходимости к построенной развертке боковой поверхности призмы пристраиваются натуральные фигуры оснований призмы.
Способ нормальных сечений эффективен, если ребра призмы являются линиями уровня. Если же при этом основания призмы расположены в плоскостях уровня, то реализуется частный случай этого способа — способ раскатки (рисунок 10.4).
Построение развертки поверхности пирамиды сводится к отысканию истинных величин граней этой пирамиды и последующему совмещению их с плоскостью. Для нахождения истинных величин граней необходимо (каким-либо способом) найти натуральные длины всех ребер пирамиды (рисунок 11.33).
Приближенное построение разверток
Выше было отмечено, что для всех поверхностей строятся приближенные развертки. Однако для таких поверхностей, как цилиндрическая и коническая поверхности вращения, могут быть вычислены все параметры необходимые для точной развертки.
Отсек цилиндра вращения радиуса R и высоты h развертывается в прямоугольник 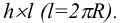 Развертка усеченного цилиндра представлена на рисунке 11.31.
Развертка усеченного цилиндра представлена на рисунке 11.31.
Отсек конуса вращения с высотой h и радиусом основания R развертывается в круговой сектор, радиус которого равен длине образующей отсека конической поверхности 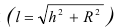 ,а его центральный угол a—
,а его центральный угол a—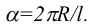
Построение разверток поверхностей начинается с аппроксимации их многогранными поверхностями, базирующейся на линейной аппроксимации направляющих. Как правило, кривая заменяется вписанной ломаной. Проиллюстрируем все выше сказанное примерами.
Развертка боковой поверхности усеченного конуса вращения представлена на рисунке 10.3.
Развертывание боковой поверхности усеченного конуса, в общем случае, производится по схеме развертывания поверхности пирамиды.
Коническая поверхность заменяется вписанной в нее поверхностью пирамиды. Построение развертки будет тем точнее, чем больше граней имеет пирамида, заменяющая коническую поверхность.
Истинные величины отрезков образующих 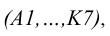 определятся на очерковой образующей конуса.
определятся на очерковой образующей конуса.
Развертка боковой поверхности наклонного кругового цилиндра показана на рисунке 10.4.
На первом этапе в цилиндрическую поверхность вписывается призма, основанием которой служит многоугольник с n сторонами. Достаточная точность аппроксимации может быть получена при длине стороны равной четверти радиуса окружности. В силу того, что рассматриваемая поверхность симметрична относительно фронтальной плоскости уровня, достаточно построить развертку лишь одной ее половинки.
Развертка вписанной призмы выполняется по способу раскатки. Некоторая фронтальная плоскость совмещается с ребром 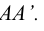 Затем с ней совмещаются боковые грани призмы последовательным вращением их вокруг соответствующих ребер.
Затем с ней совмещаются боковые грани призмы последовательным вращением их вокруг соответствующих ребер.
Вращением вокруг ребра 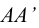 грань
грань 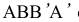 совмещается с плоскостью. Построение совмещенного положения ребра ВВ’ базируется на том, что точки В и В’ вращаются в плоскостях перпендикулярных ребру
совмещается с плоскостью. Построение совмещенного положения ребра ВВ’ базируется на том, что точки В и В’ вращаются в плоскостях перпендикулярных ребру 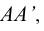 и равно отстоят от точек
и равно отстоят от точек 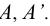 Для построения точек В и В ‘ на развертке через их фронтальные проекции
Для построения точек В и В ‘ на развертке через их фронтальные проекции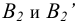 проводятся следы фронтально-проецирующих плоскостей
проводятся следы фронтально-проецирующих плоскостей 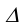 и
и 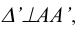 на которых фиксируется положение точек В. Далее, аналогичным образом строится грань
на которых фиксируется положение точек В. Далее, аналогичным образом строится грань 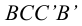 и т. д.
и т. д.
Условные развертки поверхностей
Для неразвертывающихся поверхностей строят условные развертки. Для этого, исходя из требуемой точности развертки, исходную поверхность разрезают на несколько равных частей. Затем полученные отсеки аппроксимируются отсеками развертывающихся поверхностей, для которых (по рассмотренной выше методике) и выполняют развертки. Последние и принимают за условную развертку исходной поверхности.
Рассмотрим построение разверток поверхностей вращения по описанной выше методике на примерах, приведенных на рисунках 10.5 и 10.6.
Условные развертки поверхностей вращения выполняют в основном двумя способами: способом цилиндров и способом конусов.
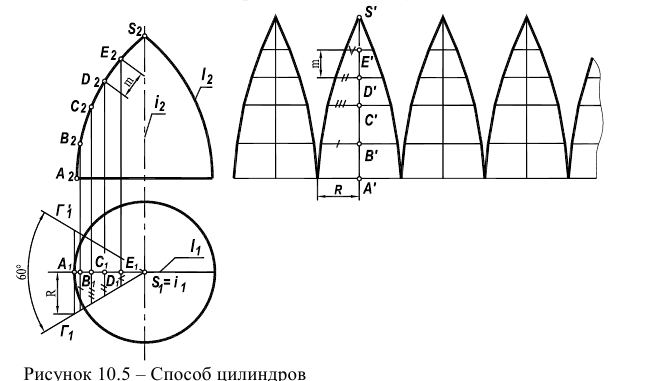
При построении условной развертки способом цилиндров исходная поверхность разрезается плоскостями, проходящими через ее ось вращения (рисунок 10.5).
Каждый выделенный отсек заменяется отсеком цилиндрической поверхности, которая касается исходной поверхности по ее среднему меридиану. Образующие отсека цилиндра ограничены плоскостями меридианов, ограничивающих отсек исходной поверхности.
При этом дуги параллелей исходной поверхности аппроксимируются отрезками образующих соответствующих цилиндров.
Для построения развертки поверхности вращения способом конусов исходная поверхность разрезается плоскостями перпендикулярными ее оси вращения, на несколько частей — «поясов». Каждый из поясов аппроксимируется отсеком конуса вращения.
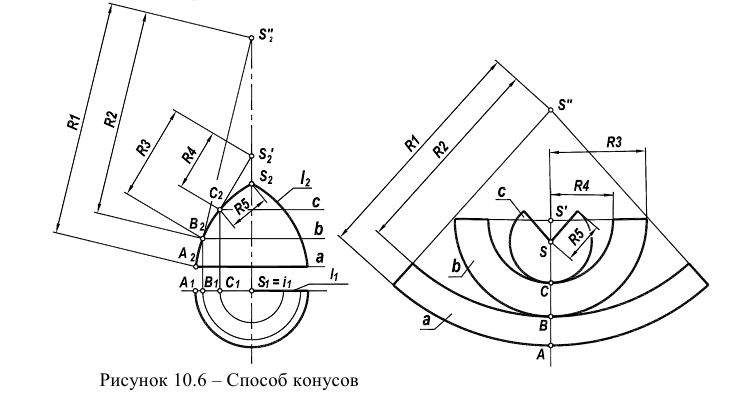
Таким образом, задача сводится к построению разверток отсеков аппроксимирующих конусов.
Выбор способа построения условной развертки поверхности вращения, в реальном проектировании, во многом зависит от конкретных размеров поверхности и технологии изготовления изделия.
Развертки поверхностей
Разверткой называется плоская фигура, в которую преобразуется поверхность предмета при ее совмещении с плоскостью. При этом подразумевается, что поверхность – это гибкая, но нерастяжимая и несжимаемая пленка и при ее развертке не происходит разрывов и образования складок.
Поверхности, которые допускают такое преобразование, называются развертывающимися.
К развертывающимся поверхностям относятся многогранники и некоторые линейчатые поверхности – цилиндрические, конические и поверхности с ребром возврата (торсы – развертка торсов не рассматривается).
Развертки можно построить точные и приближенные.
Точные развертки можно строить для гранных поверхностей призмы и пирамиды (не считая графических погрешностей построения), для круговых цилиндров (развертка – прямоугольник с размерами (π·d)×H) и круговых конусов (круговой сектор с углом φ = R·360o/L, где R – радиус основания конуса; L – длина его образующей).
Развертки, которые можно построить графически, заменяя (аппроксимируя) заданные поверхности участками развертывающихся призматических, пирамидальных или цилиндрических поверхностей, называются приближенными. К поверхностям, развертку которых можно построить приближенно, относятся круговые наклонные конуса, эллиптические цилиндры с круговыми сечениями, сферические, торовые, а также комбинированные поверхности, участки которых состоят из развертывающихся поверхностей.
Каждой точке на поверхности соответствует единственная точка на развертке, т. е. между поверхностью и ее разверткой существует взаимно однозначное соответствие, которое обладает следующими основными свойствами:
- а) длины соответствующих линий на поверхности и на развертке равны;
- б) линии, параллельные на поверхности, сохраняют параллельность на развертке;
- в) углы между соответствующими пересекающимися линиями на поверхности и на развертке равны;
- г) площади соответствующих фигур на поверхности и на развертке, ограниченные замкнутыми линиями, равны.
Развертки многогранников
Построение развертки многогранников сводится к определению натуральных величин боковых граней или ребер этих поверхностей. Натуральные величины граней (плоскостей) или ребер (прямых) могут быть определены любым из рассмотренных выше способов преобразования чертежа (см. тему «Преобразование чертежа»).
Развертка поверхности призмы
Построение развертки поверхности призмы можно выполнить несколькими способами:
- Способ нормального сечения.
- Способ раскатки.
- Способ треугольников (триангуляции) – здесь не рассматривается.
Рассмотрим на примерах построение развертки поверхности призмы первыми двумя способами.
1-й способ. Способ нормального сечения (нормальное сечение перпендикулярно ребрам призмы).
Этот способ развертки боковой поверхности призмы можно применить, если на чертеже:
- – ребра призмы являются прямыми уровня, то есть имеют на одной из заданных проекций натуральную величину,
- – на проекциях нет натуральных величин оснований призмы.
!!! Если на чертеже ребра призмы являются прямыми общего положения, то следует изменить положение призмы относительно плоскостей проекций, преобразовав ребра в прямые уровня, например, способом замены плоскостей проекций.
Построение развертки боковой поверхности призмы способом нормального сечения выполняется по следующему графическому алгоритму:
1-е действие. Провести на проекции призмы, на которую ребра призмы проецируются в натуральную величину, плоскость нормального сечения, перпендикулярную ее ребрам (в произвольном месте по длине ребер).
2-е действие. Построить натуральную величину многоугольника нормального сечения (например, способом замены плоскостей проекций).
3-е действие. Развернуть на свободном поле чертежа натуральный многоугольник сечения в прямую и через точки его вершин провести перпендикулярные прямые
- – направления ребер.
4-е действие. Отложить на направлениях ребер в обе стороны от линии нормального сечения натуральные отрезки соответствующих ребер.
5-е действие. Соединить построенные конечные точки ребер отрезками прямых и достроить плоскую фигуру развертки боковой поверхности призмы.
6-е действие. Оформить чертеж развертки, проведя линии сгиба в местах расположения ребер тонкими штрихпунктирными линиями с двумя короткими пунктирами.
На рис. 9.1 показан пример построения развертки поверхности треугольной призмы способом нормального сечения, так как на чертеже призмы ее ребра являются горизонтальными прямыми уровня, а основания являются плоскостями общего положения, т. е. не имеют натуральной величины.
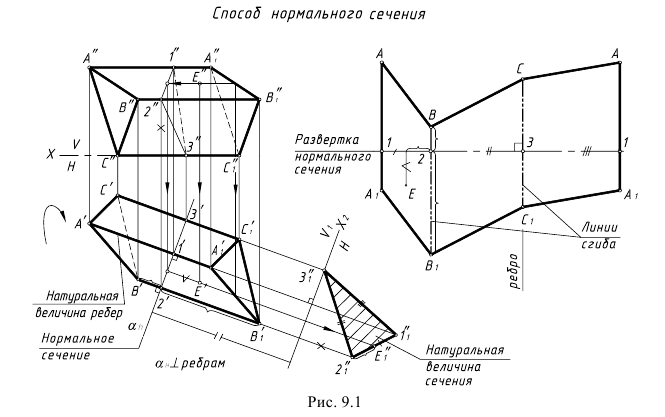
Поверхность призмы «разрезана» по ребру А и развернута по часовой стрелке.
Для построения развертки выполнены графические действия предложенного алгоритма.
1-е действие. Провести горизонтально-проецирующую плоскость нормального сечения α(αh) перпендикулярно горизонтальным проекциям ребер призмы (произвольно по длине ребер).
2-е действие. Способом замены плоскостей проекций построить натуральную величину нормального сечения
- – треугольник 11“-21“-31“, стороны которого определяют ширину каждой грани призмы.
3-е действие. На свободном поле чертежа треугольник 11“-21“-31” нормального сечения развернуть в горизонтальную линию и отметить натуральные величины его сторон; из отмеченных на линии сечения точек 1, 2, 3 и 1 провести перпендикулярные прямые – направления ребер.
4-е действие. Отложить на проведенных направлениях ребер вверх и вниз отрезки натуральных величин ребер (см. ребро B’-B’1), взятых с заданной горизонтальной проекции призмы, где ребра имеют натуральную величину.
5-е действие. Соединить отрезками прямых построенные конечные точки ребер и достроить плоскую фигуру развертки.
6-е действие. Оформить чертеж развертки, выполнив линии сгиба по ребрам призмы тонкими штрихпунктирными линиями с двумя короткими штрихами.
На этом же рис. 9.1 показано также построение на развертке точки Е(Е”,Е’), лежащей на грани АВ призмы.
2-й способ. Способ раскатки
Этот способ развертки применяется, если на чертеже:
- – ребра призмы являются прямыми уровня;
- – основания призмы (или одно из оснований) лежат в плоскости уровня, т. е. имеют на чертеже натуральную величину.
Суть способа в том, что, «разрезав» поверхность призмы по одному из ее ребер, вращением призмы (раскаткой) вокруг этого ребра ближайшая грань призмы совмещается с плоскостью развертки (за плоскость развертки принимается плоскость проекций, которой параллельны ребра призмы). Затем последовательным вращением призмы вокруг следующих ребер с плоскостью развертки совмещаются все прочие грани призмы, т. е. выполняется полная раскатка ее боковой поверхности.
На рис. 9.2 показан пример построения развертки способом раскатки, так как на чертеже ребра призмы являются фронтальными прямыми, а оба основания лежат в горизонтальных плоскостях уровня и на горизонтальной проекции призмы имеют натуральную величину. За плоскость развертки принята фронтальная плоскость проекций, так как ребра призмы фронтальные прямые.
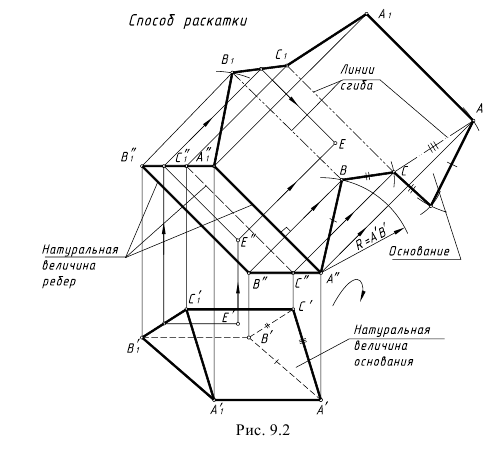
Построение развертки способом раскатки выполняется по следующему графическому алгоритму:
1-е действие. «Разрезать» поверхность призмы по очерковому ребру A-A1(A”-A1“) и повернуть вокруг этого ребра грань АВ призмы до совмещения с плоскостью развертки, построив ребро В-B1; чтобы построить на развертке это ребро, нужно провести из вершин оснований В(B”) и B1(B1“) перпендикуляры к ребру A-A1(A”-A1“) и на пересечении этих перпендикуляров с дугой-засечкой, равной стороне основания AВ(A’B’), построить точки B и B1, определяющие положение ребра В-B1 на развертке (ребро В-B1 параллельно ребру А-A1).
2-е действие. Повторить последовательное вращение каждой грани вокруг следующего ребра и совместить каждую грань с плоскостью развертки, построив конечные точки каждого ребра с помощью дуг-засечек, равных следующим сторонам основания BC(B’C’) и CА(C’А’).
3-е действие. Соединить построенные конечные точки ребер отрезками прямых и достроить плоскую фигуру развертки (достроено также одно основание призмы).
4-е действие. Оформить чертеж развертки, выполнив линии сгиба по ребрам тонкими штрихпунктирными линиями с двумя короткими пунктирами.
На этом же рисунке показано построение на развертке точки E, лежащей на грани BC призмы.
Развертка поверхности пирамиды
Построение развертки боковой поверхности пирамиды по натуральным величинам ее ребер выполняется по следующему графическому алгоритму.
1-е действие. Построить на заданных проекциях пирамиды натуральные величины всех ее боковых ребер (например, способом вращения вокруг проецирующей прямой) и натуральные величины сторон многоугольника основания пирамиды (если основание лежит в плоскости уровня, то натуральные величины даны на одной из проекций).
2-е действие. Построить на свободном поле чертежа последовательно грани пирамиды по натуральным величинам ребер и натуральным величинам сторон основания (с помощью дуг-засечек) так, чтобы они имели общую вершину S и примыкали друг к другу.
3-е действие. Оформить чертеж развертки, выполнив линии сгиба по ребрам пирамиды тонкими штрихпунктирными линиями.
На рис. 9.3 показан пример построения развертки поверхности правильной треугольной пирамиды, основание которой треугольник АВС на горизонтальной проекции имеет натуральные величины сторон, так как лежит в горизонтальной плоскости уровня.
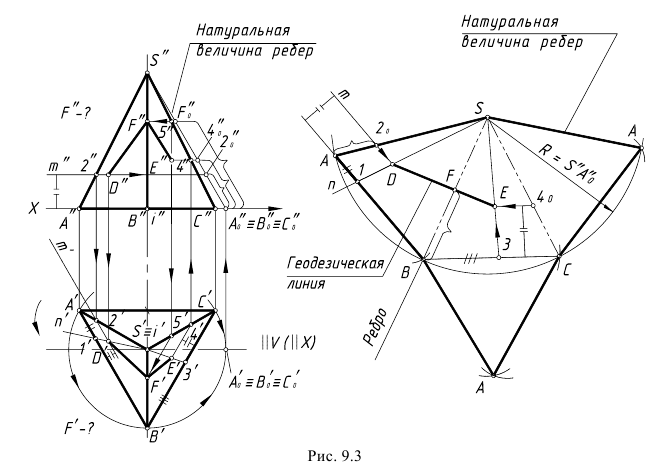
Для построения развертки выполнены графические действия предложенного алгоритма.
1-е действие. Построить на заданной фронтальной проекции натуральные величины ребер пирамиды способом вращения вокруг горизонтально-проецирующей оси i(i’), проходящей через вершину пирамиды точку S (S’) и совпадающую с ее высотой. Напоминаем графические действия этого способа преобразования:
1.1. Повернуть горизонтальные проекции ребер S’А’, S’В’ и S’С’ вокруг оси i(i’) так, чтобы они расположились параллельно фронтальной плоскости проекций V (все ребра правильной пирамиды равны по длине), и получить совмещенные проекции точек Ao‘≡Bo‘≡Co‘.
1.2. На фронтальной проекции пирамиды конечные точки А”, В” и С” ребер перемещаются по горизонтальной линии, перпендикулярной оси i(i”), и на пересечении с линией связи от точек Ao‘(Bo‘≡Co‘) построить точки Ao“(Bo“≡Co“).
1.3. Соединить вершину пирамиды S(S”) с совпадающими точками Ao“(Bo≡Co“)
– полученный отрезок S”A”(S”B”≡S”C”) и есть натуральная величина всех ребер пирамиды.
2-е действие. На свободном поле чертежа построить последовательно (например, против часовой стрелки) от ребра SA, по которому «разрезается» поверхность, треугольники граней пирамиды с общей вершиной S следующим образом:
2.1. Провести дугу радиусом R равным натуральной величине ребер S”Ao” пирамиды из произвольной точки S плоскости чертежа.
2.2. На дуге отметить (произвольно) вершину основания точку A, то есть построить ребро SA пирамиды.
2.3. На проведенной дуге засечками, равными длине сторон основания пирамиды A’В’=В’C’=C’A’ отметить следующие точки вершин основания
– B, C и точку A.
2.4. Построить треугольники граней пирамиды, соединив вершину S с вершинами основания и достроить основание пирамиды к стороне, например, ВС грани SBC.
3-е действие. Оформить чертеж развертки, выполнив линии сгиба по ребрам пирамиды тонкими штрихпунктирными линиями с двумя короткими пунктирами.
Геодезическая линия
Геодезическая линия – это линия кратчайшего расстояния между двумя точками на поверхности. На развертке этой линии соответствует прямая. Геодезическая линия строится на развертке по двум ее конечным точкам, заданным на проекциях предмета, а затем достраивается на заданных проекциях по дополнительным промежуточным точкам, взятым на построенной развертке.
На рис. 9.3 показано построение проекций геодезической линии на поверхности пирамиды по двум заданным на проекциях конечным точкам D(D”,D’-?) и E(E’,E”-?). Порядок графических действий для построения геодезической линии:
1-е действие. Построить полную развертку поверхности (в данном примере развертка пирамиды уже построена).
2-е действие. Построить на развертке геодезическую линию.
2.1. Построить на развертке заданные точки D(D”,D’) и E(E’,E”):
– точка D определяется на развертке на пересечении вспомогательной линии m, проведенной параллельно стороне АВ основания на расстоянии А-2o, равным отрезку Ao“-2o“, взятому на построенной натуральной величине ребер и отложенному по ребру SA развертки, и линии, проведенной через точку S и точку 1, построенную на стороне АВ развертки по отрезку A’-1′, взятому на горизонтальной проекции А’В’ стороны основания;
- – точка E определяется на пересечении аналогично построенных линий 4o-Е и S-3;
2.2. Соединить построенные на развертке точки геодезической линией D-E, которая пересекает ребро SB в точке F.
3-е действие. Достроить фронтальную и горизонтальную проекции геодезической линии D-F-E на проекциях пирамиды по промежуточной точке F с учетом видимости линии на поверхности (на проекциях пирамиды проекции геодезической линии – ломаные линии):
3.1. Отрезок B-F, взятый на развертке (отмечен скобкой), отложить на натуральной величине ребер, построенных на фронтальной проекции, и определить положение точки Fо“.
3.2. Провести через точку Fо” линию, параллельную основанию пирамиды, и на пересечении с проекцией ребра SB(S”B”) построить фронтальную проекцию точки F(F”) геодезической линии.
3.3. Достроить горизонтальную проекцию точки F(F’) по вспомогательной точке 5(5′), лежащей на ребре SC.
3.4. Соединить на проекциях пирамиды заданные проекции точек D и E с построенной точкой F, определив видимость участков ломаной геодезической линии.
На рис. 9.4 показан пример построения развертки неправильной треугольной пирамиды SABC и геодезической линии D-E-F на развертке и на проекциях пирамиды по заданным конечным точкам D и E. Основание пирамиды лежит в горизонтальной плоскости и на горизонтальной проекции пирамиды стороны основания имеют натуральную величину.
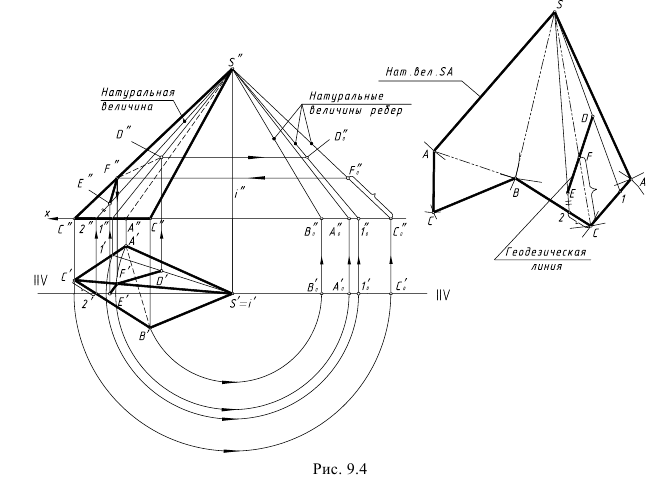
Построение развертки поверхности пирамиды выполнено по приведенному выше алгоритму с дополнительными графическими действиями по построению геодезической линии:
1-е действие. Построить на фронтальной проекции пирамиды способом вращения вокруг горизонтально-проецирующей оси i(i’), проходящей через вершину пирамиды S(S’), натуральные величины всех ребер пира-миды и вспомогательной линий S-1, проведенной на грани пирамиды SAC через заданную точку D, и определить проекцию Dо” точки D на натуральной величине S”-1o” вспомогательной линии S-1: вспомогательная линия S-2, проведенная через точку E(E’,E”), является фронтальной (//V), и проекция S”-2″ есть ее натуральная величина, которую можно использовать для построения точки E на развертке.
2-е действие. Построить на свободном поле чертежа последовательно от ребра SA по часовой стрелке треугольники граней пирамиды с общей вершиной S по натуральным величинам ее ребер и сторон основания дугами-засечками соответствующей величины и достроить основание пирамиды к стороне АВ.
3-е действие. Оформить чертеж развертки, проведя линии сгиба.
4-е действие. Построить геодезическую линию на развертке и заданных проекциях пирамиды.
4.1. Построить на развертке конечные точки D и E на вспомогательных линиях S-1 и S-2 по натуральным величинам отрезков 1-D(1o“-Dо“) и 2-E(2″-E”) и соединить эти точки прямой геодезической линией D-E, которая пересекает ребро SC в точке F.
4.2. Достроить фронтальную и горизонтальную проекции ломаной геодезической линии D-F-E на проекциях пирамиды с учетом ее видимости, определив проекции точки F(F’,F”) на ребре SC(S’C’,S”C”) по ее положению на развертке (по отрезку C-F).
Приближенные развертки цилиндрических и конических поверхностей
Развертки цилиндрических и конических поверхностей выполняются аналогично разверткам призматических и пирамидальных поверхностей. При этом цилиндрическая поверхность заменяется (аппроксимируется) вписанной многоугольной призматической поверхностью (обычно 12-угольной), а коническая поверхность заменяется вписанной многоугольной пирамидальной поверхностью, т. е. строятся приближенные развертки.
Развертка кругового цилиндра
Развертку поверхности прямого кругового цилиндра можно выполнять следующими способами:
- – способом нормального сечения на свободном поле чертежа, если образующие являются прямыми уровня, а основания не перпендикулярны образующим;
- – способом раскатки при тех же условиях (развертка является при этом продолжением проекции).
Развертка эллиптического цилиндра (нормальное сечение – эллипс) выполняется способом раскатки, если образующие являются прямыми уровня, и на проекциях есть круговое основание (не рассматривается).
Графические алгоритмы для построения разверток поверхности цилиндра этими способами аналогичны вышеприведенным графическим алгоритмам для построения разверток призмы такими же способами.
На рис. 9.5 показан пример построения развертки боковой поверхности прямого кругового цилиндра, наклоненного относительно горизонтальной плоскости проекций H и срезанного по одному торцу профильной плоскостью.
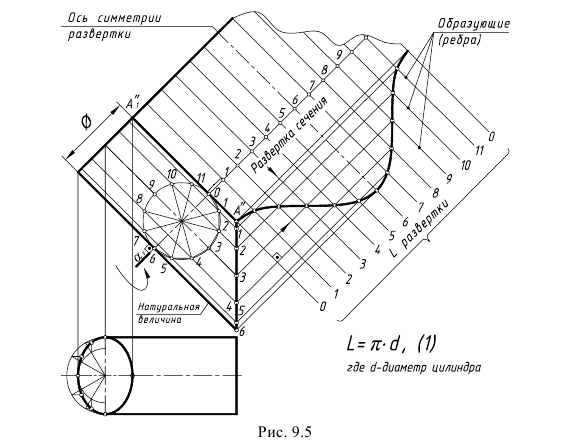
Поскольку по условию задачи образующие являются фронтальными прямыми уровня, а нормальным сечением кругового цилиндра является окружность, то здесь для построения развертки можно объединить и способы построения, и графические действия алгоритмов.
Развертка выполняется по предлагаемому графическому алгоритму.
1-е действие. Провести на фронтальной проекции цилиндра фронтально-проецирующую плоскость нормального сечения α(αV) перпендикулярно фронтальным проекциям образующих (в произвольном месте по длине образующих) и построить окружность нормального сечения, повернув плоскость этой окружности вокруг линии сечения.
1.1. Окружность нормального сечения разделить на двенадцать частей и точки деления пронумеровать от точки O на очерковой образующей А”-A1“, то есть цилиндр заменить (аппроксимировать) двенадцатиугольной вписанной призмой; из точек деления окружности сечения провести на фронтальной проекции образующие до их пересечения с проекциями оснований.
2-е действие. На продолжении линии нормального сечения отметить двенадцать отрезков – сторон двенадцатиугольника (хорды окружности), которым заменяется окружность сечения, и провести направления ребер (образующих), перпендикулярно линии сечения (линии пронумеровать), то есть выполнить от ребра А”-A1” последовательную раскатку граней призмы, заменившей цилиндр.
3-е действие. Построить конечные точки каждой образующей (ребра) на пересечении образующих с линиями, проведенными перпендикулярно образующим из одноименных точек нижнего основания.
4-е действие. Оформить чертеж развертки боковой поверхности цилиндра, соединив построенные конечные точки образующих плавными кривыми линиями (в примере развертка оборвана из-за недостатка места). Для построения более точной развертки следует по формуле (1) (рис. 9.5, где L – диаметр цилиндра) вычислить длину развертки и разделив эту длину на 12 равных частей, провести образующие и далее выполнить 3 и 4 действия алгоритма.
Развертка кругового конуса
На рис. 9.6 показан пример построения развертки боковой поверхности прямого кругового конуса со срезом фронтально-проецирующей плоскостью α(αV), которая пересекает его поверхность по эллипсу.
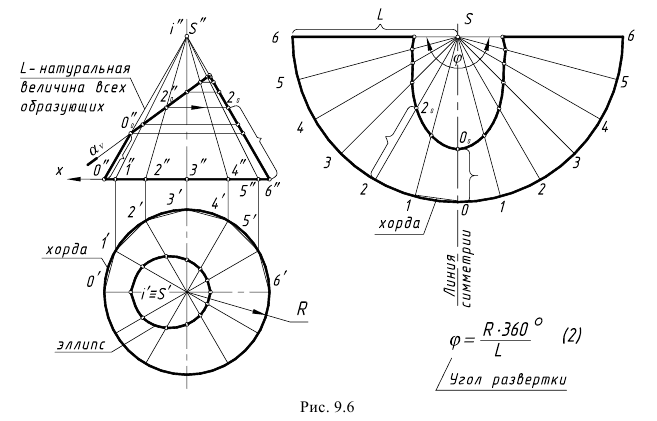
Построение развертки боковой поверхности конуса выполняется по алгоритму, приведенному выше для построения развертки пирамиды, с некоторыми дополнениями.
Развертка выполняется по предлагаемому алгоритму.
1-е действие. Заменить прямой круговой конус вписанной правильной 12-угольной пирамидой с ребрами-образующими.
2-е действие. Построить развертку боковой поверхности пирамиды по натуральным величинам ребер (образующих) и сторон основания, выполнив следующие графические действия:
2.1. Отметить на свободном поле чертежа точку S и провести дугу радиусом L, равным натуральной величине всех образующих конуса (ребер пирамиды).
2.2. Отметить на дуге точку O на вертикальной линии симметрии развертки и построить вправо и влево на дуге засечками, равными сторонам-хордам 12-угольника, точки, соответствующие вершинам этого многоугольника; пронумеровать эти точки и соединить их с вершиной развертки, построив таким образом вспомогательные ребра-образующие (грани пирамиды).
3-е действие. Достроить на развертке линию среза конуса фронтально-проецирующей плоскостью α(αV), выполнив следующие графические действия:
3.1. На фронтальной проекции конуса перенести горизонтально на натуральную величину образующей S”-6″ точки сечения, отмеченные на вспомогательных образующих, то есть вращением вокруг оси i(i”,i’) построить натуральные величины отрезков образующих-ребер сечения.
3.2. Отложить на соответствующих образующих развертки натуральные величины отрезков образующих-ребер до точек сечения (отмечены на фронтальной проекции и на развертке фигурными скобками отрезки O”-Oo” образующей для точки Oo и 2″-2o” образующей для точки 2o) и соединить построенные точки сечения на развертке плавной кривой линией.
4-е действие. Оформить чертеж развертки, проведя сплошными толстыми линиями контур построенной развертки.
Для построения более точной развертки следует вычислить по формуле (2) (рис. 9.6, где R – радиус основания конуса; L – длина образующей конуса) угол развертки и разделить дугу развертки на 12 равных частей, провести образующие и далее выполнить 3 и 4 действия алгоритма.
На рис. 9.7, а дан чертеж поверхностей кругового цилиндра и кругового конуса, описанных вокруг сферы, и построена линия пересечения этих поверхностей по теореме Г. Монжа.
На рис. 9.7, б построена развертка конической части этой конструкции по следующему графическому алгоритму:
1-е действие. Провести произвольное сечение, перпендикулярное оси конуса, и повернуть половину окружности сечения в очерковую плоскость конуса.
2-е действие. Разделить окружность сечения на 6 частей и перенести точки 1-6 параллельно оси конуса на линию сечения (проекцию окружности), то есть построить точки 1o-6o.
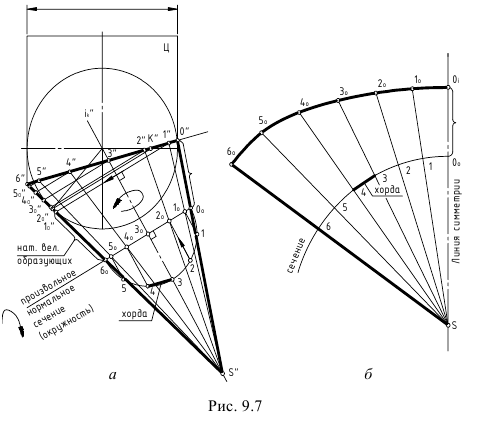
3-е действие. Через вершину конуса S(S”) и точки 1o-6o провести образующие конуса до пересечения с проекцией линии пересечения с проекцией линии пересечения цилиндра и конуса О1“-6”.
4-е действие. Вращением построенных образующих вокруг оси конуса перенести точки 1o“-5o” на очерковую образующую S”-6″, имеющую на чертеже натуральную величину.
5-е действие. На свободном поле чертежа провести радиусом R=S”Oo дугу и отложить на этой дуге шесть отрезков-хорд, на которые было поделено сечение конуса.
6-е действие. Через точку S на развертке и построенные точки Oo-6 провести семейство образующих.
7-е действие. Отложить от точек Oo-6 на каждой образующей развертки соответствующие натуральные величины образующих, взятые с чертежа, то есть отрезки 6o-1o, 6o-2o и т. д.
8-е действие. Построенные на концах семейства образующих точки соединить плавной кривой и оформить чертеж развертки (построена половина развертки).
На рис. 9.8 показано построение развертки боковой поверхности боковой поверхности усеченного конуса (если вершину конуса на чертеже достроить нельзя) с основаниями, равными d и D.
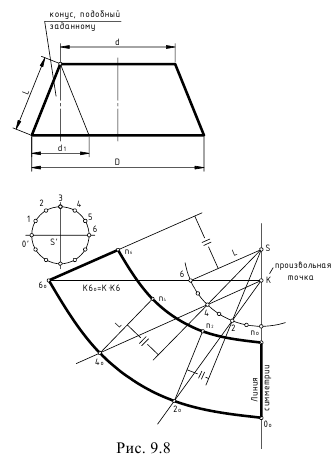
Предварительно на чертеже усеченного конуса строится вспомогательный неусеченный конус подобный заданному так, чтобы отношение диаметра D исходного конуса к диаметру вспомогательного конуса d, было целым число, то есть K = D/d1 – целое число, где K – коэффициент кратности оснований конусов.
Примем K = 3 и впишем в заданный конус вспомогательный конус с вершиной S”.
Достроим горизонтальную проекцию вспомогательного конуса и разделим половину окружности основания d1 на 6 частей (1-6).
Далее приступаем к построению развертки половины усеченного конуса по следующему графическому алгоритму:
1-е действие. На свободном поле чертежа построить развертку вспомогательного конуса с вершиной S (см. рис. 9.8), то есть построить точки 0-2-4-6 на дуге развертки.
2-е действие. На оси симметрии развертки (биссектриса полной развертки) выбрать произвольную точку К и провести семейство лучей, соединяющих соответственно произвольную точку К с точками 0-2-4-6 развертки вспомогательного конуса.
3-е действие. Отложить на проведенных лучах отрезки, величины которых определяются произведениями:
- KOo = K×KO;
- K2o = K×K2;
- K4o = K×K4;
- K6o = K×K6,
где К – принятый коэффициент пропорциональности, а величины KO, K2, K4 и K6 следует измерить на строящейся развертке. На концах лучей определяются точки Oo, 2o, 4o и 6o.
4-е действие. Через построенные точки на концах лучей провести прямые n0-n6, каждая из которых должна быть соответственно параллельна образующим вспомогательного конуса на его развертке.
5-е действие. На проведенных прямых n0-n6 отложить натуральную величину длин образующих заданного усеченного конуса L.
6-е действие. Оформить чертеж развертки, соединив построенные точки развертки лекальными прямыми.
Условные развертки поверхностей
Условные развертки можно выполнить для некоторых неразвертывающихся поверхностей.
Рассмотрим построение условных разверток неразвертывающихся поверхностей сферы и открытого тора (кругового кольца).
Развертка сферической поверхности
На рис. 9.9 показано построение условной развертки сферической поверхности.
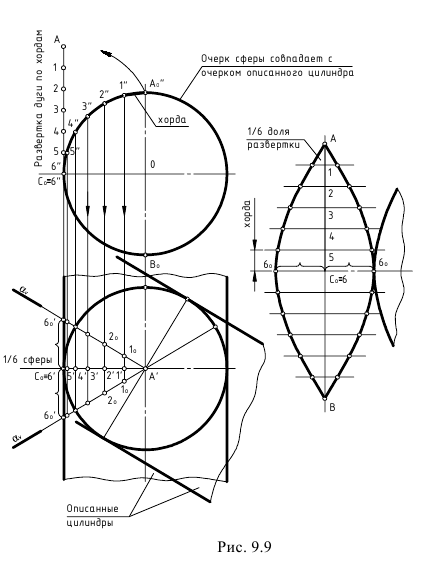
Поверхность сферы условно разрезают на какое-то количество частей (6, 12 и более) и каждую часть заменяют (аппроксимируют) цилиндрической описанной поверхностью, фронтальная проекция которой совпадает с фронтальным очерком сферы – окружностью.
Далее выполнятся развертка одной доли поверхности сферы как сектора цилиндрической поверхности по следующему графическому алгоритму:
1-е действие. На горизонтальной проекции разрезать поверхность сферы на 6 частей и рассмотреть эту 1/6 часть (сектор) как фронтально-проецирующий цилиндр, описанный вокруг сферы.
2-е действие. Разделить дугу очерковой окружности A0B0 сферы, которая совпадает с окружностью описанного цилиндра, на 12 частей (поскольку есть симметрия, рассматриваем дугу A0С0) и заменить участки хордами (то есть вписать 12-угольную призму) – A0“-1″, 1″-2” и т. д.
3-е действие. Спроецировать точки 1″-6″ на стороны взятого сектора его горизонтальной проекции.
4-е действие. Свободном поле чертежа провести вертикальную линию и отложить от точки C0 вверх и вниз по 6 отрезков, равных величине хорд (точки пронумеровать).
5-е действие. Через каждую построенную точку А-6 провести горизонтальные линии и на каждой отложить величину соответствующей образующей: 10-10, 20-20 и т. д.
6-е действие. Конечные точки соединить лекальной кривой.
Таким образом построена 1/6 доля условной поверхности сферы, а 6 таких долей составят развертку всей поверхности.
С увеличением количества долей (1/12, 1/24 и т. д.) точность развертки увеличивается.
Развертка поверхности открытого тора
На рис. 9.10 показана условная развертка поверхности открытого тора.
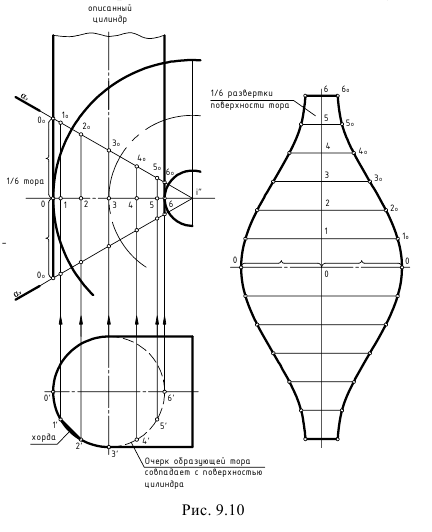
Поверхность кольца разрезают на какое-то количество долей (6, 12 и более) плоскостями, проходящими через его ось i”, и заменяют каждую долю (сектор) поверхности описанной цилиндрической поверхностью.
Далее выполняют развертку одной доли поверхности по графическому алгоритму, приведенному для построения развертки одной доли поверхности сферы.
На рис. 9.11 приведен чертеж построения части (правой) развертки комбинированной геометрической поверхности, состоящей из трех полых цилиндров, сообщенных двумя коническими рукавами, в котором подытоживается изученный материал данной темы. Показано, что развертка каждой части комбинированной поверхности строится отдельно.
Структуризация материала девятой лекции в рассмотренном объеме схематически представлена на рис. 9.12 (лист 1). На последующих листах 2–5 компактно приведены иллюстрации к этой схеме для визуального закрепления изученного материала при повторении (рис. 9.13–9.16).
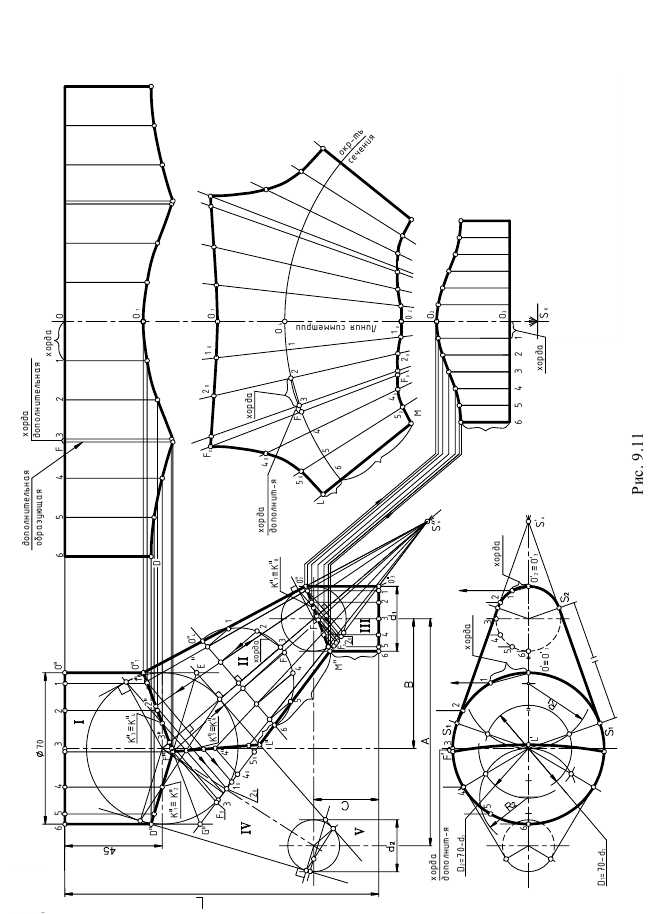
Развертки поверхностей:
Развертка – плоская фигура, в которую преобразовывается поверхность при ее совмещении с плоскостью без разрывов и складок.
Геодезическая линия – кратчайшее расстояние между двумя точками на поверхности. На развертке этой линии соответствует прямая.
Развертка гранных поверхностей
Развертка призмы.
а. Способ нормального сечения (применяется, если на чертеже ребра призмы являются прямыми уровня)
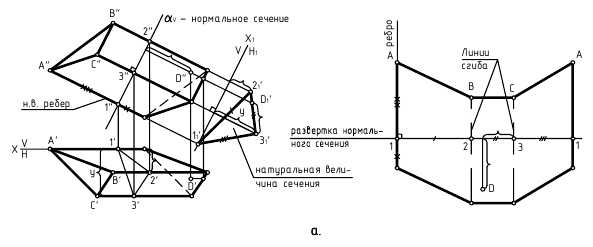
Графический алгоритм:
1. Построить натуральную величину нормального сечения, перпендикулярного к ребрам призмы.
2. Развернуть стороны сечения в линию и из вершин, провести направления ребер перпендикулярно к линии развертки.
3. Отложить вверх и вниз от точек вершин натуральные отрезки ребер и соединить построенные вершины; провести линии сгиба на месте ребер тонкими штрихпунктирными линиями с двумя штрихами.
б. Способ раскатки (применяется, если на чертеже ребра являются прямыми уровня и есть натуральная величина основания) Графический алгоритм построения на чертеже геодезической линии:
1. Построить развертку поверхности призмы.
2. Построить на развертке заданные на поверхности точки (M и N) и соединить прямой геодезической линией, которая пересекает ребро A в т.K.
3. Вернуть построенную т.K на проекции призмы и соединить с заданными точками M и N ломаной линией с учетом ее видимости на поверхности.

Развертка поверхности пирамиды.
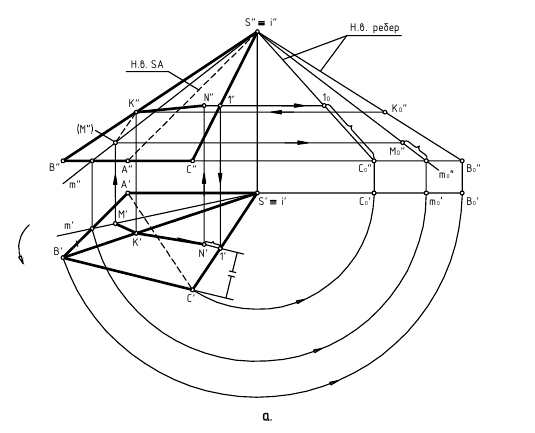
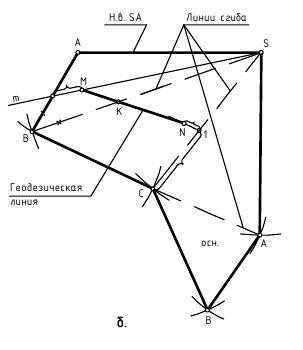
Графический алгоритм построения развертки поверхности пирамиды:
1. Построить натуральные величины всех ребер пирамиды (способом вращения вокруг проецирующей оси).
2. Выполнить развертку поверхности, построив по натуральным величинам ребер треугольники граней и основание.
3. Соединить отрезками построенные на развертке вершины и оформить линии сгиба.
Развертка цилиндрических поверхностей
1. Способ нормального сечения
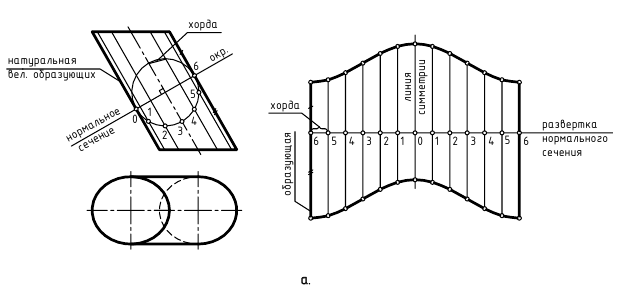
2. Способ раскатки
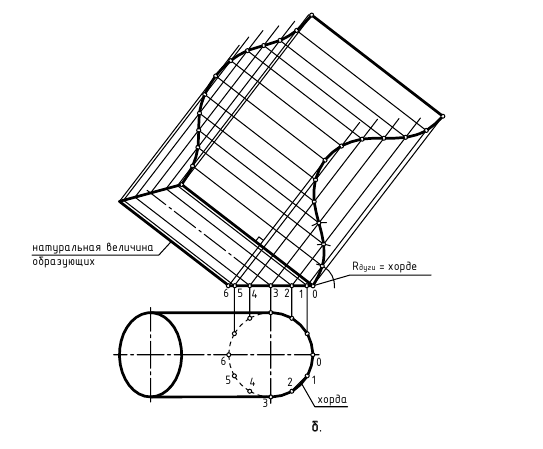
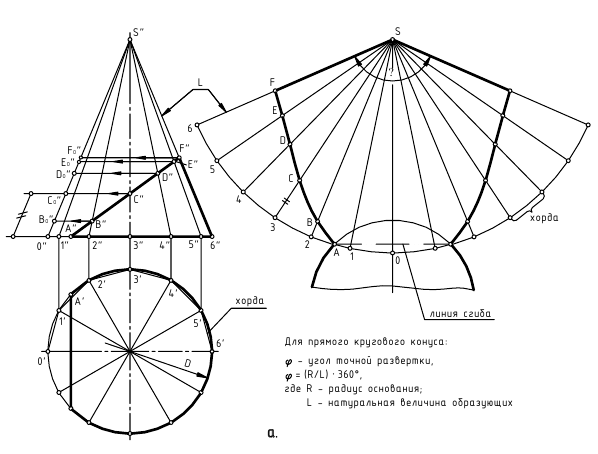
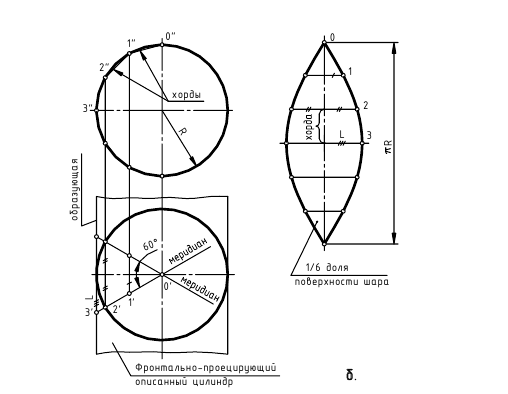
- Способы преобразования проекций
- Взаимное положение прямой и плоскости
- Решение метрических задач
- Тени в ортогональных проекциях
- Преобразование чертежа
- Кривые линии
- Образование и задание поверхности на чертеже
- Пересечение поверхности плоскостью и прямой
Мониторы
Как устроена электронно-лучевая трубка
Классификация мониторов по типу маски
Теневая маска
Щелевая маска
Апертурная решетка
Разрешение
Dot Pitch, Slot Pitch, Strip Pitch и качество монитора
Горизонтальная развертка
Вертикальная развертка, или частота кадров
Полоса пропускания
Защитная (антибликовая) панель и антибликовое покрытие
Светопередача монитора
Яркость
Контраст
Равномерность
Сведение
Динамическая фокусировка
Мерцание
Муар
Дрожание (Jitter)
Особенности жидкокристаллических мониторов
Технология плоскопанельных ЖК-мониторов
Синхронизация и фаза
Двойное преобразование ЦАП-АЦП. Цифровой интерфейс
Яркость и контрастность
Равномерность заполнения поля
Дефектные пикселы
Рабочее разрешение. Интерполяция пикселов
Инертно ли изображение ЖК-панелей?
Габариты и вес
Поворачивающийся экран
Сертификаты и стандарты безопасности
Как монитор влияет на здоровье человека
Как выбирать монитор
Международные стандарты безопасности
Когда рассуждают о том, какой компьютер купить, вопрос выбора
монитора рассматривается особо (многие фирмы даже позиционируют системные блоки
и мониторы отдельно). И если на других компонентах компьютера мы можем как-то
сэкономить, то на мониторе экономить не следует. Он по-прежнему самый дорогой
компонент компьютерной системы, его нельзя модернизировать в процессе эксплуатации,
и «время жизни» у него наибольшее по сравнению со всеми другими компонентами.
Именно посредством монитора мы воспринимаем всю визуальную
информацию от компьютера. Неважно, работаем ли мы с офисной программой, рисуем,
играем, пишем письма или находимся в Интернете — монитор нам необходим всегда.
Кроме того, от качества и безопасности монитора напрямую зависит наше здоровье.
Какие бывают мониторы? Как правильно выбрать монитор, чтобы
было удобно работать, комфортно играть, сохранять свое здоровье и меньше уставать?
На эти и другие вопросы мы и попытаемся ответить.
В рекламных проспектах продавцы и производители делают акцент
на тех характеристиках монитора, которые им выгодны (и которые зачастую только
им и понятны). Мы же постараемся дать вам общие рекомендации, объяснить смысл
и важность тех или иных характеристик и укажем, на что следует обратить особое
внимание.
Кроме того, мы рассмотрим преимущества и недостатки разных
типов мониторов — начиная с традиционных, на базе электронно-лучевой трубки,
и заканчивая современными плоскими панелями на базе жидкокристаллических матриц.
Также мы ознакомим вас со стандартами безопасности, расскажем,
чем может угрожать некачественный монитор, и дадим советы по покупке конкретного
экземпляра.
Мониторы становятся все дешевле и лучше, и этот факт, безусловно, очень радует
тех, кто нуждается в высоком качестве изображения на экране, да и просто старается
беречь свое зрение. И если раньше такие люди предпочитали работать только на
моделях от известных фирм (хороших, конечно, но довольно дорогих), то теперь
на рынке появляется все больше дисплеев, обладающих даже более высокими потребительскими
характеристиками и к тому же позволяющих сэкономить ощутимую сумму. А небольшой
разброс в качестве и ценах, а также отсутствие явных провалов у различных экземпляров
только подтверждают тот факт, что дисплейные технологии приближаются к совершенству.
Сегодня на этом рынке особенно сильно сказывается давление ЖК-мониторов, которые
в IV квартале прошлого года снова подешевели на 14-16%. Если такая тенденция
сохранится, то средняя цена на ЖК-дисплеи с диагональю 15 дюймов (сравнимые
по потребительским характеристикам с 17-дюймовыми ЭЛТ-мониторами для дома и
офиса) к концу 2001 года должна снизиться до 450-500 долл., что уже вполне сравнимо
с ценой аппаратов, основанных на ЭЛТ-технологии. Однако, как планируют производители,
столь низкие цены сильно стимулируют спрос, так что в дальнейшем их падение
замедлится или они даже опять начнут расти, что снова отсрочит поражение в конкурентной
борьбе традиционных технологий на базе электронно-лучевой трубки.
Сейчас же по-прежнему самый распространенный тип мониторов — это CRT (Cathode
Ray Tube), или ЭЛТ (электронно-лучевая трубка). Еще несколько лет назад самыми
распространенными были мониторы с диагональю 14 дюймов (на рынке традиционных
ЭЛТ-мониторов в качестве диагонали экрана в технических характеристиках указывается
размер трубки по диагонали, а видимая ее область при этом в среднем на 1 дюйм
меньше, так как края трубки скрыты в корпусе). Сегодня найти в магазине подобный
монитор практически невозможно, стандартными являются 15-дюймовые мониторы,
и наблюдается явная тенденция перехода к 17-дюймовым. Компании-производители
сворачивают выпуск 15-дюймовых ЭЛТ-устройств, поэтому ни о каких современных
технологиях в таких моделях речь идти уже не может. Даже если для вас важнее
качество, а не размер, то оптимальным выбором по этому критерию среди ЭЛТ-мониторов
может быть только дисплей с диагональю 17 дюймов и более или 15-дюймовый ЖК-монитор
(диагональ ЖК-монитора, которая указывается в технических характеристиках, совпадает
с диагональю видимой области). ![]()
Однако габариты устройства сводят на нет преимущества ЭЛТ-мониторов с диагональю
19 дюймов и более — в современной квартире бывает довольно трудно выделить место
для огромного тяжелого ящика шириной более полуметра и весом более 20 кг. Так
что оптимальной покупкой для домашнего компьютера сегодня является 17-дюймовый
ЭЛТ-монитор или 15-дюймовая ЖК-панель.
Для домашнего монитора не будет лишним наличие у него портов USB. Во-первых,
таким монитором удобнее управлять прямо из оболочки операционной системы, не
пользуясь кнопками управления на самом мониторе и его экранным меню, часто не
очень удобным. А во-вторых, появляется все больше полезных и необходимых периферийных
устройств, включая сканеры, цифровые камеры, принтеры, накопители, планшеты,
клавиатуры и т.д., которые соединяются с компьютером по USB-кабелю. Это наиболее
легкий и удобный на сегодня способ подключения периферии, применимый как на
компьютерах Macintosh, так и на РС. Встроенный в монитор USB-концентратор не
только предоставляет в ваше распоряжение больше портов, но и дает возможность
использовать более короткие кабели, удобнее разместить оборудование на рабочем
столе и, наконец, отказаться от устаревших, медленных способов подключения внешних
устройств к компьютеру: последовательного и параллельного порта.
Как устроена электронно-лучевая трубка
Электронно-лучевая трубка (ЭЛТ, или CRT, Cathode Ray Tube) — это традиционная
технология формирования изображения на дне герметично запечатанной стеклянной
«бутылки». Мониторы получают сигнал от компьютера и преобразуют его в форму,
воспринимаемую электронно-лучевой пушкой, расположенной в «горлышке» этой огромной
бутылки. Пушка «стреляет» в нашу сторону, а широкое дно (куда мы, собственно,
и смотрим) состоит из маски и люминесцентного покрытия, на котором создается
изображение. В качестве люминофоров для цветных ЭЛТ используются довольно сложные
составы на основе редкоземельных металлов (иттрия, эрбия и т.п.). Люминофор —
это вещество, испускающее свет при бомбардировке его заряженными частицами.
Электромагнитные поля управляют пучком электронов: поток на пути к люминофору
проходит через модулятор интенсивности и ускоряющую систему, работающие по принципу
разности потенциалов; отклоняющая система изменяет направление потока частиц
таким образом, что они достигают нужного места на экране, проходя через теневую
маску, падают на фосфоресцирующую поверхность и формируют на нем изображение
(активизированный электронным лучом участок экрана испускает свет, видимый глазом,
рис. 1). Такая технология называется эмиссионной.
Цвет — одно из свойств объектов материального мира, воспринимаемое нами как
зрительное ощущение. Зрительные ощущения возникают под действием на органы зрения
излучений видимого диапазона, длины волн которых находятся примерно в пределах
380-780 мкм. Физические свойства излучения тесно связаны со свойствами вызываемого
ими ощущения: с изменением мощности изменяется светлота, а с изменением длины
волны — цветность (характеристиками цвета являются цветовой тон и насыщенность).
Таким образом, восприятие цвета — продукт нашего мозга, поэтому у каждого человека
оно индивидуально. ![]()
Цвета на мониторе (впрочем, как и на телевизионном экране) получаются аддитивным
(суммарным) смешением трех основных цветов — RGB, то есть красного (Red), зеленого
(Green) и синего (Blue). Эта триада, смешанная с одинаковой интенсивностью,
дает нам белый цвет, а для того чтобы добиться цветовых оттенков, интенсивность
каждого из этих цветов дозируется в необходимой пропорции.
ЭЛТ-мониторы, как правило, имеют три отдельные электронные пушки (по одной на
каждый из основных цветов триады), которые бьют по небольшому участку люминофора
своего цвета с различной интенсивностью.
Экран монитора представляет собой матрицу, состоящую из гнезд-триад, определенной
структуры и формы (зависящей от конкретной технологии изготовления). Каждое
такое гнездо состоит из трех элементов (точек, полос или других структур), формирующих
RGB-триаду, в которой основные цвета располагаются настолько близко друг к другу,
что отдельные элементы неразличимы для глаза.
Таким образом, электронно-лучевые трубки, используемые в современных мониторах,
имеют следующие основные элементы:
- электронные пушки (по одной на каждый цвет RGB-триады или одну, но испускающую
три пучка); - отклоняющую систему, то есть набор электронных «линз», формирующих пучок
электронов; - маску, обеспечивающую точное попадание электронов от пушки каждого цвета
в «свои» точки экрана; - слой люминофора, формирующий изображение при попадании электронов в точку
соответствующего цвета.
Указанные элементы и находятся в центре непрерывной борьбы производителей за
качество изображения.
Электронная пушка состоит из подогревателя, катода, испускающего поток электронов,
и модулятора, ускоряющего и фокусирующего электроны. В современных кинескопах
применяются оксидные катоды, в которых электроны испускаются эмиссионным покрытием
из редкоземельных элементов, нанесенным на никелевый колпачок с расположенной
внутри него нитью накала. Подогреватель обеспечивает нагревание катода до температуры
850-880 °C, при которой происходит испускание (эмиссия) электронов с поверхности
катода. Остальные электроды трубки используются для ускорения и формирования
пучка электронов. Соответственно каждая из трех электронных пушек создает пучок
электронов для формирования своего цвета. Электронные лучи, расходясь после
соответствующей маски, попадают на точки люминофора нужного цвета и заставляют
их светиться.
Классификация мониторов по типу маски
Современные мониторы с любым типом маски имеют практически плоский по форме
экран, благодаря чему существенно снижаются искажения геометрии, особенно по
углам. Поэтому тип маски по форме экрана определить не так просто.
На сегодняшний день в ЭЛТ-дисплеях используются три основные технологии формирования
матриц и масок для RGB-триад:
- трехточечная теневая маска (DOT-TRIO SHADOW-MASK CRT — рис.
2); - щелевая или гнездовая (SLOT-MASK CRT — рис. 3);
- апертурная решетка (APERTURE-GRILLE CRT — рис. 4);
Тип маски можно определить, посмотрев на экран в 10-20-кратную лупу.
При создании мониторов помимо масок используются различные отклоняющие системы
и прочая сложная электроника. Хотя сам экран и является наиболее важным фактором,
определяющим эксплуатационные параметры дисплея, отклоняющая система и видеоусилитель
также играют значительную роль. Поэтому не следует думать, что при использовании
одной и той же трубки изготовители получают мониторы с одинаковыми параметрами.
Производители различных моделей говорят о преимуществах именно своей технологии,
но тот факт, что на рынке предлагается несколько моделей и, кроме того, многие
производители мониторов выпускают модели с различными типами матриц, свидетельствует,
что однозначного выбора быть не может. Предпочтения определяются только вкусами
и целями пользователей.
Теневая маска
Итак, каждая пушка излучает пучок электронов, который влияет на люминофорные
элементы разного цвета (зеленого, красного или синего). Понятно, что электронный
луч, предназначенный для красных люминофорных элементов, не должен влиять на
люминофор зеленого или синего цвета. Чтобы добиться такого действия, используется
специальная маска, структура которой зависит от типа кинескопов разных производителей
и обеспечивает дискретность изображения (растр). Самые распространенные типы
масок — теневые, которые бывают двух типов: трехточечная теневая маска и щелевая
маска. Электронный луч достигает экрана, пройдя через теневую маску, которая
может иметь различную (точечную или линейную) структуру.
Наиболее старая и широко распространенная технология — трехточечная теневая
маска. Она использует перфорированную металлическую пластину с однородными точками
(они называются триадами, так как каждая такая точка состоит из трех элементов
люминофора основных цветов — зеленого, красного и синего), которые светятся
с различной интенсивностью под воздействием лучей из электронных пушек. Изменением
тока каждого из трех электронных лучей можно добиться произвольного цвета элемента
(пиксела) изображения, образуемого триадой. В современных моделях с теневой
маской применяется инвар — специальный сплав железа и никеля с очень небольшим
коэффициентом температурного расширения, поэтому смещение масок при нагреве
остается минимальным. Однако практика показывает, что ни один из мониторов не
обеспечивает идеального выполнения этой задачи по всей поверхности экрана.
Ранние ЭЛТ-дисплеи с теневой маской имели выраженную криволинейную (сферическую)
поверхность. Это позволяло добиваться лучшей фокусировки и уменьшало нежелательные
эффекты и отклонения, вызываемые нагревом. В настоящее время большинство современных
мониторов имеет практически плоский прямоугольный экран (типа FST).
Мониторы с теневой маской имеют следующие преимущества:
- текст выглядит лучше (особенно при малом размере точек);
- цвета натуральнее и точнее (что особенно важно для компьютерной графики
и в полиграфии); - отлаженная технология обеспечивает лучшее соотношение стоимости и эксплуатационных
качеств.
Следовательно, такие мониторы можно рекомендовать для универсального применения,
офисных приложений и домашнего использования.
Из минусов можно отметить меньшую яркость этих мониторов, недостаточную контрастность
изображения и более короткий срок службы по сравнению с другими типами дисплеев.
Расстояние между люминофорными элементами одинакового цвета здесь называется
Dot Pitch, или шаг точки, и является индексом качества изображения. Шаг точки
обычно измеряется в миллиметрах. Чем меньше значение шага точки, тем выше возможное
разрешение монитора.
Щелевая маска
Щелевые маски (Slot Mask) используются в кинескопах с планарным расположением
пушек, а люминофор трех основных цветов здесь наносится на экран не в виде точек,
а в виде вертикальных чередующихся полосок (пунктиром) таким образом, чтобы
одному щелевидному отверстию соответствовала своя RGB-триада. Вертикальные полосы
фактически разделены на эллиптические ячейки, которые содержат группы из трех
люминофорных элементов трех основных цветов. В таких ЭЛТ все три электронные
пушки соосны друг другу, расположены в одной вертикальной плоскости и наклонены
под небольшим углом к горизонтальной плоскости. Подобная гибридная технология
позволяет сочетать все преимущества других типов масок — при отсутствии их недостатков.
Четкий и ясный текст, натуральные, но достаточно яркие цвета и высокая контрастность
изображения неизменно привлекают к этим мониторам внимание всех групп пользователей.
Расходясь после точки схождения, лучи образуют эллипс, охватывающий одновременно
только одно отверстие щелевой маски и соответственно три полоски люминофора,
находящиеся за ней. Отверстие щелевой маски находится напротив средней (зеленой)
полоски люминофора.
Отношение площади отверстий к общей площади маски в электронно-лучевых трубках
такого типа значительно выше, чем у обычной теневой маски, поэтому тот же уровень
яркости свечения может быть достигнут при значительно меньшей мощности электронных
пучков, следовательно, срок службы таких кинескопов существенно больше.
Минимальное расстояние между двумя ячейками называется Slot Pitch, или щелевой
шаг. Чем меньше значение щелевого шага, тем выше возможное разрешение монитора.
Апертурная решетка
Апертурная решетка (Aperture Grill) — это тип маски, которую впервые предложила
фирма Sony, выпустив мониторы с трубкой Trinitron. Теперь подобные технологии
используются разными производителями кинескопов, в частности Diamondtron от
Mitsubishi. В электронных пушках этих трубок используются динамические квадрупольные
магнитные линзы, позволяющие формировать очень тонкий и точно направленный пучок
электронов. Благодаря такому решению значительно снижается астигматизм — рассеивание
электронного пучка, приводящее к недостаточной резкости и контрастности изображения
(особенно по горизонтали). Но главное отличие от технологии теневой маски здесь
состоит в том, что вместо металлической пластины с круглыми отверстиями, выполняющей
функции маски, здесь используется вертикальная проволочная сетка (апертурная
решетка), люминофор наносится не в виде точек, а в виде вертикальных полос трех
основных цветов. Для гашения поперечных колебаний и придания проволочной сетке
дополнительной жесткости применяются горизонтальные проволочки, которые называются
Damper Wire — демпферные нити (одна в 15-дюймовых, две — в 17-дюймовых и больших
мониторах). Тени от нитей видны на экране, особенно на светлом фоне, и вызывают
раздражение у некоторых пользователей. Кроме того, если в процессе работы такой
монитор слегка качнуть, то колебания изображения будут видны даже невооруженным
глазом. Именно поэтому мониторы с этими трубками не рекомендуется ставить на
системные блоки типа desktop. Остается добавить, что в электронно-лучевых трубках
Sony Trinitron используется система трех пучков электронов, излучаемых одной
пушкой, а в трубках Diamondtron с подобной апертурной решеткой компании Mitsubishi
— система из трех лучей с тремя пушками. ![]()
Мониторы с апертурной решеткой имеют много преимуществ:
- в тонкой сетке меньше металла, что позволяет использовать больше энергии
электронов на реакцию с люминофором, а значит, меньше рассеивается на решетке
и уходит в тепло; - увеличенная площадь покрытия люминофором позволяет повысить яркость излучения
при той же интенсивности пучка электронов; - в связи со значительным общим повышением яркости можно использовать более
темное стекло и получать на экране более контрастное изображение; - экран монитора с апертурной решеткой более плоский, чем у дисплеев с теневой
маской, а в последних моделях даже не цилиндрический, как раньше, а почти
абсолютно ровный, что гораздо удобнее в работе и уменьшает количество бликов
и отражений; - расширены возможности регулировки цветовой температуры и насыщенности цвета;
- дисплей с такой ЭЛТ можно откалибровать точнее, чем с теневой маской.
Такие дисплеи можно порекомендовать для профессионального использования, презентационной
графики, мультимедиа и работы с цветом.
Минимальное расстояние между полосами люминофора одинакового цвета здесь называется
Strip Pitch, или шаг полосы, и измеряется в миллиметрах. Чем меньше значение
Strip Pitch, тем выше возможное разрешение монитора.
Разрешение
Разрешающая способность характеризует качество воспроизведения изображения монитором.
Для получения высокого разрешения высококачественным в первую очередь должен
быть видеосигнал. Электронные цепи должны обработать его таким образом, чтобы
обеспечить правильные уровни и сочетания фокусировки, цвета, яркости и контраста.
Разрешающая способность характеризуется числом точек или, как еще говорят, пикселов
(Dot) на число строк (Line). Например, разрешение монитора 1024×768 означает
возможность различить до 1024 точек по горизонтали при числе строк до 768.
Dot Pitch, Slot Pitch, Strip Pitch и качество монитора
Под шагом точки (величиной «зерна») монитора понимается расстояние между соседними
точками одного цвета. С этим параметром обычно связывается разрешающая способность,
а следовательно, и качество той или иной модели монитора.
Заметим, однако, что размер шага для трубок разных типов нельзя сравнивать напрямую:
шаг точек (или триад) электронно-лучевой трубки с трехточечной теневой маской
измеряется по диагонали, а шаг щелевой маски или апертурной решетки — по горизонтали.
Поэтому при одинаковом шаге трубка с теневой маской имеет большую плотность
точек по горизонтали, чем трубка с щелевой маской или апертурной решеткой. Так,
0,27 мм Dot Pitch равны примерно 0,22 мм шага по горизонтали, а с учетом конфигурации
триад и полосок в других типах масок монитор с трехточечной теневой маской и
шагом 0,27 мм Dot Pitch эквивалентен по разрешению монитору с щелевой маской
на 0,26 мм Slot Pith (то есть меньшим примерно на 0,01) или монитору с апертурной
решеткой 0,25 Strip Pitch (меньшим примерно на 0,02). Не следует забывать и
о том, что некоторые производители используют в своих кинескопах переменный
шаг полосы, например в мониторах с трубкой от Mitsubishi.
Отсюда, кстати, следует простой вывод о максимальном разрешении мониторов с
различными типами масок: если вы аккуратно выполните все расчеты (поделите ширину
и высоту рабочей области экрана на шаг точки), то получите, что оптимальным
разрешением экрана, например, для 17-дюймовых мониторов с 0,27 мм Dot Pitch,
0,26 мм Slot Pith или 0,25 Strip Pitch является 1024×768 пикселов, а для того
чтобы повысить его до 1280×1024, необходимо иметь 0,26 мм Dot Pitch на трехточечной
теневой маске, 0,25 мм Slot Pith на щелевой маске или не более 0,24 Strip Pitch
на апертурной решетке, что бы ни писали производители. Имея хорошую видеокарту
и электронику монитора, можно, конечно, повысить рабочее разрешение, но тогда
вы получите недостаточно четкое, размытое изображение и рискуете испортить себе
зрение.
Горизонтальная развертка
Кроме шага точки, или величины «зерна», на максимально поддерживаемое монитором
разрешение напрямую влияет частота горизонтальной развертки электронного луча,
измеряемая в килогерцах (кГц). Время горизонтального перемещения луча от левого
до правого края экрана называется периодом горизонтальной развертки. Величина,
обратно пропорциональная этому периоду, называется частотой горизонтальной развертки,
или просто горизонтальной разверткой (иногда встречаются названия «частота строчной
развертки», «строчная частота»). Например, для монитора с разрешением 1024×768
пикселов горизонтальная развертка обратно пропорциональна времени, за которое
луч сканирует 1024 пиксела. При увеличении разрешающей способности за тот же
период времени луч должен отсканировать большее число пикселов. При увеличении
частоты кадров также должна быть увеличена частота горизонтальной развертки.
Соответственно, чем больше предельное значение (именно оно, как правило, указывается
на коробке для монитора), тем выше разрешение может поддерживать монитор при
приемлемой частоте кадров. Предельная частота строк является критичным параметром
при разработке CRT-монитора. В таких мониторах используются магнитные системы
отклонения электронного луча, представляющие собой обмотки с довольно большой
индуктивностью. Амплитуда импульсов перенапряжения на катушках строчной развертки
возрастает с частотой строк, поэтому данный узел оказывается одним из самых
«узких мест» конструкции и одним из главных источников помех в широком диапазоне
частот. Мощность, потребляемая узлами строчной развертки, также серьезно учитывается
при проектировании мониторов.
Вертикальная развертка, или частота кадров
Частота регенерации (обновления) экрана — важный параметр, определяющий, как
часто перерисовывается все изображение. Монитор с электронно-лучевой трубкой
обновляет изображение на экране десятки раз в секунду. Это число называется
частотой вертикальной развертки, или частотой кадровой развертки, и измеряется
в герцах (Гц). Один герц соответствует одному циклу в секунду. Монитор с вертикальной
разверткой 60 Гц имеет такую же частоту мерцания, как лампа дневного света в
США, что несколько выше, чем в Европе, где частота сети 50 Гц. Если частота
обхода экрана становится меньше 70 Гц, то инерционности зрительного восприятия
будет недостаточно для того, чтобы изображение не мерцало. Обычно при частотах
выше 75 Гц мерцание незаметно для глаза (режим без мерцания). Однако стандарт
VESA рекомендует работу на частоте 85 Гц, считая это важным потребительским
показателем эргономичности монитора.
При этом чем выше частота регенерации, тем более устойчивым выглядит изображение
на экране: правда, исследования показали, что при частоте вертикальной развертки
выше 110 Гц глаз человека уже не может заметить никакого мерцания. Но здесь
следует опять же вспомнить о лампочке (частота сети питания у нас — 50 Гц) и
других электроприборах. В этом случае следует учесть эффект наложения частот
при искусственном освещении (особенно люминесцентном) и различных наводках в
сети питания, порождающий неприятное мерцание экрана, приводящее, в свою очередь,
к утомлению глаз, головным болям и даже к ухудшению зрения. Решением этой проблемы
может быть повышение рабочей частоты до 100 Гц (удвоенная частота сети — 2×50)
или даже выше — до 150 Гц (3×50). Заметим, что, чем больше экран монитора,
тем более заметно такое мерцание, особенно для периферийного (бокового) зрения,
так как угол обзора изображения увеличивается. ![]()
Поэтому при работе с плохой электропроводкой (недостаточно хорошо или вообще
не экранированной) или окружающим электрическим оборудованием желательно иметь
монитор, обеспечивающий частоту регенерации не менее 100 Гц.
Заметим, что значение частоты регенерации зависит не только от используемого
разрешения или электрических параметров монитора, но и от возможностей видеоадаптера.
Расчет необходимой частоты горизонтальной развертки исходя из частоты кадров
следующий:
Горизонтальная развертка = (число строк)×(вертикальная развертка)×1,05.
Так, например, требуемая горизонтальная развертка при вертикальной частоте 85
Гц и разрешении 1024×768 составляет:
768×85×1,05 = 68 500 Гц = 68,5 кГц.
Полоса пропускания
Под частотой точек (Dot Rate) понимают максимальное число входящих точек в секунду,
которое определяется разрешением по горизонтали и периодом сканирования по горизонтали
источника сигнала. Полоса пропускания видеоусилителя характеризует то, насколько
полно исходный видеосигнал преобразуется в выходной. Грубо говоря, это максимальная
частота, с которой электронный луч перескакивает с пиксела на пиксел. Таким
образом, видеоусилитель и генератор строчной развертки должны соответствовать
друг другу по качеству:
Частота точек = (разрешение по горизонтали) : (горизонтальная развертка).
Полоса пропускания = 0,35 × 2 : (время нарастания или спада сигнала).
Защитная (антибликовая) панель и антибликовое покрытие
Вопреки распространенному заблуждению, так называемые защитные экраны (даже
если они оборудованы питанием и заземлением) практически не снижают уровень
электромагнитных излучений. Впрочем, и электромагнитные излучения современных
компьютеров вместе с мониторами находятся примерно в пределах между электронными
часами и тостером и в 20 раз ниже, чем у бытового фена или пылесоса. Специальные
панели предназначены в основном для минимизации отражающих свойств экрана и
являются скорее антибликовыми, а для уменьшения электромагнитного излучения
монитора следовало бы закрывать его боковые панели, а не экран.
В последнее время вместо антибликовой панели на мониторах используют антибликовое
покрытие. Такое покрытие, как и панели, ограничивает и излучение в соответствии
со стандартами ТСО.
Используя те же принципы и свойства, что и в антибликовых панелях, для придания
монитору антибликовых свойств непосредственно на экран наносят многослойное
защитное покрытие, не ухудшающее фокусировку. Наиболее распространенным и доступным
видом антибликовой обработки экрана является покрытие диоксидом кремния. Это
химическое соединение внедряется в поверхность экрана тонким слоем. Если поместить
обработанный диоксидом кремния экран под микроскоп, то можно увидеть шершавую,
неровную поверхность, которая отражает световые лучи от поверхности под различными
углами, устраняя блики на экране, но не ухудшая изображения.
Такое покрытие одновременно является антистатическим, обеспечивая с помощью
напыления специального химического состава удаление электростатического заряда.
Оно требуется в соответствии с рядом стандартов по безопасности и эргономике,
начиная с MPR II. В наиболее передовых технологиях обработки экрана для улучшения
качества изображения используются многослойные покрытия из различных видов химических
соединений. Следует обратить внимание на то, что подобные средства эффективно
работают только при правильном заземлении электроприборов.
Светопередача монитора
Отношение полезной световой энергии, прошедшей через переднее стекло монитора,
к излученной внутренним фосфоресцирующим слоем называется коэффициентом светопередачи.
Как правило, чем темнее выглядит экран при выключенном мониторе, тем ниже данный
коэффициент.
При высоком коэффициенте светопередачи для обеспечения требуемой яркости изображения
нужен небольшой уровень видеосигнала, а схемотехнические решения упрощаются.
Однако при этом уменьшается перепад между излучающими участками и соседними,
что влечет за собой ухудшение четкости и снижение контрастности изображения
и, как следствие, — ухудшение его общего качества.
При низком же коэффициенте светопередачи улучшаются фокусировка изображения
и качество цвета, но для получения достаточной яркости необходим мощный видеосигнал
и усложнение схемы монитора.
Монитор должен позволять осуществлять регулировку яркости и контрастности в
широких пределах. Именно «заделы» яркости и контрастности являются показателями
качества.
Обычно 17-дюймовые мониторы имеют коэффициент светопередачи 52-53%, а 15-дюймовые
— 56-58%, хотя в зависимости от конкретно выбранной модели эти значения могут
варьироваться. Поэтому для определения точного значения коэффициента светопередачи
следует обращаться к документации производителя.
Яркость
Регулировкой яркости устанавливается ее уровень на экране в целом, включая
зону растра. Управление контрастом позволяет устанавливать яркость зоны данных,
изменяя коэффициент усиления входного видеосигнала и не влияя на яркость зоны
растра (рис. 5).
Контраст
Контраст характеризует яркость экрана по сравнению с темной зоной в отсутствие
видеосигнала. Контраст можно настроить специальной регулировкой, воздействующей
на входной видеосигнал.
Равномерность
Под равномерностью понимается постоянство уровня яркости по всей поверхности
экрана монитора, обеспечивающее пользователю комфортные условия для работы.
Временная неравномерность цвета может быть устранена размагничиванием экрана.
Принято различать термины «равномерность распределения яркости» и «равномерность
белого»:
- равномерность распределения яркости — большинство мониторов имеют разную
яркость в различных участках экрана. Отношение яркости в наиболее светлой
части к яркости в наиболее темной называется равномерностью распределения
яркости; - равномерность белого (White Uniformity) — характеризует различие в яркости
белого цвета на экране монитора по всей его поверхности (при выводе изображения
белого цвета). Численно равномерность белого равна отношению максимальной
и минимальной яркости.
Сведение
Для получения четкого изображения и чистых цветов на экране монитора красный,
зеленый и синий лучи, исходящие из всех трех электронных пушек, должны попадать
в точно заданное место на экране. Термин «несведение лучей» означает отклонение
красного и синего от центрирующего зеленого.
- статическое несведение — разброс «смещений» в тройке цветов (RGB-триаде),
которые должны быть одинаковыми по всей поверхности экрана; вызывается незначительной
погрешностью при сборке электронной пушки. Изображение на экране может быть
откорректировано регулировкой статического сведения; - динамическое несведение — в то время как в центре экрана монитора изображение
остается четким, на его краях может проявиться несведение. Оно вызывается
ошибками в обмотках или при их установке и может быть устранено с помощью
магнитных пластин.
Динамическая фокусировка
Если не предприняты специальные меры, электронный луч расфокусируется (увеличивается
в диаметре) по мере своего удаления от центра экрана. Для компенсации искажения
формируется специальный компенсирующий сигнал. Величина компенсирующего сигнала
зависит от свойств ЭЛТ и ее отклоняющей системы. Чтобы устранить смещение фокуса,
вызванное различием в путях пробега луча (расстоянии) от электронно-лучевой
пушки до центра и до краев экрана, требуется с помощью высоковольтного трансформатора
увеличивать напряжение в соответствии с ростом отклонения луча от центра.
Мерцание
Монитору в принципе свойственно мерцание. Оно вызывается тем, что по прошествии
определенного времени происходит ослабление излучения света фосфором. Чтобы
поддерживать свечение, экран должен подвергаться периодическому воздействию
луча от электронно-лучевой трубки. Мерцание становится заметным, если слишком
велик интервал времени между воздействиями или если недостаточно время послесвечения
фосфоресцирующего вещества экрана. Эффект мерцания может также усугубляться
ярким экраном и большим углом зрения к нему. Устранению мерцания как проблеме
эргономики в последнее время уделяется все больше внимания; уровень мерцание
экрана, таким образом, становится ключевым коммерческим показателем товара.
Уменьшение мерцания достигается увеличением частоты регенерации (обновления)
экрана на каждом уровне разрешения. Стандарт VESA рекомендует использовать частоту
не менее 85 Гц.
Муар
Муаром называются искажения, воспринимаемые глазом как волокноподобные, волнообразные
разводы изображения, вызванные неправильным взаимодействием теневой маски и
сканирующего луча. Фокус и муар являются взаимосвязанными показателями мониторов
на базе ЭЛТ. Вообще, муар должен допускаться в некоторой мере для обеспечения
хорошего фокуса.
Дрожание (Jitter)
Дрожание изображения возникает вследствие высокочастотных вибраций отверстий
маски монитора, вызванных как взаимовлиянием сети, сигналов видео, смещения,
блока управления микропроцессорными цепями, так и неправильной организацией
заземления. Термин «дрожание» относится к колебаниям с частотами выше 30 Гц.
При частотах от 1 до 30 Гц чаще употребляют термин «плавание», а ниже 1 Гц —
«дрейф». Дрожание в той или иной степени свойственно всем мониторам. Хотя незначительное
дрожание может остаться для пользователя незаметным, оно все же вызывает утомление
глаз и должно быть отрегулировано. В предписаниях по эргономике допускается
диагональное отклонение точки не более 0,1 мм. Если вы не можете устранить дрожание
электрическими средствами, попробуйте увеличить частоту регенерации экрана.
![]()
Развертки
развертываемых кривых поверхностей
можно построить методом нормального
сечения и методом раскатки.
Разверткой
прямого кругового конуса является
сектор окружности с радиусом, равным
длине образующей конуса и углом при
вершине конуса.
Разверткой
прямого кругового цилиндра является
прямоугольник шириной, равной высоте
цилиндра и длиной, равной длине окружности
основания.
Сечение
прямого кругового конуса, основание
которого расположено в горизонтальной
плоскости П1,
фронтально-проецирующей плоскостью Р
рассмотрено на рис. 9.5. В зависимости от
расположения секций плоскости Р
относительно оси прямого кругового
конуса получаются различные фигуры
сечения, ограниченные кривыми линиями.
Фигура сечения в данном случае будет
ограничена эллипсом.
Фронтальная
проекция фигуры сечения расположена
на фронтальном следе плоскости РП2
(рис. 9.5,
а).
Горизонтальную
проекцию контура фигуры сечения –
окружность делят, например, на 12 равных
частей. Через точки деления на
горизонтальной и фронтальной проекциях
проводят вспомогательные образующие.
Находят фронтальные проекции точек 12,
…, 122,
лежащих на плоскости
PП2.
Затем
с помощью линии связи находят их
профильные проекции. Найденные проекции
точек контура сечения соединяют по
лекалу.
Натуральная
величина фигуры сечения в данном примере
найдена способом замены плоскости
проекций. Горизонтальная плоскость
проекций П1
заменяется новой плоскостью проекции
П4.
На
фронтальной плоскости проекции П2
фигура сечения – эллипс изображается в
виде отрезка 1272,
совпадающего с фронтальной проекцией
секущей плоскости Р.
Отрезок 1272
является
большой осью эллипса. Малая ось эллипса
перпендикулярна большой оси 1272.
Чтобы найти малую ось сечения, через
середину большой оси 1272
эллипса проводят горизонтальную
плоскость
N
(на рисунке видим фронтальный след
плоскости NП2)
которая рассечет конус по окружности,
диаметр которой будет равняться малой
оси эллипса АВ.
Построение развертки
поверхности конуса (рис. 9.5, б)
начинают с проведения
дуги окружности радиусом, равным длине
образующей конуса, из точки S.
Длина дуги определяется углом α:
α = 1800
*(d/l),
где d
– диаметр
окружности основания конуса;
l
– длина образующей конуса.
Дугу делят на 12 частей, и
полученные точки соединяют с вершиной
S.
От вершины откладывают натуральные
длины образующих от вершины конуса до
секущей плоскости Р.
Натуральные размеры этих
отрезков находят, как и в примере с
пирамидой, способом вращении около
вертикальной оси, проходящей через
вершину конуса. Так, например, чтобы
получить действительную длину отрезка
S2
(рис.
9.5, а),
надо из 22
провести горизонтальную прямую до
пересечения с контурной образующей
конуса, являющейся действительной ее
длиной.
К развертке конической
поверхности пристраивают фигуры сечения
и основания конуса.
9.4. Развертки неразвертываемых поверхностей
По
возможности развертываться кривые
поверхности делятся на развертываемые
и неразвертываемые (условно-развертываемые).
Развертки условно развертываемых
поверхностей могут быть выполнены
только приближенно путем аппроксимации
отсеков поверхностей.
Аппроксимация
– это приближенная замена отсеков
неразвертываемой поверхности отсеками
развертываемой поверхности. В качестве
аппроксимирующих поверхностей используют
плоскости, конические и цилиндрические
поверхности.
К неразвертываемым поверхностям
относится поверхность сферы. Для
построения развертки сферы её
горизонтальную проекцию делим
горизонтально-проецирующими плоскостями
на несколько равных частей (клиньев),
например на 12 (рис. 9.6,
а).
Фронтальную проекцию сферической
поверхности тоже делят на несколько
равных частей (желательно на 12).
Через
полученные точки деления II,
…,
VI
проводят
фронтально-проецирующие плоскости РV1,
…, PV5
(рис. 9.6,
а).
Для
построения развертки сферической
поверхности на горизонтальной прямой
откладывают длину окружности диаметра
D,
равную
πD
(рис.
9.6, б).
Полученный отрезок делят на 12 равных
частей.
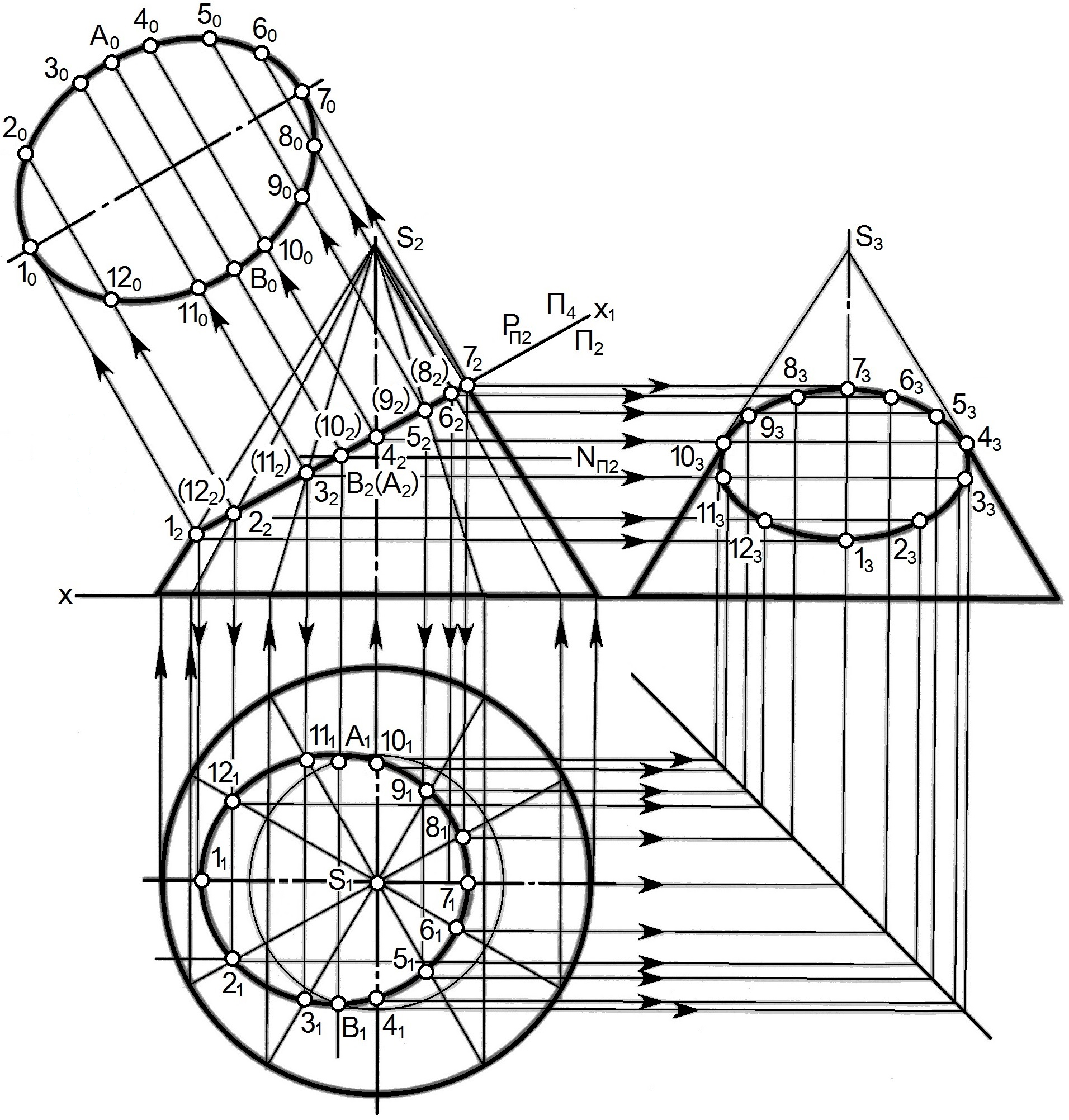
а)
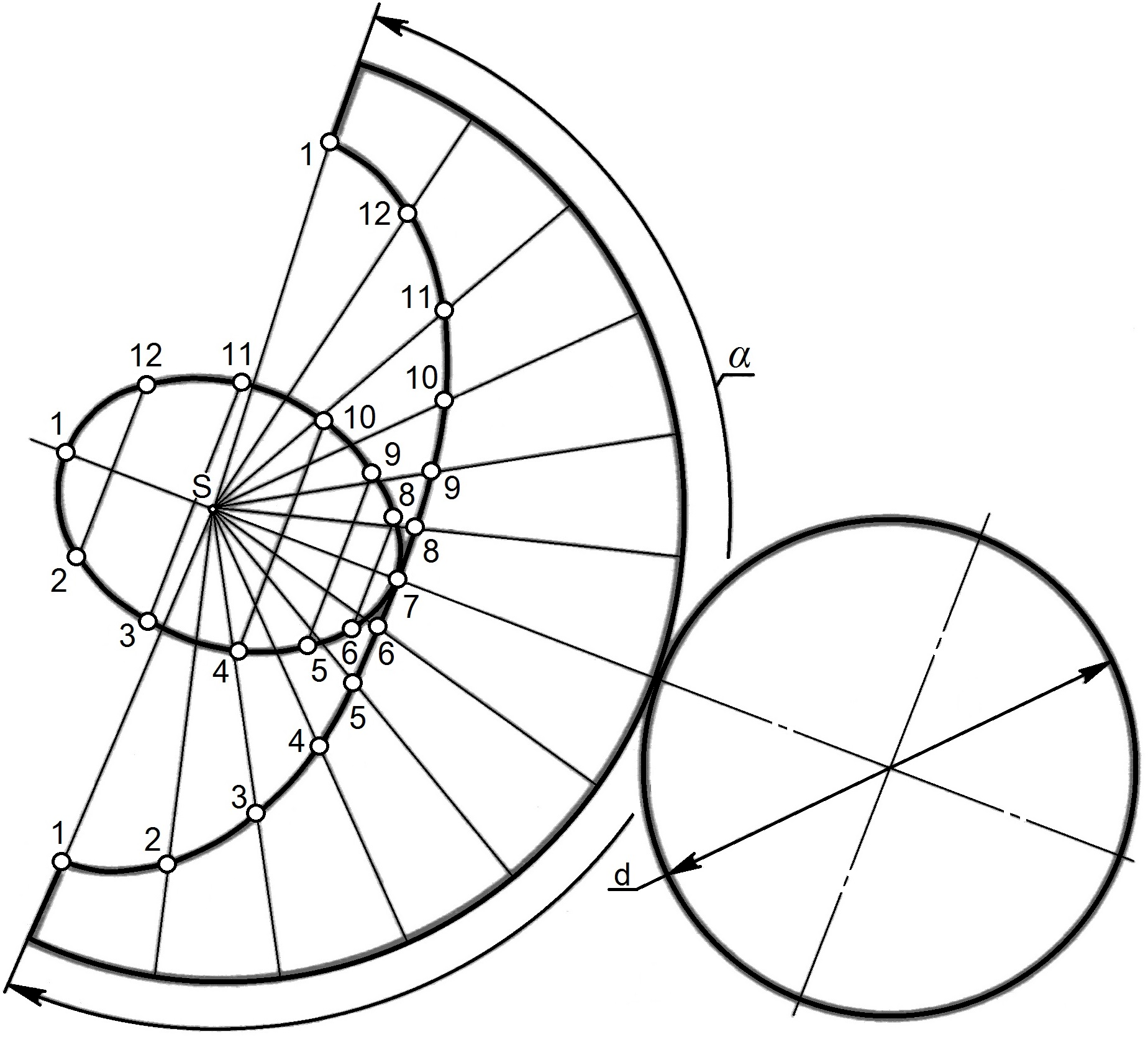
б)
Рис. 9.5. Выполнение развертки боковой
поверхности конуса
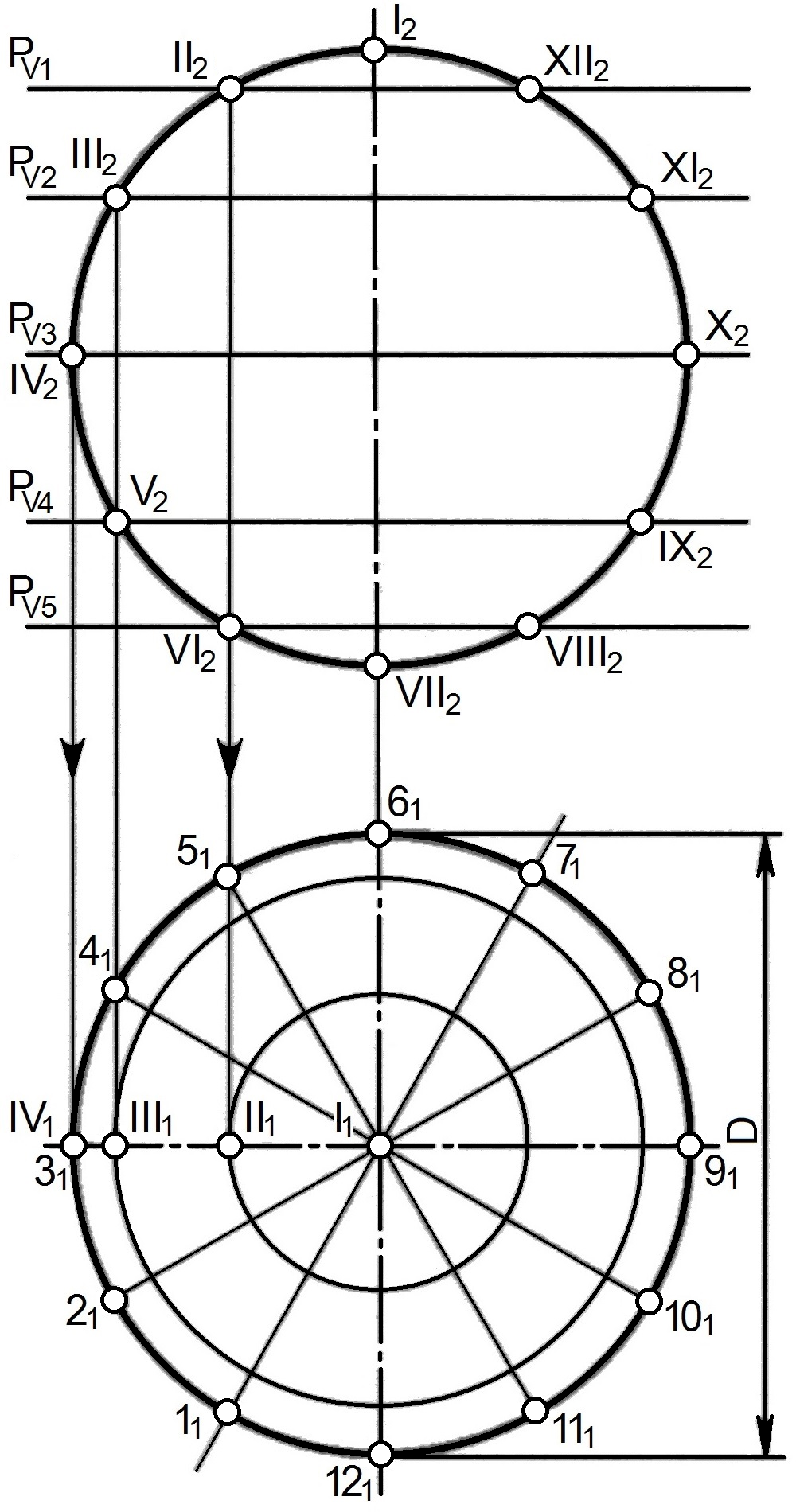
а)
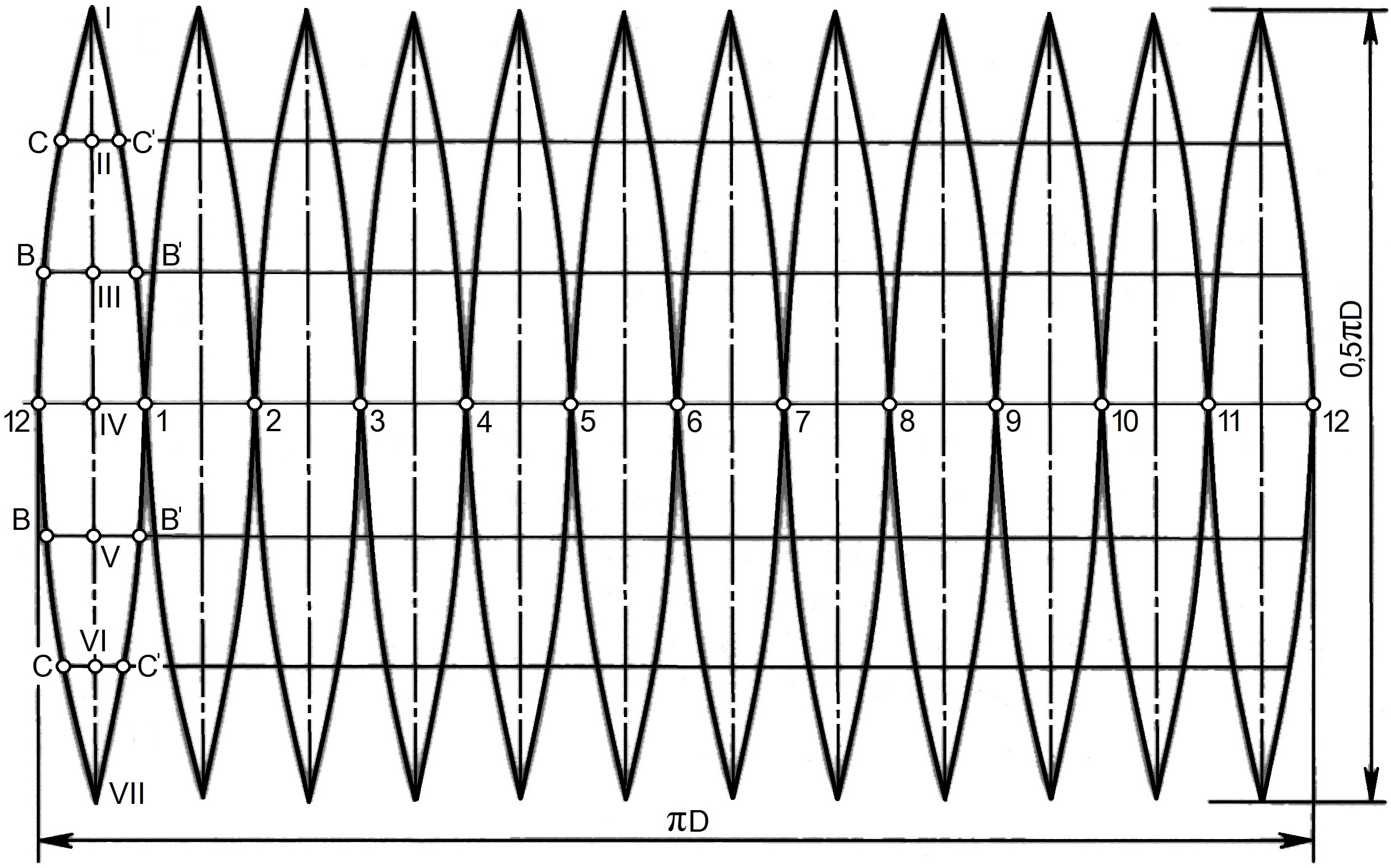
б)
Рис. 9.6. Выполнение развертки боковой
поверхности сферы
Через
середину каждого деления проводят
перпендикуляр и откладывают на нем
отрезок I
-VII,
равный 0,5 длине окружности диаметра
D.
Отрезок делят на 6 равных частей, через
полученные точки деления проводят
горизонтальные прямые, на которых
откладывают отрезки, равные 1/12 части
окружности соответствующего радиуса,
например, отрезок CC‘
соответствует 1/12 длины окружности
радиуса I-II,
взятого с горизонтальной проекции.
Полученные точки соединяют по лекалу.
Развертки остальных одиннадцати клиньев
строят аналогично.
Вопросы для самоконтроля
-
Что называется разверткой поверхности?
-
Для чего нужны развертки?
-
Какими линиями на чертеже изображаются
линии сгиба разверток? -
Каким методом можно найти натуральной
величины бокового ребра пирамиды для
построения её развертки? -
В чем суть метода нормального сечения?
-
В чем суть метода раскатки?
-
Порядок построения развертки
многогранника. -
Порядок построения развертки кривой
поверхности. -
Что такое аппроксимация?
-
В чем особенности
выполнения разверток неразворачиваемых
поверхностей?
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Необходимо построить развертки гранных тел и нанесения на развертку линии пересечения призмы и пирамиды.
Для решения этой задачи по начертательной геометрии необходимо знать:
— сведения о развертках поверхностей, способах их построения и, в частности, построение разверток гранных тел;
— взаимно-однозначные свойства между поверхностью и ее разверткой и способы перенесения точек, принадлежащих поверхности, на развертку;
— методы определения натуральных величин геометрических образов (линии, плоскости и др.).
Порядок решения Задачи
Разверткой называется плоская фигура, которая получается при разрезании и разгибании поверхности до полного совмещения с плоскостью. Все развертки поверхностей (заготовки, выкройки) строятся только из натуральных величин.
1. Поскольку развертки строятся из натуральных величин, приступаем к их определению, для чего па кальку (миллиметровку или другую бумагу) формата A3, переносится задача № з со всеми точками и линиями пересечений многогранников.
2. Для определения натуральных величин ребер и основания пирамиды используем метод прямоугольного треугольника. Безусловно, можно и другие, но на мой взгляд, этот метод более доходчив для студентов. Суть его заключается в том, что «на построенном прямом угле откладывается на одном катете проекционная величина отрезка прямой, а на другом — разность координат концов данного отрезка, взятая с сопряженной плоскости проекций. Тогда гипотенуза полученного прямого угла дает натуральную величину данного отрезка прямой».
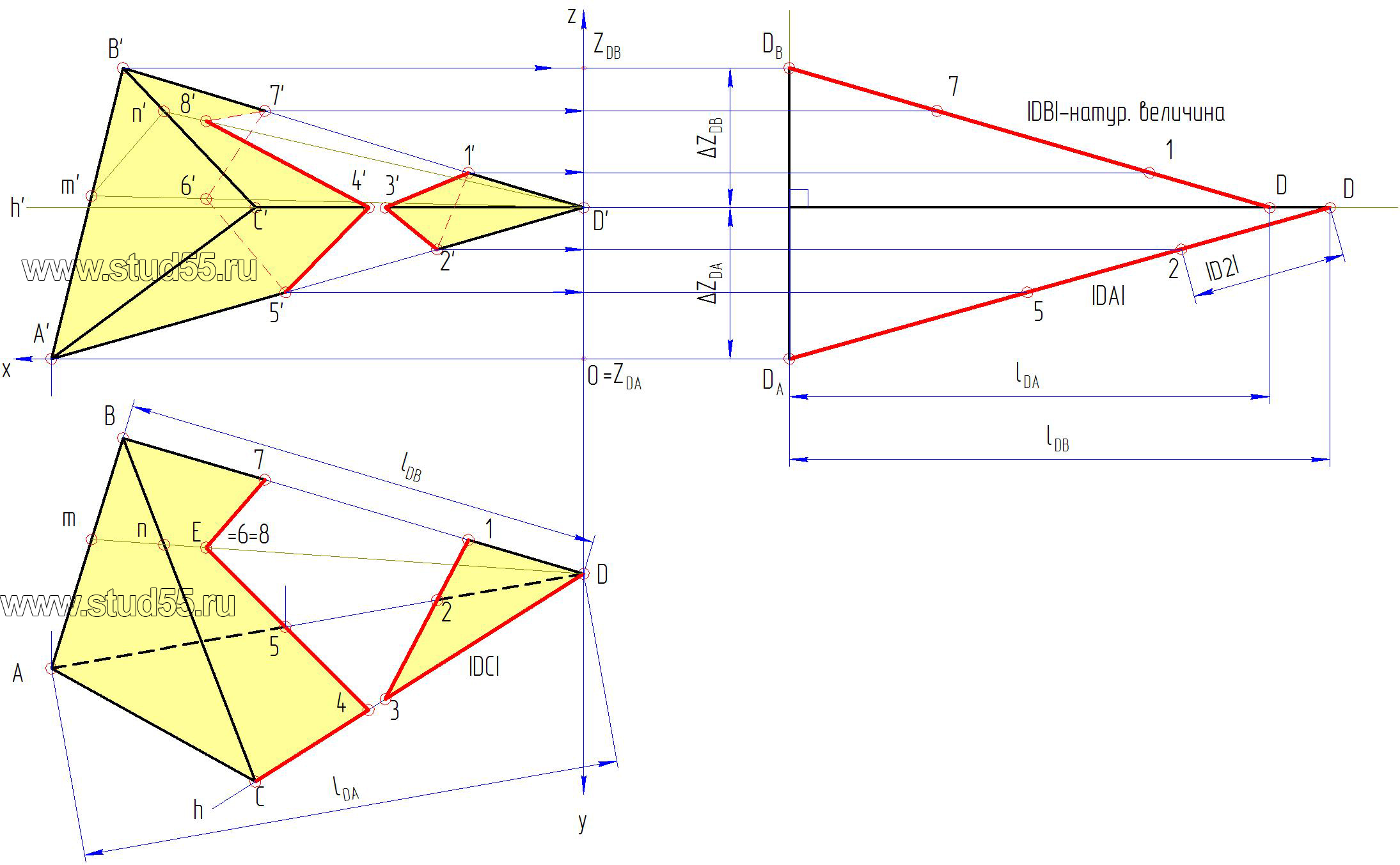
Рис.4.1

Рис.4.2
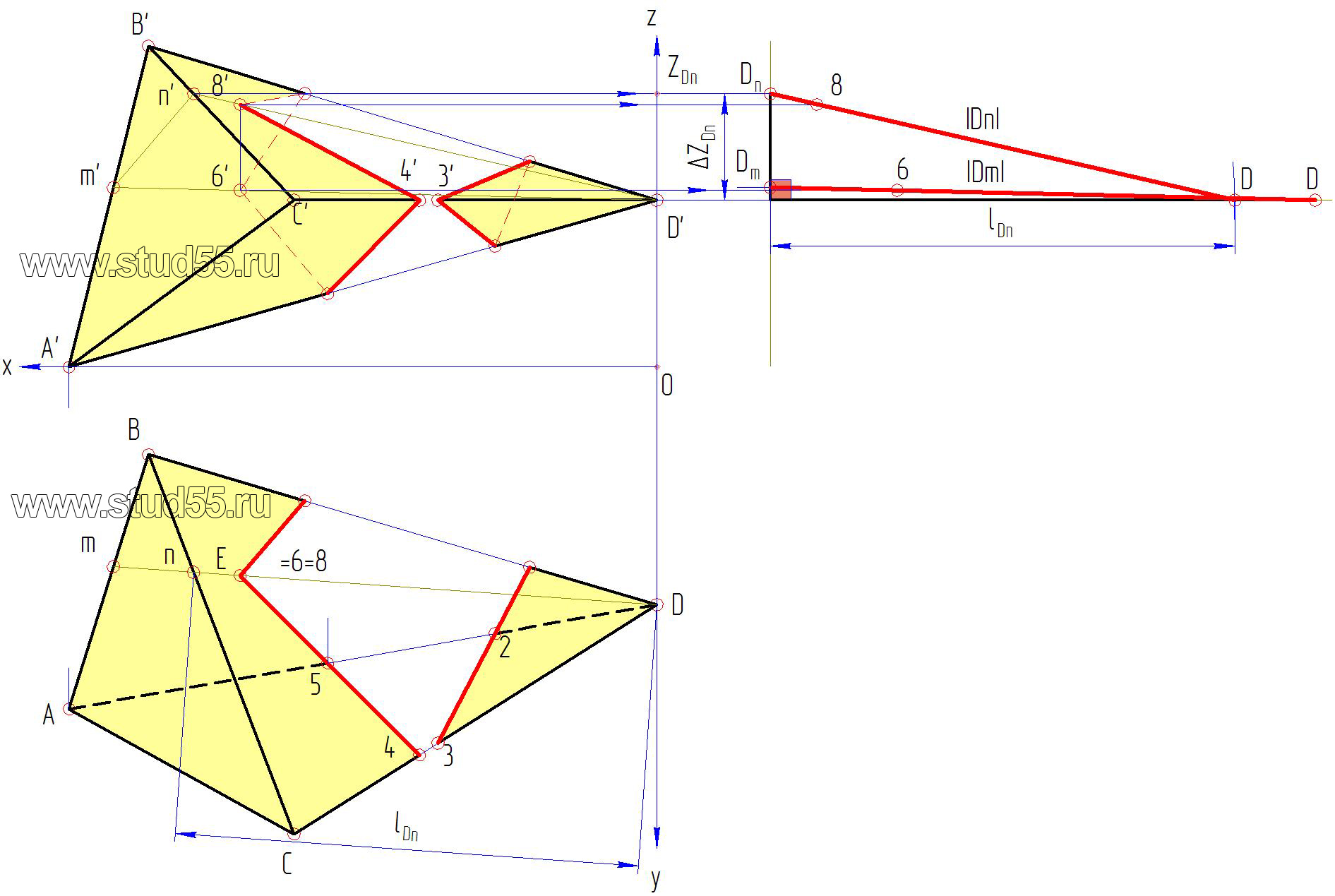
Рис.4.3
3. Итак, на свободном месте чертежа (рис.4.1.а) строим прямой угол.
По горизонтальной линии этого угла откладываем проекционную величину ребра пирамиды DA взятую с горизонтальной плоскости проекций — lDA. По вертикальной линии прямого угла откладываем разность координат точек D’ и A’, взятых с фронтальной плоскости проекций (по оси z вниз) — . Соединив полученные точки гипотенузой, получим натуральную величину ребра пирамиды |DA|.
Таким образом определяем натуральные величины других ребер пирамиды DB и DC, а также основания пирамиды АВ, ВС, АС (рис.4.2), для которых строим второй прямой угол. Заметим, что определение натуральной величины ребра DC производится в тех случаях, когда на исходном чертеже он дан проекционно. Это легко определяется, если вспомним правило: «если прямая па какой-либо плоскости проекций параллельна оси координат, то на сопряженной плоскости она проецируется в натуральную величину».
В частности, в примере нашей задачи фронтальная проекция ребра D’C’ параллельна оси х, следовательно, в горизонтальной плоскости DC сразу выражена в натуральной величине |DC| (рис.4.1).
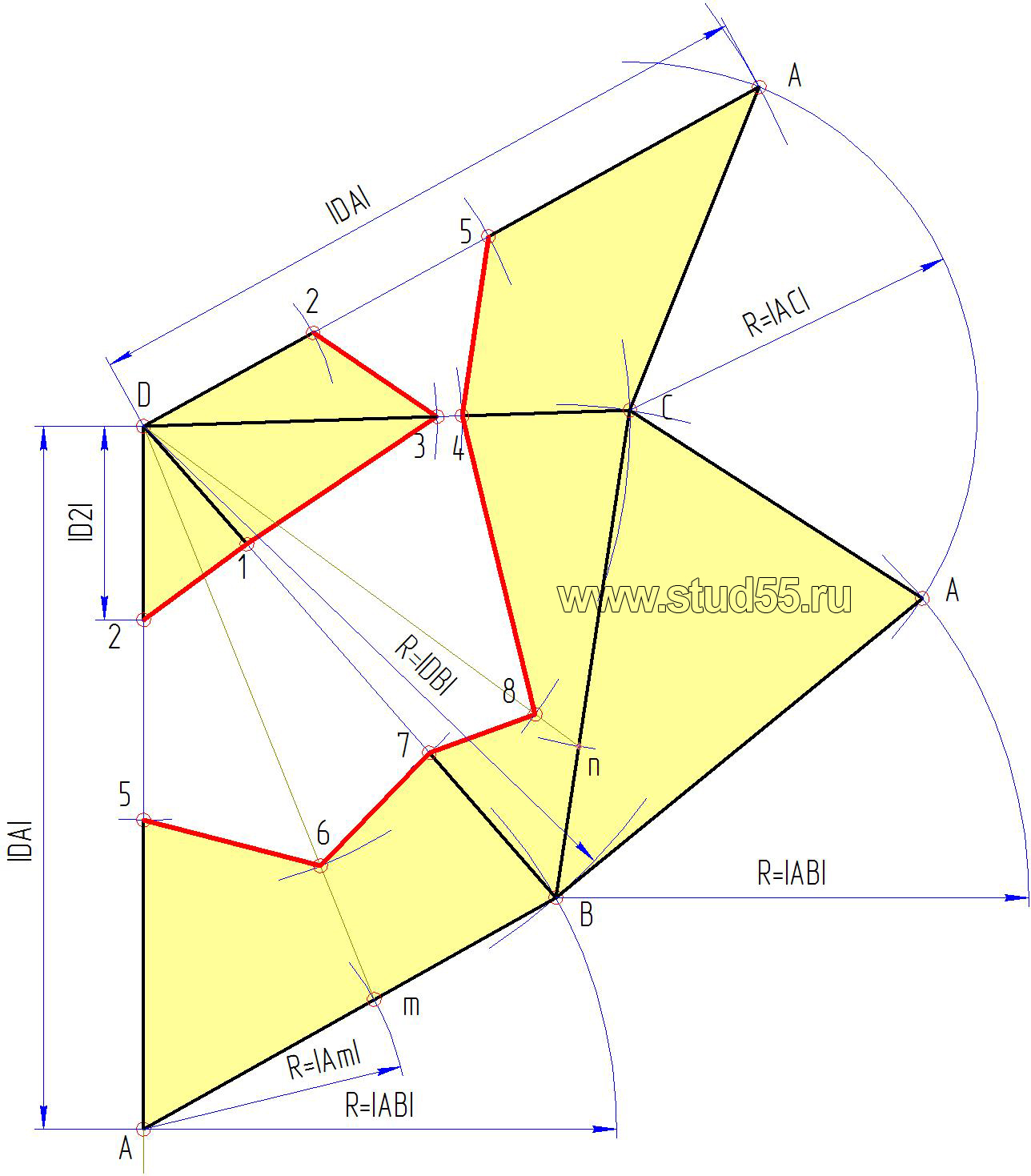
Рис.4.4
4. Определив натуральные величины ребер и основания пирамиды, приступаем к построению развертки (рис.4.4). Для этого на листе формата бумаги ближе к левой стороне рамки берем произвольную точку D считая, что это вершина пирамиды. Проводим из точки D произвольную прямую и откладываем на ней натуральную величину ребра |DA|, получая точку А. Тогда из точки А, взяв на раствор циркуля натуральную величину основания пирамиды R=|АВ| и поместив ножку циркуля в точку А делаем дуговую засечку. Далее берем на раствор циркуля натуральную величину ребра пирамиды R=|DB| и, поместив ножку циркуля в точку D делаем вторую дуговую засечку. В пересечении дуг получаем точку В, соединив ее с точками А и D получаем грань пирамиды DАВ. Аналогичным образом пристраиваем к ребру DB грань DBC, а к ребру DC — грань DCА.
К одной из сторон основания, например ВC, пристраиваем основание пирамиды также методом геометрических засечек, беря на раствор циркуля величины сторон АB и AС и делая дуговые засечки из точек B и C получая точку A (рис.4.4).
5. Построение развертки призмы упрощается тем, что на исходном чертеже в горизонтальной плоскости проекций основанием, а во фронтальной – высотой 85мм, она задана сразу в натуральную величину
Для построения развертки мысленно разрежем призму по какому-либо ребру, например по E, закрепив его на плоскости, развернем другие грани призмы до полного совмещения с плоскостью. Вполне очевидно, что получим прямоугольник, у которого длиной является сумма длин сторон основания, а высотой — высота призмы – 85мм.
Итак, для построения развертки призмы поступаем:
— на том же формате, где построена развертка пирамиды, с правой стороны проводим горизонтальную прямую линию и от произвольно взятой точки на ней, например E, последовательно откладываем отрезки основания призмы EK, KG, GU, UE, взятые с горизонтальной плоскости проекций;
— из точек E, K, G, U, E восстанавливаем перпендикуляры, на которых откладываем высоту призмы, взятую с фронтальной плоскости проекций (85мм);
— соединяя полученные точки прямой, получаем развертку боковой поверхности призмы и к одной из сторон основания, например, GU пристраиваем верхнее и нижнее основание методом геометрических засечек, как выполняли при построении основания пирамиды.
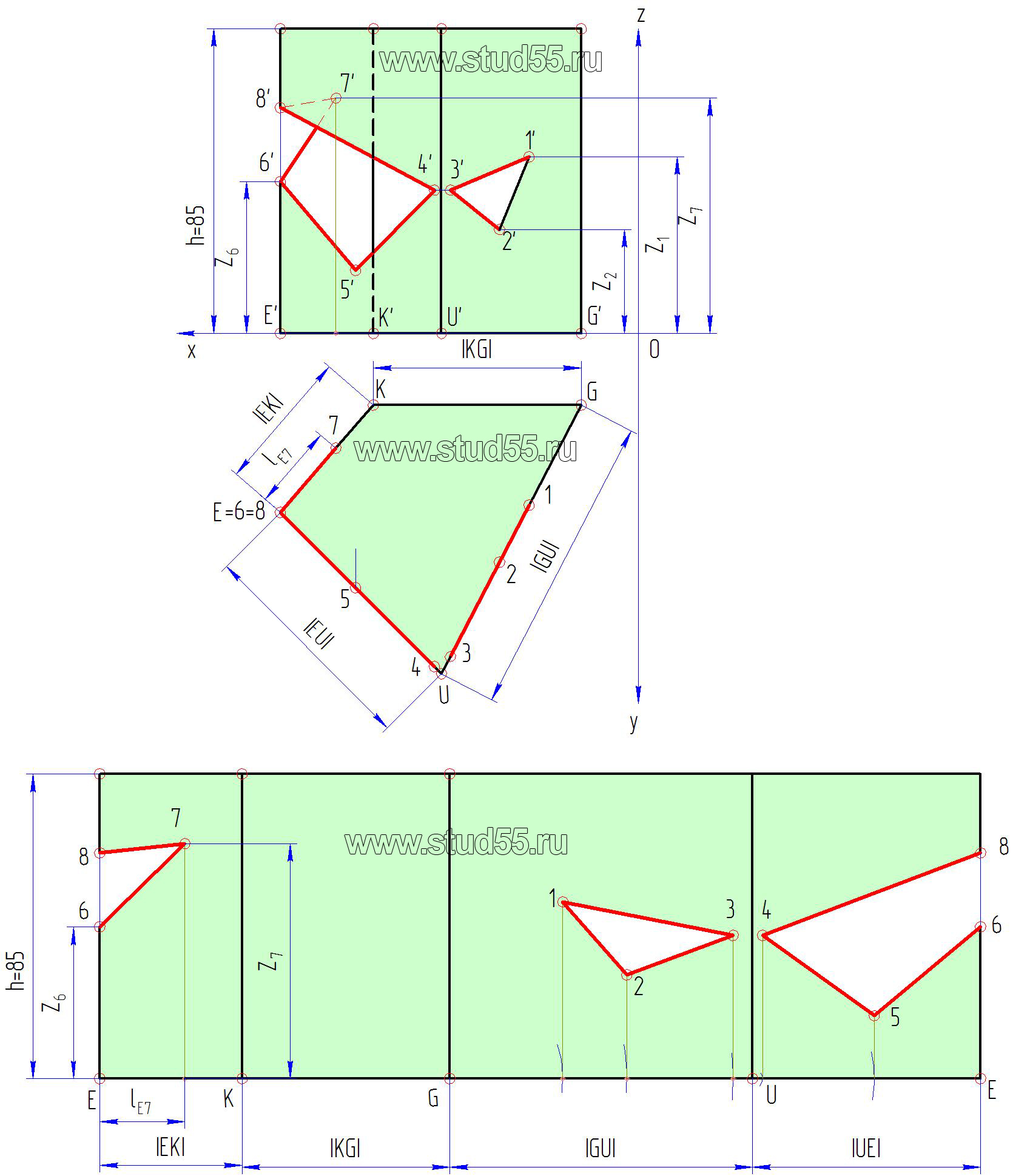
Рис.4.5
6. Для построения линии пересечения на развертке используем правило, гласящее о том, что «любой точке на поверхности соответствует точка на развертке». Возьмем, например, грань призмы GU, где проходит линия пересечения с точками 1-2-3;. Отложим на развертке основания GU точки 1,2,3 по расстояниям, взятым с горизонтальной плоскости проекции. Восстановим из этих точек перпендикуляры и отложим на них высоты точек 1’, 2’, 3’, взятые с фронтальной плоскости проекции – z1, z2 и z3. Таким образом, на развертке получили точки 1, 2, 3, соединив которые получаем первую ветвь линии пересечения.
Аналогично переносятся, все остальные точки. Построенные точки соединяются, получая вторую ветвь линии пересечения. Выделяем красным цветом – искомая линия. Добавим, что при неполном пересечении гранных тел, на развертке призмы будет одна замкнутая ветвь линии пересечения.
7. Построение (перенесение) линии пересечения на развертке пирамиды производится таким же образом, но с учетом следующего:
— поскольку развертки строятся из натуральных величин, необходимо перенести положение точек 1-8 линии пересечения проекций на линии ребер натуральных величин пирамиды. Для этого возьмем, например, точки 2 и 5 во фронтальной проекции ребра DA перенесем их на проекционную величину этого ребра прямого угла (рис.4.1) по линиям связи параллельным оси х, получим искомые отрезки |D2| и |D5| ребра DA в натуральных величинах, которые и откладываем (переносим) на развертку пирамиды;
— аналогично переносятся все другие точки линии пересечения, в том числе и точки 6 и 8, лежащие на образующих Dm и Dn для чего на прямом угле (рис.4.3) определяются натуральные величины этих образующих, а затем на них переносятся точки 6 и 8;
— на втором прямом угле, где определены натуральные величины основания пирамиды, переносятся точки m и n пересечений образующих с основанием, которые впоследствии переносятся на развертку.
Таким образом, полученные на натуральных величинах точки 1-8 и перенесенные на развертку, соединяем последовательно прямыми линиями и окончательно получаем линию пересечения пирамиды на ее развертке.
Раздел: Начертательная геометрия /
- Рекомендуем
- Комментарии
- Наши товары
Горизонтальная развертка
Cтраница 1
Горизонтальная развертка контролируется линейно возрастающим напряжением, которое воздействует на пластины горизонтального отклонения, расположенные слева и справа от электронной пушки. Вертикальная развертка контролируется более медленно возрастающим напряжением, которое воздействует на пластины вертикального отклонения, расположенные под и над электронной пушкой. После определенного количества разверток ( от 400 до 1000) напряжение на пластинах вертикального и горизонтального отклонения спадает, и луч возвращается в верхний левый угол экрана.
[1]
Горизонтальная развертка синхронизована с исследуемым процессом. Частота пилообразных импульсов велика и яркие точки, вспыхивающие на экране, в моменты отпирания луча сливаются в сплошную линию. Если набег фазы в измерительном канале постоянен ( плазма отсутствует или ее свойства строго неизменны), линии на экране осциллографа – горизонтальные прямые.
[3]
Горизонтальная развертка в осциллографе получается при помощи генератора на неоновой лампе. Для фиксации изображения в распоряжении оператора имеются регулятор времени по частоте и регулятор синхронизации.
[4]
Горизонтальная развертка типа А ( рис. 47, а) синхронизирована с перемещением импульса в изделии. Отклонение луча в вертикальном направлении пропорционально амплитуде принятого эхо-сигнала. Сигнал 1 соответствует зондирующему импульсу, сигнал 2 – донному сигналу; между ними располагается эхо-сигнал 3 от дефекта.
[6]
Горизонтальная развертка луча трубки осуществляется генератором 4 пилообразного напряжения. Полученный импульс подается на генератор горизонтальной развертки. Вследствие такого устройства на экране получается устойчивое изображение синусоиды.
[7]
Длительность горизонтальной развертки при использовании внутреннего генератора регулируется двумя ручками время развертки, причем левая устанавливает диапазон длительности скачкообразно, а правая позволяет установить длительность плавно в пределах выбранного диапазона.
[8]
Система горизонтальной развертки рассчитана на осциллогра-фирование трансформированного импульса, поэтому ее реализация не встречает трудностей.
[9]
Генератор горизонтальной развертки в таких осциллографах запускается самим исследуемым напряжением. Это запаздывание ( доли микросекунды) обеспечивается цепью задержки ( состоящей из катушек индуктивности И конденсаторов), включаемой на пути прохождения исследуемого напряжения к отклоняющим пластинам; цепь задержки вместе с тем вносит амплитудные и фазовые искажения в исследуемый импульс напряжения.
[10]
Неисправности горизонтальной развертки и АПЧ и Ф строк телевизора по внешним признакам могут быть следующие: нарушение частоты строчной развертки; недостаточная яркость свечения экрана кинескопа; уменьшение размера изображения по горизонтали; нарушение линейности по горизонтали; искажение растра типа трапеция или параллелограмм; перекос изображения; вырывание отдельных строк; яркая вертикальная полоса по центру экрана кинескопа; неприятно слышимый писк ( свист), частота которого равна частоте строчной развертки; быстрое пропадание растра, сопровождаемое щелчком в громкоговорителе, а затем его появление.
[11]
Когда горизонтальную развертку осуществляют от внешнего источника напряжения, то, выбирая осциллограф, следует проверить соответствие чувствительности, полосы пропускания и входных параметров канала горизонтального отклонения характеристикам развертывающего напряжения.
[12]
Не работает горизонтальная развертка. Неисправность может быть вызвана как отказом генераторе 1 000 гц так и отказом усилителя горизонтальной развертки. В обоих случаях при вращении ручки переменного резистора 220 Усиление горизонтальная развертка не регулируется.
[13]
Так как горизонтальная развертка луча осциллографической трубки осуществляется также гармоническим напряжением частотой 50 Гц, синфазным с током модуляции, на экране трубки наблюдается четкий сигнал ЯМР.
[14]
Частота генератора горизонтальной развертки должна быть равна скорости передачи телеграфных сигналов. Регулируется она посредством переменного сопротивления Частота. Стопирование обоих генераторов развертки производится стартстопным устройством в конце стартстопного цикла. В моменты изменения полярности входящих посылок происходит резкое увеличение яркости светового пятна: на экране трубки. При отсутствии искажений светящиеся точки находятся на одной вертикали, а при наличии искажений они отклоняются от вертикали.
[15]
Страницы:
1
2
3
4
5
