ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Наиболее простым и наглядным методом решения задачи линейного программирования (ЗЛП) является графический метод. Он основан на геометрической интерпретации задачи линейного программирования и применяется при решении ЗЛП с двумя неизвестными:
Будем рассматривать решение этой задачи на плоскости. Каждое неравенство системы функциональных ограничений геометрически определяет полуплоскость с граничной прямой апх, + + aj2х2 = bn i = 1, т. Условия неотрицательности определяют полуплоскости с граничными прямыми х <= 0, х2 = 0 соответственно. Если система совместна, то полуплоскости, пересекаясь, образуют общую часть, которая является выпуклым множеством и представляет собой совокупность точек; координаты каждой из этих точек являются решением данной системы. Совокупность этих точек называют многоугольником решений. Он может быть точкой, отрезком, лучом, ограниченным и неограниченным многоугольником.
Геометрически ЗЛП представляет собой отыскание такой угловой точки многоугольника решений, координаты которой доставляют максимальное (минимальное) значение линейной целевой функции, причем допустимыми решениями являются все точки многоугольника решений.
Линейное уравнение описывает множество точек, лежащих на одной прямой. Линейное неравенство описывает некоторую область на плоскости.
Определим, какую часть плоскости описывает неравенство 2х <+ Зх2 0, j = 1, п). Координаты любой точки, принадлежащей области определения, являются допустимым решением задачи.
Для нахождения экстремального значения целевой функции при графическом решении ЗЛП используют вектор-градиент, координаты которого являются частными производными целевой функции:
Этот вектор показывает направление наискорейшего изменения целевой функции. Прямая c[xl + с2х2 = f(x0), перпендикулярная вектору-градиенту, является линией уровня целевой функции (рис. 2.2.2). В любой точке линии уровня целевая функция принимает одно и то же значение. Приравняем целевую функцию постоянной величине а. Меняя значение а, получим семейство параллельных прямых, каждая из которых является линией уровня целевой функции.
Рис. 2.2.2. Вектор-градиент и линии уровня
Важное свойство линии уровня линейной функции состоит в том, что при параллельном смещении линии в одну сторону уровень только возрастает, а при смещении в д р у г у ю сторону — только убывает.
Графический метод решения ЗЛП состоит из четырех этапов:
- 1. Строится область допустимых решений (ОДР) ЗЛП.
- 2. Строится вектор-градиент целевой функции (ЦФ) с началом в точке х0 (0; 0): V = (с,, с2).
- 3. Линия уровня CjXj + с2х2 = а (а — постоянная величина) — прямая, перпендикулярная вектору-градиенту V, — передвигается в направлении вектора-градиента в случае максимизации целевой функции f(xv х2) до тех пор, пока не покинет пределов ОДР. При минимизации /(*,, х2) линия уровня перемещается в направлении, противоположном вектору-градиенту. Крайняя точка (или точки) ОДР при этом движении и является точкой максимума (минимума) f(xpjc2).
Если прямая, соответствующая линии уровня, при своем движении не покидает ОДР, то минимума (максимума) функции f(xр х2) не существует.
Если линия уровня целевой функции параллельна функциональному ограничению задачи, на котором достигается оптимальное значение ЦФ, то оптимальное значение ЦФ будет достигаться в любой точке этого ограничения, лежащей между двумя оптимальными угловыми точками, и, соответственно, любая из этих точек является оптимальным решением ЗЛП.
4. Определяются координаты точки максимума (минимума). Для этого достаточно решить систему уравнений прямых, дающих в пересечении точку максимума (минимума). Значение f(x<, х2), найденное в полученной точке, является максимальным (минимальным) значением целевой функции.
Возможные ситуации графического решения ЗЛП представлены в табл. 2.2.1.
Как построить вектор градиент целевой функции
Графический метод характеризуется простотой и наглядностью, однако он недостаточно точен и применим только для задач с не более чем тремя переменными. Последнее обусловлено тем, что человек, живущий в трехмерном пространстве, практически не способен представить себе визуально пространство более высокого порядка.
Метод основан на том, что каждое ограничение неравенство отсекает в n -мерном пространстве n -мерную полуплоскость (в данной курсовой работе это двухмерное пространство (плоскость) и простая полуплоскость). Совокупность этих полуплоскостей (если ограничения совместны) образует n -мерный многогранник допустимых решений. Оптимальное решение достигается в одной из вершин многогранника. Для определения этой вершины необходимо построить поверхность уровня целевой функции (в курсовом проекте линию уровня). Затем следует перемещать эту поверхность (линию) в направлении градиента до крайней точки области допустимых решений (ОДР).
Рассмотрим следующий простой пример решения задачи линейного программирования (ЗЛП) графическим методом.
Математическая модель: 2Х1+3Х2≤60;
3Х1+2Х2≤60;
4Х1+20Х2≤200;
Х1≥0; Х2≥0;
F=40Х1+30Х2→Мах.
Перейдем от неравенств к равенствам: 2Х1+3Х2=60;
3Х1+2Х2=60;
4Х1+20Х2=200.
Это уравнения прямых линий, которые могут быть легко построены по двум точкам:
для первого ограничения Х1=0; Х2=20;
Х2=0; Х1=30.
для второго ограничения Х1=0; Х2=30;
Х2=0; Х1=20.
для третьего ограничения Х1=0; Х2=10;
Х2=0; Х1=50.
Градиент целевой функции это вектор, характеризующий направление и скорость изменения функции (в данном случае целевой функции). Он определяется ее частными производными по каждой переменной:
Линия уровня целевой функции перпендикулярна градиенту.
Графическое решение данной задачи приведено на рисунке 6.1.
Рис. 6.1. Графическое решение задачи
Область допустимых решений (ОДР) в данном случае образуется четырехугольником ОВСД. Ни одна точка внутри его или на его границе не противоречит ни одному из ограничений. Оптимальное решение находится в одной из вершин четырехугольника. Для нахождения оптимального решения перемещаем линию уровня целевой функции в направлении градиента до крайней точки ОДР. Такой точкой является точка С с координатами: Х1=16; Х2=8. Значение целевой функции F=40×16+30×8=880. Очевидно, что это решение не отличается высокой точностью, что характерно для графического метода.
Из рисунка видно, что ресурсы второго и третьего видов использованы полностью, а ресурс первого вида оказался в избытке. Для количественной оценки этого избытка определим сначала расход данного ресурса: 2×16+3×8=56. Запас равен 60, тогда остаток составит 6056=4.
6.1.2. Симплексный метод решения
задач линейного программирования
В отличие от графического метода, симплексный метод абсолютно точен. Кроме того, он дает возможность для точной количественной оценки излишков имеющихся ресурсов, а применение двойственного симплекс-метода дает еще и большие возможности для технико-экономического анализа полученного решения с целью выработки обоснованных рекомендаций по улучшению условий функционирования системы.
Приведем задачу, рассмотренную в предыдущем разделе, к канонической форме: 2Х1+3Х2+Х3=60;
3Х1+2Х2+Х4=60;
4Х1+20Х2+Х5=200;
F-40Х1 -30Х2 =0.
Дополнительные переменные Х3, Х4 и Х5 равны разности между левой и правой частями ограничений и характеризуют недовыполнение данного ограничения (в данном случае излишний запас).
Задача решается в стандартных симплексных таблицах. Исходная таблица (см. табл. 6.1) заполняется коэффициентами модели.
| Базис | Х1 | Х2 | Х3 | Х4 | Х5 | а io | a io / a ip |
|---|---|---|---|---|---|---|---|
| Х3 | 2 | 3 | 1 | 0 | 0 | 60 | 20 |
| Х4 | 3 | 2 | 0 | 1 | 0 | 60 | 30 |
| Х5 | 4 | 20 | 0 | 0 | 1 | 200 | 10 |
| F | 4 | 3 | 0 | 0 | 0 | 0 |
Исходная таблица
Базисными переменными являются переменные, входящие только в одно уравнение, с коэффициентом +1. Базисным переменным соответствует единичный вектор-столбец. Базисные переменные равны свободным членам. Свободные переменные (переменные, не вошедшие в базис) равны нулю. Таким образом, Х1=0; Х2=0; Х3= 60; Х4= 60; Х5=200; F=0.
Данное решение является опорным, так как в столбце свободных членов нет отрицательных элементов.
В качестве разрешающего столбца выбирается любой столбец с отрицательной оценкой в строке целевой функции F. Выберем в данном случае в качестве разрешающего второй столбец. Для всех его элементов вычисляем симплексные отношения a io /a ip (отношение элемента столбца свободных членов к соответствующему элементу разрешающего столбца) и записываем их в последний столбец таблицы. Разрешающий элемент определяется минимальным симплексным отношением (в таблице он выделен жирным шрифтом). На месте разрешающего элемента ставится 1, а остальные элементы данного столбца равны нулю.
Остальные столбцы, соответствующие базисным переменным остаются без изменения. Столбец, соответствующий выводимой из базиса переменной, пересчитывается по общему правилу, описанному ниже. В данном случае Х2 вводится в базис вместо Х5 и столбец Х5 пересчитывается. Элементы разрешающей строки делятся на разрешающий элемент. Все остальные элементы таблицы пересчитываются по правилу прямоугольника. Пересчитываемый элемент образует с разрешающим элементом и соответствующими элементами разрешающей строки и столбца прямоугольник, изображенный на рисунке 6.2.
Рис. 6.2. Прямоугольник пересчета элементов симплексной таблицы
Пересчет производится по следующей формуле:
т.е. пересчитываемый элемент умножается на решающий элемент, минус элемент соответствующего разрешающего столбца, умноженный на соответствующий элемент разрешающей строки, и эта разность делится на разрешающий элемент. Или иначе: произведение элементов главной диагонали минус произведение элементов побочной диагонали, деленное на разрешающий элемент.
Например, пересчет элемента первого столбца первой строки:
| Базис | Х1 | Х2 | Х3 | Х4 | Х5 | а io | a io / a ip |
|---|---|---|---|---|---|---|---|
| Х3 | 1,4 | 0 | 1 | 0 | 0,15 | 30 | 21,4 |
| Х4 | 2,6 | 0 | 0 | 1 | 0,10 | 40 | 15,4 |
| Х2 | 0,2 | 1 | 0 | 0 | 0,05 | 10 | 50 |
| F | 3,4 | 0 | 0 | 0 | 0,150 | 300 |
Первая итерация расчета
Решение задачи на любой итерации читается следующим образом: базисные переменные равны свободным членам (предпоследний столбец в таблице) а свободные переменные (те, которые не входят в базис) равны нулю. В данном случае Х3 = 30; Х4 = 40; Х2 = 10; Х1 = Х5 = 0.
Или в краткой форме записи: Х1 = (0; 10; 30; 40; 0), F = 300.
Здесь значения переменных приводятся в порядке возрастания их индексов.
Технико-экономический анализ полученного решения
Выпускается десять единиц продукции второго вида (Х2 = 10). При этом ресурс второго вида останется в количестве тридцати единиц (Х3 = 30), ресурс первого вида останется в количестве сорока единиц (Х4 = 40), а ресурс третьего вида оказывается израсходованным полностью (Х5 = 0).
Проверка полученного решения: 2·0+3·10+30=60;
3·0+2·10+40=60;
4·0+20·10+0=200;
F=40·0+30·10=300.
Данное решение не является оптимальным, так как в строке целевой функции еще есть отрицательный элемент а 1F = 3,4.
Вторая и все последующие итерации выполняются аналогично.
| Базис | Х1 | Х2 | Х3 | Х4 | Х5 | а io | a io / a ip |
|---|---|---|---|---|---|---|---|
| Х3 | 0 | 0 | 1 | 0,54 | 0,1 | 8,5 | |
| Х1 | 1 | 0 | 0 | 0,38 | 0,04 | 15,4 | |
| Х2 | 0 | 1 | 0 | 0,74 | 0,17 | 6,9 | |
| F | 0 | 0 | 0 | 1,3 | 0,28 | 823 |
Вторая итерация расчета
Х2=(15,4; 6,9; 8,5; 0; 0) → F=823.
Это решение оптимально, так как в строке целевой функции нет отрицательных оценок.
Технико-экономический анализ полученного решения
При имеющихся ресурсах следует выпустить 15,4 единицы (Х1=15,4) продукции первого вида и 6,9 единицы продукции второго вида (Х2=6,9). При этом ресурсы первого вида остаются в количестве 8,5 единицы (Х3=8,5), а ресурсы второго и третьего вида израсходованы полностью (Х4=Х5=0). Прибыль составит 823 у.е.
Проверка: 2·15,4+3·6,9+8,5=60;
3·15,4+2·6,9+0=60;
4·15,4+20·6,9+0=200;
F=40·15,4+30·6,9=823.
Сравнение полученных результатов с результатами графического метода подтверждает, что графический метод при всей своей наглядности не отличается достаточной точностью.
© ФГОУ ВПО Красноярский государственный аграрный университет
Как построить вектор градиент целевой функции
ПРИМЕР ГРАФИЧЕСКОГО РЕШЕНИЯ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
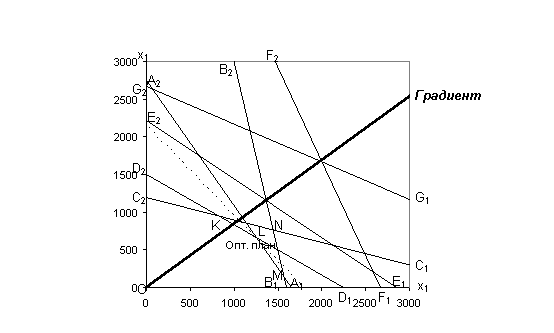
Построение градиента и определение оптимального плана
Обратимся к целевой функции. Ее градиент есть вектор (32; 27). Для решения задачи следует изобразить этот вектор в виде стрелки с началом в точке (0; 0) и концом в точке (32; 27).
Такая стрелка является короткой и поэтому плохо различимой на чертеже. Однако длина этой стрелки не играет никакой роли при решении задачи. Важно лишь ее направление. Если обе координаты точки (32; 27) умножить или разделить на одно и то же положительное число, то изменится лишь длина стрелки, но не ее направление. Поэтому на результате решения задачи это не скажется.
Удлиним стрелку до границы нашего рисунка ( Рис. 2.5 ).
Все линии уровня целевой функции параллельны друг другу и перпендикулярны градиенту. На Рис. 2.5 пунктиром изображены линии, соответствующие различным значениям целевой функции, начиная от 10000 и с шагом 16000. Разумеется, такие линии могут быть построены для любых значений целевой функции, они параллельны и все вместе покрывают координатную плоскость.
Градиент показывает направление роста целевой функции. Мы решаем задачу на максимум. Чем больше значение целевой функции, тем лучше. Однако при слишком больших значениях пунктирная линия уровня окажется за пределами области допустимых планов.
Рис. 2 . 6 . Построение оптимального плана
В своем крайнем положении линия уровня проходит через точку L . Таким образом, точка L является оптимальным планом задачи. Это единственная точка, принадлежащая одновременно области допустимых планов и линии уровня в ее крайнем положении. Следовательно, наша задача обладает единственным оптимальным планом.
Найдем координаты оптимального плана. Приближенно их можно определить по чертежу. Для точного расчета необходимо решить соответствующую систему уравнений. Точка L лежит на границе первого и четвертого ограничений. Составляем систему уравнений:
Решив эту систему, получаем компоненты оптимального плана: x 1 = 1250 и x 2 = 667. Таким образом, оптимальный план X*max равен:
.
Он предписывает выпустить 1250 кг Печенья и 667 (точнее, 666,667) кг Бисквитов.
Для определения оптимума следует подставить компоненты оптимального плана в целевую функцию задачи. Оптимум Z*max определяется равенством:
.
Таким образом, реализация выпущенной продукции даст выручку в размере 58000 руб. Задача решена. Теперь следует обратиться к экономическому содержанию задачи и проанализировать полученный результат.
Рассмотрим, для полноты картины, задачу, когда при той же системе ограничений и той же целевой функции требуется найти не максимальное, а минимальное ее значение. В этой ситуации все рассуждения, связанные с построением области допустимых планов и градиента полностью сохраняются. Однако для нахождения оптимального плана следует теперь смещать линию уровня до крайнего положения в направлении, противоположном градиенту. Оптимальным планам для задачи на минимум окажется точка О – начало координат. Оптимум будет равен 0.
[spoiler title=”источники:”]
http://www.kgau.ru/distance/fub_03/eldeshtein/logistika/kurs/06_01.html
http://ecocyb.narod.ru/217-220/s11.htm
[/spoiler]
Уважаемые студенты!
Заказать задачи по физике, информатике, экономике, праву, химии, теормеху, сопромату и другим предметам можно здесь всего за 10 минут.
Градиент функции
Как найти?
Постановка задачи
Найти градиент функции $ f(x,y,z) $ в точке $ M(x_0,y_0,z_0) $
План решения
Градиент функции $ f(x,y,z) $ – это вектор, каждая координата которого является частной производной первого порядка этой функции:
$$ grad f = frac{partial f}{partial x} overline {i} + frac{partial f}{partial y} overline{j} + frac{partial f}{partial z} overline {k} $$
- Берём частные производные первого порядка от функции $ f(x,y,z) $:
$$ frac{partial f}{partial x}, frac{partial f}{partial y}, frac{partial f}{partial z} $$ - Вычисляем полученные производные в точке $ M(x_0,y_0,z_0) $:
$$ frac{partial f}{partial x} bigg |_{M(x_0,y_0,z_0)}, frac{partial f}{partial y} bigg |_{M(x_0,y_0,z_0)}, frac{partial f}{partial z} bigg |_{M(x_0,y_0,z_0)} $$ - Подставляем, полученные данные в формулу градиента функции:
$$ grad f bigg |_M = frac{partial f}{partial x} bigg |_M overline{i} + frac{partial f}{partial y} bigg |_M overline{j} + frac{partial f}{partial z} bigg |_M overline{k} $$
Примеры решений
| Пример 1 |
| Найти градиент функции $ u = x + ln (z^2+y^2) $ в точке $ M(2,1,1) $ |
| Решение |
|
Находим частные производные первого порядка функции трёх переменных: Вычисляем значение производных в точке $ M(2,1,1) $: $$ frac{partial f}{partial x} bigg |_{M(2,1,1)} = 1 $$ $$ frac{partial f}{partial y} bigg |_{M(2,1,1)} = frac{2 cdot 1}{1^2+1^2} = frac{2}{2}=1 $$ $$ frac{partial f}{partial z} bigg |_{M(2,1,1)} = frac{2cdot 1}{1^2 + 1^2} = frac{2}{2}=1 $$ Подставляем в формулу градиента функции полученные данные: $$ grad f = 1 cdot overline{i} + 1 cdot overline{j} + 1 cdot overline{k} = overline{i}+overline{j}+overline{k} $$ Запишем ответ в координатной форме: $$ grad f = overline{i}+overline{j}+overline{k} = (1,1,1) $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ grad f = (1,1,1) $$ |
| Пример 2 |
| Найти градиент функции $ u = sin(x+2y)+2sqrt{xyz} $ в точке $ M bigg (frac{pi}{2},frac{3pi}{2},3 bigg ) $ |
| Решение |
|
Находим частные производные: $$ frac{partial f}{partial x} = cos(x+2y) + frac{yz}{sqrt{xyz}} $$ $$ frac{partial f}{partial y} = 2cos(x+2y) + frac{xz}{sqrt{xyz}} $$ $$ frac{partial f}{partial z} = frac{xy}{sqrt{xyz}} $$ Вычисляем значения производных в точке $ M bigg (frac{pi}{2},frac{3pi}{2},3 bigg ) $: $$ frac{partial f}{partial x} bigg |_{M(frac{pi}{2},frac{3pi}{2},3)} = cos(frac{pi}{2}+3pi)+ frac{frac{9pi}{2}}{sqrt{frac{9pi^2}{4}}} = cos frac{7pi}{2} + sqrt{9} = 3 $$ $$ frac{partial f}{partial y} bigg |_{M(frac{pi}{2},frac{3pi}{2},3)} = 2 cos(frac{pi}{2}+3pi) + frac{frac{3pi}{2}}{sqrt{frac{9pi^2}{4}}} = 2 cos frac{7pi}{2} + 1 = 2 cdot 0 + 1 = 1 $$ $$ frac{partial f}{partial y} bigg |_{M(frac{pi}{2},frac{3pi}{2},3)} = frac{frac{3pi^2}{4}}{sqrt{frac{9pi^2}{4}}} = sqrt{frac{pi^2}{4}} = frac{pi}{2} $$ Подставляем вычисленные недостающие данные в формулу и получаем: $$ grad f = 3 cdot overline{i}+ 1 cdot overline{j} + frac{pi}{2} cdot overline{k} = 3overline{i}+overline{j}+frac{pi}{2} overline{k} $$ Записываем ответ в координатной форме: $$ grad f = (3,1,frac{pi}{2}) $$ |
| Ответ |
| $$ grad f = (3,1,frac{pi}{2}) $$ |
Построение градиента и определение оптимального плана
Обратимся
к целевой функции. Ее градиент есть
вектор (32; 27). Для решения задачи следует
изобразить этот вектор в виде стрелки
с началом в точке (0; 0) и концом в точке
(32; 27).
Такая
стрелка является короткой и поэтому
плохо различимой на чертеже. Однако
длина этой стрелки не играет никакой
роли при решении задачи. Важно лишь ее
направление. Если обе координаты точки
(32; 27) умножить или разделить на одно и
то же положительное число, то изменится
лишь длина стрелки, но не ее направление.
Поэтому на результате решения задачи
это не скажется.
Удлиним
стрелку до границы нашего рисунка (Error: Reference source not found).
Все
линии уровня целевой функции параллельны
друг другу и перпендикулярны градиенту.
На Error: Reference source not foundпунктиром изображены
линии, соответствующие различным
значениям целевой функции, начиная от
10000 и с шагом 16000. Разумеется, такие линии
могут быть построены для любых значений
целевой функции, они параллельны и все
вместе покрывают координатную плоскость.
Градиент
показывает направление роста целевой
функции. Мы решаем задачу на максимум.
Чем больше значение целевой функции,
тем лучше. Однако при слишком больших
значениях пунктирная линия уровня
окажется за пределами области допустимых
планов.
Рис.
Сложение матриц..5. Построение оптимального
плана
В
своем крайнем положении линия уровня
проходит через точку L.
Таким образом, точка L
является оптимальным планом задачи.
Это единственная точка, принадлежащая
одновременно области допустимых планов
и линии уровня в ее крайнем положении.
Следовательно, наша задача обладает
единственным оптимальным планом.
Найдем
координаты оптимального плана. Приближенно
их можно определить по чертежу. Для
точного расчета необходимо решить
соответствующую систему уравнений.
Точка L
лежит на границе первого и четвертого
ограничений. Составляем систему
уравнений:

Решив
эту систему, получаем компоненты
оптимального плана: x1
= 1250 и x2
= 667. Таким образом, оптимальный план
X*max
равен:
.
Он
предписывает выпустить 1250 кг Печенья
и
667 (точнее, 666,667) кг Бисквитов.
Для
определения оптимума следует подставить
компоненты оптимального плана в целевую
функцию задачи. Оптимум Z*max
определяется равенством:
.
Таким
образом, реализация выпущенной продукции
даст выручку в размере 58000 руб. Задача
решена. Теперь следует обратиться к
экономическому содержанию задачи и
проанализировать полученный результат.
Рассмотрим,
для полноты картины, задачу, когда при
той же системе ограничений и той же
целевой функции требуется найти не
максимальное, а минимальное ее значение.
В этой ситуации все рассуждения, связанные
с построением области допустимых планов
и градиента полностью сохраняются.
Однако для нахождения оптимального
плана следует теперь смещать линию
уровня до крайнего положения в направлении,
противоположном градиенту. Оптимальным
планам для задачи на минимум окажется
точка О – начало координат. Оптимум будет
равен 0.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Приветствую всех. Сегодня на занятии хотелось бы затронуть немало важную тему, связанную одновременно с дифференциальным исчислением и векторной алгеброй. Мы постараемся как можно меньше углубляться в теоретические тезисы и побольше сделаем упор на решение практических задач. Незамедлительно начнём.
Определение слова “градиент” в математике нужно усвоить.
Градиент – это вектор показывающий направление наибольшего возрастания функции. Модуль вектора градиента показывает скорость изменения функции.
Запишем формулу для нахождения вектора градиента:
При нашем раскладе можно с теорией закончить, этого будет достаточно.
Разберём простенький примерчик для начала.
Никто ведь не забыл как брать частные производные? Если подзабыли, ссылочка (на статью) будет в конце урока.
Было слишком уж просто для нас, возьмём что-нибудь посложнее.
Такого плана примеры уже устно не решишь, хотя… Нет, всё же возможно.
Не будем перенапрягаться сильно, рассмотрим последний пример и пойдём отдыхать.
Берёмся за дело.
Не отчаиваемся что уже конец практики, у вас всегда есть возможность найти похожие задачки в интернете или взять в библиотеке задачник по высшей математике. Практикуйтесь, практикуйтесь, и ещё раз практикуйтесь. Спасибо за внимание.
Другие темы: