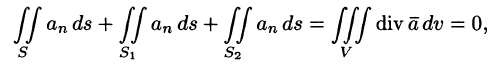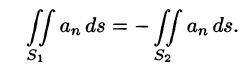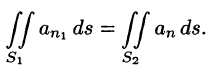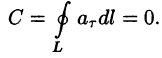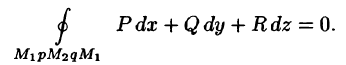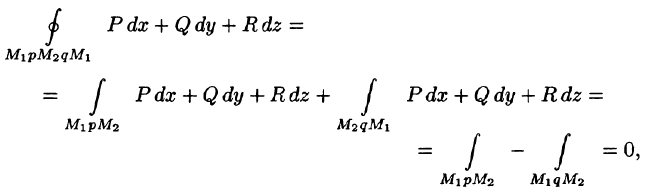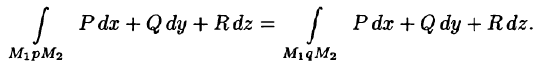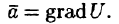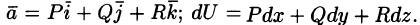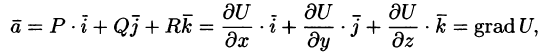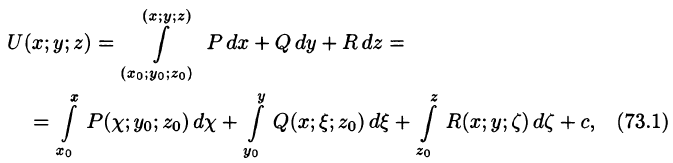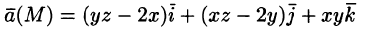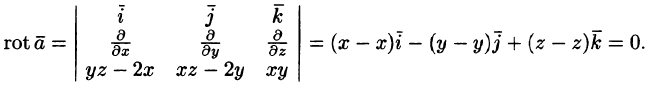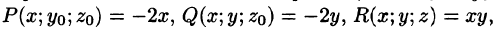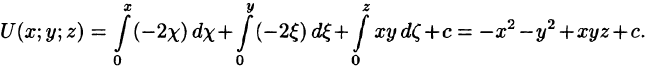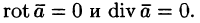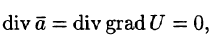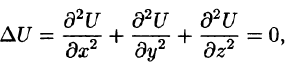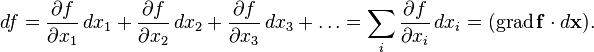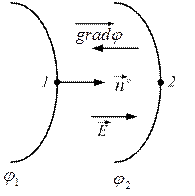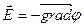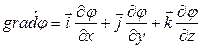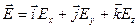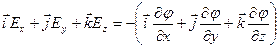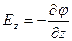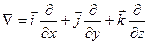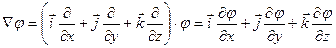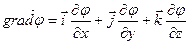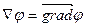Оператор градиента преобразует холм (слева), если смотреть на него сверху, в поле векторов (справа). Видно, что векторы направлены «в горку» и чем они длиннее, тем круче наклон
Градие́нт (от лат. gradiens — «шагающий, растущий») — вектор, своим направлением указывающий направление наискорейшего роста некоторой скалярной величины 
Градиент поля 



Пространство, на котором определена функция и её градиент, может быть, вообще говоря, как обычным трёхмерным пространством, так и пространством любой другой размерности.
Термин впервые появился в метеорологии для исследования изменений температуры и давления атмосферы, а в математику был введён Максвеллом в 1873 году; обозначение 


Иллюстрация применения[править | править код]
Градиент 2D функции отображен на графике в виде синих стрелок
Пусть температура в комнате задана с помощью скалярного поля T таким образом, что в каждой точке, заданной координатами (x, y, z) температура равняется T(x, y, z) (предположим, что температура не изменяется с течением времени). В каждой точке комнаты градиент функции T будет показывать направление, в котором температура возрастает быстрее всего. Величина градиента определяет, насколько быстро температура возрастает в данном направлении.
Определение и вычисление[править | править код]
Для случая трёхмерного пространства градиентом дифференцируемой в некоторой области
скалярной функции 



[3]
Или, использовав для единичных векторов по осям прямоугольных декартовых координат 
Если 



компоненты которого равны частным производным 
- Размерность вектора градиента определяется, таким образом, размерностью пространства (или многообразия), на котором задано скалярное поле, о градиенте которого идёт речь.
- Оператором градиента называется оператор, действие которого на скалярную функцию (поле) даёт её градиент. Этот оператор иногда коротко называют просто «градиентом».
Смысл градиента любой скалярной функции 




Стоит здесь заметить, что поскольку формула полного дифференциала не зависит от вида координат 

или, опуская по правилу Эйнштейна знак суммы,
(в ортонормированном базисе мы можем писать все индексы нижними, как мы и делали выше).
Однако градиент оказывается настоящим ковариантным вектором в любых криволинейных координатах.
Используя интегральную теорему
,
градиент можно выразить в интегральной форме:
здесь 

Пример[править | править код]
Например, градиент функции 
Некоторые применения[править | править код]
Геометрический смысл[править | править код]
Рассмотрим семейство линий уровня функции 
Нетрудно показать, что градиент функции 


В физике[править | править код]
В различных отраслях физики используется понятие градиента различных физических полей.
Например, напряжённость электростатического поля есть минус градиент электростатического потенциала, напряжённость гравитационного поля (ускорение свободного падения) в классической теории гравитации есть минус градиент гравитационного потенциала. Консервативная сила в классической механике есть минус градиент потенциальной энергии.
В других естественных науках[править | править код]
Понятие градиента находит применение не только в физике, но и в смежных и даже сравнительно далёких от физики науках (иногда это применение носит количественный, а иногда и просто качественный характер).
Например, градиент концентрации — нарастание или уменьшение по какому-либо направлению концентрации растворённого вещества, градиент температуры — увеличение или уменьшение по какому-то направлению температуры среды и т. д.
Градиент таких величин может быть вызван различными причинами, например, механическим препятствием, действием электромагнитных, гравитационных или других полей или различием в растворяющей способности граничащих фаз.
В экономике[править | править код]
В экономической теории понятие градиента используется для обоснования некоторых выводов и для оптимизации. В частности, используемые для нахождения оптимума потребителя метод множителей Лагранжа и условия Куна — Таккера (позаимствованные из естественных наук) основаны на сопоставлении градиентов функции полезности и функции бюджетного ограничения.
Связь с производной по направлению[править | править код]
Используя правило дифференцирования сложной функции, нетрудно показать, что
производная функции 



Таким образом, для вычисления производной скалярной функции векторного аргумента по любому направлению достаточно знать
градиент функции, то есть вектор, компоненты которого являются её частными производными.
Градиент в ортогональных криволинейных координатах[править | править код]
где 
Полярные координаты (на плоскости)[править | править код]
Коэффициенты Ламе:
Отсюда:
Цилиндрические координаты[править | править код]
Коэффициенты Ламе:
Отсюда:
Сферические координаты[править | править код]
Коэффициенты Ламе:
Отсюда:
Вариации и обобщения[править | править код]
Пусть 


выполняется для произвольной спрямляемой кривой 



См. также[править | править код]
- 4-градиент
- Векторный анализ
- Градиент концентрации
- Градиентные методы
- Оператор Кэнни
- Теорема Остроградского — Гаусса
- Формулы векторного анализа
Примечания[править | править код]
- ↑ Градиент // Советский энциклопедический словарь. — 2-е изд.. — М.: Советская энциклопедия, 1982. — С. 332. — 1600 с.
- ↑ Математическая энциклопедия, 1977.
- ↑ Коваленко Л. И. Методические указания по математическому анализу для студентов второго курса. Элементы векторного анализа.. — МФТИ, 2001. — С. 5. — 35 с. Архивная копия от 7 ноября 2020 на Wayback Machine
- ↑ 6.2 в Heinonen, Juha, et al. Sobolev spaces on metric measure spaces. Vol. 27. Cambridge University Press, 2015.
Литература[править | править код]
- Дубровин Б. А., Новиков С. П., Фоменко А. Т. Современная геометрия. Методы и приложения: уч. пособие для физико-математических специальностей университетов. — М.: Наука, 1986. — 759 с.
- Кочин Н. Е. Векторное исчисление и начала тензорного исчисления. — 9-е изд. — М. : Наука, 1965.
- Купцов Л. П. Градиент // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1977. — Т. 1. — Стб. 1080. — 1152 с.
- Рашєвский П. К. Риманова геометрия и тензорный анализ. — 3-е изд. — М. : Наука, 1967.
Ссылки[править | править код]
- Что такое градиент на YouTube
- Weisstein, Eric W. Gradient (англ.) на сайте Wolfram MathWorld.
Теория поля — крупный раздел физики, механики, математики, в котором изучаются скалярные, векторные, тензорные поля.
К рассмотрению скалярных и векторных полей приводят многие задачи физики, электротехники, математики, механики и других технических дисциплин. Изучение одних физических полей способствует изучению и других. Так, например, силы всемирного тяготения, магнитные, электрические силы — все они изменяются обратно пропорционально квадрату расстояния от своего источника; диффузия в растворах происходит по законам, общим с распространением тепла в различных средах; вид силовых магнитных линий напоминает картину обтекания препятствий жидкостью и т. д.
Математическим ядром теории поля являются такие понятия, как градиент, поток, потенциал, дивергенция, ротор, циркуляция и другие. Эти понятия важны и в усвоении основных идей математического анализа функций многих переменных.
Полем называется область V пространства, в каждой точке которой определено значение некоторой величины. Если каждой точке М этой области соответствует определенное число U = U(M), говорят, что в области определено (задано) скалярное поле (или функция точки). Иначе говоря, скалярное поле — это скалярная функция U(М) вместе с ее областью определения. Если же каждой точке М области пространства соответствует некоторый вектор 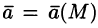
Примерами скалярных полей могут быть поля температуры (воздуха, тела, …), атмосферного давления, плотности (массы, воздуха, …), электрического потенциала и т.д. Примерами векторных полей являются поле силы тяжести, поле скоростей частиц текущей жидкости (ветра), магнитное поле, поле плотности электрического тока и т. д.
Если функция 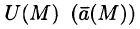
Далее будем рассматривать только стационарные поля.
Если V — область трехмерного пространства, то скалярное поле U можно рассматривать как функцию трех переменных х, у, z (координат точки М):
(Наряду с обозначениями 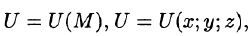
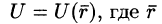
Если скалярная функция U (М) зависит только от двух переменных, например х и у, то соответствующее скалярное поле U(х; у) называют плоским.
Аналогично: вектор 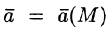
Вектор 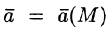
где P(x;y;z), Q(x;y;z ), R(x;y;z) — проекции вектора 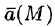
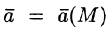
Векторное поле называется однородным, если 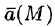
В дальнейшем будем предполагать, что скалярные функции (U(x;y;z) — определяющая скалярное поле, P(x;y;z), Q(x;y;z) и R(x; у; z) — задающие векторное поле) непрерывны вместе со своими частными производными.
Пример:
Функция 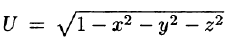
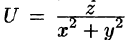
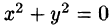
Пример:
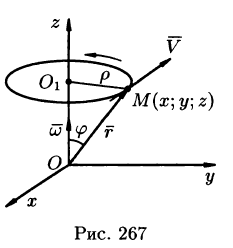
Найти поле линейной скорости 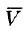
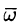
Решение:
Угловую скорость представим в виде вектора 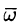
Построим радиус-вектор 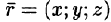
Численное значение линейной скорости 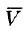
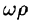
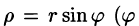
Вектор скорости 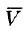
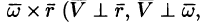
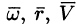
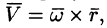
или
Поле линейных скоростей 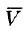
Скалярное поле
Поверхности и линии уровня:
Рассмотрим скалярное поле, задаваемое функцией U = U(x,y,z). Для наглядного представления скалярного поля используют поверхности и линии уровня.
Поверхностью уровня скалярного поля называется геометрическое место точек, в которых функция U(М) принимает постоянное значение, т. е.
Давая в уравнении (70.1) величине с различные значения, получим различные поверхности уровня, которые в совокупности как бы расслаивают поле. Через каждую точку поля проходит только одна поверхность уровня. Ее уравнение можно найти путем подстановки координат точки в уравнение (70.1).
Для скалярного поля, образованного функцией
поверхностями уровня является множество концентрических сфер с центрами в начале координат: 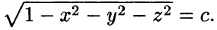
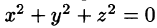
Для равномерно раскаленной нити поверхности уровня температурного поля (изотермические поверхности) представляют собой круговые цилиндры, общей осью которых служит нить.
В случае плоского поля U — U(х; у) равенство U(x; у) = с представляет собой уравнение линии уровня поля, т. е. линия уровня —это линия на плоскости Оху, в точках которой функция U (х; у) сохраняет постоянное значение.
В метеорологии, например, сети изобар и изотерм (линии одинаковых средних давлений и одинаковых средних температур) являются линиями уровня и представляют собой функции координат точек местности.
Линии уровня применяются в математике при исследовании поверхностей методом сечений (см. п. 12.9).
Производная по направлению
Для характеристики скорости изменения поля U =U(М) в заданном направлении введем понятие «производной по направлению».
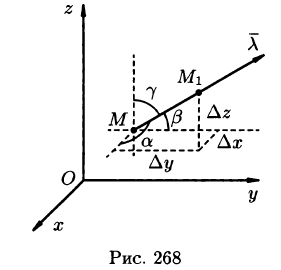
Возьмем в пространстве, где задано поле U = U(x;y;z), некоторую точку М и найдем скорость изменения функции U при движении точки М в произвольном направлении 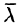
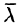
Приращение функции U, возникающее при переходе от точки М к некоторой точке 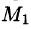
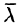
или
(см. рис. 268).
Тогда
Производной от функции U = U(M) в точке М по направлению 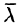
Производная по направлению 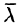
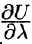
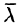
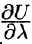
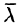
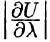
собой мгновенную скорость изменения функции U в направлении 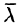
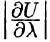
Выведем формулу для вычисления производной по направлению, считая, что функция U(x;y;z) дифференцируема в точке М. Тогда ее полное приращение в этой точке М можно записать так:
где 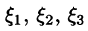
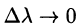
то
Переходя к пределу при 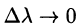
В случае плоского поля U = U(x;y) имеем:
Формула (70.2) принимает вид:
Замечание:
Понятие производной по направлению является обобщением понятия частных производных 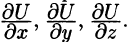
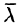
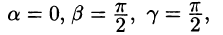
Пример:
Найти производную функции 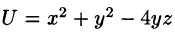
Решение:
Находим вектор 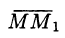
Находим частные производные функции и вычисляем их значения в точке М:
Следовательно, по формуле (70.2) имеем:
Поскольку jj^- < 0, то за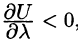
Градиент скалярного поля и его свойства
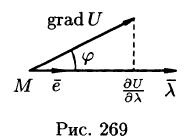
В каком направлении 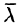
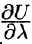
Можно заметить, что правая часть равенства (70.2) представляет собой скалярное произведение единичного вектора
и некоторого вектора
Вектор, координатами которого являются значения частных производных функции U(x,y,z) в точке M(x;y,z), называют градиентом функции и обозначают gradU, т. е.
или
Отметим, что grad U есть векторная величина. Говорят: скалярное поле U порождает векторное поле градиента U. Теперь равенство (70.2) можно записать в виде
или
где 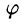
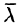
Из формулы (70.3) сразу следует, что производная по направлению достигает наибольшего значения, когда 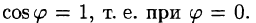
В этом состоит физический смысл градиента. На указанном свойстве градиента основано его широкое применение в математике и других дисциплинах.
Приведем важные свойства градиента функции.
1.Градиент направлен по нормали к поверхности уровня, проходящей через данную точку.
Действительно, по любому направлению вдоль поверхности уровня 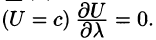
Доказываются эти свойства на основании определения градиента. Докажем, например, последнее свойство. Имеем:
Замечание. Приведенные свойства градиента функции остаются справедливыми и для плоского поля.
Пример:
Найти наибольшую скорость возрастания функции
Решение:
Имеем:
Наибольшая скорость возрастания функции равна
Отметим, что функция U будет убывать с наибольшей скоростью 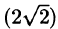
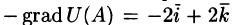
Векторное поле
Векторные линии поля:
Рассмотрим векторное поле, задаваемое вектором 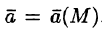
Векторной линией поля 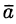
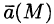
Это понятие для конкретных полей имеет ясный физический смысл. Например, в поле скоростей текущей жидкости векторными линиями будут линии, по которым движутся частицы жидкости (линии тока); для магнитного поля векторными (силовыми) линиями будут линии, выходящие из северного полюса и оканчивающиеся в южном.
Совокупность всех векторных линий поля, проходящих через некоторую замкнутую кривую, называется векторной трубкой.
Изучение векторного поля обычно начинают с изучения расположения его векторных линий. Векторные линии поля
описываются системой дифференциальных уравнений вида
Действительно, пусть PQ — векторная линия поля, 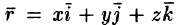
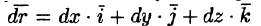
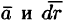
Пример:
Найти векторные линии поля линейных скоростей тела, вращающегося с постоянной угловой скоростью 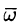
Решение:
Это поле определено вектором 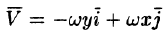
Интегрируя, получим: 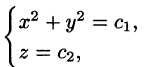
Поток поля
Пусть векторное поле образовано вектором (71.1). Для наглядности будем считать 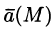
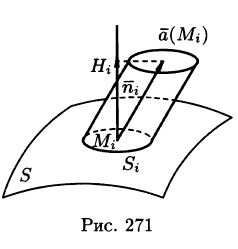
Выберем определенную сторону поверхности S. Пусть 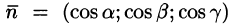
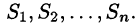
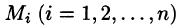
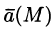
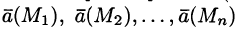
Будем приближенно считать каждую площадку плоской, а вектор 
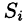
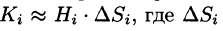
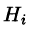
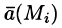
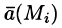
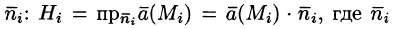
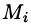
Точное значение искомого количества жидкости получим, взяв предел найденной суммы при неограниченном увеличении числа элементарных площадок и стремлении к нулю их размеров (диаметров 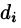
Независимо от физического смысла поля 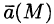
Потоком вектора 
Рассмотрим различные формы записи потока вектора. Так как
(см. (6.2)), то
где 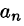
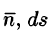
Иногда формулу (71.3) записывают в виде
где вектор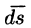
Так как
— проекции вектора 

Используя взаимосвязь поверхностных интегралов I и II рода (см. формулу (58.8)), поток вектора можно записать как
Отметим, что поток К вектора а есть скалярная величина. Величина К равна объему жидкости, которая протекает через поверхность S за единицу времени. В этом состоит физический смысл потока (независимо от физического смысла поля).
Особый интерес представляет случай, когда поверхность замкнута и ограничивает некоторый объем V. Тогда поток вектора записывается в виде
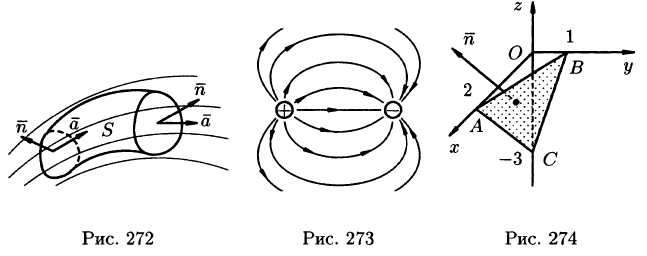
В этом случае за направление вектора п обычно берут направление внешней нормали и говорят о потоке изнутри поверхности S (см. рис. 272).
Если векторное поле 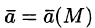

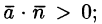
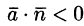
При этом если К > 0, то из области V вытекает больше жидкости, чем в нее втекает. Это означает, что внутри области имеются дополнительные источники.
Если К < 0, то внутри области V имеются стоки, поглощающие избыток жидкости.
Можно сказать, что источники — точки, откуда векторные линии начинаются, а стоки — точки, где векторные линии кончаются. Так, в электростатическом поле источником является положительный заряд, стоком — отрицательный заряд магнита (см. рис. 273).
Если К = 0, то из области V вытекает столько же жидкости, сколько в нее втекает в единицу времени; внутри области либо нет ни источников, ни стоков, либо они таковы, что их действие взаимно компенсируется.
Пример:
Найти поток вектора 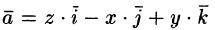
Решение:
Поток найдем методом проектирования на три координатные плоскости. Для этого воспользуемся формулой (71.5). В нашем случае Р = z, Q = —х, R = у. Имеем:
Расчленим этот поверхностный интеграл на три слагаемых, затем сведем их вычисление к вычислению двойных интегралов. Нормаль к верхней стороне треугольника образует с осью Ох тупой угол, с осью Оу — тупой, а с осью Oz — острый угол. (Единичный вектор данной плоскости есть 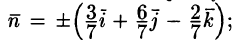
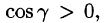
Итак, 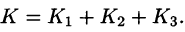
В результате имеем:
Пример:
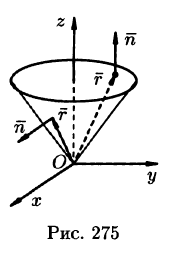
Найти поток радиус-вектора 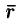
Решение:
Очевидно, что
т. к.
Дивергенция поля. Формула Остроградского-Гаусса
Важной характеристикой векторного поля (71.1) является так называемая дивергенция, характеризующая распределение и интенсивность источников и стоков поля.
Дивергенцией (или расходимостью) векторного поля
в точке М называется скаляр вида 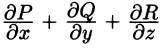
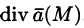
Отметим некоторые свойства дивергенции.
- Если
— постоянный вектор, то
где с = const.
т. е. дивергенция суммы двух векторных функций равна сумме дивергенции слагаемых.
- Если U — скалярная функция,
— вектор, то
Эти свойства легко проверить, используя формулу (71.6). Докажем, например, справедливость свойства 4.
Так как 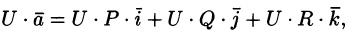
Используя понятия потока и дивергенции векторного поля, запишем известную в анализе (см. (58.9)) формулу Остроградского-Гаусса
в так называемой векторной форме.
Рассматривал область V, ограниченную замкнутой поверхностью S, в векторном поле (71.1), можно утверждать, что левая часть формулы (71.7) есть поток вектора 

(в котором она чаще всего и встречается).
Формула Остроградского-Гаусса означает, что поток векторного поля через замкнутую поверхность S (в направлении внешней нормали, т. е. изнутри) равен тройному интегралу от дивергенции этого поля по объему V, ограниченному данной поверхностью.
Используя формулу (71.8), можно дать другое определение дивергенции векторного поля 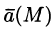
По теореме о среднем для тройного интеграла (см. п. 54.1) имеем:
где 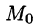
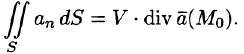
Пусть поверхность S стягивается в точку. Тогда 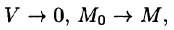
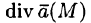
Дивергенцией векторного поля в точке М называется предел отношения потока поля через (замкнутую) поверхность S, окружающую точку М, к объему тела, ограниченного этой поверхностью, при условии, что вся поверхность стягивается в точку
Определение (71.9) дивергенции эквивалентно (можно показать) определению (71.6).
Как видно из определения, дивергенция векторного поля в точке является скалярной величиной. Она образует скалярное поле в данном векторном поле.
Исходя из физического смысла потока (обычно условно считают, что 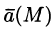
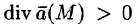
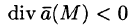
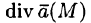
Понятно, что если в объеме V, ограниченном замкнутой поверхностью S, нет ни источников, ни стоков, то
Векторное поле, в каждой точке которого дивергенция поля равна нулю, т. е. 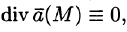
Пример:
Найти дивергенцию поля линейных скоростей 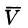
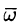
Решение:
Примем ось вращения жидкости за ось Oz. Тогда, как показано ранее (см. пример 69.2), 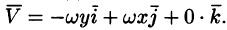
Поле 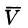
Циркуляция поля
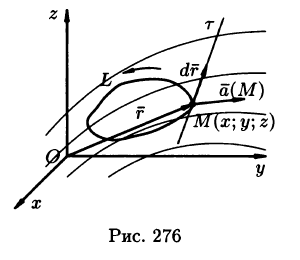
Пусть векторное поле образовано вектором (71.1). Возьмем в этом поле некоторую замкнутую кривую L и выберем на ней определенное направление.
Пусть 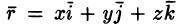
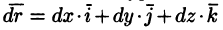
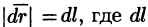
Криволинейный интеграл по замкнутому контуру L от скалярного произведения вектора 
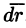
Рассмотрим различные формы записи циркуляции. Так как
где 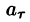

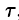
или
Циркуляция С, записанная в виде (71.12) имеет простой физический смысл: если кривая L расположена в силовом поле, то циркуляция — это работа силы 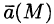
Отметим, что вдоль замкнутых векторных линий циркуляция отлична от нуля, потому что в каждой точке векторной линии скалярное произведение 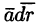

Пример:
Найти циркуляцию вектора поля линейных скоростей вращающегося тела (см. пример 69.2) 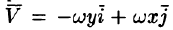
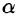
Решение:
Будем считать, что направление нормали к плоскости 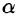
где S — площадь поверхности, ограниченной кривой L (см. 56.17).
Заметим, что если нормаль к поверхности S образует угол 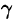
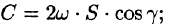
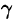
Пример:
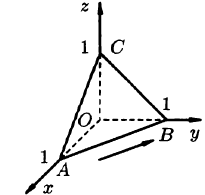
Вычислить циркуляцию векторного поля
вдоль периметра треугольника с вершинами A(1;0;0), В(0;1;0), С(0;0;1) (см. рис. 277).
Решение:
Согласно формуле (71.12), имеем:
На отрезке AB: x + у = 1, z = 0, следовательно,
На отрезке ВС: у + z = 1, х = 0, следовательно,
На отрезке СА: х + z = 1, у = 0, следовательно,
Следовательно,
Ротор поля. Формула Стокса
Ротором (или вихрем) векторного поля
называется вектор, обозначаемый 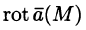
Формулу (71.13) можно записать с помощью символического определителя в виде, удобном для запоминания:
Отметим некоторые свойства ротора.
- Если
— постоянный вектор, то
т. е. ротор суммы двух векторов равен сумме роторов слагаемых.
- Если U — скалярная функция, а
— векторная, то
Эти свойства легко проверить, используя формулу (71.13). Покажем, например, справедливость свойства 3:
Используя понятия ротора и циркуляции, векторного поля, запишем известную в математическом анализе (см. п. 58.4) формулу Стокса:
Левая часть формулы (71.14) представляет собой циркуляцию вектора 
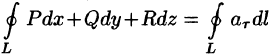
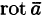
Следовательно, формулу Стокса можно записать в виде
Такое представление формулы Стокса называют ее векторной формой. В этой формуле положительное направление на контуре L и выбор стороны у поверхности S согласованы между собой так же, как в теореме Стокса.
Формула (71.15) показывает, что циркуляция вектора 

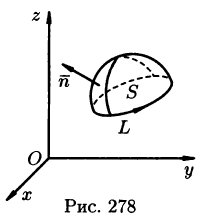
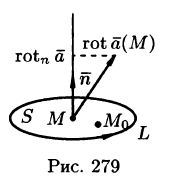
Используя формулу (71.14), можно дать другое определение ротора поля, эквивалентное первому и не зависящее от выбора координатной системы.
Для этого применим формулу Стокса (71.15) для достаточно малой плоской площадки S с контуром L, содержащей точку М.
По теореме о среднем для поверхностного интеграла (п. 57.1, свойство 7) имеем:
где 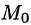
Тогда формулу (71.15) можно записать в виде
Отсюда:
Пусть контур L стягивается в точку М. Тогда 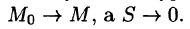
Ротором вектора 
Как видно из определения, ротор вектора 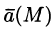
Дадим физическое истолкование понятия ротора векторного поля. Найдем ротор поля линейных скоростей твердого тела, вращающегося вокруг оси Oz с постоянной угловой скоростью (пример 69.2) 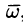
По определению ротора
Ротор этого поля направлен параллельно оси вращения, его модуль равен удвоенной угловой скорости вращения.
С точностью до числового множителя ротор поля скоростей 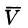
Замечание:
Из определения (71.13) ротора вытекает, что направление ротора — это направление, вокруг которого циркуляция имеет наибольшее значение (плотность) по сравнению с циркуляцией вокруг любого направления, не совпадающего с нормалью к площадке S.
Так что связь между ротором и циркуляцией аналогична связи между градиентом и производной по направлению (см. п. 70.3).
Оператор Гамильтона
Векторные дифференциальные операции первого порядка:
Основными дифференциальными операциями (действиями) над скалярным полем U и векторным полем
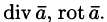
Эти операции удобно записывать с помощью так называемого оператора Гамильтона
Этот символический вектор называют также оператором 


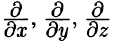
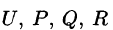
Применяя оператор Гамильтона, получим дифференциальные операции первого порядка:
Оператор Гамильтона применяется для записи и других операций и для вывода различных формул в теории поля. При действиях с ним надо пользоваться правилами векторной алгебры и правилами дифференцирования.
В частности, производная по направлению (70.2) может быть записана в виде
где
Векторные дифференциальные операции второго порядка
После применения оператора Гамильтона к скалярному или векторному полю получается новое поле, к которому можно снова применить этот оператор. В результате получаются дифференциальные операции второго порядка. Нетрудно убедиться, что имеется лишь пять дифференциальных операций второго порядка:
(Понятно, что операция 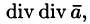
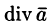
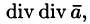
Запишем явные выражения для дифференциальных операций второго порядка, используя оператор Гамильтона. Заметим при этом, что оператор действует только на множитель, расположенный непосредственно за оператором.
Правая часть этого равенства называется оператором Лапласа скалярной функции U и обозначается 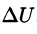
Дифференциальное уравнение Лапласа 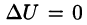
Замечание. К равенству (72.1) можно прийти, введя в рассмотрение скалярный оператор дельта:
(который тоже называют оператором Лапласа).
2. 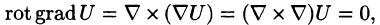
4. 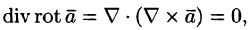
так как двойное векторное произведение обладает свойством
Здесь 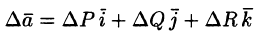

Некоторые свойства основных классов векторных полей
Соленоидальное поле
Напомним, что векторное поле 
Примерами соленоидальных полей являются: поле линейных скоростей вращающегося твердого тела (см. пример 71.4); магнитное поле, создаваемое прямолинейным проводником, вдоль которого течет электрический ток, и другие.
Приведем некоторые свойства соленоидального поля.
- В соленоидальном поле
поток вектора через любую замкнутую поверхность равен нулю. Это свойство непосредственно вытекает из формулы (71.8). Таким образом, соленоидальное поле не имеет источников и стоков.
- Соленоидальное поле является полем ротора некоторого векторного поля, т. е. если
, то существует такое поле
, что
. Вектор
называется векторным потенциалом поля
.
Любое из свойств 1-2 можно было бы взять в качестве определения соленоидального поля.
Доказывать свойство 2 не будем. Отметим лишь, что обратное утверждение — поле ротора векторного поля есть соленоидальное — нами доказано (выше мы показали, что 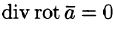
3. В соленоидальном поле 
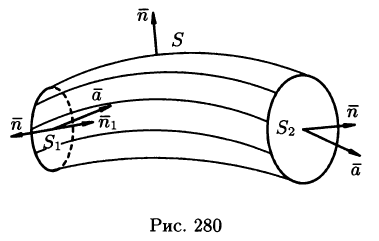
Рассмотрим векторную трубку между двумя ее произвольными сечениями 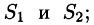
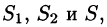
где n — внешняя нормаль.
Так как на боковой поверхности векторной трубки нормаль п перпендикулярна к векторам поля, то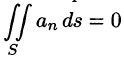
Переменив направление нормали на площадке 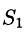
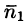
В поле скоростей текущей жидкости полученный результат означает, что количество жидкости, втекающей в трубку за единицу времени, равно количеству жидкости, вытекающей из нее.
Потенциальное поле
Векторное поле 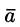
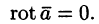
Приведем основные свойства потенциального поля.
Свойство 1. Циркуляция потенциального поля 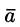
Это непосредственно вытекает из формулы (71.14). Следовательно,
В частности, для силового потенциального поля это означает, что работа силы по любому замкнутому контуру равна нулю; в поле скоростей текущей жидкости равенство С = 0 означает, что в потоке нет замкнутых струек, т. е. нет водоворотов.
Свойство 2. В потенциальном поле 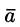
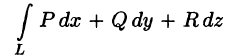
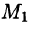
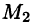
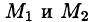
Это свойство вытекает из свойства 1. Действительно, взяв в поле две точки 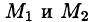
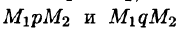
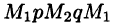
Учитывая свойства криволинейного интеграла, получаем:
т. e.
Свойство 3. Потенциальное поле является полем градиента некоторой скалярной функции U(x; y; z), т. е. если 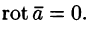
Из равенства 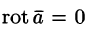
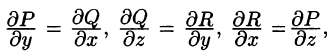
Отсюда: 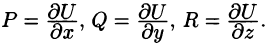
т. е. вектор поля 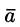
Замечание. Из равенства rot grad U = 0 следует обратное утверждение — поле градиента скалярной функции U = U(x;y; z) является потенциальным.
Из равенства 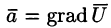
где 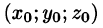
Произвольное же векторное поле требует задания трех скалярных функций (P(x;y;z), Q(x;y;z), R(x;y,z) — проекции вектора поля на оси координат).
Замечание. Определение потенциального поля может быть дано иначе — векторное поле 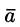
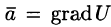
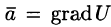
Пример:
Установить потенциальность поля
и найти его потенциал.
Решение:
Имеем:
Следовательно, поле вектора 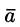
Найдем потенциал U по формуле (73.1), выбирая в качестве фиксированной точки начало координат, т. е. 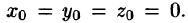
то
Гармоническое поле
Векторное поле 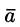
Примером гармонического поля является поле линейных скоростей стационарного безвихревого потока жидкости при отсутствии в нем источников и стоков.
Так как поле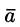
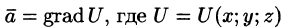
Но так как поле одновременно и соленоидальное, то
или, что то же самое,
т. е. потенциальная функция U гармонического поля а является решением дифференциального уравнения Лапласа. Такая функция называется, как уже упоминали, гармонической.
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
Градие́нт — вектор,
своим направлением указывающий
направление наибольшего возрастания
некоторой величины ,
значение которой меняется от одной
точки пространства к другой (скалярного
поля),
а по величине (модулю) равный быстроте
роста этой величины в этом направлении.
Градиент
скалярной величины – векторная величина,
численно равная производной от этой
функции по направлению нормалей к
поверхности уровня.
Смысл
градиента любой скалярной функции в
том, что его скалярное произведение с
бесконечно малым вектором
перемещения дает полный
дифференциал этой
функции при соответствующем изменении
координат в пространстве, на котором
определена ,
то есть линейную (в случае общего
положения она же главная) часть
изменения при
смещении на .
Применяя одну и ту же букву для обозначения
функции от вектора и соответствующей
функции от его координат, можно написать:
Градиент
численно равен максимальной скорости
изменения функции. Направление градиента
совпадает с направлением быстрейшего
изменения функции.
Вихревые
поля – поля с замкнутыми силовыми линиями.
Создается магнитным полем и индукционным
электрическим полем (при изменении
магнитного потока).
Индукционное
электрическое поле является
вихревым.
Направление
силовых линий вихревого эл. поля совпадает
с направлением индукционного тока
4.Дивергенция вектора. Принцип непрерывности линий магнитной индукции.
Дивергенция
– скалярная характеристика векторного
поля.
Дивергенция
векторного поля скалярная величина,
равная пределу отношения потока через
замкнутую поверхность к объёму,
заключенному внутри этой поверхности,
при условии, что эта плоскость стягивается
к точке.
Она
характеризует интенсивность источников
поля ( если div
F
= 0, то источники поля отсутствуют)
Поток
вектора магнитной индукции сквозь
любую замкнутую поверхность равен
нулю:
,
где
для однородных изотропных сред
;
–напряженность
магнитного поля; –
абсолютная магнитная проницаемость
среды; –
относительная магнитная проницаемость
среды; –
магнитная постоянная.
Геометрический
смысл закона: линии вектора магнитной
индукции всюду непрерывны и замкнуты.
Этот
принцип определяет, что линии магнитной
индукции непрерывны (магнитное поле не
имеет ни стоков, ни истоков). Линии
магнитной индукции – линии проведенные
(построенные) в магнитном поле так, что
в каждой их точке касательные совпадают
по направлению с вектором .
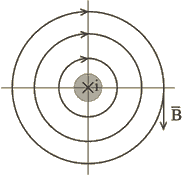
Рассмотрим
один из простых и наглядных примеров.
На рис.1.5 представлен прямолинейный
провод круглого сечения, ток i в котором
направлен от наблюдателя. Линии магнитной
индукции – концентрические окружности
с центром на оси провода. Направление
линий связано с направлением тока
правилом правого винта.
Рис.1.5
Источниками
магнитных полей являются электрические
токи.
Принцип
непрерывности магнитного потока
математически записывается так:
–
(1.6.)
магнитный
поток сквозь любую замкнутую поверхность
равен нулю.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Вектор градиента потенциала электростатического поля
§7 Работа силы электростатического поля при перемещении заряда.
Потенциальный характер сил поля.
Циркуляция вектора напряженности
Рассмотрим электростатическое поле, создаваемое зарядом q . Пусть в нем перемещается пробный заряд q 0 . В любой точке поля на заряд q 0 действует сила
де – модуль силы, – орт радиус-вектора , определяющего положение заряда q 0 относительно заряда q . Так как сила меняется от точки к точке, то работу силы электростатического поля запишем как работу переменной силы:
Ввиду того, что рассматривали перемещение заряда из точки 1 в точку 2 по произвольной траектории, можно сделать вывод, что работа по перемещению точечного заряда в электростатическом поле не зависит от формы пути, а определяется лишь начальным и конечным положением заряда. Это свидетельствует о том, что электростатическое поле является потенциальным, а сила Кулона – консервативной силой. Работа по перемещению заряда в таком поле по замкнутому пути всегда рвана нулю.
– проекция на направление контура ?.
Учтем, что работа по замкнутому пути равно нулю
– ЦИРКУЛЯЦИЯ вектора напряженности.
Циркуляция вектора напряженности электростатического поля, взятая по произвольному замкнутому контуру всегда равна нулю.
§7 Потенциал.
Связь между напряженностью и потенциалом.
Градиент потенциала.
Эквипотенциальные поверхности
Поскольку электростатическое поле является потенциальным работа по перемещению заряда в таком поле может быть представлена, как разность потенциальных энергий заряда в начальной и конечной точках пути. (Работа равна уменьшению потенциальной энергии, или изменению потенциальной энергии, взятому со знаком минус.)
Постоянную определяют из условия, что при удалении заряда q 0 на бесконечность его потенциальная энергия должна быть равна нулю.
.
Различные пробные заряды q 0 i , помещенные в данную точку поля будут обладать в этой точке различными потенциальными энергиями:
…
Отношение W пот i к величине пробного заряда q 0 i , помещенного в данную точку поля является величиной постоянной для данной точки поля для всех пробных зарядов. Это отношение называется ПОТЕНЦИАЛОМ.
ПОТЕНЦИАЛ – энергетическая характеристика электрического поля. ПОТЕНЦИАЛ численно равен потенциальной энергии, которой обладает в данной точке поля единичный положительный заряд.
Работу по перемещению заряда можно представить в виде
.
Потенциал измеряется в Вольтах
ЭКВИПОТЕНЦИАЛЬНЫМИ ПОВЕРХНОСТЯМИ называются поверхности равного потенциала (φ = const ). Работа по перемещению заряда вдоль эквипотенциальной поверхности равна нулю.
Связь между напряженностью и потенциалом φ можно найти, исходя из того, что работу по перемещению заряда q на элементарном отрезке d ? можно представить как
С другой стороны
– градиент потенциала.
Напряженность поля равна градиенту потенциала, взятому со знаком минус.
Градиент потенциала показывает, как меняется потенциал на единицу длины. Градиент перпендикулярен функции и направлен в сторону возрастания функции. Следовательно, вектор напряженности перпендикулярен эквипотенциальной поверхности и направлен в сторону убывания потенциала.
Рассмотрим поле, создаваемое системой N точечных зарядов q 1 , q 2 , … qN . Расстояния от зарядов до данной точки поля равны r 1 , r 2 , … rN . Работа, совершаемая силами этого поля над зарядом q 0 , будет равна алгебраической сумме работ сил, каждого заряда в отдельности.
гле
Потенциал поля, создаваемого системой зарядов, определяется как алгебраическая сумма потенциалов, создаваемых в этой же точке каждым зарядом в отдельности.
§9 Вычисление разности потенциалов плоскости, двух плоскостей, сферы, шара, цилиндра
Используя связь между φ и определим разность потенциалов между двумя произвольными точками
Разность потенциалов поля равномерно заряженной бесконечной плоскости с поверхностной плотностью заряда σ.
2. Разность потенциалов поля двух бесконечных параллельных разноименно заряженных плоскостей с поверхностной плотностью заряда σ.
Если х1 = 0; х2 = d , то или
3. Разность потенциалов поля равномерно заряженной сферической поверхности радиуса R .
Внутри сферической поверхности потенциал всюду одинаков и равен
4. Разность потенциалов поля объемно заряженного шара радиуса R с общим зарядом Q.
Вне шара r 1 , r 2 > R ,
Внутри шара
5. Разность потенциалов поля равномерно заряженного цилиндра (или бесконечно длинной нити).
r > R :
Градиент потенциала
Градиент потенциала – это скорость возрастания потенциала в направлении кротчайшем между двумя точками.
Между двумя точками имеется некоторая разность потенциалов. Если эту разность разделить на кратчайшее расстояние между взятыми точками, то полученное значение будет характеризовать скорость изменения потенциала в направлении кратчайшего расстояния между точками.
Градиент потенциала показывает направление наибольшего возрастания потенциала, численно равен модулю напряженности и отрицательно направлен по отношению к нему.
В определении градиента существенны два положения:
1) Направление, в котором берутся две близлежащие точки, должно быть таким, чтобы скорость изменения была максимальной.
2) Направление таково, что скалярная функция в этом направлении возрастает.
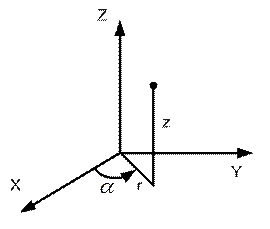
Для декартовой системы координат:
Скорость изменения потенциала в направлении оси Х, Y, Z:
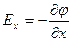
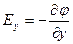
Два вектора равны только тогда, когда равны друг другу их проекции. Проекция вектора напряженности на ось Х равна проекции скорости изменения потенциала вдоль оси Х, взятой с обратным знаком. Аналогично для осей Y и Z.
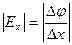
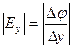
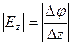
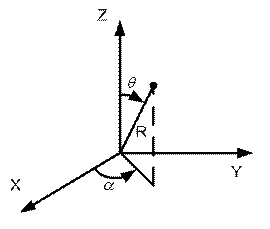
В цилиндрической системе координат выражение градиента потенциала будет иметь следующий вид:
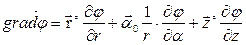
А в сферической системе координат:
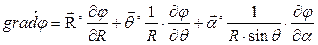
Дифференциальный оператор Гамильтона (оператор Набла)
Для сокращения записи операций над скалярными и векторными величинами употребляют дифференциальный оператор Гамильтона или оператор Набла:
Под дифференциальным оператором Гамильтона понимают сумму частных производных по 3-м координатным осям, умноженных на соответствующие единичные векторы (орты).
Применим оператор Гамильтона к потенциалу:
Правые части одинаковы, значит, будут одинаковы и левые части:
Оператор Гамильтона сочетает в себе как векторные, так и скалярные свойства и может быть применен к скалярным и векторным функциям.
Дата добавления: 2015-07-30 ; просмотров: 19610 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Градиент потенциальных характеристик, как его рассчитать и пример
градиент потенциала является вектором, который представляет отношение изменения электрического потенциала по отношению к расстоянию в каждой оси декартовой системы координат. Таким образом, вектор градиента потенциала указывает направление, в котором скорость изменения электрического потенциала больше, в зависимости от расстояния.
В свою очередь, модуль градиента потенциала отражает скорость изменения электрического потенциала в определенном направлении. Если значение этого известно в каждой точке пространственной области, то электрическое поле может быть получено из градиента потенциала.
Электрическое поле определяется как вектор, с которым оно имеет определенное направление и величину. Определяя направление, в котором электрический потенциал уменьшается быстрее, удаляясь от контрольной точки, и деля это значение на пройденное расстояние, получается величина электрического поля..
- 1 Характеристики
- 2 Как рассчитать?
- 3 Пример
- 3.1 Упражнение
- 4 Ссылки
черты
Градиент потенциала представляет собой вектор, ограниченный конкретными пространственными координатами, который измеряет отношение изменения между электрическим потенциалом и расстоянием, пройденным этим потенциалом.
Наиболее выдающиеся характеристики градиента электрического потенциала подробно описаны ниже:
1- Потенциальный градиент – это вектор. Следовательно, он имеет определенную величину и направление.
2- Поскольку потенциальный градиент является вектором в пространстве, он имеет величины, адресованные по осям X (ширина), Y (высокая) и Z (глубина), если в качестве эталонной системы координат берется декартова система координат.
3- Этот вектор перпендикулярен эквипотенциальной поверхности в точке, в которой оценивается электрический потенциал.
4- Вектор градиента потенциала направлен в направлении максимального изменения функции электрического потенциала в любой точке..
5- Модуль градиента потенциала равен модулю, полученному из функции электрического потенциала по отношению к расстоянию, пройденному в направлении каждой из осей декартовой системы координат..
6- Потенциальный градиент имеет нулевое значение в стационарных точках (максимальная, минимальная и седловая точки).
7- В международной системе единиц (СИ) единицами измерения градиента потенциала являются вольт / метры.
8. Направление электрического поля такое же, в котором электрический потенциал уменьшает свою величину быстрее. В свою очередь, градиент потенциала указывает в направлении, в котором потенциал увеличивает свое значение по отношению к изменению положения. Тогда электрическое поле имеет то же значение градиента потенциала, но с противоположным знаком.
Как рассчитать?
Разность электрических потенциалов между двумя точками (точка 1 и точка 2) определяется следующим выражением:
V1: электрический потенциал в точке 1.
V2: электрический потенциал в точке 2.
E: величина электрического поля.
Ѳ: угол наклона вектора электрического поля, измеренного относительно системы координат.
Выражая указанную формулу дифференциальным способом, получаем следующее:
Коэффициент E * cos (Ѳ) относится к модулю компонента электрического поля в направлении dl. Пусть L – горизонтальная ось плоскости отсчета, тогда cos (Ѳ) = 1, вот так:
Далее, отношение между изменением электрического потенциала (dV) и изменением пройденного расстояния (ds) является модулем градиента потенциала для упомянутого компонента.
Из этого следует, что величина градиента электрического потенциала равна компоненте электрического поля в направлении исследования, но с противоположным знаком.
Однако, поскольку реальная среда является трехмерной, градиент потенциала в данной точке должен быть выражен как сумма трех пространственных компонентов на осях X, Y и Z декартовой системы..
Разбивая вектор электрического поля на три прямоугольных компонента, мы получаем следующее:
Если в плоскости имеется область, в которой электрический потенциал имеет одинаковое значение, частная производная этого параметра по каждой из декартовых координат будет равна нулю.
Таким образом, в точках, которые находятся на эквипотенциальных поверхностях, напряженность электрического поля будет иметь нулевую величину.
Наконец, вектор градиента потенциала может быть определен как точно такой же вектор электрического поля (по величине) с противоположным знаком. Таким образом, мы имеем следующее:
пример
Из приведенных выше расчетов необходимо:
Теперь, прежде чем определять электрическое поле как функцию градиента потенциала или наоборот, сначала необходимо определить направление, в котором разность электрических потенциалов растет..
После этого определяется коэффициент изменения электрического потенциала и изменения пройденного расстояния..
Таким образом, мы получаем величину соответствующего электрического поля, которая равна величине градиента потенциала в этой координате.
осуществление
Есть две параллельные пластины, как показано на следующем рисунке.
Шаг 1
Направление роста электрического поля на декартовой системе координат определяется.
Электрическое поле растет только в горизонтальном направлении, учитывая расположение параллельных пластин. Следовательно, можно сделать вывод, что компоненты градиента потенциала на оси Y и оси Z равны нулю..
Шаг 2
Данные, представляющие интерес различаются.
– Разность потенциалов: dV = V2 – V1 = 90 В – 0 В => dV = 90 В.
– Разница в расстоянии: дх = 10 сантиметров.
Чтобы обеспечить соответствие единиц измерения, используемых в соответствии с Международной системой единиц, величины, не выраженные в СИ, должны быть соответственно преобразованы. Таким образом, 10 сантиметров равны 0,1 метра, и, наконец, dx = 0,1 м.
Шаг 3
Величина вектора градиента потенциала рассчитывается соответствующим образом.
[spoiler title=”источники:”]
http://helpiks.org/4-37431.html
http://ru.thpanorama.com/articles/electrnica/gradiente-de-potencial-caractersticas-cmo-calcularlo-y-ejemplo.html
[/spoiler]
Градиент (от , род. падеж gradientis — шагающий болт ) — характеристика, показывающая направление наискорейшего возрастания некоторой величины, значение которой меняется от одной точки пространства к другой. Например, если взять высоту поверхности Земли над уровнем моря (2-мерное пространство), то её градиент в каждой точке поверхности будет показывать «в горку».
Как видно из объяснения, градиент является векторной функцией, а величина, которую он характеризует — функцией скалярной.
Формально, для случая трёхмерного пространства, градиентом называется векторная функция с компонентами 


Если 

,
компоненты которого равны частным производным 
Градиент обозначается 

Из определения градиента следует, что:

Свойства
Для любого постоянного числа 

Линейность
Правило Лейбница
Пример
Например, градиент функции 
В физике
В различных отраслях физики используется понятие градиента различных физических полей.
Например, градиент концентрации — нарастание или уменьшение по какому-либо направлению концентрации растворённого вещества, градиент температуры – увеличение или уменьшение по направлению температуры среды и т.д.. Градиент может быть вызван различными причинами, например, механическим препятствием, действием электромагнитных, гравитационных или других полей или различием в растворяющей способности граничащих фаз, например, октанол/вода.
Связь с производной по направлению
Используя правило дифференцирования сложной функции, нетрудно показать, что
производная функции 

произведению градиента 

Таким образом, для вычисления производной по любому направлению достаточно знать
градиент функции, то есть набор всех её частных производных.
Градиент в ортогональных криволинейных координатах
,
где Hi – коэффициенты Ламе.
Цилиндрические координаты
Коэффициенты Ламе:
.
Отсюда:
.
Сферические координаты
Коэффициенты Ламе:
.
Отсюда:
.
См. также
- Векторный анализ
- Теорема Остроградского-Гаусса
- Формулы векторного анализа
- Теория поля
bg:Градиент
cs:Gradient
he:גרדיאנט
nl:Gradiënt
pl:Gradient (matematyka)
sl:Gradient
sv:Gradient
uk:Градієнт






















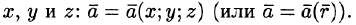
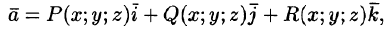
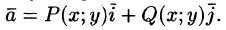
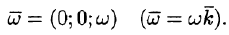
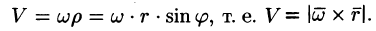
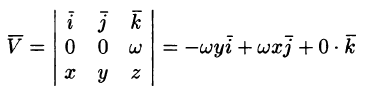
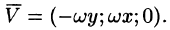


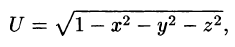
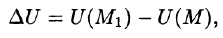
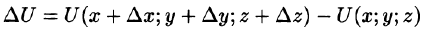
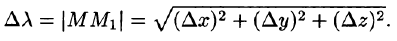
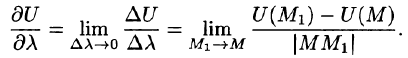
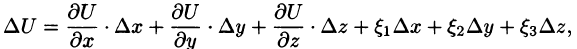
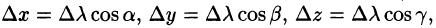
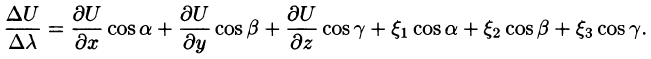
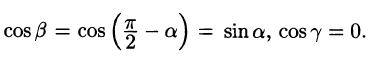
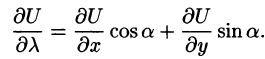
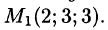
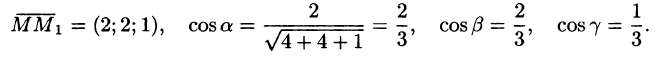
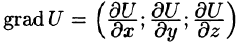
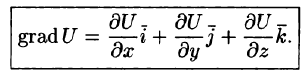
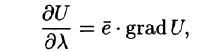
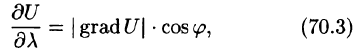
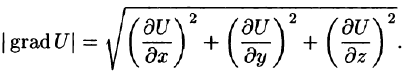
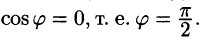
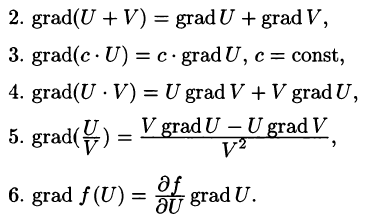
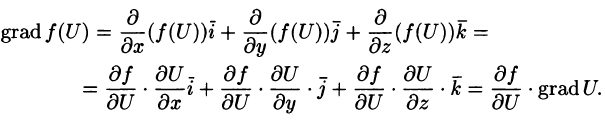
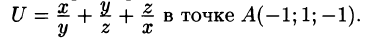
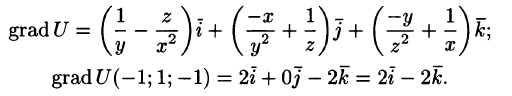
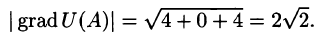
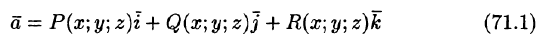
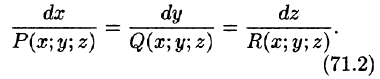
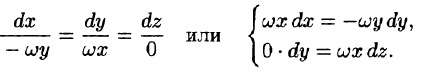
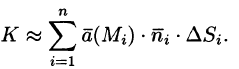
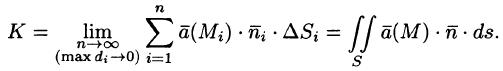

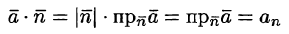

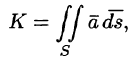
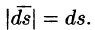
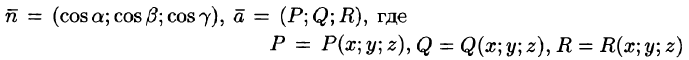
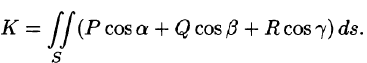
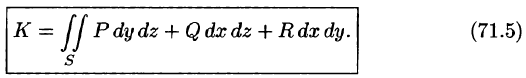
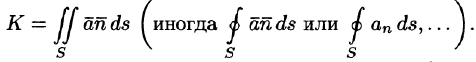
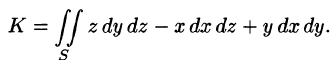
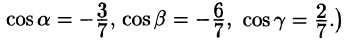
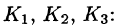
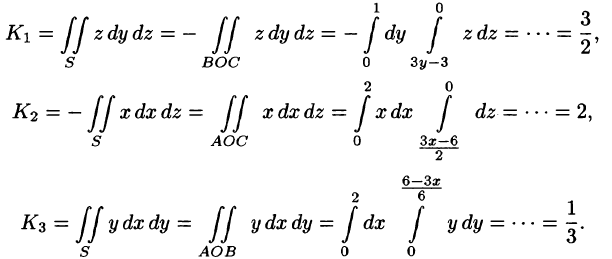
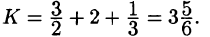
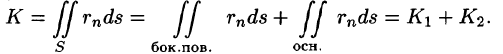
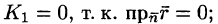
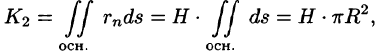
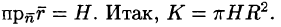
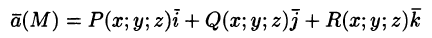
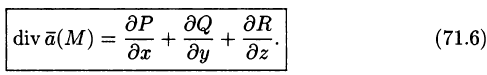
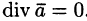
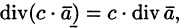 где с = const.
где с = const.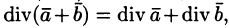 т. е. дивергенция суммы двух векторных функций равна сумме дивергенции слагаемых.
т. е. дивергенция суммы двух векторных функций равна сумме дивергенции слагаемых.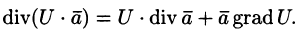
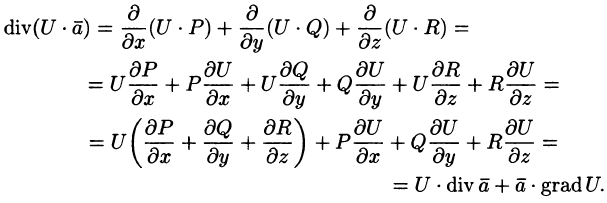
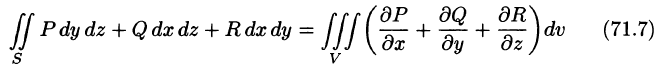
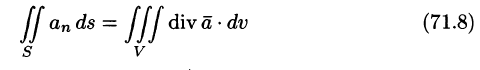
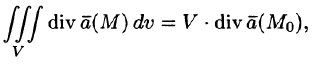
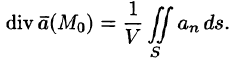
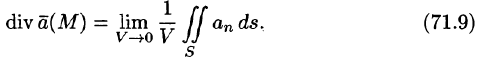
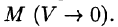
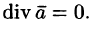
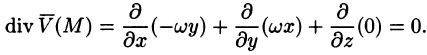
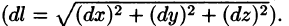

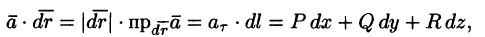

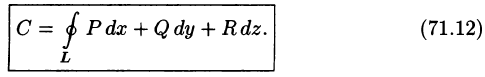
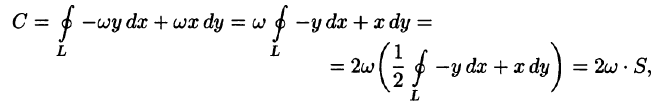
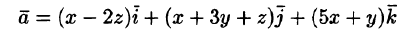
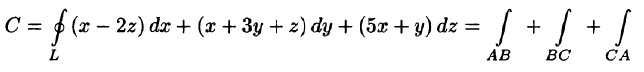
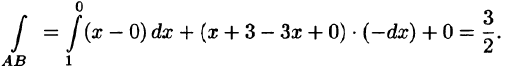
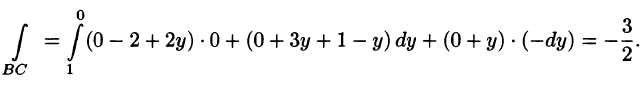
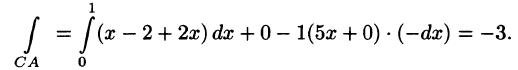
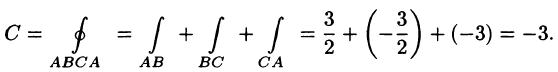
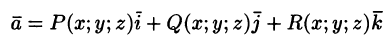
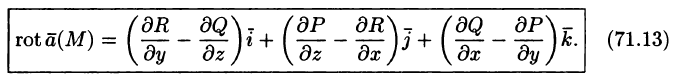
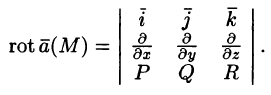
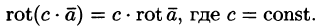
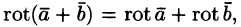 т. е. ротор суммы двух векторов равен сумме роторов слагаемых.
т. е. ротор суммы двух векторов равен сумме роторов слагаемых.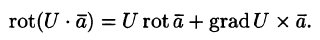
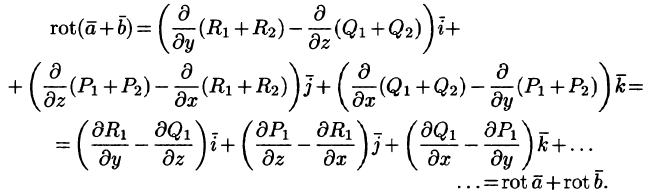
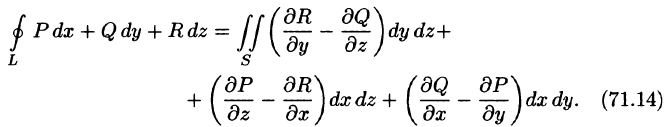
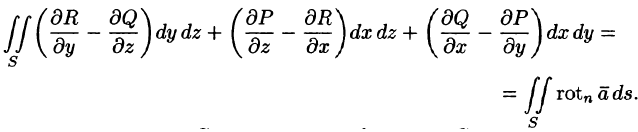
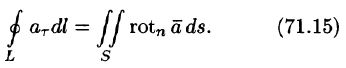
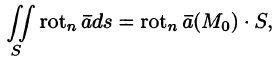
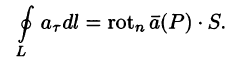
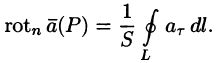
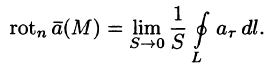
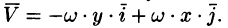
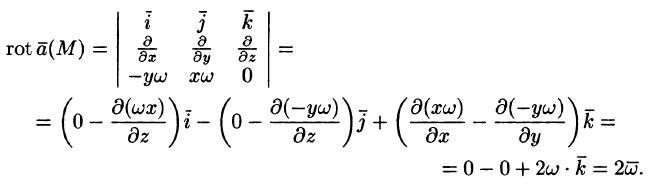
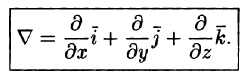
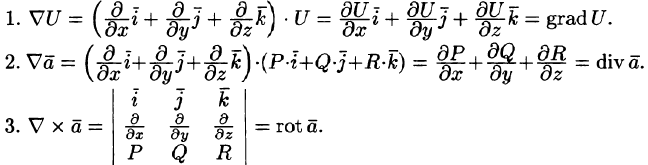
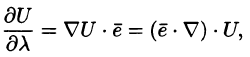
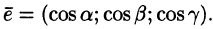
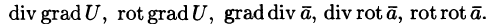
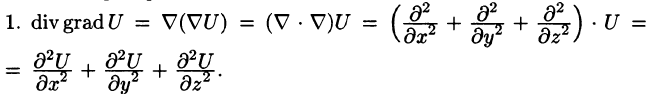
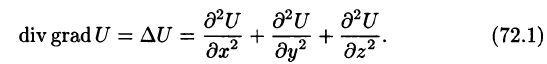
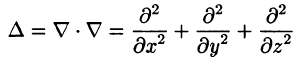
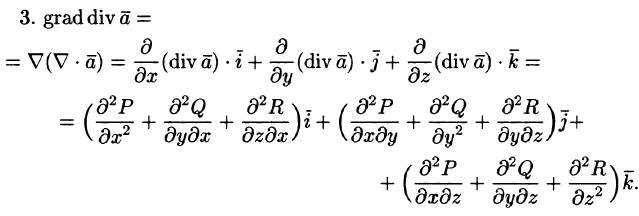
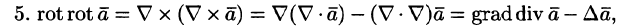
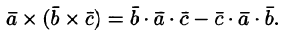
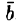 , что
, что 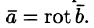 . Вектор
. Вектор