Градиент функции
Градиент — вектор, своим направлением указывающий направление наискорейшего возрастания некоторой величины u. Другими словами, направление градиента есть направление наибыстрейшего возрастания функции.
![]()
Назначение сервиса. Онлайн калькулятор используется для нахождения градиента функции нескольких переменных. (см. пример) При этом решаются следующие задачи:
- нахождение частных производных функции, запись формулы градиента, вычисление наибольшой скорости возрастания функции в указанной точке;
- вычисление градиента в точке A, нахождение производной в точке A по направлению вектора a;
- нахождение полного дифференциала функции.
- Шаг №1
- Шаг №2
- Видеоинструкция
- Оформление Word
Решение со всеми исходными формулами сохраняется в формате Word.
Полный дифференциал для функции двух переменных: 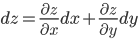
Полный дифференциал для функции трех переменных равен сумме частных дифференциалов: d f(x,y,z)=dxf(x,y,z)dx+dyf(x,y,z)dy+dzf(x,y,z)dz
Алгоритм нахождения градиента
- Вычисление частных производных по формуле:
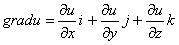
- Вычисление частных производных в точке A.
- Нахождение направляющих углов вектора a.
- Вычисление производной в точке A по направлению вектора a по формуле;
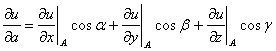
- Наибольшая скорость возрастания функции в указанной точке равна модулю градиента функции в этой точке.
Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).
Зафиксируем
значение
![]() ,
,
получим уравнение![]() первой степени с двумя переменными,
первой степени с двумя переменными,
которое геометрически задает прямую.
В каждой точке данной прямой функция
принимает одно и то же значение![]() и являетсялинией
и являетсялинией
уровня.
Придавая
![]() различные значения, например,
различные значения, например,![]()
![]() ,
,
… , получим множество линий уровня,
которые образуютсовокупность
параллельных
прямых.
Для линейной
функции
![]() градиент
градиент
– это вектор
![]() ,
,
координаты которого равны частным
производным функции![]() по
по![]() и по
и по![]() (значениям коэффициентов при переменных
(значениям коэффициентов при переменных
в целевой функции). Данный вектор
перпендикулярен каждой прямой (линии
уровня)![]() и показывает направление возрастания
и показывает направление возрастания
целевой функции.
Пример 4.
Построить линии уровня и градиент
функции
![]() .
.

![]()
![]()
![]()
![]()
![]()
![]()
Линии уровня
при
![]() ,
,![]() ,
,![]() – это прямые
– это прямые![]()
![]() ,
,![]()
![]() ,
,![]()
![]() ,параллельные
,параллельные
друг другу.
Градиент
– это вектор
![]() ,
,
перпендикулярный каждой линии уровня.
2.4. Графическое нахождение наибольшего и наименьшего значений линейной функции в области
Геометрическая
постановка задачи.
Найти в
области решений системы линейных
неравенств точку, через которую проходит
линия уровня, соответствующая наибольшему
(наименьшему) значению линейной функции
с двумя переменными.
Последовательность
действий:
-
Построить
область допустимых решений системы
линейных неравенств
 Если область непустая, то можно говорить
Если область непустая, то можно говорить
о целесообразности нахождения в ней
наибольшего и наименьшего значений
функции.
![]()

В
A
![]()
![]()
-
Построить градиент
 и одну из линий уровня
и одну из линий уровня

функции
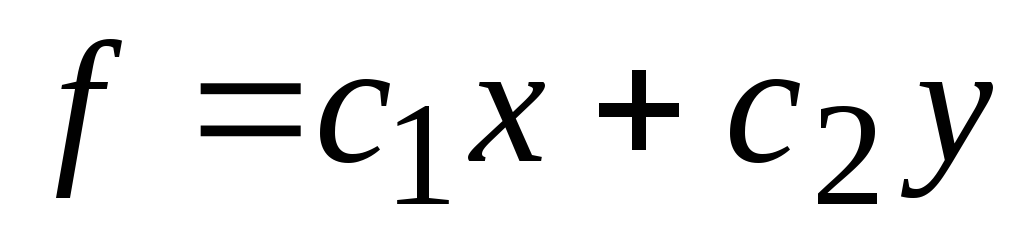 .
. -
Параллельным
перемещением прямой
 в направлении вектора
в направлении вектора геометрически найти две точки:
геометрически найти две точки:
-
точку А «входа»
в область. Эта точка определяет точку
наименьшего значения функции
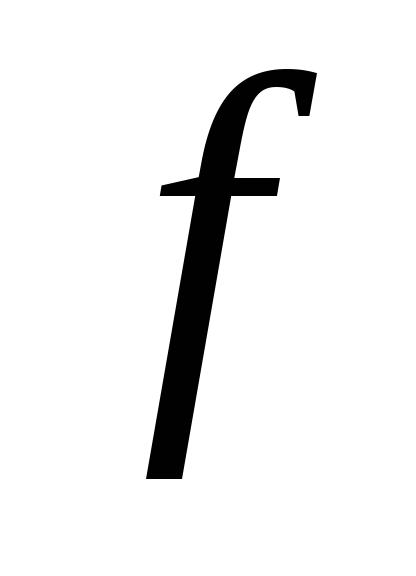 ;
; -
точку В «выхода»
из области. Эта точка определяет точку
наибольшего значения функции
 .
.
4. Найти координаты
точки А, решая систему уравнений прямых,
пересекающихся в точке А. Вычислить
наименьшее значение функции
![]() .
.
Аналогично – для точки В и наибольшего
значения функции![]() .
.
Пример 5.
Найти наибольшее и наименьшее значения
функции
![]()
в области решений
системы линейных неравенств

Решение
1.
Построим область решений системы
линейных неравенств.

у
![]()
1
![]()
![]()
О 2 x
![]()
![]()
![]()
Прямая (![]() )
)![]() ,
,
точки для построения![]() и
и![]() .
.
Так как![]() верно, то полуплоскость обращена в
верно, то полуплоскость обращена в
сторону точки![]() .
.
Прямую (![]() )
)![]() строим по точкам
строим по точкам![]() и
и![]() ;
;
неравенство![]() верное, полуплоскость направлена к
верное, полуплоскость направлена к
началу координат.
Прямая (![]() )
)![]() построена по точкам
построена по точкам![]() и
и![]() ;
;
полуплоскость обращена в сторону![]() .
.
Неравенства
![]() и
и![]() показывают, что искомая область
показывают, что искомая область
(пересечение всех полуплоскостей)
находится в первой координатной четверти.
2. Построим
градиент функции
![]() .
.
Это вектор с координатами![]() с началом в точке
с началом в точке![]() .
.
Перпендикулярно градиенту построимодну из линий
уровня.
3. Параллельным
движением линии уровня в направлении
градиента
![]() найдем точку
найдем точку
«входа» линии уровня в область
– это точка О(0,0). Вычислим значение
функции в
этой точке:
![]() .
.
4. Продолжая движение
линии уровня в направлении градиента
![]() ,
,
найдемточку
«выхода» линии уровня из области
– это точка А. Для определения ее
координат решим систему уравнений
прямых
![]() и
и![]() :
: Решение системы уравнений
Решение системы уравнений![]() и
и![]() .
.
Вычислимзначение
функции в точке
![]() :
:![]() .
.
Ответ:
![]() ,
,![]() .
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Приветствую всех. Сегодня на занятии хотелось бы затронуть немало важную тему, связанную одновременно с дифференциальным исчислением и векторной алгеброй. Мы постараемся как можно меньше углубляться в теоретические тезисы и побольше сделаем упор на решение практических задач. Незамедлительно начнём.
Определение слова “градиент” в математике нужно усвоить.
Градиент – это вектор показывающий направление наибольшего возрастания функции. Модуль вектора градиента показывает скорость изменения функции.
Запишем формулу для нахождения вектора градиента:
При нашем раскладе можно с теорией закончить, этого будет достаточно.
Разберём простенький примерчик для начала.
Никто ведь не забыл как брать частные производные? Если подзабыли, ссылочка (на статью) будет в конце урока.
Было слишком уж просто для нас, возьмём что-нибудь посложнее.
Такого плана примеры уже устно не решишь, хотя… Нет, всё же возможно.
Не будем перенапрягаться сильно, рассмотрим последний пример и пойдём отдыхать.
Берёмся за дело.
Не отчаиваемся что уже конец практики, у вас всегда есть возможность найти похожие задачки в интернете или взять в библиотеке задачник по высшей математике. Практикуйтесь, практикуйтесь, и ещё раз практикуйтесь. Спасибо за внимание.
Другие темы:
Градиент функции
Как найти?
Постановка задачи
Найти градиент функции $ f(x,y,z) $ в точке $ M(x_0,y_0,z_0) $
План решения
Градиент функции $ f(x,y,z) $ – это вектор, каждая координата которого является частной производной первого порядка этой функции:
$$ grad f = frac{partial f}{partial x} overline {i} + frac{partial f}{partial y} overline{j} + frac{partial f}{partial z} overline {k} $$
- Берём частные производные первого порядка от функции $ f(x,y,z) $:
$$ frac{partial f}{partial x}, frac{partial f}{partial y}, frac{partial f}{partial z} $$ - Вычисляем полученные производные в точке $ M(x_0,y_0,z_0) $:
$$ frac{partial f}{partial x} bigg |_{M(x_0,y_0,z_0)}, frac{partial f}{partial y} bigg |_{M(x_0,y_0,z_0)}, frac{partial f}{partial z} bigg |_{M(x_0,y_0,z_0)} $$ - Подставляем, полученные данные в формулу градиента функции:
$$ grad f bigg |_M = frac{partial f}{partial x} bigg |_M overline{i} + frac{partial f}{partial y} bigg |_M overline{j} + frac{partial f}{partial z} bigg |_M overline{k} $$
Примеры решений
| Пример 1 |
| Найти градиент функции $ u = x + ln (z^2+y^2) $ в точке $ M(2,1,1) $ |
| Решение |
|
Находим частные производные первого порядка функции трёх переменных: Вычисляем значение производных в точке $ M(2,1,1) $: $$ frac{partial f}{partial x} bigg |_{M(2,1,1)} = 1 $$ $$ frac{partial f}{partial y} bigg |_{M(2,1,1)} = frac{2 cdot 1}{1^2+1^2} = frac{2}{2}=1 $$ $$ frac{partial f}{partial z} bigg |_{M(2,1,1)} = frac{2cdot 1}{1^2 + 1^2} = frac{2}{2}=1 $$ Подставляем в формулу градиента функции полученные данные: $$ grad f = 1 cdot overline{i} + 1 cdot overline{j} + 1 cdot overline{k} = overline{i}+overline{j}+overline{k} $$ Запишем ответ в координатной форме: $$ grad f = overline{i}+overline{j}+overline{k} = (1,1,1) $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ grad f = (1,1,1) $$ |
| Пример 2 |
| Найти градиент функции $ u = sin(x+2y)+2sqrt{xyz} $ в точке $ M bigg (frac{pi}{2},frac{3pi}{2},3 bigg ) $ |
| Решение |
|
Находим частные производные: $$ frac{partial f}{partial x} = cos(x+2y) + frac{yz}{sqrt{xyz}} $$ $$ frac{partial f}{partial y} = 2cos(x+2y) + frac{xz}{sqrt{xyz}} $$ $$ frac{partial f}{partial z} = frac{xy}{sqrt{xyz}} $$ Вычисляем значения производных в точке $ M bigg (frac{pi}{2},frac{3pi}{2},3 bigg ) $: $$ frac{partial f}{partial x} bigg |_{M(frac{pi}{2},frac{3pi}{2},3)} = cos(frac{pi}{2}+3pi)+ frac{frac{9pi}{2}}{sqrt{frac{9pi^2}{4}}} = cos frac{7pi}{2} + sqrt{9} = 3 $$ $$ frac{partial f}{partial y} bigg |_{M(frac{pi}{2},frac{3pi}{2},3)} = 2 cos(frac{pi}{2}+3pi) + frac{frac{3pi}{2}}{sqrt{frac{9pi^2}{4}}} = 2 cos frac{7pi}{2} + 1 = 2 cdot 0 + 1 = 1 $$ $$ frac{partial f}{partial y} bigg |_{M(frac{pi}{2},frac{3pi}{2},3)} = frac{frac{3pi^2}{4}}{sqrt{frac{9pi^2}{4}}} = sqrt{frac{pi^2}{4}} = frac{pi}{2} $$ Подставляем вычисленные недостающие данные в формулу и получаем: $$ grad f = 3 cdot overline{i}+ 1 cdot overline{j} + frac{pi}{2} cdot overline{k} = 3overline{i}+overline{j}+frac{pi}{2} overline{k} $$ Записываем ответ в координатной форме: $$ grad f = (3,1,frac{pi}{2}) $$ |
| Ответ |
| $$ grad f = (3,1,frac{pi}{2}) $$ |
Пусть F(x,y,z)F(x,y,z) – функция трех переменных, (x,y,z)(x,y,z) – декартовы координаты.
Градиентом функции F(x,y,z)F(x,y,z) называется векторное поле
∇F(x,y,z)=∂F∂xi+∂F∂yj+∂F∂zk,
nabla F(x,y,z)=frac{partial F}{partial x}mathbf{i}+frac{partial F}{partial y}mathbf{j}+frac{partial F}{partial z}mathbf{k},
где ∂F∂xfrac{partial F}{partial x}, ∂F∂yfrac{partial F}{partial y} и ∂F∂zfrac{partial F}{partial z} – частные производные функции F(x,y,z)F(x,y,z), а imathbf{i}, jmathbf{j} и kmathbf{k} – базис декартовой системы координат (x,y,z)(x,y,z).
Иногда градиент обозначается так: gradF(x,y,z)operatorname{grad} F(x,y,z).
Градиент функции в данной точке показывает направление наибольшего роста функции.
Пример 1
Найти градиент функции F(x,y,z)=ln(x2+y2+z2)F(x,y,z)=ln(x^2+y^2+z^2) в точке M(1,2,3)M(1,2,3).
Вычислим частные производные:
∂F∂x=∂∂xln(x2+y2+z2)=2xx2+y2+z2,
frac{partial F}{partial x}=frac{partial }{partial x}ln(x^2+y^2+z^2)=frac{2x}{x^2+y^2+z^2},
∂F∂y=∂∂yln(x2+y2+z2)=2yx2+y2+z2,
frac{partial F}{partial y}=frac{partial }{partial y}ln(x^2+y^2+z^2)=frac{2y}{x^2+y^2+z^2},
∂F∂z=∂∂zln(x2+y2+z2)=2zx2+y2+z2.
frac{partial F}{partial z}=frac{partial }{partial z}ln(x^2+y^2+z^2)=frac{2z}{x^2+y^2+z^2}.
Градиент в точке M(1,2,3)M(1,2,3) (подставляем в формулы для частных производных значения x=1x=1, y=2y=2, z=3z=3):
∇F(M)=17 i+27 j+37 k=17 OM→.
nabla F(M)=frac{1}{7},,mathbf{i}+frac{2}{7},,mathbf{j}+frac{3}{7},,mathbf{k}=frac{1}{7},,overrightarrow{OM}.
Производная по направлению
Пусть FF – функция на плоскости или в пространстве.
Производной функции FF по направлению вектора amathbf{a} в точке MM называется число
∂F∂a(M)=1∥a∥ddεF(M+εa)∣ε=0,
frac{partial F}{partialmathbf{a}}(M)=frac{1}{|mathbf{a}|}left.frac{d}{dvarepsilon}Fleft(M+varepsilon mathbf{a}right)right|_{varepsilon=0},
если производная в правой части существует.
Пример 2
Найдем производную функции F(x,y,z)=x2y−y2z+z2xF(x,y,z)=x^2y-y^2z+z^2x по направлению вектора a=i−2j+2kmathbf{a}=mathbf{i}-2mathbf{j}+2mathbf{k} в точке M(−1,0,1)M(-1,0,1).
Вычисляем значение функции в точке M+εaM+varepsilon mathbf{a} с координатами (−1+ε,−2ε,1+2ε)(-1+varepsilon,-2varepsilon,1+2varepsilon):
F(M+εa)=(−1+ε)2(−2ε)−(−2ε)2(1+2ε)+(1+2ε)2(−1+ε)=−6ε3−5ε−1.
Fleft(M+varepsilon mathbf{a}right)=(-1+varepsilon)^2(-2varepsilon)-(-2varepsilon)^2(1+2varepsilon)+(1+2varepsilon)^2(-1+varepsilon)=-6{varepsilon^{3}}-5varepsilon-1.
Длина вектора amathbf{a}:
∥a∥=a12+a22+a32=12+(−2)2+22=9=3.
|mathbf{a}|=sqrt{a_1^2+a_2^2+a_3^2}=sqrt{1^2+(-2)^2+2^2}=sqrt{9}=3.
Производная по направлению:
∂F∂a(M)=1∥a∥ddεF(M+εa)∣ε=0=13ddε(−6ε3−5ε−1)∣ε=0=−53
frac{partial F}{partialmathbf{a}}(M)=frac{1}{|mathbf{a}|}left.frac{d}{dvarepsilon}Fleft(M+varepsilon mathbf{a}right)right|_{varepsilon=0}=frac{1}{3}left.frac{d}{dvarepsilon}left(-6{varepsilon^{3}}-5varepsilon-1right)right|_{varepsilon=0}=-frac{5}{3}
Выражение производной по направлению через градиент
Используя формулу Тейлора для функций нескольких переменных, легко получить выражение производной по направлению через градиент. Действительно, из равенства
F(M+εa)=F(M)+ε(∇F(M),a)+o(ε2)Fleft(M+varepsilon mathbf{a}right)=F(M)+varepsilonleft(nabla F(M),mathbf{a}right)+oleft(varepsilon^2right)
следует, что
ddεF(M+εa)∣ε=0=(∇F(M),a).
left.frac{d}{dvarepsilon}Fleft(M+varepsilon mathbf{a}right)right|_{varepsilon=0}=left(nabla F(M),mathbf{a}right).
Таким образом,
∂F∂a(M)=(∇F(M),a)∥a∥.
frac{partial F}{partialmathbf{a}}(M)=frac{left(nabla F(M),mathbf{a}right)}{|mathbf{a}|}.
Пример 2′2′
Найдем производную функции F(x,y,z)=x2y−y2z+z2xF(x,y,z)=x^2y-y^2z+z^2x по направлению вектора a=i−2j+2kmathbf{a}=mathbf{i}-2mathbf{j}+2mathbf{k} в точке M(−1,0,1)M(-1,0,1) используя градиент.
Частные производные:
∂F∂x(M)=2xy+z2∣(x,y,z)=(−1,0,1)=1,
frac{partial F}{partial x}(M)=left.2xy+z^2right|_{(x,y,z)=(-1,0,1)}=1,
∂F∂y(M)=x2−2yz∣(x,y,z)=(−1,0,1)=1,
frac{partial F}{partial y}(M)=left.x^2-2yzright|_{(x,y,z)=(-1,0,1)}=1,
∂F∂z(M)=−y2+2zx∣(x,y,z)=(−1,0,1)=−2.
frac{partial F}{partial z}(M)=left.-y^2+2zxright|_{(x,y,z)=(-1,0,1)}=-2.
Градиент:
∇F(M)=i+j−2k.
nabla F(M)=mathbf{i}+mathbf{j}-2mathbf{k}.
Скалярное произведение:
(∇F(M),a)=(i+j−2k,i−2j+2k)=1−2−4=−5.
left(nabla F(M),mathbf{a}right)=left(mathbf{i}+mathbf{j}-2mathbf{k},mathbf{i}-2mathbf{j}+2mathbf{k}right)=1-2-4=-5.
Производная по направлению:
∂F∂a(M)=(∇F(M),a)∥a∥=−53.
frac{partial F}{partialmathbf{a}}(M)=frac{left(nabla F(M),mathbf{a}right)}{|mathbf{a}|}=-frac{5}{3}.
