Математика
5 класс
Урок № 27
Углы. Измерение углов
Перечень рассматриваемых вопросов:
– понятие «угол», «величина угла»;
– виды углов;
– построение углов;
– измерение величины угла.
Тезаурус
Угол – геометрическая фигура, образованная двумя лучами (сторонами угла), выходящими из одной точки, которая называется вершиной угла.
Градус – единица измерения углов, составляющая часть развёрнутого угла.
Градусная мера угла – число, которое показывает, сколько единиц измерения (градусов) содержится между сторонами этого угла.
Обязательная литература
Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.
Дополнительная литература
1. Чулков П. В. Математика: тематические тесты. 5 класс. // П. В. Чулков, Е. Ф. Шершнёв, О.Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы. // И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95 с.
Теоретический материал для самостоятельного изучения
«Я думаю, что никогда до настоящего времени мы не жили в такой геометрический период. Всё вокруг – геометрия», – сказал в своё время французский архитектор Ле Корбюзье, и трудно с ним не согласиться. Геометрические фигуры постоянно встречаются в творениях природы и человека.
Сегодня мы рассмотрим ещё одну геометрическую фигуру – угол, разберём его виды и опишем процесс построения и измерения углов.
Для начала определим, что называют углом.
Углом называют геометрическую фигуру, образованную двумя лучами, выходящими из одной точки.
Построим угол. Для этого отметим на плоскости точку О и проведём два луча – ОК и ОМ. Получим геометрическую фигуру, образованную точкой О и двумя лучами, исходящими из этой точки. Такую геометрическую фигуру и называют углом.

Лучи ОК и ОМ называют сторонами угла, точку О – общее начало этих лучей – называют вершиной угла.
Обозначается угол чаще всего тремя буквами. Например, ∠КОМ или ∠МОК. В середине пишется буква, которой обозначена вершина угла. Также угол можно обозначать и одной буквой, поставленной у вершины угла. Например, ∠О.
Начертим два луча, исходящих из точки О и принадлежащих одной прямой.
Лучи ОС и OК вместе с точкой О дополняют друг друга до прямой – это дополнительные лучи. Угол называют развёрнутым, если его стороны являются дополнительными лучами.
Угол СОК – развёрнутый.

Построим развёрнутый угол АОВ и полуокружность с центром в точке О. Полуокружность разделим на 180 равных частей. Если построим углы с вершиной в точке О, стороны которых проходят через точки деления полуокружности, то таких углов будет 180. Один такой угол будет составлять часть развёрнутого угла.
рисунок
Меру угла, составляющего часть развёрнутого угла, принимают за единицу измерения углов и называют градусом. Обозначают: 1º.
Градусной мерой угла называют число, которое показывает, сколько единиц измерения (градусов) содержится между сторонами этого угла.
Например, градусная мера угла КOВ равна 25 градусам, так как в нём единица измерения градус содержится двадцать пять раз. Записывают: ∠КОВ = 25º.
рисунок
Стоит отметить, что для более точного измерения угла используют доли градуса:
– минуты, которые обозначают одной чёрточкой сверху над цифрой справа,
– секунды, которые обозначаются двумя чёрточками над цифрой справа.
В одном градусе содержится 60 минут, а в одной минуте – 60 секунд.
Например, если угол А равен 10 градусам 5 минутам, записывают: ∠А = 10º5′.
Градусная мера развёрнутого угла равна 180º.
Для измерения углов в градусах пользуются прибором, который называется транспортиром. На транспортире имеется шкала – полуокружность, разделённая на 180 равных частей. На линейке транспортира чёрточкой отмечен центр полуокружности транспортира.
Чтобы найти градусную меру угла, например, угла АВС, нужно совместить центр транспортира с вершиной угла, в данном случае точкой В; расположить линейку транспортира так, чтобы одна из сторон угла прошла через начало отсчёта шкалы транспортира – ноль градусов (в данном случае сторона АВ), и найти на шкале транспортира деление, через которое проходит другая сторона угла – в данном случае сторона ВС.
Это деление шкалы покажет градусную меру угла. В нашем случае – это 120º.
Транспортир применяется также для построения угла, мера которого известна. Построим, например, угол KNM, равный 60º. Для этого:
– проведём луч NM;
– совместим центр транспортира с точкой N;
– расположим линейку транспортира так, чтобы луч NM прошёл через начало отсчёта шкалы транспортира;
– найдём на шкале транспортира деление, соответствующее шестидесяти градусам, и отметим напротив него точку К;
– проведём луч NK. Мы построили угол KNM, равный 60º.
Ответить на вопрос, равны ли углы, и, если не равны, то какой из них больше или меньше, можно, сравнивая их градусные меры. Углы с равными градусными мерами равны. Из двух углов больше тот, который имеет большую градусную меру; а меньше тот, который имеет меньшую градусную меру.
Углы можно сравнить также наложением. Если при этом они совпадают, то равны.
Помимо развёрнутого, углы можно разделить на следующие виды: прямой, острый и тупой.
Угол называют прямым, если его градусная мера равна 90º.

Острым – если его градусная мера меньше 90º.

Тупым – если его градусная мера больше 90º и меньше 180º.

Рассмотрим ещё два вида углов, которые встречаются в геометрических задачах: это вертикальные углы, то есть пара углов с общей вершиной, которые образованы при пересечении двух прямых так, что стороны одного угла являются продолжением сторон другого. Например, угол один и два.

И смежные углы – это два угла, у которых одна сторона общая, а две другие являются дополнительными полупрямыми.
Например, угол САВ и угол САD.

Вместе смежные углы составляют развёрнутый угол. Следовательно, сумма величин смежных углов составляет 180º.
Итак, сегодня мы познакомились с разными видами углов и научились строить их с помощью транспортира.
Для определения величины углов используется прибор, который называют транспортир. Но существуют и более высокоточные приборы.
Так, гониометр использовался для определения положения судна в море или океане.

Теодолит – прибор для измерения горизонтальных и вертикальных углов при геодезических работах, в строительстве и т. п.

Секстант применялся для измерения высоты Солнца над горизонтом с целью определения географических координат той местности, в которой производится измерение, и на судах.

Посох Якова, служащий для измерения углов, – один из первых инструментов для астрономических наблюдений.

Геометрическая фигура угол образуется из двух лучей с общей начальной точкой.
Общая точка называется вершиной угла, а лучи — сторонами угла.
Для названия угла часто используют три большие латинские буквы, название вершины угла пишется посередине.
Иногда угол можно назвать только одной буквой, которая находится у вершины.
Можно также познакомиться с греческим алфавитом и использовать маленькие буквы для названий углов.
Чаще используют:
α,β,γ,δ,ϵ,η,ϕ,ω
— и другие.
Попытаемся представить точку как что-то бесконечно маленькое, а прямую — как что-то бесконечно простирающееся в обе стороны.

Рис. (1). Угол
∡ABC
,
∡B
или
∡α
.
Если угол образован дополнительными (или противоположными) лучами, то он называется развёрнутым.

Рис. (2). Развёрнутый угол
∡KLM
.
Так же как каждый отрезок имеет длину, которую можно измерить линейкой и выразить в единицах измерения, так и каждый угол имеет величину.
За единицу измерения углов принимают градус, что является
1180
частью развёрнутого угла.
Величина развёрнутого угла — (180°).
Углы измеряют транспортиром.

Рис. (3). Транспортир.
Особый угол, половина развёрнутого угла — прямой угол.
Прямой угол обозначают маленьким квадратиком внутри угла.
Величина прямого угла равна (90°).

Рис. (4). Прямой угол.
Углы, величина которых меньше (90°), называются острыми.
Углы, величина которых больше (90°), называются тупыми.
Источники:
Рис. 1. Угол, © ЯКласс.
Рис. 2. Развёрнутый угол, © ЯКласс.
Рис. 3. Транспортир. © ЯКласс.
Рис. 4. Прямой угол, © ЯКласс.
Рассказываем, как решать на нахождение градусной меры угла. Приводим алгоритм и примеры решения. Задачи для самостоятельного решения.
Суть задач на нахождение градусной меры угла
Задачи на нахождение градусной меры угла – это геометрические задачи на построение и нахождение величины угла, выраженной в градусах.
Алгоритм решения задач
Алгоритм решения задач на нахождение градусной меры угла:
- Выполняем краткую запись задачи;
- Определяем способ и решаем задачу;
- Выписываем полный ответ.
Определяем способ решения:
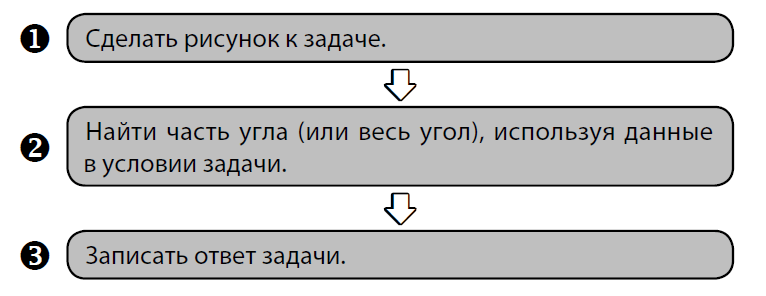
Способы решения задач
Примеры решения задачи
Задача 1. Угол AOB — развернутый. Провели луч OD. Найти градусную меру угла AOD, если угол AOD в 4 раза больше угла BOD.
Краткая запись:
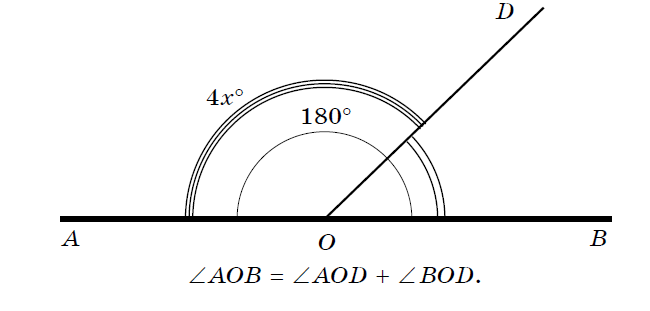
Решение:
- Пусть ∠ BOD = x°, тогда ∠ AOD = 4x°.
Так как их сумма равна 180°, составим и решим уравнение:
(4x+x=180)
(5x=180)
(x=180:5)
(x=36).
Итак, ∠ BOD = 36°, тогда ∠ AOD = 4 ⋅ 36° = 144° (или ∠ AOB = 180° – 36° = 144°).
Ответ: ∠ AOD = 144°.
Задачи для самостоятельного решения
- Луч BD — биссектриса ∠ ABC. Найти градусную меру ∠ DBC, если ∠ ABC = 160°.
- ∠ AOC = 132°, провели луч OB внутри ∠ AOC. Найти градусную меру ∠ AOB, если ∠ BOC = 35°.
- Внутри прямого угла ACB провели луч CD. Найти градусные меры углов ACD и BCD, если разность градусных мер углов ACD и BCD равна 40°.
- Определить градусную меру ∠ KON, изображенного на рисунке, если ∠ EOP = ∠ DOP, ON — биссектриса ∠ DOP.
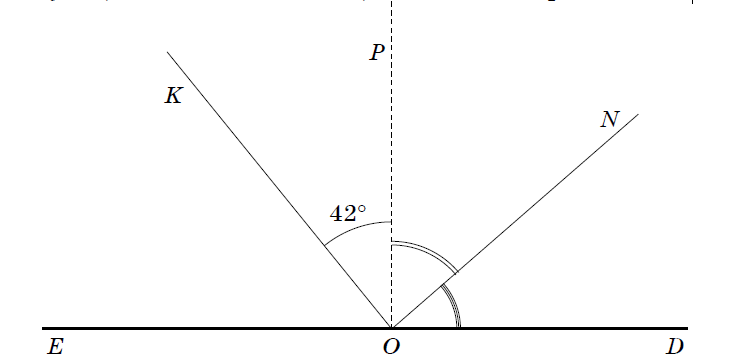
Посмотреть еще в категории: Задачи по математике 5-6 класс
- Задачи на сложение и вычитание
- Задачи на движение навстречу друг другу
- Задачи на движение в одном направлении
- Задачи на движение в противоположных направлениях
- Задачи на движение по реке
- Задачи на нахождение дроби от числа
- Задачи на нахождение числа по его дроби
- Задачи на нахождение процента от числа
- Задачи на нахождение числа по его процентам
- Задачи на процентное отношение двух чисел
- Задачи на проценты (с помощью пропорции)
- Задачи на нахождение периметра и площади треугольника
- Задачи с использованием формул площадей прямоугольника и квадрата
- Задачи на нахождение объема прямоугольного параллелепипеда и куба
- Задачи на проценты
- Задачи на нахождение длины окружности и площади круга
На этом уроке мы познакомимся с прибором для
измерения углов – транспортиром. Научимся с помощью транспортира измерять и
строить углы.
Коснёмся истории, чтобы узнать, как появился транспортир.
Понятие «градуса» и появление первых инструментов для
измерения углов связывают с развитием цивилизации в древнем Вавилоне. Хотя само
слово градус имеет латинское происхождение (градус
– от лат. gradus – “шаг, ступень”). Предполагают, что создание
транспортира было связано с созданием первого календаря.
Древние вавилонские математики и астрономы полный
оборот (окружность) разделили на столько частей, сколько дней в году. Они
думали, что в году 360 дней. Поэтому круг,
обозначающий год, они разделили на 360
равных частей. Такое изображение было очень удобным. На нём можно было отмечать
каждый прошедший день, и видеть, сколько дней осталось до конца года. Каждой
части дали название – градус.
Каждый градус разделили на 60 минут,
а минуту – на 60 секунд.
Градусная мера сохранилась и до наших дней.
Итак, для измерения углов применяют транспортир.
Транспортир
состоит из линейки (прямолинейной шкалы) и полуокружности
(угломерной шкалы). Центр этой полуокружности отмечен на транспортире
или штрихом, или отверстием. Штрихи шкалы транспортира делят полуокружность на 180 долей. В некоторых моделях – на 360 долей – это круглые транспортиры.
Если из центра этой полуокружности провести лучи
через каждый штрих, то получится 180 углов.
Каждый, из которых равен доле
развернутого угла.
Определение
Такие углы принято называть градусами.
Градусы обозначают вот таким знаком °.
Каждое деление шкалы транспортира равно 1°. Кроме делений по 1°
на шкале транспортира есть ещё деления по 5°
и по 10°.
А
теперь давайте разберёмся, как с помощью транспортира измерить угол. Запомните алгоритм
измерения углов:
1)
Совместить вершину угла с центром транспортира.
2)
Расположить транспортир так, чтобы одна из сторон угла проходила через
начало отсчёта на шкале транспортира; 0 –
начало отсчёта.
3)
Найдём штрих на шкале, через который пройдёт вторая сторона угла; (заметьте,
используем ту шкалу для определения градусной меры угла, где располагается
нулевой градус).
4)
Смотрим, через какой штрих проходит вторая сторона и какой градус
соответствует этому штриху.
На нашем слайде угол АОВ
равен 50°. Пишут так:
Развёрнутый угол равен 180°.
Так как мы с вами выяснили, что прямой угол равен половине развёрнутого угла,
то он равен
Прямой угол
равен 90°.
Так как равные углы полностью совмещаются при наложении,
то равные углы имеют равные градусные меры. Следовательно, больший
угол имеет большую градусную меру, меньший угол имеет меньшую
градусную меру.
Транспортир применяют и не только для измерения углов, а
также и для их построения.
Запомним алгоритм построения углов.
Алгоритм будем исследовать на конкретном примере:
построить угол МКN
равный 110°.
1.
Отметим
произвольную точку и обозначим её буквой К.
2.
Начертим
луч с началом в точке А и на нём отметим произвольную точку М. Получили луч КМ.
3.
Наложим
транспортир так, чтобы центр его совпал с точкой К, а луч КМ прошёл через
начало отсчёта на шкале.
4.
На
этой же шкале транспортира найдём штрих, который соответствует 110°. Отметим на
чертеже точку N
против штриха с отметкой 110°.
5.
Проведём
луч КN.
Построенный нами угол МКN и есть искомый.
6.
Не
забудем записать МКN = 110°.
Такой же угол можно построить и по другую сторону от луча КМ.
Повсюду есть углы
любые:
Прямые, острые, тупые,
Есть смежные, развёрнутые есть,
Их много, всех не перечесть.
Определение
Если угол меньше 90°,
то его называют острым углом.
Если угол больше 90°,
но меньше 180°, то его называют тупым
углом.
На экране изображены угол АОС
– острый и угол МКN – тупой. Градусная мера угла АОС
равна 30°,
т.е. меньше 90°, следовательно, он острый.
Градусная мера угла МКN
равна 120°, т.е. больше 90°, но меньше 180°,
следовательно, он тупой.
Итоги
Итак, сегодня на уроке мы познакомились с прибором для
измерения углов – транспортиром. Научились с помощью него измерять и строить
углы.
Слайд 1.
Цели:
- Образовательные:
- познакомить учащихся с единицей измерения
углов, с прибором для измерения углов; - научить пользоваться транспортиром.
- познакомить учащихся с единицей измерения
- Развивающие:
- развивать внимание, мышление учащихся;
- развивать самостоятельность учащихся,
используя проблемные ситуации, творческие
задания; - развивать познавательный интерес к предмету.
- Воспитательные:
- воспитывать чувство взаимоуважения;
- воспитывать у учащихся навыки учебного труда.
ХОД УРОКА
I. Организационный момент
II. Вступительное слово учителя
Мы познакомимся с измерительным прибором (как
он называется, вы узнаете немного позже),
научимся с его помощью измерять, а затем и
строить углы. Вы покажите свои знания, докажите
насколько внимательны.
Будем учиться не только математике, но и умению
общаться, уважению друг к другу.
Для того чтобы достичь наших целей, вы должны
быть волевыми, настойчивыми, целеустремленными,
поэтому эпиграфом нашего урока будут слова:
Слайд 2
«Усердие все превозмогает»
III. Устная работа
Какие из углов, изображенных на рисунке,
являются:
а) острыми;
б) тупыми;
в) есть ли среди этих углов прямые?
Слайд 3.
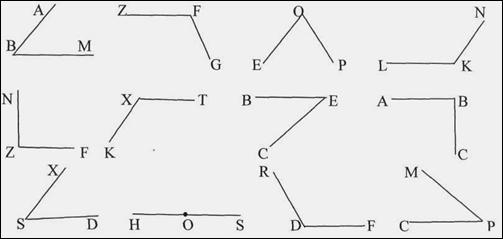
О каком угле мы с вами еще не вспомнили? [О
развернутом]
Какой угол называется развернутым? Острым?
Прямым? Тупым?
Мы знаем, что два угла можно сравнивать друг с
другом.
Какой способ для этого мы использовали?
[Наложение]
Но углы, также как и отрезки, можно сравнивать
не только наложением, но и с помощью измерения.
IV. Изучение нового материала
Для построения и измерения углов используют
специальный прибор. Как он называется, вы
узнаете, отгадав кроссворд.
Слайд 4.
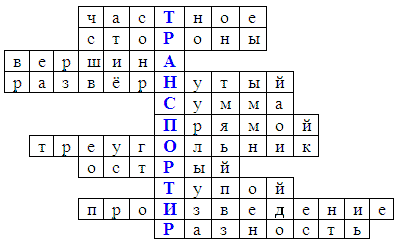
1. Результат деления.
2. Лучи образующие угол.
3. Точка, из которой выходят лучи образующие
угол.
4. Угол, который образуют два дополнительных
друг другу луча.
5. Результат сложения.
6. Угол, который составляет половину
развернутого угла.
7. Инструмент, который используют для
построения прямого угла.
8. Угол, меньше прямого.
9. Угол, больше прямого, но меньше
развернутого.
10. Результат умножения.
11. Результат вычитания.
Учитель демонстрирует учащимся транспортир
или показывает на плакате:
– Для измерения углов применяют транспортир.
Положите перед собой транспортиры. Вы видите,
какие они разные, но у всех есть нечто общее, о чем
мы сейчас будем говорить.
Слайд 5. Итак, шкала транспортира.
Она расположена на полуокружности и
пронумерована
от 0 до 180. Бывают шкалы двойные: нумерация идет
слева направо и справа налево.

Слайд 6. Также есть круглые транспортиры, шкала
идет по кругу от 0 до 360, но она также разделена на
две полуокружности.

Центр этой полуокружности отмечен на
транспортире точкой или черточкой. Найдите на
своем транспортире центр и покажите его.
Штрихи шкалы транспортира делят
полуокружность на 180 равных частей. Лучи,
проведенные из центра полуокружности через эти
штрихи, образуют 180 углов, каждый из которых равен
![]() доле
доле
развернутого угла. Такие углы называют
градусами.
Слайд 7. Итак, градусом называют ![]() долю
долю
развернутого угла. Градусы обозначают знаком
°. Каждое деление шкалы транспортира равно 1°.
Слайд 8.
Историческая справка
Слово «градус» – латинское,
означает «шаг», «ступень». Измерение углов в
градусах появилось более 3 тыс. лет назад в
Вавилоне. В расчетах там использовались
шестидесятеричная система счисления,
шестидесятеричные дроби.
С этим связано, что вавилонские математики и
астрономы, а вслед за ними греческие и индийские,
полный оборот (окружность) делили на 360 частей – градусов
(шесть раз по шестьдесят), каждый градус – на 60
минут, а минуту – на 60 секунд:
![]()
Объяснение учителя (с демонстрацией
на доске), как с помощью транспортира можно
измерить угол.
Слайд 9.
– Как измеряют углы с помощью транспортира?
1) Нужно вершину угла совместить с центром
транспортира.
2) Одна сторона угла должна проходить через
нулевую отметку (0° по шкале).
3) Вторая сторона угла должна пересекать шкалу.
Нужно посмотреть, через какую
отметку проходит вторая сторона угла. Это и есть
величина этого угла.
Если у транспортира есть две шкалы, то надо
смотреть на отметку той шкалы, через ноль которой
проходит одна из сторон угла.
V. Практическая работа
Каждому ученику выдается набор углов: острый,
прямой, тупой и развернутый.
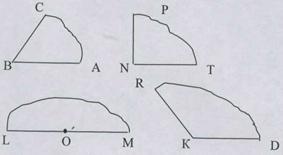
Задания
- Выберите из предложенных вам углов острый,
тупой, прямой, развернутый. - Измерьте их градусную меру и запишите в
тетрадях эти данные. - Сделайте вывод о градусной мере:
а) развернутого угла;
б) прямого угла;
в) острого угла;
г) тупого угла.
Вывод:
Слайд 10.
– развернутый угол равен 180°;
– прямой угол равен 90° (половина
развернутого угла);
– острый угол меньше 90°;
– тупой угол больше 90°, но меньше
180°.
VI. Физкультурная пауза
- Покажите руками угол 90°, 180°.
- Покажите руками острый угол, тупой угол.
- Покажите рукой, где вокруг нас есть прямые углы.
- Повернитесь на 180°. А теперь на 90°.
Продолжаем работать.
Задание: Начертите в тетради угол
любой величины. Предложите соседу по парте его
измерить.
VII. Работа по карточкам
У всех учеников карточки с одинаковым заданием.
Задание: Измерьте углы и запишите
результаты измерений в тетрадях.
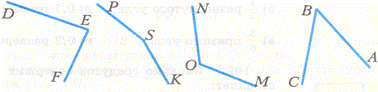
Слайд11.
Задание: Выполняется устно с
использованием модели часов.
Какой угол образуют часовая и минутная стрелки
часов:
а) в 3
ч;
в) в 10
ч;
д) в 2 ч 30 мин;
б) в 5
ч;
г) в 6
ч;
е) в 5 ч 30 мин?
Слайд 12.
Задача №1652
Луч ОС лежит внутри угла АОВ,
причем ![]() АОС = 37°,
АОС = 37°, ![]() ВОС = 19°?.
ВОС = 19°?.
Чему равен угол АОВ°
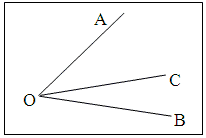
Слайды 13, 14, 15.
VIII. Итог урока
IX. Задание на дом
п. 42, №1651, №1683, №1672.
