Как найти градусную меру дуги развертки конуса

Как найти градусную меру дуги развертки конуса

Калькулятор рассчитывает параметры развертки прямого кругового конуса на плоскости. Картинка ниже иллюстрирует задачу.

conus.jpg

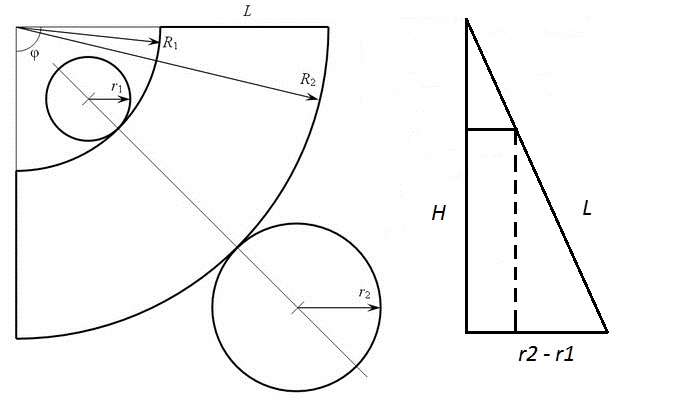
Про конус нам известен радиус основания и высота конуса (или высота усеченного конуса). Для описания развертки нам надо найти радиус внешней дуги, радиус внутренней дуги (если конус усеченный), длину образующей и центральный угол.

Длину образующей можно посчитать по теореме Пифагора:
L = sqrt{ (r_2 - r_1)^2 + H^2 },
при этом для полного конуса r1 просто обращается в ноль.

Радиус внутренней дуги можно найти из подобия треугольников:
R_1=frac{L*r_1}{r_2-r_1},
опять же, для полного конуса она равна нулю.

Соответственно, радиус внешней дуги:
R_2=L+R_1,
для полного конуса он совпадает с L.

Ну и центральный угол:
phi=360*frac{r_2}{R_2}

PLANETCALC, Развертка (выкройка) конуса

Развертка (выкройка) конуса

Радиус основания конуса r2

Радиус второго основания r1

Радиус второго основания (для случая усеченного конуса)

Точность вычисления

Знаков после запятой: 2

Радиус внешней дуги выкройки R2

Радиус внутренней дуги выкройки R1

Центральный угол выкройки (в градусах)

Длина хорды, соединяющей края внешней дуги

Источник

Построение развертки конуса

Развертка поверхности конуса – это плоская фигура, полученная путем совмещения боковой поверхности и основания конуса с некоторой плоскостью.

Варианты построения развертки:

  • Прямой круговой конус
  • Наклонный конус
  • Усеченный конус

Развертка прямого кругового конуса

Развертка боковой поверхности прямого кругового конуса представляет собой круговой сектор, радиус которого равен длине образующей конической поверхности l, а центральный угол φ определяется по формуле φ=360*R/l, где R – радиус окружности основания конуса.

В ряде задач начертательной геометрии предпочтительным решением является аппроксимация (замена) конуса вписанной в него пирамидой и построение приближенной развертки, на которую удобно наносить линии, лежащие на конической поверхности.

Алгоритм построения

  1. Вписываем в коническую поверхность многоугольную пирамиду. Чем больше боковых граней у вписанной пирамиды, тем точнее соответствие между действительной и приближенной разверткой.
  2. Строим развертку боковой поверхности пирамиды способом треугольников. Точки, принадлежащие основанию конуса, соединяем плавной кривой.

Пример

На рисунке ниже в прямой круговой конус вписана правильная шестиугольная пирамида SABCDEF, и приближенная развертка его боковой поверхности состоит из шести равнобедренных треугольников – граней пирамиды.

Рассмотрим треугольник S0A0B0. Длины его сторон S0A0 и S0B0 равны образующей l конической поверхности. Величина A0B0 соответствует длине A’B’. Для построения треугольника S0A0B0 в произвольном месте чертежа откладываем отрезок S0A0=l, после чего из точек S0 и A0 проводим окружности радиусом S0B0=l и A0B0= A’B’ соответственно. Соединяем точку пересечения окружностей B0 с точками A0 и S0.

Грани S0B0C0, S0C0D0, S0D0E0, S0E0F0, S0F0A0 пирамиды SABCDEF строим аналогично треугольнику S0A0B0.

Точки A, B, C, D, E и F, лежащие в основании конуса, соединяем плавной кривой – дугой окружности, радиус которой равен l.

Развертка наклонного конуса

Рассмотрим порядок построения развертки боковой поверхности наклонного конуса методом аппроксимации (приближения).

Алгоритм

  1. Вписываем в окружность основания конуса шестиугольник 123456. Соединяем точки 1, 2, 3, 4, 5 и 6 с вершиной S. Пирамида S123456, построенная таким образом, с некоторой степенью приближения является заменой конической поверхности и используется в этом качестве в дальнейших построениях.
  2. Определяем натуральные величины ребер пирамиды, используя способ вращения вокруг проецирующей прямой: в примере используется ось i, перпендикулярная горизонтальной плоскости проекций и проходящая через вершину S.
    Так, в результате вращения ребра S5 его новая горизонтальная проекция S’5’1 занимает положение, при котором она параллельна фронтальной плоскости π2. Соответственно, S’’5’’1 – натуральная величина S5.
  3. Строим развертку боковой поверхности пирамиды S123456, состоящую из шести треугольников: S01060, S06050, S05040, S04030, S03020, S02010. Построение каждого треугольника выполняется по трем сторонам. Например, у △S01060 длина S010=S’’1’’0, S060=S’’6’’1, 1060=1’6’.

Степень соответствия приближенной развертки действительной зависит от количества граней вписанной пирамиды. Число граней выбирают, исходя из удобства чтения чертежа, требований к его точности, наличия характерных точек и линий, которые нужно перенести на развертку.

Перенос линии с поверхности конуса на развертку

Линия n, лежащая на поверхности конуса, образована в результате его пересечения с некоторой плоскостью (рисунок ниже). Рассмотрим алгоритм построения линии n на развертке.

Алгоритм

  1. Находим проекции точек A, B и C, в которых линия n пересекает ребра вписанной в конус пирамиды S123456.
  2. Определяем натуральную величину отрезков SA, SB, SC способом вращения вокруг проецирующей прямой. В рассматриваемом примере SA=S’’A’’, SB=S’’B’’1, SC=S’’C’’1.
  3. Находим положение точек A0, B0, C0 на соответствующих им ребрах пирамиды, откладывая на развертке отрезки S0A0=S’’A’’, S0B0=S’’B’’1, S0C0=S’’C’’1.
  4. Соединяем точки A0, B0, C0 плавной линией.

Развертка усеченного конуса

Описываемый ниже способ построения развертки прямого кругового усеченного конуса основан на принципе подобия.

Алгоритм

  1. Строим вспомогательный конус ε, подобный конусу ω, как это показано на рисунке выше. Для удобства построения величину диаметра d выбираем таким образом, чтобы соотношение t=D/d выражалось целым числом. В рассматриваемом примере t=2.
  2. Строим развертку боковой поверхности конуса ε – S0A01020304050A0 и на биссектрисе угла A0S0A0 отмечаем точку O0, выбрав ее расположение произвольно.
  3. Проводим прямые O0A0, O010, O020, O030, O040, O050, O0A0 и на них откладываем отрезки [O0A10]=t×|O0A0|, [O0110]= t×|O010|, [O0210]=t×|O020|, [O0310]=t×|O030|, [O0410]=t×|O040|, [O0510]=t×|O050|, [O0A10]=t×|O0A0| соответственно, где t=D/d. Соединяем точки A10, 110, 210, 310, 410, 510, A10 плавной линией.
  4. Из точек A10, 110, 210, 310, 410, 510, A10 проводим лучи, которые параллельны соответственно прямым A0S0, 10S0, 20S0, 30S0, 40S0, 50S0, A0S0, и на них откладываем отрезки A10B10, 110120, 210220, 310320, 410420, 510520, A10B10, равные l – образующей усеченного конуса. Проводим линию B10120220320420520B10.
Источник

На этом уроке мы познакомимся с понятием конуса. Дадим
определение конуса. Рассмотрим, какими элементами он обладает. А также
разберемся, как находят объем, площадь боковой поверхности  и площадь полной
поверхности конуса.

Итак, рассмотрим понятие конуса. Вокруг нас существует множество предметов, имеющих
форму конуса. Вафельные рожки для мороженного имеют форму конуса, дорожный
конус, шляпа ведьмочки для хэлоуина, колпак у Буратино, колпаки для дня
рождения, некоторые архитектурные сооружения, декоративным растениям, придают
форму конуса и многое другое.

Конус – это один из видов тел вращения. Итак, если
взять прямоугольный треугольник, например, треугольник ABC
и вращать его вокруг катета AB, то в результате
получится тело, которое называется конусом.

Прямая AB называется осью
конуса. А отрезок AB – его высотой.

При вращении катета AC
образуется круг, он называется основанием конуса.

Иногда радиус этого круга называют радиусом конуса.

При вращении гипотенузы BC
образуется поверхность, состоящая из отрезков с общим концом B.
Ее называют конической поверхностью или боковой поверхностью конуса.

Отрезки, из которых она составлена, называются
образующими конуса.

Точка B называется вершиной
конуса.

Определение. Конус – это тело, ограниченное
кругом и конической поверхностью.

Пользуясь принципом Кавальери, можно доказать, что объем конуса
, где r –
радиус основания конуса, h – его высота.

На рисунке изображен конус, у которого радиус равен r, а образующая равна l. Боковую
поверхность конуса, как и боковую поверхность цилиндра, можно развернуть на
плоскость, разрезав ее по одной из образующих.

Давайте представим, что боковую поверхность конуса
разрезали по образующей AB и
развернули таким образом, что получился круговой сектор ABB’.
Стороны AB и A’B которого являются двумя краями
разреза боковой поверхности конуса.

Разверткой боковой поверхности конуса является
круговой сектор. Обратите внимание, радиус сектора равен образующей конуса,
т.е. l. А длина дуги сектора равна длине окружности
основания конуса, т.е. равна 2πr.

За площадь боковой поверхности конуса принимается
площадь ее развертки. Выразим площадь боковой поверхности конуса через его
образующую l и радиус основания r.

Площадь кругового сектора – развертки боковой поверхности конуса –
равна , где α – градусная мера дуги
сектора.

Длина дуги окружности с градусной мерой α и радиусом l равна пи эль альфа деленное на сто восемьдесят. С другой
стороны, длина этой дуги равна два пи эр, т.е. . Отсюда, площадь боковой поверхности
конуса
. Т.е. площадь боковой поверхности
конуса с образующей l и радиусом основания r выражается формулой: .

Площадью полной поверхности конуса называется сумма площадей боковой
поверхности и основания. Отсюда видим,
.

Задача. Радиус основы конуса  метра,
высота  метра. Найдите площади боковой и
полной поверхностей конуса.

Решение.

 – прямоугольный.

 

 

 (м)

 (м2)

 (м2)

Ответ: , .

Задача. Радиус основы конуса  см,
высота  см. Найдите объем конуса, .

Решение.

 

 (см3)

Ответ: .

Конус в переводе с греческого «konos»
означает «сосновая шишка». С конусом люди знакомы с глубокой древности. В 1906
году была обнаружена книга «О методе», написанная Архимедом. В этой книге
дается решение задачи об объеме общей части пересекающихся цилиндров. Архимед
приписывает честь открытия этого принципа древнегреческому философу Демокриту.
С помощью этого принципа Демокрит получил формулы для вычисления объема
пирамиды и конуса.

Подведем итоги. На этом уроке мы познакомились с
понятием конуса. Узнали, что конус – это тело, ограниченное кругом и конической
поверхностью. Рассмотрели, какими элементами он обладает. А также разобрались,
как находят объем, площадь боковой поверхности  и площадь полной поверхности
конуса.

Источник

Развертка (выкройка) конуса

Калькулятор рассчитывает развертку (выкройку) на плоскости прямого кругового конуса и усеченного прямого кругового конуса.

Калькулятор рассчитывает параметры развертки прямого кругового конуса на плоскости. Картинка ниже иллюстрирует задачу.

Про конус нам известен радиус основания и высота конуса (или высота усеченного конуса). Для описания развертки нам надо найти радиус внешней дуги, радиус внутренней дуги (если конус усеченный), длину образующей и центральный угол.

Длину образующей можно посчитать по теореме Пифагора:
,
при этом для полного конуса r1 просто обращается в ноль.

Радиус внутренней дуги можно найти из подобия треугольников:
,
опять же, для полного конуса она равна нулю.

Соответственно, радиус внешней дуги:
,
для полного конуса он совпадает с L.

Радиус и высота конуса

Свойства

Через радиус конуса можно найти все параметры конуса, связанные с основанием, а значение высоты позволяет вычислить площади, объемы и все остальные объемные параметры конуса. Так, диаметр конуса равен удвоенному радиусу, периметр окружности в основании вычисляется по стандартной формуле через радиус, равно как и площадь основания. d=2r P=2πr S_(осн.)=πr^2

Прямоугольный треугольник, образованный высотой конуса, радиусом основания и образующей конуса, связывает эти три значения теоремой Пифагора, по которой можно вычислить неизвестную образующую, а также угол между образующей и основанием. Тем временем, угол α рассчитывается из равнобедренного треугольника, сформированного двумя образующими и диаметром из того принципа, что сумма всех углов в треугольнике равна 180 градусам. (рис.40.1, 40.2) l=√(h^2+r^2 ) tan⁡β=h/r α=180°-2β

Чтобы найти площадь боковой поверхности конуса, необходимо умножить радиус и апофему на число π. Площадь полной поверхности конуса состоит из площади его основания и площади боковой поверхности. В обеих формулах вместо апофемы нужно подставить квадратный корень через высоту и радиус, полученный по теореме Пифагора. S_(б.п.)=πrl=πr√(h^2+r^2 ) S_(п.п.)=S_(б.п.)+S_(осн.)=πrl+πr^2=πr(l+r)=πr(√(h^2+r^2 )+r)

Чтобы найти объем конуса, достаточно знать значения радиуса и высоты, тогда формула объема выглядит как произведение числа π на квадрат радиуса и высоту, деленное на три. V=1/3 S_(осн.) h=(πr^2 h)/3

Радиус сферы, вписанной в конус, зависит не только от радиуса основания конуса и его высоты, но и от образующей, поэтому чтобы вычислить радиус вписанной сферы конуса через радиус конуса и высоту, нужно вместо образующей подставить полученное для нее выше выражение. Радиус описанной сферы может быть представлен сразу формулой только с переменными радиуса и высоты. (рис.40.3, 40.4) r_1=hr/(l+r)=rh/(√(h^2+r^2 )+r) R=(h^2+r^2)/2h

Калькуляторы расчета размеров развертки конуса

Иногда в ходе выполнения тех или иных хозяйственных работ мастер встаёт перед проблемой изготовления конуса – полного или усеченного. Это могут быть операции, скажем, с тонким листовым металлом, эластичным пластиком, обычной тканью или даже бумагой или картоном. А задачи встречаются самый разные – изготовление кожухов, переходников с одного диаметра на другой, козырьков или дефлекторов для дымохода или вентиляции, воронок для водостоков, самодельного абажура. А может быть даже просто маскарадного костюма для ребенка или поделок, заданных учителем труда на дом.

Калькуляторы расчета размеров развертки конуса

Чтобы из плоского материала свернуть объёмную фигуру с заданными параметрами, необходимо вычертить развертку. А для этого требуется рассчитать математически и перенести графически необходимые точные размеры этой плоской фигуры. Как это делается – рассмотрим в настоящей публикации. Помогут нам в этом вопросе калькуляторы расчета размеров развертки конуса.

Калькуляторы расчета размеров развертки конуса

Несколько слов о рассчитываемых параметрах

Понять принцип расчета будет несложно, разобравшись со следующей схемой:

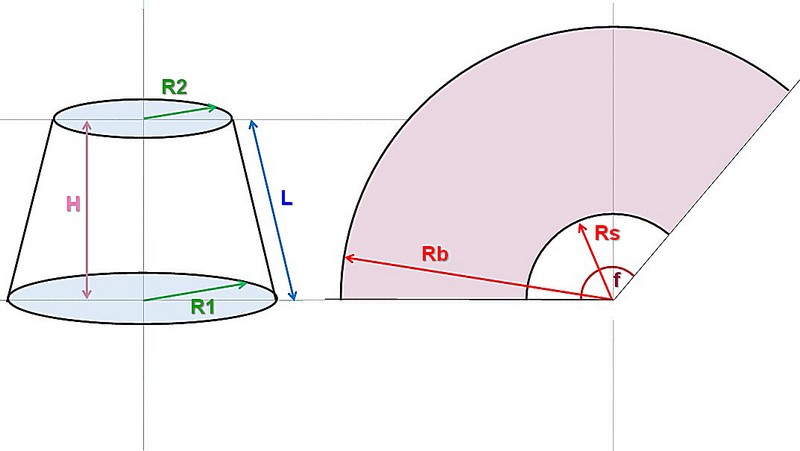Усеченный конус с определяющими размерами и его развёртка. Показан усеченный конус, но с полным — принцип не меняется, а расчеты и построение становятся даже проще.

Итак, сам конус определяется радиусами оснований (нижней и верхней окружности) R1 и R2, и высотой Н. Понятно, что если конус не усеченный, то R2 просто равно нулю.

Буквой L обозначена длина боковой стороны (образующей) конуса. Она в некоторых случаях уже известна – например, требуется сделать конус по образцу или выкроить материал для обтяжки уже имеющегося каркаса. Но если она неизвестна – не беда, ее несложно рассчитать.

Справа показана развёртка. Она для усеченного конуса ограничена сектором кольца, образованного двумя дугами, внешней и внутренней, с радиусами Rb и Rs. Для полного конуса Rs также будет равен нулю. Хорошо видно, что Rb = Rs + L

Угловую длину сектора определяет центральный угол f, который в любом случае предстоит рассчитать.

Все расчеты займут буквально минуту, если воспользоваться предлагаемыми калькуляторами:

Шаг 1 – определение длины образующей L

(Если она уже известна – шаг пропускается)

Шаг 2 – определение радиусов внутренней и внешней дуги развертки

Радиусы рассчитываются поочередно – с выбором в соответствующем поле калькулятора.

[spoiler title=”источники:”]

http://geleot.ru/education/math/geometry/calc/cone/radius_and_height

http://stroyday.ru/kalkulyatory/obshhestroitelnye-voprosy/kalkulyatory-rascheta-razmerov-razvertki-konusa.html

[/spoiler]

Источник
  1. Главная
  2. Справочники
  3. Справочник по геометрии 7-9 класс
  4. Многогранники
  5. Конус

Конус – это объемное тело, которое получается при вращении прямоугольного треугольника вокруг одного из его катетов.

Возьмем прямоугольный треугольник АВС. Будем вращать этот треугольник вокруг катета АС.

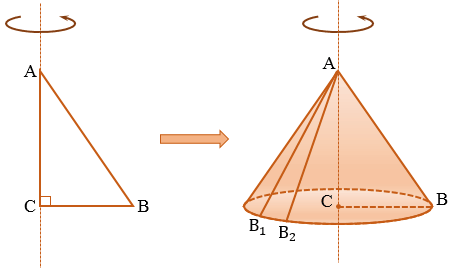
Прямая АС – ось косинуса.

Отрезок АС – высота конуса.

Основание конуса – круг, образованный при вращении катета ВС.

Коническая поверхность (или боковая поверхность конуса) – поверхность, образованная при вращении гипотенузы АВ и состоящая из отрезков с общим концом А.

Образующие конуса – отрезки, из которых составлена боковая поверхность конуса (на рисунке выше указаны образующие АВ, АВ1 и АВ2).

Определение

Конус – это тело, ограниченное кругом и конической поверхностью.

Объем конуса

Объем конуса равен одной трети произведения площади основания на высоту.

Доказательство

Дано: конус с площадью основания S, высотой h и объемом V.

Доказать: V = 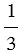Sh.

Доказательство:

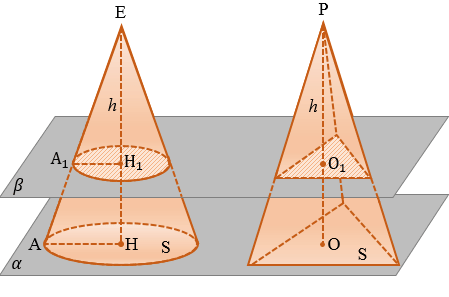
Воспользуемся принципом Кавальери. Рассмотрим конус и пирамиду с площадями оснований S и высотами ЕН = h и РО = h соответственно, “стоящие” на одной плоскости .

Проведем секущую плоскость 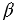, параллельную плоскости и пересекающую высоты ЕН и РО в точках Н1 и О1 соответственно. В сечении конуса плоскостью 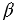получится круг радиуса Н1А1.

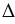ЕН1А1 подобен 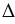ЕНА по двум углам (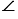Е – общий, 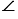ЕН1А1 = 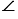ЕНА = 900, т.к. в противном случае прямые НА и Н1А1, а значит, и плоскости и 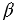пересекались бы, что противоречит условию). Поэтому  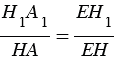, откуда 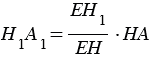и площадь сечения конуса равна .

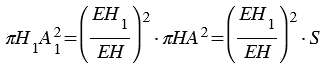Площадь сечения пирамиды равна 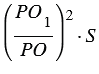. По условию ЕН = РО = h, значит, ЕН1 = РО1 (т.к. ЕН1 = h – НН1 и РО1 = h – ОО1, параллельные плоскости отсекают одинаковые отрезки НН1 и ОО1 от отрезков ЕН и РО, т.е. НН1 = ОО1).

Следовательно, площадь сечения конуса равна площади сечения пирамиды. Поэтому и его объем равен объему пирамиды, т.е. V = 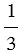Sh. Что и требовалось доказать.

Площадь боковой поверхности конуса

Рассмотрим конус с радиусом основания 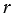и образующей .

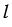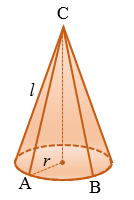
Представим, что его боковую поверхность разрезали по одной из образующих и развернули так, что получился круговой сектор.

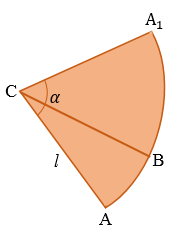
Радиус этого сектора равен образующей конуса, т.е. равен 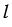, а длина дуги сектора равна длине окружности основания конуса, т.е. равна 2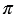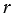, – градусная мера дуги сектора, тогда площадь данного сектора: 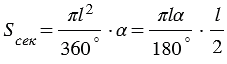.   (1)

Длина дуги окружности с градусной мерой и радиусом 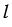равна 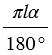. С другой стороны, длина этой дуги равна 2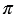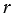, поэтому учитывая (1), получим: .

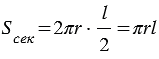Площадь боковой поверхности конуса равна площади ее развертки, т.е. .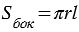

Советуем посмотреть:

Предмет стереометрии

Параллельность и перпендикулярность прямых и плоскостей в пространстве

Многогранник

Призма

Параллелепипед

Объём тела

Свойства прямоугольного параллелепипеда

Пирамида

Цилиндр

Сфера и шар

Многогранники


Правило встречается в следующих упражнениях:

7 класс

Задание 1219,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1220,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1221,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1222,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1224,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1228,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1230,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 20,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1250,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1310,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Источник

Добавить комментарий