Как найти градусную меру двух смежных углов

Как найти градусную меру двух смежных углов

Смежные углы в геометрии

15 июня 2022

Два угла называются смежными, если у них общая вершина, общая сторона, а две других стороны образуют прямую.

В этом уроке:

  1. Что такое смежные углы
  2. Основное свойство смежных углов
  3. Биссектрисы смежных углов
  4. Тренировочные задачи

Это довольно простая, но очень важная тема.

1. Что такое смежные углы

Возьмём прямую $AB$ и отметим на ней точку $M$. Получим развёрнутый угол $AMB:$

Развёрнутый угол

Проведём из точки $M$ луч $MN$, не совпадающий с лучами $MA$ и $MB$.

Смежный угол

Получим два новых угла: $angle AMN$ и $angle BMN$. Эти углы и называются смежными.

Определение. Два угла называются смежными, если у них одна общая сторона, а две других образуют прямую (или, что то же самое, являются дополнительными лучами).

Обратите внимание: чтобы углы стали смежными, им недостаточно просто иметь общую сторону. Вот эти углы — не смежные, хотя они и имеют общую сторону:

Углы с общей стороной

А вот дальше — смежные, хотя и расположены немного непривычно:

Нестандартные смежные углы

Часто смежные углы возникают в точке пересечения прямых. Например, при пересечении двух прямых

Пересечение двух прямых

образуется четыре пары смежных углов: $angle ASM$ и $angle ASN$; $angle BSM$ и $angle MSN$; $angle ASN$ и $angle BSN$; наконец, $angle ASM$ и $angle BSM$.

2. Основное свойство внешних углов

У смежных углов есть замечательное свойство, которое будет преследовать нас на протяжении всей геометрии, до конца 11 класса.

Теорема. Сумма смежных углов равна 180°.

Доказательство. Рассмотрим смежные углы $AMN$ и $BMN$ с общей стороной $MN$:

Смежный угол

Поскольку луч $MN$ делит угол $AMB$ на смежные углы $AMN$ и $BMN$, по основному свойству углов

[angle AMB=angle AMN+angle BMN]

Но угол $AMB$ — развёрнутый, поэтому

[angle AMN+angle BMN={180}^circ ]

Другими словами, если один угол равен $alpha $, то смежный с ним равен ${180}^circ -alpha $. Или если известно, что углы $alpha $ и $beta $ — смежные, то $alpha +beta ={180}^circ $.

Казалось бы, элементарные рассуждения, но их вполне достаточно, чтобы решать большой класс задач.

Задача 1. Найдите угол, смежный с углом $ABC$, если:

  1. $angle ABC={36}^circ $.
  2. $angle ABC={121}^circ $.

Решение

1) Обозначим смежный угол $DBC=x$. Он будет тупым:

Смежный угол 36 градусов

Тогда $x=180-36=144$.

2) Обозначим смежный угол $DBC=x$. Он будет острым:

Смежный угол 121 градус

Тогда $x=180-121=59$.

Немного усложним задачу.

Задача 2. Найдите смежные углы, если:

  1. один из них на 68° больше другого.
  2. один из них в 5 раз больше другого.
  3. их градусные меры относятся как 5 : 4.

Решение.

1) Пусть один из углов равен $x$. Тогда другой (очевидно, больший) будет равен $x+68$.

Один смежный угол на 68 больше другого

Поскольку углы смежные, их сумма равна 180 градусов:

[begin{align}2x+68&=180 \ 2x&=112 \ x&=56 end{align}]

Итак, один угол равен 56 градусов. Тогда другой равен $x+68=124$ градуса.

2) Пусть меньший угол равен $x$. Тогда смежный с ним равен $5x$.

Один смежный угол в 5 раз больше другого

Сумма смежных углов равна 180 градусов, поэтому

[begin{align}5x+x&=180 \ 6x&=180 \ x&=30 end{align}]

Мы нашли меньший угол — он равен 30 градусов. Тогда второй угол равен $5x=150$ градусов.

3) В задачах с отношениями величинам удобно обозначать их кратными некоторой переменной. Например, если углы относятся как 5 к 4, то пусть величина одного угла будет $5x$, а другого — $4x$.

Смежные углы относятся как 5 к 4

Сумма смежных углов вновь равна 180 градусов:

[begin{align}5x+4x&=180 \ 9x&=180 \ x&=20 end{align}]

Поэтому сами углы равны $4x=80$ и $5x=100$ градусов.

3. Биссектрисы смежных углов

Вновь рассмотрим смежные углы $AMN$ и $BMN$:

Смежный угол

Построим биссектрису $MC$ угла $AMN$ и биссектрису $MD$ угла $BMN$:

Биссектрисы смежных углов

Если $angle AMC=x$ и $angle BMD=y$, то $angle AMN=2x$ и $angle BMN=2y$. Это смежные углы, поэтому

[begin{align}2x+2y&={180}^circ \ x+y&={90}^circ end{align}]

Получается, что биссектрисы смежных углов всегда пересекаются под углом 90°. Этот факт известен далеко не всем ученикам. Хотя он вполне может встретиться, например, на ЕГЭ.

Задача 3. Углы $ABC$ и $MBC$ смежные, $angle ABC={70}^circ $. Луч $BD$ принадлежит углу $ABC$, причём $angle ABD={40}^circ $. Найдите угол между биссектрисами углов $CBD$ и $MBC$.

Решение. Изобразим все углы на рисунке:

Смежный угол 40 и биссектрисы

Видим, что углы $ABD$ и $MBD$ — смежные. Следовательно

[begin{align}angle MBD&={180}^circ -angle ABD= \ &={180}^circ -{40}^circ ={140}^circ end{align}]

Синим цветом отмечены биссектрисы углов $CBD$ и $MBC$. Обозначим величину углов переменными: $angle CBD=2x$, $angle MBD=2y$. Но $angle MBD=angle MBC+angle CBD$, поэтому

[begin{align}2x+2y&=140 \ x+y&=70 end{align}]

Это и есть искомый угол между биссектрисами. Он равен 70 градусов.

Задача 4. Дан треугольник $ABC$. Лучи $AM$ и $CN$ лежат на одной прямой со стороной $AB$ (см. рисунок). Известно, что $angle MAC+angle ABC={180}^circ $. Докажите, что $angle MAC=angle NBC$.

Треугольник ABC и смежные углы

Пусть $angle ABC=x$. Тогда из условия следует, что $angle MAC={180}^circ -x$.

С другой стороны, углы $ABC$ и $NBC$ смежные, поэтому $angle NBC={180}^circ -x$.

Получается, что углы $MAC$ и $NBC$ равны одному и тому же выражению. Следовательно, $angle MAC=angle NBC$, что и требовалось доказать.

Смотрите также:

  1. Что такое вертикальные углы
  2. Перпендикулярные прямые — определение и свойства
  3. Правила комбинаторики в задаче B6
  4. Метод координат в пространстве
  5. Четырехугольная пирамида: как найти координаты вершин
  6. Задача B4 про три дороги — стандартная задача на движение
Источник
  1. Главная
  2. Справочники
  3. Справочник по геометрии 7-9 класс
  4. Начальные геометрические сведения
  5. Смежные углы

Смежные углы – это два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой.

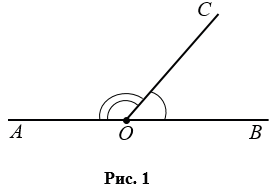
На Рис.1 ОС – общая сторона, ОА и ОВ продолжают друг друга, значит АОС и СОВ – смежные.

Вместе смежные углы составляют развернутый угол, т.е. угол равный 1800. На Рис.1 АОВ = АОС + СОВ = 1800. Значит:

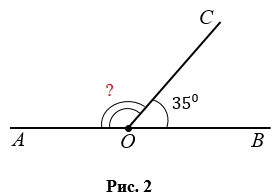
  1. Зная один из смежных углов, всегда можно найти второй. На Рис.2  СОВ = 350, тогда АОС = 1800 – СОВ = 1800 – 350 = 1450.

         

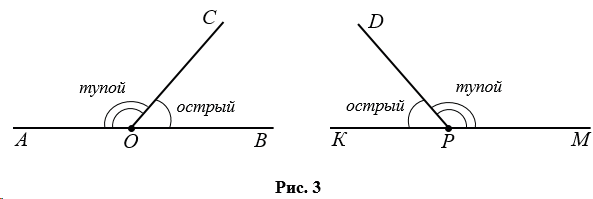
  1. Если один из смежных углов острый, то второй будет тупой и наоборот (Рис.3).

         

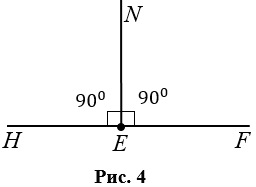
  1. Если один из смежных углов прямой т.е. равен 900, то второй также будет прямой (Рис.4).

         

Советуем посмотреть:

Точки, прямые, отрезки

Провешивание прямой на местности

Луч

Угол

Равенство геометрических фигур

Сравнение отрезков

Сравнение углов

Длина отрезка

Единицы измерения длины, расстояний

Градусная мера угла

Измерение углов на местности

Вертикальные углы

Перпендикулярные прямые

Построение прямых углов на местности

Начальные геометрические сведения


Правило встречается в следующих упражнениях:

7 класс

Задание 68,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 152,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 192,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 238,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 296,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 337,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 346,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 362,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 2,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 715,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Источник

Что такое смежные углы? Какие у них свойства?

Определение.

Смежные углы — это углы, у которых одна сторона — общая, а другие стороны лежат на одной прямой.

smezhnyie uglyi

∠1 и ∠2 — смежные углы

Сколько смежных углов образуется при пересечении двух прямых?

При пересечении двух прямых образуется четыре пары смежных углов:

skolko smezhnyih uglov pri peresechenii pryamyih

∠1 и ∠2, ∠3 и ∠4,

∠1 и ∠3,  ∠2 и ∠4

Но, так как ∠1 =∠4,  ∠2=∠3 (как вертикальные), то достаточно рассмотреть только одну из этих пар.

Свойство смежных углов.

Сумма смежных углов равна 180º.

Задачи.

1) Даны два смежных угла. Один на 42 градуса больше другого. Найти эти углы.

dva smezhnyih ugla

Дано:

∠AOC и ∠BOC — смежные,

∠AOC на 42º  больше, чем ∠BOC

Найти: ∠AOC и ∠BOC.

Решение:

Пусть ∠BOC=хº, тогда ∠AOC= х+42º. Так как сумма смежных углов равна 180º, то ∠BOC+∠AOC=180º.

Имеем уравнение:

х+х+42=180

2х=180-42

2x=138

x=69

Значит, ∠BOC= 69º, ∠AOC=69+42=111º.

Ответ: 69º и 111º.

2) Найти смежные углы, если их градусные меры относятся как 4:5.

danyi smezhnyie uglyi

Дано:

∠1 и ∠2 — смежные,

∠1 : ∠2= 4:5

Найти:∠1 и ∠2

Решение:

Пусть k — коэффициент пропорциональности. Тогда ∠2 =4kº , ∠1=5kº. Так как сумма смежных углов равна 180º, ∠1 +∠2=180º.

Имеем уравнение:

4k+5k=180

9k=180

k=20

Значит, смежные углы равны 4∙20=80º и 5∙20=100º.

Ответ: 80º и 100º.

3) Один из углов, образованных при пересечении двух прямых, в 5 раз больше другого. Найти эти углы.

ugol peresecheniya dvuh pryamyih

Дано: AB и CD — прямые, O — точка их пересечения,

∠AOD  в 5 раз больше, чем ∠BOD

Найти: ∠AOD, ∠BOD

Решение:

При пересечении двух прямых образуются смежные и вертикальные углы. Так как вертикальные углы равны между собой, то углы∠AOD и ∠BOD —  смежные. Пусть ∠BOD=xº, тогда ∠AOD=5xº. Так как сумма смежных углов равна 180º, ∠AOD +∠BOD=180º.

Имеем уравнение:

x+5x=180

6x=180

x=30

Значит, ∠BOD=30º, ∠AOD=5∙30=150º.

Ответ: 30º и 150º.

Могут ли смежные углы быть равными?

Да. Если смежные углы равны между собой, то, так как сумма смежных углов равна 180º, каждый из них равен половине суммы, то есть 90º.

Вывод:

угол, смежный с прямым, есть прямой угол.

Могут ли два смежных угла быть тупыми? Острыми?

Нет. Так как градусная мера тупого угла больше 90º, то сумма двух тупых углов больше 180º. А сумма смежных углов равна 180º.

Градусная мера острого угла меньше 90º. Значит, сумма двух острых углов меньше 180º.

Таким образом, в паре смежных углов один — тупой, другой — острый (или оба прямые).

Источник

Углы на плоскости можно объединять в типы по градусам (например, тип «острый угол» $0^circleq{x}<90^circ$). Также в геометрии выделяются и виды углов, куда входят составные углы-фигуры. В следующих уроках текущего раздела вас ждет подробное изучение подобных фигур и их свойств. А открывать тему мы будем, давая определение смежных углов.

❓Мы разберем:

— какие углы называются смежными;
— свойства смежных углов;
— и узнаем, чему равняется сумма смежных углов.

Определение смежных углов

Построим на плоскости развернутый угол $angle{ABC}$ и проведем через вершину угла $B$ луч $BD$. Рассмотрим полученную в результате построений фигуру.

Для углов $angle{ABD}$ и $angle{DBC}$ сторона $BD$ является общей. При этом, как мы можем заметить, другие стороны данных углов являются дополнительными лучами. Если два угла имеют такую ориентацию на плоскости, они называются смежными.

Дадим определение смежных углов:

Два угла называются смежными, если у них одна сторона общая, а другие стороны являются дополнительными лучами.   

Смежные углы и их свойства

Смежные углы — соседи, живущие через стенку.

Из свойств лучей нам известно, что вкупе дополнительные лучи образуют прямую. Таким образом, смежные углы — углы-соседи, «проживающие» на одной прямой. Эта геометрическая особенность подразумевает ряд интересных свойств, одно из которых — связь смежных с развернутыми углами.

Градусная мера смежных углов

Теорема о сумме смежных углов. Сумма смежных углов равняется $180^circ$.  

Доказательство

Пусть $angle{ABD}$ и $angle{DBC}$ — произвольные смежные углы. Докажем, что сумма смежных углов равняется $180^circ$. Заметим, что луч $BD$ проходит между сторонами развернутого угла $angle{ABC}$. Градусная мера развернутого угла равняется $180^circ$.

По аксиоме $A_8$ мы помним, что градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами. Значит:

$$angle{ABC}=angle{ABD}+angle{DBC}=180^circ$$

Градусная мера смежных углов в сумме составляет $180^circ$. Что и требовалось доказать.

Задача. Какова градусная мера смежных углов, если про смежные углы известно, что один их них в три раза больше другого?

Решение. Обозначим градусную меру меньшего угла как $x$. Если больший угол больше меньшего в три раза, его градусную меру можно обозначить как $3x$. Сумма смежных углов составляет $180^circ$. Пользуясь данным свойством, составим следующее уравнение:

$$x+3x=180^circ$$

Откуда получаем значение меньшего угла $x=45^circ$. Больший угол по условию больше в три раза и, следовательно, будет равняться $135^circ$. Градусная мера смежных углов найдена и составляет $45^circ$ и $135^circ$.

Ответ: $45^circ$, $135^circ$.

Сумма смежных углов: следствие из теоремы

Поскольку градусная мера смежных углов в сумме строго определяется как $180^circ$, это позволяет сделать вывод о том, что если два угла равны, то равны будут и смежные с ними углы. В геометрии бездоказательно выводы приводить нельзя, так что оформим данное наблюдение в виде следствия из теоремы и докажем его.

Итак:

Следствие из теоремы о сумме смежных углов. Если два угла равны, то смежные с ними углы также равны.

Доказательство

Рассмотрим два равных угла — $angle{1}$ и $angle{2}$. Если углы равны, равны их градусные меры. Обозначим градусную меру углов как $x$ и запишем следующее:

$$begin{cases}angle{1}=x^circ\angle{2}=x^circend{cases}$$

Сумма смежных углов равняется $180^circ$. Тогда смежный угол с $angle{1}$ равен «$180^circ-x^circ$». То же самое заключаем про градусную меру угла, смежного с $angle{2}$: «$180^circ-x^circ$». У равных углов $angle{1}$ и $angle{2}$ равные смежные углы. Что и требовалось доказать.

Острые, тупые и прямые углы

Рассмотрим три возможные ситуации на предмет типов углов по градусам, которые могут встретиться в составе смежных.


Один из углов — острый. Если градусная мера одного угла $0^circleq{angle{alpha}}<90^circ$, то второй угол в паре смежных получается тупым (в границах $90^circ<x<180^circ$).


Один из углов — тупой. Известно, что один из углов в паре $90^circ<angle{alpha}<180^circ$. В таком случае второй, с ним смежный, будет иметь градусную меру $0^circleq{x}<90^circ$.

Один из углов — прямой. Если один из углов имеет градусную меру $90^circ$, то второй также равняется $90^circ$. Угол, смежный с прямым, тоже будет прямым.  

Задача для самостоятельного решения

Не получается решить? Мы поможем: готовое решение задачи скрыто ниже. Можно, если что, подсмотреть. Только чуть-чуть!

Задача. Чему равен $angle{alpha}$, если $angle{ABE}=125^circ$ и $angle{DBC}=115^circ?$

Показать решение

Свернуть решение

Дано:

$angle{ABE}=125^circ$ $angle{DBC}=115^circ$

Найти:

$angle{alpha}$ — ?

Решение. Во-первых, найдем значения углов, смежных с $angle{ABE}$ и $angle{DBC}$. По теореме о сумме смежных углов находим следующие значения:

$$angle{EBC}=180^circ-angle{ABE}=55^circ\angle{ABD}=180^circ-angle{DBC}=65^circ$$

Развернутый угол $angle{ABC}$ состоит из суммы углов $angle{ABD}$, $angle{DBE}$ и $angle{EBC}$. Заметим, что $angle{DBE}$ и есть искомый по условию $angle{alpha}$. Градусная мера развернутого угла составляет $180^circ$, откуда получаем:

$$angle{ABC}=65^circ+angle{alpha}+55^circ=180^circ$$

Находим, что градусная мера $angle{alpha}=60^circ$.

Ответ: $60^circ$.

Источник

Смежные углы

Определение

Смежные углы — это два угла, у которых есть общая вершина и одна сторона, а две другие стороны являются продолжением друг друга и лежат на одной прямой.

Развёрнутый угл

 

Свойства и виды смежных углов в геометрии

  1. Так как две стороны смежных углов образуют прямую линию, то вместе они составляют развернутый угол. Его градусная мера составляет 180^circ. Следовательно — сумма смежных углов тоже равна (180^circ.)
  2. Если две прямые пересекаются, то они образуют две пары смежных углов: (angle1) и (angle2), (angle3) и (angle4), а также (angle1) и (angle3), ( angle2) и (angle4). При этом объединение пар, которые обозначены обозначениями 1 и 4, 2 и 3, представляют из себя вертикальные углы, а значит — они равны. Поэтому рассматривать можно только одну из пар смежных углов, другая окажется идентична по всем показателям.Виды смежных углов
  3. У смежных углов одинаковые синусы.
  4. Для косинусов и тангенсов тоже распространяется равенство, но их значения противоположны по знаку.
  5. Чтобы построить смежный угол уже заданному, требуется продлить одну из сторон существующего угла дальше вершины.

Примечание

В паре, если один угол тупой, то по правилу другой обязательно острый.

Если один из углов является прямым, то второй тоже прямой.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Как найти, чему равна сумма

Сумма смежных углов всегда составляет 180 градусов.

Отсюда следует формула:

(anglealpha+anglebeta=180^circ)

(anglealpha=180^circ-anglebeta)

(anglebeta=180^circ-anglealpha)

Смежных углы

Примеры решения задач

Задача №1

Дано: (anglealpha) и (anglebeta) — смежные, (anglebeta=60^circ).

Найти: чему равен (anglealpha).

Решение

Так как углы смежные, значит:

(anglealpha+anglebeta=180^circ.)

(anglealpha=180^circ-anglebeta.)

(anglealpha=180^circ-60^circ=120^circ.)

Ответ: (;anglealpha=120^circ).

Задача №2

Дано: ( anglealpha) и (anglebeta) — смежные, (anglealpha) на (30^circ) больше, чем (anglebeta.)

Найти: чему равны (anglealpha) и (anglebeta.)

Решение

Допустим,( anglebeta=x), тогда (anglealpha=x+30^circ.) 

Так как сумма смежных углов равна 180 градусов, то получаем уравнение, которое выглядит, как:

(x+x+30^circ=180^circ)

(2x=180^circ-30^circ)

(2x=150^circ)

(x=75^circ)

Значит, величина (anglebeta=75^circ.)

Чтобы найти (anglealpha), нужно выполнить стандартные вычисления согласно теореме о сумме:

(anglealpha=180^circ-anglebeta=180^circ-75^circ=105^circ.)

Ответ: (anglealpha=105^circ.)

Насколько полезной была для вас статья?

У этой статьи пока нет оценок.

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Текст с ошибкой:

Расскажите, что не так

Поиск по содержимому

Источник

Добавить комментарий