Как найти градусную меру каждого угла

Как найти градусную меру каждого угла

При рассмотрении основных составляющих измерения углов, следует изучить исходные геометрические сведения:

  • Угол.
  • Развернутый угол, неразвернутый угол.
  • Градус, секунда и минута.
  • Градусная мера.
  • Острый, прямой или тупой.

Геометрическая фигура, которая представляет собой точку — называется вершиной. А исходящие из этой вершины два луча, являются ее сторонами.

Измерение углов производится с помощью градусной меры угла. Углы измеряются таким же способом, как и отрезки, при помощи специальных единиц измерения – градусов.

Развернутый и обычный углы

Определение

Градус — геометрическая единица измерения, представляющая собой угол, который сравнивается с другими углами.

Равенство градуса таково: [frac{1}{180}] от развернутого угла. Исходя из этого, можно понять, что развернутый угол равен 180 градусам, а неразвернутый угол любой меньше 180 градусов.

Чему равна градусная мера угла

Определение

Градусная мера угла – это положительное число, которое показывает сколько раз градус и его части укладываются в данном углу.

А для их измерения используется инструмент – транспортир.

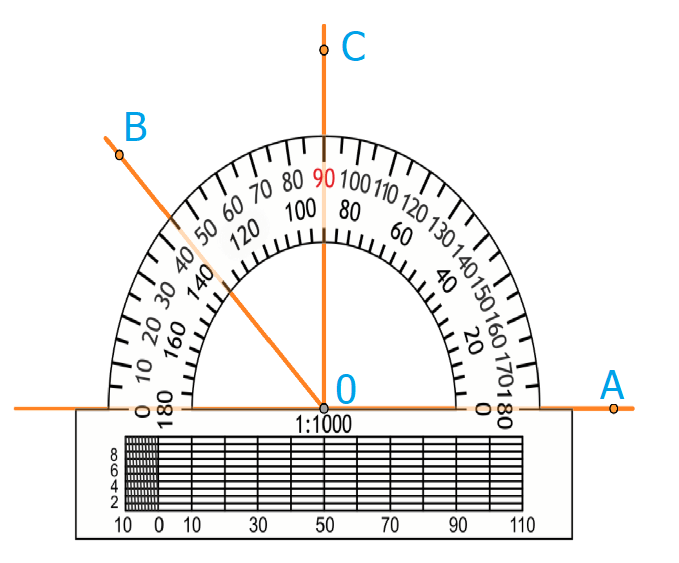
Транспортир

Рисунок 1. Транспортир

Транспортир используется следующим образом:

  • Совместить вершину угла с центром транспортира, при этом одна сторона угла должна пройти по линейке.
  • Штрих на шкале транспортира, через который пройдет 2-я сторона, покажет его градусную меру.

Как найти градусную меру угла

На рисунке угол АОВ = 135 градусов. Угол АОС = 90 градусов, угол ВОС = 45 градусов. Градусная мера углов равна сумме углов, на которые он разбит лучом, который проходит между его сторонами.

Отсюда следует, что величина угла AOB на рисунке 1 равна сумме величин углов AOC и [B O C: angle A O B=angle A O C+angle B O C].

Какие бывают названия углов можно понять, разобравшись со следующими обозначениями.

  • Минута – 1/60 часть градуса. Обозначается знаком ‘
  • Секунда – 1/60 часть минуты. Обозначают знаком»

Например: угол в 65 градусов, 35 минут,18 секунд записывается так: 75°45’28». Если градусная мера у нескольких углов одинаковая, эти углы считаются равными. Сравнить их можно по размерам – больше или меньше. Развернутый и неразвернутый углы.

Нет времени решать самому?

Наши эксперты помогут!

Градусная мера вписанного угла

Градусная мера вписанного угла равняется половине градусной меры дуги, опирающуюся на нее, и половине градусной меры угла, находящегося по центру, которая опирается на эту же дугу.

Вписанный угол равняется половине градусной меры дуги, на которую он опирается.

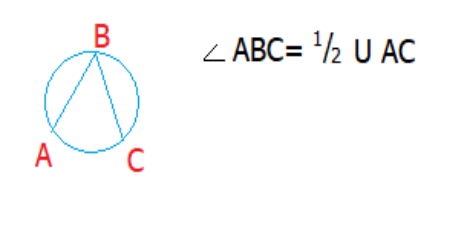
Вписанный угол
Рисунок.2.

АВ-хорда

ВС-хорда

В-точка окружности.

Углы также различаются несколькими типами:

  • Прямыми
  • Острыми
  • Тупыми

Равность прямого угла составляет — 90 градусов. Острый равен цифре меньше 90 градусов. А тупой же – больше 90 и меньше 180 градусов. В чем же заключается важность умения измерения углов и градусной меры в жизни? Оно пригодится в исследованиях, таких как: астрономия. Например, чтобы вычислить положение различных тел в космосе. Чтобы попрактиковаться, необходимо прочертить несколько неразвернутых углов, отличающихся друг от друга. Также важно потренироваться чертить развернутые. А еще, можно при помощи транспортира поупражняться, задавая случайные цифры, в правильности воспроизведения углов.

Существует еще такое понятие, как, биссектриса.

Определение

Биссектриса— луч, который исходит из вершины этого угла и делит его пополам.

Пример 1. Задача с биссектрисой и развернутым углом.

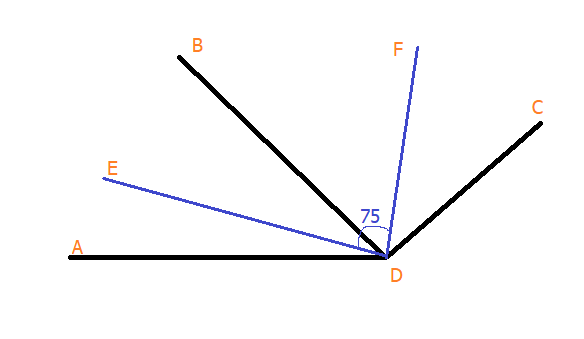
Биссектриса и развернутый угол

Рисунок.3.

Рис.3 Лучи DЕ и DF – это биссектрисы, которые соответствуют углам ADB и BDC.

Теперь нужно найти угол ADC, при этом угол EDF = 75°

Ответ. Угол EDF имеет по половинке от углов ADB и BDC, это значит, что EDF – это половина самого угла ADC. Теперь получили вычисление угол ADC = 75 умножить на 2 = 150°.

Ответ: 150°

Пример 2. Задача с биссектрисой и прямым углом.

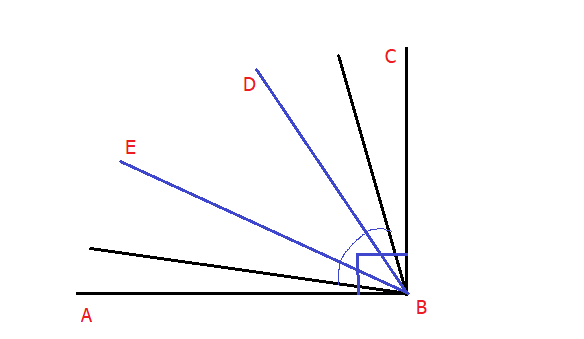
Биссектриса и прямой угол

Рисунок.4.

Рисунок 4.  По рисунку 4 видно, что угол АВС прямой, а углы ABE EBD DBC равны. Нужно найти угол, который образовали биссектрисы — ABE и DBC.

Решение будет таким: угол АВС прямой, и исходя из этого, можно понять что он равен 90°. Угол ЕВD=90/3=30°. Согласно правилу, углы ABE EBD DBC равны и поэтому каждый из них будет = 30°. Далее видно, что биссектриса любого из трех углов делит любой из этих углов на 2 угла, которые будут равны 15°. Обе половины углов ABE и DBC относятся к углу, который необходимо найти, то можно смело утверждать, что угол, который мы вычисляем, равен 30+15+15=60°.

Решение: 60°

Градусная мера углов треугольника

У любой геометрической фигуры, кроме округлой, имеются углы. При рассмотрении углов треугольника можно увидеть следующее: Сумма углов треугольника всегда равняется 180°. Если рассматривать прямоугольный треугольник, то можно увидеть, что один из углов равен 90°. А сумма двух других углов тоже равняется 90°.

Поэтому, если известно сколько градусов составляет один из острых углов треугольника, второй угол можно найти по формуле:

[angle a=90^{circ}-angle beta]

У прямоугольного треугольника один из углов прямой, соответственно, два других – острые.

Разъяснение острого угла таково: острым углом называется угол, значение которого составляет менее 90 градусов.

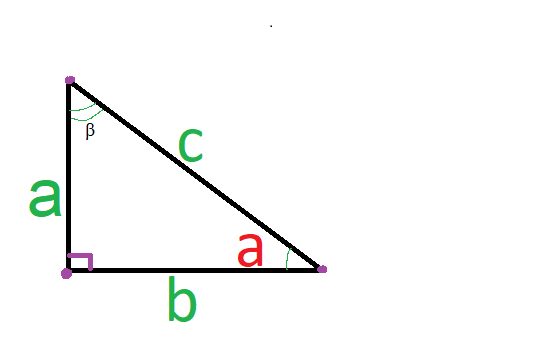
Прямоугольный треугольник

Рисунок 5. Прямоугольный треугольник

Исходя из вышесказанного, можно отметить, что прямоугольный треугольник — это геометрическая фигура, которая образовалась из трех отрезков. Эти отрезки соединяются между собой тремя точками. Углы у нее все внутренние, а один из них — прямой и равняется 90°. Пример —  рисунок 5.

Источник

Как определить градусную меру угла

Содержание:

  • Градусная мера угла — формулировка

    • Что отражает величина
    • Обозначение
  • Мера прямого угла
  • Мера развернутого угла
  • Мера тупого угла
  • Мера острого угла
  • Как найти градусную меру

    • Описание
  • Свойства углов

    • Мера больше нуля
    • Мера соответствует сумме градусных мер углов, разбиваемых лучом
    • Отложение угла от луча
  • Примеры нахождения меры угла

Градусная мера угла — формулировка

Градусная мера, в первую очередь, делает возможным измерение углов в геометрии.

Это число – показатель того, сколько градусов, минут и секунд содержится в данном угле. 

Примечание

Оно всегда больше нуля.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Что отражает величина

Количество градусов, минут и секунд, которые находятся между сторонами угла.

Обозначение

С помощью символов градусов ((º)), минут ((′)) и секунд ((″)).

В одном градусе содержится шестьдесят минут, в одной минуте — шестьдесят секунд.

Пример

(125º) (22′) (15″) (сто двадцать пять градусов, двадцать две минуты, пятнадцать секунд).

Примечание

Если настолько точно, как показано выше определить меру невозможно, пользуются дробной мерой градуса. Например, (123,5º).

Пример

Обозначение на чертеже:

120 градусов

Источник: https://www.budu5.com/

Мера прямого угла

 Прямой всегда равен (90º). В него входит (5400′) или (324000″). Является половиной развернутого.

Прямой угол

Источник: webmath.ru

Мера развернутого угла

Развернутый всегда равен (180º). Представляет собой прямую.

Развернутый угол

Источник: syl.ru

Мера тупого угла

Тупой всегда больше (90º), но меньше (180º).

Тупой угол

Источник: ru.solverbook.com

Мера острого угла

Острый всегда меньше (90º).

Примечание

Выглядит как нечто с острым концом, способным «уколоть».

Острый угол

Источник: impariamoninsieme.com

Как найти градусную меру

С помощью специального измерительного инструмента – транспортира. Он может быть сделан из разного материала (пластик, дерево, тонкий металл) и выглядеть по-разному. 

Виды транспортиров

Источник: infourok.ru

Разница только во внешнем виде. Устроены инструменты одинаково. Состоят из:

  • основания (часто со шкалой-линейкой),
  • дуги (полукруга) с двумя шкалами с градусной сеткой.

Примечание

Круглый транспортир имеет отличие в строении сетки: на нем указан полный круг в (360°).

Описание

Как производить измерения:

  • найти в середине транспортира специальную метку (это может быть отверстиештрихточка и т.п.), она проходит через «0º» на сетке дуги;
  • приложить инструмент этой отметкой к вершине угла, т.е. совместить «0º» с точкой вершины;
  • повернуть так, чтобы основание инструмента совпадало с одной из сторон угла;
  • следить, чтобы при повороте транспортира отметка «0º» не сходила с вершины;
  • проводим мысленно дугу справа налево (снизу, от основания, вверх по дуге) до второй стороны угла;
  • вторая сторона угла покажет на отметку с цифрой на шкале инструмента;
  • это и будет градусная мера данного угла.

Примечание

Если после того, как вы приложили центральную метку транспортира к вершине угла, одна из его сторон прошла через отметку «0º» на внешней шкале полукруга, то дальше измерение проводите только по внешней шкале. Если же сторона прошла через внутренний «0º», то пользуйтесь внутренней шкалой, на внешнюю уже смотреть не нужно.

Чтобы не сделать ошибку при измерении, воспользуйтесь образцом: https://yadi.sk/i/LVbtcivDBPzimw

Свойства углов

Градусная мера меньшего всегда меньше.

Если углы равны, то их градусные меры тоже равны (и наоборот: равные меры говорят о равенстве углов).

Ниже представлены основные свойства.

Мера больше нуля

Градусная мера любого угла всегда больше (0º).

Мера соответствует сумме градусных мер углов, разбиваемых лучом

Если угол разделен лучом на несколько углов, то его градусная мера  будет равна сумме всех этих углов.

Отложение угла от луча

От любого луча можно построить только один угол с градусной мерой меньше (180º).

Примеры нахождения меры угла

Задача №1

Луч ОС лежит внутри (∠АОВ). При этом (∠АОС = 36º), а (∠ВОС = 18º). Чему равен (∠АОВ)?

Решение

  1. Луч  делит исходный угол на два.
  2. Значит, чтобы найти (∠АОВ), нужно сложить меры углов, полученных при проведении луча.
  3. (36º+18º=54º.)

Задача №2

Луч (ОК) делит (∠АОВ) на два угла. Один из них больше другого в два раза и равен (60º). Чему равен (∠АОВ)?

Здесь, как и в задаче выше, решение будет простое. Специальная формула не требуется.

Решение:

  1. (∠AOK = 60º,)
  2. Известно также, что второй — вдвое меньше него, значит, (∠KOB = 60º:2 = 30º,)
  3. Мы знаем что (∠АОВ = ∠АОК+∠КОВ,)
  4. Нам остается только выполнить сложение:( 60º+30°= 90º). Это и есть величина (∠AOB.)
Источник
  1. Главная
  2. Справочники
  3. Справочник по геометрии 7-9 класс
  4. Начальные геометрические сведения
  5. Градусная мера угла

Нам известно, что при измерении отрезков, мы сравниваем измеряемый отрезок с отрезком, который принят за единицу измерения. Аналогично происходит измерение углов: чтобы измерить угол его сравнивают с углом, который принят за единицу измерения –  с  градусом.

Градус – это угол, который равен 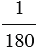части развернутого угла,обозначается знаком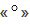

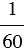часть градуса называется минутой, обозначается знаком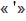

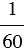часть минуты называется секундой, обозначается знаком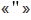

Пример: 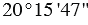(двадцать градусов пятнадцать минут сорок семь секунд)

Градусная мера угла – это положительное число, которое показывает, сколько раз градус и его части укладываются в данном угле.

Пример:

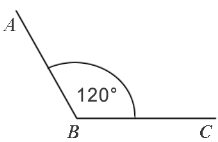
Градусная мера угла ABC равна 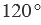. Говорят: “Угол ABC равен 120 градусам”. Пишут: .

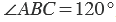Транспортир – это измерительный инструмент, который используется для измерения и построения углов. Состоит из линейки (прямолинейной шкалы) и полукруга (угломерной шкалы: внутренней и внешней), который разделен на градусы от 0 до .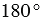

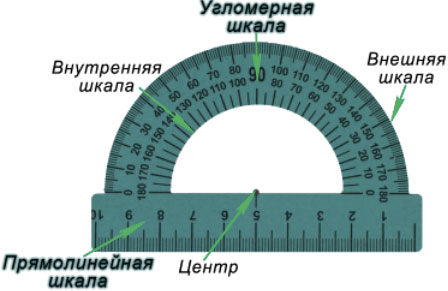
Для того чтобы измерить угол, необходимо совместить вершину угла с центром транспортира, при этом одна из сторон угла должна пройти через нулевое деление шкалы, тогда вторая сторона угла укажет градусную меру угла.

Пример: Измерим угол ABC, для этого совместим точку B с центром транспортира, и расположим транспортир так, чтобы сторона BC прошла через нулевое деление шкалы (обратите внимание отсчёт угла ведётся по той шкале, через нулевое деление которой пройдет одна из сторон угла: в нашем случае по внутренней шкале).

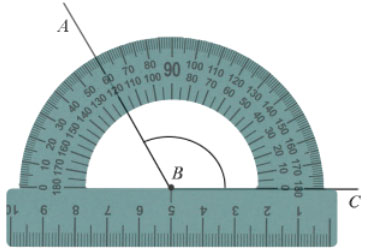
Вторая сторона при этом, как мы видим, проходит через деление шкалы 120, значит: .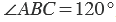

Свойства:

Основные типы углов:

  1. Острый угол – угол, градусная мера которого меньше 90°.

  1. Прямой угол – угол, градусная мера которого равна 90°.

  1. Тупой угол – угол, градусная мера которого больше 90°, но меньше 180°.

  1. Развернутый угол – угол, градусная мера которого равна 180°.

Советуем посмотреть:

Точки, прямые, отрезки

Провешивание прямой на местности

Луч

Угол

Равенство геометрических фигур

Сравнение отрезков

Сравнение углов

Длина отрезка

Единицы измерения длины, расстояний

Измерение углов на местности

Смежные углы

Вертикальные углы

Перпендикулярные прямые

Построение прямых углов на местности

Начальные геометрические сведения


Правило встречается в следующих упражнениях:

7 класс

Задание 56,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 67,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 17,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 226,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 346,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 465,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 646,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 896,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 14,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Источник

Анна Куличёва

Мастер

(1293)


10 лет назад

Положительное число, которое показывает, сколько раз градус и его части укладываются в данном угле, называется градусной мерой угла. Для измерения углов используется транспортир. равные углы имеют равные градусные меры. Меньший угол имеет меньшую градусную меру. Если луч делит угол на два угла, то градусная мера всего угла равна сумме градусных мер этих углов.

Источник: Новейший полный справочник школьника : 5-11 классы.

анжела денегаМастер (1646)

10 лет назад

Начертить 2 угла 100 и 60 градусов с общей вершиной, так чтобы они имелиобщую сторону и лежали по разные стороны от нее. Найти градусную меру угла , образованного двумя другими сторонами этих углов. Это надо сложить градусы обоих углов?

Naumenko

Высший разум

(856093)


10 лет назад

Читайте замечательный по языку и содержанию Кур Геометрии Никитина:
http://oldskola1.narod.ru/Nikitin/0013.htm

Чтобы более точно определять величину углов, применяются особые меры дуг и углов.

Для измерения дуг служат дуговые градусы, а для измерения углов — угловые.

Дуговым градусом, или градусом дуги, называется 1/360 часть окружности
(черт. 92).

VideoПросветленный (28010)

10 лет назад

чтож очередной раз пытаешься очистить свою черепную коробку от фекальных отложений…
так и быть 1балл в качестве поощрения

Источник

Угол – это фигура, образованная  точкой – вершиной угла и двумя различными лучами (полупрямыми), исходящими из этой точки, – сторонами угла.

Ugly12Угол можно обозначить одной буквой, которая называет его вершину. Но из одной точки могут быть построены несколько углов, тогда для их разграничения можно обозначать углы указанием их сторон, либо указанием  трёх точек: вершины и двух точек на сторонах угла.

Углы измеряются в градусах. Если взять развёрнутый угол и разделить его на 180 равных углов, то градусная мера каждого из этих углов называется градусом (его обозначение º). Итак, единица измерения угла – градус – это поворот луча на 1/360  полного оборота. Получается, полный оборот луча равен 360º. Один градус можно разделить на  60 минут (обозначение ′); одну минуту – соответственно на 60 секунд  (обозначение ″).

В зависимости от градусной меры углы можно классифицировать на:

острые (градусная мера менее 90º);

прямые (угол равен 90º);

тупые  (градусная меру более  90º);

развернутые  (угол равен 180º). Развёрнутым угол является, если стороны его являются дополнительными лучами (полупрямыми).

Получается, острый угол меньше прямого, а тупой угол больше прямого.

Ugly11Биссектриса угла – это луч, который исходит из его вершины, проходит между его сторонами и делит угол пополам.

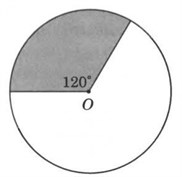
В геометрии существует понятие плоского угла. Плоский угол – это часть плоскости, которая ограничена двумя различными лучами, исходящими из одной точки. Эти лучи – стороны угла. Существуют два плоских угла с данными сторонами. Они называются дополнительными.

Если плоский угол является частью полуплоскости, то его градусной мерой будет градусная мера обычного угла с теми же сторонами. Если плоский угол содержит полуплоскость, то его градусная мера равна 360˚ – α, где α – градусная мера дополнительного плоского угла.

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Остались вопросы?

Задайте свой вопрос и получите ответ от профессионального преподавателя.

Источник

Добавить комментарий