Алгебра и начала математического анализа, 10 класс
Урок №29. Радианная мера угла
Перечень вопросов, рассматриваемых в теме:
1) Понятие тригонометрической окружности;
2) Поворот точки вокруг начала координат;
3) Длина дуги окружности и площадь кругового сектора.
Глоссарий по теме
Окружность – это замкнутая линия, все точки которой равноудалены от центра.
Радиус окружности – отрезок, соединяющий её центр с любой лежащей на окружности точкой.
Круг – часть плоскости, ограниченная окружностью.
Дуга окружности – кривая линия, лежащая на окружности и ограниченная двумя точками.
Круговой сектор – часть круга, ограниченная двумя радиусами.
Угол в 1 радиан – центральный угол, опирающийся на дугу, равную по длине радиусу окружности.
Основная литература:
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл.– М.: Просвещение, 2014.
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Учебно-методический комплект: Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл.– М.: Просвещение, 2014.
Теоретический материал для самостоятельного изучения
На уроках геометрии мы с вами изучали окружность, её элементы, свойства. Повторим понятие окружности. Это замкнутая линия, все точки которой равноудалены от центра.
Радиусом окружности называется отрезок, соединяющий её центр с любой лежащей на окружности точкой.
На окружности можно выделить дугу. А если рассмотреть круг – часть плоскости, ограниченной окружностью – то можно выделить круговой сектор.
«Окружность бесконечно большого круга и прямая линия – одно и то же» Г. Галилей
Действительно, и окружность и прямая – бесконечны. Рассмотрим окружность радиуса, равному 1 единичному отрезку, в прямоугольной системе координат хОу с центром в начале координат. Такую окружность называют единичной или тригонометрической. (рис.1)

Длина этой окружности (в предыдущей задаче велотрека), как мы помним из уроков геометрии,  . А учитывая, что R=1,
. А учитывая, что R=1,  , осями координат она поделена на четыре дуги, которые находятся соответственно в I, II, III и IV координатных четвертях.
, осями координат она поделена на четыре дуги, которые находятся соответственно в I, II, III и IV координатных четвертях.
Вычислите длину каждой дуги.
Ответ. длина каждой дуги равна  части окружности или
части окружности или 
Длина полуокружности равна  А так как образовался развернутый угол, то
А так как образовался развернутый угол, то  180
180 .
.
Рассмотрим дугу, равную по длине радиусу единичной окружности. Полученный центральный угол РОМ равен длине дуги МР=R.
 рис.3
рис.3
Определение. Углом в 1 радиан называется центральный угол, опирающийся на дугу, равную по длине радиусу окружности.
Обозначается 1рад.
 ;
;

 α рад=(180/π α)° (1)
α рад=(180/π α)° (1)
Длину дуги l окружности радиуса R (рис.4)

можно вычислять по формуле (3)
(3)
А площадь S кругового сектора радиуса R и дугой  рад (рис.5)
рад (рис.5)

находят по формуле:  , где
, где (4)
(4)
Вернёмся к единичной окружности в координатной плоскости.
Каждая точка этой окружности будет иметь координаты х и у такие, что выполняются неравенства -1≤ х ≤ 1; -1≤ у ≤ 1.
Введём понятие поворота точки. (рис.2)

- Пусть
 Тогда точка А(1;0) будет двигаться по единичной окружности против часовой стрелки. Она пройдёт путь α рад от точки А(1;0) до точки В. Говорят, точка В получена из точки А поворотом на угол
Тогда точка А(1;0) будет двигаться по единичной окружности против часовой стрелки. Она пройдёт путь α рад от точки А(1;0) до точки В. Говорят, точка В получена из точки А поворотом на угол 
- Пусть
 точка А(1;0) будет двигаться по единичной окружности по часовой стрелки . Она пройдёт путь α рад от точки А(1;0)до точки С. Говорят, точка С получена из точки А поворотом на угол – α.
точка А(1;0) будет двигаться по единичной окружности по часовой стрелки . Она пройдёт путь α рад от точки А(1;0)до точки С. Говорят, точка С получена из точки А поворотом на угол – α.
При повороте на 0 рад точка остаётся на месте.
Давайте рассмотрим такой пример:
при повороте точки М(1;0) на угол  получается точка N (0;1). В эту же точку можно попасть из точки М(1;0) при повороте на
получается точка N (0;1). В эту же точку можно попасть из точки М(1;0) при повороте на
угол  (рис.6)
(рис.6)

(рис.6)
Примеры и разбор решения заданий тренировочного модуля
Пример 1.
Найти градусную меру угла, равного  рад.
рад.
Решение: Используя формулу (1),
находим  .
.
Так как  , то
, то  рад, тогда
рад, тогда  (2)
(2)
Ответ:  .
.
Пример 2. Найти радианную меру угла, равного 60 .
.
Решение:
Вычисляем по формуле (2):  рад
рад
 рад
рад
При обозначении мер угла, наименование «рад» опускают.
Ответ:  рад,
рад,  рад.
рад.
Пример 3. Найти длину дуги окружности радиуса 6 см, если её радианная мера  .
.
Решение: Используя формулу (3),
получим: 
Ответ:  .
.
Пример 4. Найти площадь сектора, если радиус окружности 10 м, а радианная мера центрального угла  .
.
Решение:
По формуле (4) вычисляем 
Ответ: 45  м2
м2
Пример 5. Найти координаты точки М, полученной из точки N(1;0) поворотом на угол, равный  .
.
Решение: Абсцисса точки М равна отрезку ОК, ордината отрезку ОТ=МК. Так как  то
то
прямоугольный равнобедренный треугольник ОМК имеет равные катеты и гипотенузу ОМ=R=1. По теореме Пифагора можно найти длины катетов. Они равны  Учитывая, что точка М находится в I координатной четверти, её координаты положительны.
Учитывая, что точка М находится в I координатной четверти, её координаты положительны. 
На окружности можно найти координаты любой точки.
Ответ: 
Курс тригонометрии. Как найти радианную и градусную меру угла
При рассмотрении основных составляющих измерения углов, следует изучить исходные геометрические сведения:
- Угол.
- Развернутый угол, неразвернутый угол.
- Градус, секунда и минута.
- Градусная мера.
- Острый, прямой или тупой.
Геометрическая фигура, которая представляет собой точку — называется вершиной. А исходящие из этой вершины два луча, являются ее сторонами.
Измерение углов производится с помощью градусной меры угла. Углы измеряются таким же способом, как и отрезки, при помощи специальных единиц измерения – градусов.
Определение
Градус — геометрическая единица измерения, представляющая собой угол, который сравнивается с другими углами.
Равенство градуса таково: [frac{1}{180}] от развернутого угла. Исходя из этого, можно понять, что развернутый угол равен 180 градусам, а неразвернутый угол любой меньше 180 градусов.
Чему равна градусная мера угла
Определение
Градусная мера угла – это положительное число, которое показывает сколько раз градус и его части укладываются в данном углу.
А для их измерения используется инструмент – транспортир.
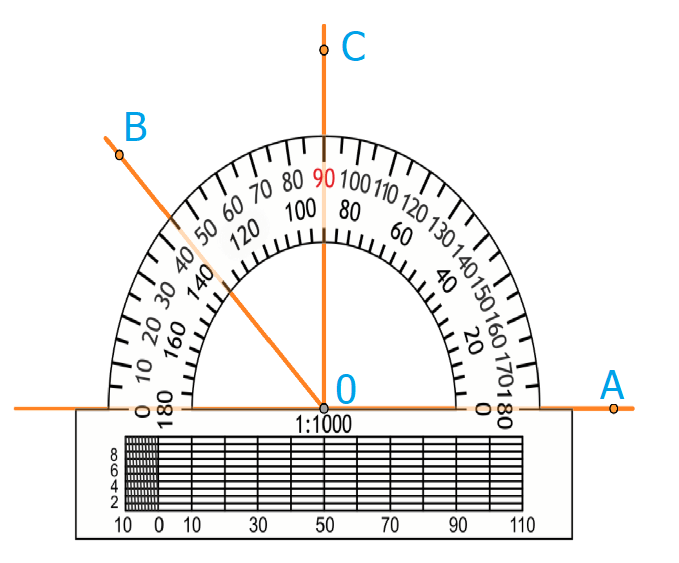
Транспортир используется следующим образом:
- Совместить вершину угла с центром транспортира, при этом одна сторона угла должна пройти по линейке.
- Штрих на шкале транспортира, через который пройдет 2-я сторона, покажет его градусную меру.
Как найти градусную меру угла
На рисунке угол АОВ = 135 градусов. Угол АОС = 90 градусов, угол ВОС = 45 градусов. Градусная мера углов равна сумме углов, на которые он разбит лучом, который проходит между его сторонами.
Отсюда следует, что величина угла AOB на рисунке 1 равна сумме величин углов AOC и [B O C: angle A O B=angle A O C+angle B O C].
Какие бывают названия углов можно понять, разобравшись со следующими обозначениями.
- Минута – 1/60 часть градуса. Обозначается знаком ‘
- Секунда – 1/60 часть минуты. Обозначают знаком»
Например: угол в 65 градусов, 35 минут,18 секунд записывается так: 75°45’28». Если градусная мера у нескольких углов одинаковая, эти углы считаются равными. Сравнить их можно по размерам – больше или меньше. Развернутый и неразвернутый углы.
Нет времени решать самому?
Наши эксперты помогут!
Градусная мера вписанного угла
Градусная мера вписанного угла равняется половине градусной меры дуги, опирающуюся на нее, и половине градусной меры угла, находящегося по центру, которая опирается на эту же дугу.
Вписанный угол равняется половине градусной меры дуги, на которую он опирается.
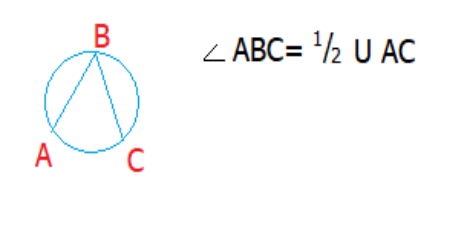
АВ-хорда
ВС-хорда
В-точка окружности.
Углы также различаются несколькими типами:
- Прямыми
- Острыми
- Тупыми
Равность прямого угла составляет — 90 градусов. Острый равен цифре меньше 90 градусов. А тупой же – больше 90 и меньше 180 градусов. В чем же заключается важность умения измерения углов и градусной меры в жизни? Оно пригодится в исследованиях, таких как: астрономия. Например, чтобы вычислить положение различных тел в космосе. Чтобы попрактиковаться, необходимо прочертить несколько неразвернутых углов, отличающихся друг от друга. Также важно потренироваться чертить развернутые. А еще, можно при помощи транспортира поупражняться, задавая случайные цифры, в правильности воспроизведения углов.
Существует еще такое понятие, как, биссектриса.
Определение
Биссектриса— луч, который исходит из вершины этого угла и делит его пополам.
Пример 1. Задача с биссектрисой и развернутым углом.
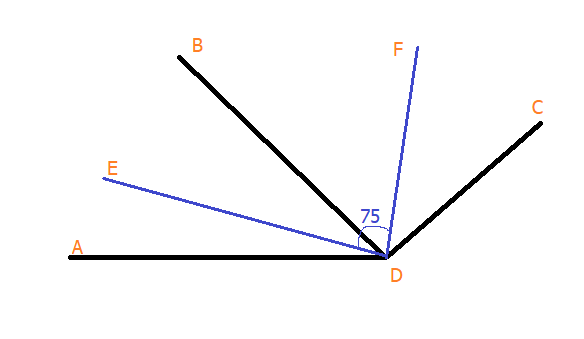
Рис.3 Лучи DЕ и DF – это биссектрисы, которые соответствуют углам ADB и BDC.
Теперь нужно найти угол ADC, при этом угол EDF = 75°
Ответ. Угол EDF имеет по половинке от углов ADB и BDC, это значит, что EDF – это половина самого угла ADC. Теперь получили вычисление угол ADC = 75 умножить на 2 = 150°.
Ответ: 150°
Пример 2. Задача с биссектрисой и прямым углом.
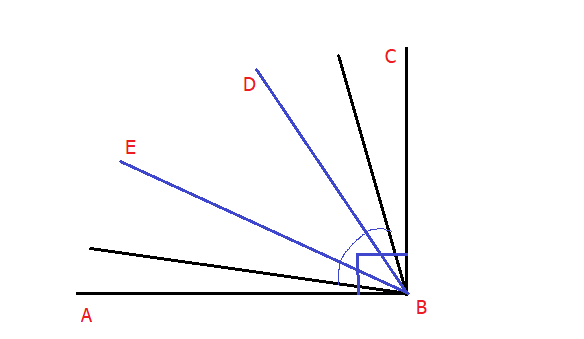
Рисунок 4. По рисунку 4 видно, что угол АВС прямой, а углы ABE EBD DBC равны. Нужно найти угол, который образовали биссектрисы — ABE и DBC.
Решение будет таким: угол АВС прямой, и исходя из этого, можно понять что он равен 90°. Угол ЕВD=90/3=30°. Согласно правилу, углы ABE EBD DBC равны и поэтому каждый из них будет = 30°. Далее видно, что биссектриса любого из трех углов делит любой из этих углов на 2 угла, которые будут равны 15°. Обе половины углов ABE и DBC относятся к углу, который необходимо найти, то можно смело утверждать, что угол, который мы вычисляем, равен 30+15+15=60°.
Решение: 60°
Градусная мера углов треугольника
У любой геометрической фигуры, кроме округлой, имеются углы. При рассмотрении углов треугольника можно увидеть следующее: Сумма углов треугольника всегда равняется 180°. Если рассматривать прямоугольный треугольник, то можно увидеть, что один из углов равен 90°. А сумма двух других углов тоже равняется 90°.
Поэтому, если известно сколько градусов составляет один из острых углов треугольника, второй угол можно найти по формуле:
[angle a=90^{circ}-angle beta]
У прямоугольного треугольника один из углов прямой, соответственно, два других – острые.
Разъяснение острого угла таково: острым углом называется угол, значение которого составляет менее 90 градусов.
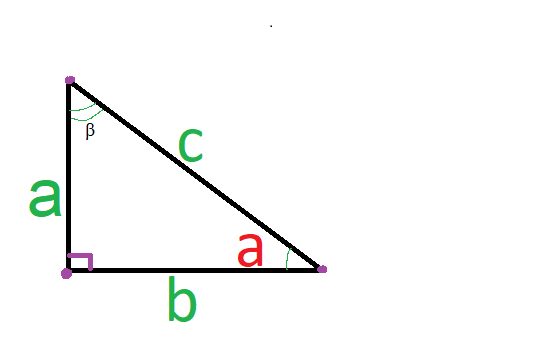
Исходя из вышесказанного, можно отметить, что прямоугольный треугольник — это геометрическая фигура, которая образовалась из трех отрезков. Эти отрезки соединяются между собой тремя точками. Углы у нее все внутренние, а один из них — прямой и равняется 90°. Пример — рисунок 5.
Углы в математике (а также в тригонометрии и физике) высчитываются и измеряются в градусах или в радианах. Важно понимать и определять связь между этими единицами измерения, и переводить их из одной в другую. Понимание и определение этой связи позволяет оперировать углами и перевести градусы в радианы, а также осуществить перевод из радиан в градусы с помощью специальной тригонометрической формулы – формулы перевода градусов в радианы. В данной статье мы разберемся, зачем все это нужно конвертировать (и что делать с конвертируемым), выведем формулу для перевода градусов в радианы и обратно – из радианов в градусы, а также разберем несколько примеров из практики по конвертации.
Связь между градусами и радианами
Что такое радиан? Радиан вместе с градусом является выражением угловой меры: это величина, которая используется для измерения плоских углов. Поэтому, когда говорят о таблице градусов и радиан, то имеют в виду таблицу, в которой представлены соответствия угловых градусов радианам (что позволяет вам не находить и не считать самостоятельно на калькуляторе, к примеру).
Как перевести радианы в градусы — есть формула? Для нахождения связи между градусами и радианами, необходимо узнать, сколько будет градусная и ридианная (радиальная) мера какого-либо угла (и для этого нам не нужно пользоваться каким-либо переводчиком онлайн). Например, возьмем центральный угол, который опирается на диаметр окружности радиуса r. Чтобы вычислить радианную меру этого угла, необходимо рассчитать определенные данные: длину дуги разделить на длину радиуса окружности. Рассматриваемому углу соответствует длина дуги, равная половине длины окружности π·r. Разделим длину дуги на радиус и получим радианную меру угла: π·rr=π рад.
Итак, рассматриваемый угол равен π радиан. С другой стороны, это развернутый угол, равный 180°. Следовательно, 180°=π рад.
Связь между радианами и градусами выражается следующей полной формулой
π радиан =180°
Формулы перевода из градусов в радианы и наоборот
Как перевести градусы в радианы не более, чем за минуту? Что делать с координатами в градусах, если нужны в радианах? Из содержания формулы, полученной выше, можно вывести другие формулы для перевода углов из радианов в градусы и обратно из градусов в радианы (взаимно преобразовывать и пересчитывать).
Как онлайн найти градусную меру угла и сделать пересчет? Выразим 1 радиан в градусах. Для этого разделим левую и правую части радиуса на пи.
1 рад=180π° – град. мера угла в 1 радиан равна 180π.
Также можно выразить один градус в радианах. Чему равен 1 радиан и во что он будет переходить? Вот простой расчет.
1°=π180рад
Можно произвести приблизительные вычисления величин угла в радианах и наоборот. Для этого возьмем значения числа π с точностью до десятитысячных и подставим в полученные формулы.
1 рад=180π°=1803,1416°=57,2956°
Значит, в одном радиане примерно 57 градусов
1°=π180рад=3,1416180рад=0,0175 рад
Один градус содержит 0,0175 радиана.
По какой формуле перевести радианы в градусы?
x рад=х·180π°
Чтобы перевести угол из радианов в градусы, нужно значение угла в радианах умножить на 180 и разделить на пи.
Примеры перевода градусов в радианы и радианов в градусы
Рассмотрим пример, как перевести градусы в радианы по формуле.
Конечно, в интернете это все может считаться за секунду, но у самостоятельного подсчета другие преимущества.
Пусть α=3,2 рад. Нужно узнать градусную меру этого угла.
Применим формулу перехода от радианов к градусам и получим:
3,2 рад=3,2·180π°≈3,2·1803,14°≈5763,14°≈183,4°
Аналогично можно получить формулу перевода в радианы из градусов.
y°=y·π180рад
Переведем 47 градусов в радианы.
Согласно формуле, умножим 47 на пи и разделим на 180.
47°≈47·3,14180≈0,82 рад
![]()
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Материалы урока
Прежде, чем приступить к рассмотрению новой темы, давайте вспомним, что градусом называют величину центрального угла, которому соответствует 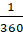 часть окружности. Градусная мера угла – это положительное число, которое показывает, сколько раз градус и его части укладываются в измеряемом угле.
часть окружности. Градусная мера угла – это положительное число, которое показывает, сколько раз градус и его части укладываются в измеряемом угле.
А углы можно измерять только в градусах? Сегодня на уроке мы рассмотрим ещё одну единицу измерения углов.
Давайте изобразим окружность с центром в точке 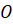 и радиусом
и радиусом  . Затем проведём вертикальную прямую, которая касается окружности в точке
. Затем проведём вертикальную прямую, которая касается окружности в точке 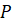 . Эту прямую мы будем считать числовой осью с началом отсчёта в точке
. Эту прямую мы будем считать числовой осью с началом отсчёта в точке 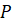 . Положительным направлением на прямой будем считать направление вверх. За единичный отрезок на числовой оси возьмём радиус окружности.
. Положительным направлением на прямой будем считать направление вверх. За единичный отрезок на числовой оси возьмём радиус окружности.
Отметим на прямой несколько точек:  и
и 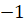 ,
,  и
и 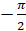 ,
, 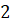 и
и 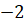 ,
, 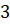 и
и 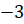 ,
, 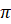 и
и 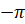 .
.
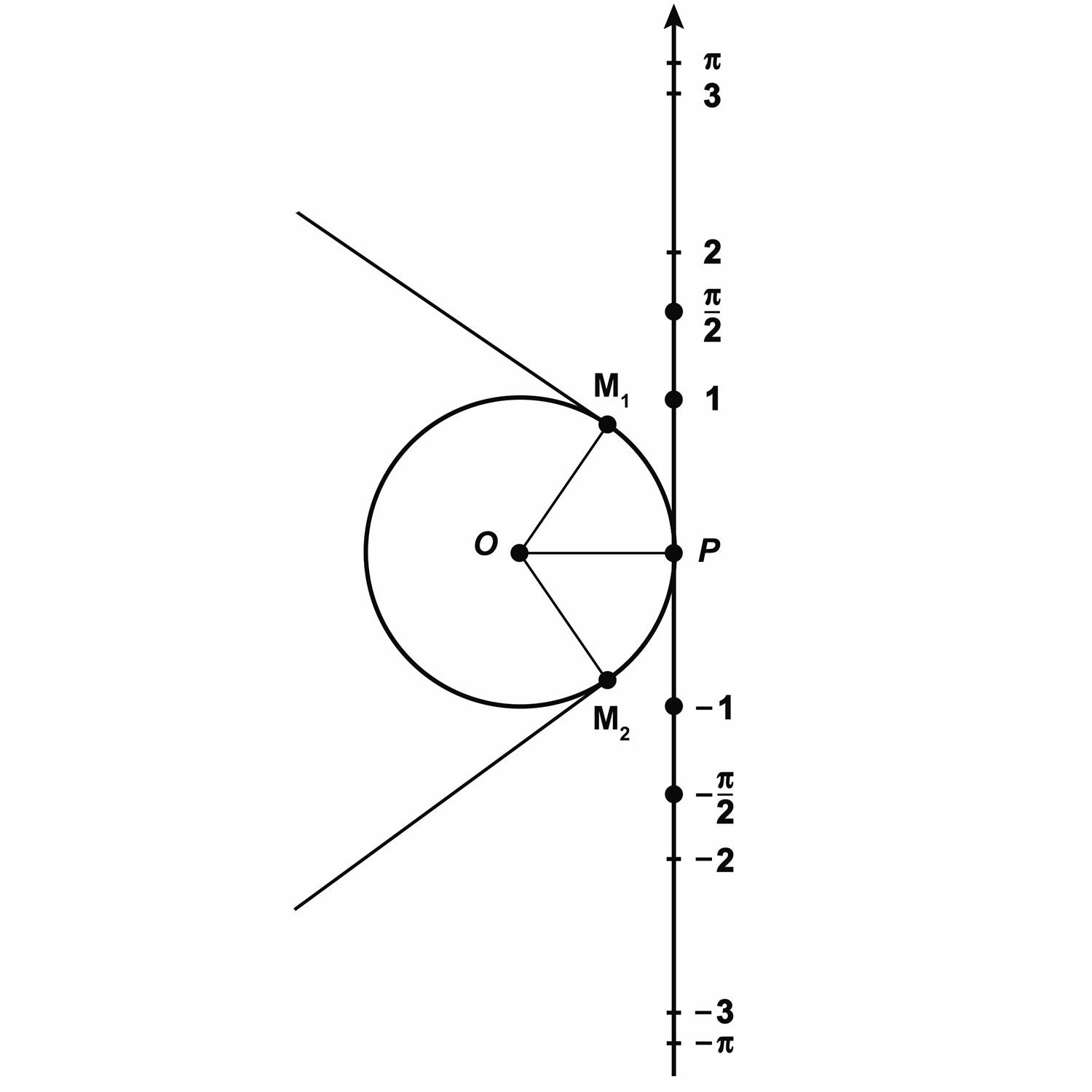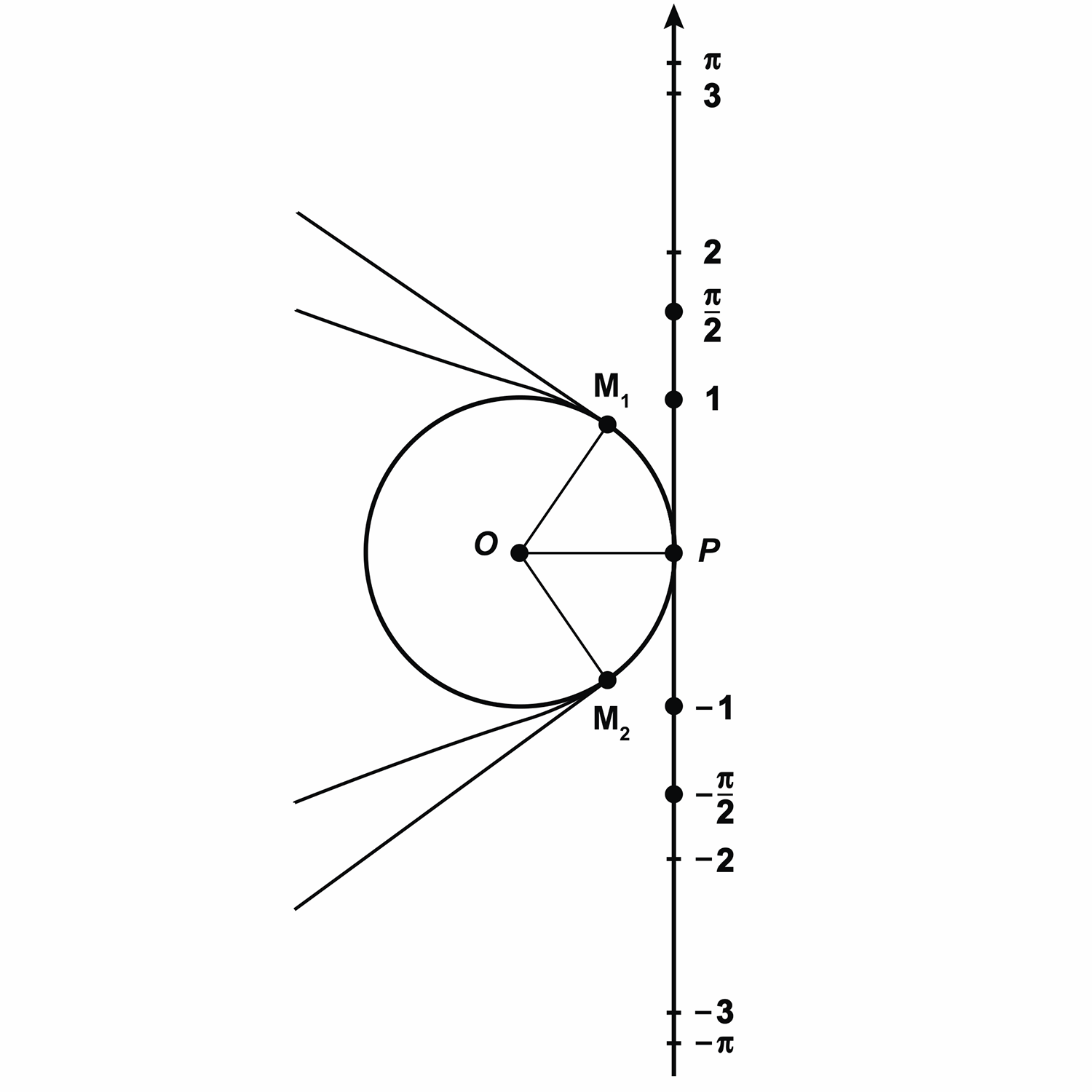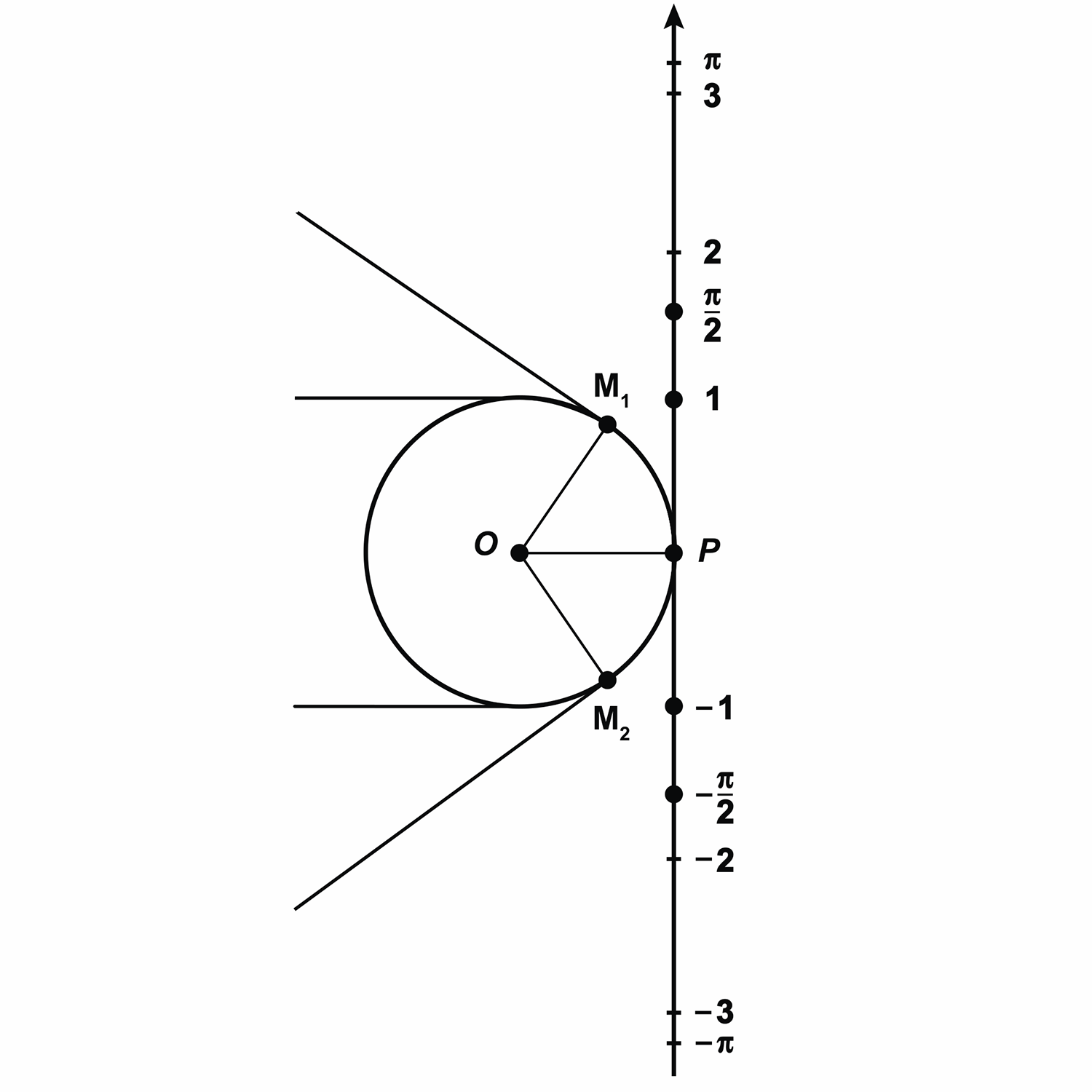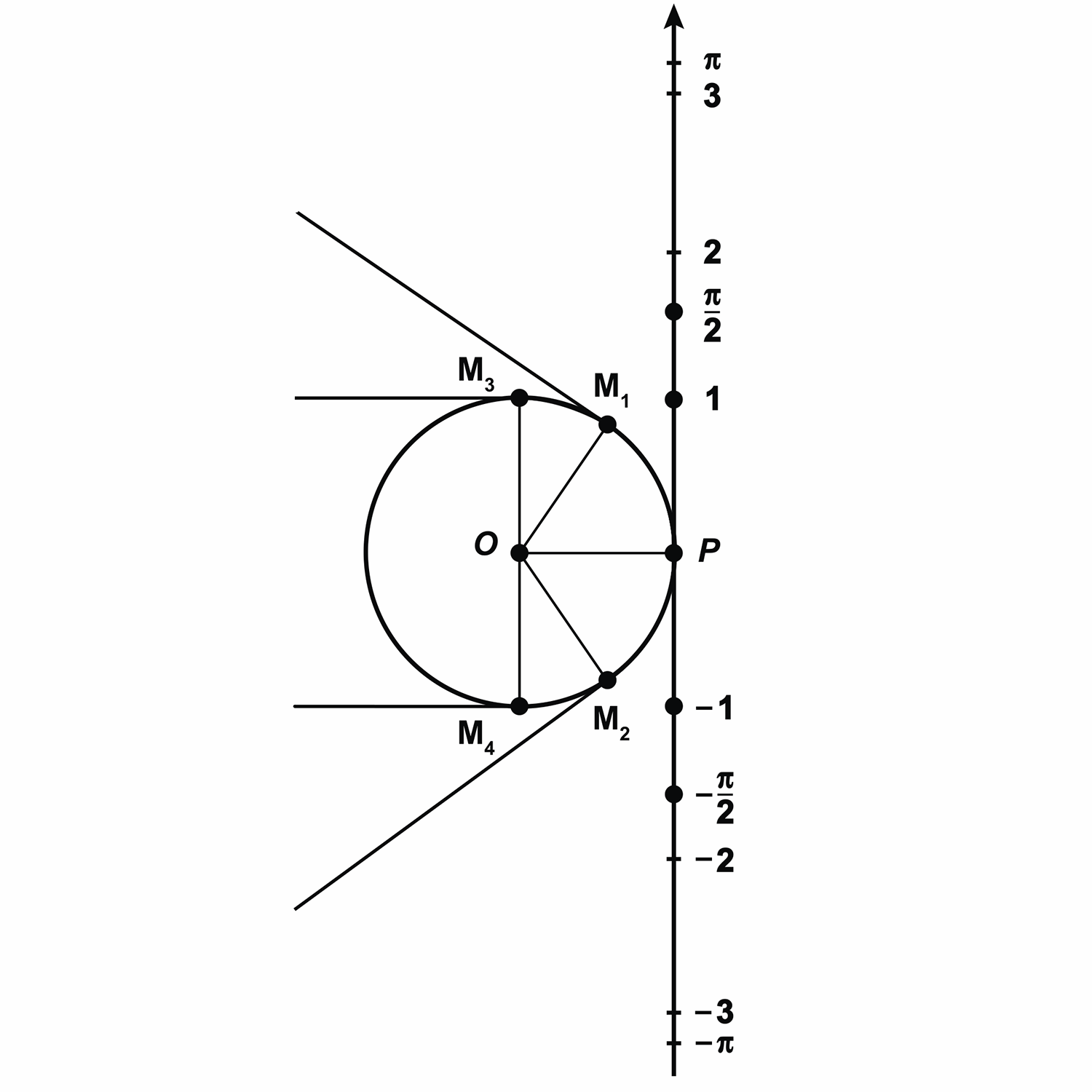
Теперь представим нашу прямую в виде нерастяжимой нити, которая закреплена на окружности в точке 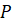 . Будем наматывать нить на окружность. При этом точки на числовой прямой с координатами
. Будем наматывать нить на окружность. При этом точки на числовой прямой с координатами  ,
, 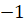 ,
,  ,
, 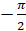 перейдут соответственно в точки окружности
перейдут соответственно в точки окружности 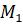 ,
, 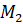 ,
, 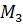 ,
, 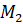 . При этом длина дуги
. При этом длина дуги 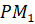 равна
равна  , длина дуги
, длина дуги 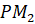 равна
равна 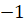 , длина дуги
, длина дуги 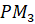 равна
равна  , длина дуги
, длина дуги 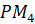 равна
равна 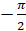 .
.
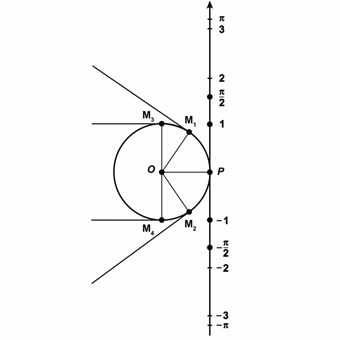
Получается, что каждой точке прямой ставится в соответствие некоторая точка окружности.
Так, точке прямой с координатой  ставится в соответствие точка
ставится в соответствие точка 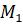 . А значит, угол
. А значит, угол 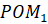 можем считать единичным? Да, и его мерой мы будем измерять другие углы. Например, угол
можем считать единичным? Да, и его мерой мы будем измерять другие углы. Например, угол 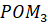 следует считать равным
следует считать равным  , а угол
, а угол 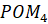 равным
равным 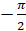 .
.
А где используют такой способ измерения углов? Такой способ измерения углов широко используется в математике и физике. Говорят, что углы измеряются в радианной мере.
Единичный угол 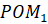 называют углом в один радиан. Записывают так:
называют углом в один радиан. Записывают так:  рад.
рад.
И напомним, что длина дуги 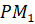 равна радиусу нашей окружности.
равна радиусу нашей окружности.
Сейчас давайте рассмотрим окружность радиуса 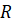 . И отметим на ней дугу
. И отметим на ней дугу 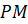 , равную длине радиуса окружности, и угол
, равную длине радиуса окружности, и угол 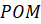 .
.

И такой угол называется углом в один радиан? Верно.
Запомните! Центральный угол, опирающийся на дугу, длина которой равна радиусу окружности, называется углом в один радиан.
Интересно, а скольким градусам равен угол в один радиан? Давайте найдём градусную меру угла в один радиан. Мы знаем из курса геометрии, что дуге длиной 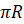 , то есть полуокружности, соответствует центральный угол, равный
, то есть полуокружности, соответствует центральный угол, равный 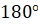 . Следовательно, дуге окружности длиной
. Следовательно, дуге окружности длиной 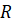 соответствует угол в
соответствует угол в 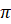 раз меньший.
раз меньший.
Выше мы назвали такой угол углом в один радиан, а значит, можем записать, что 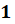 рад
рад 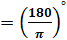 .
. 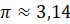 , тогда
, тогда 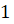 рад
рад 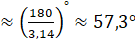 .
.
Если угол содержит 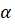 рад, то
рад, то 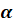 рад
рад 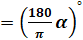 . Эту формулу называют формулой перехода от радианной меры к градусной.
. Эту формулу называют формулой перехода от радианной меры к градусной.
Давайте с вами найдём градусную меру угла, равного  рад. Для этого воспользуемся формулой перехода от радианной меры к градусной. Подставим
рад. Для этого воспользуемся формулой перехода от радианной меры к градусной. Подставим  вместо
вместо 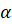 :
: 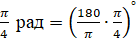 . Сократим на
. Сократим на 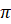 и на
и на 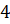 . И в результате получим
. И в результате получим 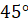 .
.
Можно ли, наоборот, перейти от градусной меры к радианной? Конечно, можно, но такой переход будет чуть сложнее. Так как угол в 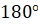 равен
равен  рад, то
рад, то 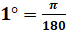 рад. Тогда
рад. Тогда 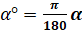 рад. Такую формулу называют формулой перехода от градусной меры к радианной.
рад. Такую формулу называют формулой перехода от градусной меры к радианной.
Найдём радианную меру угла, равного 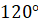 . Воспользуемся формулой перехода от градусной меры к радианной. Подставим
. Воспользуемся формулой перехода от градусной меры к радианной. Подставим 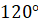 вместо
вместо 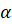 :
: 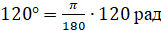 . Сократим
. Сократим 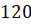 и
и 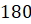 на
на 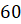 . И в результате получим
. И в результате получим 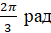 .
.
Обратите внимание, что при обозначении меры угла в радианах слово «радиан» обычно не пишут: 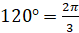 . При этом обозначение градуса в записи меры угла пропускать нельзя.
. При этом обозначение градуса в записи меры угла пропускать нельзя.
В следующей таблице представлены углы в градусной и радианной мере, с которыми мы будем встречаться чаще всего.

Отметим, что радианная мера углов позволяет значительно упростить многие формулы в математике, физике, механике. В частности, радианная мера угла удобна для вычисления длины дуги окружности. Так, выше мы выяснили, что угол в  рад стягивает дугу, длина которой равна радиусу
рад стягивает дугу, длина которой равна радиусу 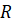 , а значит, угол в
, а значит, угол в 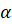 рад стягивает дугу длиной:
рад стягивает дугу длиной: 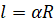 . Если
. Если 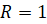 , то эта формула принимает совсем простой вид:
, то эта формула принимает совсем простой вид: 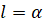 , то есть длина дуги равна величине центрального угла, стягиваемого этой дугой.
, то есть длина дуги равна величине центрального угла, стягиваемого этой дугой.
Сейчас, прежде чем приступить к выполнению заданий, мы докажем, что площадь кругового сектора радиуса 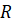 , образованного углом в
, образованного углом в 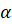 рад, равна
рад, равна 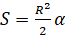 , где
, где 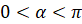 .
.
Докажем это. Известно, что площадь круга вычисляется по формуле: 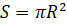 . Площадь полукруга, то есть кругового сектора в
. Площадь полукруга, то есть кругового сектора в 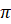 рад:
рад: 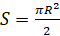 . Тогда площадь сектора в
. Тогда площадь сектора в  рад в
рад в 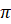 раз меньше, то есть
раз меньше, то есть 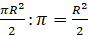 . Следовательно, площадь сектора в
. Следовательно, площадь сектора в 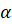 рад равна
рад равна 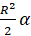 .
.
Ну а сейчас давайте выполним несколько заданий.
Первое задание. Найдите градусную меру угла, выраженную в радианах: а) 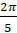 ; б)
; б) 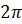 ; в)
; в) 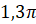 ; г)
; г) 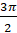 ; д)
; д) 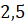 .
.
Решение.
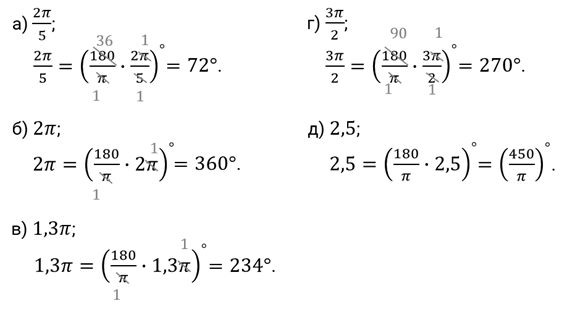
Второе задание. Найдите радианную меру угла, выраженного в градусах: а) 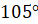 ; б)
; б) 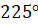 ; в)
; в) 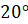 ; г)
; г) 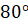 .
.
Решение.
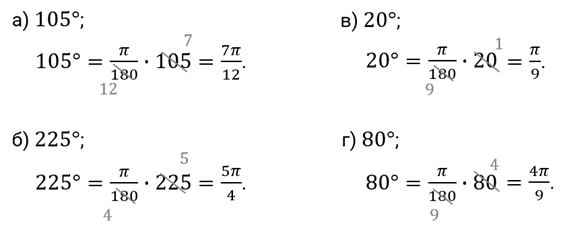
Следующее задание. Чему равен радиус окружности, если дуге длиной 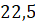 см соответствует центральный угол в
см соответствует центральный угол в 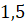 рад?
рад?
Решение.

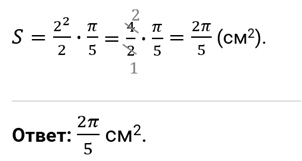
И ещё одно задание. Дуге кругового сектора соответствует угол, равный  рад. Чему равна площадь сектора, если радиус круга равен
рад. Чему равна площадь сектора, если радиус круга равен 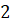 см?
см?
Решение.
Ну а сейчас немного истории.
Впервые радиан как единица измерения был использован английским математиком Роджером Котсом в 1713 году. Он считал, что радиан является наиболее естественной единицей измерения углов. Термин «радиан» впервые появился в печати в 1873 году в экзаменационных билетах Университета Квинса в Белфасте, составленных британским инженером и физиком Джеймсом Томсоном.
В 1960 году XI Генеральной конференцией по мерам и весам радиан был принят в качестве единицы измерения плоских углов в Международной системе единиц (СИ).

