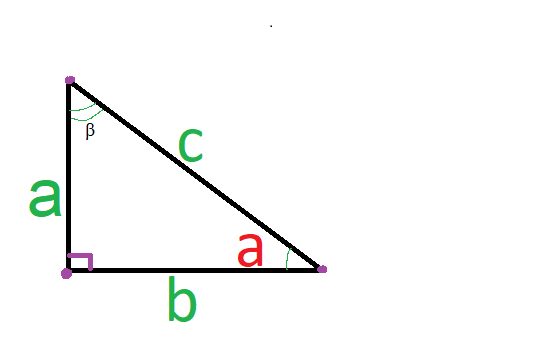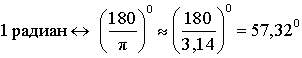Дорогие друзья! Мы уже рассматривали с вами задачи на вписанный в окружность угол. Если вы давно не решали подобных заданий, и не помните свойство вписанного угла, то обязательно ознакомьтесь с материалами и решите несколько задач, посмотрите статьи на блоге «Угол вписанный в окружность. Часть 1!» и про вписанный четырёхугольник, либо соответствующий раздел в учебной литературе.
Есть ещё один тип заданий с вписанным углом, которые входят в состав ЕГЭ. Их мы и рассмотрим в этой статье. В заданиях имеется одна особенность – окружность и угол заданы (построены) на листе в клетку и никаких градусных величин в условии не задано. Возникает вопрос: а как тогда углы-то вычислять?
Всё просто! Нужно понимать как «установить» угол, если он построен на листе в клетку, а далее использовать свойство вписанного угла. Запутал?
Начнём с самого простого. Чему равен данный угол?
Конечно же, 90 градусам.
Чему равен этот угол?
Понятно, что 45 градусам.
А этот?
Правильно, 135 градусам (90 + 45 или по-другому 180 – 45).
А такой?
225 градусов (180 + 45 или 360 – 135).
Понимания того, как стороны угла расположены относительно клеток вполне достаточно, чтобы решать такие задачи.
Ещё раз напомню основное свойство вписанного угла.
«Вписанный угол равен половине центрального,
опирающегося на ту же дугу»
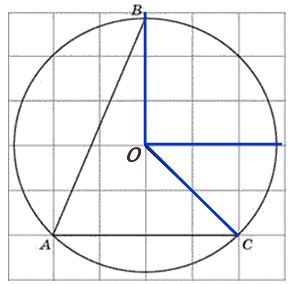
27891. Найдите градусную величину дуги BC окружности, на которую опирается угол BAC. Ответ дайте в градусах.
Все подобные задания, в которых дан вписанный в окружность угол (либо центральный угол) на листе в клетку, решаются просто – угол определяется по расположению его сторон относительно клеток. Если необходимо, то используется свойство вписанного угла.
Построим центральный угол соответствующий дуге ВС:
Градусная величина дуги на которую опирается вписанный угол равна центральному углу опирающемуся на эту дугу, то есть нам необходимо найти угол ВОС:
По клеткам видно, что угол ВОС равен 900 + 450 = 1350 (ОС проходит по диагонали клеток).
Ответ: 135
27887. Найдите величину угла ABC. Ответ дайте в градусах.
Посмотреть решение
27888. Найдите величину угла ABC. Ответ дайте в градусах.
Посмотреть решение
27889. Найдите величину угла ABC. Ответ дайте в градусах.
Посмотреть решение
27890. Найдите градусную величину дуги AC окружности, на которую опирается угол ABC. Ответ дайте в градусах.
Посмотреть решение
Небольшой итог!
Нужно знать свойство вписанного угла (обязательно).
Для решения подобных задач достаточно построить центральный угол и далее использовать указанное свойство.
На этом всё. Успеха Вам!
С уважением, Александр Крутицких
Когда маленький Дракула не вернулся домой из школы, его мама так и подумала: «Наверное, кол поставили».
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
|
Как вычислить градусную меру угла по клеточкам ? Определить размер угла в градусах по клеточкам можно, выполнив следующие действия:
По клеточкам можно найти косинус или синус угла без рисования окружности. Знаете ответ? |
При рассмотрении основных составляющих измерения углов, следует изучить исходные геометрические сведения:
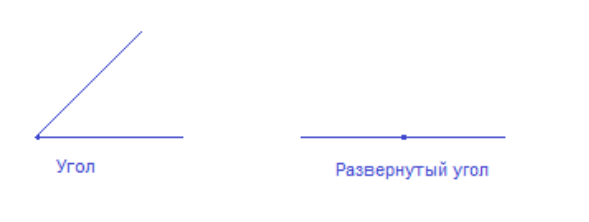
- Угол.
- Развернутый угол, неразвернутый угол.
- Градус, секунда и минута.
- Градусная мера.
- Острый, прямой или тупой.
Геометрическая фигура, которая представляет собой точку — называется вершиной. А исходящие из этой вершины два луча, являются ее сторонами.
Измерение углов производится с помощью градусной меры угла. Углы измеряются таким же способом, как и отрезки, при помощи специальных единиц измерения – градусов.
Определение
Градус — геометрическая единица измерения, представляющая собой угол, который сравнивается с другими углами.
Равенство градуса таково: [frac{1}{180}] от развернутого угла. Исходя из этого, можно понять, что развернутый угол равен 180 градусам, а неразвернутый угол любой меньше 180 градусов.
Чему равна градусная мера угла
Определение
Градусная мера угла – это положительное число, которое показывает сколько раз градус и его части укладываются в данном углу.
А для их измерения используется инструмент – транспортир.
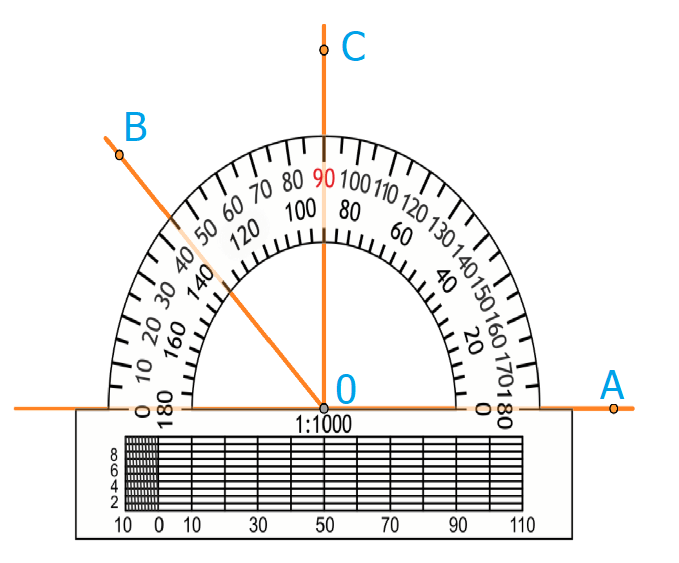
Транспортир используется следующим образом:
- Совместить вершину угла с центром транспортира, при этом одна сторона угла должна пройти по линейке.
- Штрих на шкале транспортира, через который пройдет 2-я сторона, покажет его градусную меру.
Как найти градусную меру угла
На рисунке угол АОВ = 135 градусов. Угол АОС = 90 градусов, угол ВОС = 45 градусов. Градусная мера углов равна сумме углов, на которые он разбит лучом, который проходит между его сторонами.
Отсюда следует, что величина угла AOB на рисунке 1 равна сумме величин углов AOC и [B O C: angle A O B=angle A O C+angle B O C].
Какие бывают названия углов можно понять, разобравшись со следующими обозначениями.
- Минута – 1/60 часть градуса. Обозначается знаком ‘
- Секунда – 1/60 часть минуты. Обозначают знаком»
Например: угол в 65 градусов, 35 минут,18 секунд записывается так: 75°45’28». Если градусная мера у нескольких углов одинаковая, эти углы считаются равными. Сравнить их можно по размерам – больше или меньше. Развернутый и неразвернутый углы.
Нет времени решать самому?
Наши эксперты помогут!
Градусная мера вписанного угла
Градусная мера вписанного угла равняется половине градусной меры дуги, опирающуюся на нее, и половине градусной меры угла, находящегося по центру, которая опирается на эту же дугу.
Вписанный угол равняется половине градусной меры дуги, на которую он опирается.
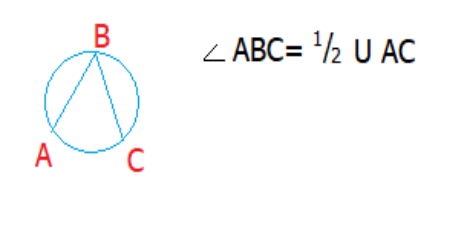
АВ-хорда
ВС-хорда
В-точка окружности.
Углы также различаются несколькими типами:
- Прямыми
- Острыми
- Тупыми
Равность прямого угла составляет — 90 градусов. Острый равен цифре меньше 90 градусов. А тупой же – больше 90 и меньше 180 градусов. В чем же заключается важность умения измерения углов и градусной меры в жизни? Оно пригодится в исследованиях, таких как: астрономия. Например, чтобы вычислить положение различных тел в космосе. Чтобы попрактиковаться, необходимо прочертить несколько неразвернутых углов, отличающихся друг от друга. Также важно потренироваться чертить развернутые. А еще, можно при помощи транспортира поупражняться, задавая случайные цифры, в правильности воспроизведения углов.
Существует еще такое понятие, как, биссектриса.
Определение
Биссектриса— луч, который исходит из вершины этого угла и делит его пополам.
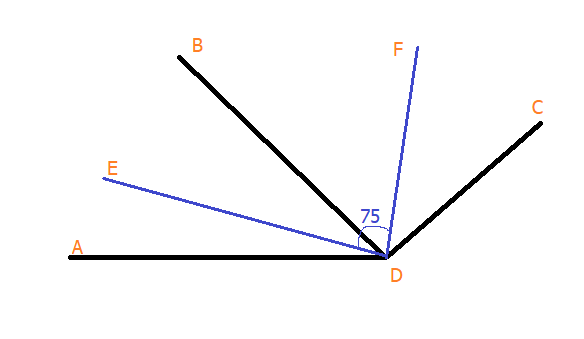
Пример 1. Задача с биссектрисой и развернутым углом.
Рис.3 Лучи DЕ и DF – это биссектрисы, которые соответствуют углам ADB и BDC.
Теперь нужно найти угол ADC, при этом угол EDF = 75°
Ответ. Угол EDF имеет по половинке от углов ADB и BDC, это значит, что EDF – это половина самого угла ADC. Теперь получили вычисление угол ADC = 75 умножить на 2 = 150°.
Ответ: 150°
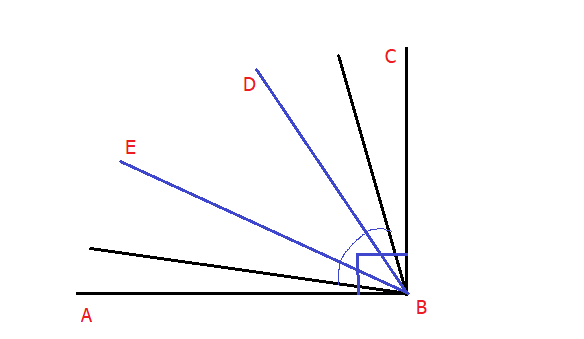
Пример 2. Задача с биссектрисой и прямым углом.
Рисунок 4. По рисунку 4 видно, что угол АВС прямой, а углы ABE EBD DBC равны. Нужно найти угол, который образовали биссектрисы — ABE и DBC.
Решение будет таким: угол АВС прямой, и исходя из этого, можно понять что он равен 90°. Угол ЕВD=90/3=30°. Согласно правилу, углы ABE EBD DBC равны и поэтому каждый из них будет = 30°. Далее видно, что биссектриса любого из трех углов делит любой из этих углов на 2 угла, которые будут равны 15°. Обе половины углов ABE и DBC относятся к углу, который необходимо найти, то можно смело утверждать, что угол, который мы вычисляем, равен 30+15+15=60°.
Решение: 60°
Градусная мера углов треугольника
У любой геометрической фигуры, кроме округлой, имеются углы. При рассмотрении углов треугольника можно увидеть следующее: Сумма углов треугольника всегда равняется 180°. Если рассматривать прямоугольный треугольник, то можно увидеть, что один из углов равен 90°. А сумма двух других углов тоже равняется 90°.
Поэтому, если известно сколько градусов составляет один из острых углов треугольника, второй угол можно найти по формуле:
[angle a=90^{circ}-angle beta]
У прямоугольного треугольника один из углов прямой, соответственно, два других – острые.
Разъяснение острого угла таково: острым углом называется угол, значение которого составляет менее 90 градусов.
Исходя из вышесказанного, можно отметить, что прямоугольный треугольник — это геометрическая фигура, которая образовалась из трех отрезков. Эти отрезки соединяются между собой тремя точками. Углы у нее все внутренние, а один из них — прямой и равняется 90°. Пример — рисунок 5.
Углы на клетках
-1-
Как построить прямой угол по клеткам? Очень просто! – скажете вы. – Отметим точку,
вершину угла, от неё чертим вправо или влево луч, затем ещё один луч вверх или
вниз. Угол между горизонталью и вертикалью – прямой. А можно и по диагоналям
соседних клеток.

Всё верно. А если один из лучей уже построен и
он не горизонтальный, не вертикальный и не проходит по диагоналям клеток? Как
начертить второй луч, чтобы угол между ними был прямым?




Найдём узел сетки, через который проходит
начерченный луч. На нашем рисунке до такого узла от начала луча нужно пройти 3
клетки ВЛЕВО и 1 клетку ВНИЗ. Поэтому чтобы получился прямой угол, надо от
начала луча отсчитать 1 клетку ВЛЕВО и 3 клетки ВВЕРХ. Почему? Обозначим
упомянутые нами точки – А, В и О. Построим векторы ОА и ОВ. Координаты вектора ОА
равны (-3; -1), вектора ОВ (-1; 3). Их скалярное произведение равно 0, поэтому
они перпендикулярны.
Можно отсчитывать клетки и так: 1 клетку
ВПРАВО и 3 клетки ВНИЗ. Тогда вектор ОВ имеет координаты (1; -3), при этом
скалярное произведение векторов ОА и ОВ также равно 0.

Вывод. Векторы с координатами (a; b) и (-b; a), или
(a; b) и (b; –a), – перпендикулярны.
Рассмотрим несколько задач, связанных с
умением находить прямой угол на рисунке.
№ 1. Найти угол АВС на рисунке.


Решение. На первом рисунке угол АОС построен
на диагоналях соседних клеток. На втором рисунке векторы ОА и ОС имеют
координаты соответственно (3; -4) и (4; 3). Поэтому на первом и втором рисунках
центральный угол АОС – прямой, а вписанный угол АВС, опирающийся на ту же дугу,
равен его половине, то есть 45°. На третьем рисунке угол АОС – половина прямого,
то есть 45°, а угол АВС соответственно равен 22,5°.
№ 2. Три квадрата расположены так, как показано на рисунке. Чему равен
угол между прямыми АС и ВD?
Решение. Отрезок ВD
переместим параллельно вниз на одну клетку. Появляется отрезок АМ, равный ВD. Угол
между прямыми АС и ВD равен углу между АС и АМ на втором рисунке.
Соединим отрезком точки С и М. Получается, что угол АМС – прямой и АМ = МС. Треугольник
АСМ прямоугольный равнобедренный, поэтому искомый угол равен 45°.
№ 3. Найти тангенс угла, изображенного на рисунке.

Решение. Выделим на этом рисунке узлы сетки –
точки А и С. Рассмотрим треугольник АВС. Заметим, что он является
прямоугольным, к тому же катет ВС в 2 раза больше катета АС. Отсюда следует,
что тангенс угла В равен 1:2 = 0,5.
-2-
Правильный треугольник и описанная около неё
окружность, построенные на клетках, несут в себе много интересных свойств. Известно,
что радиус окружности, описанной около равностороннего треугольника со стороной
а, равен , а радиус вписанной в него окружности –
, то есть в два раза меньше. Отсюда
следует, что хорда, перпендикулярная радиусу окружности и проходящая через его
середину, является стороной правильного треугольника. Другими словами, острый
вписанный угол, опирающийся на хорду, перпендикулярную радиусу и проходящую
через его середину, равен 60°, а центральный угол и тупой вписанный угол,
опирающиеся на эту хорду, – 120°.
Рассмотрим несколько примеров задач, решаемых
на основе этого свойства.
1) Угол АВС на рисунке равен 60°,
так как хорда АС проходит через середину радиуса и перпендикулярна ему.
2) Угол АВС на рисунке является половиной угла в
60° из предыдущей задачи и равен 30°.

3) Угол АВС на следующем рисунке равен 120°.
При этом четырёхугольник АВСО является ромбом и его острый угол равен 60°.

-3-
Полезным при решении
задач на клетках является знание углов правильных многоугольников. Рассмотрим
правильный шестиугольник и правильный восьмиугольник. Около них описаны
окружности. Каждый внутренний угол правильного шестиугольника равен 120°,
угол между диагоналями-диаметрами равен 60°, угол
между двумя соседними диагоналями, исходящими из одной вершины, равен 30°,
меньшая диагональ правильного шестиугольника перпендикулярна его стороне, а с другими
соседними сторонами – угол 30°. Каждый угол правильного восьмиугольника
равен 135°, угол между соседними
диагоналями-диаметрами равен 45°.

Найдите на следующих
рисунках градусные меры отмеченных углов.











Мясникова Т.Ф.
Измерение углов. Градусы и радианы
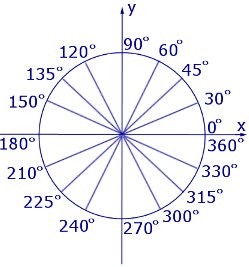
Рассмотрим тригонометрические круги, изображенные на рисунке 1 и рисунке 2.
Рис.1
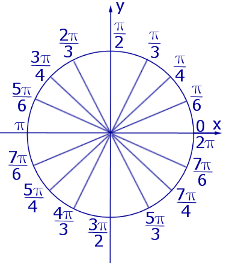
Рис.2
На тригонометрическом круге, изображенном на рисунке 1, центральные углы измерены в градусах, а на тригонометрическом круге, изображенном на рисунке 2, те же центральные углы измерены в радианах.
Углом в 1 градус называют угол, составляющий полного угла. Углом в k° называют угол в k раз больший угла в 1° .
Углом в 1 радиан называют центральный угол тригонометрического круга, которому соответствует дуга окружности тригонометрического круга длиной 1 . Углом в k радиан называют центральный угол тригонометрического круга в k раз больший угла в 1 радиан.
СЛЕДСТВИЕ 1. Углом в k радиан является центральный угол тригонометрического круга, которому соответствует дуга окружности тригонометрического круга длиной k .
СЛЕДСТВИЕ 2. Полный угол является углом в 2π радиан.
Для того, чтобы найти формулы, связывающие градусную и радианную меры угла, рассмотрим рисунки 3 и 4
На этих рисунках изображены прямые углы, причем на рисунке 3 прямой угол измерен в градусах и равен 90° , а на рисунке 4 прямой угол измерен в радианах и равен радиан. Следовательно,
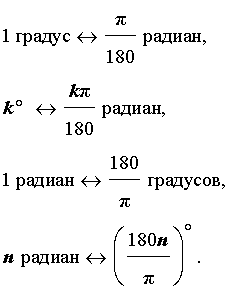
Таким образом, формулы, связывающие градусную и радианную меры угла, имеют вид
Поскольку , то
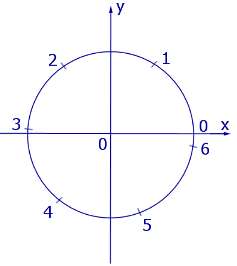
По этой причине углы, составляющие целое число радиан, изображаются на тригонометрическом круге так, как это показано на рисунке 5.
Рис.5
ЗАМЕЧАНИЕ. Тригонометрическая формула sin α означает, что рассматривается синус угла в α радиан, а тригонометрическая формула sin α° означает, что рассматривается синус угла в α градусов. По такому же правилу определяются значения косинуса, тангенса и котангенса.
ПРИМЕР. Найти наименьшее из чисел:
РЕШЕНИЕ. Поскольку
то наименьшим числом является число cos 3 .