На сайте уже были рассмотрены некоторые типы задач по стереометрии, которые входят в единый банк заданий экзамена по математике. Например, задания про составные многогранники.
Призма называется правильной если её боковые перпендикулярны основаниям и в основаниях лежит правильный многоугольник. То есть правильная призма – это прямая призма, у которой в основании правильный многоугольник.
Правильная шестиугольная призма – в основании правильный шестиугольник, боковые грани – прямоугольники.
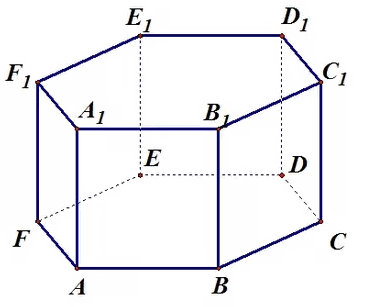
В этой статье для вас задачи на решение призмы, в основании которой лежит правильный шестиугольник. Особенностей и сложностей в решении нет никаких. В чём суть? Дана правильная шестиугольная призма, требуется вычислить расстояние между двумя вершинами или найти заданный угол. Задачи на самом деле простые, в итоге решение сводится к нахождению элемента в прямоугольном треугольнике.
Используется теорема Пифагора и теорема косинусов. Необходимо знание определений тригонометрических функций в прямоугольном треугольнике.
Обязательно посмотрите информацию о правильном шестиугольнике в этой статье (пункт 6). Ещё вам пригодится навык извлечения квадратного корня их большого числа. Можете посмотреть статью на решение многогранников, там тоже вычисляли расстояние между вершинами и углы.
Кратко: что представляет собой правильный шестиугольник?
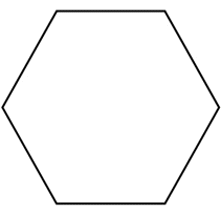
Известно, что в правильном шестиугольнике стороны равны. Кроме этого, углы между сторонами тоже равны.
*Противолежащие стороны параллельны.
Дополнительная информация
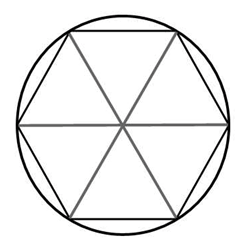
Радиус окружности описанной около правильного шестиугольника равен его стороне. *Это подтверждается очень просто: если мы соединим противоположные вершины шестиугольника, то получим шесть равных равносторонних треугольников. Почему равносторонних?
У каждого треугольника угол при его вершине лежащей в центре равен 600 (360:6=60). Так как у треугольника две стороны имеющие общую вершину в центре равны (это радиусы описанной окружности), то каждый угол при основании такого равнобедренного треугольника так же равен 60 градусам.
То есть правильный шестиугольник, образно говоря, состоит как бы из шести равных равносторонних треугольников.
Какой полезный для решения задач факт ещё следует отметить? Угол при вершине шестиугольника (угол между его соседними сторонами) равен 120 градусам.
*Умышленно не коснулись формул правильного N-угольника. Данные формулы мы подробно рассмотрим в будущем, здесь они просто не нужны.
Рассмотрим задачи:
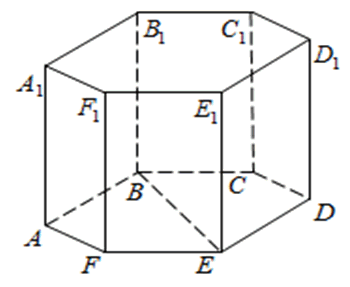
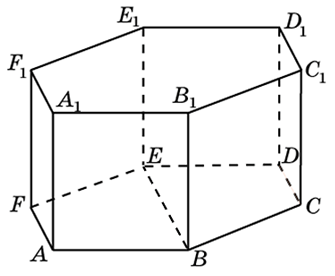
272533. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 48. Найдите расстояние между точками A и E1.
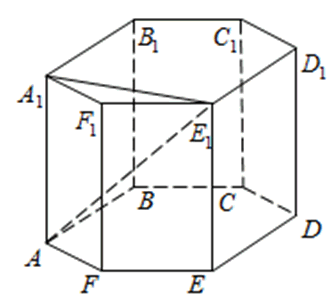
Рассмотрим прямоугольный треугольник AA1E1. По теореме Пифагора:
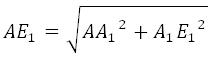
*Угол между сторонами правильного шестиугольника равен 120 градусам.
Отрезок АЕ1 является гипотенузой, АА1 и А1Е1 катеты. Ребро АА1 нам известно. Катет А1Е1 мы можем найти используя используя теорему косинусов.
Теорема: Квадрат любой стороны треугольника равен сумме квадратов двух других его сторон без удвоенного произведения этих сторон на косинус угла между ними.
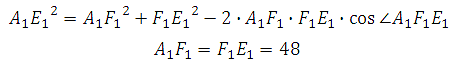
Следовательно
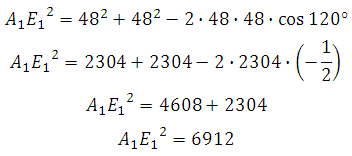
По теореме Пифагора:
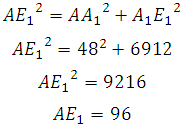
Ответ: 96
*Обратите внимание, что 48 возводить в квадрат совсем не обязательно.
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 35. Найдите расстояние между точками B и E.
Рассмотрим правильный шестиугольник:
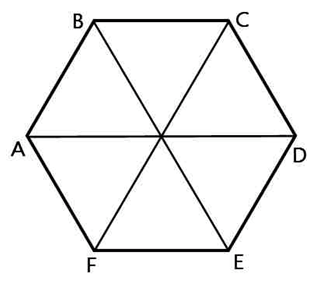
Сказано, что все рёбра равны 35, то есть сторона шестиугольника лежащего в основании равна 35. А так же, как уже сказано, радиус описанной около него окружности равен этому же числу.
Таким образом,
Ответ: 70
273353. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны сорока корням из пяти. Найдите расстояние между точками B и E1.
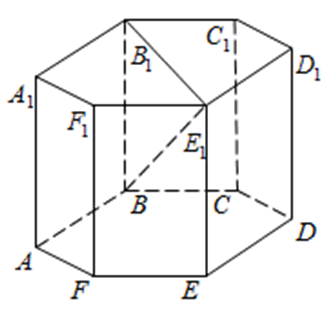
Рассмотрим прямоугольный треугольник BB1E1. По теореме Пифагора:
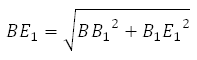
Отрезок B1E1 равен двум радиусам описанной около правильного шестиугольника окружности, а её радиус равен стороне шестиугольника, то есть
Таким образом,
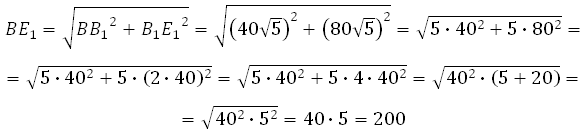
Ответ: 200
273683. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 45. Найдите тангенс угла AD1D.
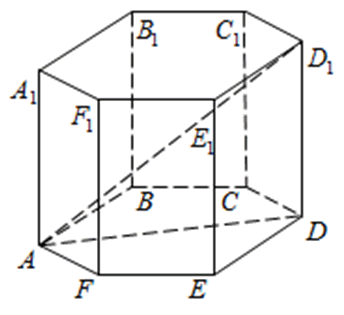
Рассмотрим прямоугольный треугольник ADD1, в котором AD равно диаметру окружности, описанной вокруг основания. Известно, что радиус окружности, описанной вокруг правильного шестиугольника равен его стороне.
Таким образом,
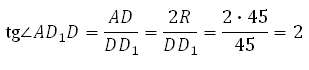
Ответ: 2
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 23. Найдите угол DAB. Ответ дайте в градусах.
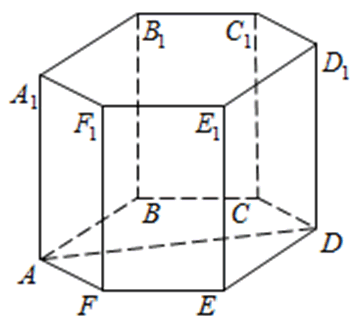
Рассмотрим правильный шестиугольник:
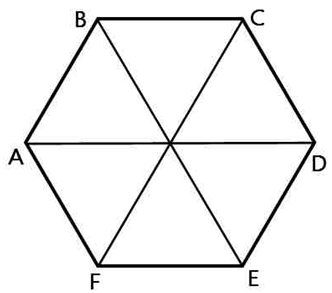
В нём углы между сторонами равны 120°. Значит,
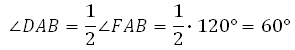
Сама длина ребра не имеет значения, на величину угла она не влияет.
Ответ: 60
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 10. Найдите угол AC1C. Ответ дайте в градусах.
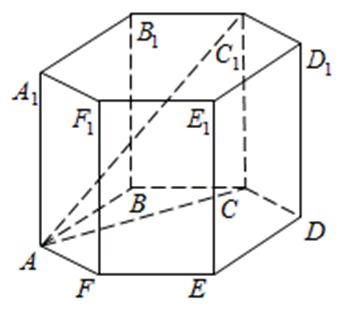
Рассмотрим прямоугольный треугольник AC1C:
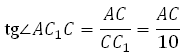
Найдём AC. В правильном шестиугольнике углы между его сторонами равны 120 градусам, тогда по теореме косинусов для треугольника АВС :
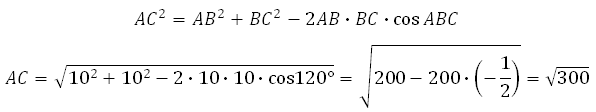
Таким образом,
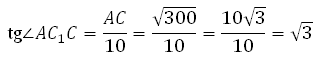
Значит, угол AC1C равен 60 градусам.
Ответ: 60
274453. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 10. Найдите угол AC1C. Ответ дайте в градусах.
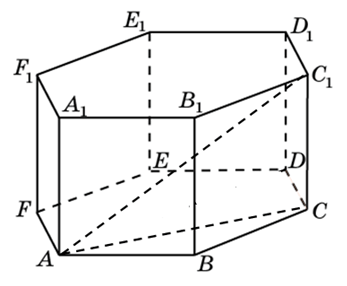
Рассмотрим треугольник AС1С, он прямоугольный. Вычислим тангенс указанного в условии угла и определим угол. Известно, что тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему, то есть
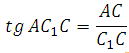
Катет С1С = 10. Отрезок АС вычислим по теореме косинусов (это мы уже делали в первой задаче, запишем ещё раз):
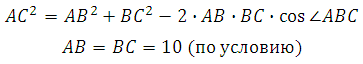
В правильном шестиугольнике углы при вершинах равны 120 градусам, то есть
Следовательно
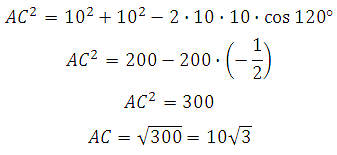
Таким образом:
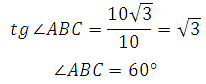
Ответ: 60
245364. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите расстояние между точками А и Е1.
Посмотреть решение
245365. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите расстояние между точками В и Е.
Посмотреть решение
245366. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1все ребра равны корню из пяти. Найдите расстояние между точками В и Е1.
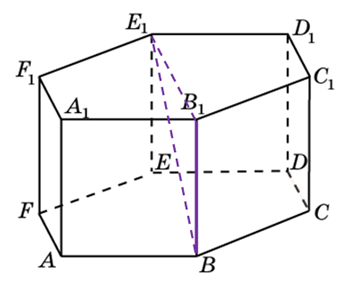
Посмотреть решение
245367. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите тангенс угла AD1D.
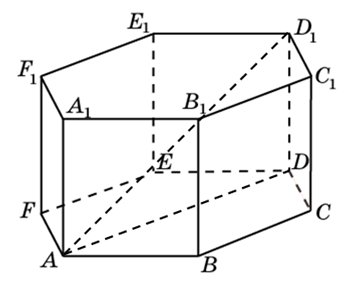
Посмотреть решение
245368. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите угол DAB. Ответ дайте в градусах.
Посмотреть решение
245369. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите угол AC1C. Ответ дайте в градусах.
Посмотреть решение
На этом всё! Успеха Вам!
В состав ЕГЭ включены и другие задачи по стереометрии, и они довольно разнообразны. Обязательно будем их рассматривать, не пропустите! Успехов вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Угол призмы Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Угол падения: 40 степень –> 0.698131700797601 Радиан (Проверьте преобразование здесь)
Угол выхода: 4 степень –> 0.0698131700797601 Радиан (Проверьте преобразование здесь)
Угол отклонения: 12.5 степень –> 0.21816615649925 Радиан (Проверьте преобразование здесь)
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
0.549778714378111 Радиан –>31.5 степень (Проверьте преобразование здесь)
8 Основы оптики Калькуляторы
Угол призмы формула
Угол призмы = Угол падения+Угол выхода–Угол отклонения
A = i+e–D
Какой минимальный угол отклонения?
Этот угол падения, при котором угол отклонения призмы минимален, называется положением минимального отклонения призмы, а сам угол отклонения известен как минимальный угол отклонения.
В основании правильной четырехугольной призмы лежит квадрат. В условии не сказано, что призма прямая, может просто пропущено. Если призма не прямая, то данных для решения задачи недостаточно, а решение будет очень сложным, поэтому будем решать задачу для прямой призмы. Чертим призму, так, как она будет выглядеть, если одна грань призмы обращена к нам, а мы смотрим на призму спереди и чуть справа, то есть видим переднюю и правую грани. Обозначим вершины при нижнем основании. Ближнюю левую вершину – точкой А, и дальше по ходу часовой стрелки (дальнюю левую В, дальнюю правую С, ближнюю правую D. Вершины при верхнем основании обозначим соответствующими буквами с индексом 1. Примем, что задана диагональ призмы АС1. Она равна (а) . Проведем диагональ АВ1 левой боковой грани АА1В1В. Получили прямоугольный треугольник АВ1С1 с прямым углом АВ1С1 и гипотенузой АС1. Угол В1АС1 этого треугольника и есть заданный угол между диагональю призмы и плоскостью боковой грани. По условию он равен 30 градусам. В1С1 – катет, лежащий против угла в 30 градусов, значит он равен половине гипотенузы, т. е. а/2 (это сторона основания, вопрос № 1). Катет АВ1 очевидно равен а*sqrt(3)/2. В1С1 – это сторона основания (квадрата) . Значит все стороны оснований равны а/2. Из прямоугольного треугольника АВ1В с прямым углом В1ВА и гипотенузой АВ1 по Пифагору находим ВВ1=sqrt(AB1^2-AB^2)=sqrt((а*sqrt(3)/2)^2-(a/2)^2)=sqrt(3*a^2/4-a^2/4)=sqrt(2*a^2/4)=a*sqrt(2)/2. Это высота призмы. Проведем диагонали (АС) и (ВD) нижнего основания призмы (квадрата) . Точку их пересечения обозначим К. Очевидно, что если сторона квадрата равна а/2, то его диагональ равна a*sqrt(2)/2. Рассмотрим прямоугольный треугольник АС1С. В нем АС=a*sqrt(2)/2 и СС1=ВВ1=a*sqrt(2)/2. Значит треугольник АС1С – прямоугольный равнобедренный. Углы С1АС и АС1С равны 45 градусам. Угол С1ФС и есть искомый по вопросу № 2 угол между диагональю призмы и плоскостью основания. Площадь одной боковой грани АА1В1В равна АВ*ВВ1=а/2*a*sqrt(2)/2=а^2*sqrt(2)/4, а площадь боковой поверхности (вопрос № 3) равна 4*а^2*sqrt(2)/4=а^2*sqrt(2). Построим сечение призмы плоскостью, проходящей через диагональ основания параллельно диагонали призмы. Поскольку она параллельна диагонали АС1, значит ни одна из ее точек (нас интересует точка А) не принадлежит этой плоскости. Отсюда следует, что искомая плоскость проходит через диагональ ВD. Поскольку искомая плоскость параллельна АС1, в ней должны быть прямые, параллельные АС1 и пересекающие ВD. Рассмотрим треугольник АС1С. Точка К лежит на середине АС. Проведем через нее прямую, параллельную АС1. Это будет средняя линия треугольника АС1С, значит она равна а/2 и пересечет ребро СС1 посередине. Обозначим эту точку М. Теперь мы можем построить сечение. Это будет треугольник ВМD. Очевидно, что он равнобедренный (ВМ=DМ) , а КМ является его медианой, и высотой.
Площадь треугольника ВМD (вопрос № 4) равна ВD*МК/2=(a*sqrt(2)/2)*а/2)/2=а^2*sqrt(2)/8
1. Углы между прямыми и плоскостями
Угол между прямой l и плоскостью L – это угол между прямой l и ее проекцией на плоскость l’.
Угол между плоскостями L и M – это угол между прямыми l и m, лежащими в этих плоскостях, такими, что 
и
(линейный угол). Угол между плоскостями также называется двугранным углом.
Угол между скрещивающимися прямыми l и m, лежащими в параллельных плоскостях, равен углу между проекцией l’ прямой l на плоскость, где лежит прямая m, и прямой m.
Расстояние от точки до плоскости равно длине перпендикуляра, опущенного из точки на плоскость.
Признак параллельности плоскостей:
Если AB||A’B’ и BC||B’C’, то плоскости ABC и A’B’C’ параллельны.
Теорема о трех перпендикулярах:
Прямая BC, лежащая в плоскости ABC, перпендикулярна наклонной DB, тогда и только тогда, когда она перпендикулярна ее проекции на плоскость AB.
2. Призма
Объем наклонной призмы: V=Sосн∙H , где Sосн – площадь основания призмы.
Площадь поверхности: S=2Sосн+Sбок, где Sбок – площадь боковой поверхности, равная сумме площадей всех граней.
Прямая призма – призма, боковое ребро которой перпендикулярно основанию.
Объем: V=Sосн∙l .
Площадь боковой поверхности: Sбок=P∙l, где P – периметр основания.
Правильная призма – прямая призма, основание которой – правильный многоугольник.
Параллелепипед – призма, основание которой – параллелограмм. Все грани параллелепипеда являются параллелограммами.
Прямоугольный параллелепипед – призма, все грани которой – прямоугольники.
Свойства диагоналей: AC1=BD1=CA1=DB1=d; d2=a2+b2+c2.
Объем: V=abc.
Площадь поверхности: S=2∙(ab+ac+bc).
Куб – призма, все грани которой – квадраты (a=b=c). Куб является параллелепипедом и обладает всеми его свойствами.
; V=a3; S=6a2.
Пример 1. Чему равна полная поверхность прямой треугольной призмы, если ее высота равна 50, а стороны основания 13, 37 и 40?
Решение:
Периметр основания призмы равен P=13+17+40=90. Площадь боковой поверхности Sбок= 90∙50=4500.
Площадь основания найдем по формуле Герона. Его полупериметр p=45 и 
.
Осталось вычислить полную поверхность призмы: S=2∙240+4500=4980.
Ответ: 4980.
Пример 2. В основании прямой призмы ABCDA1B1C1D1 лежит квадрат со стороной 2. Боковое ребро призмы равно 
. Найдите градусную меру угла между плоскостью треугольника AB1C и плоскостью основания призмы.
Решение:
Плоскость AB1C пересекает плоскость основания про прямой AC. Построим линейный угол, соответствующий углу между этими плоскостями. Т.к. ABCD – квадрат, то его диагонали пересекаются под прямым углом, т.е. 
. Далее, т.к. призма правильная, то B1A=B1C. Треугольник AB1C – равнобедренный. Его медиана B1O является также его высотой, т.е. 
. Следовательно, линейный 
равен углу между плоскостями.
Рассмотрим треугольник B1OB. Поскольку призма – прямая, то угол B в треугольнике – прямой. B1B=по условию задачи. 
. Т.к. катеты в прямоугольном треугольнике B1OB равны, то =450.
Ответ: 450.
3. Пирамида
Объем: 
.
Площадь поверхности:
.
Особые случаи пирамиды:
1. Если все боковые ребра равны, то
- высота проходит через центр описанной окружности основания;
- боковые ребра образуют с плоскостью основания равные углы.
2. Если боковые грани наклонены к плоскости основания под одним углом, то
- высота проходит через центр вписанной окружности;
- высоты боковых граней равны.
Правильная n-угольная пирамида – пирамида, в основании которой лежит правильный n-угольник, а высота проходит через центр основания. Все боковые ребра правильной пирамиды равны. Все боковые грани – равные между собой равнобедренные треугольники. Высота h боковой грани называется апофемой. Правильная треугольная пирамида, все ребра которой равны, называется тетраэдром.
Площадь боковой поверхности правильной пирамиды: , где P – периметр основания.
Усеченная пирамида
Плоскость ABC параллельна плоскости A1B1C1. Грани ABC и A1B1C1 – основания усеченной пирамиды; h – апофема (в правильной пирамиде).
Объем: 
, где S1 и S2 – площади оснований.
Площадь боковой поверхности: S=S1+S2+Sбок .
Площадь боковой поверхности правильной усеченной пирамиды: 
, где P1 и P2 – периметры оснований.
Пример 3. Высота правильной пирамиды равна 
, апофема 4. Найдите длину бокового ребра.
Решение:
На чертеже изобразим пирамиду SABC, ее высоту SO и апофему SD. Т.к. пирамида правильная, точка O является центром вписанной окружности – точкой пересечения биссектрис, которые также являются высотами и медианами.
Найдем отрезок OD, как катет прямоугольного треугольника SOD: 
.
Медианы AD и BM правильного треугольника ABC равны и точкой O делятся в отношении 2:1. Следовательно 
.
Рассмотрим прямоугольный треугольник SOB. Боковое ребро SB является его гипотенузой. По теореме Пифагора 
.
Ответ: 7.
Пример 4. Площадь основания правильной треугольной пирамиды равна 
, а ее грани наклонены к плоскости основания под углом 600. Найдите объем пирамиды.
Решение:
Воспользуемся чертежом к предыдущей задаче. Т.к. SABC правильная пирамида, точка O является центром вписанной окружности – точкой пересечения биссектрис, которые также являются высотами и медианами. Следовательно,
. SD также является медианой и высотой равнобедренного треугольника CSB. Значит, 
.
Таким образом, линейный угол SDO равен двугранному углу между плоскостью основания пирамиды и плоскостью грани SBC и равен 600.
Рассмотрим правильный треугольник ABC. Путь его сторона равна a. Тогда его площадь равна 
, откуда 
. Найдем высоту треугольника: 
. По свойству медиан
.
Рассмотрим прямоугольный треугольник SOD.
.
Вычислим объем пирамиды: 
.
Ответ: 3.
Пример 5. Все ребра правильной четырехугольной пирамиды равны 2. Через середины боковых ребер проведена плоскость. Найти объем многогранника, заключенного между этой плоскостью и плоскостью основания пирамиды.
Решение:
Отрезки, A1B1, B1C1, C1D1, и D1A1, соединяющие середины боковых ребер, являются средними линиями боковых граней. Таким образом, A1B1||AB и A1C1||AC, и, в соответствии с признаком параллельности плоскостей плоскость, содержащая точки A1, B1, C1 и D1 параллельна плоскости основания. Следовательно, многогранник ABCDA1B1C1D1 является усеченной пирамидой.
По свойству средней линии сторона верхнего основания равна 
. Площадь верхнего основания: S1=12=1.
Площадь нижнего основания S2=22=4 . Диагональ нижнего основания – квадрата ABCD: 
. Поскольку пирамида правильная, то O – центр квадрата, т.е. точка пересечения диагоналей, и 
.
Рассмотрим прямоугольный треугольник SOD. Вычислим высоту пирамиды SO как длину одного из катетов этого треугольника: 
. Отрезок O1D1 – средняя линия этого треугольника, т.к. параллелен основанию OD и проходит через середину стороны SD. Таким образом, 
– высота усеченной пирамиды.
Вычислим объем усеченной пирамиды:
.
Ответ: 
.
4. Цилиндр
OO1 – ось цилиндра; A1ABB1 – осевое сечение.
Объем: 
.
Площадь боковой поверхности:
.
Площадь поверхности: 
.
Пример 6. Осевое сечение цилиндра – квадрат со стороной 50. Найдите площадь сечения цилиндра плоскостью, проходящей параллельно оси цилиндра на расстоянии 7 от нее.
Решение:
Высота и диаметр цилиндра равны 50, его радиус равен 25.
Поскольку плоскость параллельна оси OO1, то она пересекает боковую поверхность цилиндра по прямым AA1 и BB1, параллельным OO1 и перпендикулярным основаниям. Таким образом, сечение, площадь которого требуется найти, представляет собой прямоугольник, стороны
AA1 и BB1 которого равны 50.
Расстояние от оси цилиндра до плоскости AA1B равно длине перпендикуляра OE, опущенного из точки O на прямую AB. Чтобы вычислить длину AB, рассмотрим верхнее основание подробнее. является высотой и, следовательно, медианой равнобедренного треугольника AOB. Таким образом, AE=EB.
В прямоугольном треугольнике OEB гипотенуза OB является радиусом цилиндра и равна 25; катет OE равен 7 по условию задачи. Найдем катет EB: 
. Отсюда AB=2•24=48.
Площадь сечения AA1BB1 равна 48•50=2400.
Ответ: 2400.
5. Конус
L – образующая конуса; OO1 – ось конуса; 
– осевое сечение; 
– угол раствора конуса.
Объем: 
.
Площадь боковой поверхности: 
.
Площадь поверхности:
.
Усеченный конус
Объем:
.
Площадь боковой поверхности:
.
Площадь поверхности:
.
Пример 7. Образующая конуса наклонена к плоскости основания под углом 450. Расстояние от центра основания до образующей равно
. Найдите высоту конуса.
Решение:
Рассмотрим осевое сечение конуса. Оно представляет собой равнобедренный треугольник ABC, углы при основании которого равны 450. Угол в вершине B треугольника – прямой. BO – ось конуса – является также высотой треугольника ABC, а, следовательно, биссектрисой угла B. Таким образом, 
.
Опустим перпендикуляр OE на отрезок BC. Его длина и есть расстояние от центра основания O до образующей BC, которое равно 
.
Рассмотрим прямоугольный треугольник OBE. Высота конуса BO является его гипотенузой.
.
Ответ: 6.
6. Шар и сфера
Объем шара: 
.
Площадь сферы: 
.
Объем шарового сегмента:
.
Площадь сферического сегмента: 
.
Объем шарового сектора: 
.
Площадь боковой поверхности сектора: 
.
Пример 8. Шар, радиус которого равен 13, пересечен плоскостью на расстоянии 10 от центра. Найдите площадь сечения.
Решение:
Проведем осевое сечение шара плоскостью, перпендикулярной той, которая дана в условии задачи. Две плоскости пересекаются по прямой AB.
Искомое сечение является окружностью, диаметр которой равен длине отрезка AB. В плоскости AOB опустим перпендикуляр OH из точки O на прямую AB. Поскольку плоскости перпендикулярны, длина OH и есть расстояние от точки O до заданной плоскости, т.е. OH=10.
Рассмотрим прямоугольный треугольник OHB. Его гипотенуза OB является радиусом сферы и равна 13. Найдем катет HB: 
.
Поскольку OH – высота равнобедренного треугольника AOB, то O – середина AB, т.е. радиус сечения. Таким образом, площадь сечения равна 
.
Ответ: 
.
Задачи для самостоятельного решения
1) В основании прямой призмы лежит прямоугольный треугольник с катетами, равными 5 и 12. Высота призмы равна 8. Найдите полную поверхность призмы.
2) В прямой треугольной призме основания равны 36, 29 и 25, а полная поверхность призмы 1620. Найдите высоту призмы.
3) В основании прямой призмы лежит равнобедренный прямоугольный треугольник с гипотенузой, равной 
. Диагональ боковой грани, соответствующей катету, равна 13. Найдите объем призмы.
4) Стороны основания прямой треугольной призмы равны 10, 17 и 21, а ее боковое ребро равно меньшей из высот основания. Найдите объем призмы.
5) Объем правильной треугольный призмы равен 
. Найдите высоту призмы, если радиус описанной около основания окружности равен 2.
6) Высота правильной треугольной призмы равна 8, а площадь основания 
. Найдите диагональ боковой грани призмы.
7) Все ребра прямой треугольной призмы равны. Найдите площадь основания призмы, если площадь ее полной поверхности равна 
.
8) Высота правильной четырёхугольной призмы равна 
, а диагональ призмы наклонена к плоскости основания под углом 300. Найти сторону основания призмы.
9) Основание прямой призмы – прямоугольный треугольник с катетами 6м и 8м, а диагональ большей по площади боковой грани равна 
м. Найдите объём призмы.
10) Найдите площадь поверхности куба, диагональ которого равна 
.
11) Площадь диагонального сечения куба равна 
. Найдите ребро куба.
12) Сумма длин всех ребер куба равна 48. Чему равна площадь всех его граней?
13) Если ребро куба уменьшить на 10%, на сколько процентов уменьшится его объем?
14) В прямом параллелепипеде проведено сечение через диагональ нижнего основания и середину непересекающегося с этой диагональю бокового ребра. Расстояние от плоскости сечения до вершины нижнего основания, не лежащей в плоскости сечения, равно 5см. Площадь сечения равна 10см2. Найти объём параллелепипеда.
15) В прямом параллелепипеде проведено сечение через диагональ нижнего основания и середину непересекающегося с этой диагональю бокового ребра. Объём меньшего из двух многогранников, на которые параллелепипед делится плоскостью сечения, равен 40см3. Найдите объём параллелепипеда.
16) Стороны основания прямоугольного параллелепипеда 6м и 8м, а угол между диагональю параллелепипеда и плоскостью основания 300. Найдите диагональ параллелепипеда.
17) Стороны основания прямоугольного параллелепипеда равны 4м и 3м, а угол между диагональю параллелепипеда и плоскостью основания 450. Найдите длину диагонали параллелепипеда.
18) Сторона основания правильной треугольной призмы ABCDA1B1C1D1 равна 12, а боковое ребро . Найдите градусную меру угла между плоскостями A1BC и ABC.
19) ABCDA1B1C1D1 – призма, в основании которой лежит квадрат, боковые ребра которой наклонены к плоскости основания под углом 300. Диагональ AD1 перпендикулярна плоскости основания. Площадь боковой поверхности призмы равна 
. Найдите объем призмы.
20) В основании прямой призмы ABCDA1B1C1D1 лежит квадрат. Боковое ребро равно 
. Найдите длину стороны основания, если угол между плоскостью AB1C и плоскостью основания призмы равен 300.
21) Ребра треугольной пирамиды длины 4, 5 и 9 взаимно перпендикулярны. Чему равен объем пирамиды?
22) Пирамида имеет 28 ребер. Сколько у нее граней?
23) Высота правильной треугольной пирамиды равна 15, а высота ее основания 12. Найдите длину бокового ребра.
24) Высота правильной треугольной пирамиды в два раза меньше стороны основания. Найдите угол между боковой гранью пирамиды и плоскостью основания.
25) Сторона основания правильной треугольной пирамиды равна 10 см. Боковые грани наклонены к плоскости основания под углом 450. Найдите высоту пирамиды.
26) Боковое ребро правильной треугольной пирамиды равно 10, а периметр основания 36. Найдите высоту пирамиды.
27) В правильной четырёхугольной пирамиде высота равна 3см, а площадь боковой поверхности 80см2. Найти объём пирамиды.
28) Боковые грани правильной четырёхугольной пирамиды наклонены к плоскости основания под углом 600. Площадь основания равна 14м2. Найти площадь боковой поверхности пирамиды.
29) В правильной четырёхугольной пирамиде боковое ребро образует с плоскостью основания угол 600. Сторона основания пирамиды равна 6см. Найдите объём пирамиды.
30) В правильной четырёхугольной пирамиде апофема образует с плоскостью основания угол 600. Высота пирамиды равна 8см. Найдите площадь поверхности пирамиды.
31) В правильной треугольной пирамиде высота равна 
, а величина двугранного угла при основании 600. Найдите сторону основания пирамиды.
32) В правильной треугольной пирамиде высота равна 4, а апофема равна 5. Найдите сторону основания пирамиды.
33) Высота треугольной пирамиды SABC равна 8, а площадь треугольника ABC 12. Точки A1, B1, C1 делят ребра SA, SB и SC в отношении 1 : 1. Найдите объем усеченной пирамиды ABCA1B1C1.
34) В основании пирамиды SABC лежит прямоугольный треугольник ABC с катетами AC=4 и BC=3. Все боковые ребра пирамиды наклонены к плоскости основания под одним и тем же углом, тангенс которого равен 4/5. Найдите объем пирамиды.
35) Найдите площадь боковой поверхности цилиндра, если площадь его осевого сечения равна 12.
36) Площадь основания цилиндра равна 4, а площадь его боковой поверхности равна 
. Найдите высоту цилиндра.
37) Высота и радиус основания цилиндра равны, соответственно, 9 и 6. Концы отрезка AB длины 
лежат на окружностях верхнего и нижнего оснований. Найдите расстояние от оси цилиндра до отрезка AB.
38) Радиус основания конуса равен 6, а образующая составляет с плоскостью основания угол, равный 300. Найдите расстояние от центра основания до образующей.
39) Образующая конуса равна диаметру его основания. Найдите площадь боковой поверхности конуса, если его высота равна 
.
40) Площадь осевого сечения конуса равна 8, а радиус основания 2. Найдите площадь боковой поверхности конуса.
41) Осевое сечение конуса – правильный треугольник со стороной 
. Найдите полную поверхность конуса.
42) Из точки M вне шара проведена касательная AM к его поверхности. Кратчайшее расстояние от этой точки до поверхности шара равно 6, а до центра шара 15. Найдите длину AM.
43) Если радиус сферы увеличить на 50%, на сколько процентов увеличится площадь ее поверхности?
44) Радиус шара равен 
. Через конец радиуса под углом 600 к нему проведена плоскость. Найти площадь сечения шара плоскостью.
45) Стороны треугольника, равные 10, 10 и 12 касаются поверхности шара Найдите радиус шара, если расстояние от центра шара до плоскости треугольника равно 4.
46) Как относятся объемы куба и описанного около него шара?
47) В шар объема 
вписан конус, таким образом, что основанием конуса является осевое сечение шара. Найдите площадь осевого сечения конуса.
