Как найти градусную меру угла вписанного четырехугольника

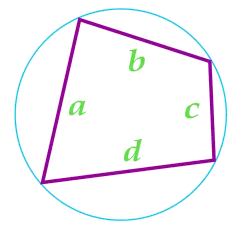
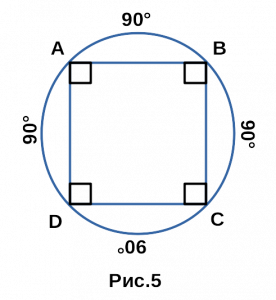
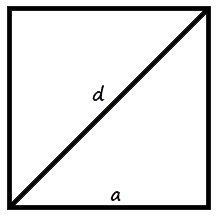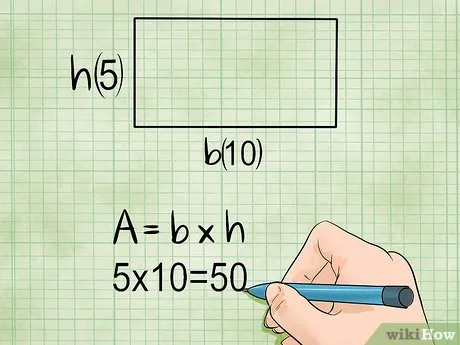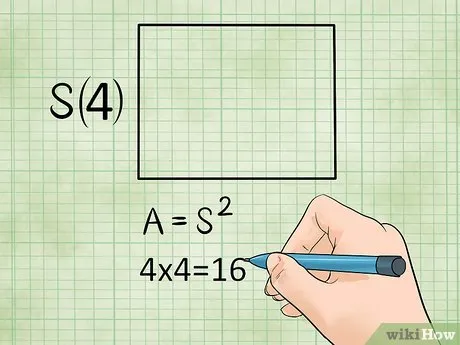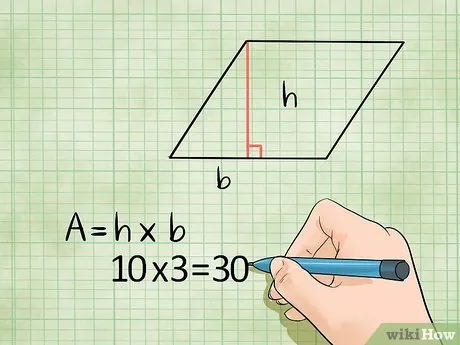Сумма углов четырехугольника

Свойства

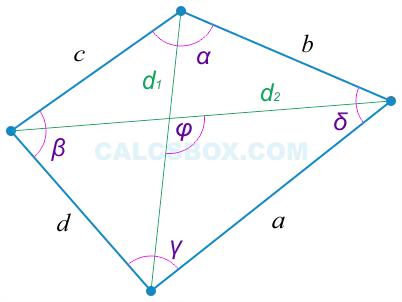
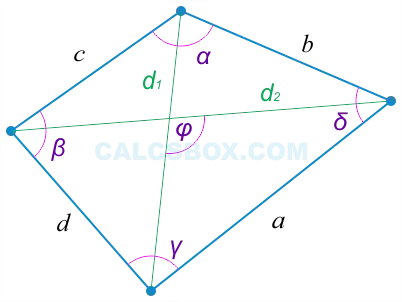
1. Сумма углов четырехугольника равна 360°.
   ∠A + ∠B + ∠C + ∠D = 360°.
   
2. Если четырехугольник правильный, то каждый угол по 90°
   и этот четырехугольник является квадратом.
   ∠A = ∠B = ∠C = ∠D, ⇒ ∠A = ∠B = ∠C = ∠D = 90°,
   ABCD — квадрат.
   
3. Сумма противоположных углов четырехугольника равна 180°,
   если около четырехугольника описана окружность.
   ∠A + ∠С = ∠В + ∠D = 180°.
   

Такие четырехугольники называют вписанными.

Это все виды четырехугольников,
которые изучаются в школьном
курсе по геометрии.

Четырехугольники, вписанные в окружность. Теорема Птолемея

Вписанные четырёхугольники и их свойства

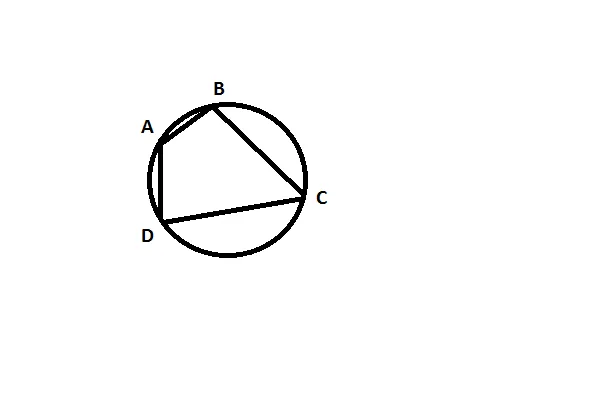
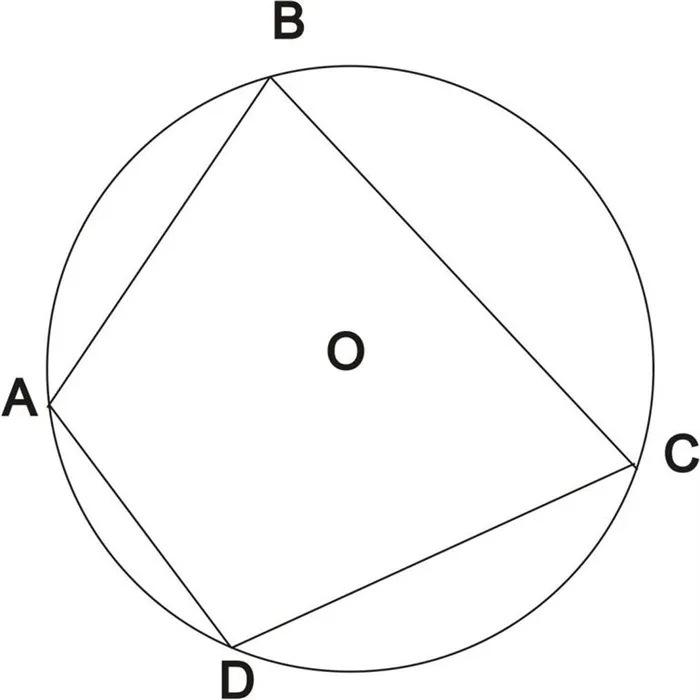
Определение 1 . Окружностью, описанной около четырёхугольника, называют окружность, проходящую через все вершины четырёхугольника (рис.1). В этом случае четырёхугольник называют четырёхугольником, вписанным в окружность, или вписанным четырёхугольником .

Теорема 1 . Если четырёхугольник вписан в окружность, то суммы величин его противоположных углов равны 180° .

Доказательство . Угол ABC является вписанным углом, опирающимся на дугу ADC (рис.1). Поэтому величина угла ABC равна половине угловой величины дуги ADC . Угол ADC является вписанным углом, опирающимся на дугу ABC . Поэтому величина угла ADC равна половине угловой величины дуги ABC . Отсюда вытекает, что сумма величин углов ABC и ADC равна половине угловой величины дуги, совпадающей со всей окружностью, т.е. равна 180° .

Если рассмотреть углы BCD и BAD , то рассуждение будет аналогичным.

Теорема 1 доказана.

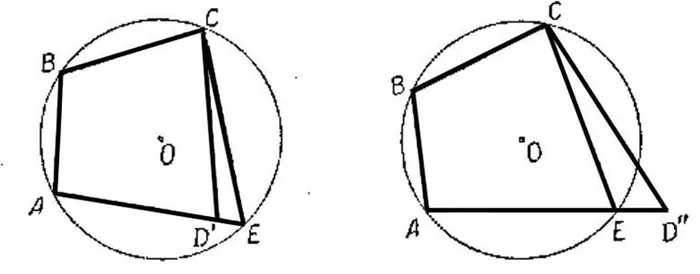
Теорема 2 (Обратная к теореме 1) . Если у четырёхугольника суммы величин его противоположных углов равны 180°, то около этого четырёхугольника можно описать окружность.

Доказательство . Докажем теорему 2 методом «от противного». С этой целью рассмотрим окружность, проходящую через вершины A , B и С четырёхугольника, и предположим, что эта окружность не проходит через вершину D . Приведём это предположение к противоречию. Рассмотрим сначала случай, когда точка D лежит внутри круга (рис.2).

Продолжим отрезок CD за точку D до пересечения с окружностью в точке E , и соединим отрезком точку E с точкой A (рис.2). Поскольку четырёхугольник ABCE вписан в окружность, то в силу теоремы 1 сумма величин углов ABC и AEC равна 180° . При этом сумма величин углов ABC и ADC так же равна 180° по условию теоремы 2. Отсюда вытекает, что угол ADC равен углу AEC . Возникает противоречие, поскольку угол ADC является внешним углом треугольника ADE и, конечно же, его величина больше, чем величина угла AEC , не смежного с ним.

Случай, когда точка D оказывается лежащей вне круга, рассматривается аналогично.

Теорема 2 доказана.

Перечисленные в следующей таблице свойства вписанных четырёхугольников непосредственно вытекают из теорем 1 и 2.

Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты:

где a, b, c, d – длины сторон четырёхугольника,
а p – полупериметр, т.е.

Фигура	Рисунок	Свойство
Окружность, описанная около параллелограмма		Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.
Окружность, описанная около ромба		Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом.
Окружность, описанная около трапеции		Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией.
Окружность, описанная около дельтоида		Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников.
Произвольный вписанный четырёхугольник

Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты:

где a, b, c, d – длины сторон четырёхугольника,
а p – полупериметр, т.е.

Окружность, описанная около параллелограмма
	Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.
Окружность, описанная около ромба
	Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом.
Окружность, описанная около трапеции
	Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией.
Окружность, описанная около дельтоида
	Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников.
Произвольный вписанный четырёхугольник

Окружность, описанная около параллелограмма

Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.

Окружность, описанная около ромба

Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом.

Окружность, описанная около трапеции

Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией.

Окружность, описанная около дельтоида

Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников.

Произвольный вписанный четырёхугольник

Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты:

где a, b, c, d – длины сторон четырёхугольника,
а p – полупериметр, т.е.

Теорема Птолемея

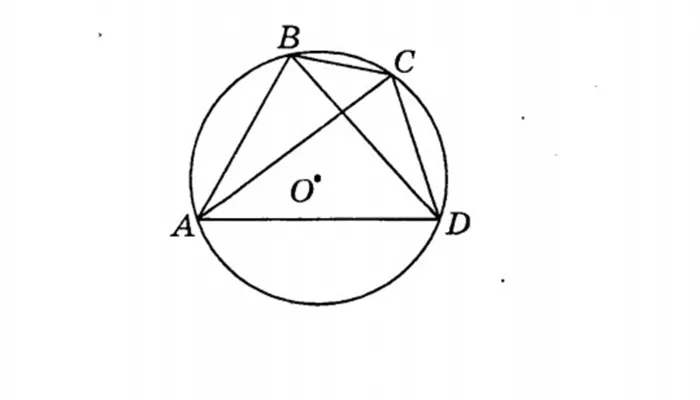
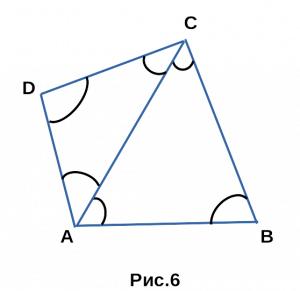
Теорема Птолемея . Произведение диагоналей вписанного четырёхугольника равно сумме произведений противоположных сторон.

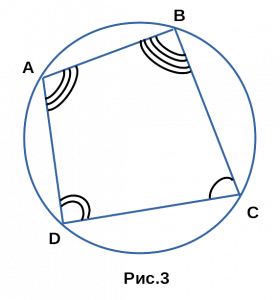
Доказательство . Рассмотрим произвольный четырёхугольник ABCD , вписанный в окружность (рис.3).

Докажем, что справедливо равенство:

Для этого выберем на диагонали AC точку E так, чтобы угол ABD был равен углу CBE (рис. 4).

Заметим, что треугольник ABD подобен треугольнику BCE . Действительно, у этих треугольников по два равных угла: угол ABD равен углу CBE (по построению точки E ), угол ADB равен углу ACB (эти углы являются вписанными углами, опирающимися на одну и ту же дугу). Следовательно, справедлива пропорция:

откуда вытекает равенство:

(1)

Заметим, что треугольник ABE подобен треугольнику BCD . Действительно, у этих треугольников по два равных угла: угол ABE равен углу DBC (углы ABD и EBC равны по построению, угол DBE – общий), угол BAC равен углу BDC (эти углы являются вписанными углами, пирающимися на одну и ту же дугу). Следовательно, справедлива пропорция:

Вписанный четырехугольник. Задание 6

Вписанный четырехугольник. Задание 6

При решении задач на нахождение углов вписанного четырехугольника нам нужно вспомнить, что

1. Четырехугольник называется вписанным в окружность, если все его вершины лежат на окружности:

2. Сумма противоположных углов вписанного четырехугольника равна 180°:

Рассмотрим решение задач из Открытого банка заданий по математике:

1 .Задание B7 (№ 27871)

Угол A четырехугольника ABCD, вписанного в окружность, равен 58°. Найдите угол C этого четырехугольника. Ответ дайте в градусах.

Сумма углов А и С равна 180°, поэтому угол С равен 180°-58°=122°

Ответ: 122°

2 . Задание B7 (№ 27927)

Два угла вписанного в окружность четырехугольника равны 82° и 58°. Найдите больший из оставшихся углов. Ответ дайте в градусах.

Углы 82° и 58° не могут быть противоположными, так как их сумма не равна 180°. Значит, оставшиеся углы являются противоположными к этим. очевидно. что величина большего угла равна 180°-58°=122°

3 . Задание B7 (№ 27928)

Углы A, B и C четырехугольника ABCD относятся как 1:2:3. Найдите угол D, если около данного четырехугольника можно описать окружность. Ответ дайте в градусах.

Введем единичный угол. Тогда величины углов А, В и С можно записать так:

А=х, В=2х, С=3х. Суммы противоположных углов вписанного четырехугольника равны и равны 180°. Сумма углов А и С равна 4х и равна 180°. Отсюда х=45°.

Очевидно, что величина угла D равна 4х-2х=90°

[spoiler title=”источники:”]

http://www.resolventa.ru/spr/planimetry/ofcircle.htm

http://ege-ok.ru/2012/03/23/vpisannyiy-chetyirehugolnik-zadanie-6

[/spoiler]

Вписанный четырёхугольник — это четырёхугольник, вершины которого лежат на одной окружности. Эта окружность называется описанной. Обычно предполагается, что четырёхугольник выпуклый, но бывают и самопересекающиеся вписанные четырёхугольники. Формулы и свойства, данные ниже, верны только для выпуклых четырёхугольников.

Все треугольники имеют описанные окружности, но не все четырёхугольники.
Примером четырёхугольника, который нельзя вписать в окружность, может служить ромб (если только он не является квадратом). Секция «Свойства» ниже даёт необходимые и достаточные условия, чтобы вокруг четырёхугольника можно было описать окружность.

Специальные случаи[править | править код]

Любые квадраты, прямоугольники, равнобедренные трапеции или антипараллелограммы можно вписать в окружность. Дельтоид можно вписать в том и только в том случае, когда у него два угла прямые. Бицентричный четырёхугольник^[en] — это вписанный четырёхугольник, который также является и описанным, а внешне бицентричный четырёхугольник — это вписанный четырёхугольник, который является также
внешне описанным^[en].

Свойства[править | править код]

• Первый критерий вписанности четырёхугольника. Выпуклый невырожденный четырёхугольник является вписанным тогда и только тогда, когда четыре серединных перпендикуляра, проведённых к каждой из сторон, пересекаются в одной точке^[1].
• Второй критерий вписанности четырёхугольника. Выпуклый четырёхугольник является вписанным тогда и только тогда, когда противоположные углы в сумме дают 180°, то есть^[2].

• Другой вариант первого критерия вписанности четырёхугольника. Теорема была Предложением 22 в книге 3 Евклида Начала^[3]. Эквивалентно, выпуклый четырёхугольник является вписанным тогда и только тогда, когда смежный угол равен противоположному внутреннему углу.
• Третий критерий вписанности четырёхугольника. Около четырёхугольника можно описать окружность тогда и только тогда, когда любая пара его противоположных сторон антипараллельна.
• Четвертый критерий вписанности четырёхугольника. Другой критерий для того, чтобы выпуклый четырёхугольник был вписанным, требует, чтобы угол между стороной и диагональю был равен углу между противоположной стороной и другой диагональю^[4]. Например,

• Пятый критерий вписанности четырёхугольника. Неравенство Птолемея утверждает, что произведение длин двух диагоналей p и q четырёхугольника равно сумме произведений противоположных сторон, только если четырёхугольник вписан: ^[5]

.

• Шестой критерий вписанности четырёхугольника. Около четырёхугольника можно описать окружность тогда и только тогда, когда любая пара его противоположных сторон антипараллельна.Если две прямые, из которых одна содержит отрезок AC, а другая — отрезок BD, пересекаются в точке E, то четыре точки A, B, C, D лежат на окружности тогда и только тогда, когда^[6]

Точка пересечения E может лежать как внутри, так и вне окружности. В первом случае это будет вписанный четырёхугольник ABCD, а во втором — вписанный четырёхугольник ABDC. Если пересечение лежит внутри, равенство означает, что произведение отрезков, на которые точка E делит одну диагональ, равно произведению отрезков другой диагонали. Это утверждение известно как теорема о пересекающихся хордах, поскольку диагонали вписанного четырёхугольника являются хордами описанной окружности.

• Седьмой критерий вписанности четырёхугольника. Выпуклый четырёхугольник ABCD является вписанным тогда и только тогда, когда ^[7]

.

(1) является циклическим четырехугольником тогда и только тогда, когда точки и коллинеарные с центром окружности .^{[10] [11]}

(2) является циклическим четырехугольником тогда и только тогда, когда точки и являются серединами сторон и .^[10][11] .

• Замечание. Седьмой и восьмой критерии вписанности четырёхугольника очень похожи и рисунки у них очень похожи. Возможно, что это – один и тот же критерий вписанности четырёхугольника, взятый из разных первоисточников. На обоих рисунках и – точки Паскаля. Есть и другие сходные точки. Хотя формально звучат оба критерия по-разному.
• Десятый критерий вписанности четырёхугольника. Условие, при котором совмещение двух треугольников с одной равной стороной даёт четырёхугольник, вписанный в окружность^[12]. Для того, чтобы два треугольника с тройками длин сторон соответственно (a, b, f) и (c, d, f) при их совмещении вдоль общей стороны с длиной, равной f, давали в итоге четырёхугольник, вписанный в окружность с последовательностью сторон (a, b, c, d), необходимо условие^[13]:84

• Замечание. Последнее условие даёт выражение для диагонали f четырёхугольника, вписанного в окружность, через длины четырёх его сторон (a, b, c, d). Эта формула немедленно следует при перемножении и при приравнивании друг другу левых и правых частей формул, выражающих суть первой и второй теорем Птолемея.

• Одиннадцатый критерий вписанности четырёхугольника. Выпуклый четырёхугольник (см. рис. справа), образованный четырьмя данными прямыми Микеля, вписан в окружность тогда и только тогда, когда точка Микеля M четырёхугольника лежит на прямой, соединяющей две из шести точек пересечения прямых (те, которые не являются вершинами четырёхугольника). То есть, когда M лежит на EF (см. рис. справа).

Площадь[править | править код]

Площадь S вписанного четырёхугольника со сторонами a, b, c, d задаётся формулой Брахмагупты^[14]

где p, полупериметр, равен . Утверждение является следствием соотношения Бретшнайдера, поскольку противоположные углы в сумме дают 180°. Если же d= 0, вписанный четырёхугольник становится треугольником, и равенство превращается в формулу Герона.

Вписанный четырёхугольник имеет максимальную площадь среди всех четырёхугольников, имеющих ту же последовательность длин сторон. Это другое следствие соотношения Бретшнайдера. Утверждение можно доказать с помощью математического анализа^[15].

Четыре неравные длины, каждая из которых меньше суммы остальных трёх, являются сторонами трёх неконгруэнтных вписанных четырёхугольников^[16], и по формуле Брахмагупты все эти треугольники имеют одинаковую площадь. В частности, для сторон a, b, c и d сторона a может быть противоположной любой из сторон b, c или d. Любые два из этих трёх вписанных четырёхугольников имеют диагональ одинаковой длины^[17].

Площадь вписанного четырёхугольника с последовательными сторонами a, b, c, d и углом B между сторонами a и b можно выразить формулой^[5]

или^[18]

где θ — любой угол между диагоналями. Если угол A не является прямым, площадь можно выразить формулой ^[18]

Ещё одна формула площади ^[19]

где R — радиус описанной окружности. Прямым следствием будет ^[20]

,

и неравенство превращается в равенство в том и только в том случае, когда четырёхугольник является квадратом.

Диагонали[править | править код]

Во вписанном четырёхугольнике с вершинами A, B, C, D (в указанной последовательности) и сторонами a = AB, b = BC, c = CD и d = DA длины диагоналей p = AC и q = BD можно выразить через стороны ^[21][22][17]

и

что даёт равенство Птолемея

Согласно второй теореме Птолемея^[21][22],

при тех же обозначениях, что и прежде.

Для суммы диагоналей имеем неравенство ^[23]

Неравенство становится равенством в том и только в том случае, когда диагонали имеют одинаковую длину, что можно показать, используя неравенство между средним арифметическим и средним геометрическим.

Более того^[24],

В любом выпуклом четырёхугольнике две диагонали делят четырёхугольник на четыре треугольника. Во вписанном четырёхугольнике противоположные пары этих четырёх треугольников подобны.

Если M и N являются средними точками диагоналей AC и BD, то^[25]

где E и F — точки пересечения противоположных сторон.

Если ABCD — вписанный четырёхугольник и AC пересекает BD в точке P, то ^[26]

Формулы углов[править | править код]

Для вписанного четырёхугольника со сторонами a, b, c, d, полупериметром p и углом A между сторонами a и d тригонометрические функции угла A равны^[27]

Для угла θ между диагоналями выполняется^[18]

Если продолжения противоположных сторон a и c пересекаются под углом , то

где p — полупериметр^[28]

Формула Парамешвары[править | править код]

Для вписанного четырёхугольника со сторонами , , и (в указанной последовательности) и полупериметром радиус описанной окружности задаётся формулой^[22][29]

Формула была выведена индийским математиком Ватассери Парамешварой^[en] в 15 веке.

Используя формулу Брахмагупты, формулу Парамешвары можно преобразовать в

,

где — площадь вписанного четырёхугольника.

Антицентр и коллинеарность[править | править код]

Четыре отрезка прямых, перпендикулярных одной стороне вписанного четырёхугольника и проходящих через середину противоположной стороны, пересекаются в одной точке^[30][31]. Эта точка пересечения называется антицентром. Антицентр симметричен центру описанной окружности относительно “вершинного центроида”. Таким образом, во вписанном четырёхугольнике центр описанной окружности, “вершинный центроид” и антицентр лежат на одной прямой^[31].

Если диагонали вписанного четырёхугольника пересекаются в точке P, а середины диагоналей — V и W, то антицентр четырёхугольника является ортоцентром треугольника VWP, а вершинный центроид находится в середине отрезка, соединяющего середины диагоналей ^[31].

Во вписанном четырёхугольнике “центроид площади” G_a, “центроид вершин” G_v и пересечение P диагоналей лежат на одной прямой. Для расстояний между этими точками выполняется равенство^[32]

Другие свойства[править | править код]

• Теорема Монжа об ортоцентре вписанного четырехугольника. 4 отрезка прямых (4 антимедатрисы), проведенных из середин 4 сторон вписанного четырехугольника перпендикулярно к противолежащим сторонам, пересекаются в ортоцентре Н этого четырехугольника.^[33],^[34]

• Японская теорема о вписанном четырёхугольнике. Во вписанном четырёхугольнике ABCD центры вписанных окружностей треугольников ABC, BCD, CDA и DAB являются вершинами прямоугольника. Это одна из теорем, известных как японская теорема. Ортоцентры тех же четырёх треугольников являются вершинами четырёхугольника, равного ABCD. Центроиды этих четырёх треугольников являются вершинами другого вписанного четырёхугольника^[4].

• Следствие теоремы о вписанном угле. Во вписанном четырёхугольнике ABCD с центром описанной окружности O пусть P — точка пересечения диагоналей AC и BD. Тогда угол APB является средним арифметическим углов AOB и COD. Это является прямым следствием теоремы о вписанном угле и теоремы о внешнем угле треугольника^[en].

• Теорема о перпендикулярности внутренних биссектрис углов при вершинах E и F, образованных на пересечениях двух пар противоположных сторон вписанного четырёхугольника. Если противоположные стороны вписанного четырёхугольника продолжить до пересечения в точках E и F, то внутренние биссектрисы углов в E и F перпендикулярны^[16].

• Теорема о числовом четырехугольнике. Не существует вписанных четырёхугольников с рациональной площадью и неравными рациональными сторонами, образующими арифметическую, либо геометрическую прогрессию^[36].

• Теорема о числовом четырехугольнике. Если вписанный четырёхугольник имеет длины сторон, образующие арифметическую прогрессию, то четырёхугольник является также внешне описанным^[en].

Четырёхугольники Брахмагупты[править | править код]

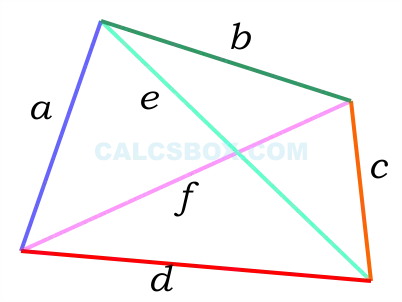
Четырёхугольник Брахмагупты^[37] — это вписанный четырёхугольник с целочисленными длинами сторон, целочисленными длинами диагоналей и целочисленной площадью.
Все четырёхугольники Брахмагупты со сторонами a, b, c, d, диагоналями e, f, площадью S, и радиусом описанной окружности R можно получить путём избавления от знаменателя в следующих выражениях (при рациональных параметрах t, u и v):

Свойства ортодиагональных вписанных четырёхугольников[править | править код]

Площадь и радиус описанной окружности[править | править код]

Пусть для вписанного четырёхугольника, являющегося также ортодиагональным (т.е. имеющим перпендикулярные диагонали), пересечение диагоналей делит одну диагональ на отрезки длиной p₁ и p₂, а другую делит на отрезки длиной q₁ и q₂. Тогда^[38] (первое равенство является Предложением 11 в книге Архимеда «Леммы»)

,

где D — диаметр описанной окружности. Равенство выполняется ввиду того, что диагонали являются перпендикулярными хордами окружности. Отсюда следует, что радиус описанной окружности R удовлетворяет равенству

или, через стороны четырёхугольника

Отсюда также следует, что

Таким образом, согласно формуле Эйлера, радиус можно выразить через диагонали p и q и расстояние x между серединами диагоналей

Формула для площади K вписанного ортодиагонального четырёхугольника можно получить непосредственно через стороны, если скомбинировать теорему Птолемея (см. выше) и формулу площади ортодиагонального четырёхугольника. В результате получим

Другие свойства[править | править код]

• Во вписанном ортодиагональном четырёхугольнике антицентр совпадает с точкой пересечения диагоналей^[39].

• Теорема Брахмагупты утверждает, что во вписанном четырёхугольнике, являющемся также ортодиагональным, перпендикуляр от любой стороны через точку пересечения диагоналей делит противоположную сторону пополам^[39].

• Если вписанный четырёхугольник является также ортодиагональным, расстояние от центра описанной окружности до любой стороны равно половине длины противоположной стороны ^[39].

• Во вписанном ортодиагональном четырёхугольнике расстояние между серединами диагоналей равно расстоянию между центром описанной окружности и точкой пересечения диагоналей ^[39].

См. также[править | править код]

• Теорема о бабочке
• Описанная окружность
• Степень точки относительно окружности
• Таблица хорд Птолемея^[en]
• Пятиугольник Роббинса
• Внеописанный четырёхугольник
• Четырёхугольник

Примечания[править | править код]

Литература[править | править код]

• Claudi Alsina, Roger Nelsen. When Less is More: Visualizing Basic Inequalities, Сhapter 4.3 Cyclic, tangential, and bicentric quadrilaterals. — Mathematical Association of America, 2009. — ISBN 978-0-88385-342-9.
• Claudi Alsina, Roger B. Nelsen. On the diagonals of a cyclic quadrilateral // Forum Geometricorum. — 2007. — Т. 7.
• Nathan Altshiller-Court. College Geometry: An Introduction to the Modern Geometry of the Triangle and the Circle. — 2nd. — Courier Dover, 2007. — ISBN 978-0-486-45805-2. (org. 1952)
• =Titu Andreescu, Bogdan Enescu. Mathematical Olympiad Treasures. — Springer, 2004. — ISBN 978-0-8176-4305-8.
• Christopher Bradley. Three Centroids created by a Cyclic Quadrilateral. — 2011.
• Christopher J. Bradley. The Algebra of Geometry: Cartesian, Areal and Projective Co-Ordinates. — Highperception, 2007. — ISBN 1906338000.
• R. H. Buchholz, J. A. MacDougall. Heron quadrilaterals with sides in arithmetic or geometric progression // Bulletin of the Australian Mathematical Society. — 1999. — Т. 59, вып. 2. — doi:10.1017/S0004972700032883.
• Harold Scott MacDonald Coxeter, Samuel L. Greitzer. Geometry Revisited. 3.2 Cyclic Quadrangles; Brahmagupta’s formula. — Mathematical Association of America, 1967. — ISBN 978-0-88385-619-2. Перевод Г. С. М. Коксетер, С. Л. Грейтцер. Новые встречи с геометрией. 3.2 Вписанные четырёхугольники; Теорема Брахмагупты. — Москва: «Наука», 1978. — (Библиотека математического кружка).
• Crux Mathematicorum. Inequalities proposed in Crux Mathematicorum. — 2007.
• D. Fraivert. The theory of an inscribable quadrilateral and a circle that forms Pascal points // Journal of Mathematical Sciences: Advances and Applications. — 2016. — Т. 42. — P. 81–107. — doi:10.18642/jmsaa_7100121742.
• C. V. Durell, A. Robson. Advanced Trigonometry. — Courier Dover, 2003. — ISBN 978-0-486-43229-8. (orig. 1930)
• Mowaffaq Hajja. A condition for a circumscriptible quadrilateral to be cyclic // Forum Geometricorum. — 2008. — Т. 8.
• Larry Hoehn. Circumradius of a cyclic quadrilateral // Mathematical Gazette. — 2000. — Т. 84, вып. 499 March. — JSTOR 3621477.
• Ross Honsberger. Episodes in Nineteenth and Twentieth Century Euclidean Geometry. — Cambridge University Press, 1995. — Т. 37. — (New Mathematical Library). — ISBN 978-0-88385-639-0.
• Roger A. Johnson. Advanced Euclidean Geometry. — Dover Publ, 2007. (orig. 1929)
• Thomas Peter. Maximizing the area of a quadrilateral // The College Mathematics Journal. — 2003. — Т. 34, вып. 4 September. — JSTOR 3595770.
• Alfred S. Posamentier, Charles T. Salkind. Challenging Problems in Geometry. — 2nd. — Courier Dover, 1970. — ISBN 978-0-486-69154-1. Глава: Solutions: 4-23 Prove that the sum of the squares of the measures of the segments made by two perpendicular chords is equal to the square of the measure of the diameter of the given circle.

• , <http://students.imsa.edu/~tliu/Math/planegeo.pdf> Архивная копия от 21 сентября 2018 на Wayback Machine Перевод с русского издания В.В. Прасолов. Задачи по планиметрии. Учебное пособие. — 5-е. — Москва: МЦНМО OAO «Московские учебники», 2006. — ISBN 5-94057-214-6.
• K.R.S. Sastry. Brahmagupta quadrilaterals // Forum Geometricorum. — 2002. — Т. 2.
• A. W. Siddons , R. T. Hughes. Trigonometry. — Cambridge University Press, 1929.
• Zalman Usiskin, Jennifer Griffin, David Witonsky, Edwin Willmore. The Classification of Quadrilaterals: A Study of Definition. — IAP, 2008. — (Research in mathematics education). — ISBN 978-1-59311-695-8.
• D. E. Joyce. Euclid’s Elements. — Clark University, 1997.
• D. Fraivert. Pascal-points quadrilaterals inscribed in a cyclic quadrilateral // The Mathematical Gazette. — 2019. — Т. 103, вып. 557.

Внешние ссылки[править | править код]

• Derivation of Formula for the Area of Cyclic Quadrilateral
• Incenters in Cyclic Quadrilateral at cut-the-knot
• Four Concurrent Lines in a Cyclic Quadrilateral at cut-the-knot
• Weisstein, Eric W. Cyclic quadrilateral (англ.) на сайте Wolfram MathWorld.
• Euler centre and maltitudes of cyclic quadrilateral at Dynamic Geometry Sketches, interactive dynamic geometry sketch.

Площадь ромба также можно найти, умножив его стороны на высоту, приходящуюся на эту сторону. Однако не путайте высоту с прилегающей стороной. Высота — это линия, которая выходит из любой вершины ромба на противоположную сторону и пересекает противоположную сторону под прямым углом.

Четырёхугольник

Сегодня мы рассмотрим геометрическую фигуру четырехугольник. Из названия этой фигуры уже понятно, что она имеет четыре угла. Однако мы обсудим и другие свойства.

Четырехугольник — это многоугольник, состоящий из четырех точек (вершин) и четырех отрезков (сторон), попарно соединенных этими точками. Площадь четырехугольника равна половине произведения его диагоналей и угла между ними.

Четырехугольник — это многоугольник с четырьмя вершинами, три из которых не лежат на одной прямой.

Четырехугольник — это геометрическая фигура, состоящая из четырех точек, три из которых не лежат на одной прямой и последовательно соединены отрезками.

Виды четырехугольников

• Четырехугольник, у которого противоположные стороны попарно параллельны, называется параллелограммом.
• Четырехугольник, у которого две противоположные стороны параллельны, а две другие − нет, называется трапецией.
• Четырехугольник, у которого все углы прямые, является прямоугольником.
• Четырехугольник, у которого все стороны равны, является ромбом.
• Четырехугольник, у которого все стороны равны и все углы прямые, называется квадратом.

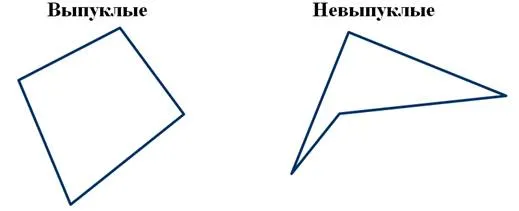
Четырехугольник может быть:

Единственный пересекающийся четырехугольник — это четырехугольник с точкой пересечения (показана синим цветом) по обе стороны.

Невыпуклые четырехугольники — это четырехугольники, один из внутренних углов которых превышает 180° (на рисунке выделен оранжевым цветом).

Сумма углов несамостоятельных четырехугольников всегда равна 360 градусам.

Четырехугольник и окружность

Четырехугольники с контуром, нарисованным вокруг окружности (окружность, вписанная в четырехугольник).

Основные характеристики очерченного четырехугольника:.

Четырехугольник может быть описан вокруг окружности только в том случае, если суммы противоположных длин равны.

Вписанный четырехугольник (круг, нарисованный вокруг четырехугольника).

Основные свойства вписанного четырехугольника:.

Четырехугольник может быть вписан в окружность только в том случае, если сумма противоположных углов равна 180 градусам.

Радиус четырехугольной окружности R с половиной периметра p и сторонами a, b, c и d определяется по формуле Парамешвары: r = (¼)*((a * b + c * d)*(a * c + b * d)*(a * d + b * c))/((p-a)*(p-b)*(p-c)*(p-d))^(½). Аналогия возникла благодаря индийскому математику XV века Ватасери Парамешваре.

Четырёхугольник

В этом уроке мы рассмотрим геометрические фигуры, такие как четырехугольники. Вводится понятие четырехугольника. Сформируйте представление о его верхней и боковых поверхностях. Вы узнаете, какие четырехугольники называются выпуклыми, а какие невыпуклыми. Мы также обсудим диагонали и периметры четырехугольника. Затем они узнают, что сумма углов выпуклого четырехугольника равна 360°. Он также закрепляет то, чему вы научились в практической части урока.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам из набора, вам необходимо приобрести их в каталоге и добавить в свой личный стенд.

Конспект урока «Четырёхугольник»

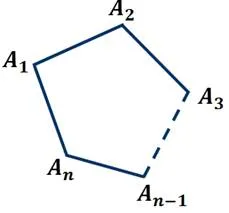
В предыдущем уроке мы обсудили многоугольники. Помните, что многоугольник — это геометрическая фигура, состоящая из частей и внутренних областей. Точка А.₁, A₂, A₃ и т.д._n-1, A_n называется многоугольником, а вершины отрезка A₁A₂, A₂A₃,…, A_n-1A_n, A_n называемые ребрами многоугольника.

Многоугольник с n вершинами называется n-прямоугольником.

В этом уроке мы обсудим четырехугольники. Таким образом, четырехугольник — это геометрическая фигура, состоящая из четырех точек и четырех последовательных отрезков, соединяющих их.

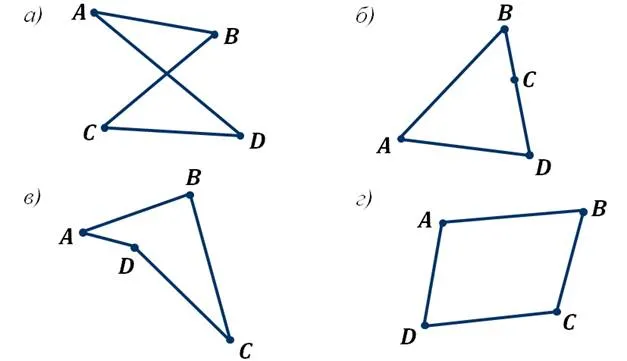
Нет трех точек на одной прямой, и соединяющие их отрезки не пересекаются.

Точки A, B, C и D называются вершинами четырехугольника. А отрезки прямых AB, BC, CD и DA, соединяющие эти точки, называются сторонами четырехугольника.

Давайте рассмотрим следующие элементы.

Каждая из них состоит из четырех точек и четырех частей, соединяющих эти точки в непрерывной последовательности. Обратите внимание, что первая фигура не является четырехугольником, так как отрезки AD и BC пересекаются. Следующая фигура имеет точки B, C и D на одной прямой и не является четырехугольной. Следующая фигура — четырехугольник. Это происходит потому, что ни одна из трех точек не лежит на одной прямой и их соединения не пересекаются. Последняя фигура также является четырехугольником, потому что ни одна из трех точек не лежит на одной прямой и их соединения не пересекаются.

Вершины четырехугольника, принадлежащие одной и той же стороне, называются смежными. Например, вершины A и B и A и D являются смежными.

Вершины, которые не являются соседними, называются противоположными вершинами. Таким образом, в четырехугольниках A и C, B и D симметричны.

Стороны четырехугольника, начинающиеся от одной вершины, называются смежными. Например, BC и CD являются смежными.

Грани, не имеющие общей вершины, называются противоположными. Таким образом, AB и CD, AD и BC взаимозаменяемы.

Четырехугольники могут быть выпуклыми или невыпуклыми.

Выпуклые четырехугольники лежат по одну сторону от прямой, проходящей через две соседние вершины. Однако если четырехугольник лежит по обе стороны хотя бы одной прямой, проходящей через две соседние вершины, он является невыпуклым.

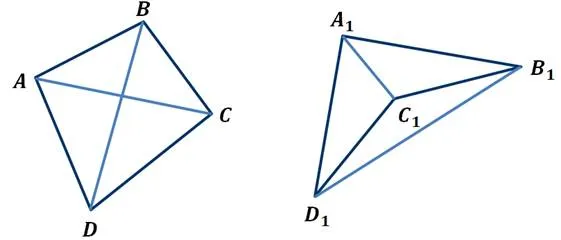
Отрезки, соединяющие противоположные вершины четырехугольника, называются диагоналями.

Так, в выпуклом четырехугольнике ABCD отрезки AC и BD являются диагоналями. Каждая диагональ делит этот четырехугольник на два треугольника.

У четырехугольника есть два противоположных угла, сумма которых равна ⌘ (⌘ displaystyle 180)<>^ }} то такой четырехугольник является вписанным.

Площадь четырехугольника, заданного координатами

Тип площади четырехугольника на основе координат используется для вычисления площади координатной фигуры. В этом случае сначала необходимо рассчитать требуемую длину сторон. Сам тип может отличаться в зависимости от типа четырехугольника. Рассмотрим пример вычисления площади четырехугольника с помощью квадрата в системе координат XY.

Мы знаем, что все стороны фигуры равны, и формула площади квадрата находится по формуле: Найдем одну из сторон, к примеру, AB : Подставим значения в формулу: Знаем, что все стороны одинаковые. Подставляем значение в формулу расчета площади:

Нахождение площади четырёхугольника различными способами и методами

Вы узнаете, как найти площадь четырехугольника, учитывая его диагонали и острые углы, образованные их пересечениями. Затем площадь четырехугольника вычисляется по формуле: s = 1/2 * d1 * d2 * sin (d1, d2).

Рассмотрим его пример. Пусть d1 = 15 см, d2 = 12 см, а угол между ними равен 30 градусам. Пусть S. S = 1/2 * 15 * 12 * sin30 = 1/2 * 15 * 12 * 1/2 = 45 см квадратных.

Теперь посмотрите на стороны и противоположные углы четырехугольника.

Пусть a, b, c и d — известные стороны многоугольника, а p — его периметр. Квадратный корень из формулы называется rad (от латинского radical). Формула для площади четырехугольника дается следующим образом (a, b) + (c, d))/ 2), где p = 1/2 * (a + b + c + d).

На первый взгляд, формула кажется очень сложной и изощренной. Однако здесь нет ничего сложного. Мы докажем это на примере. Рассмотрим данные нашей ситуации: α = 18 мм, β = 23 мм, γ = 22 мм, δ = 17 мм. Противоположные углы равны (a, b) = 0,5° и (c, d) = 1,5°. Сначала найдите длину полуокружности: p = 1/2 * (18 + 23 + 22 + 17) = 1/2 * 80 = 40 мм.

Теперь найдите квадрат синуса запятой противоположного угла: co s ^ 2 ((a, b) + (c, d)) / 2) = c o s ^ 2 (0,5 + 1,5) / 2 = c o s1 * c o s1 = (1/2) * (1/2) = 0,9996.

Эти данные заменяются формулой: s = rad((40-18)*(40-23)*(40-22)*(40-17)-18 * 23 * 22 * 17 * 0,97) = rad((22 * 17 * 18 * 23-18 * 23 * 22 * 17 * 1/4) * (1-0,9996)) = рад (154836 * 0,0004) = рад62 = 7 875 мм в квадрате.

Узнайте, как вычислить площадь с помощью конечных циклов и окружностей. При устранении этой проблемы рекомендуется приложить к действию план поддержки, но это требование не является обязательным.

Если у вас есть акроцикл и вам нужно найти площадь четырехугольника, формула будет такой: α = 16,5, α = 16,5, α = 16,5, α = 16,5, α = 16,5.

Рассмотрим другой пример: α = 16 метров, β = 30 метров, γ = 28 метров, δ = 14 метров, r = 6 метров. Подставляя цены в прессе, получаем

S = ((16 +30 + 28 + 14) / 2) * 6 = 44 * 6 = 264 кв. м.

Давайте теперь обсудим случай, когда окружность нарисована вокруг четырехугольника. Здесь можно использовать следующее уравнение

S = rad((p —a)*(p — b)*(p — c)*(p — d), где p — половина длины периметра. В этом случае значения сторон: α = 26 метров в десятичной дроби, β = 35 метров в десятичной дроби, γ = 39 метров в десятичной дроби, δ = 30 метров в десятичной дроби.

Сначала определим полудесятичную длину, p = (26 + 35 + 39 + 30) / 2 = 65 дециметров. Подставим найденную цену в формулу. Мы получаем:.

S = rad ((65-26)*(65-35)*(65-39)*(65-30)) = rad (39 * 30 * 26 * 35) = 1032 (округленно) десятичных.

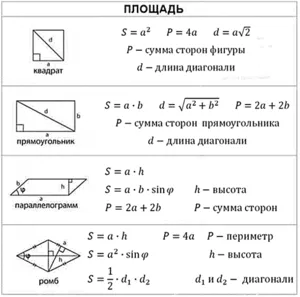
Квадрат, прямоугольник и другие параллелограммы

Определение прямоугольника. Прямоугольник — это четырехугольник с равными противоположными сторонами, параллельными друг другу. Квадраты, прямоугольники и ромбы — это прямоугольники.

• Квадрат — это параллелограмм, у которого все стороны равны и пересекаются под прямым углом.
• Прямоугольник — это параллелограмм, у которого все стороны пересекаются под прямым углом.
• Ромб — это параллелограмм, у которого все стороны равны.

Площадь прямоугольника. Чтобы вычислить площадь прямоугольника, нужно знать его ширину (короткая сторона — считается высотой) и длину (длинная сторона — считается стороной, на которой проведена высота). Площадь прямоугольника равна произведению его длины и ширины.

• ‘ Площадь = длина х высота , или S = a х h .
• Пример: если длина прямоугольника равна 10 см, а ширина равна 5 см, то площадь этого прямоугольника: S = 10 х 5 = 50 квадратных сантиметров .
• Не забывайте, что площадь измеряется в квадратных единицах (квадратных метрах, квадратных сантиметрах и так далее).

Площадь квадрата. Поскольку квадрат является частным случаем прямоугольника, используйте ту же формулу, что и для нахождения площади прямоугольника. Однако в квадрате все стороны равны, поэтому площадь квадрата равна любой из его сторон, возведенной в квадрат (т.е. умноженной на себя). 1

• Площадь = сторона х сторона , или S = a 2 .
• Пример: если сторона квадрата равна 4 см (a = 4), то площадь этого квадрата: S = a 2 = 4 х 4 = 16 квадратных сантиметров .

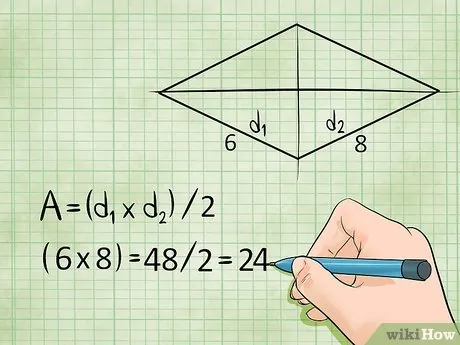
Площадь ромба равна его диагонали, деленной на 2. Диагональ — это часть ромба, соединяющая противоположные вершины. 2

• Площадь = (диагональ1 х диагональ2)/2 , или S = (d₁ ×x d₂)/2
• Пример: если диагонали ромба равны 6 см и 8 см, то площадь этого ромба: S = (6 х 8)/2 = 24 квадратных сантиметров.

Площадь ромба также можно найти, умножив его стороны на высоту, приходящуюся на эту сторону. Однако не путайте высоту с прилегающей стороной. Высота — это линия, которая выходит из любой вершины ромба на противоположную сторону и пересекает противоположную сторону под прямым углом.

• Пример: если длина ромба равна 10 см, а его высота равна 3 см, то площадь такого ромба равна 10 х 3 = 30 квадратных сантиметров .

Площади двумерных фигур — это геометрические понятия, которые указывают на их числовые свойства или размер. В большинстве случаев они обозначаются буквой S. Она измеряется в квадратных метрах (см 2, м 2, и т.д.). Фигура с характеристикой S называется квадратом.

Найдите углы вписанного в окружность четырехугольника, если три угла(в последовательном порядке) относятся как 4 : 7 : 6?

Если три угла (последовательно) равны 4:7:6, найдите угол четырехугольника, записанного в круге.

Ответ Максимальная степень ответа.

Четырехугольник может быть зарегистрирован в круге только в том случае, если сумма противоположных углов равна 180°.

4: 7: 6: x x конг угловых пар4 + 6 = 7 + x

Цикл составляет 360°.

А сумма отрезков, на которые он разделен, равна 10 + 10 = 20, шкала оценки отрезка

Четырехугольник ABCD вписан в окружность, угол А = 108 *, угол В = 70 * ?

Четырехугольник ABCD описан на окружности под углом a = 108 * и углом b = 70 *.

Найдите минимальное значение остальных углов.

Какой угол четырехугольника записан в круге, если три угла (в последовательном порядке) на этой странице связаны с категорией геометрии 4:7:6? Этот вопрос имеет те же трудности, с которыми сталкиваются учащиеся 5-9 классов. Здесь вы можете найти и обсудить правильный ответ и сравнить его с мнением других пользователей сайта. Используйте автоматический поиск на этой же странице, чтобы найти похожие вопросы и ответы к категории геометрия. Если вы не уверены в ответе, переформулируйте свой вопрос. Для этого нажмите кнопку вверху.

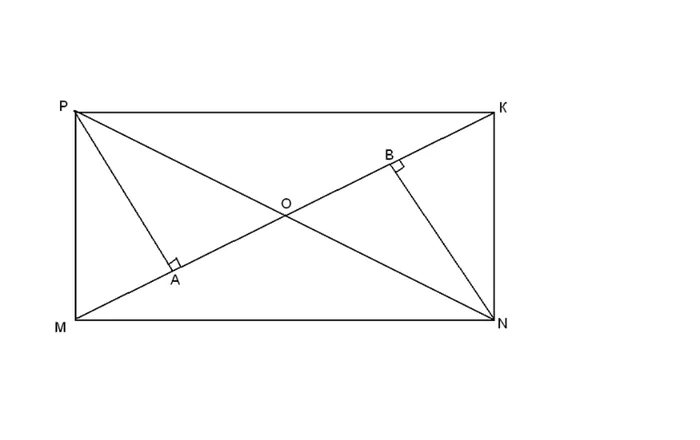
ДОКАЗАТЕЛЬСТВО: Предположим, что отрезки AC и BD пересекаются в точке o треугольника. aob = треугольник с первым знаком (угол aob, угол sod перпендикулярны, bo = od, ao = os, так как o — середина ac и ua) треугольник abc = треугольник SOD с первым знаком (ac — общий. …

AC = 16 + 2 = 18 (см) BC = 18-8 = 10 (см) p = 16 + 18 + 10 = 44 (см) Ответ: 44 см.

Да, так как это проекция, то возможно отображение.

AC = AD + DC = 6 + 8 = 14. Спроектируйте CH, которая является высотой ABC. Это также высота треугольника ABD. SABC = 1/2 AC -BHBH = 2SABC /AC = 2-42 /14 = 6SABD = 1/2 AB -BH = 1 /2-6-6-6 = 18 кв.м. изд.

Невыпуклые четырехугольники — это четырехугольники, один из внутренних углов которых превышает 180° (на рисунке выделен оранжевым цветом).

Вписанный четырехугольник и его свойства (ЕГЭ 2022)

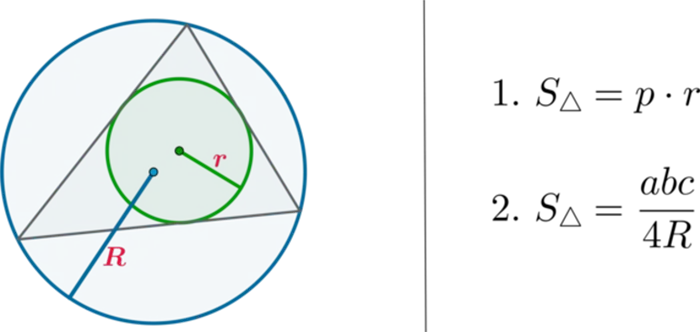
Оказывается, можно описать круг вокруг треугольника. Например, такой:

Вопрос: Могу ли я получить записанный четырехугольник?

Верно ли, что всегда существует круг, на котором сидят все четырехугольники всех четырех вершин?

Вписанный четырехугольник — коротко о главном

Если четырехугольник вписан в окружность, то сумма двух противоположных углов равна ߡ(ߡ displaystyle 180<>^ круг )

У четырехугольника есть два противоположных угла, сумма которых равна ⌘ (⌘ displaystyle 180)<>^ }} то такой четырехугольник является вписанным.

Четырехугольник будет зарегистрирован как круг, только если сумма двух противоположных углов равна ⌘ (⌘ displaystyle 180), тогда четырехугольник будет зарегистрирован как круг.<>^ circ ).

)<>^ circ ).

Прямоугольник, вписанный в окружность, обязательно является прямоугольником, и его центр совпадает с точкой пересечения диагоналей.

Вписанный четырехугольник — определения и теоремы

Оказывается, это не так!

Не всегда можно записать четырехугольную окружность.

Существует очень важное условие:

Четырехугольник может быть зарегистрирован как круг, только если сумма двух противоположных углов равна ⌘ (⌘ displaystyle 180.<>^ circ ).

В нашей диаграмме: ⌘ (⌘ displaystyle alpha + ⌘ beta = 180)<>^ круг )

Смотрите, углы ( displaystyle alpha ) и ( displaystyle beta ) противоположны друг другу и поэтому противоположны. Как насчет углов ⌘ (⌘ displaystyle varphi ) и ⌘ (⌘ displaystyle psi )? Разве они не противоположны?

Углы ⌘ (⌘ displaystyle alpha ) и ⌘ (⌘ displaystyle beta ) можно заменить углами ⌘ (⌘ displaystyle varphi ) и ⌘ (⌘ displaystyle ).

Главное — найти два противоположных угла четырехугольника. Сумма этих углов равна ᢙ (ᢙ displaystyle 180).<>^ circ ).

Два других угла добавляются к (⌘ displaystyle 180)<>^ circ ). Вы мне не верите, давайте проверим.

displaystyle alpha + beta = 180)<>^ circ ). Помните ли вы, чему равна сумма всех четырех углов четырехугольника? Определенно, ዄ (ዄ displaystyle 360).<>^ circ ).

Следовательно, ( displaystyle альфа + бета + варфи + пси = 360<>^ circ ) — всегда! displaystyle 180<>^ круг )

Однако 팀 (팀 displaystyle alpha + beta = 180<>^ circ ), -> ᢙ (ᢙ displaystyle varphi + psi = 360)<>^ circ -180<>^ окружность = 180<>^ circ )

Поэтому хорошо запомните это.

Если четырехугольник вписан в окружность, то сумма любых двух противоположных углов равна ⌘ (⌘ displaystyle 180<>^ \\ circ \ circ \ circ \\ }

Если четырехугольник имеет два противоположных угла, то сумма любых двух противоположных углов равна ⌘ (⌘ displaystyle 180 ^ ⌘ displaystyle 180 ^ ⌘ displaystyle 180 ^ ⌘ displaystyle 180 ^ ⌘ displaystyle 180).<>^ \\ circ \) Далее, четырехугольник вписан.

Смотрите чек чуть ниже.

А пока давайте посмотрим, к чему приведет этот примечательный факт. Вписанный четырехугольник — это четырехугольник, сумма противоположных углов которого равна ⌘ (⌘ displaystyle 180).<>^ circ ).

Теперь возникает вопрос, например, можно ли нарисовать круг вокруг прямоугольника?

Вписанный параллелограмм

Сначала попробуйте применить «научный метод».

Это не работает. Теперь давайте применим наши знания.

Предположим, что вам каким-то образом удалось вписать круг в прямоугольник ⌘ (⌘ displaystyle ABCD ). Тогда нам нужно сделать следующее: ( displaystyle alpha + beta = 180)<>^ circ ), поэтому: ( displaystyle угол B + угол D = 180)<>^ circ ).

Вспомним свойства прямоугольников. Каждый прямоугольник имеет равный и противоположный угол.

Следовательно, 퓡 (퓡 displaystyle угол B = 퓡 угол D 퓡).

displaystyle left < beginangle B=angle D\angle B+angle D=180<>^ circ end right.) → 섹 (섹 displaystyle left )< beginangle B=90<>^ circ\\ угол D=90<>^ displaystyle left ^ displaystyle right).

Как насчет углов ⌘ (⌘ displaystyle A ) и 섹 (섹 displaystyle C )?

Вписанный четырехугольник — это четырехугольник, все вершины которого лежат на одной окружности.

Центр окружности, описанной около четырехугольника — точка пересечения серединных перпендикуляров, проведенных к сторонам четырехугольника.

Признаки вписанного четырехугольника

Для того, чтобы четырехугольник был вписанным, необходимо и достаточно, чтобы выполнялось одно из следующих равенств:

Специальные случаи

Любые квадраты, прямоугольники, равнобедренные трапеции можно вписать в окружность.

Свойства вписанного четырехугольника

• Произведение диагоналей вписанного четырехугольника равняется сумме произведений его противолежащих сторон.
• Диагонали вписанного четырехугольника относятся как суммы, произведений сторон, сходящихся в концах диагоналей.
• Диагонали вписанного четырехугольника разбивают его на две пары подобных треугольников.
• Сумма квадратов противолежащих сторон четырехугольника равна квадрату диаметра описанной окружности.
• Сумма противолежащих углов четырехугольника равна .

Использование свойств и признаков вписанного четырехугольника при решении геометрических задач.

Задача 1. Высоты и остроугольного треугольника пересекаются в точке  . Докажите, что .

Решение. Рассмотрим четырехугольник .

.

Следовательно, вокруг четырехугольника можно описать окружность и по свойству вписанных углов, опирающихся на одну дугу .

Рассмотрим четырехугольник .

.

Следовательно, вокруг четырехугольника можно описать окружность и по свойству вписанного четырехугольника .

  — свойство смежных углов.

Следовательно, .

   

   

ч.т.д.

Задача 2. В остроугольном треугольнике  проведены высоты и . На них из точек и опущены перпендикуляры   и соответственно. Докажите, что прямые и параллельны.

Решение. Рассмотрим четырехугольник .

.

Следовательно, вокруг четырехугольника можно описать окружность и по свойству вписанных углов, опирающихся на одну дугу .

Рассмотрим четырехугольник .

.

Следовательно, вокруг четырехугольника можно описать окружность и по свойству вписанных углов, опирающихся на одну дугу .

   

— соответственные углы, образованные при пересечении прямых и секущей .

Следовательно, прямые и параллельны.

ч.т.д.