- Главная
- Справочник
- Теорема о внешнем угле треугольника
Поможем решить контрольную, написать реферат, курсовую и диплом от 800р
Узнать стоимость
Теорема о внешнем угле треугольника
Содержание:
- Формулировка теоремы о внешнем угле треугольника
- Примеры решения задач
Формулировка теоремы о внешнем угле треугольника
Теорема
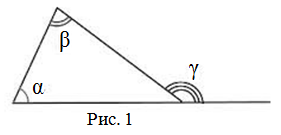
Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним:
$$angle gamma=angle alpha+angle beta$$
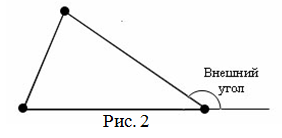
Внешним углом треугольника при данной вершине называется угол, смежный с углом треугольника при этой вершине
(внутренним углом) (рис. 2).
Следствие
Внешний угол треугольника больше любого внутреннего угла, не смежного с ним.
Примеры решения задач
Пример
Задание. В треугольнике
$ABC$ угол
$A$ равен
$30^{circ}$, угол
$B – 80^{circ}$. Найти
градусную меру угла, смежного с
третьим углом треугольника.
Решение. Согласно теореме о внешнем угле треугольника, искомый угол равен сумме углов не смежных с ним, то есть:
$$alpha=30^{circ}+80^{circ}=110^{circ}$$
Ответ. $alpha=110^{circ}$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. В треугольнике $ABC$ угол
$A$ равен
$30^{circ}$, а внешний угол при вершине
$C$ равен
$45^{circ}$. Найти остальные углы треугольника
$ABC$ .
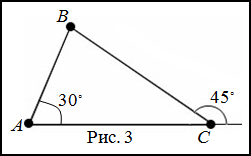
Решение. Сделаем чертеж к задаче (рис. 3).
Согласно теореме о внешнем угле треугольника, получаем равенство для нахождения градусной меры угла
$B$:
$$45^{circ}=30^{circ}+angle B Rightarrow angle B=15^{circ}$$
Угол $C$, как смежный угол, равен
$$angle C=180^{circ}-45^{circ}=135^{circ}$$
Ответ. $angle B=15^{circ}, angle C=135^{circ}$
Статьи по теме
- Теоремы по математике и геометрии
- Теорема Пифагора
- Теорема о среднем
- Теорема о сумме углов треугольника
- Теорема о трех перпендикулярах
- Все темы раздела “Теоремы по математике и геометрии”

Разделы
- Формулы сокращенного умножения
- Формулы по физике
- Логарифмы
- Векторы
- Матрицы
- Комплексные числа
- Пределы
- Производные
- Интегралы
- СЛАУ
- Числа
- Дроби
Все еще сложно?
Не получается написать работу самому?
Доверь это кандидату наук!
Ищещь ответ на вопрос с которым нужна помощь?
80% ответов приходят в течение 10 минут
250 ответов по вашей теме сегодня
2 специалиста свободны онлайн
Ответы приходят уже через 10 минут
90% ответов положительные
Внешним углом DCA плоского треугольника ABC при данной вершине C называется угол, смежный внутреннему углу ACB треугольника при этой вершине
Теорема о внешнем угле треугольника — одна из основных теорем планиметрии.
Формулировка[править | править код]
Внешним углом плоского треугольника при данной вершине называется угол, смежный с внутренним углом треугольника при этой вершине (см. рис.).
Если внутренний угол при данной вершине треугольника образован двумя сторонами, выходящими из данной вершины, то внешний угол треугольника образован одной стороной, выходящей из данной вершины и продолжением другой стороны, выходящей из той же вершины.
- Внешний угол равен разности между 180° и его внутренним углом, смежным с ним. Внешний угол может принимать значения от 0 до 180° не включительно.
- Теорема о внешнем угле треугольника: Внешний угол треугольника равен сумме двух оставшихся углов треугольника, не смежных с этим внешним углом. Иными словами, (см. рис.):
История[править | править код]
В евклидовом доказательстве теоремы о внешнем угле треугольника, принадлежащем Евклиду, (а также и результата о том, то сумма всех трех внутренних углов треугольника равна 180°) сначала проводится прямая, параллельна стороне AB, проходящая через вершину C, а затем, используя свойство соответственных углов при двух параллельных прямых и одной секущей и о внутренних накрест лежащих углах при двух параллельных прямых, требуемое утверждение получают как иллюстрацию (см. рис.).[1].
Применение[править | править код]
Теорема о внешнем угле треугольника используется тогда, когда пытаются вычислить меры неизвестных углов в геометрии, в задачах с многоугольниками, где используются треугольники.
Примечания[править | править код]
- ↑ Heath, 1956, Vol. 1, p. 316
Литература[править | править код]
- Faber, Richard L. (1983), Foundations of Euclidean and Non-Euclidean Geometry, New York: Marcel Dekker, Inc., ISBN 0-8247-1748-1
- Greenberg, Marvin Jay (1974), Euclidean and Non-Euclidean Geometries/Development and History, San Francisco: W.H. Freeman, ISBN 0-7167-0454-4
- Heath, Thomas L. (англ.) (рус.. The Thirteen Books of Euclid’s Elements (неопр.). — 2nd ed. [Facsimile. Original publication: Cambridge University Press, 1925]. — New York: Dover Publications, 1956.
- (3 vols.): ISBN 0-486-60088-2 (vol. 1), ISBN 0-486-60089-0 (vol. 2), ISBN 0-486-60090-4 (vol. 3).
- Henderson, David W. & Taimiņa, Daina (2005), Experiencing Geometry/Euclidean and Non-Euclidean with History (3rd ed.), Pearson/Prentice-Hall, ISBN 0-13-143748-8
- Venema, Gerard A. (2006), Foundations of Geometry, Upper Saddle River, NJ: Pearson Prentice Hall, ISBN 0-13-143700-3
- Wylie Jr., C.R. (1964), Foundations of Geometry, New York: McGraw-Hill
- Wheater, Carolyn C. (2007), Homework Helpers: Geometry, Franklin Lakes, NJ: Career Press, с. 88–90, ISBN 978-1-56414-936-7
Внешний угол треугольника
Углы треугольника бывают внутренние и внешние. Что такое внешний угол треугольника? Как его найти?
Внешний угол треугольника при данной вершине — это угол, смежный с внутренним углом треугольника при этой вершине.
Как построить внешний угол треугольника? Нужно продлить сторону треугольника.
∠3 — внешний угол при вершине А,
∠2 — внешний угол при вершине С,
∠1 — внешний угол при вершине В.
Сколько внешних углов у треугольника?
При каждой вершине треугольника есть два внешних угла. Чтобы построить внешний угол при вершине треугольника, можно продлить любую из двух сторон, на которых лежит данная вершина. Таким образом получаем 6 внешних углов.
Внешние углы каждой пары при данной вершины равны между собой (как вертикальные):
Поэтому, когда говорят о внешнем угле треугольника, не важно, какую из сторон треугольника продлили.
Чему равен внешний угол?
Теорема (о внешнем угле треугольника)
Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
Дано : ∆АВС, ∠1 — внешний угол при вершине С.
∠1 и ∠С (∠АСВ) — смежные, поэтому их сумма равна 180º, значит, ∠1=180º-∠С=180º-(180º-(∠А+∠В))=180º-180º+(∠А+∠В)=∠А+∠В.
Теорема о внешнем угле треугольника: формулировка и задачи
В данной публикации мы рассмотрим одну из основных теорем в геометрии 7 класса – о внешнем угле треугольника. Также разберем примеры решения задач, чтобы закрепить представленный материал.
Определение внешнего угла
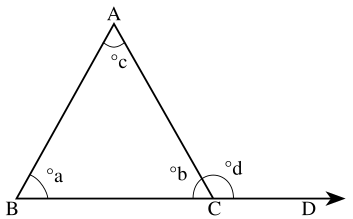
Для начала вспомним, что такое внешний угол. Допустим у нас есть треугольник:
Смежный с внутренним углом ( λ ) треугольника угол при той же вершине является внешним. На нашем рисунке он обозначен буквой γ .
-
сумма данных углов равна 180 градусам, т.е. γ + λ = 180° (свойство внешнего угла);
Формулировка теоремы
Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
Из данной теоремы следует, что внешний угол треугольника больше любого из несмежных с ним внутренних углов.
Примеры задач
Задание 1
Дан треугольник, в котором известны значения двух углов – 45° и 58°. Найдите внешний угол, смежный с неизвестным углом треугольника.
Решение
Воспользовавшись формулой теоремы получаем: 45° + 58° = 103°.
Задание 1
Внешний угол треугольника равен 115°, а один из несмежных с ним внутренних углов – 28°. Вычислите значения оставшихся углов треугольника.
Решение
Для удобства будем использовать обозначения, указанные на рисунках выше. Известный внутренний угол примем за α .
Исходя из теоремы: β = γ – α = 115° – 28° = 87° .
Угол λ является смежным с внешним, а значит вычисляется по следующей формуле (следует из свойства внешнего угла): λ = 180° – γ = 180° – 115° = 65° .
Внешний угол треугольника. Синус и косинус внешнего угла
В некоторых задачах ЕГЭ требуется найти синус, косинус или тангенс внешнего угла треугольника. А что такое внешний угол треугольника?
Давайте вспомним сначала, что такое смежные углы. Вот они, на рисунке. У смежных углов одна сторона общая, а две другие лежат на одной прямой. Сумма смежных углов равна .
Возьмем треугольник и продолжим одну из его сторон. Внешний угол при вершине — это угол, смежный с углом . Если угол острый, то смежный с ним угол — тупой, и наоборот.

Обратите внимание, что:
Запомните эти важные соотношения. Сейчас мы берем их без доказательств. В разделе «Тригонометрия», в теме «Тригонометрический круг», мы вернемся к ним.
Легко доказать, что внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
Ты нашел то, что искал? Поделись с друзьями!
1. В треугольнике угол равен , . Найдите тангенс внешнего угла при вершине .
Пусть — внешний угол при вершине .
Зная , найдем по формуле
2. В треугольнике угол равен , . Найдите синус внешнего угла при вершине .
Задача решается за четыре секунды. Поскольку сумма углов и равна , . Тогда и синус внешнего угла при вершине также равен .
[spoiler title=”источники:”]
http://ege-study.ru/ru/ege/materialy/matematika/vneshnij-ugol-treugolnika/
[/spoiler]
Мы привыкли рассматривать треугольники, в особенности их углы, только «изнутри». Однако, знаете ли, «снаружи» треугольника тоже кипит жизнь. В этом уроке предлагаем узнать, что в геометрии треугольников имеется также внешний угол. А что же такое внешний угол? Какие свойства внешнего угла треугольника существуют? Может, есть какая-нибудь теорема о внешнем угле треугольника? Вот, сейчас будем все выяснять.
Что такое внешний угол?
Начертим треугольник $bigtriangleup{ABC}$ и построим при вершине $B$ угол, смежный с $angle{B}$. Теперь в $bigtriangleup{ABC}$ при вершине $B$ появилось два угла — один «внутри», другой «снаружи». Угол «снаружи» называется внешним углом при вершине $B$. Дадим ему определение.
Внешний угол при данной вершине — угол, смежный с углом треугольника при этой вершине.
Как обозначается внешний угол?
Углы в треугольнике обозначаются согласно вершинам, где они располагаются, либо по трем точкам.
Например, в треугольнике $bigtriangleup{ABC}$ угол при вершине $B$ обозначается как $angle{B}$, либо как $angle{ABC}$. А если при вершине $B$ в том числе имеется внешний угол? Его тоже обозначать как $angle{B}$?
Или лучше указать дополнительную точку на продолжении стороны? Вопрос отличный. Для того, чтобы подобной путаницы не возникало, в геометрии принят термин «внутренний угол».
К примеру, в ходе задачи или доказательства вы пользуетесь внешним углом при некоторой вершине. Скажем, вновь при вершине $B$ в треугольнике $bigtriangleup{ABC}$. Когда вы ссылаетесь к углу треугольника внутри, можно уточнить: «Внутренний угол $angle{B}$».
Когда ссылаетесь к углу снаружи, уточняйте: «Внешний угол $angle{B}$».
Способ с уточнениями «внутренний угол», «внешний угол» проще и не требует дополнительных точек. К тому же, такое обозначение облегчает понимание, где в треугольнике располагается угол. Ведь вы акцентируете внимание только на вершине.
Такое особенно полезно, когда решения или чертежи к задачам громоздкие. Бывает, что при одной вершине нужно рассматривать два внешних угла. Они все равно равны как вертикальные, но все же… Мало ли. Тут удобнее дать углам обозначение в стиле «$angle{1}$» или, например, «$angle{x}$».
Теорема о внешнем угле треугольника
Применим наши знания теоремы о сумме углов треугольника к внешним углам. Рассмотрим внешний угол $angle{B}$ в треугольнике $bigtriangleup{ABC}$. Сумма $angle{B}$ внешнего и $angle{B}$ внутреннего равняется $180^circ$, как смежных.
По теореме о сумме углов треугольника: $$angle{A}+angle{B}+angle{C}=180^circ$$
Если:
- внутр. $angle{B}+$ внеш. $angle{B}=180^circ$
- $angle{A}+$ внутр. $angle{B}+angle{C}=180^circ$
То:
- внеш. $angle{B}=180^circ-$ внутр. $angle{B}$
- внутр. $angle{B}=180^circ-angle{A}-angle{C}$
- внеш. $angle{B}=180^circ-180^circ+angle{A}+angle{C}$
Методом подстановки переменных из одного уравнения в другое мы обнаружили, что внешний угол равняется сумме двух других углов, с ним не смежных. Так, величина внешнего $angle{B}$ равна сумме $angle{A}+angle{C}$ внутренних.
Теорема о внешнем угле треугольника. Внешний угол треугольника равен сумме двух внутренних углов, с ним не смежных.
Обратим ваше внимание вот еще на что.
Раз внешний угол по величине — это сумма двух внутренних углов, внешний угол всегда будет по величине больше любого внутреннего угла, не смежного с ним. Полезное следствие, особенно если вдруг придется, скажем, доказывать возможность или невозможность существования некоторого треугольника. Или еще для чего-нибудь.
Теорема о внешнем угле треугольника: доказательство Евклида
Официально теорему о внешнем угле треугольника впервые доказал Евклид — древнегреческий математик, считающийся «отцом геометрии». Примечательно, что его доказательство не имеет ничего общего с теоремой о сумме углов треугольника — математик воспользовался свойствами углов при параллельных и секущей. Оно в принципе и понятно: Евклид огромное количество времени посвятил изучению параллельных прямых.
В качестве практики и повторения материала по параллельным прямым и секущим мы приводим евклидовое доказательство. Оно очень даже достойно внимания. Итак, посмотрим, как внешний угол треугольника «общается» с параллельными прямыми.

Доказательство
Рассмотрим $bigtriangleup{ABC}$ с внешним углом при вершине $B$. Проведем через эту вершину луч, параллельный стороне $AC$. Отметим на полученном луче точку $B_1$. На продолжении стороны $AB$ отметим точку $B_2$.
Теперь рассмотрим параллельные отрезки $BB_1$ и $AC$ при секущей $AB$. Внутренний угол $angle{A}$ и угол $angle{B_{1}BB_2}$ равны как соответственные. Далее рассмотрим отрезки $BB_1$ и $AC$ при секущей $CB$. Углы $angle{B_{1}BC}$ и $angle{ACB}$ равны как накрест лежащие.
Видим, что внешний $angle{B}$ состоит из суммы внутренних углов $angle{A}$ и $angle{C}$. Что и требовалось доказать.
Свойства внешнего угла
Не сказать, что свойства внешнего угла многочисленные. В основном, когда затрагивается внешний угол, для решения задач или доказательства чего-либо хватает теоремы о внешнем угле треугольника. Ну, и смежности внутреннего и внешнего углов.
То есть базового определения.
Правда если к делу подключается биссектриса, свойства внешнего угла, помимо «классических», таки обнаруживаются. Разберем одно наиболее полезное.
Свойство биссектрис внешнего и внутреннего углов треугольника. Биссектрисы внутреннего и внешнего углов являются перпендикулярными друг к другу.
Доказательство
Проведем в треугольнике $bigtriangleup{ABC}$ биссектрисы при внешнем $angle{B}$ и при внутреннем $angle{B}$. Для удобства разметим все полученные углы следующим образом: $x$ и $y$ — значения внутренних углов при вершинах $A$ и $C$ соответственно; $z$ — половина внутреннего $angle{B}$; $f$ — половина внешнего $angle{B}$.
Нам требуется установить, чему равняется $z+f$. Если сумма будет равна $90^circ$ — свойство доказано. Воспользуемся теоремой о внешнем угле и теоремой о сумме углов треугольника.
$$2f=x+y\2z+x+y=180^circ$$
Так как нам нужно найти сумму $z+f$, сложим уравнения выше:
$$2f+2z+x+y=x+y+180^circ$$
Видим, что после сокращения $2(f+z)=180^circ$.
Следовательно сумма $f$ и $z$ равняется $90^circ$. Биссектрисы перпендикулярны друг к другу. Свойство доказано.
Задача для самостоятельного решения
Свойства внешнего угла треугольника — нет. Теорема о внешнем угле треугольника — однозначное да. Решите данную задачу, не используя свойство смежности внешнего и внутреннего углов.
Условие. В треугольнике $bigtriangleup{ABH}$ величина внешних углов $angle{1}$ и $angle{2}$ равняется $97^circ$ и $125^circ$ соответственно. Найдите, чему равняется внутренний $angle{A}$.
Показать решение
Спрятать решение
Дано:
$bigtriangleup{ABH}$
$angle{1}=97^circ$
$angle{2}=125^circ$
Найти:
внутр. $angle{A}$ — ?
Решение. Воспользуемся теоремой о внешнем угле треугольника. Так как рассматривать мы будем только два внешних угла — $angle{1}$ и $angle{2}$, договоримся, что $angle{A}$, $angle{B}$ и $angle{H}$ далее в решении относятся к обозначению только внутренних углов треугольника $bigtriangleup{ABH}$.
Имеем следующие равенства:
$$angle{1}=angle{A}+angle{B}\angle{2}=angle{A}+angle{H}$$
Сложим между собой данные равенства и подставим имеющиеся по условию значения внешних углов $angle{1}$ и $angle{2}$:
$$2angle{A}+angle{B}+angle{H}=angle{1}+angle{2}=222^circ$$
Сумма углов $angle{A}$, $angle{B}$ и $angle{H}$ составляет $180^circ$. Вычтем из полученного выше равенства равенство $angle{A}+angle{B}+angle{H}=180^circ$.
Получаем следующее:
$$2angle{A}+angle{B}+angle{H}=222^circ\angle{A}+angle{B}+angle{H}=180^circ\angle{A}=222^circ-180^circ$$
Откуда получаем, что значение внутреннего угла $angle{A}$ равняется $42^circ$.
Ответ: $42^circ$.
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Основные определения
Прежде чем рассмотреть определение внешнего угла треугольника, напомним несколько основных определений из начального курса геометрии, а именно:
- угла и треугольника;
- смежных углов;
- параллельных прямых.
Угол и треугольник являются геометрическими фигурами. Угол состоит из точки (вершины) и двух лучей (сторон угла), которые исходят из данной точки. Треугольник представляет собой три точки (вершины), соединённые отрезками (сторонами). Треугольник имеет три угла.
Определение 1
Смежными называют два угла, имеющие одну общую сторону, а другие две стороны являются продолжениями друг друга.
На рисунке ниже смежными углами являются углы $ADB$ и $BDC$. $angle ADB + angle BDC = angle ADC = 180^{circ}$.
Рисунок 1. Смежные углы. Автор24 — интернет-биржа студенческих работ
Параллельными называются две непересекающиеся прямые на одной плоскости. Секущей по отношению к двум прямым называется прямая, которая пересекает две прямые в двух точках. Если две прямые параллельны, то в случае пересечения пары этих прямых секущей, получившиеся в результате этого действа накрест лежащие углы равны, а сумма односторонних углов равна $180^{circ}$.
Теорема о сумме углов треугольника
Понятие внешнего угла треугольника встречается в теореме о сумме углов треугольника, которая звучит следующим образом:
Сумма углов треугольника равна $180^{circ}$.
«Внешний угол треугольника: определение и свойство» 👇
Приведём её доказательство.
Пусть дан произвольный $triangle ABC$. Нужно доказать, что $angle A + angle B + angle C=180^{circ}$.
Рисунок 2. Теорема о сумме углов треугольника. Автор24 — интернет-биржа студенческих работ
Проведём прямую $b$ через вершину $B$, которая будет параллельна стороне $AC$.
Рисунок 3. Теорема о сумме углов треугольника. Автор24 — интернет-биржа студенческих работ
Видим, что углы 1 и 5 – накрест лежащие углы при пересечении параллельных прямых $b$ и $AC$ секущей $AB$. Углы 3 и 4 также являются накрест лежащими углами при пересечении тех же параллельных прмяых секущей $BC$. Делаем вывод, что: $angle 5 = angle 1, angle 4 = angle 3$.
Очевидно, глядя на рисунок, что сумма углов 2, 4 и 5 равна $180^{circ}$. Отсюда следует, что $angle 1 +angle 2 +angle 3 = 180^{circ}$ или $angle A + angle B + angle C=180^{circ}$. Ч.т.д.
Внешний угол треугольника
В доказательстве теоремы о сумме углов треугольника есть два примера внешнего угла треугольника. Это углы 4 и 5. Дадим определение:
Определение 2
Внешний угол треугольника – это угол, являющийся смежным с каким-нибудь углом данного треугольника.
Имеем теорему:
Теорема 2
Внешний угол треугольника равен сумме двух углов данного треугольника, не являющихся смежным с внешним углом.
Докажем эту теорему.
Рассмотрим следующий рисунок:
Рисунок 4. Внешний угол треугольника. Автор24 — интернет-биржа студенческих работ
Мы видим, что угол 4 является внешним углом, смежным с 2 углом треугольника. Очевидно, что $angle 4 +angle 2 = 180^{circ}$. По теореме о сумме углов:
$(angle 1 +angle 3)+angle 2=180^{circ}$. Отсюда следует, $angle 4 = angle 1 +angle 3$. Ч.т.д.
Рассмотрим пример задачи на данную тему.
Пример 1
Задача. $triangle ABC$ – равнобедренный. $AC$ – основание этого треугольника. $AC$=37 см, внешний угол при $B$ равняется $60^{circ}$. Нужно найти расстояние от точки $C$ до прямой $AB$.
Решение. Сделаем рисунок:
Рисунок 5. Треугольник. Автор24 — интернет-биржа студенческих работ
На рисунке прямая, обозначающая расстояние от точки $C$ до прямой $AB$ обозначена как $CD$. В математике такое расстояние называют высотой. По определению высоты треугольника, прямая высоты перпендикулярна той стороне, на которую опущена. То есть $angle ADC = 90^{circ}$.
По теореме о внешнем угле треугольника находим $angle B$: $angle B=180-60=120^{circ}$. По теореме о сумме углов треугольника получается, что $angle A + angle C = 180-120=60$. Так как треугольник равнобедренный, углы у основания равны по $30^{circ}$.
Рассмотрим $triangle ADC$. Из вышеуказанного следует, что он прямоугольный. Из свойства прямоугольных треугольников известно, что катет такого треугольника, который лежит против угла $30^{circ}$, равен половине гипотенузы. В нашем случае, $СD$ является катетом против угла $30^{circ}$, а $AC$ – гипотенуза. Поэтому справедливо утверждать, что $CD=37/2=18,5$ см.
Ответ: 18,5 см.
Таким образом, в данной статье мы получили полное представление о том, что такое внешний угол треугольника и разобрали сопутствующие теоремы.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме