![]()
Дорогие друзья! Мы уже рассматривали с вами задачи на вписанный в окружность угол. Если вы давно не решали подобных заданий, и не помните свойство вписанного угла, то обязательно ознакомьтесь с материалами и решите несколько задач, посмотрите статьи на блоге «Угол вписанный в окружность. Часть 1!» и про вписанный четырёхугольник, либо соответствующий раздел в учебной литературе.
Есть ещё один тип заданий с вписанным углом, которые входят в состав ЕГЭ. Их мы и рассмотрим в этой статье. В заданиях имеется одна особенность – окружность и угол заданы (построены) на листе в клетку и никаких градусных величин в условии не задано. Возникает вопрос: а как тогда углы-то вычислять?
Всё просто! Нужно понимать как «установить» угол, если он построен на листе в клетку, а далее использовать свойство вписанного угла. Запутал?
Начнём с самого простого. Чему равен данный угол?

Конечно же, 90 градусам.
Чему равен этот угол?

Понятно, что 45 градусам.
А этот?

Правильно, 135 градусам (90 + 45 или по-другому 180 – 45).
А такой?

225 градусов (180 + 45 или 360 – 135).
Понимания того, как стороны угла расположены относительно клеток вполне достаточно, чтобы решать такие задачи.
Ещё раз напомню основное свойство вписанного угла.
«Вписанный угол равен половине центрального,
опирающегося на ту же дугу»



27891. Найдите градусную величину дуги BC окружности, на которую опирается угол BAC. Ответ дайте в градусах.

Все подобные задания, в которых дан вписанный в окружность угол (либо центральный угол) на листе в клетку, решаются просто – угол определяется по расположению его сторон относительно клеток. Если необходимо, то используется свойство вписанного угла.
Построим центральный угол соответствующий дуге ВС:

Градусная величина дуги на которую опирается вписанный угол равна центральному углу опирающемуся на эту дугу, то есть нам необходимо найти угол ВОС:
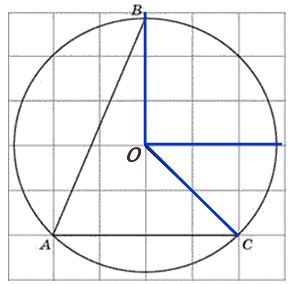
По клеткам видно, что угол ВОС равен 900 + 450 = 1350 (ОС проходит по диагонали клеток).
Ответ: 135
![]()
27887. Найдите величину угла ABC. Ответ дайте в градусах.

Посмотреть решение
27888. Найдите величину угла ABC. Ответ дайте в градусах.

Посмотреть решение
27889. Найдите величину угла ABC. Ответ дайте в градусах.

Посмотреть решение
27890. Найдите градусную величину дуги AC окружности, на которую опирается угол ABC. Ответ дайте в градусах.

Посмотреть решение
Небольшой итог!
Нужно знать свойство вписанного угла (обязательно).
Для решения подобных задач достаточно построить центральный угол и далее использовать указанное свойство.
На этом всё. Успеха Вам!
С уважением, Александр Крутицких
Когда маленький Дракула не вернулся домой из школы, его мама так и подумала: «Наверное, кол поставили».
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

© 2007 – 2023 Сообщество учителей-предметников “Учительский портал”
Свидетельство о регистрации СМИ: Эл № ФС77-64383 выдано 31.12.2015 г. Роскомнадзором.
Территория распространения: Российская Федерация, зарубежные страны.
Учредитель / главный редактор: Никитенко Е.И.
Сайт является информационным посредником и предоставляет возможность пользователям размещать свои материалы на его страницах.
Публикуя материалы на сайте, пользователи берут на себя всю ответственность за содержание этих материалов и разрешение любых спорных вопросов с третьими лицами.
При этом администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта.
Если вы обнаружили, что на сайте незаконно используются материалы, сообщите администратору через форму обратной связи — материалы будут удалены.
Все материалы, размещенные на сайте, созданы пользователями сайта и представлены исключительно в ознакомительных целях. Использование материалов сайта возможно только с разрешения администрации портала.
Фотографии предоставлены 

СДАМ ГИА:
РЕШУ ЕГЭ
Образовательный портал для подготовки к экзаменам
Математика профильного уровня
Математика профильного уровня
≡ Математика
Базовый уровень
Профильный уровень
Информатика
Русский язык
Английский язык
Немецкий язык
Французский язык
Испанский язык
Физика
Химия
Биология
География
Обществознание
Литература
История
Сайты, меню, вход, новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Об экзамене
Каталог заданий
Варианты
Ученику
Учителю
Школа
Эксперту
Справочник
Карточки
Теория
Сказать спасибо
Вопрос — ответ
Чужой компьютер
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
Играть в ЕГЭ-игрушку
Новости
1 мая
Новый сервис: можно исправить ошибки!
29 апреля
Разместили актуальные шкалы ЕГЭ — 2023
24 апреля
Учителю: обновленный классный журнал
7 апреля
Новый сервис: ссылка, чтобы записаться к учителю
30 марта
Решения досрочных ЕГЭ по математике
31 октября
Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР
НАШИ БОТЫ
Все новости
ЧУЖОЕ НЕ БРАТЬ!
Экзамер из Таганрога
10 апреля
Предприниматель Щеголихин скопировал сайт Решу ЕГЭ
Наша группа
Задания
Версия для печати и копирования в MS Word
Задания Д4 № 324461 

i
На клетчатой бумаге с размером клетки 1 см
1 см изображён угол. Найдите его градусную величину.
Спрятать решение
Решение.
Изображённый на рисунке угол равен сумме прямого угла и угла 45°, поэтому он равен 135°.
Ответ: 135.
Кодификатор ФИПИ/Решу ЕГЭ: 5.5.1 Величина угла, градусная мера угла
Спрятать решение
·
Видеокурс
·
Помощь
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
На клетчатой бумаге изображён вписанный угол
Дорогие друзья! Мы уже рассматривали с вами задачи на вписанный в окружность угол. Если вы давно не решали подобных заданий, и не помните свойство вписанного угла, то обязательно ознакомьтесь с материалами и решите несколько задач, посмотрите статьи на блоге « Угол вписанный в окружность. Часть 1! » и про вписанный четырёхугольник , либо соответствующий раздел в учебной литературе.
Есть ещё один тип заданий с вписанным углом, которые входят в состав ЕГЭ. Их мы и рассмотрим в этой статье. В заданиях имеется одна особенность – окружность и угол заданы (построены) на листе в клетку и никаких градусных величин в условии не задано. Возникает вопрос: а как тогда углы-то вычислять?
Всё просто! Нужно понимать как «установить» угол, если он построен на листе в клетку, а далее использовать свойство вписанного угла. Запутал?
Начнём с самого простого. Чему равен данный угол?
Конечно же, 90 градусам.
Чему равен этот угол?
Понятно, что 45 градусам.
Правильно, 135 градусам (90 + 45 или по-другому 180 – 45).
225 градусов (180 + 45 или 360 – 135).
Понимания того, как стороны угла расположены относительно клеток вполне достаточно, чтобы решать такие задачи.
Ещё раз напомню основное свойство вписанного угла.
«Вписанный угол равен половине центрального,
опирающегося на ту же дугу»
27891. Найдите градусную величину дуги BC окружности, на которую опирается угол BAC . Ответ дайте в градусах.
Все подобные задания, в которых дан вписанный в окружность угол (либо центральный угол) на листе в клетку, решаются просто – угол определяется по расположению его сторон относительно клеток. Если необходимо, то используется свойство вписанного угла.
Построим центральный угол соответствующий дуге ВС:
Градусная величина дуги на которую опирается вписанный угол равна центральному углу опирающемуся на эту дугу, то есть нам необходимо найти угол ВОС:
По клеткам видно, что угол ВОС равен 90 0 + 45 0 = 135 0 (ОС проходит по диагонали клеток).
27887. Найдите величину угла ABC . Ответ дайте в градусах.
27888. Найдите величину угла ABC. Ответ дайте в градусах.
27889. Найдите величину угла ABC . Ответ дайте в градусах.
27890. Найдите градусную величину дуги AC окружности, на которую опирается угол ABC . Ответ дайте в градусах.
Нужно знать свойство вписанного угла (обязательно).
Для решения подобных задач достаточно построить центральный угол и далее использовать указанное свойство.
На этом всё. Успеха Вам!
С уважением, Александр Крутицких
Когда маленький Дракула не вернулся домой из школы, его мама так и подумала: «Наверное, кол поставили».
Как найти величину угла в окружности на клетчатой бумаге
На окружности отмечены точки A и B так, что меньшая дуга AB равна 72°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
Пусть точка O — центр окружности. Угол AOB — центральный и равен дуге, на которую опирается. Значит, угол AOB равен 72°. Треугольник AOB — равнобедренный. Значит,
Таким образом, поскольку угол OBC прямой, угол ABC равен 90° − 54° = 36°.
Читатели, знакомые с теоремой «Угол между хордой и касательной равен половине дуги, стягиваемой хордой», могут решить эту задачу в одно действие: ∠ABC = 72° : 2 = 36°.
На окружности отмечены точки A и B так, что меньшая дуга AB равна 56°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
Пусть точка O — центр окружности. Угол AOB — центральный и равен дуге, на которую опирается. Значит, угол AOB равен 56°. Треугольник AOB — равнобедренный. Значит,
Таким образом, поскольку угол OBC прямой, угол ABC равен 90° − 62° = 28°.
Читатель, знающий правило «Угол между хордой и касательной равен половине дуги, стягиваемой хордой», может решить эту задачу в одно действие:
Найдите угол ABC. Ответ дайте в градусах.
Впишем в окружность квадрат так, как показано на рисунке. Стороны квадрата отсекают на окружности равные дуги. Поэтому градусная мера дуги AC, на которую опирается угол ABC, составляет полного угла 360°, т. е. равна 270°. Угол ABC вписанный, поэтому он равен половине дуги, на которую опирается. Следовательно, угол ABC равен 135°.
Как находить угол в окружности по клеточкам
На клетчатой бумаге изображён вписанный угол
Дорогие друзья! Мы уже рассматривали с вами задачи на вписанный в окружность угол. Если вы давно не решали подобных заданий, и не помните свойство вписанного угла, то обязательно ознакомьтесь с материалами и решите несколько задач, посмотрите статьи на блоге « Угол вписанный в окружность. Часть 1! » и про вписанный четырёхугольник , либо соответствующий раздел в учебной литературе.
Есть ещё один тип заданий с вписанным углом, которые входят в состав ЕГЭ. Их мы и рассмотрим в этой статье. В заданиях имеется одна особенность – окружность и угол заданы (построены) на листе в клетку и никаких градусных величин в условии не задано. Возникает вопрос: а как тогда углы-то вычислять?
Всё просто! Нужно понимать как «установить» угол, если он построен на листе в клетку, а далее использовать свойство вписанного угла. Запутал?
Начнём с самого простого. Чему равен данный угол?
Конечно же, 90 градусам.
Чему равен этот угол?
Понятно, что 45 градусам.
Правильно, 135 градусам (90 + 45 или по-другому 180 – 45).
225 градусов (180 + 45 или 360 – 135).
Понимания того, как стороны угла расположены относительно клеток вполне достаточно, чтобы решать такие задачи.
Ещё раз напомню основное свойство вписанного угла.
«Вписанный угол равен половине центрального,
опирающегося на ту же дугу»
27891. Найдите градусную величину дуги BC окружности, на которую опирается угол BAC . Ответ дайте в градусах.
Все подобные задания, в которых дан вписанный в окружность угол (либо центральный угол) на листе в клетку, решаются просто – угол определяется по расположению его сторон относительно клеток. Если необходимо, то используется свойство вписанного угла.
Построим центральный угол соответствующий дуге ВС:
Градусная величина дуги на которую опирается вписанный угол равна центральному углу опирающемуся на эту дугу, то есть нам необходимо найти угол ВОС:
По клеткам видно, что угол ВОС равен 90 0 + 45 0 = 135 0 (ОС проходит по диагонали клеток).
27887. Найдите величину угла ABC . Ответ дайте в градусах.
27888. Найдите величину угла ABC. Ответ дайте в градусах.
27889. Найдите величину угла ABC . Ответ дайте в градусах.
27890. Найдите градусную величину дуги AC окружности, на которую опирается угол ABC . Ответ дайте в градусах.
Нужно знать свойство вписанного угла (обязательно).
Для решения подобных задач достаточно построить центральный угол и далее использовать указанное свойство.
На этом всё. Успеха Вам!
С уважением, Александр Крутицких
Когда маленький Дракула не вернулся домой из школы, его мама так и подумала: «Наверное, кол поставили».
Круг на клетчатой бумаге
Рассмотрим задачи, в которых изображён круг на клетчатой бумаге и требуется по известной площади круга найти площадь заштрихованного сектора либо найти площадь круга по данному значению площади сектора.
Для решения обеих задач надо определить величину соответствующего ему центрального угла.
Градусная мера окружности — 360°. Зная центральный угол, найдем, какую часть площадь закрашенного сектора составляет от площади круга.
Самые простые задания этого вида — те, в которых центральный угол — прямой. 90° составляют четверть от 360°. Отсюда, для нахождения площади сектора площадь круга следует разделить на 4. И наоборот, для нахождения площади круга по известной площади сектора площадь сектора умножаем на 4.
Стороны прямого угла, чаще всего, либо проведены по клеточкам (одна сторона — горизонтально, другая — вертикально), либо делят каждую клеточку по диагонали (как диагональ квадрата).
Определить прямой угол можно даже с помощью листа бумаги (приложив его к центру круга).
1) На клетчатой бумаге изображён круг площадью 60.
Найти площадь заштрихованного сектора.
Так как центральный угол, соответствующий данному сектору, равен 90º, то
2) На клетчатой бумаге изображён круг.
Какова площадь круга, если площадь заштрихованного сектора равна 17?
Так как стороны угла делят каждую клеточку по диагонали, образуя с горизонтальной прямой, проходящей из вершины угла, углы по 45°, то центральный угол равен 90º.
Следовательно, площадь сектора составляет 1/4 от площади круга: Sкруга=Sсектора:(1/4)=17·4=68.
3) Найти площадь круга, если площадь заштрихованного сектора равна 21.
Площадь заштрихованного сектора составляет 3/4 площади круга.
Следовательно, чтобы найти площадь круга, надо площадь сектора разделить на 3/4:
4) Какова площадь круга если известно, что площадь закрашенного сектора равна 11?
Соответствующий центральный угол равен 45° (одно сторона угла проведена по горизонтали, другая делит каждую клеточку по диагонали (является диагональю квадрата).
Так как 45° составляет от 360° 1/8 часть, то
5) На клетчатой бумаге изображен круг площадью 96.
Найдите площадь заштрихованного сектора.
Центральный угол, соответствующий незакрашенной части, равен 45°, то есть составляет 1/8 площади круга.
Sзакрашенного сектора=Sнезакрашенного сектора-Sкруга=96-12=84.
А как определить на клетчатой бумаге центральные углы в 60° и 30°?
Можно рассуждать следующим образом.
Рассмотрим треугольник ABC.
Так как BH — его высота и медиана, то ABC — равнобедренный с основанием AO. Значит, AB=BO.
Но AO=BO (как радиусы).
Следовательно, AB=BO=AO, то есть треугольник ABC — равносторонний. Следовательно, все его углы равны по 60°, в частности, ∠AOB=60°.
6) Найти площадь заштрихованного сектора, если площадь круга равна 30.
Соответствующий центральный угол равен 60°. Значит, площадь сектора составляет 1/6 от площади круга и Sсектора=Sкруга:6=30:6=5.
7) Найти площадь круга, если площадь заштрихованного сектора равна 24.
Так как центральный угол заштрихованного сектора равен 30°, то площадь сектора составляет 1/12 часть от площади круга.
8) Найти площадь круга, изображенного на клетчатой бумаге, если площадь заштрихованного сектора равна 60.
Центральный угол, соответствующий незакрашенному сектору, равен 60°. Значит, площадь незакрашенной части составляет 1/6 площади круга.
Следовательно, на площадь закрашенной части приходится 5/6 круга:
В некоторых случаях центральный угол можно найти как сумму или разность других центральных углов.
9) Центральный угол равен 30+45=75°,
площадь заштрихованного сектора составляет
1/12+1/8=5/24 площади круга, то есть
10) Центральный угол равен 180-30=150°,
площадь заштрихованного сектора составляет 1/2-1/12=5/12 площади круга,
11) Центральный угол равен 60-45=15°,
площадь заштрихованного сектора составляет 1/24 площади круга
12) Центральный угол равен 15+90=105°
Как находить угол в окружности по клеточкам
На окружности отмечены точки A и B так, что меньшая дуга AB равна 72°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
Пусть точка O — центр окружности. Угол AOB — центральный и равен дуге, на которую опирается. Значит, угол AOB равен 72°. Треугольник AOB — равнобедренный. Значит,
Таким образом, поскольку угол OBC прямой, угол ABC равен 90° − 54° = 36°.
Читатели, знакомые с теоремой «Угол между хордой и касательной равен половине дуги, стягиваемой хордой», могут решить эту задачу в одно действие: ∠ABC = 72° : 2 = 36°.
На окружности отмечены точки A и B так, что меньшая дуга AB равна 56°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
Пусть точка O — центр окружности. Угол AOB — центральный и равен дуге, на которую опирается. Значит, угол AOB равен 56°. Треугольник AOB — равнобедренный. Значит,
Таким образом, поскольку угол OBC прямой, угол ABC равен 90° − 62° = 28°.
Читатель, знающий правило «Угол между хордой и касательной равен половине дуги, стягиваемой хордой», может решить эту задачу в одно действие:
Найдите угол ABC. Ответ дайте в градусах.
Впишем в окружность квадрат так, как показано на рисунке. Стороны квадрата отсекают на окружности равные дуги. Поэтому градусная мера дуги AC, на которую опирается угол ABC, составляет полного угла 360°, т. е. равна 270°. Угол ABC вписанный, поэтому он равен половине дуги, на которую опирается. Следовательно, угол ABC равен 135°.
[spoiler title=”источники:”]
http://oge.sdamgia.ru/search?search=%D0%9D%D0%B0%D0%B9%D0%B4%D0%B8%D1%82%D0%B5%20%D1%83%D0%B3%D0%BE%D0%BB%20ABC
http://b4.cooksy.ru/articles/kak-nahodit-ugol-v-okruzhnosti-po-kletochkam
[/spoiler]
Рассказываем, как решать на нахождение градусной меры угла. Приводим алгоритм и примеры решения. Задачи для самостоятельного решения.
Суть задач на нахождение градусной меры угла
Задачи на нахождение градусной меры угла – это геометрические задачи на построение и нахождение величины угла, выраженной в градусах.
Алгоритм решения задач
Алгоритм решения задач на нахождение градусной меры угла:
- Выполняем краткую запись задачи;
- Определяем способ и решаем задачу;
- Выписываем полный ответ.
Определяем способ решения:
Способы решения задач
Примеры решения задачи
Задача 1. Угол AOB — развернутый. Провели луч OD. Найти градусную меру угла AOD, если угол AOD в 4 раза больше угла BOD.
Краткая запись:
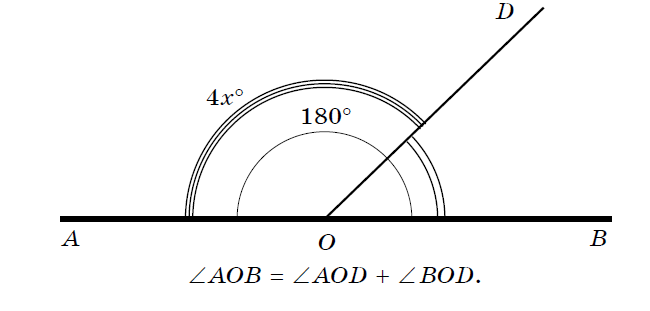
Решение:
- Пусть ∠ BOD = x°, тогда ∠ AOD = 4x°.
Так как их сумма равна 180°, составим и решим уравнение:
(4x+x=180)
(5x=180)
(x=180:5)
(x=36).
Итак, ∠ BOD = 36°, тогда ∠ AOD = 4 ⋅ 36° = 144° (или ∠ AOB = 180° – 36° = 144°).
Ответ: ∠ AOD = 144°.
Задачи для самостоятельного решения
- Луч BD — биссектриса ∠ ABC. Найти градусную меру ∠ DBC, если ∠ ABC = 160°.
- ∠ AOC = 132°, провели луч OB внутри ∠ AOC. Найти градусную меру ∠ AOB, если ∠ BOC = 35°.
- Внутри прямого угла ACB провели луч CD. Найти градусные меры углов ACD и BCD, если разность градусных мер углов ACD и BCD равна 40°.
- Определить градусную меру ∠ KON, изображенного на рисунке, если ∠ EOP = ∠ DOP, ON — биссектриса ∠ DOP.
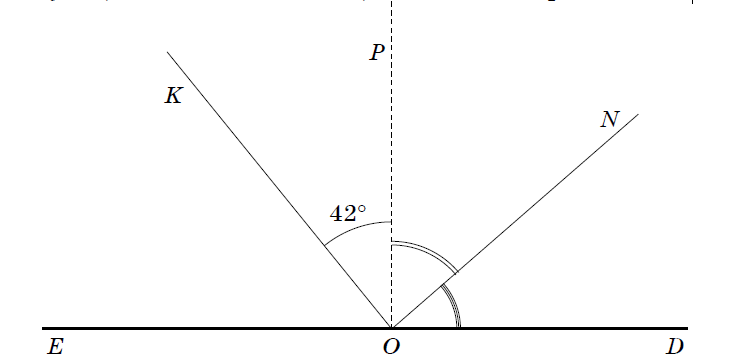
Посмотреть еще в категории: Задачи по математике 5-6 класс
- Задачи на сложение и вычитание
- Задачи на движение навстречу друг другу
- Задачи на движение в одном направлении
- Задачи на движение в противоположных направлениях
- Задачи на движение по реке
- Задачи на нахождение дроби от числа
- Задачи на нахождение числа по его дроби
- Задачи на нахождение процента от числа
- Задачи на нахождение числа по его процентам
- Задачи на процентное отношение двух чисел
- Задачи на проценты (с помощью пропорции)
- Задачи на нахождение периметра и площади треугольника
- Задачи с использованием формул площадей прямоугольника и квадрата
- Задачи на нахождение объема прямоугольного параллелепипеда и куба
- Задачи на проценты
- Задачи на нахождение длины окружности и площади круга
