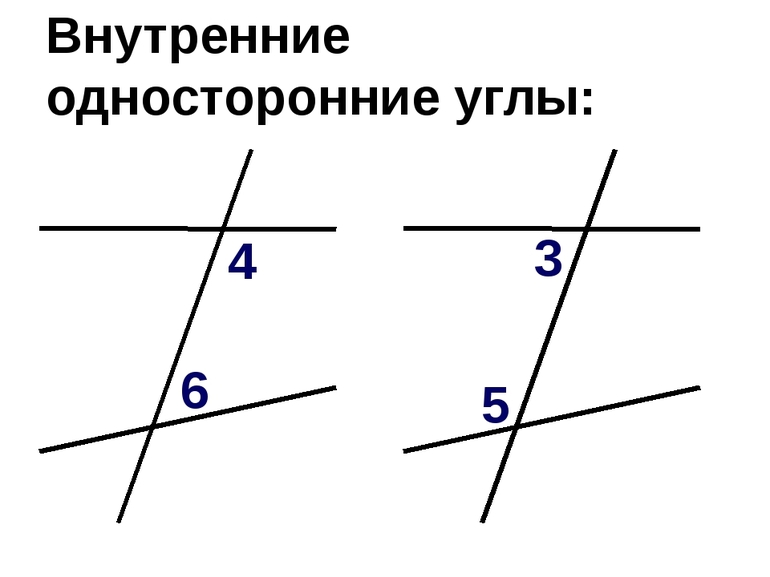
Внутренние односторонние углы — теория, правило и свойства
Чтобы дать верное определение внутренним односторонним углам, нужно отличать их от вертикальных, смежных, соответственных и накрест лежащих. Их объединяет то, что они могут быть образованы двумя параллельными прямыми и пересекающей их линией. Утверждение о том, что сумма внутренних односторонних углов составляет 180 градусов, позволяет доказать теорему о параллельности прямых.
Углы по определению
Прямая, которая пересекает другие линии, идущие параллельно друг другу, образует не только внутренние, но и внешние углы. Один из них дополняет другой до 180 градусов. Это свойство можно доказать как для смежных, так и односторонних внутренних, каждый из которых имеет соответственный внешний.
Углы, расположенные на одной стороне от секущей, пересекающей 2 линии, идущие параллельно, называются накрест лежащими. Они отличаются от односторонних, образуя с ними смежные. В сумме они составляют 180 градусов.
Отрезок между линиями, проведенными параллельно между собой, можно обозначить AB. Если представить, что AB=0, то параллельные будут совпадать, а соответственные углы и односторонние станут смежными. Их сумма должна быть 180 градусов.
Доказательство теоремы
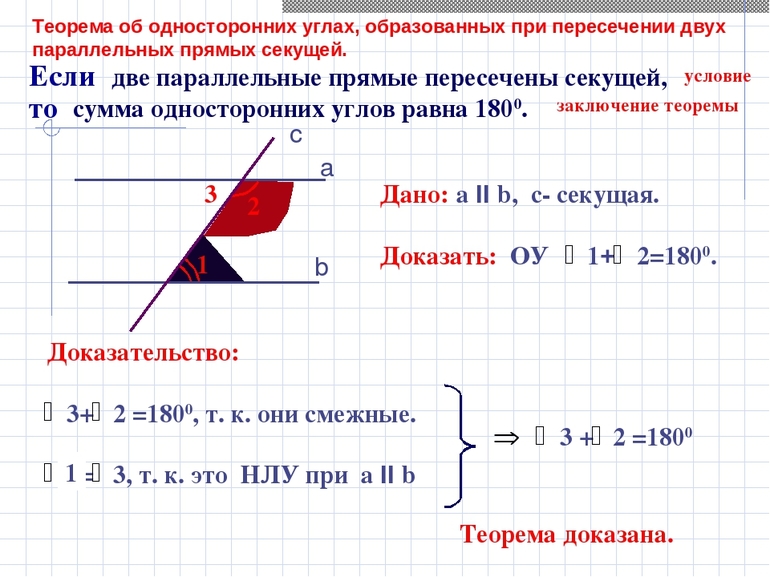
Прямые являются параллельными, если сумма односторонних внутренних углов равна 180. Нужно доказать теорему по исходным данным. Секущая АВ является линией пересечения параллельных а и b.
Для доказательства теоремы можно допустить, что линии не являются параллельными, значит они пересекают друг друга в определенной точке С. Секущая АВ образует с а и b треугольник АВС, поскольку точка С лежит в одной из двух плоскостей относительно АВ. На линии а расположена сторона треугольника АС, а на b — ВС.
Если в противоположной полуплоскости отложить точку С1, то она образует с АВ другой треугольник АВС1. При этом по построению углы ВАС и АВС1 равны. Сумма САВ и СВА составляет 180, что указано в условии задачи. Следовательно, сторона АС1 принадлежит а, аналогично, ВС1 — линии b.
Точка пересечения С линий а и b принадлежит этим прямым. Вместе с тем точка С1 не может лежать на каждой из них, поскольку она находится в полуплоскости, где линии по построению не пересекаются.
Если в сумме односторонние углы составляют 180, то треугольника АВС1 не существует, значит а || b.
Следствие из свойства прямых
На прямую а может быть опущен единственный перпендикуляр из любой точки А, которая не принадлежит данной линии. Доказательство утверждения состоит из следующих шагов:
Итак, отрезок АВ является единственным перпендикуляром, проходящим через точку А.
Построение параллелограмма
Если односторонние углы не прямые, то один из них является острым, а другой — тупым, то есть меньшим или большим по величине. Если через каждый из них провести биссектрисы, то они должны пересечь противоположные стороны в определенных точках. Для этого достаточно отложить отрезки на параллельных линиях, равные AB, используя циркуль.
Секущая и отрезки, принадлежащие проведенным биссектрисам, образуют 2 треугольника вместе с параллельными. Напротив большего угла будет находиться биссектриса, отсекающая наибольший отрезок. Это подтверждает теорема о соотношении между углами и сторонами разностороннего треугольника.
Соединив точки пересечения биссектрис с параллельными прямыми, можно построить четырехугольник ABCD. Чтобы доказать, что полученная фигура является параллелограммом, достаточно учесть следующее:
Отложив от A и B равноудаленные точки C и D, можно получить линию CD, которая параллельна AB. Тогда CD — отрезок, перпендикулярный параллельным прямым BC и AD. Поскольку все отрезки полученной фигуры ABCD пересекаются перпендикулярно, то она является прямоугольником по построению.
Доказательство теоремы позволяет определять, какой является величина второго из двух внутренних односторонних углов при параллельных прямых и секущей. Решение задач по геометрии позволяет найти их градусную меру и в зависимости от разности между ними.
Углы при пересечении двух прямых
Если какие-нибудь две прямые пересечены третьей прямой, то пересекающая их прямая называется секущей по отношению к прямым, которые она пересекает.
При пересечении двух прямых третьей, образуется два вида углов: внешние и внутренние.
На рисунке изображены две прямые a и b, пересекаемые прямой c. Прямая c по отношению к прямым a и b является секущей. Синим цветом на рисунке обозначены внешние углы (∠1, ∠2, ∠7 и ∠8), а красным — внутренние углы (∠3, ∠4, ∠5 и ∠6).
Также при пересечении двух прямых третьей, образовавшиеся углы получают попарно следующие названия:
Углы при пересечении параллельных прямых
Если секущая пересекает две параллельные прямые линии, то:
- внутренние накрест лежащие углы равны;
- сумма внутренних односторонних углов равна 180°;
- соответственные углы равны;
- внешние накрест лежащие углы равны;
- сумма внешних односторонних углов равна 180°.
Углы при параллельных прямых и секущей. Вертикальные, смежные, односторонние, соответственные, накрест лежащие углы
Пусть прямая с пересекает параллельные прямые и . При этом образуется восемь углов. Углы при параллельных прямых и секущей так часто используются в задачах, что в геометрии им даны специальные названия.
Углы и — вертикальные. Очевидно, вертикальные углы равны, то есть
Конечно, углы и , и — тоже вертикальные.
Углы и — смежные, это мы уже знаем. Сумма смежных углов равна .
Углы и (а также и , и , и ) — накрест лежащие. Накрест лежащие углы равны.
Углы и — односторонние. Они лежат по одну сторону от всей «конструкции». Углы и — тоже односторонние. Сумма односторонних углов равна , то есть
Углы и (а также и , и , и ) называются соответственными.
Соответственные углы равны, то есть
Углы и (а также и , и , и ) называют накрест лежащими.
Накрест лежащие углы равны, то есть
Чтобы применять все эти факты в решении задач ЕГЭ, надо научиться видеть их на чертеже. Например, глядя на параллелограмм или трапецию, можно увидеть пару параллельных прямых и секущую, а также односторонние углы. Проведя диагональ параллелограмма, видим накрест лежащие углы. Это — один из шагов, из которых и состоит решение.
Ты нашел то, что искал? Поделись с друзьями!
1. Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении , считая от вершины тупого угла. Найдите большую сторону параллелограмма, если его периметр равен .

Пусть — биссектриса тупого угла . По условию, отрезки и равны и соответственно.
Рассмотрим углы и . Поскольку и параллельны, — секущая, углы и являются накрест лежащими. Мы знаем, что накрест лежащие углы равны. Значит, треугольник — равнобедренный, следовательно, .
Периметр параллелограмма — это сумма всех его сторон, то есть
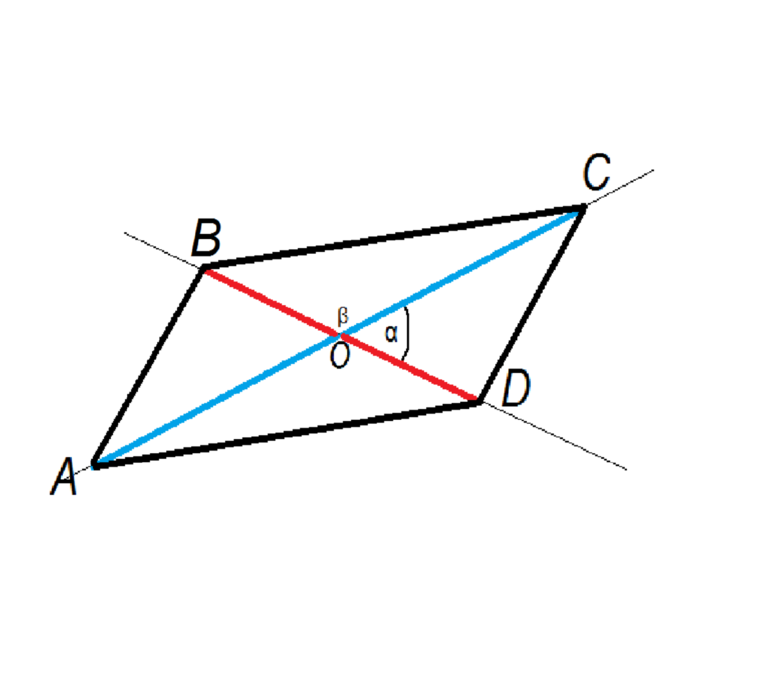
2. Диагональ параллелограмма образует с двумя его сторонами углы и . Найдите больший угол параллелограмма. Ответ дайте в градусах.
Нарисуйте параллелограмм и его диагональ. Заметив на чертеже накрест лежащие углы и односторонние углы, вы легко получите ответ: .
3. Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна ? Ответ дайте в градусах.

Давайте посмотрим на чертеж. По условию, , то есть .
Углы и — односторонние при параллельных прямых и секущей, следовательно,
[spoiler title=”источники:”]
http://izamorfix.ru/matematika/planimetriya/ugly_dvuh_pryam.html
http://ege-study.ru/ru/ege/materialy/matematika/ugly-pri-parallelnyx-pryamyx/
[/spoiler]
Углы по определению
Прямая, которая пересекает другие линии, идущие параллельно друг другу, образует не только внутренние, но и внешние углы. Один из них дополняет другой до 180 градусов. Это свойство можно доказать как для смежных, так и односторонних внутренних, каждый из которых имеет соответственный внешний.
Углы, расположенные на одной стороне от секущей, пересекающей 2 линии, идущие параллельно, называются накрест лежащими. Они отличаются от односторонних, образуя с ними смежные. В сумме они составляют 180 градусов.
Отрезок между линиями, проведенными параллельно между собой, можно обозначить AB. Если представить, что AB=0, то параллельные будут совпадать, а соответственные углы и односторонние станут смежными. Их сумма должна быть 180 градусов.
Доказательство теоремы
Прямые являются параллельными, если сумма односторонних внутренних углов равна 180. Нужно доказать теорему по исходным данным. Секущая АВ является линией пересечения параллельных а и b.
Для доказательства теоремы можно допустить, что линии не являются параллельными, значит они пересекают друг друга в определенной точке С. Секущая АВ образует с а и b треугольник АВС, поскольку точка С лежит в одной из двух плоскостей относительно АВ. На линии а расположена сторона треугольника АС, а на b — ВС.
Если в противоположной полуплоскости отложить точку С1, то она образует с АВ другой треугольник АВС1. При этом по построению углы ВАС и АВС1 равны. Сумма САВ и СВА составляет 180, что указано в условии задачи. Следовательно, сторона АС1 принадлежит а, аналогично, ВС1 — линии b.
Точка пересечения С линий а и b принадлежит этим прямым. Вместе с тем точка С1 не может лежать на каждой из них, поскольку она находится в полуплоскости, где линии по построению не пересекаются.
Если в сумме односторонние углы составляют 180, то треугольника АВС1 не существует, значит а || b.
Следствие из свойства прямых
На прямую а может быть опущен единственный перпендикуляр из любой точки А, которая не принадлежит данной линии. Доказательство утверждения состоит из следующих шагов:
- Вначале следует отметить на прямой а произвольную точку, обозначив ее С1.
- Далее можно провести через С1 линию с, перпендикулярную а.
- Затем через точку А нужно начертить АС2, которая параллельна с.
- После этого следует предположить о существовании перпендикуляра, который вместе с АС2 пересекает линию а с образованием третьего отрезка АС3.
- Поскольку из точки А нельзя проводить перпендикуляр АС3 и править треугольник АС2С3, дополняя его другим перпендикулярным отрезком, то согласно свойству параллельных прямых АС2||АС3.
Итак, отрезок АВ является единственным перпендикуляром, проходящим через точку А.
Построение параллелограмма
Если односторонние углы не прямые, то один из них является острым, а другой — тупым, то есть меньшим или большим по величине. Если через каждый из них провести биссектрисы, то они должны пересечь противоположные стороны в определенных точках. Для этого достаточно отложить отрезки на параллельных линиях, равные AB, используя циркуль.
Секущая и отрезки, принадлежащие проведенным биссектрисам, образуют 2 треугольника вместе с параллельными. Напротив большего угла будет находиться биссектриса, отсекающая наибольший отрезок. Это подтверждает теорема о соотношении между углами и сторонами разностороннего треугольника.
Соединив точки пересечения биссектрис с параллельными прямыми, можно построить четырехугольник ABCD. Чтобы доказать, что полученная фигура является параллелограммом, достаточно учесть следующее:
- По построению AB=BD=AD.
- Следовательно, AB=CD.
- Точки C и D равноудалены от A и B.
- Отрезки AB и CD параллельны.
- Полученная фигура ABCD представляет собой параллелограмм, так как ее стороны попарно равны и параллельны.
Отложив от A и B равноудаленные точки C и D, можно получить линию CD, которая параллельна AB. Тогда CD — отрезок, перпендикулярный параллельным прямым BC и AD. Поскольку все отрезки полученной фигуры ABCD пересекаются перпендикулярно, то она является прямоугольником по построению.
Доказательство теоремы позволяет определять, какой является величина второго из двух внутренних односторонних углов при параллельных прямых и секущей. Решение задач по геометрии позволяет найти их градусную меру и в зависимости от разности между ними.
Пересечение двух параллельных прямых секущей
Параллельными называются пара прямых, которые при продолжении не пересекаются.
Когда две паралелльные прямые $a$ и $b$ пересекаются секущей $c$ , то образуется много разнообразных углов.
Некоторые пары углов имеют свои имена – названия:
пара накрест лежащие углы : ∠3 и ∠5, ∠4 и ∠6;
пара односторонние углы : ∠4 и ∠5, ∠3 и ∠6;
пара соответственные углы : ∠1 и ∠5, ∠4 и ∠8, ∠2 и ∠6, ∠3 и ∠7.
Свойства:
- накрест лежащие углы равны: 3 = 5, 4 = 6.
- соответственные углы равны: 1 = 5, 4 = 8, 2 = 6, 3 = 7.
- сумма односторонних углов равна 180 градусов: 3 + 6 = 180 градусов, 4 + 5 = 180 градусов.

_____________________________________________________________________________________
Теорема Если две параллельные линии пересекаются третьей (Секущей), тогда выполняется следующее:
ТеоремаТеорема * накрест лежащие углы равны ;
ТеоремаТеорема * соответственные углы равны ;
ТеоремаТеорема * сумма односторонних углов 180 град. ;
ТеоремаТеорема * вертикальные равны ∠3 = ∠1, ∠8 = ∠6 .
_____________________________________________________________________________________
Теорема Если две прямые перпендикулярны (обе одновременно) к третьей, то они параллельны друг другу.
_____________________________________________________________________________________
Теорема Если две прямые не параллельны друг другу, то равенства для сумм углов не выполняются: 3 + 6 < 180 ; 4 + 5 > 180 .
_____________________________________________________________________________________
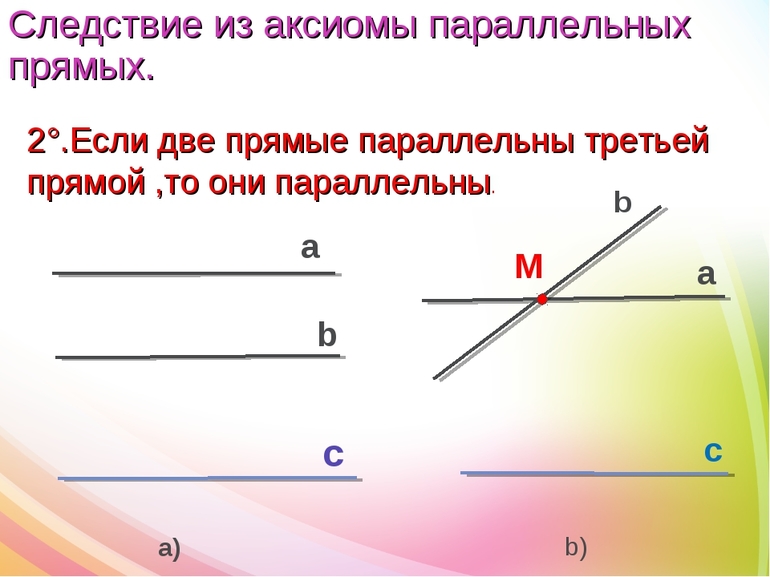
Теорема Если одна прямая параллельна второй, а вторая параллельна третьей, то первая прямая так же параллельна третьей.
_____________________________________________________________________________________
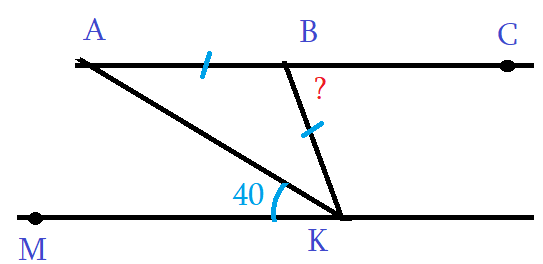
Задача 1: На рисунке АС и МК параллельны, отрезки АВ = ВК равные. Дан угол ∠АКМ = 40°. Найти ∠КВС.
- Решение: АС ║ МК параллельны, АК – секущая, $Rightarrow$ ∠АКМ и ∠КАВ накрест лежащие, $Rightarrow$ ∠КАВ = 40°.
- ∆АВК – равнобедренный, АВ = ВК $Rightarrow$ углы у основания ∠КАВ = ∠АКВ значит, $Rightarrow$ ∠АКВ = 40°.
- Значит, углы ∠АКВ = ∠АКМ равные. Угол ∠МКВ состоит из частей, аддитивность, ∠МКВ = ∠АКВ + ∠АКМ = 80°.
- АС ║ МК параллельны, АК – секущая, $Rightarrow$ ∠ВКМ и ∠КВС накрест лежащие, $Rightarrow$ Ответ: ∠КВС = 80°.
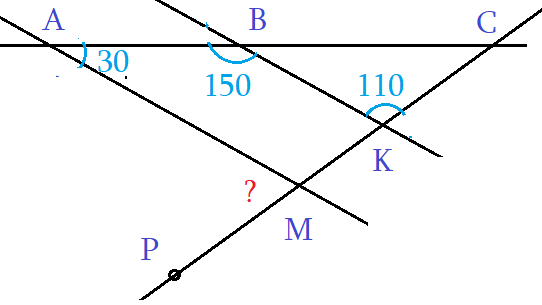
Задача 2: На рисунке, даны углы ∠ВАМ = 30°, ∠АВК = 150°, ∠ВКС = 110°. Найти ∠АМР.
- Решение: Углы ∠ВАМ и ∠АВК – односторонные от секущей АВ. Их сумма ∠ВАМ + ∠АВК = 180°.
- Сумма односторонных 180°? … по теореме “о параллельных”, прямые АМ и ВК должны быть параллельными. АМ ║ ВК.
- Теперь: АМ ║ ВК, СР – секущая. Односторонные углы равные, ∠ВКС = ∠АМК. Значит, ∠АМК = 110°.
- Наконец, углы ∠АМК и ∠АМР – смежные. Значит, ∠АМК + ∠АМР = 180°. $Rightarrow$ ∠АМР = 180° – ∠АМК = 70°.
- Ответ: ∠АМР = 70°. Замечание: “надо видеть все секущие к параллельным, и углы к ним”.
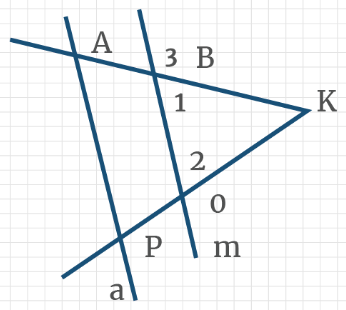
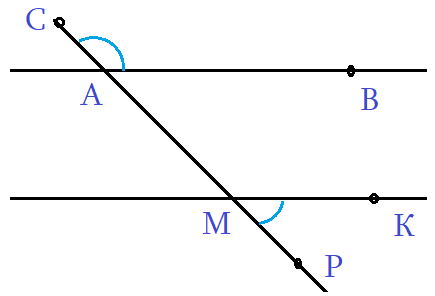
Задача 3: На рисунке, АВ параллельно МК, угол ∠РМК составляет треть угла ∠САВ. Найти эти углы.
- Решение: Дано: отношение углов ∠РМК : ∠САВ = 1 : 3. Выразим: ∠САВ = 3∠РМК
- Как связаны искомые углы по рисунку? ∠САВ и ∠МАВ – смежные, значит ∠МАВ = 180° – ∠САВ.
- Углы ∠МАВ и ∠РМК односторонные углы при параллельных АВ ║ МК и секущей РС. Значит, ∠МАВ = ∠РМК
- Из двух равенств получаем ∠РМК = 180° – ∠САВ. Вспомним ∠САВ = 3∠РМК, подставим: ∠РМК = 180° – 3∠РМК
- ∠РМК = 45°, значит ∠САВ = 3∠РМК = 135°. Ответ: 45°, 135°
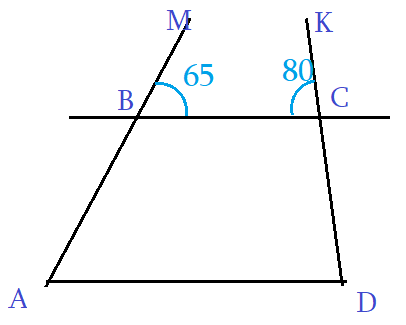
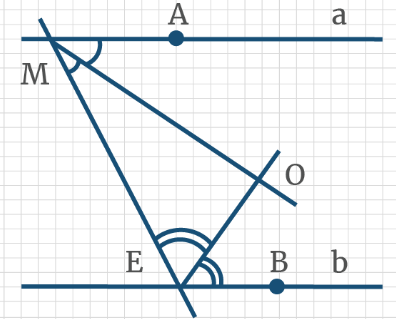
Задача 4: На рисунке, АD параллельно ВС, угол ∠МВС = 65°, ∠ВСК = 80°. Найти четырехугольника АВСD.
- Трапеция АВСD: Четырехугольник с двумя параллельными сторонами называется трапецией. АD ║ ВС.
- Решение: Угол трапеции ∠АВС смежен с ∠МВС, значит ∠АВС = 180° – ∠МВС = 115°.
- Аналогично, угол трапеции ∠ВСD смежный к углу ∠ВСК, значит ∠ВСD = 180° – ∠ВСК = 100°.
- АМ секущая к АD ║ ВС $Rightarrow$ ∠ВАD и ∠МВС соответственные, значит равные ∠ВАD = ∠МВС = 65°.
- Аналогично, КD секущая к АD ║ ВС $Rightarrow$ ∠АDС и ∠ВСК соответственные, значит равные ∠АDС = ∠ВСК = 80°.
- Ответ: Углы трапеции ∠ВАD = 65° ∠АВС = 115° ∠ВСD = 100° ∠АDС= 80°
Задача 4, продолжение, “углы в трапеции”: Пусть углы любые: ∠МВС = х, ∠ВСК = у.
- Такими же рассуждениями о смежных и односторонных, получим: ∠А = х ∠В = 180° – х ∠С = 180° – у ∠D = у
- Видно: ∠А + ∠В = 180° ∠С + ∠D = 180°. Сумма углов при боковой стороне трапеции 180° . Односторонные!
- Видно: ∠А + ∠В + ∠С + ∠D = 180°. Сумма всех углов трапеции равна 360°. . Как у четырехугольника?
Факты, Следствия из теорем о углах при параллельных и секущей к ним:
- В параллелограмме и трапеции диагонали образуют со сторонами равные накрест лежащие углы. Что секущая?
- В паралеллограмме сумма углов у одной стороны равен 180 град. – внутренные односторонные. Что секущая?
- В трапеции сумма углов у боковых сторон равен 180 град. – внутренные односторонные. Что секущая?
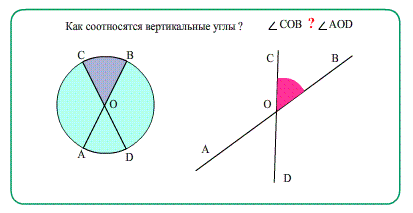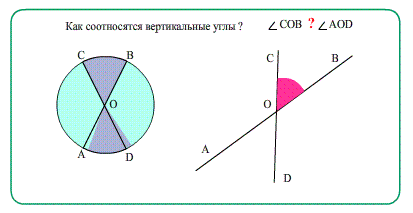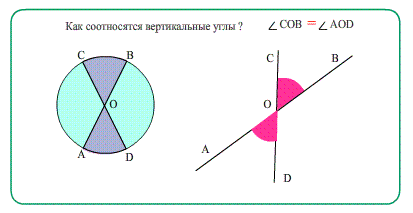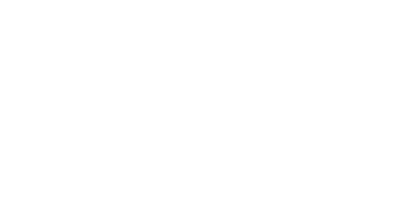
- Еще о углах: Диаметры в окружности при пересечении образуют равные вертикальные углы.
- Сумма углов треугольника 180 градусов . Достроить параллельную, увидеть секущую!
Интерактивные Упражнения:
Задачи из сайта https://resh.edu.ru :
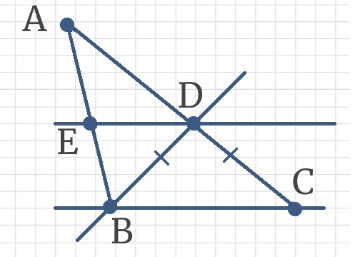
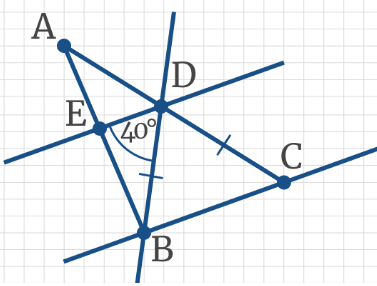
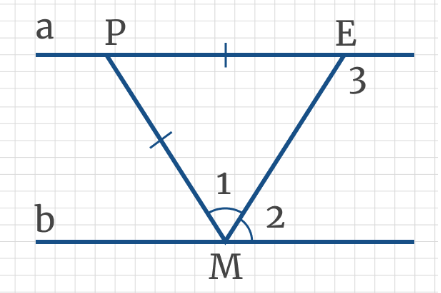
Задача 1: Установите соответствие между углами и их градусными мерами, если ∠РМЕ = 50°, а ∠1 = ∠2 и РМ = РЕ.
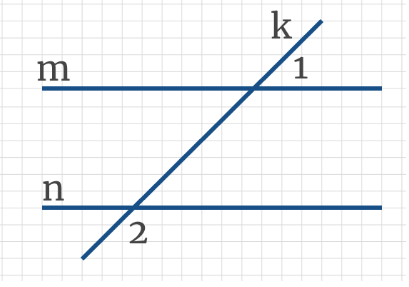
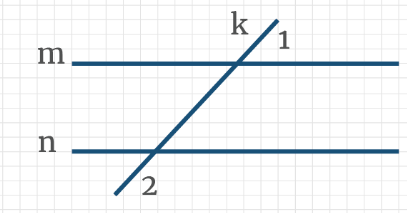
Задача 2: На рисунке через параллельные прямые m и n проведена секущая k, угол 1 составляет 50% угла 2. Найдите угол 1.
Задача 3: По рисунку найдите градусную меру неизвестного угла х. Параллельные прямые а и b пересечены секущими МК и МF.
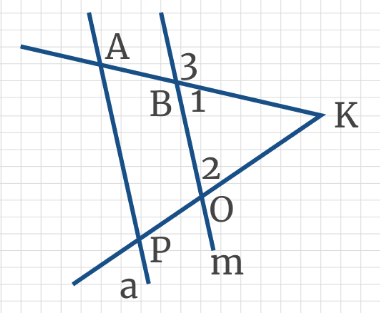
Задача 4: Прямые а и m параллельны. АК и КР – секущие, ∆ВКО – равнобедренный. ∠3 = 120°. Чему равен ∠2?
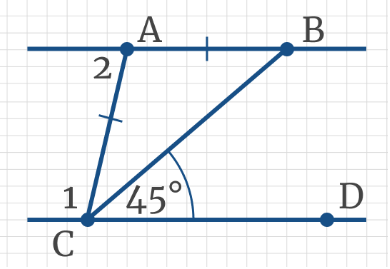
Задача 5: На рисунке прямые AB║CD, при этом AB = AC, ∠BCD = 45°. Найдите угол 2
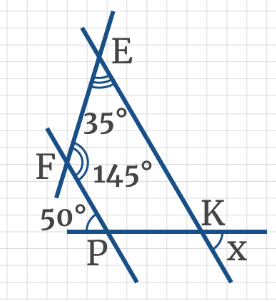
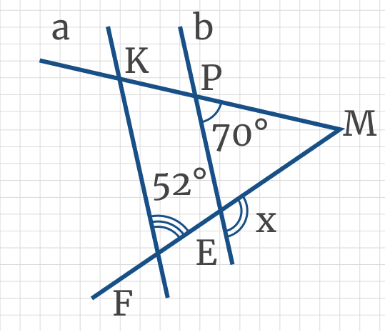
Задача 6: Прямые FP и EK параллельны, чему равна градусная мера угла x?
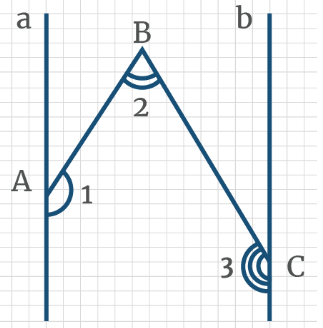
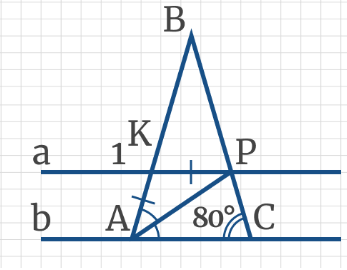
Задача 7: Через параллельные прямые а и b проведены секущие ВА и ВС, так что АВ = ВС, при этом ∠ВСА = 80°. Найдите градусную меру угла 1.
Задача 8: В треугольнике АВС BD – секущая к параллельным прямым BC и DE, при этом ВD = DC, ∠BDE = 40°. Чему равен угол ADВ?
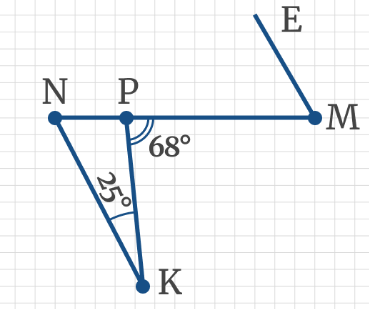
Задача 9: Прямые KN и ME параллельны. По рисунку найдите угол ЕМР, если сумма углов треугольника равна 180°.
Задача 10: На рисунке через параллельные прямые m и n проведена секущая k, угол 1 составляет 20 % угла 2. Найдите угол 1.
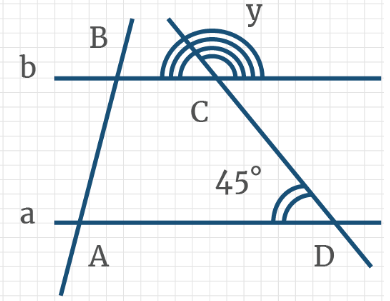
Задача 11: Прямые a и b параллельны. Основываясь на рисунке, определите, чему равна градусная мера угла y.
Задача 12: ∆ВКО – равнобедренный. ∠3 = 110°. Чему равен ∠2?
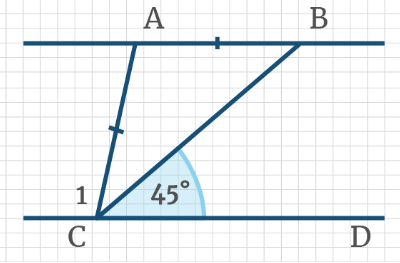
Задача 13: На рисунке AB║CD, при этом AB=AC, ∠BCD = 45°. Найдите угол BAC.
Задача 14: На рисунке прямые а║b, при этом MO и ЕО – биссектрисы углов М и Е соответственно, пересекаются в точке О. Чему равна градусная мера угла МОЕ?
Задача 15: Дан треугольник АВС. BD – секущая к параллельным прямым BC и DE, при этом ВD = DC, ∠BDE = 50°. Чему равен угол ADE?
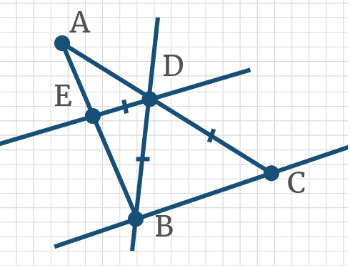
Задача 16: Прямые а и b параллельны. Чему равна градусная мера суммы углов 1, 2, 3?
Задача 17: Проведена секущая к прямым BC и DE, при этом ВD = DC, BC || DE, ∠BDE = 40°. Чему равен ∠ADE?
Задача 18: Один из односторонних углов при двух параллельных прямых и секущей на 66º меньше другого. Найдите меньший из односторонних углов.
Задача 19: Сумма пары накрест лежащих углов, образованных при пересечении параллельных прямых секущей, равна 110°. Найдите, чему равен один накрест лежащий угол.
Задача 20: “углы в параллелограмме и трапеции”:
-
один из углов параллелограмма 40. найти остальные
-
найти углы параллелограмма, если известно, что сумма двух 80. (100, 160)
-
найти углы параллелограмма, если известно, что разность двух 70. (110, 130)
-
Диагональ параллелограмма состовляет с одной из сторон углы 25 и 35. найти все углы параллелограмма
-
Углы параллелограмма относятся как 2:3 найти все углы
-
Чему равны углы равнобедренной трапеции, если разность противолежащих 40
Еще один вид углов, образованных при пересечении двух прямых секущей — внутренние односторонние углы.
Две прямые разбивают плоскость на части. Та часть, которая лежит между прямыми — внутренняя. Углы, которые расположены в этой части, так и называются — внутренние. Внутренние односторонние углы — это углы, которые лежат внутри между прямыми по одну сторону от секущей (поэтому они так и называются).
При пересечении двух прямых секущей образуется две пары внутренних односторонних углов.

∠3 и∠4
— внутренние односторонние углы при прямых a и b и секущей c.
Наибольший интерес вызывают внутренние накрест лежащие углы, образованные параллельными прямыми.
Свойство параллельных прямых
Если две параллельные прямые пересечены третьей прямой, то сумма внутренних односторонних углов равна 180º.

∠1 +∠2 =180º
(как внутренние односторонние при a ∥ b и секущей c).
Признак параллельных прямых
Если сумма внутренних односторонних углов равна 180º, то прямые параллельны.

А так как эти углы — внутренние односторонние при a и b и секущей c,
то a ∥ b (по признаку параллельных прямых).
Могут ли быть внутренние односторонние углы равны?
Да. Внутренние односторонние углы равны, если прямые параллельны, а секущая им перпендикулярна.

∠1 =∠2
тогда и только тогда, когда a ∥ b, а секущая c перпендикулярна и прямой a, и прямой b.
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Параллельные прямые
- Теорема об односторонних углах
Советуем посмотреть:
Параллельные прямые
Признаки параллельности двух прямых
Практические способы построения параллельных прямых
Аксиомы геометрии
Аксиома параллельных прямых
Теорема о накрест лежащих углах
Теорема о соответственных углах
Теорема об углах с соответственно параллельными сторонами
Теорема об углах с соответственно перпендикулярными сторонами
Параллельные прямые
Правило встречается в следующих упражнениях:
7 класс
Задание 215,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 16,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 298,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 377,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 390,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 440,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 826,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 891,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1043,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1233,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник