ГДЗ и решебники
вип уровня
- ГДЗ
- 5 класс
- Математика
- Виленкин
- Задание 1685

Условие
Найдите градусные меры углов треугольника MNKy если угол М меньше угла N на 40° и больше угла К на 10°.
Решение 1

Решение 2
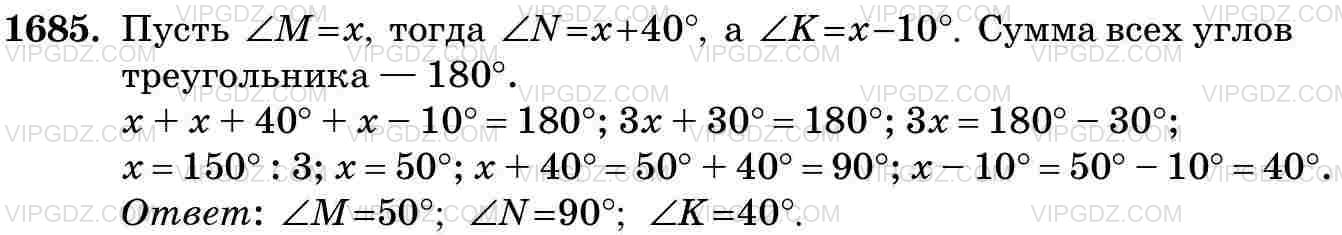
Решение 3

Популярные решебники
- Учебники
- 5 класс
- Математика 👍
- Виленкин
- №1685

Найдите градусные меры углов треугольника MNKy если угол М меньше угла N на 40° и больше угла К на 10°.

reshalka.com
Математика 5 класс Виленкин. Номер №1685
Решение
Пусть градусная мера ∟M равна х, тогда ∟N = (х + 40)°, а ∟К = (х − 10)°.
Составим и решим уравнение:
x + x + 40 + x − 10 = 180
3x + 30 = 180
х = (180 − 30) : 3 = 50°.
∟M = 50°, ∟N = 50 + 40 = 90°, ∟K = 50 − 10 = 40°.
- Предыдущее
- Следующее
Нашли ошибку?
Если Вы нашли ошибку, неточность или просто не согласны с ответом, пожалуйста сообщите нам об этом

grav81
+20
Решено
8 лет назад
Математика
5 – 9 классы
Найдите градусные меры углов треугольника МНК, если угол М меньше угла Н на 40 градусов и больше угла К на 10 градусов.
Смотреть ответ
1
Ответ
2
(3 оценки)
3

belcatya
8 лет назад
Светило науки – 1247 ответов – 0 раз оказано помощи
сумма углов треугольника=180°
пусть угол К=х°, тогда М=(х+10)°, а угол Н=((х+10)+40)°=(х+50)°
сумма углов=х+(х+10)+х+50=180°
3х+60=180°
3х=120°
х=40° – угол К
х+10=40+10=50° – угол М
х+50=40+50=90° – угол Н
Ответ: 40° – угол К, 50° – угол М, 90° – угол Н
(3 оценки)
https://vashotvet.com/task/7613562
Рассмотрим разновидность задания № (23) — геометрическая задача на нахождение градусной меры угла.
Для выполнения необходимо вспомнить теорию.
Пример:
в треугольнике
MNK
угол
M=45°
и угол
K=54°
. Вычисли градусную меру угла между высотой
NH
и биссектрисой
NL
.
Как решить задание из примера?
Для получения максимального балла задание нужно оформлять разборчивым почерком с подробным решением. Обязательно должны присутствовать чертёж, дано и решение.

Рис. (1). Чертёж
Дано:
ΔMNK
;
NH⊥MK
;
NL
— биссектриса;
∠M=45°
;
∠K=54°
.
Решение:
рассмотрим
ΔMNK
. Найдём в нём
∠N
.
(теорема о сумме углов в треугольнике).
∠N=180°−45°−54°=81°.
Так как
NL
— биссектриса, то
∠MNL=∠LNK=∠MNK:2.
∠MNL=∠LNK=81°:2=40,5°.
Рассмотрим
ΔKHN
— прямоугольный, так как
NH⊥MK
.
(свойство острых углов в прямоугольном треугольнике).
∠LNH=40,5°−36°=4,5°.
Обрати внимание!
Записываем ответ с единицами измерения.
Источники:
Рис. 1. Чертёж. © ЯКласс.
Найдите градусные меры углов треугольника MNK , если угол М меньше угла N на 40 градусов и больше угла К на 10 градусов.

Светило науки – 91 ответ – 2309 раз оказано помощи
Пусть угол М=х градусов, тогда по условиям задачи угол N=(х+40)градусов, а угол К=(х-10)градусов. Поскольку сума внутренних углов треугольника равна 180 градусам, то составим простое уравнение:
угол М+ угол N+ угол К=180 градусов
х+ (х+40)+ (х-10)=180
3х+30=180
3х=180-30
3х=150
х=50- угол М
(х+40)=50+40=90- угол N
(х-10)=50-10=40- угол К
Ответ: 50; 90; 40 градусов
Светило науки – 2 ответа – 24 помощи
Сумма всех углов в треугольнике равна 180 градусам. Составляем уравнение: угол М + угол N + угол Л = 180 градусов. заменяем углы K и N небольшим уравнением: угол М + ( угол М + 40 градусов) + (угол М – 10 градусов) = 180 соответственно раскрываем скобки и получаем следующее: угол М+угол М+угол М= 180-40+10 3М = 150 М = 50 Полученное значение угла подставляем и выясняем, что угол N= М+40, угол N = 90 градусов угол К = М-10 угол К = 40 градусов
Думаю так

