Смежные углы в геометрии
15 июня 2022
Два угла называются смежными, если у них общая вершина, общая сторона, а две других стороны образуют прямую.
В этом уроке:
- Что такое смежные углы
- Основное свойство смежных углов
- Биссектрисы смежных углов
- Тренировочные задачи
Это довольно простая, но очень важная тема.
1. Что такое смежные углы
Возьмём прямую $AB$ и отметим на ней точку $M$. Получим развёрнутый угол $AMB:$
Проведём из точки $M$ луч $MN$, не совпадающий с лучами $MA$ и $MB$.
Получим два новых угла: $angle AMN$ и $angle BMN$. Эти углы и называются смежными.
Определение. Два угла называются смежными, если у них одна общая сторона, а две других образуют прямую (или, что то же самое, являются дополнительными лучами).
Обратите внимание: чтобы углы стали смежными, им недостаточно просто иметь общую сторону. Вот эти углы — не смежные, хотя они и имеют общую сторону:
А вот дальше — смежные, хотя и расположены немного непривычно:
Часто смежные углы возникают в точке пересечения прямых. Например, при пересечении двух прямых
образуется четыре пары смежных углов: $angle ASM$ и $angle ASN$; $angle BSM$ и $angle MSN$; $angle ASN$ и $angle BSN$; наконец, $angle ASM$ и $angle BSM$.
2. Основное свойство внешних углов
У смежных углов есть замечательное свойство, которое будет преследовать нас на протяжении всей геометрии, до конца 11 класса.
Теорема. Сумма смежных углов равна 180°.
Доказательство. Рассмотрим смежные углы $AMN$ и $BMN$ с общей стороной $MN$:
Поскольку луч $MN$ делит угол $AMB$ на смежные углы $AMN$ и $BMN$, по основному свойству углов
[angle AMB=angle AMN+angle BMN]
Но угол $AMB$ — развёрнутый, поэтому
[angle AMN+angle BMN={180}^circ ]
Другими словами, если один угол равен $alpha $, то смежный с ним равен ${180}^circ -alpha $. Или если известно, что углы $alpha $ и $beta $ — смежные, то $alpha +beta ={180}^circ $.
Казалось бы, элементарные рассуждения, но их вполне достаточно, чтобы решать большой класс задач.
Задача 1. Найдите угол, смежный с углом $ABC$, если:
- $angle ABC={36}^circ $.
- $angle ABC={121}^circ $.
Решение
1) Обозначим смежный угол $DBC=x$. Он будет тупым:
Тогда $x=180-36=144$.
2) Обозначим смежный угол $DBC=x$. Он будет острым:
Тогда $x=180-121=59$.
Немного усложним задачу.
Задача 2. Найдите смежные углы, если:
- один из них на 68° больше другого.
- один из них в 5 раз больше другого.
- их градусные меры относятся как 5 : 4.
Решение.
1) Пусть один из углов равен $x$. Тогда другой (очевидно, больший) будет равен $x+68$.
Поскольку углы смежные, их сумма равна 180 градусов:
[begin{align}2x+68&=180 \ 2x&=112 \ x&=56 end{align}]
Итак, один угол равен 56 градусов. Тогда другой равен $x+68=124$ градуса.
2) Пусть меньший угол равен $x$. Тогда смежный с ним равен $5x$.
Сумма смежных углов равна 180 градусов, поэтому
[begin{align}5x+x&=180 \ 6x&=180 \ x&=30 end{align}]
Мы нашли меньший угол — он равен 30 градусов. Тогда второй угол равен $5x=150$ градусов.
3) В задачах с отношениями величинам удобно обозначать их кратными некоторой переменной. Например, если углы относятся как 5 к 4, то пусть величина одного угла будет $5x$, а другого — $4x$.
Сумма смежных углов вновь равна 180 градусов:
[begin{align}5x+4x&=180 \ 9x&=180 \ x&=20 end{align}]
Поэтому сами углы равны $4x=80$ и $5x=100$ градусов.
3. Биссектрисы смежных углов
Вновь рассмотрим смежные углы $AMN$ и $BMN$:
Построим биссектрису $MC$ угла $AMN$ и биссектрису $MD$ угла $BMN$:
Если $angle AMC=x$ и $angle BMD=y$, то $angle AMN=2x$ и $angle BMN=2y$. Это смежные углы, поэтому
[begin{align}2x+2y&={180}^circ \ x+y&={90}^circ end{align}]
Получается, что биссектрисы смежных углов всегда пересекаются под углом 90°. Этот факт известен далеко не всем ученикам. Хотя он вполне может встретиться, например, на ЕГЭ.
Задача 3. Углы $ABC$ и $MBC$ смежные, $angle ABC={70}^circ $. Луч $BD$ принадлежит углу $ABC$, причём $angle ABD={40}^circ $. Найдите угол между биссектрисами углов $CBD$ и $MBC$.
Решение. Изобразим все углы на рисунке:
Видим, что углы $ABD$ и $MBD$ — смежные. Следовательно
[begin{align}angle MBD&={180}^circ -angle ABD= \ &={180}^circ -{40}^circ ={140}^circ end{align}]
Синим цветом отмечены биссектрисы углов $CBD$ и $MBC$. Обозначим величину углов переменными: $angle CBD=2x$, $angle MBD=2y$. Но $angle MBD=angle MBC+angle CBD$, поэтому
[begin{align}2x+2y&=140 \ x+y&=70 end{align}]
Это и есть искомый угол между биссектрисами. Он равен 70 градусов.
Задача 4. Дан треугольник $ABC$. Лучи $AM$ и $CN$ лежат на одной прямой со стороной $AB$ (см. рисунок). Известно, что $angle MAC+angle ABC={180}^circ $. Докажите, что $angle MAC=angle NBC$.
Пусть $angle ABC=x$. Тогда из условия следует, что $angle MAC={180}^circ -x$.
С другой стороны, углы $ABC$ и $NBC$ смежные, поэтому $angle NBC={180}^circ -x$.
Получается, что углы $MAC$ и $NBC$ равны одному и тому же выражению. Следовательно, $angle MAC=angle NBC$, что и требовалось доказать.
Смотрите также:
- Что такое вертикальные углы

- Перпендикулярные прямые — определение и свойства

- Правила комбинаторики в задаче B6

- Метод координат в пространстве

- Четырехугольная пирамида: как найти координаты вершин

- Задача B4 про три дороги — стандартная задача на движение

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 6 октября 2021 года; проверки требуют 5 правок.

Смежные углы — это два угла, у которых одна сторона общая, а две другие дополняют друг друга до прямой. Таким образом, вместе смежные углы составляют развёрнутый угол, а сумма их угловых величин смежных всегда равна 
Таким образом, величина угла, являющимся смежным для угла величиной 

Так, например, для угла карп 


Тригонометрические соотношения[править | править код]
Синусы смежных углов равны. Их косинусы и тангенсы равны по величине, но имеют противоположные знаки (за исключением неопределённых значений).
См. также[править | править код]
- Угол
- Прилежащие углы
- Дополнительные углы
- Треугольник
Ссылки[править | править код]
- Никитин Н. Н. Геометрия. Смежные углы.
- Animated demonstration
- Angle definition pages
Как найти смежный угол
Плоским углом называют фигуру, образованную двумя лучами, исходящими из одной точки. Эта точка называется вершиной угла, а лучи – его сторонами. Если один из лучей продолжить за его начальную точку, то есть сделать прямой линией, то его продолжение образует со вторым лучом еще один угол – он называется смежным. Так как стороны угла равнозначны и продолжить можно любую из них, у каждого угла есть по два смежных.
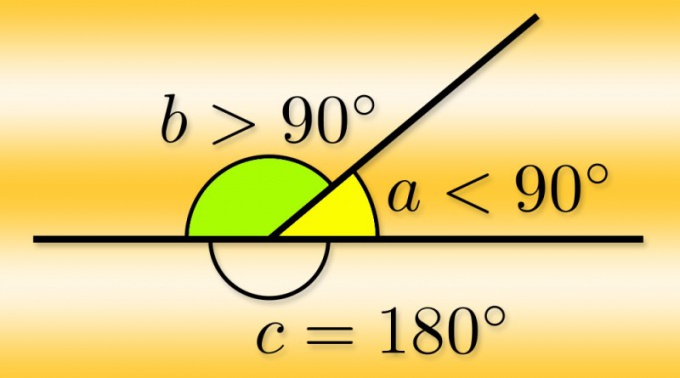
Инструкция
Если вам известна величина основного угла (α) в градусах, рассчитать градусную меру любого из пары смежных (α₁ и α₂) будет очень просто. Каждый из них дополняет основной угол до развернутого, то есть равного 180°, поэтому для их нахождения вычтите из этого числа известную величину основного угла α₁ = α₂ = 180°-α.
Величина исходного угла может быть приведена в радианах. Если и результат нужно получить в этих единицах, исходите из того, что развернутому углу соответствует количество радиан, равное числу Пи. Значит, формулу вычисления можно записать в таком виде: α₁ = α₂ = π-α.
Вместо градусной или радианной меры основного угла в условиях может быть дано соотношение величин основного и смежного углов. В этом случае составьте уравнение пропорции. Например, обозначьте через Y величину доли пропорции, относящуюся к основному углу, через X – относящуюся к смежному, а количество градусов, приходящееся на каждую единицу пропорции, обозначьте через k. Тогда общую формулу можно будет записать так: k*X+k*Y=180° или k*(X+Y)=180°. Выразите из нее общий множитель: k=180°/(X+Y). Затем рассчитайте величину смежного угла, умножив полученный коэффициент на долю этого угла в заданной пропорции: k*X = 180°/(X+Y)*X. Например, если это соотношение равно 5/13, величина смежного угла должна составлять 180°/(5+13)*13 = 10°*13 = 130°.
Если в исходных условиях ничего не сказано об основном угле, но дана величина вертикального угла, для вычисления смежных углов используйте формулы двух предыдущих шагов. Согласно определению вертикальный угол образуется двумя лучами, исходящими из той же точки, что и лучи основного угла, но направленными в строго противоположные стороны. Это значит, что градусная или радианная мера основного и вертикального угла равны, а значит, равны и величины смежных им углов.
Видео по теме
Источники:
- как найти смежный угол в треугольнике если
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Всем привет! Сегодня решил поговорить о геометрии и начать хочется с одной из первых тем 7 класса – смежные и вертикальные углы.
Смежные углы
Два угла, у которых одна сторона общая, а две другие являются продолжениями друг друга, называются смежными.
Здесь смежными углы это DOA и DOC (сторона DO общая, АО продолжение ОС и наоборот), COB и AOB (сторона ВО общая, АО продолжение ОС и наоборот).
Теперь об особенностях.
Сумма смежных углов равна 180 градусов.
Значит, DOA + DOC и COB + AOB = 180 градусов.
Теперь о вертикальных углах.
Вертикальные углы
Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого.
Если говорить простым языком, то по сути это два угла в виде “крест на крест”.
На этом рисунке углы DOA и COB, DOC и AOB – вертикальные, поскольку OC является продолжением AO, а OB продолжением DO.
Свойства:
Вертикальные углы всегда равны.
То есть DOA = COB, DOC = AOB.
Эти две теоремы нужно запомнить, чтобы решать задачи по геометрии и номер 19 из первой части ОГЭ.
Теории не очень много, поэтому эту тему можно назвать простой. Но в любой теме важна практика, так что давайте решать задачи.
Практика
1. Смежные углы относятся как 4:5. Найдите эти углы.
1) Нам известно, что сумма любых смежных углов 180 градусов.
Возьмем градусы в одной части за “икс” и составим уравнение.
4х + 5х = 180
9х = 180 х = 180 /9
х = 20
Теперь найдем углы, умножив значение “иск” на число частей угла.
2) 4х = 4 · 20 = 80 градусов 5х = 5 · 20 = 100 градусов
Ответ: Углы равны 80 и 100 градусов.
2. Найдите величину каждого из двух вертикальных углов, если их сумма равна 30 градусов.
Вертикальные углы равны, следовательно их сумму нужно разделить пополам, на 2.
30 / 2 = 15 градусов.
Ответ: 15 градусов
3. Один из смежных углов в 8 раз больше другого. Найдите оба угла.
1) Сумма смежных углов 180 градусов, зная это мы можем составить уравнение, обозначив за “икс” меньший угол.
8х + х = 180
9х =180
х = 180 / 9
х = 20
2) 8 · х = 8 · 20 = 160 градусов
Ответ: углы равны 20 и 160 градусов.
Домашка
Без нее никак)
1) Смежные углы относятся как 2:4. Найдите эти углы.
2) Один из смежных углов в 6 раз больше другого. Найдите оба угла.
3) Найдите величину каждого из двух вертикальных углов, если их сумма равна 20 градусов.
На этом все, надеюсь, что мой урок был полезен для вас. Все оставшиеся вопросы можете задавать в комментарии или мне в личные сообщения. Подписывайтесь на канал и ставьте лайки.
#математика #огэ 2022 #школа #россия #образование #огэ по математике #2021 #огэшники #подготовка к огэ по математике #геометрия













