Уважаемые студенты!
Заказать задачи по физике, информатике, экономике, праву, химии, теормеху, сопромату и другим предметам можно здесь всего за 10 минут.
Градиент функции
Как найти?
Постановка задачи
Найти градиент функции $ f(x,y,z) $ в точке $ M(x_0,y_0,z_0) $
План решения
Градиент функции $ f(x,y,z) $ – это вектор, каждая координата которого является частной производной первого порядка этой функции:
$$ grad f = frac{partial f}{partial x} overline {i} + frac{partial f}{partial y} overline{j} + frac{partial f}{partial z} overline {k} $$
- Берём частные производные первого порядка от функции $ f(x,y,z) $:
$$ frac{partial f}{partial x}, frac{partial f}{partial y}, frac{partial f}{partial z} $$ - Вычисляем полученные производные в точке $ M(x_0,y_0,z_0) $:
$$ frac{partial f}{partial x} bigg |_{M(x_0,y_0,z_0)}, frac{partial f}{partial y} bigg |_{M(x_0,y_0,z_0)}, frac{partial f}{partial z} bigg |_{M(x_0,y_0,z_0)} $$ - Подставляем, полученные данные в формулу градиента функции:
$$ grad f bigg |_M = frac{partial f}{partial x} bigg |_M overline{i} + frac{partial f}{partial y} bigg |_M overline{j} + frac{partial f}{partial z} bigg |_M overline{k} $$
Примеры решений
| Пример 1 |
| Найти градиент функции $ u = x + ln (z^2+y^2) $ в точке $ M(2,1,1) $ |
| Решение |
|
Находим частные производные первого порядка функции трёх переменных: Вычисляем значение производных в точке $ M(2,1,1) $: $$ frac{partial f}{partial x} bigg |_{M(2,1,1)} = 1 $$ $$ frac{partial f}{partial y} bigg |_{M(2,1,1)} = frac{2 cdot 1}{1^2+1^2} = frac{2}{2}=1 $$ $$ frac{partial f}{partial z} bigg |_{M(2,1,1)} = frac{2cdot 1}{1^2 + 1^2} = frac{2}{2}=1 $$ Подставляем в формулу градиента функции полученные данные: $$ grad f = 1 cdot overline{i} + 1 cdot overline{j} + 1 cdot overline{k} = overline{i}+overline{j}+overline{k} $$ Запишем ответ в координатной форме: $$ grad f = overline{i}+overline{j}+overline{k} = (1,1,1) $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ grad f = (1,1,1) $$ |
| Пример 2 |
| Найти градиент функции $ u = sin(x+2y)+2sqrt{xyz} $ в точке $ M bigg (frac{pi}{2},frac{3pi}{2},3 bigg ) $ |
| Решение |
|
Находим частные производные: $$ frac{partial f}{partial x} = cos(x+2y) + frac{yz}{sqrt{xyz}} $$ $$ frac{partial f}{partial y} = 2cos(x+2y) + frac{xz}{sqrt{xyz}} $$ $$ frac{partial f}{partial z} = frac{xy}{sqrt{xyz}} $$ Вычисляем значения производных в точке $ M bigg (frac{pi}{2},frac{3pi}{2},3 bigg ) $: $$ frac{partial f}{partial x} bigg |_{M(frac{pi}{2},frac{3pi}{2},3)} = cos(frac{pi}{2}+3pi)+ frac{frac{9pi}{2}}{sqrt{frac{9pi^2}{4}}} = cos frac{7pi}{2} + sqrt{9} = 3 $$ $$ frac{partial f}{partial y} bigg |_{M(frac{pi}{2},frac{3pi}{2},3)} = 2 cos(frac{pi}{2}+3pi) + frac{frac{3pi}{2}}{sqrt{frac{9pi^2}{4}}} = 2 cos frac{7pi}{2} + 1 = 2 cdot 0 + 1 = 1 $$ $$ frac{partial f}{partial y} bigg |_{M(frac{pi}{2},frac{3pi}{2},3)} = frac{frac{3pi^2}{4}}{sqrt{frac{9pi^2}{4}}} = sqrt{frac{pi^2}{4}} = frac{pi}{2} $$ Подставляем вычисленные недостающие данные в формулу и получаем: $$ grad f = 3 cdot overline{i}+ 1 cdot overline{j} + frac{pi}{2} cdot overline{k} = 3overline{i}+overline{j}+frac{pi}{2} overline{k} $$ Записываем ответ в координатной форме: $$ grad f = (3,1,frac{pi}{2}) $$ |
| Ответ |
| $$ grad f = (3,1,frac{pi}{2}) $$ |
Как найти градиент
Пример №1. Даны функция u = f(x,y,z); точка A(x0;y0) и вектор a(a1;a2).
Найти:
а) grad u в точке А.
б) Производную в точке А по направлению вектора а
u = x2 + 2xy + y2 + z2
A(1;1;1)
a(2;-1;0)
Решение находим с помощью калькулятора.
Градиент grad u
Как найти производную
grad u в точке А
grad u(A) = (2·1+2·1)i + (2·1+2·1)j + 2·1·k = 4i+4j+2k
Модуль grad u
Вектор а(2;-1;0)
Направляющие углы
Модуль вектора |a|.
Производная в точке А по направлению вектора а.
![]()
Пример №2. Найти grad u в точке М(0,0,0), если u=х*sin(z)-y*cos(z).
Найти производную функции u=х*y2+z3-x*y*z в точке М(1,1,2) в направлении, образующем с осями координат углы соответственно в 60о, 45о, 60о.
Пример №3. Даны функция z = f(x,y), точка A и вектор a. Найти: 1) наибольшую скорость возрастания функции в точке A; 2) скорость изменения функции в точке A по направлению вектора a.
z = ln(x2 + 3y2), A(1,1), a(3,2).
Примечание: наибольшая скорость возрастания функции в указанной точке равна модулю градиента функции в этой точке.
Скачать решение
Задача 1. Найти проекции grad z в точке М(1,2), где z=ln(4x2-y).
Задача 2. Найти производную функции z=х3-3x2y +3xy2+1 в точке М(3,1) в направлении, идущем от этой точки к точке N(6,5).
Задача 3. Даны функция z = f(x,y), точка A(x0,y0) и вектор a(a1,a2). Найти:
1) grad z в точке A;
2) производную в точке A по направлению вектора a.
Решение.
z = ln(5x2+3y2), A(1;1), a(3;2)
Скачать решение
см. также Производная функции в точке в направлении вектора
Как найти градиент
Решение находим с помощью калькулятора.
Градиент grad u
grad u в точке А
Вектор а(2;-1;0)
Направляющие углы
Модуль вектора |a| .
Производная в точке А по направлению вектора а .
Пример №2 . Найти grad u в точке М(0,0,0), если u=х*sin(z)-y*cos(z) .
Найти производную функции u=х*y 2 +z 3 -x*y*z в точке М(1,1,2) в направлении, образующем с осями координат углы соответственно в 60 о , 45 о , 60 о .
Пример №3 . Даны функция z = f(x,y) , точка A и вектор a . Найти: 1) наибольшую скорость возрастания функции в точке A ; 2) скорость изменения функции в точке A по направлению вектора a.
z = ln(x 2 + 3y 2 ), A(1,1), a(3,2).
Примечание: наибольшая скорость возрастания функции в указанной точке равна модулю градиента функции в этой точке.
Скачать решение
Задача 1. Найти проекции grad z в точке М(1,2) , где z=ln(4x 2 -y).
Задача 2. Найти производную функции z=х 3 -3x 2 y +3xy 2 +1 в точке М(3,1) в направлении, идущем от этой точки к точке N(6,5) .
Задача 3. Даны функция z = f(x,y) , точка A(x0,y0) и вектор a(a1,a2). Найти:
1) grad z в точке A ;
2) производную в точке A по направлению вектора a .
Решение.
z = ln(5x 2 +3y 2 ), A(1;1), a(3;2)
Скачать решение
Градиент функции онлайн
Градиент функции – это вектор координатами которого являются частные производные этой функции по всем её переменным.
Градиент обозначается символом набла . Выражение градиента некоторой функции записывается следующим образом:
где , , – частные производные функции по переменным , , соответственно.
Вектор градиента указывает направление наискорейшего роста функции. Рассмотрим график функции .
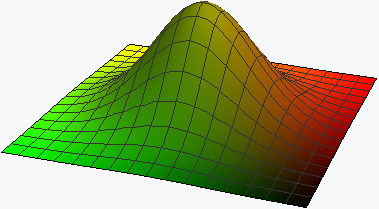
Эта функция достигает своего единственного максимума в точке . График градиентного поля данной функции имеет вид:
Из данного градика видно, что в каждой точке вектор градиента направлен в сторону наискорейшего роста функции, т.е. в точку . При этом модуль вектора отражает скорость роста (крутизну подъёма) функции в этом направлении.
Задача вычисления градиента функции очень часто возникает при поиске эстремумов функции с использованием различных численных методов.
Наш онлайн калькулятор позволяет вычислить градиент практически любой функции как общем виде, так и в конкретной точке с описанием подробного хода решения на русском языке.
Производная по направлению, градиент функции: объяснение, примеры
Понятие производной по направлению
Понятие производной по направлению рассматривается для функций двух и трёх переменных. Чтобы понять смысл производной по направлению, нужно сравнить производные по определению
Рассматривая функцию одной переменной, мы выяснили, что на оси Oy отображается приращение функции f(x) , соответствующее приращению аргумента x . Если мы имеем дело с функцией трёх переменных, то приращения аргументов x , y , z отображаются на осях Оx , Оy , Оz . Сам собой напрашивается вопрос: а где можно отобразить приращение уже не аргументов, а функции трёх переменных?
И вот ответ на этот вопрос: приращение функции трёх переменных отображается на некоторой прямой, направление которой определяется вектором, произвольно заданным в задаче.
Если рассматривается функция двух или трёх переменных, то два или три измерения задают аргументы, а упомянутая прямая, на которой отображается приращение функции, – это ещё одно измерение и для его акцентирования назовём это измерение не третьим или четвёртым, а нулевым, следуя программистской традиции (в программировании отсчёт чаще начинается не с единицы, а с нуля).
Для того, чтобы перейти к строгому математическому определению производной по направлению, нужно рассмотреть:
1) функцию u = f(M) , определённую в окрестности точки M с координатами x , y , z ;
Через точку M проводим прямую, одно из двух возможных направлений которых совпадает с направлением вектора l . На получившейся прямой отметим точку M 1 , координаты которой образуют суммы координат точки M и приращений соответствующих аргументов функции трёх переменных:
Величину отрезка MM 1 можно обозначить .
Функция u = f(M) при этом получит приращение
.
Определение производной по направлению. Предел отношения при , если он существует, называется производной функции u = f(M) по направлению вектора l и обозначается , то есть
.
Формула, которой нужно пользоваться для нахождения производной по направлению, следующая:
.
Смысл этой формулы: производная по направлению является линейной комбинацией частных производных, причём направляющие косинусы показывают вклад в производную по направлению соответствующей частной производной.
Примеры нахождения производной по направлению
Пример 1. Найти производную функции в точке M 0 (1; 2; 3) по направлению вектора .
Найдём направляющие косинусы, пользуясь определением скалярного произведения векторов:
Теперь можем найти производную по направлению данной функции по её формуле:
А сейчас – домашнее задание. В нём дана функция не трёх, а лишь двух переменных, но несколько иначе задан направляющий вектор. Так что придётся вновь повторить векторную алгебру.
Пример 2. Найти производную функции в точке M 0 (1; 2) по направлению вектора , где M 1 – точка с координатами (3; 0) .
Вектор, задающий направление производной, может быть дан и в такой форме, как в следующем примере – в виде разложения по ортам координатных осей, но эта хорошо знакомая тема из самого начала векторной алгебры.
Пример 3. Найти производную функции в точке M 0 (1; 1; 1) по направлению вектора .
Решение. Найдём направляющие косинусы вектора
Найдём частные производные функции в точке M 0 :
Следовательно, можем найти производную по направлению данной функции по её формуле:
.
Градиент функции
Градиент функции нескольких переменных в точке M 0 характеризует направление максимального роста этой функции в точке M 0 и величину этого максимального роста.
Как найти градиент?
Нужно определить вектор, проекциями которого на оси координат являются значения частных производных , , этой функции в соответствующей точке:
.
То есть, должно получиться представление вектора по ортам координатных осей, в котором на каждый орт умножается соответствующая его оси частная производная.
Для градиента функции двух переменных формула короче:
.
Пример 4. Найти градиент функции в точке M 0 (2; 4;) .
Решение. Найдём частные производные функции в точке M 0 :
Следовательно, можем записать искомый градиент данной функции:
.
[spoiler title=”источники:”]
http://mathforyou.net/online/calculus/gradient/
http://function-x.ru/derivative_directional.html
[/spoiler]
Приветствую всех. Сегодня на занятии хотелось бы затронуть немало важную тему, связанную одновременно с дифференциальным исчислением и векторной алгеброй. Мы постараемся как можно меньше углубляться в теоретические тезисы и побольше сделаем упор на решение практических задач. Незамедлительно начнём.
Определение слова “градиент” в математике нужно усвоить.
Градиент – это вектор показывающий направление наибольшего возрастания функции. Модуль вектора градиента показывает скорость изменения функции.
Запишем формулу для нахождения вектора градиента:
При нашем раскладе можно с теорией закончить, этого будет достаточно.
Разберём простенький примерчик для начала.
Никто ведь не забыл как брать частные производные? Если подзабыли, ссылочка (на статью) будет в конце урока.
Было слишком уж просто для нас, возьмём что-нибудь посложнее.
Такого плана примеры уже устно не решишь, хотя… Нет, всё же возможно.
Не будем перенапрягаться сильно, рассмотрим последний пример и пойдём отдыхать.
Берёмся за дело.
Не отчаиваемся что уже конец практики, у вас всегда есть возможность найти похожие задачки в интернете или взять в библиотеке задачник по высшей математике. Практикуйтесь, практикуйтесь, и ещё раз практикуйтесь. Спасибо за внимание.
Другие темы:
Щебетун Виктор
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Определение 1
Если для каждой пары $(x,y)$ значений двух независимых переменных из некоторой области ставится в соответствие определенное значение $z$, то говорят, что $z$ является функцией двух переменных $(x,y)$. Обозначение: $z=f(x,y)$.
Рассмотрим функцию $z=f(x,y)$, которая определена в некоторой области в пространстве $Oxy$.
Для заданной функции определим вектор, для которого проекциями на оси координат являются значения частных производных заданной функции в некоторой точке $frac{partial z}{partial x} ;frac{partial z}{partial y} $.
Определение 2
Градиентом заданной функции $z=f(x,y)$ называется вектор $overrightarrow{gradz} $ следующего вида:
[overrightarrow{gradz} =frac{partial z}{partial x} cdot overrightarrow{i} +frac{partial z}{partial y} cdot overrightarrow{j} .]
Сделаем домашку
с вашим ребенком за 380 ₽
Уделите время себе, а мы сделаем всю домашку с вашим ребенком в режиме online
Бесплатное пробное занятие
*количество мест ограничено
Пусть в некотором скалярном поле $z=z(x,y)$ определено поле градиентов
[overrightarrow{gradz} =frac{partial z}{partial x} cdot overrightarrow{i} +frac{partial z}{partial y} cdot overrightarrow{j} .]
Производная $frac{partial z}{partial s} $ по направлению заданного вектора $overrightarrow{s} $ равна проекции вектора градиента $overrightarrow{gradz} $ на заданный вектор $overrightarrow{s} $.
Теорема 2
Для функции двух переменных вектор $overrightarrow{gradz} $ направлен перпендикулярно к линии уровня $z(x,y)=c$, которая лежит в плоскости $Oxy$ и проходит через соответствующую точку.
Пример 1
Определить градиент заданной функции
[z=x^{2} +2y^{2} .]
Решение:
Выражение для градиента находим по формуле
[overrightarrow{gradz} =frac{partial z}{partial x} cdot overrightarrow{i} +frac{partial z}{partial y} cdot overrightarrow{j} .]
Частные производные имеют вид:
[frac{partial z}{partial x} =2x;frac{partial z}{partial y} =4y.]
Следовательно,
[overrightarrow{gradz} =2xcdot overrightarrow{i} +4ycdot overrightarrow{j} .]
«Градиент заданной функции» 👇
Пример 2
Определить градиент заданной функции
[z=x+y^{2} ]
в точке $M(1;2)$. Вычислить $left(|overrightarrow{gradz} |right)_{M} $.
Решение:
Выражение для градиента в заданной точке находим по формуле
[left(overrightarrow{gradz} right)_{M} =left(frac{partial z}{partial x} right)_{M} cdot overrightarrow{i} +left(frac{partial z}{partial y} right)_{M} cdot overrightarrow{j} .]
Частные производные имеют вид:
[frac{partial z}{partial x} =1;frac{partial z}{partial y} =2y.]
Производные в точке $M(1;2)$:
[frac{partial z}{partial x} =1;frac{partial z}{partial y} =2cdot 2=4.]
Следовательно,
[left(overrightarrow{gradz} right)_{M} =overrightarrow{i} +4cdot overrightarrow{j} ]
и
[left(|overrightarrow{gradz} |right)_{M} =sqrt{1^{2} +4^{2} } =sqrt{1+16} =sqrt{17} .]
Пример 3
Записать уравнение линии уровня в условиях примера 2.
Решение:
Выражение для линии уровня имеет вид:
[z(x,y)=c.]
В условиях примера 2 получаем:
[x+y^{2} =c.]
Подставив координаты точки, вычислим значение константы:
[1+2^{2} =1+4=5.]
Следовательно,
[x+y^{2} =5.]
Определение 3
Если для каждой тройки $(x,y,z)$ значений трех независимых переменных из некоторой области ставится в соответствие определенное значение $w$, то говорят, что $w$ является функцией трех переменных $(x,y,z)$ в данной области.
Обозначение: $w=f(x,y,z)$.
Рассмотрим функцию $w=f(x,y,z)$, которая определена в некоторой области в пространстве $Oxyz$.
Для заданной функции определим вектор, для которого проекциями на оси координат являются значения частных производных заданной функции в некоторой точке $frac{partial z}{partial x} ;frac{partial z}{partial y} $.
Определение 4
Градиентом заданной функции $w=f(x,y,z)$ называется вектор $overrightarrow{gradw} $ следующего вида:
[overrightarrow{gradw} =frac{partial w}{partial x} cdot overrightarrow{i} +frac{partial w}{partial y} cdot overrightarrow{j} +frac{partial w}{partial z} cdot overrightarrow{k} .]
Теорема 3
Пусть в некотором скалярном поле $w=f(x,y,z)$ определено поле градиентов
[overrightarrow{gradw} =frac{partial w}{partial x} cdot overrightarrow{i} +frac{partial w}{partial y} cdot overrightarrow{j} +frac{partial w}{partial z} cdot overrightarrow{k} .]
Производная $frac{partial w}{partial s} $ по направлению заданного вектора $overrightarrow{s} $ равна проекции вектора градиента $overrightarrow{gradw} $ на заданный вектор $overrightarrow{s} $.
Пример 4
Определить градиент заданной функции
[w=x^{2} +2y^{2} +2z.]
Решение:
Выражение для градиента находим по формуле
[overrightarrow{gradw} =frac{partial w}{partial x} cdot overrightarrow{i} +frac{partial w}{partial y} cdot overrightarrow{j} +frac{partial w}{partial z} cdot overrightarrow{k} .]
Частные производные имеют вид:
[frac{partial w}{partial x} =2x;frac{partial w}{partial y} =4y;frac{partial w}{partial z} =2.]
Следовательно,
[overrightarrow{gradw} =2xcdot overrightarrow{i} +4ycdot overrightarrow{j} +2cdot overrightarrow{k} .]
Пример 5
Определить градиент заданной функции
[w=x^{2} +2y^{2} +2z^{3} ]
в точке $M(1;2;1)$. Вычислить $left(|overrightarrow{gradz} |right)_{M} $.
Решение:
Выражение для градиента в заданной точке находим по формуле
[left(overrightarrow{gradw} right)_{M} =left(frac{partial w}{partial x} right)_{M} cdot overrightarrow{i} +left(frac{partial w}{partial y} right)_{M} cdot overrightarrow{j} +left(frac{partial w}{partial z} right)_{M} cdot overrightarrow{k} .]
Частные производные имеют вид:
[frac{partial w}{partial x} =2x;frac{partial w}{partial y} =4y;frac{partial w}{partial z} =6z^{2} .]
Производные в точке $M(1;2)$:
[frac{partial w}{partial x} =2cdot 1=2;frac{partial w}{partial y} =4cdot 2=8;frac{partial w}{partial z} =6cdot 1^{2} =6.]
Следовательно,
[left(overrightarrow{gradw} right)_{M} =2cdot overrightarrow{i} +8cdot overrightarrow{j} +6cdot overrightarrow{k} ]
и
[left(|overrightarrow{gradw} |right)_{M} =sqrt{2^{2} +8^{2} +6^{2} } =sqrt{4+64+36} =sqrt{104} .]
Перечислим некоторые свойства градиента:
-
Производная заданной функции в заданной точке по направлению некоторого вектора $overrightarrow{s} $ имеет наибольшее значение, если направление данного вектора $overrightarrow{s} $ совпадает с направлением градиента. При этом данное наибольшее значение производной совпадает с длиной вектора градиента, т.е. $|overrightarrow{gradw} |$.
-
Производная заданной функции по направлению вектора, который перпендикулярен к вектору градиента, т.е. $overrightarrow{gradw} $, равна 0. Так как $varphi =frac{pi }{2} $, то $cos varphi =0$; следовательно, $frac{partial w}{partial s} =|overrightarrow{gradw} |cdot cos varphi =0$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме

