В данной публикации мы рассмотрим, что такое гипербола, приведем формулу, с помощью которой задается ее функция, а также на практических примерах разберем алгоритм построения данного вида графика.
- Определение и функция гиперболы
-
Алгоритм построения гиперболы
- Пример 1
-
Пример 2
Определение и функция гиперболы
Гипербола – это график функции обратной пропорциональности, которая в общем виде задается следующей формулой:
Здесь:
- x – независимая переменная;
- k ≠ 0;
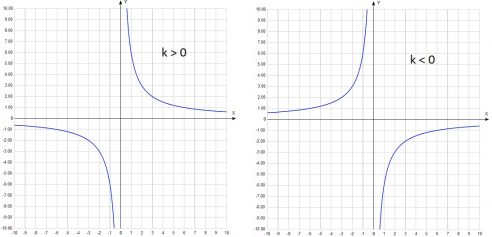
- при k > 0 гипербола расположена в I и III четвертях координатной плоскости;
- при k < 0 график находится во II и IV четвертях.
На рисунке ниже изображен пример гиперболы.
- Линии графика (зеленым цветом) называются его ветвями.
- Оси абсцисс и ординат (Ox и Oy) являются асимптотами гиперболы, т.е. ветви бесконечно к ним приближаются, но никогда их не коснутся и не пересекут.
- Ось симметрии (синим цветом) – это прямая:
- y = x (при k > 0)
- y = -x (при k < 0)
Смещение асимптот
Допустим у нас есть функция, заданная формулой:
В этом случае:
- x = a – это вертикальная асимптота графика (при a ≠ 0) вместо оси Oy;
- y = b – горизонтальная асимптота (при b ≠ 0) вместо оси Ox.
Канонический вид уравнения гиперболы (координатные оси совпадают с осями графика):
Алгоритм построения гиперболы
Пример 1
Дана функция y = 4/x. Построим ее график.
Решение
Так как k > 0, следовательно, гипербола будет находиться в I и III координатных четвертях.
Чтобы построить график, сначала нужно составить таблицу соответствия значений x и y. То есть мы берем конкретное значение x, подставляем его в формулу функции и получаем y.
| x | y | Расчет y |
| 0,5 | 8 | 4 / 0,5 = 8 |
| 1 | 4 | 4 / 1 = 4 |
| 2 | 2 | 4 / 2 = 2 |
| 4 | 1 | 4 / 4 = 1 |
| 8 | 0,5 | 4 / 8 = 0,5 |
Теперь отмечаем найденные точки на координатной плоскости и соединяем их плавной линией, которая будет стремиться к осям координат. В итоге получится ветвь гиперболы, расположенная в первой четверти.
Чтобы построить ветвь в третьей четверти, вместо x в формулу подставляем -x. Так мы вычислим значения y.
| x | y | Расчет y |
| -0,5 | -8 | 4 / -0,5 = -8 |
| -1 | -4 | 4 / -1 = -4 |
| -2 | -2 | 4 / -2 = -4 |
| -4 | -1 | 4 / -4 = -1 |
| -8 | -0,5 | 4 / -8 = -0,5 |
Соединив полученные точки получаем следующий результат. На этом построение гиперболы завершено.
Пример 2
Рассмотренный выше пример был одним из самых простых (без смещения асимптот). Давайте усложним задачу и построим гиперболу, заданную функцией ниже:
Решение
Так как k < 0, график будет располагаться во второй и четвертой четвертях.
Теперь определяемся с асимптотами, в нашем случае это x = 3 и y = 4 (см. информацию выше про их смещение).
Составим таблицу соответствия значений x и y.
| x II четв. | y II четв. | x IV четв. | y IV четв. |
| -1 | 4,5 | 3,5 | 0 |
| 1 | 5 | 4 | 2 |
| 2 | 6 | 5 | 3 |
| 2,5 | 8 | 7 | 3.5 |
Остается только нанести рассчитанные точки на координатную плоскость и соединить их плавными линиями.
Что такое гипербола? Как построить гиперболу? (Для школьников (7-11 классов)).
Математическая гипербола.
Функция заданная формулой (y=frac{k}{x}), где к неравно 0. Число k называется коэффициентом обратной пропорциональности.
Определение гиперболы.
График функции (y=frac{k}{x}) называют гиперболой. Где х является независимой переменной, а у — зависимой.
Что нужно знать, чтобы построить гиперболу?
Теперь обсудим свойства гиперболы:
1. Ветви гиперболы. Если k>o, то ветви гиперболы находятся в 1 и 3 четверти. Если k<0, то ветви гиперболы находятся во 2 и 4 четверти.


2.Асимптоты гиперболы. Чтобы найти асимптоты гиперболы необходимо,иногда, уравнение гиперболы упростить. Рассмотрим на примере:
Пример №1:
$$y=frac{1}{x}$$
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому х не равен 0.
$$yneqcolor{red} {frac{1}{x}}+0$$
(frac{1}{x}) дробь отбрасываем, для того чтобы найти вторую асимптоту.
Остается простое число
y≠0 это вторая асимптота.
И так, асимптоты x≠0 и y≠0 в данном примере совпадают с осями координат OX и OY.
k=1, значит гипербола будет находится в первой и третьей четверти. k всегда находится в числители.
Построим примерный график гиперболы.
Пример №2:
$$y=frac{1}{x+2}-1$$
Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому х+2 неравен 0.
х+2≠0
х≠-2 это первая асимптота
Находим вторую асимптоту.
$$y=color{red} {frac{1}{x+2}}-1$$
Дробь (color{red} {frac{1}{x+2}}) отбрасываем
Остается y≠ -1 это вторая асимптота.
Строим примерный график, отмечаем асимптоты (красным проведены прямые х≠-2 и y≠-1):
Пример №3:
$$begin{align*}
&y=frac{2+x}{1+x} \\
&y=frac{color{red} {1+1}+x}{1+x} \\
&y=frac{1}{1+x}+frac{1+x}{1+x}\\
&y=frac{1}{1+x}+1\\
&y=frac{1}{color{red} {1+x}}+1
end{align*}$$
Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому 1+х неравен 0.
1+х≠0
х≠-1 это первая асимптота.
Находим вторую асимптоту.
$$y=color{red}{frac{1}{1+x}}+1$$
(color{red}{frac{1}{1+x}}) Дробь убираем.
Остается y≠1 это вторая асимптота.
Строим примерный график, отмечаем асимптоты (красным проведены прямые х≠-1 и y≠1):
3. У гиперболы есть центр симметрии относительно начала координат. Рассмотрим на примере:
$$y=frac{1}{x}$$
Возьмем точку А(1;1) с координатами, которая находится на графике у=1/х. На этом же графике лежит точка B(-1;-1). Видно, что точка А симметрична точке В относительна начала координат.
4. Оси симметрии гиперболы. У гиперболы две оси симметрии. Рассмотрим пример:
$$y=frac{1}{x}$$
Первой осью симметрии является прямая y=x. Посмотрим точки (0,5;2) и (2;0,5) и еще точки (-0,5;-2) и (-2;-0,5). Эти точки расположены по разные стороны данной прямой, но на равных расстояниях от нее, они симметричны относительно этой прямой.
Вторая ось симметрии это прямая y=-x.
5. Гипербола нечетная функция.
$$f(-x)=frac{1}{-x}=-frac{1}{x}=-f(x)$$
6. Область определения гиперболы и область значения гиперболы. Область определения смотрим по оси х. Область значения смотрим по оси у. Рассмотрим на примере:
$$y=frac{-1}{x-1}-1$$
а) Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому x-1 неравен 0.
x-1≠0
х≠1 это первая асимптота.
Находим вторую асимптоту.
$$y=color{red} {frac{-1}{x-1}}-1$$
Дробь (color{red} {frac{-1}{x-1}}) удаляем.
Остается y≠ -1 это вторая асимптота.
б) k=-1, значит ветви гиперболы будут находится во второй и четвертой четверти.
в) Возьмем несколько дополнительных точек и отметим их на графике.
х=0 y=0
x=-1 y=-0,5
x=2 y=-2
x=3 y=-1,5
г) Область определения смотрим по оси х. Графика гиперболы не существует по асимптоте х≠1, поэтому область определения будет находится
х ∈ (-∞;1)U(1;+∞).
д) Область значения смотрим по оси y. График гиперболы не существует по асимптоте y≠ -1, поэтому область значения будет находится
y ∈ (-∞;-1)U(-1;+∞).
е) функция возрастает на промежутке x ∈ (-∞;1)U(1;+∞).
7. Убывание и возрастание функции гиперболы. Если k>0, функция убывающая. Если k<0 функция возрастающая.
8. Для более точного построения взять несколько дополнительных точек. Пример смотреть в пункте №6.
Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.
реклама
Свойства гиперболы
1) Область определения и область значений
По аналитическому заданию функции видно, что х ≠-a, поскольку знаменатель дроби не может ровняться нулю. Таким образом получим:
D(f)=(-∞;-а) U (-a;+∞)
Область значений
Е(f)=(-∞;+∞)
2) Нули функции
Если b=0, то график функции не пересекает ось ОХ;
Если b≠0, то гипербола имеет одну точку пересечения с ОХ:*
x=-(k+ab)/b
3) Промежутки знакопостоянства
Рассмотрим только 2 простых случая, остальные случаи вы можете рассмотреть аналитически самостоятельно по алгоритму из раздела Свойства функций -> Знакопостоянство
Случай 1: a=0, b=0, k>0
f(x)>0, при x ∈ (0; +∞)
f(x)<0, при x ∈ (-∞;0)
Случай 1: a=0, b=0, k<0
f(x)<0, при x ∈ (0; +∞)
f(x)>0, при x ∈ (-∞;0)
4) Промежутки монотонности
Аналогично с промежутками знакопостоянства рассмотрим только 2 случая
Случай 1: a=0, b=0, k>0
Функция убывает при
x ∈ (-∞;0) U (0; +∞)
Функция возрастает при
x ∈ (-∞;0) U (0; +∞)
5) Четность и нечетность
Функция является нечетной при a=0, b=0, то есть если имеет вид y=k/x
Обратная пропорциональность — коротко о главном
Определение:
Функция, описывающая обратную пропорциональность, – это функция вида ( displaystyle y=frac{k}{x-a}+b ), где ( kne 0), ( xne 0) и ( xne а)
По-другому эту функцию называют обратной зависимостью.
Область определения и область значений функции:
( Dleft( y right)=left( -infty ;0 right)cup left( 0;+infty right)) или, что то же самое, ( Dleft( y right)=mathbb{R}backslash left{ 0 right})
( Eleft( y right)=left( -infty ;0 right)cup left( 0;+infty right)) или ( Eleft( y right)=mathbb{R}backslash left{ 0 right}).
График обратной пропорциональности (зависимости) – гипербола.
Коэффициент ( displaystyle k)
( displaystyle k) – отвечает за «пологость» и направление графика. Чем больше этот коэффициент, тем дальше от начала координат располагается гипербола, и, следовательно, она менее круто «поворачивает» (см. рисунок).
Знак коэффициента ( displaystyle k) влияет на то, в каких четвертях расположен график:
если ( displaystyle k>0), то ветви гиперболы расположены в ( displaystyle I) и ( displaystyle III) четвертях;
если ( displaystyle k<0), то во ( displaystyle II) и ( displaystyle IV).
Коэффициент ( displaystyle a)
Если внимательно посмотреть на знаменатель, видим, что ( displaystyle a) – это такое число, которому не может равняться ( displaystyle x).
То есть ( x=a) – это вертикальная асимптота, то есть вертикаль, к которой стремится график функции
Коэффициент ( b)
Число ( b) отвечает за смещение графика функции вверх на величину ( b), если ( b>0), и смещение вниз, если ( b<0).
Следовательно, ( y=b) – это горизонтальная асимптота.
Алгоритм построения графика функции ( displaystyle y=frac{k}{x-a}+b)
- Определяем коэффициенты ( displaystyle k), ( displaystyle a) и ( displaystyle b).
- Строим график функции ( displaystyle y=frac{k}{x}) (сначала по 3-4 точкам правую ветвь, потом симметрично рисуем левую ветвь).
- График должен быть сдвинут вправо на ( displaystyle a). Но проще двигать не график, а оси, так что ось ( displaystyle Oy) сдвигаем влево на ( displaystyle a).
- График должен быть сдвинут вверх на ( displaystyle b). Но проще двигать не график, а оси, так что ось ( displaystyle Ox) сдвигаем вниз на ( displaystyle b).
- Старые оси (прямые, которые служили нам осями в пункте 2) оставляем в виде пунктирных линий. Это теперь просто вертикальная и горизонтальная асимптоты.
Что такое функция
Ты помнишь, что функция – это определенного рода зависимость?
Если ты еще не читал тему «Функции», настоятельно рекомендую бросить все и прочитать, ведь нельзя изучать какую-либо конкретную функцию, не понимая, что это такое – функция.
Также очень полезно перед началом этой темы освоить две более простые функции: линейную и квадратичную.
Там ты закрепишь понятие функции и научишься работать с коэффициентами и графиками.
Ну и на всякий случай немного повторим…
Функция – это правило, по которому каждому элементу одного множества (аргументу) ставится в соответствие некоторый (единственный!) элемент другого множества (множества значений функции).
То есть, если у тебя есть функция ( y=fleft( x right)), это значит что каждому допустимому значению переменной ( x) (которую называют «аргументом») соответствует одно значение переменной ( y) (называемой «функцией»).
Что значит «допустимому значению»?
Если не можешь ответить на этот вопрос, еще раз вернись к теме «Функции»!
Все дело в понятии «область определения»: для некоторых функций не все аргументы можно подставить в зависимость. Например, для функции ( y=sqrt{x}) отрицательные значения аргумента ( x) – недопустимы.
Функция, описывающая обратную зависимость
Это функция вида ( displaystyle y=frac{k}{x}), где ( kne 0).
По-другому ее называют обратной пропорциональностью: увеличение аргумента вызывает пропорциональное уменьшение функции.
Давай определим область определения. Чему может быть равен ( x)? Или, по-другому, чему он не может быть равен?
Единственное число, на которое нельзя делить – это ( 0), поэтому ( xne 0):
( Dleft( y right)=left( -infty ;0 right)cup left( 0;+infty right))
или, что то же самое,
( Dleft( y right)=mathbb{R}backslash left{ 0 right})
Такая запись означает, что ( x) может быть любым числом, кроме ( 0).
- Знак «( mathbb{R})» обозначает множество действительных чисел, то есть всех возможных чисел.
- Знаком «( backslash )» обозначается исключение чего-нибудь из этого множества (аналог знака «минус»).
- Число ( 0) в фигурных скобках означает просто число ( 0).
Получается, что из всех возможных чисел мы исключаем ( 0)).
Множество значений функции, оказывается, точно такое же: ведь если ( kne 0), то на что бы мы его не делили, ( 0) не получится:
( Eleft( y right)=left( -infty ;0 right)cup left( 0;+infty right)) или ( Eleft( y right)=mathbb{R}backslash left{ 0 right}).
Также возможны некоторые вариации формулы ( y=frac{k}{x}). Например, ( y=frac{k}{x+a}) – это тоже функция, описывающая обратную зависимость.
Определи самостоятельно область определения и область значений этой функции. Должно получиться:
- ( Dleft( y right)=left( -infty ;-a right)cup left( -a;+infty right))
- ( Eleft( y right)=left( -infty ;0 right)cup left( 0;+infty right)).
Давай посмотрим на такую функцию: ( displaystyle y=frac{x-5}{{{x}^{2}}-25}).
Является ли она обратной зависимостью?
На первый взгляд сложно сказать: ведь при увеличении ( x) увеличивается и знаменатель дроби, и числитель, так что непонятно, будет ли функция уменьшаться, и если да, то будет ли она уменьшаться пропорционально?
Чтобы понять это, нам необходимо преобразовать выражение таким образом, чтобы в числителе не было переменной:
( displaystyle y=frac{x-5}{{{x}^{2}}-25}=frac{x-5}{left( x-5 right)left( x+5 right)}=frac{1}{x+5},text{ }xne 5).
Действительно, мы получили обратную зависимость, но с оговоркой: ( xne 5).
Почему так? А потому, что выражение ( left( x-5 right)) было в исходном выражении в знаменателе, поэтому если мы возьмём значение ( x=5) и подставим его в исходную функцию (а ведь именно её нам нужно исследовать), то что мы получим?
Ноль, делённый на ноль. Но ведь на ноль нельзя делить ничего, даже другой ноль. Поэтому ( x) никак не может быть равен ( 5).
Но почему тогда мы также не пишем ( xne -5)? Оно ведь тоже в знаменателе!
А всё потому, что оно как было в знаменателе, так там и осталось, следовательно мы и так видим, что такое значение икса невозможно.
А поэтому — зачем лишний раз писать? Да-да, математики — народ ленивый, без надобности напрягаться не станут:)
Решения
Пример 1
( displaystyle y=1-frac{3}{x+2})
Пример 2
Здесь нужно вспомнить, как квадратный трехчлен раскладывается на множители (это подробно описано в теме «Разложение на множители»).
Напомню, что для этого надо найти корни соответствующего квадратного уравнения: ( displaystyle {{x}^{2}}+4{x}-5=0).
Я найду их устно с помощью теоремы Виета: ( displaystyle {{x}_{1}}=-5), ( displaystyle {{x}_{2}}=1). Как это делается? Ты можешь научиться этому, прочитав тему «Квадратные уравнения».
Итак, получаем: ( displaystyle {{x}^{2}}+4{x}-5=left( x+5 right)left( x-1 right)), следовательно:
( displaystyle y=frac{x+5}{left( x+5 right)left( x-1 right)}=frac{1}{x-1},text{ }xne -5)
Пример 3
Ты уже попробовал решить сам? В чем загвоздка?
Наверняка в том, что в числителе у нас ( displaystyle 2x), а в знаменателе – просто ( displaystyle x).
Это не беда. Нам нужно будет сократить на ( displaystyle left( x+2 right)), поэтому в числителе следует вынести ( displaystyle 2) за скобки (чтобы в скобках ( displaystyle x) получился уже без коэффициента):
( displaystyle y=frac{2{x}-3}{x+1}=frac{2left( x-frac{3}{2} right)}{x+1}=2cdot frac{x-1,5}{x+1}=2cdot frac{x+1-1-1,5}{x+1}=…) дальше сам.
Ответ: ( displaystyle y=2-frac{5}{x+1}).
График обратной пропорциональности
Как всегда, начнем с самого простого случая: ( displaystyle y=frac{1}{x}).
Составим таблицу.
Таблица обратной пропорциональности (зависимости)
| ( displaystyle mathbf{x}) | ( displaystyle -3) | ( displaystyle -2) | ( displaystyle -1) | ( displaystyle -0,5) | ( displaystyle 0,5) | ( displaystyle 1) | ( displaystyle 2) | ( displaystyle 3) | ( displaystyle 4) |
| ( displaystyle mathbf{y}) | ( displaystyle -frac{1}{3}) | ( displaystyle -frac{1}{2}) | ( displaystyle -1) | ( displaystyle -2) | ( displaystyle 2) | ( displaystyle ;1) | ( displaystyle frac{1}{2}) | ( displaystyle frac{1}{3}) | ( displaystyle frac{1}{4}) |
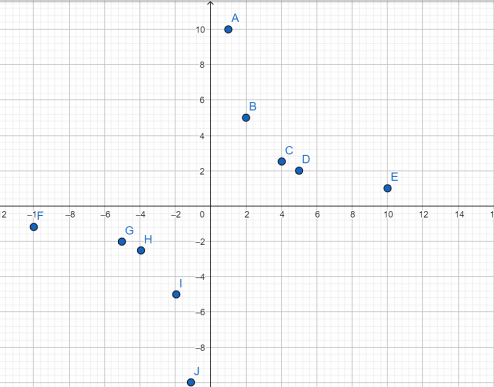
Нарисуем точки на координатной плоскости:
Теперь их надо плавно соединить, но как?
Видно, что точки в правой и левой частях образуют будто бы несвязанные друг с другом кривые линии. Так оно и есть.
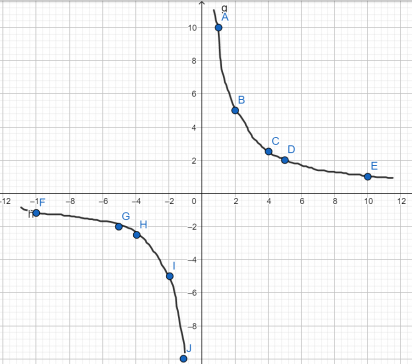
Это график гиперболы и выглядит он так:
Этот график называется «гипербола» (есть что-то похожее на «параболу» в этом названии, правда?). Как и у параболы, у гиперболы две ветки, только они не связаны друг с другом.
Каждая из них стремится своими концами приблизиться к осям ( displaystyle Ox) и ( displaystyle Oy), но никогда их не достигает. Если посмотреть на эту же гиперболу издалека, получится такая картина:
Оно и понятно: так как ( displaystyle xne 0), график не может пересекать ось ( displaystyle Oy). Но и ( displaystyle yne 0), так что график никогда не коснется и оси ( displaystyle Ox).
Ну что же, теперь посмотрим на что влияют коэффициенты.
На что влияют коэффициенты
Рассмотрим такие функции:
( displaystyle y=frac{1}{x};text{ }y=frac{2}{x};text{ }y=frac{4}{x};text{ }y=-frac{1}{x};text{ }y=-frac{3}{x}):
Ух ты, какая красота!
Все графики построены разными цветами, чтобы легче было их друг от друга отличать.
Итак, на что обратим внимание в первую очередь?
Например, на то, что если у функции перед дробью стоит минус, то график переворачивается, то есть симметрично отображается относительно оси ( displaystyle Ox).
Второе: чем больше число в знаменателе, тем дальше график «убегает» от начала координат.
А что, если функция выглядит сложнее, например, ( displaystyle y=frac{1}{x-1}+2)?
В этом случае гипербола будет точно такой же, как обычная ( displaystyle y=frac{1}{x}), только она немного сместится. Давай думать, куда?
Чему теперь не может быть равен ( x)? Правильно, ( xne 1). Значит, график никогда не достигнет прямой ( x=1).
А чему не может быть равен ( y)? Теперь ( yne 2). Значит, теперь график будет стремиться к прямой ( y=2), но никогда ее не пересечет.
Итак, теперь прямые ( x=1) и ( y=2) выполняют ту же роль, которую выполняют координатные оси для функции ( displaystyle y=frac{1}{x}).
Такие прямые называются асимптотами (линии, к которым график стремится, но не достигает их):
Более подробно о том, как строятся такие графики, мы выучим чуть позже.
А теперь попробуй решить несколько примеров для закрепления.
Обратная пропорциональность в жизни
Где же нам встречается такая функция на практике? Примеров множество. Самый распространенный – это движение: чем больше скорость, с которой мы движемся, тем меньшее время нам потребуется, чтобы преодолеть одно и то же расстояние.
И правда, вспомним формулу скорости: ( displaystyle v=frac{S}{t}), где ( v) – скорость, ( t) – время в пути, ( S) – расстояние (путь).
Отсюда можно выразить время: ( displaystyle t=frac{S}{v})
Пример:
Человек едет на работу со средней скоростью ( 40) км/ч, и доезжает за ( 1) час. Сколько минут он потратит на эту же дорогу, если будет ехать со скоростью ( 60) км/ч?
Решение:
Вообще, такие задачи ты уже решал в 5 и 6 классе. Ты составлял пропорцию:
( displaystyle 60) км/ч – ( 60) мин.
( displaystyle 60) км/ч – ( x) мин.
Далее ты определял, что это обратная пропорциональность, так как чем больше скорость, тем меньше время. Значит, чтобы решить эту пропорцию, нужно поделить числа «крест-накрест»:
( displaystyle frac{40}{x}=frac{60}{60}text{ }Rightarrow text{ }x=40)(мин).
То есть понятие обратной пропорциональности тебе уже точно знакомо. Вот и вспомнили. А теперь то же самое, только по-взрослому: через функцию.
Функция (то есть зависимость) времени в минутах от скорости:
( displaystyle tleft( v right)=frac{S}{v}).
Известно, что ( tleft( 40 right)=60), тогда:
( frac{S}{40}=60text{ }Rightarrow text{ }S=40cdot 60=2400).
Нужно найти ( tleft( 60 right)):
( displaystyle tleft( 60 right)=frac{2400}{60}=40) (мин).
Теперь придумай сам несколько примеров из жизни, в которых присутствует обратная пропорциональность.
Придумал? Молодец, если да. Удачи!
Принципы построения графика обратной пропорциональности (гиперболы)
Теперь давай научимся строить простейшую гиперболу – ( displaystyle y=frac{k}{x}).
Достаточно помнить, как она выглядит, и тогда нам хватит всего трех-четырех точек.
Например, построим гиперболу ( displaystyle y=frac{3}{x}).
Составим таблицу из ( 4) точек, которые принадлежат одной ветке (например, правой):
| ( x) | ( frac{1}{2}) | ( displaystyle 1) | ( displaystyle 3) | ( displaystyle 6) |
| ( y) | ( displaystyle 6) | ( displaystyle 3) | ( displaystyle 1) | ( frac{1}{2}) |
Отмечаем точки на рисунке:
Проводим через них плавную линию, которая краями приближается к осям:
Это одна ветвь гиперболы
Проверить правильность построения этой кривой можно так: она должна быть симметрична относительно биссектрисы угла между осями координат:
Отлично, осталось вспомнить, что собой представляет вторая ветвь?
Это точно такая же кривая, расположенная симметрично относительно начала координат. То есть как будто оси теперь направлены не снизу вверх и слева направо, а наоборот: сверху вниз и справа налево, и мы рисуем ту же самую ветвь гиперболы.
Вот:
Еще один полезный факт.
Посмотри на красные точки на графике. Видно, что их абсцисса совпадает с ординатой. Так вот, эти абсцисса с ординатой равны ( sqrt{k}) для правой ветви гиперболы, и ( -sqrt{k}) для левой.
Для функций, у которых ( k) – точный квадрат (например, ( 1), ( 4) или ( displaystyle frac{1}{4})), эту точку, относительно которой ветвь гиперболы симметрична, будет очень легко поставить.
В этом случае достаточно даже трех точек, чтобы построить график.
Например, построим график функции ( displaystyle y=frac{4}{x})
Как и в прошлый раз, начнем с правой ветви.
Точка симметрии: ( displaystyle x=y=2). Выберем еще одну точку, например, ( displaystyle x=1), ( displaystyle y=4). У третьей точки координаты будут наоборот: ( displaystyle x=4), ( displaystyle y=1).
Рисуем:
И теперь симметрично отображаем эту ветвь в третью координатную четверть:
Теперь выясним, что будет, если ( displaystyle k<0)?
Очень просто: если есть график функции с таким же по величине, но положительным ( displaystyle k), то нужно просто отразить его относительно оси ( displaystyle Ox)
То есть правая ветвь теперь будет ниже оси ( displaystyle Ox) (в ( displaystyle IV) четверти), а левая – выше (в ( displaystyle III) четверти).
Принцип построения же останется прежним:
Ну что же, осталось объединить все то, что мы уже выяснили в один алгоритм:
Графиком функции у=kx, где k≠0 число, а х – переменная, является кривая, которую называют гиперболой.
Гипербола имеет две ветви и может располагаться в 1 и 3 координатных четвертях, либо во 2 и 4. Это зависит от знака числа k. Рассмотрим данную кривую на рисунке, где показано ее расположение в зависимости от знака k.
Свойства гиперболы (у=kx)
График функции симметричен относительно начала координат (0;0). Поэтому функцию еще называют – обратная пропорциональность.
- Область определения – любое число, кроме нуля.
- Область значения – любое число, кроме нуля.
- Функция не имеет наибольших или наименьших значений.
Построение графика функции
Для построения графика функции необходимо подбирать несколько положительных и несколько отрицательных значений переменной х, затем подставлять их в заданную функцию для вычисления значений у. После этого по найденным координатам построить точки и соединить их плавной линией. Рассмотрим построение графиков на примерах.
Построить график функции у=10x.
Для этого построим две таблицы для положительных и отрицательных значений х. Подбирать желательно такие значения х, чтобы число 10 на них делилось
| х | 1 | 2 | 4 | 5 | 10 |
| у |
| х | –1 | –2 | –4 | –5 | –10 |
| у |
Теперь делим на эти числа 10, получим значения у:
| х | 1 | 2 | 4 | 5 | 10 |
| у | 10 | 5 | 2,5 | 2 | 1 |
| х | –1 | –2 | –4 | –5 | –10 |
| у | –10 | –5 | –2,5 | –2 | –1 |
Выполняем построение точек, они будут располагаться в первой и третьей координатных четвертях, так как число k положительное.
Теперь для построения гиперболы соединим точки плавной линией.
Построить график функции у=−5x.
Для этого построим также две таблицы для положительных и отрицательных значений х. Подбирать желательно такие значения х, чтобы число минус 5 на них делилось. Выполняем деление и получаем значения у. При делении обращаем внимание на знаки, чтобы не допускать ошибок.
| х | 1 | 2 | 5 | 10 |
| у | –5 | –2,5 | –1 | –0,5 |
| х | –1 | –2 | –5 | –10 |
| у | 5 | 2,5 | 1 | 0,5 |
Теперь отмечаем точки во 2 и 4 координатных четвертях (число k отрицательное) и соединяем их для получения ветвей гиперболы.
Задание OM1104o
Установите соответствие между графиками функций и формулами, которые их задают.

2) y = x/2
3) y = 2/x
Для решения данной задачи необходимо знать вид графиков функций, а именно:
y = x² – парабола, в общем виде это y = ax²+bx+c, но в нашем случае b = c = 0, а а = 1
x/2 – прямая, в общем виде график прямой имеет вид y = ax + b, в нашем случае b = 0, а = 1/2
y = 2/x – гипербола, в общем виде график функции y = a/x + b, в данном примере b = 0, a = 2
Парабола изображена на рисунке А, гипербола на рисунке Б, а прямая – В.
Ответ:
А 1
Б 3
В 2
Ответ: 132
pазбирался: Даниил Романович | обсудить разбор
Задание OM1102o
Установите соответствие между функциями и их графиками.
Функции:
A) y = -3/x
Б) y = 3/x
В) y = 1/(3x)
Графики:
В данной ситуации можно воспользоваться двумя подходами — можно руководствоваться общими соображениями, а можно просто решить задачу подстановкой. Я рекомендую решать задачу общими соображениями, а проверять подстановкой.
Общие правила:
- если уравнение гиперболы положительное (то есть не стоит знак -, как во втором и третьем случае), то график функции лежит в первой и третьей координатной четверти
- если перед уравнением гиперболы стоит знак — (как в первом случае), то график лежит во второй и четвертой четвертях
Таким образом можно сразу определить, что первое уравнение соответствует графику под номером 2.
Второе правило, которым я пользуюсь, звучит так:
- чем больше число в знаменателе гиперболы (рядом с x), тем сильнее гипербола жмется к осям координатной плоскости
и наоборот:
- чем больше число в числителе уравнения гиперболы, тем слабее и медленнее график функции прижимается к осям
Следовательно, функция Б слабее прижимается к осям и ей соответствует график 3, а функции В соответствует график 1, так как она сильнее прижимается к осям.
Ответ:
A) 2
Б) 3
В) 1
Ответ: 231
pазбирался: Даниил Романович | обсудить разбор
Даниил Романович | Просмотров: 11.4k