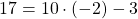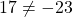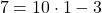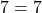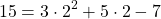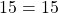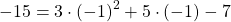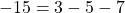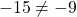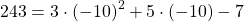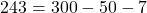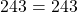Как найти график функции в точке формула

Принадлежит ли графику функции точка

Как определить, принадлежит ли графику функции точка? Это можно сделать, не выполняя построения графика.

График функции проходит через точку, если координаты этой точки обращают формулу функции в верное числовое равенство.

Таким образом, чтобы выяснить, принадлежит ли графику функции точка, надо подставить координаты точки в формулу функции. Если получится верное числовое равенство, точка лежит на графике.

1) Принадлежат ли графику функции y=10x-3 точки A(-2; 17) и B(1; 7)?

График функции проходит через точки A и B, если их координаты обращают формулу y=10x-3 в верное числовое равенство.

Подставляем в формулу функции вместо y ординату точки A (y=17), а вместо x — абсциссу (x=-2). Имеем:

Значит, точка A графику функции y=10x-3 не принадлежит.

Ординату 7 точки B подставляем в формулу функции y=10x-3 вместо y, абсциссу 1 — вместо x. Имеем:

Следовательно, точка B принадлежит графику функции y=10x-3.

Ответ: точка B принадлежит графику функции, точка A — не принадлежит.

2) Какие из точек A(2;15), B(-1;-15), C(-10; 243) принадлежат графику функции y=3x²+5x-7?

В формулу функции y=3x²+5x-7 вместо y подставляем ординату точки, вместо каждого x — абсциссу.

Верные равенства получили для точек A и C. Значит, эти точки принадлежат графику функции y=3x²+5x-7, а точка B — не принадлежит.

Ответ: точки A и C принадлежат графику функции.

Построение графиков функций

О чем эта статья:

11 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Понятие функции

Функция — это зависимость y от x, где x является переменной или аргументом функции, а y — зависимой переменной или значением функции.

Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:

• Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
• Графический способ — наглядно.
• Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
• Словесный способ.

Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.

Например, для функции вида область определения выглядит так

• х ≠ 0, потому что на ноль делить нельзя. Записать можно так: D (y): х ≠ 0.

Область значений — множество у, то есть это значения, которые может принимать функция.

Например, естественная область значений функции y = x² — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.

Понятие графика функции

Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.

График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.

Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.

Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.

В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.

Отметим любые три точки на координатной плоскости, например: L (-2; -2), M (0; 0) и N (1; 1).

Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:

Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться в решении задач.

Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.

Исследование функции

Важные точки графика функции y = f(x):

• стационарные и критические точки;
• точки экстремума;
• нули функции;
• точки разрыва функции.

Стационарные точки — точки, в которых производная функции f(x) равна нулю.

Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.

Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.

Нули функции — это значения аргумента, при которых функция равна нулю.

Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.

Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:

Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.

Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.

Схема построения графика функции:

1. Найти область определения функции.
2. Найти область допустимых значений функции.
3. Проверить не является ли функция четной или нечетной.
4. Проверить не является ли функция периодической.
5. Найти нули функции.
6. Найти промежутки знакопостоянства функции, то есть промежутки, на которых она строго положительна или строго отрицательна.
7. Найти асимптоты графика функции.
8. Найти производную функции.
9. Найти критические точки в промежутках возрастания и убывания функции.
10. На основании проведенного исследования построить график функции.

У нас есть отличные курсы по математике для учеников с 1 по 11 классы!

Построение графика функции

Чтобы понять, как строить графики функций, потренируемся на примерах.

Задача 1. Построим график функции

Упростим формулу функции:

при х ≠ -1.

График функции — прямая y = x — 1 с выколотой точкой M (-1; -2).

Задача 2. Построим график функции

Выделим в формуле функции целую часть:

График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции

Выделение целой части — полезный прием, который применяется в решении неравенств, построении графиков и оценке целых величин.

Задача 3. По виду графика определить знаки коэффициентов общего вида функции y = ax2 + bx + c.

1. 
2. 
3. 

Вспомним, как параметры a, b и c определяют положение параболы.

Ветви вниз, следовательно, a 0.

Точка пересечения с осью Oy — c = 0.

Координата вершины , т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0.

Ветви вниз, следовательно, a 0.

Координата вершины , т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b

Как видим, k = 3 > 0 и угол наклона к оси Ox острый, b = -1 — смещение по оси Oy.

k = -1 > 0 и b = 2 можно сделать аналогичные выводы, как и в первом пункте.

k = 2 > 0 — угол наклона к оси Ox острый, B = 0 — график проходит через начало координат.

k = 0 — константная функция, прямая проходит через точку b = -1 и параллельно оси Ox.

Задача 5. Построить график функции

Это дробно-рациональная функция. Область определения функции D(y): x ≠ 4; x ≠ 0.

Нули функции: 3, 2, 6.

Промежутки знакопостоянства функции определим с помощью метода интервалов.

Вертикальные асимптоты: x = 0, x = 4.

Если x стремится к бесконечности, то у стремится к 1. Значит, y = 1 — горизонтальная асимптота.

Вот так выглядит график:

Задача 6. Построить графики функций:

б)

г)

д)

Когда сложная функция получена из простейшей через несколько преобразований, то преобразования графиков можно выполнить в порядке арифметических действий с аргументом.

а)

Преобразование в одно действие типа f(x) + a.

Сдвигаем график вверх на 1:

б)

Преобразование в одно действие типа f(x — a).

Сдвигаем график вправо на 1:

В этом примере два преобразования, выполним их в порядке действий: сначала действия в скобках f(x — a), затем сложение f(x) + a.

Сдвигаем график вправо на 1:

Сдвигаем график вверх на 2:

г)

Преобразование в одно действие типа

Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:

д)

Мы видим три преобразования вида f(ax), f (x + a), -f(x).

Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.

Сжимаем график в два раза вдоль оси абсцисс:

Сдвигаем график влево на 1/2 вдоль оси абсцисс:

Отражаем график симметрично относительно оси абсцисс:

Как определить a, b и c по графику параболы

Предположим, вам попался график функции (y=ax^2+bx+c) и нужно по этому графику определить коэффициенты (a), (b) и (c). В этой статье я расскажу 3 простых способа сделать это.

1 способ – ищем коэффициенты на графике

Данный способ хорош, когда координаты вершины и точка пересечения параболы с осью (y) – целые числа. Если это не так, советую использовать способ 2.

Коэффициент (a) можно найти с помощью следующих фактов:

— Если (a>0), то ветви параболы направленных вверх, если (a 1), то график вытянут вверх в (a) раз по сравнению с «базовым» графиком (у которого (a=1)). Вершина при этом остается на месте. Это наглядно видно по выделенным точкам.

Ищем 3 точки с целыми координатами, принадлежащие параболе.
Пример:

Выписываем координаты этих точек и подставляем в формулу квадратичной функции: (y=ax^2+bx+c). Получится система с тремя уравнениями.

Решаем систему.
Пример:

Вычтем из второго уравнения первое:

Подставим (9a) вместо (b):

Первое и второе уравнения совпали (это нормально для точек, симметричных относительно прямой проходящей через вершину – как точки (A) и (B) в нашем случае), но нас это не остановит – мы вычтем из второго уравнение третье:

Подставим в первое уравнение (a):

Получается квадратичная функция: (y=-x^2-9x-15).

Сразу заметим, что по графику можно сразу определить, что (c=4). Это сильно облегчит нашу систему – нам хватит 2 точек. Выберем их на параболе: (C(-1;8)), (D(1;2)) (на самом деле, если присмотреться, то можно заметить, что эти точки выделены жирно на изначальной картинке – это вам подсказка от авторов задачи).

Таким образом имеем систему:

Сложим 2 уравнения:

Подставим во второе уравнение:

Теперь найдем точки пересечения двух функций:

Теперь можно найти ординату второй точки пересечения:

3 способ – используем преобразование графиков функций

Этот способ быстрее первого и более универсальный, в частности он может пригодится и в задачах на другие функции.

Главный недостаток этого способа — вершина должна иметь целые координаты.

Сам способ базируется на следующих идеях:

График (y=-x^2) симметричен относительно оси (x) графику (y=x^2).

– Если (a>1) график (y=ax^2) получается растяжением графика (y=x^2) вдоль оси (y) в (a) раз.
– Если (a∈(0;1)) график (y=ax^2) получается сжатием графика (y=x^2) вдоль оси (y) в (a) раз.

– График (y=a(x+d)^2) получается сдвигом графика (y=ax^2) влево на (d) единиц.
— График (y=a(x-d)^2) получается сдвигом графика (y=ax^2) вправо на (d) единиц.

График (y=a(x+d)^2+e) получается переносом графика (y=a(x+d)^2) на (e) единиц вверх.
График (y=a(x+d)^2-e) получается переносом графика (y=a(x+d)^2) на (e) единиц вниз.

У вас наверно остался вопрос — как этим пользоваться? Предположим, мы видим такую параболу:

Сначала смотрим на её форму и направленность её ветвей. Видим, что форма стандартная, базовая и ветви направлены вверх, поэтому (a=1). То есть она получена перемещениями графика базовой параболы (y=x^2).

А как надо было перемещать зеленый график чтоб получить оранжевый? Надо сдвинуться вправо на пять единиц и вниз на (4).

То есть наша функция выглядит так: (y=(x-5)^2-4).
После раскрытия скобок и приведения подобных получаем искомую формулу:

Чтобы найти (f(6)), надо сначала узнать формулу функции (f(x)). Найдем её:

Парабола растянута на (2) и ветви направлены вниз, поэтому (a=-2). Иными словами, первоначальной, перемещаемой функцией является функция (y=-2x^2).

Парабола смещена на 2 клеточки вправо, поэтому (y=-2(x-2)^2).

Парабола поднята на 4 клеточки вверх, поэтому (y=-2(x-2)^2+4).

Смотрите бесплатные видео-уроки на канале Ёжику Понятно по теме “Графики функций”.

Содержание страницы:

Декартова система координат

Система координат – это две взаимно перпендикулярные координатные прямые, пересекающиеся в точке, которая является началом отсчета для каждой из них.

Координатные оси – прямые, образующие систему координат.

Ось абсцисс (ось x ) – горизонтальная ось.

Ось ординат (ось y ) – вертикальная ось.

Функция

Функция – это отображение элементов множества X на множество Y. При этом каждому элементу x множества X соответствует одно единственное значение y множества Y.

Прямая

Линейная функция – функция вида y = a x + b где a и b – любые числа.

Графиком линейной функции является прямая линия.

Рассмотрим, как будет выглядеть график в зависимости от коэффициентов a и b :

Если a > 0 , прямая будет проходить через I и III координатные четверти.

b – точка пересечения прямой с осью y .

Если a < 0 , прямая будет проходить через II и IV координатные четверти.

b – точка пересечения прямой с осью y .

Если a = 0 , функция принимает вид y = b .

Отдельно выделим график уравнения x = a .

Важно: это уравнение не является функцией так как нарушается определение функции (функция ставит в соответствие каждому элементу x множества X одно единственно значение y множества Y). Данное уравнение ставит в соответствие одному элементу x бесконечное множества элементов y. Тем не менее, график данного уравнения построить можно. Просто не будем называть его гордым словом «Функция».

Гипербола

Графиком функции y = k x является гипербола.

Характерная особенность гиперболы в том, что у неё есть асимптоты.

Асимптоты гиперболы – прямые, к которым она стремится, уходя в бесконечность.

Ось x – горизонтальная асимптота гиперболы

Ось y – вертикальная асимптота гиперболы.

На графике асимптоты отмечены зелёной пунктирной линией.

Если коэффициент k > 0 , то ветви гиперолы проходят через I и III четверти.

Если k     <     0, ветви гиперболы проходят через II и IV четверти.

Чем меньше абсолютная величина коэффиента k (коэффициент k без учета знака), тем ближе ветви гиперболы к осям x и y .

Квадратный корень

Функция y     =     x имеет следующий график:

Возрастающие/убывающие функции

Функция y   =   f ( x ) возрастает на интервале, если большему значению аргумента (большему значению x ) соответствует большее значение функции (большее значение y ) .

То есть чем больше (правее) икс, тем больше (выше) игрек. График поднимается вверх (смотрим слева направо)

Примеры возрастающих функций:

Функция y   =   f ( x ) убывает на интервале, если большему значению аргумента (большему значению x ) соответствует меньшее значение функции (большее значение y ) .

То есть чем больше (правее) икс, тем меньше (ниже) игрек. График опускается вниз (смотрим слева направо).

Примеры убывающих функций:

Для того, чтобы найти наибольшее значение функции, находим самую высокую точку на графике и смотрим, какая у нее координата по оси ординат (по оси y ) . Это значение и будет являться наибольшим значением функции.

Для того, чтобы найти наименьшее значение функции, находим самую нижнюю точку на графике и смотрим, какая у нее координата по оси ординат (по оси y ) . Это значение и будет являться наименьшим значением функции.

Задание №11 из ОГЭ 2020. Типовые задачи и принцип их решения.

Скачать домашнее задание к уроку 5.

Принадлежит ли графику функции точка

Как определить, принадлежит ли графику функции точка? Это можно сделать, не выполняя построения графика.

График функции проходит через точку, если координаты этой точки обращают формулу функции в верное числовое равенство.

Таким образом, чтобы выяснить, принадлежит ли графику функции точка, надо подставить координаты точки в формулу функции. Если получится верное числовое равенство, точка лежит на графике.

1) Принадлежат ли графику функции y=10x-3 точки A(-2; 17) и B(1; 7)?

График функции проходит через точки A и B, если их координаты обращают формулу y=10x-3 в верное числовое равенство.

Подставляем в формулу функции вместо y ординату точки A (y=17), а вместо x — абсциссу (x=-2). Имеем:

Значит, точка A графику функции y=10x-3 не принадлежит.

Ординату 7 точки B подставляем в формулу функции y=10x-3 вместо y, абсциссу 1 — вместо x. Имеем:

Следовательно, точка B принадлежит графику функции y=10x-3.

Ответ: точка B принадлежит графику функции, точка A — не принадлежит.

2) Какие из точек A(2;15), B(-1;-15), C(-10; 243) принадлежат графику функции y=3x²+5x-7?

В формулу функции y=3x²+5x-7 вместо y подставляем ординату точки, вместо каждого x — абсциссу.

Верные равенства получили для точек A и C. Значит, эти точки принадлежат графику функции y=3x²+5x-7, а точка B — не принадлежит.

Как решать задачи на функцию

Прежде чем перейти к разбору решения задач с функциями обязательно прочитайте урок «Что такое функция в математике».

После того, как вы действительно поймете, что такое функция (возможно, придется прочитать урок не один раз) вы с бóльшей уверенностью сможете решать задания с функциями.

В этом уроке мы разберем, как решать основные типы задач на функцию и графики функций.

Как получить значение функции

Рассмотрим задание. Функция задана формулой « y = 2x − 1 »

1. Вычислить « y » при « x = 15 »
2. Найти значение « x », при котором значение « y » равно « −19 ».

Для того, чтобы вычислить « y » при « x = 15 » достаточно подставить в функцию вместо « x » необходимое числовое значение.

Запись решения выглядит следующим образом.

Для того, чтобы найти « x » по известному « y », необходимо подставить вместо « y » в формулу функции числовое значение.

То есть теперь наоборот, для поиска « x » мы подставляем в функцию « y = 2x − 1 » вместо « y » число « −19 » .

Мы получили линейное уравнение с неизвестным « x », которое решается по правилам решения линейных уравнений.

Запомните!

Не забывайте про правило переноса в уравнениях.

При переносе из левой части уравнения в правую (и наоборот) буква или число меняет знак на противоположный .

Как и при решении линейного уравнения, чтобы найти неизвестное, сейчас требуется умножить и левую, и правую часть на « −1 » для смены знака.

Теперь разделим и левую, и правую часть на « 2 », чтобы найти « x » .

Как проверить верно ли равенство для функции

Рассмотрим задание. Функция задана формулой « f(x) = 2 − 5x ».

Верно ли равенство « f(−2) = −18 »?

Чтобы проверить верно ли равенство, нужно подставить в функцию « f(x) = 2 − 5x » числовое значение « x = −2 » и сопоставить с тем, что получится при расчетах.

Важно!

Когда подставляете отрицательное число вместо « x », обязательно заключайте его в скобки.

Не забывайте использовать правило знаков.

Неправильно

Правильно

С помощью расчетов мы получили « f(−2) = 12 ».

Это означает, что « f(−2) = −18 » для функции « f(x) = 2 − 5x » не является верным равенством.

Как проверить, что точка принадлежит графику функции

Рассмотрим функцию « y = x 2 −5x + 6 »

Требуется выяснить, принадлежит ли графику этой функции точка с координатами (1; 2) .

Для этой задачи нет необходимости, строить график заданной функции.

Запомните!

Чтобы определить, принадлежит ли точка функции, достаточно подставить её координаты в функцию (координату по оси « Ox » вместо « x » и координату по оси « Oy » вместо « y »).

Если получится верное равенство , значит, точка принадлежит функции.

Вернемся к нашему заданию. Подставим в функцию « y = x 2 − 5x + 6 » координаты точки (1; 2) .

Вместо « x » подставим « 1 ». Вместо « y » подставим « 2 ».

У нас получилось верное равенство, значит, точка с координатами (1; 2) принадлежит заданной функции.

Теперь проверим точку с координатами (0; 1) . Принадлежит ли она
функции « y = x 2 − 5x + 6 »?

Вместо « x » подставим « 0 ». Вместо « y » подставим « 1 ».

В этом случае мы не получили верное равенство. Это означает, что точка с координатами (0; 1) не принадлежит функции « y = x 2 − 5x + 6 »

Как получить координаты точки функции

С любого графика функции можно снять координаты точки. Затем необходимо убедиться, что при подстановке координат в формулу функции получается верное равенство.

Рассмотрим функцию « y(x) = −2x + 1 ». Её график мы уже строили в предыдущем уроке.

Найдем на графике функции « y(x) = −2x + 1 », чему равен « y » при x = 2 .

Для этого из значения « 2 » на оси « Ox » проведем перпендикуляр к графику функции. Из точки пересечения перпендикуляра и графика функции проведем еще один перпендикуляр к оси « Oy ».

Полученное значение « −3 » на оси « Oy » и будет искомым значением « y ».

Убедимся, что мы правильно сняли координаты точки для x = 2
в функции « y(x) = −2x + 1 ».

Для этого мы подставим x = 2 в формулу функции « y(x) = −2x + 1 ». Если мы правильно провели перпендикуляр, мы также должны получить в итоге y = −3 .

При расчетах мы также получили y = −3 .

Значит, мы правильно получили координаты с графика функции.

Важно!

Все полученные координаты точки с графика функции обязательно проверяйте подстановкой значений « x » в функцию.

При подстановке числового значения « x » в функцию в результате должно получиться то же значение « y », которое вы получили на графике.

При получении координат точек с графика функции высока вероятность, что вы ошибетесь, т.к. проведение перпендикуляра к осям выполняется «на глазок».

Исследование графика функции

На рисунке изображен график функции . Посмотрим, как исследовать функцию с помощью графика. Оказывается, глядя на график, можно узнать всё, что нас интересует, а именно:

• область определения функции
• область значений функции
• нули функции
• промежутки возрастания и убывания
• точки максимума и минимума
• наибольшее и наименьшее значение функции на отрезке.

Абсцисса — это координата точки по горизонтали.
Ордината — координата по вертикали.
Ось абсцисс — горизонтальная ось, чаще всего называемая ось .
Ось ординат — вертикальная ось, или ось .

Аргумент — независимая переменная, от которой зависят значения функции. Чаще всего обозначается .
Другими словами, мы сами выбираем , подставляем в формулу функции и получаем .

Область определения функции — множество тех (и только тех) значений аргумента , при которых функция существует.
Обозначается: или .

На нашем рисунке область определения функции — это отрезок . Именно на этом отрезке нарисован график функции. Только здесь данная функция существует.

Область значений функции — это множество значений, которые принимает переменная . На нашем рисунке это отрезок — от самого нижнего до самого верхнего значения .

Нули функции — точки, где значение функции равно нулю, то есть . На нашем рисунке это точки и .

Значения функции положительны там, где . На нашем рисунке это промежутки и .
Значения функции отрицательны там, где . У нас это промежуток (или интервал) от до .

Важнейшие понятия — возрастание и убывание функции на некотором множестве . В качестве множества можно взять отрезок , интервал , объединение промежутков или всю числовую прямую.

Функция возрастает на множестве , если для любых и , принадлежащих множеству , из неравенства следует неравенство .

Иными словами, чем больше , тем больше , то есть график идет вправо и вверх.

Функция убывает на множестве , если для любых и , принадлежащих множеству , из неравенства следует неравенство .

Для убывающей функции большему значению соответствует меньшее значение . График идет вправо и вниз.

На нашем рисунке функция возрастает на промежутке и убывает на промежутках и .

Определим, что такое точки максимума и минимума функции.

Точка максимума — это внутренняя точка области определения, такая, что значение функции в ней больше, чем во всех достаточно близких к ней точках.
Другими словами, точка максимума — такая точка, значение функции в которой больше, чем в соседних. Это локальный «холмик» на графике.

На нашем рисунке — точка максимума.

Точка минимума — внутренняя точка области определения, такая, что значение функции в ней меньше, чем во всех достаточно близких к ней точках.
То есть точка минимума — такая, что значение функции в ней меньше, чем в соседних. На графике это локальная «ямка».

На нашем рисунке — точка минимума.

Точка — граничная. Она не является внутренней точкой области определения и потому не подходит под определение точки максимума. Ведь у нее нет соседей слева. Точно так же и на нашем графике не может быть точкой минимума.

Точки максимума и минимума вместе называются точками экстремума функции. В нашем случае это и .

А что делать, если нужно найти, например, минимум функции на отрезке ? В данном случае ответ: . Потому что минимум функции — это ее значение в точке минимума.

Аналогично, максимум нашей функции равен . Он достигается в точке .

Можно сказать, что экстремумы функции равны и .

Иногда в задачах требуется найти наибольшее и наименьшее значения функции на заданном отрезке. Они не обязательно совпадают с экстремумами.

В нашем случае наименьшее значение функции на отрезке равно и совпадает с минимумом функции. А вот наибольшее ее значение на этом отрезке равно . Оно достигается в левом конце отрезка.

В любом случае наибольшее и наименьшее значения непрерывной функции на отрезке достигаются либо в точках экстремума, либо на концах отрезка.