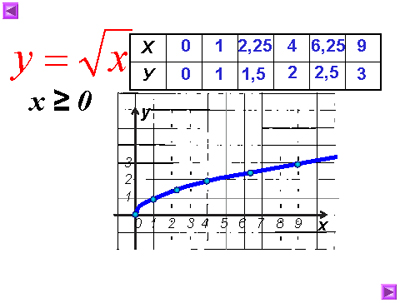
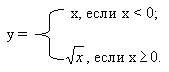Как найти график функции y корень х - Сайт, где вы сможете решить свои вопросы

График и свойства функции $y = sqrt{x}$

Составим таблицу для расчёта значений функции $y = sqrt{x}$.

x	0	0,25	1	2,25	4	6,25	9	12,25	16
$y = sqrt{x}$	0	0,5	1	1,5	2	2,25	3	3,5	4

Отметим полученные точки на координатной плоскости и соединим их кривой:

Свойства функции $y = sqrt{x}$

1. Область определения $x in [0;+infty)$ – все неотрицательные действительные числа.

2. Область значений $y in [0;+infty)$ – все неотрицательные действительные числа.

3. Наименьшее значение функции y = 0 при x = 0.

4. Функция возрастает на всей области определения.

Т.к. функция возрастает, при сравнении возводим корни в квадрат; знак сохраняется:

$$ sqrt{a} lt sqrt{b} iff a lt b $$

$$ sqrt{a} = sqrt{b} iff a = b $$

$$ sqrt{a} gt sqrt{b} iff a gt b $$

Если сравнить полученную кривую с графиком параболы $y = x^2$ (см. §18 данного справочника), то график $y = sqrt{x}$ симметричен положительной ветви параболы, ось симметрии – биссектриса 1-й четверти координатной плоскости.

Таким образом, график функции $y = sqrt{x}$ – это ветвь параболы.

Примеры

Пример 1. Используя графики функций $y = sqrt{x}$, y = x и $y = x^2$, расположите числа в порядке возрастания. Сделайте вывод.

а)

$0,8; 0,8^2 и sqrt{0,8}$

$0,8^2 lt 0,8 lt sqrt{0,8}$

б)

$1,2^2; sqrt{1,2} и 1,2$

$ sqrt{1,2} lt 1,2 lt 1,2^2$

Вывод

В зависимости от значения числа x, корень, само число и его квадрат будут упорядочены следующим образом:

Порядок $x, sqrt{x}, x^2$

0 или 1

$x = sqrt{x} = x^2$

$0 lt x lt 1$

$x^2 lt x lt sqrt{x}$

$x gt 1$

$sqrt{x} lt x lt x^2$

Пример 2. Сравните числа:

а)$ sqrt{0,7}$ и 1

$(sqrt{0,7})^2 ? 1^2$

$0,7 lt 1 Rightarrow sqrt{0,7} lt 1$

б)$ sqrt{0,17} и 0,4$

$ (sqrt{0,17})^2 ? 0,4^2 $

$ 0,17 gt 0,16 Rightarrow sqrt{0,17} gt 0,4 $

$ в) sqrt{0,7} и-1 $

$ sqrt{0,7} gt 0 gt -1 Rightarrow sqrt{0,7} gt -1 $

$ г) sqrt{2,3} и sqrt{2 frac{1}{3}} $

$ 2 frac{1}{3} = 2,333… = 2,(3) gt 2,3 $

$ 2,3 lt 2,(3) Rightarrow sqrt{2,3} lt sqrt{2 frac{1}{3}} $

Пример 3. Расположите числа в порядке возрастания:

$ а) sqrt{0,4}; frac{1}{3}; sqrt{frac{2}{9}}; sqrt{3 frac{1}{3}}; 1,8 $

Возведем весь ряд чисел в квадрат: $ 0,4; frac{1}{9}; frac{2}{9};3 frac{1}{3};3,24 $

Расположим по возрастанию: $frac{1}{9};frac{2}{9};0,4;3,24; sqrt{3 frac{1}{3}}$

Опять вернёмся к корням:

$$ frac{1}{3}; sqrt{frac{2}{9}}; sqrt{0,4}; 1,8; sqrt{3 frac{1}{3}} $$

$ б) 0,7;-1; sqrt{0,2};-0,5;sqrt{0,25} $

(!) Уберем из ряда отрицательные числа: -1;-0,5

Оставшиеся числа возведём в квадрат: 0,49;0,2;0,25

Вернёмся к корням из оставшихся чисел: $sqrt{0,2}; sqrt{0,25}; 0,7$

Расположим всё по возрастанию:

$$ -1;-0,5; sqrt{0,2}; sqrt{0,25};0,7 $$

Пример 4. Решите уравнение графически:

а)

$ sqrt{x} – frac{8}{x} = 0 $

$ sqrt{x} = frac{8}{x} $

Чертим два графика:

$y = sqrt{x} и y = frac{8}{x}$

Ответ: x = 4

б)

$x+ sqrt{x} = 2$

$ sqrt{x} = -x+2 $

Чертим два графика:

$y = sqrt{x} и y = -x+2$

Ответ: x = 1

в*)

$ sqrt{|2x-1|} = 1 $

Область определения:

$x in Bbb R$, выражение под корнем всегда неотрицательно.

$ sqrt{|2x-1|} = 1 iff |2x-1| = 1 $

Чертим два графика:

$y = |2x-1| и y = 1$

Ответ: x = 1

г*)

$ sqrt{|2x-1|} = sqrt{2-x} $

Область определения: $x le 2$

$ sqrt{|2x-1|} = sqrt{2-x} $

$ iff {left{ begin{array}{c} |2x-1| = sqrt{2-x} \ x le 2 end{array} right.}$

Чертим два графика:

y = |2x-1| и y = x

и выбираем корни слева от 2.

Ответ: $ x_1 = -1, x_2 = 1 $

Источник

Построим график функции

y=x

. При (x < 0) выражение

не имеет смысла, поэтому выберем удобные для вычисления (y) неотрицательные значения (x). Подбираем:

Заполним таблицу:

(x)	(0)	(1)	(4)	(9)
(y)	(0)	(1)	(2)	(3)

По точкам ((0; 0), (1;1), (4; 2), (9;3)) построим линию.

Обрати внимание!

График функции

y=x

касается оси (y) в точке ((0; 0)).

График функции

y=x

можно строить с помощью шаблона параболы

y=x2

, так как он является ветвью этой параболы, направленной вправо.

1. Область определения функции — луч

0;+∞

2. (y = 0) при (x = 0); (y >)0 при (x > 0).

3. Функция возрастает на луче

0;+∞

4. Функция ограничена снизу, но не ограничена сверху.

yнаим=0 при x=0;yнаиб не существует

6. Функция непрерывна на луче

0;+∞

Источник

Ученик

(45),
на голосовании

10 лет назад

Голосование за лучший ответ

V.S.

Знаток

(338)

10 лет назад

Подставляй вместо х числа из которых можно извлечь корень, т. е под корнем значения х будут, а извлечешь корень получишь значения у, отметишь полученные х и у на осях и соединишь точки, вот тебе и график

Источник

Основные цели:

1) сформировать представление о
целесообразности обобщённого исследования
зависимостей реальных величин на примере
величин, связанных отношением у=

2) формировать способность к построению графика
у= и его
свойства;

3) повторить и закрепить приёмы устных и
письменных вычислений, возведение в квадрат,
извлечение квадратного корня.

Оборудование, демонстрационный материал: раздаточный
материал.

1. Алгоритм:

2. Образец для выполнения задания в группах:

3. Образец для самопроверки самостоятельной
работы:

4. Карточка для этапа рефлексии:

1) Я понял, как построить график функции у=.

2) Я могу по графику перечислить его свойства.

3) Я не допустил ошибок в самостоятельной
работе.

4) Я допустил ошибки в самостоятельной работе
(перечислить эти ошибки и указать их причину).

Ход урока

1. Самоопределение к учебной деятельности

Цель этапа:

1) включить учащихся в учебную деятельность;

2) определить содержательные рамки урока:
продолжаем работать с действительными числами.

Организация учебного процесса на этапе 1:

– Что мы изучали на прошлом уроке? (Мы изучали
множество действительных чисел, действия с ними,
построили алгоритм для описания свойств функции,
повторяли функции изученные в 7 классе).

– Сегодня мы продолжим работать с множеством
действительных чисел, функцией.

2. Актуализация знаний и фиксация затруднений в
деятельности

Цель этапа:

1) актуализировать учебное содержание,
необходимое и достаточное для восприятия нового
материала: функция, независимая переменная,
зависимая переменна, графики

y = kx + m, y = kx, y =c, y =x², y = – x²,

2) актуализировать мыслительные операции,
необходимые и достаточные для восприятия нового
материала: сравнение, анализ, обобщение;

3) зафиксировать все повторяемые понятия и
алгоритмы в виде схем и символов;

4) зафиксировать индивидуальное затруднение в
деятельности, демонстрирующее на личностно
значимом уровне недостаточность имеющихся
знаний.

Организация учебного процесса на этапе 2:

1. Давайте вспомним как можно задать
зависимости между величинами? (С помощью текста,
формулы, таблицы, графика)

2. Что называется функцией? (Зависимость между
двумя величинами, где каждому значению одной
переменной соответствует единственное значение
другой переменной y = f(x)).

Как называется х? (Независимая переменная –
аргумент)

Как называется у? (Зависимая переменная).

3. В 7- м классе мы изучили функции? (y = kx + m, y = kx, y =c,
y =x², y = – x², ).

Индивидуальное задание:

Что является графиком функций y = kx + m, y =x², y
= ?

3. Выявление причин затруднений и постановка
цели деятельности

Цель этапа:

1) организовать коммуникативное
взаимодействие, в ходе которого выявляется и
фиксируется отличительное свойство задания,
вызвавшего затруднение в учебной деятельности;

2) согласовать цель и тему урока.

Организация учебного процесса на этапе 3:

– Что особенного в этом задании? (Зависимость
задана формулой y = с которой мы еще не встречались).

– Какая цель урока? (Познакомиться с функцией y =
, ее
свойствами и графиком. Функцией в таблице
определять вид зависимости, строить формулу и
график.)

– Можно сформулировать тему урока? (Функция у=, ее свойства и
график).

– Запишите тему в тетради.

4. Построение проекта выхода из затруднения

Цель этапа:

1) организовать коммуникативное взаимодействие
для построения нового способа действия,
устраняющего причину выявленного затруднения;

2) зафиксировать новый способ действия в
знаковой, вербальной форме и с помощью эталона.

Организация учебного процесса на этапе 4:

Работу на этапе можно организовать по группам,
предложив группам построить график y = , затем
проанализировать получившиеся результаты. Также
группам можно предложить по алгоритму описать
свойства данной функции.

5. Первичное закрепление во внешней речи

Цель этапа: зафиксировать изученное
учебное содержание во внешней речи.

Организация учебного процесса на этапе 5:

Постройте график у= – и опишите его свойства.

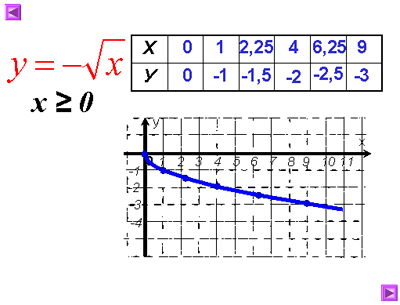
Свойства у= – .

1.Область определения функции.

D(y) =

2.Область значений функции.

E(y) =

3. y = 0, y> 0, y<0.

y =0, если x = 0.

y<0, если х(0;+)

4.Возрастания, убывания функции.

Функция убывает при х [0;+ )

5. Ограниченность функции.

Функция ограничена сверху, и не ограничена
снизу.

6.Наибольшее, наименьшее значения функции.

у _наиб. = нет у _наим. = 0.

7.Непрерывность функции.

Функция непрерывна на все области определения.

№13.2(в)

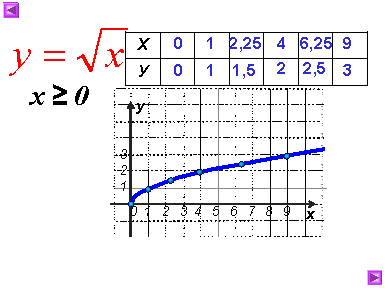
Используя график функции у=, найдите наименьшее и
наибольшее значения функции на отрезке [1; 9].

Построим график у=.

Выделим его часть на отрезке [1;9]. Заметим, что у _наим.
= 1 при х = 1, а у _наиб. =3 при х = 9.

Ответ: у _наим. = 1, у _наиб. =3

6. Самостоятельная работа с самопроверкой по
эталону

Цель этапа: проверить своё умение
применять новое учебное содержание в типовых
условиях на основе сопоставления своего решения
с эталоном для самопроверки.

Организация учебного процесса на этапе 6:

№ 13.1(в)

Учащиеся выполняют задание самостоятельно,
проводят самопроверку по эталону, анализируют,
исправляют ошибки.

Построим график у=.

С помощью графика найдите наименьшее и
наибольшее значения функции на отрезке [0; 4].

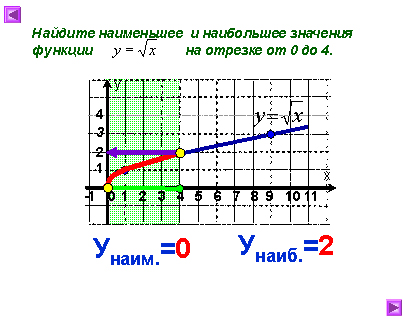
7. Включение в систему знаний и повторение

Цель этапа: тренировать навыки
использования нового содержания совместно с
ранее изученным: 2) повторить учебное содержание,
которое потребуется на следующих уроках.

Организация учебного процесса на этапе 7:

Решите графически уравнение: = х – 6.

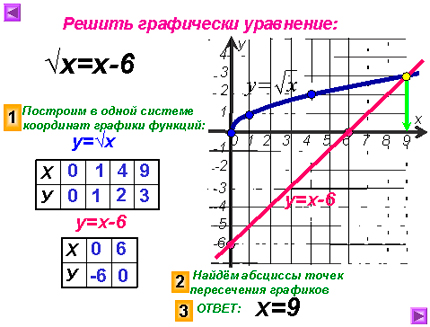
Ответ: 9.

Один ученик у доски остальные в тетрадях.

8. Рефлексия деятельности

Цель этапа:

1) зафиксировать новое содержание, изученное на
уроке;

2) оценить собственную деятельность на уроке;

3) поблагодарить одноклассников, которые
помогли получить результат урока;

4) зафиксировать неразрешённые затруднения как
направления будущей учебной деятельности;

5) обсудить и записать домашнее задание.

Организация учебного процесса на этапе 8:

– Ребята, какая цель стояла сегодня перед нами?
(Изучить функцию у=, ее свойства и график).

– Какие знания нам помогли в достижении цели?
(Умение искать закономерности, умение читать
графики.)

– Проанализируйте свою деятельность на уроке.
(Карточки с рефлексией)

Домашнее задание

п. 13 (до примера 2) № 13.3, 13.4

Решите графически уравнение:

Постройте график функции и опишите его
свойства:

Источник

Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика:Функция у = √х , ее свойства и график

Функция у = √х , ее свойства и график

Для построения графика функции дадим, как обычно, независимой переменной х несколько конкретных значений (неотрицательных, поскольку при х < 0 выражение не имеет смысла) и вычислим соответствующие значения зависимой переменной у. Разумеется, мы будем давать х такие значения, для которых известно точное значение квадратного корня. Итак:

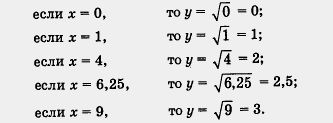
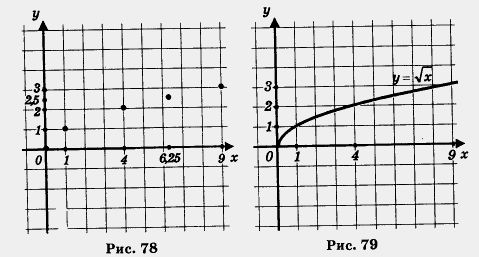
Итак, мы составили таблицу значений функции:

x	0	1	4	6,25	9
y	0	1	2	2,5	3

Построим найденные точки (0; 0), (1;1), (4; 2), (6,25; 2,5), (0;3) на координатной плоскости (рис. 78). Они располагаются некоторой линии, начертим ее (рис. 79). Получили график функции . Обратите внимание: график касается оси у в точке (0; 0). Заметим, что, имея шаблон параболы у = х², можно без труда с его помощью построить график функции , ведь это — ветвь той же параболы, только ориентированная не вверх, а вправо.

Свойства функции
Описывая свойства этой функции, мы, как обычно, будем опираться на ее геометрическую модель — ветвь параболы (рис. 79).

1. Область определения функции — луч [0, +оо).
2. у = 0 при х = 0; у > 0 при х > 0.
3. Функция возрастает на луче [0, + оо).
4. Функция ограничена снизу, но не ограничена сверху.
5. у_наим. = 0 (достигается при х = 0), у_наи6 не существует.
6. Функция непрерывна на луче [0, +оо).

Комментариев требует лишь свойство 4. Почему мы считаем, что функция не ограничена сверху? Возьмем, например, число 10. Найдется ли такое значение х, для которого будет выполнено неравенство > 10? Конечно, достаточно взять х = 121, ведь = 11, а 11 > 10. Возьмем число 40. Найдется ли такое значение х, для которого будет выполняться неравенство > 40? Конечно, достаточно взять х = 2500, ведь = 50, а 50 > 40. И вообще, какое бы положительное число т ни взять, всегда найдется такое х, что будет выполняться неравенство > m (достаточно взять х = (m + 1)²; подумайте, почему это так).

А теперь обратим внимание на одно любопытное обстоятельство. Рассмотрим две функции: у = (ее график изображен на рис. 79) и у = х2, где х> 0 (ее график изображен на рис. 80). Мы только что перечислили шесть свойств для первой функции, но абсолютно теми же свойствами обладает и вторая функция. Словесные «портреты» двух различных функций одинаковы. Математики не смогли вынести такой несправедливости, когда разные функции, имеющие разные графики, словесно описываются одинаково. Они обнаружили принципиальные различия в характере графиков, заметив, что график функции обращен выпуклостью вверх, тогда как
график функции у = х², где х > 0, обращен выпуклостью вниз.

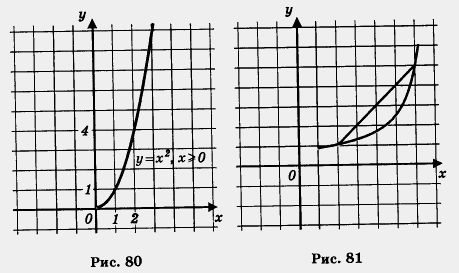
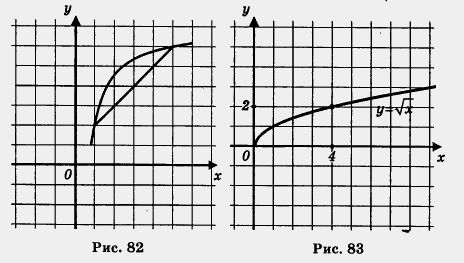
Обычно говорят, что функция выпукла вниз, если, соединив любые две точки ее графика отрезком прямой, обнаруживают, что соответствующая часть графика лежит ниже проведенного отрезка (рис. 81); функция выпукла вверх, если, соединив любые две точки ее графика отрезком прямой, обнаруживают, что соответствующая часть графика лежит выше проведенного отрезка (рис. 82).

Свойство выпуклости будем в дальнейшем включать в процедуру чтения графика.

Функция у = f (х)у где f (х) = , принимает любые неотрицательные значения. В самом деле, какое бы конкретное значение у > 0 ни задать, всегда найдется такое х, что выполняется равенство f (х) = у, т.е. = у; для этого достаточно положить х = у². Множество всех значений функции называют обычно областью значений функции. Для функции у = областью значения значений является луч [0, + оо). Это, кстати, хорошо читается по графику функции (рис. 79). Если спроецировать график на ось у, как раз и получится луч [0, + оо ).

Пример 1. Найти наименьшее и наибольшее значения функции у = на отрезке:
а) [0, 4]; б) [1, 5].

Решение, а) Построим график функции у = и выделим его часть на отрезке [0, 4] (рис. 83). Замечаем, что У_наим. = 0 (достигается при х = 0), а у_наи6 = 2 (достигается при х = 4).

б) Построим график функции у = и выделим его часть на отрезке [1, 5] (рис. 84). Замечаем, что у_наим = 1 (достигается при х = 1), а у_наиб = (достигается при х = 5).
О т в е т: а) у_наим. = 0; у_наиб = 2; б) у_наим. = 1; ушиб =

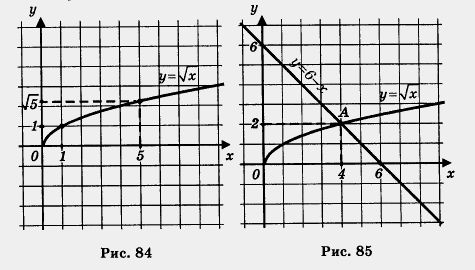
Пример 2. Решить уравнение = 6 – х.
Решение.

1) Рассмотрим две функции у = 6 – x и y =
2) Построим график функции у = (рис. 85).
3) Построим график линейной функции у = 6 – х.
Это — прямая, которую можно построить по двум точкам (0; 6) и (6; 0). Прямая изображена на том же чертеже (рис. 85).
4) По чертежу устанавливаем, что графики пересекаются в одной точке А (4; 2). Так ли это на самом деле? Проверим: пара (4; 2) удовлетворяет и уравнению у = и уравнению у = 6 – х.
Это значит, что точка (4; 2) на самом деле служит точкой пересечения построенных графиков. Заданное уравнение имеет один корень 4 — это абсцисса точки А.
Ответ: 4.
Пример 3. Построить график функции
Решение. 1) Перейдем к вспомогательной системе координат с началом в точке (1; -2) (пунктирные прямые х = 1 и у = – 2 на рис. 86).

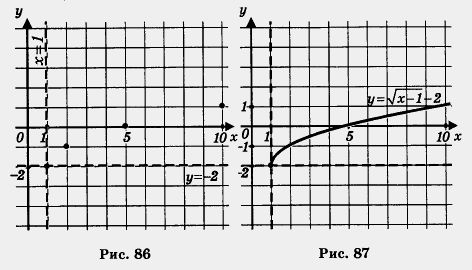
2) Привяжем функцию у = к новой системе координат.
Для этого выберем контрольные точки для функции у = . , например (0; 0), (1; 1), (4; 2), (9; 3), но строить их будем не в старой, а в новой системе координат (эти точки отмечены на рис. 86). Построим ветвь параболы, проходящую через выбранные точки, — это и есть требуемый график (рис. 87).

Пример 4. Построить и прочитать график функции y = –
Решение. Выше, в § 8, мы заметили, что график функции у = – f (х) получается из графика функции у = f (x) с помощью преобразования симметрии относительно оси х.
Воспользовавшись этим, построим график функции у = и отобразим его симметрично относительно оси х (рис. 88). Это и будет график функции у = – .

Перечислим свойства функции у = – (по графику):
1. Область определения функции — луч [0, + оо).
2. у = 0 при х = 0; у < 0 при х > 0.

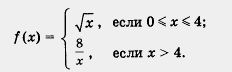
3. Функция убывает на луче [0, + оо).
4. Функция ограничена сверху и не ограничена снизу.
5 У_наиб. = 0 (достигается при х = 0), у_наим не существует.
6. Функция непрерывна на луче [0, + од).
7. Область значений функции — луч (- оо, 0].
8. Функция выпукла вниз.

Пример 5. Построить и прочитать график функции y =f(x), где

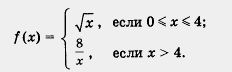
Решение. Сначала построим график функции у = и выделим его часть на отрезке [0, 4] (рис. 89). Затем построим гиперболу и выделим ее часть на открытом луче (4, + оо) (рис. 90). Наконец, оба «кусочка» изобразим в одной системе координат — это и есть график функции у = f(x) (рис. 91).
Перечислим свойства функции у — f(x), т.е. прочитаем график.

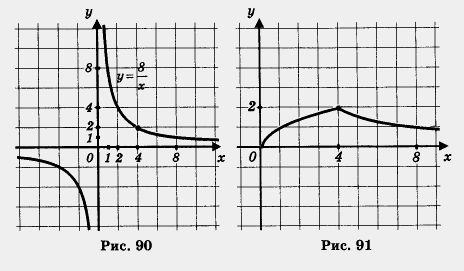
1. Область определения функции — луч [0, + °о).
2. у = 0 при x = 0; у > 0 при х > 0.
3. Функция возрастает на отрезке [0, 4] и убывает на луче [4, + оо).
4. Функция ограничена и снизу и сверху.
5 У_наим. = 0 (достигается при х = 0); у_наи6 = 2 (достигается при х = 4).
6. Функция непрерывна в заданной области определения.
7. Область значений функции — отрезок [0, 2].
8. Функция выпукла вверх на отрезке [0, 4] и выпукла вниз на луче [4, + оо).

Мордкович А. Г., Алгебра. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил.

_{Рефераты, домашняя работа по математике скачать, учебники скатать бесплатно, онлайн уроки, вопросы и ответы}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников

Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 

Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь – Образовательный форум.

При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов –
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других “взрослых” тем.

Разработка – Гипермаркет знаний 2008-

Ждем Ваши замечания и предложения на email:
По вопросам рекламы и спонсорства пишите на email: