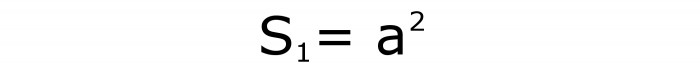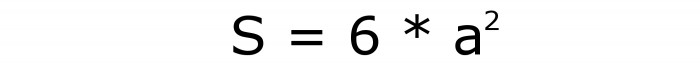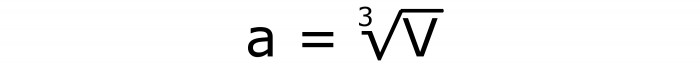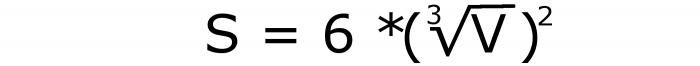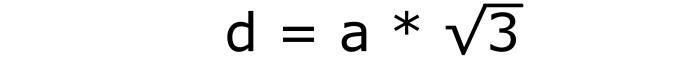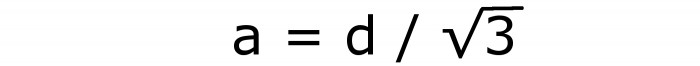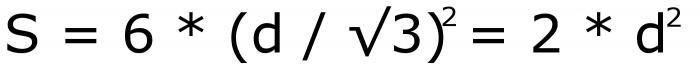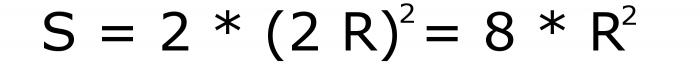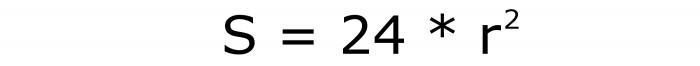Как найти грань куба когда известно ребро

формула через ребро и диагональ грани

В данной публикации мы рассмотрим, как можно найти площадь поверхности куба и разберем примеры решения задач для закрепления материала.

Формула вычисления площади куба

1. Через длину ребра

Площадь (S) поверхности куба равна произведению числа 6 на длину его ребра в квадрате.

S = 6 ⋅ a²

Данная формула получена следующим образом:

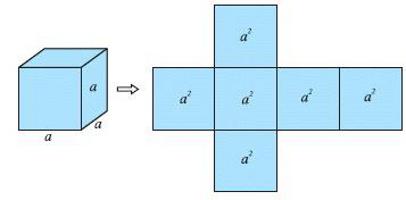
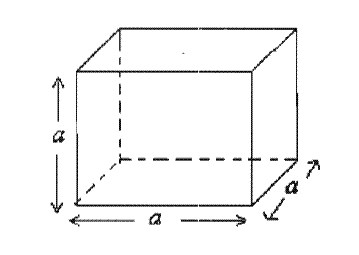
• Куб – это правильная геометрическая фигура, все грани которого являются равными квадратами с длиной стороны a (одновременно является ребром куба).
• Площадь каждой грани считается так: S = a ⋅ a = a².
• Всего у куба 6 граней, а значит, площадь его поверхности равняется шести площадям одной грани: S = 6 ⋅ a².

2. Через длину диагонали грани

Сторона любой грани куба (ребро) может быть рассчитана через длину ее диагонали по формуле:

a=d/√2.

Это значит, что вычислить площадь поверхности фигуры можно так:

S = 6 ⋅ (d/√2)²

Примеры задач

Задание 1
Найдите площадь поверхности куба, если длина его ребра составляет 12 см.

Решение:
Используем первую формулу выше и получаем:
S = 6 ⋅ (12 см)² = 864 см².

Задание 2
Площадь поверхности куба равняется 294 см². Вычислите длину его ребра.

Решение:
Примем ребро куба за a. Из формулы расчета площади следует:

Задание 3
Вычислите площадь поверхности куба, если диагональ его грани равняется 5 см.

Решение:
Воспользуемся формулой, в которой задействована длина диагонали:
S = 6 ⋅ (5 см : √2)² = 75 см².

Площадь поверхности куба, формулы и примеры / Блог :: Бингоскул

Формулы для нахождения площади поверхности куба:

Существует две формулы:

1. Через длину грани H: S=6*H^2
2. Через длину диагонали d: S=6*H^2=6*(frac { d } { sqrt { 3 } } )

Как найти площадь поверхности куба?

1. Чтобы найти с гранью H, надо сложить сумму площадей всех его граней, то есть вычислить площадь квадрата со стороной H, и умножить полученный результат на 6.
   S=6*H
2. Если известна только диагональ грани куба, надо его диагональ d поделить на квадратный корень из трёх и результат умножить на 6.
   S=6*(frac { d } { sqrt { 3 } } )

Примеры

1. Дан куб с ребром H = 7. Для начала возведем длину его грани в квадрат:
   H² = H * H = 7 * 7 = 49. Мы получили периметр одной грани.
   Для вычисления площади результат из первого действия умножим на количество граней:
   S = 6 * 49 = 294.
   Мы получили искомый результат.
   Ответ: 294.
2. Дан куб с диагональю ребра d=13. Требуется найти площадь его поверхности
   Вычислим его грань H, исходя из формулы H=frac { d } { sqrt { 3 } } = frac { 13 } { sqrt { 3 } } = 7,51.
   Теперь, когда нам известна величина грани куба, воспользуемся первой формулой, и умножим результат на 6 :
   S = 6 * H² = 6 * 7,512² = 6 * 56,43 ≈ 338.
   Мы снова получили искомый результат.
   Ответ: 338.

Площадь поверхности прямоугольного параллелепипеда равна

S_пов = (аb + bc + ac) * 2

Так как у куба а = b = c

S_{пов. куба} = (аа + аа +аа) * 2 = 6 а²

S_{пов. куба} = 6 а²

Пример. Площадь поверхности куба равна 18. Найдите его диагональ.

Пусть ребро куба равно а.

S_{пов. куба} = 6 а²

6а^2 =18

a=sqrt { 3 }

Delta BB_ { 1 } D:B_ { 1 } D=sqrt { BB_1^2+BD^2 }

B_1D=a*sqrt { 3 }

B_1D=3

---

Смотри также:

как найти вычислением площадь или диагональ и чему равны суммы длин ребер, формулы и примеры задач для этого

Куб — удивительная фигура. Он одинаковый со всех сторон. Любая его грань может вмиг стать основанием или боковой. И от этого ничего не изменится. А формулы для него всегда легко запоминаются.

И неважно, что нужно найти — объем или площадь поверхности куба. В последнем случае даже не нужно учить что-то новое. Достаточно помнить только формулу площади квадрата.

Что такое площадь?

Эту величину принято обозначать латинской буквой S. Причем это справедливо для школьных предметов, таких как физика и математика. Измеряется она в квадратных единицах длины.

Все зависит от данных в задаче величин. Это могут быть мм, см, м или км в квадрате. Причем возможны случаи, когда единицы даже не указаны. Идет речь просто о числовом выражении площади без наименования.

Так что же такое площадь? Это величина, которая является числовой характеристикой рассматриваемой фигуры или объемного тела. Она показывает размер ее поверхности, которая ограничена сторонами фигуры.

Какая фигура называется кубом?

Эта фигура является многогранником. Причем непростым. Он правильный, то есть у него все элементы равны друг другу. Будь то стороны или грани. Каждая поверхность куба представляет собой квадрат.

Другое название куба — правильный гексаэдр, если по-русски, то шестигранник. Он может быть образован из четырехугольной призмы или параллелепипеда. При соблюдении условия, когда все ребра равны и углы образуют 90 градусов.

Эта фигура настолько гармонична, что часто используется в быту. Например, первые игрушки малыша — кубики. А забава для тех, кто постарше, — кубик Рубика.

Как связан куб с другими фигурами и телами?

Если начертить сечение куба, которое проходит через три его грани, то оно будет иметь вид треугольника. По мере удаления от вершины сечение будет все больше.

Настанет момент, когда пересекаться будут уже 4 грани, и фигура в сечении станет четырехугольником.

Если провести сечение через центр куба так, чтобы оно было перпендикулярно его главным диагоналям, то получится правильный шестиугольник.

Внутри куба можно начертить тетраэдр (треугольную пирамиду). За вершину тетраэдра берется один из его углов. Остальные три совпадут с вершинами, которые лежат на противоположных концах ребер выбранного угла куба.

В него можно вписать октаэдр (выпуклый правильный многогранник, который похож на две соединенные пирамиды). Для этого нужно найти центры всех граней куба. Они будут вершинами октаэдра.

Возможна и обратная операция, то есть внутрь октаэдра реально вписать куб. Только теперь центры граней первого станут вершинами для второго.

Метод 1: вычисление площади куба по его ребру

Для того чтобы вычислить всю площадь поверхности куба, потребуется знание одного из его элементов. Самый простой способ решения, когда известно его ребро или, другими словами, сторона квадрата, из которого он состоит. Обычно эта величина обозначается латинской буквой «а».

Теперь нужно вспомнить формулу, по которой вычисляется площадь квадрата. Чтобы не запутаться, введено ее обозначение буквой S1.

Для удобства лучше задать номера всем формулам. Эта будет первой. Но это площадь только одного квадратика. Всего их шесть: 4 по бокам и 2 снизу и сверху. Тогда площадь поверхности куба вычисляется по такой формуле: S = 6 * a2. Ее номер 2.

Метод 2: как вычислить площадь, если известен объем тела

Этот способ сводится к тому, чтобы сосчитать длину ребра по известному объему. И потом уже воспользоваться известной формулой, которая здесь обозначена цифрой 2.

Из математического выражения для объема гексаэдра выводится то, по которому можно сосчитать длину ребра. Вот она:

• Нумерация продолжается, и здесь уже цифра 3.
• Теперь его можно вычислить и подставить во вторую формулу. Если действовать по нормам математики, то нужно вывести такое выражение:

Это формула площади всей поверхности куба, которой можно воспользоваться, если известен объем. Номер этой записи 4.

Метод 3: расчет площади по диагонали куба

Для того чтобы рассчитать площадь полной поверхности куба, также потребуется вывести ребро через известную диагональ. Здесь используется формула для главной диагонали гексаэдра:

1. Это формула №5.
2. Из нее легко вывести выражение для ребра куба:

Это шестая формула. После его вычисления можно снова воспользоваться формулой под вторым номером. Но лучше записать такую:

Она оказывается пронумерованной цифрой 7. Если внимательно посмотреть, то можно заметить, что последняя формула удобнее, чем поэтапный расчет.

Метод 4: как воспользоваться радиусом вписанной или описанной окружности для вычисления площади куба

Если обозначить радиус описанной около гексаэдра окружности буквой R, то площадь поверхности куба будет легко вычислить по такой формуле:

Ее порядковый номер 8. Она легко получается благодаря тому, что диаметр окружности полностью совпадает с главной диагональю.

Несколько слов о боковой поверхности гексаэдра

Если в задаче требуется найти площадь боковой поверхности куба, то нужно воспользоваться уже описанным выше приемом. Когда уже дано ребро тела, то просто площадь квадрата нужно умножить на 4. Эта цифра появилась из-за того, что боковых граней у куба всего 4. Математическая запись этого выражения такая:

Ее номер 10. Если даны какие-то другие величины, то поступают аналогично описанным выше методам.

Примеры задач

Условие первой. Известна площадь поверхности куба. Она равна 200 см². Необходимо вычислить главную диагональ куба.

Решение:

1 способ. Нужно воспользоваться формулой, которая обозначена цифрой 2. Из нее будет несложно вывести «а». Эта математическая запись будет выглядеть как квадратный корень из частного, равного S на 6. После подстановки чисел получается:

а = √ (200/6) = √ (100/3) = 10 √3 (см).

Пятая формула позволяет сразу вычислить главную диагональ куба. Для этого нужно значение ребра умножить на √3. Это просто. В ответе получается, что диагональ равна 10 см.

2 способ. На случай если забылась формула для диагонали, но помнится теорема Пифагора.

Аналогично тому, как было в первом способе, найти ребро. Потом нужно записать теорему для гипотенузы два раза: первую для треугольника на грани, вторую для того, который содержит искомую диагональ.

х² = а² + а², где х — диагональ квадрата.

d² = х² + а² = а² + а² + а² = 3 а². Из этой записи легко видно, как получается формула для диагонали. А дальше все расчеты будут, как в первом способе. Он немножко длиннее, но позволяет не запоминать формулу, а получить ее самостоятельно.

Ответ: диагональ куба равна 10 см.

Условие второй. По известной площади поверхности, которая равна 54 см2, вычислить объем куба.

Решение:

Пользуясь формулой под вторым номером, нужно узнать значение ребра куба. То, как это делается, подробно описано в первом способе решения предыдущей задачи. Проведя все вычисления, получим, что а = 3 см.

Теперь нужно воспользоваться формулой для объема куба, в которой длина ребра возводится в третью степень. Значит, объем будет считаться так: V = 33 = 27 см3.

Ответ: объем куба равен 27 см3.

Условие третьей. Требуется найти ребро куба, для которого выполняется следующее условие. При увеличении ребра на 9 единиц площадь всей поверхности увеличивается на 594.

Решение:

Поскольку явных чисел в задаче не дано, только разности между тем, что было, и тем, что стало, то нужно ввести дополнительные обозначения. Это несложно. Пусть искомая величина будет равна «а». Тогда увеличенное ребро куба будет равно (а + 9).

Зная это, нужно записать формулу для площади поверхности куба два раза. Первая — для начального значения ребра — совпадет с той, которая пронумерована цифрой 2. Вторая будет немного отличаться. В ней вместо «а» нужно записать сумму (а + 9). Так как в задаче идет речь о разности площадей, то нужно вычесть из большей площади меньшую:

6 * (а + 9)2 — 6 * а2 = 594.

Нужно провести преобразования. Сначала вынести за скобку 6 в левой части равенства, а потом упростить то, что останется в скобках. А именно (а + 9)2 — а2. Здесь записана разность квадратов, которую можно преобразовать так: (а + 9 — а)(а + 9 + а). После упрощения выражения получается 9(2а + 9).

Теперь его нужно умножить на 6, то есть то число, что было перед скобкой, и приравнять к 594: 54(2а + 9) = 594. Это линейное уравнение с одной неизвестной. Его легко решить.

Сначала нужно раскрыть скобки, а потом перенести в левую часть равенства слагаемое с неизвестной величиной, а числа — в правую. Получится уравнение: 2а = 2. Из него видно, что искомая величина равна 1.

Ответ: а = 1.

Источник: https://www.syl.ru/article/181412/mod_nemnogo-informatsii-o-kube-i-o-sposobah-togo-kak-vyichislit-ploschad-poverhnosti-kuba

Формулы объема и площади поверхности. Призма, пирамида — материалы для подготовки к ЕГЭ по Математике

Изучение стереометрии начинается со знания формул. Для решения задач ЕГЭ по стереометрии нужны всего две вещи:

1. Формулы объёма — например, объём куба, объём призмы, объем пирамиды — и формулы площади поверхности.
2. Элементарная логика.

Все формулы объёма и формулы площади поверхности многогранников есть в нашей таблице.

Проще всего найти объём куба — это куб его стороны. Вот, оказывается, откуда берётся выражение «возвести в куб».

Объём параллелепипеда тоже легко найти. Надо просто перемножить длину, ширину и высоту.

Объём призмы — это произведение площади её основания на высоту. Если в основании треугольник — находите площадь треугольника. Если квадрат — ищите площадь квадрата. Напомним, что высота — это перпендикуляр к основаниям призмы.

Объём пирамиды — это треть произведения площади основания на высоту. Высота пирамиды — это перпендикуляр, проведенный из её вершины к основанию.

Некоторые задачи по стереометрии решаются вообще без формул! Например, эта.

Объём куба равен . Найдите объём четырёхугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.

Обойдёмся без формул! Просто посчитайте, сколько нужно таких четырёхугольных пирамидок, чтобы сложить из них этот куб 🙂

Очевидно, их 6, поскольку у куба 6 граней.

Иногда в задаче  надо посчитать площадь поверхности куба или призмы.

Напомним, что площадь поверхности многогранника — это сумма площадей всех его граней.

В некоторых задачах каждое ребро многогранника увеличили, например, в три раза. Очевидно, что при этом площадь поверхности увеличится в девять раз, а объём — в раз.

Стереометрия — это просто! Для начала выучите формулы объёма и площади поверхности многогранников и тел вращения. А дальше — читайте о приемах решения задач по стереометрии.

Источник: https://ege-study.ru/ru/ege/materialy/matematika/formuly-obema/

Калькулятор площади куба

Куб — это правильный шестигранник, каждая грань которого является квадратом. Кубические фигуры часто встречаются в реальной жизни, поэтому на работе или в быту вам может понадобиться вычислить объем или площадь поверхности объекта, который имеет форму кубика.

Геометрия куба

Куб или правильный гексаэдр — это частный случай шестигранной прямоугольной призмы, все грани которой представляют собой квадраты. Кроме того, куб — это и частный случай прямоугольного параллелепипеда, у которого длина, ширина и высота абсолютно равны.

Куб — уникальная фигура, существующая в разных многомерных пространствах. К примеру, нульмерный куб — это точка, одномерный — отрезок, двухмерный — квадрат, а четырехмерный — тессеракт.

В нашем родном трехмерном пространстве куб встречается повсеместно, к примеру, в форме детских кубиков, рафинированного сахара, картонных коробок, газетных киосков или предметов интерьера.

Кубы широко используются в программировании, аналитике, научных изысканиях и прочих высоких материях.

Идеальная форма геометрической фигуры позволяет при помощи разномерных кубов выражать массивы данных, измерять объемы или визуализировать данные.

Кубические фигуры часто встречаются в реальности и абстрактных задачах, поэтому вам может понадобиться рассчитать объем или площадь поверхности кубика для решения самых разных проблем.

Площадь поверхности куба

Площадь кубической фигуры — это сумма площадей всех граней. Каждая грань куба — это квадрат. Площадь квадрата, то есть одной грани, определяется по простой формуле как:

Куб — это гексаэдр, то есть шестигранник. Таким образом, площадь поверхности кубической фигуры представляет собой сумму шести квадратов:

Определить площадь куба можно не только при помощи длины его ребра: для расчета площади поверхности вы можете использовать диагональ самого куба или диагональ одной грани.

Диагональ куба — это отрезок, который находится внутри пространства куба и соединяет две противоположные вершины. Проведенная диагональ разделяет куб на два прямоугольных треугольника. Согласно теореме Пифагора квадрат ребра куба равен одной трети от квадрата диагонали D, следовательно, формула площади полной поверхности приобретает вид:

1. S = 2 D2

Площадь поверхности куба легко определить и с помощью диагонали одной грани. Площадь квадрата через диагональ равна:

1. S = 0,5 d2.

Так как у куба 6 граней, общая площадь поверхности составит сумму шести граней куба, то есть:

1. S = 6 × 0,5 d2 = 3 d2

Таким образом, чтобы определить площадь поверхности кубической фигуры вам достаточно ввести в форму-онлайн калькулятора всего один параметр на выбор:

• длину ребра;
• диагональ куба;
• диагональ квадрата.

Рассмотрим примеры использования данных формул в реальной жизни.

Примеры из жизни

Ящик

Представьте, что вы хотите соорудить из листов ДСП ящик для хранения инструментов в форме куба. Вы знаете, что он отлично впишется в пространство на чердаке высотой 50 см.

Сколько же квадратных метров ДСП вам понадобится для создания такого контейнера? Зная высоту, равную a = 0,5 м вы можете легко подсчитать площадь общей поверхности куба, введя данный параметр в онлайн-калькулятор. Вы получите ответ в виде:

S = 1,5

Таким образом, вам понадобится всего 1,5 квадратных метра ДСП для создания ящика для инструментов. Зная всего один параметр, вы без труда порежете листы на грани куба и соорудите нужную конструкцию.

Контейнер

Допустим, вы хотите обработать антикоррозионным покрытием грузовые контейнеры, которые имеют кубическую форму. Для правильного расчета параметров покрытия вам необходимо знать площадь обрабатываемой поверхности. Вы знаете, что диагональ грани стандартного контейнера равняется d = 3 м. Зная этот параметр, вы легко рассчитаете площадь кубической поверхности, которая равна:

S = 18

Зная общую площадь покрытия, вы без проблем определите необходимое количество антикоррозионной жидкости.

Заключение

Куб встречается в реальной жизни не так часто, как призматические фигуры или параллелепипеды, однако в любом случае вам может понадобиться удобный калькулятор, при помощи которого вы определите площадь полной поверхности кубического объекта. Наш сервис поможет решить вам бытовые, производственные или школьные задачи мгновенно и без ошибок.

Источник: https://BBF.ru/calculators/153/

Чему равна площадь всех граней куба

Введите пожалуйста в соответствующее поле один, любой параметр куба, который Вам известен, остальные мы вычислим и предоставим подробный расчёт с указанием всех формул, по которым быдут произведены вычисления.

Формула объёма куба

Чтобы его найти, необходимо знать размеры рёбер: высоту, ширину и длинну. по формуле, размеры граней куба необходимо перемножить три раза, то есть возвести в третью степень. Объём куба равен длине ребра ‘в кубе’ ))).

Объём можно представить в литрах или куб.см., кубических миллиметрах.

Формула площади поверхности куба

По формуле площади куба необходимо найти площадь одной стороны/грани куба, а затем умножить это значение на 6. Потому, что граней у куба как раз шесть штук ;-). Все стороны куба равны между собой по площади, а все рёбра куба равны по длинне.

Грань куба

В некоторых случаях бывает известна площадь грани куба, тогда для того, что бы найти объём куба, нужно вычислить квадратный корень из площади сторогы куба – это будет длинна ребра, и умножить длинну ребра на площадь грани – получим объём куба. Или просто возвести в третью степень длинну ребра – получим объём куба опять. Два разных пути нахождения объёма дадут один и тот же результат.

Куб — удивительная фигура. Он одинаковый со всех сторон. Любая его грань может вмиг стать основанием или боковой. И от этого ничего не изменится. А формулы для него всегда легко запоминаются. И неважно, что нужно найти – объем или площадь поверхности куба. В последнем случае даже не нужно учить что-то новое. Достаточно помнить только формулу площади квадрата.

Что такое площадь?

Эту величину принято обозначать латинской буквой S. Причем это справедливо для школьных предметов, таких как физика и математика. Измеряется она в квадратных единицах длины. Все зависит от данных в задаче величин. Это могут быть мм, см, м или км в квадрате. Причем возможны случаи, когда единицы даже не указаны. Идет речь просто о числовом выражении площади без наименования.

Так что же такое площадь? Это величина, которая является числовой характеристикой рассматриваемой фигуры или объемного тела. Она показывает размер ее поверхности, которая ограничена сторонами фигуры.

Какая фигура называется кубом?

Эта фигура является многогранником. Причем непростым. Он правильный, то есть у него все элементы равны друг другу. Будь то стороны или грани. Каждая поверхность куба представляет собой квадрат.

Другое название куба — правильный гексаэдр, если по-русски, то шестигранник. Он может быть образован из четырехугольной призмы или параллелепипеда. При соблюдении условия, когда все ребра равны и углы образуют 90 градусов.

Эта фигура настолько гармонична, что часто используется в быту. Например, первые игрушки малыша — кубики. А забава для тех, кто постарше, — кубик Рубика.

Как связан куб с другими фигурами и телами?

Если начертить сечение куба, которое проходит через три его грани, то оно будет иметь вид треугольника. По мере удаления от вершины сечение будет все больше. Настанет момент, когда пересекаться будут уже 4 грани, и фигура в сечении станет четырехугольником. Если провести сечение через центр куба так, чтобы оно было перпендикулярно его главным диагоналям, то получится правильный шестиугольник.

Внутри куба можно начертить тетраэдр (треугольную пирамиду). За вершину тетраэдра берется один из его углов. Остальные три совпадут с вершинами, которые лежат на противоположных концах ребер выбранного угла куба.

В него можно вписать октаэдр (выпуклый правильный многогранник, который похож на две соединенные пирамиды). Для этого нужно найти центры всех граней куба. Они будут вершинами октаэдра.

Возможна и обратная операция, то есть внутрь октаэдра реально вписать куб. Только теперь центры граней первого станут вершинами для второго.

Метод 1: вычисление площади куба по его ребру

Для того чтобы вычислить всю площадь поверхности куба, потребуется знание одного из его элементов. Самый простой способ решения, когда известно его ребро или, другими словами, сторона квадрата, из которого он состоит. Обычно эта величина обозначается латинской буквой «а».

Теперь нужно вспомнить формулу, по которой вычисляется площадь квадрата. Чтобы не запутаться, введено ее обозначение буквой S₁.

Для удобства лучше задать номера всем формулам. Эта будет первой.

Но это площадь только одного квадратика. Всего их шесть: 4 по бокам и 2 снизу и сверху. Тогда площадь поверхности куба вычисляется по такой формуле: S = 6 * a 2 . Ее номер 2.

Метод 2: как вычислить площадь, если известен объем тела

Этот способ сводится к тому, чтобы сосчитать длину ребра по известному объему. И потом уже воспользоваться известной формулой, которая здесь обозначена цифрой 2.

Из математического выражения для объема гексаэдра выводится то, по которому можно сосчитать длину ребра. Вот она:

Нумерация продолжается, и здесь уже цифра 3.

Теперь его можно вычислить и подставить во вторую формулу. Если действовать по нормам математики, то нужно вывести такое выражение:

Это формула площади всей поверхности куба, которой можно воспользоваться, если известен объем. Номер этой записи 4.

Метод 3: расчет площади по диагонали куба

Для того чтобы рассчитать площадь полной поверхности куба, также потребуется вывести ребро через известную диагональ. Здесь используется формула для главной диагонали гексаэдра:

Из нее легко вывести выражение для ребра куба:

Это шестая формула. После его вычисления можно снова воспользоваться формулой под вторым номером. Но лучше записать такую:

Она оказывается пронумерованной цифрой 7. Если внимательно посмотреть, то можно заметить, что последняя формула удобнее, чем поэтапный расчет.

Метод 4: как воспользоваться радиусом вписанной или описанной окружности для вычисления площади куба

Если обозначить радиус описанной около гексаэдра окружности буквой R, то площадь поверхности куба будет легко вычислить по такой формуле:

Ее порядковый номер 8. Она легко получается благодаря тому, что диаметр окружности полностью совпадает с главной диагональю.

Обозначив радиус вписанной окружности латинской буквой r, можно получить такую формулу для площади всей поверхности гексаэдра:

Несколько слов о боковой поверхности гексаэдра

Если в задаче требуется найти площадь боковой поверхности куба, то нужно воспользоваться уже описанным выше приемом. Когда уже дано ребро тела, то просто площадь квадрата нужно умножить на 4. Эта цифра появилась из-за того, что боковых граней у куба всего 4. Математическая запись этого выражения такая:

Ее номер 10. Если даны какие-то другие величины, то поступают аналогично описанным выше методам.

Примеры задач

Условие первой. Известна площадь поверхности куба. Она равна 200 см². Необходимо вычислить главную диагональ куба.

1 способ. Нужно воспользоваться формулой, которая обозначена цифрой 2. Из нее будет несложно вывести «а». Эта математическая запись будет выглядеть как квадратный корень из частного, равного S на 6. После подстановки чисел получается:

а = √ (200/6) = √ (100/3) = 10 √3 (см).

Пятая формула позволяет сразу вычислить главную диагональ куба. Для этого нужно значение ребра умножить на √3. Это просто. В ответе получается, что диагональ равна 10 см.

2 способ. На случай если забылась формула для диагонали, но помнится теорема Пифагора.

Аналогично тому, как было в первом способе, найти ребро. Потом нужно записать теорему для гипотенузы два раза: первую для треугольника на грани, вторую для того, который содержит искомую диагональ.

х² = а² + а², где х — диагональ квадрата.

d² = х² + а² = а² + а² + а² = 3 а². Из этой записи легко видно, как получается формула для диагонали. А дальше все расчеты будут, как в первом способе. Он немножко длиннее, но позволяет не запоминать формулу, а получить ее самостоятельно.

Ответ: диагональ куба равна 10 см.

Условие второй. По известной площади поверхности, которая равна 54 см 2 , вычислить объем куба.

Пользуясь формулой под вторым номером, нужно узнать значение ребра куба. То, как это делается, подробно описано в первом способе решения предыдущей задачи. Проведя все вычисления, получим, что а = 3 см.

Теперь нужно воспользоваться формулой для объема куба, в которой длина ребра возводится в третью степень. Значит, объем будет считаться так: V = 3 3 = 27 см 3 .

Ответ: объем куба равен 27 см 3 .

Условие третьей. Требуется найти ребро куба, для которого выполняется следующее условие. При увеличении ребра на 9 единиц площадь всей поверхности увеличивается на 594.

Поскольку явных чисел в задаче не дано, только разности между тем, что было, и тем, что стало, то нужно ввести дополнительные обозначения. Это несложно. Пусть искомая величина будет равна «а». Тогда увеличенное ребро куба будет равно (а + 9).

Зная это, нужно записать формулу для площади поверхности куба два раза. Первая – для начального значения ребра – совпадет с той, которая пронумерована цифрой 2. Вторая будет немного отличаться. В ней вместо «а» нужно записать сумму (а + 9). Так как в задаче идет речь о разности площадей, то нужно вычесть из большей площади меньшую:

6 * (а + 9) 2 – 6 * а 2 = 594.

Нужно провести преобразования. Сначала вынести за скобку 6 в левой части равенства, а потом упростить то, что останется в скобках. А именно (а + 9) 2 – а 2 . Здесь записана разность квадратов, которую можно преобразовать так: (а + 9 – а)(а + 9 + а). После упрощения выражения получается 9(2а + 9).

Теперь его нужно умножить на 6, то есть то число, что было перед скобкой, и приравнять к 594: 54(2а + 9) = 594. Это линейное уравнение с одной неизвестной. Его легко решить. Сначала нужно раскрыть скобки, а потом перенести в левую часть равенства слагаемое с неизвестной величиной, а числа — в правую. Получится уравнение: 2а = 2. Из него видно, что искомая величина равна 1.

Куб – одна из простейших трехмерных фигур. Каждому знакомы кубики льда, квадратные коробки или кристаллы соли – все они являются такими фигурами. Площадь поверхности куба – это общая площадь всех сторон на его поверхности. Все шесть его граней соразмерны, поэтому, зная длину одной из них, можно рассчитать боковую площадь и площадь поверхности любой фигуры.

Куб – это трехмерная фигура, которая имеет одинаковые размеры. Его длина, ширина и высота идентичны, а каждое ребро встречает другие края под одним углом. Поиск площади поверхности куба быстрый и удобный, поскольку он состоит из конгруэнтных или соразмерных квадратов. Итак, как только вы найдете размер одного из квадратов, вы узнаете площадь всей фигуры.

Из иллюстрации видно, что куб имеет переднюю и заднюю грань, две боковые и верхнюю с нижней стороны. Площадь любого куба будут составлять шесть конгруэнтных квадратов. Фактически, если развернуть его, можно четко увидеть шесть квадратов, которые составляют общую поверхность фигуры.

Площадь куба состоит из площади шести граней. Поскольку все они равны, достаточно знать площадь одной из них и умножить значение на 6. Площадь фигуры также находят по простой формуле: S = 6 x а², где «а» – одна из сторон куба.

• Предположим, что высота куба составляет 2 см. Поскольку его поверхность состоит из квадратов, все его края будут иметь одинаковую длину. Поэтому, исходя из размеров высоты, его длина и ширина будут составлять 2 см.
• Чтобы найти площадь одного из квадратов, вспомните базовые знания геометрии, где S = а², где а – длина одной из сторон. В нашем случае, а = 2 см, так что S = (2 см)² = 2 см х 2 см = 4 см².
• Площадь одного из квадратов поверхности составляет 4 см². Не забудьте указать свое значение в квадратных единицах.

Поскольку вся поверхность фигуры состоит из шести соразмерных квадратов, нужно умножить площадь одной стороны на 6, следуя формуле S = 6 x а². В нашем случае S = 6 х 4 см² = 24 см². Площадь трехмерной фигуры составляет 24 см².

Если вам сложно работать с дробью, конвертируйте ее в десятичную.
Например, высота куба 2 ½ см.

• S = 6 х (2½ см) ²
• S = 6 х (2,5 см) ²
• S = 6 х 6,25 см ²
• S = 37,5 см ²
• Площадь поверхности куба – 37,5 см ².

Если площадь поверхности куба известна, можно определить длину его сторон.

• Площадь куба составляет 86,64 см². Необходимо определить длину грани.
• Решение. Поскольку известна площадь поверхности, нужно считать в обратном порядке, разделив значение на 6, а затем извлечь квадратный корень.
• Сделав необходимые вычисления, получаем длину 3,8 см.

Используя калькулятор на сайте OnlineMSchool , можно быстро вычислить площадь куба. Достаточно ввести нужное значение стороны и сервис выдаст детальное пошаговое решение задания.

Итак, чтобы знать площадь куба, вычислите площадь одной из сторон, затем умножьте результат на 6, так как фигура имеет 6 равных сторон. Можно при подсчете использовать формулу S = 6а². Если задана площадь поверхности, возможно определить длину боковой части, проделав обратные шаги.

Поделиться советом: “Как найти площадь куба”

как найти площадь грани куба

Вы искали как найти площадь грани куба? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и площадь грани куба, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «как найти площадь грани куба».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как как найти площадь грани куба,площадь грани куба,площадь грани куба как найти,площадь грани формула куба. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и как найти площадь грани куба. Просто введите задачу в окошко и нажмите
«решить» здесь (например, площадь грани куба как найти).

Где можно решить любую задачу по математике, а так же как найти площадь грани куба Онлайн?

Решить задачу как найти площадь грани куба вы можете на нашем сайте https://pocketteacher.ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать — это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора.

Куб — Формулы | Свойства

Грань куба

— это часть плоскости, ограниченная сторонами квадрата

• У куба шесть граней
• Каждая грань куба пересекается с четырьмя другими гранями под прямым углом и параллельная противоположной грани
• Грани имеют одинаковую площадь, а так как являются квадратами, то формула площади грани S = a²

Ребро куба

— это отрезок, образованный пересечением двух граней куба.

• У куба двенадцать рёбер
• Каждое ребро перпендикулярно по отношению к примыкающим рёбрам
• Все ребра куба имеет одинаковую длину

Ось куба

— это прямая, проходящая через центр куба и центры двух параллельных граней куба

• У куба три оси
• Оси куба взаимно перпендикулярны

Диагональ куба

— отрезок, который соединяет противоположные вершины куба и проходит через центр куба.

• куб имеет четыре диагонали;
• диагонали куба пересекаются под прямым углом и делятся пополам в центре куба;
• диагонали куба имеют одинаковую длину;

Диагональ куба

$$
D_K = a * sqrt{3}
$$

Диагональ грани куба

$$
D_Г = a * sqrt{2}
$$

Объём куба

• через длину ребра
  $$
  V = a^3
  $$
• через длину диагонали куба
  $$
  V = {D_K^3 over 3 * sqrt{3}}
  $$

Площадь поверхности куба

$$
S_П = 6 * a^2
$$

Периметр куба

$$
P = 12 * a
$$

Сфера, вписанная в куб

— это сфера, центр которой совпадает с центром куба и которая касается центров граней куба.

Радиус вписанной сферы через длину ребра

$$
R_В = {a over 2}
$$

Объем вписанной сферы через длину ребра

$$
V_В = {pi * a^3 over 6}
$$

Сфера, описанная вокруг куба

— это сфера, центр которой совпадает с центром куба и которая соприкасается с восьмью вершинами

Радиус описанной сферы через длину ребра

$$
R_О = {a * sqrt{3} over 2}
$$

Объем сферы описанной вокруг куба V через длину ребра

$$
V_О = {pi * a^3 * sqrt{3} over 2}
$$

Объём сферы (шара) через радиус, V_C

$$
V_C = {4 over 3} * pi * R^3
$$

Площадь поверхности сферы (шара), S_C

$$
S_C = 4 * pi * R^2
$$

Куб ℹ️ определение, свойства геометрической фигуры, виды, обозначения, формулы нахождения площади, объема, диагоналей, вершин и других элементов фигуры

Среди многогранников куб – это один из наиболее известных объектов, знакомых с далёкого детства. Более подробно эта тема изучается на уроках геометрии в старших классах, когда от фигур на плоскости переходят к телам в пространстве.

Кубу можно дать определение различными способами, каждый из которых только подчеркнёт тот или иной класс тел в пространстве, выделит основные признаки и особенности:

• многогранник, у которого все рёбра равны, а грани попарно перпендикулярны;

• прямая призма, все грани которой есть квадраты;

•  прямоугольный параллелепипед, все рёбра которого равны.

Всеми этими и многими другими подобными формулировками геометрия позволяет описывать одну и ту же фигуру в пространстве.

Элементы куба

Основными элементами многогранника считаются грани, рёбра, вершины.

Грань

Плоскости, образующие поверхность куба, называются гранями. Другое название – стороны.

Интересно, сколько граней у куба и каковы их особенности. Всего граней шесть. Две из них, параллельные друг другу, считаются основаниями, остальные – боковыми.

Грани куба попарно перпендикулярны, являются квадратами, равны между собой.

Ребро

Линии пересечения сторон называются рёбрами.

Не каждый школьник может ответить, сколько рёбер у куба. Их двенадцать. Они имеют одинаковые длины. Те из них, что обладают общим концом, расположены под прямым углом по отношению к любому из двух остальных.

Рёбра могут пересекаться в вершине, быть параллельными. Не лежащие в одной грани ребра, являются скрещивающимися.

Вершина

Точки пересечения рёбер называются вершинами. Их число равно восьми.

Центр грани

Отрезок, соединяющий две вершины, не являющийся ребром, называется диагональю. 

Пересечение диагоналей грани считается центром грани – точкой, равноудалённой от всех вершин и сторон квадрата. Это есть центр симметрии грани.

Центр куба

Пересечение диагоналей куба является его центром – точкой, равноудалённой от всех вершин, рёбер и сторон многогранника. 

Это есть центр симметрии куба.

Ось куба

Рассматриваемый многогранник имеет несколько осей ортогональной (под прямым углом) симметрии. К ним относятся: диагонали куба и прямые, проходящие через его центр параллельно рёбрам.

Диагональ куба

Отрезок, соединяющий две вершины, не принадлежащие одной стороне, называется диагональю рассматриваемого многогранника.

Учитывая, что ребра куба имеют равные измерения a, можно найти длину диагонали:

Формула доказывается с помощью дважды применённой теоремы Пифагора.

Диагональ куба — одна из осей симметрии.

Все диагонали куба равны между собой и точкой пересечения делятся пополам.

Диагональ грани куба

Длина диагонали грани в √2 раз больше ребра, то есть:

Эта формула доказывается также с помощью теоремы Пифагора.

Объем куба

Как для любого параллелепипеда, объём куба равен произведению всех трёх измерений, которые в данном случае равны:

Периметр куба

Сумма длин всех рёбер равна:

Площадь поверхности

Сумма площадей всех граней называется площадью поверхности куба. Она равна:

Сфера, вписанная в куб

Такая сфера имеет центр, совпадающий с центром куба. 

Радиус равен половине ребра:

Сфера, описанная вокруг куба

Как для вписанной сферы, центр совпадает с точкой пересечения диагоналей, радиус равен половине диагонали:

Координаты вершин куба

В зависимости от расположения фигуры в системе координат, можно по-разному рассчитывать координаты вершин.

Наиболее часто используют следующий способ. Одна из вершин совпадает с началом координат, рёбра параллельны осям координат или совпадают с ними, координаты единичного куба в этом случае будут равны:

Такое расположение удобно для введения четырёхмерного пространства (вершины задаются всеми возможными бинарными наборами длины 4).

Свойства куба

Плоскость, рассекающая куб на две части, есть сечение. Его форма выглядит как выпуклый многоугольник.

Построение сечений необходимо для решения многих задач. Как правило, используется метод следов или условие параллельности прямых и плоскостей.

Прочие свойства:

• у куба все грани равны, являются квадратами;

• у куба все рёбра равны;

• один центр и несколько осей симметрии.

Площадь куба с вычислителем

Площадь поверхности куба с калькулятором — Math Open Reference

Определение:
Количество квадратных единиц, которые точно покроют поверхность куба.

Попробуй это
Перетащите ползунок, чтобы изменить размер куба. Площадь поверхности рассчитывается при перетаскивании.
Также поверните куб, перетащив его.

Как найти площадь поверхности куба

Напомним, что все ребра куба имеют одинаковую длину (см. Определение куба).Это означает, что каждая из шести граней куба представляет собой
квадрат.
Таким образом, общая площадь поверхности в шесть раз больше площади одного лица.

Или как формула:

Где s — длина любого ребра куба.

Если вы знаете площадь поверхности

Если вы уже знаете площадь, вы можете найти длину края, изменив формулу выше:
где a — площадь поверхности.

Квартир

Помните, что длина края и площадь поверхности будут в одинаковых единицах.Таким образом, если длина края указана в милях, то площадь поверхности будет в квадратных милях и так далее.

Калькулятор

Воспользуйтесь калькулятором выше, чтобы вычислить свойства куба.

Введите любое одно значение, и остальные будут рассчитаны. Например, введите длину стороны, и будет рассчитан объем.

Точно так же, если вы введете площадь поверхности, будет рассчитана длина стороны, необходимая для получения этой площади.

Что попробовать

• Установите флажок «взорвать».Поверните куб, перетащив его, чтобы более четко увидеть, что куб имеет шесть одинаковых квадратных граней.
• На рисунке выше перетащите ползунок, чтобы изменить размер куба. Обратите внимание, как пересчитывается площадь поверхности.
• Нажмите «скрыть детали». Измените размер куба с помощью ползунка. Рассчитайте площадь поверхности, затем нажмите «Показать подробности», чтобы проверить свой ответ.

Связанные темы

(C) Открытый справочник по математике, 2011 г.
Все права защищены.

,

Площадь поверхности куба

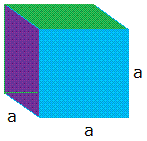
Чтобы вывести формулу площади поверхности куба, вам нужно будет начать с куба, как показано ниже, и назвать длину одной стороны a.

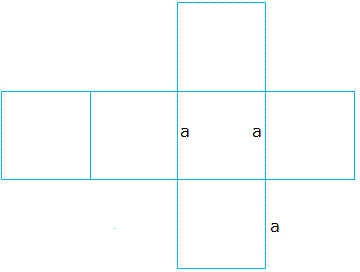
Для того, чтобы сделать куб, подобный показанному выше, вам в основном необходимо использовать следующий шаблон куба:

Глядя на шаблон куба, легко увидеть, что куб имеет шесть сторон, и каждая сторона представляет собой квадрат.

Поскольку длина ребра равна a, площадь одного квадрата равна a × a = a ²

Поскольку имеется шесть сторон, общая площадь поверхности, назовем ее SA, может быть найдена, как показано ниже:

SA = a ² + a ² + a ² + a ² + a ² + a ²

SA = 6 × a ²

Несколько примеров, показывающих, как найти площадь поверхности куба

Пример № 1:

Найдите площадь поверхности, если длина одной стороны составляет 3 см.

Площадь поверхности = 6 × a ²

Площадь поверхности = 6 × 3 ²

Площадь поверхности = 6 × 3 × 3

Площадь поверхности = 6 × 9

Площадь поверхности = 54 см ²

Пример № 2:

Найдите площадь поверхности, если длина одной стороны составляет 5 см.

Площадь поверхности = 6 × a ²

Площадь поверхности = 6 × 5 ²

Площадь поверхности = 6 × 5 × 5

Площадь поверхности = 6 × 25

Площадь поверхности = 150 см ²

Пример № 3:

Найдите площадь поверхности, если длина одной стороны составляет 1/2 см.

Площадь поверхности = 6 × a ²

Площадь поверхности = 6 × (1/2) ²

Площадь поверхности = 6 × 1/2 × 1/2

Площадь поверхности = 6 × 1/4

Площадь поверхности = 6/4 см ²

Площадь поверхности = 3/2 см ²

Площадь поверхности = 1,5 см ²

Пример № 4:

Найдите площадь поверхности, если длина одной стороны 2 1/3 см.

Сначала преобразуйте 2 1/3 в правильную дробь.

2 1/3 = (2 × 3 + 1) / 3 = (6 + 1) / 3 = 7/3

Площадь поверхности = 6 × a ²

Площадь поверхности = 6 × (7/2 ) ²

Площадь поверхности = 6 × 7/2 × 7/2

Площадь поверхности = 6 × 49/4

Площадь поверхности = 294/4 см ²

Площадь поверхности = 73,5 см ²

Новые уроки математики

Ваша электронная почта в безопасности. Мы будем использовать его только для информирования вас о новых уроках математики.

,

Формулы площади поверхности

Формулы площади поверхности

(Математика | Геометрия | Формулы площади поверхности)

( пи
= = 3,141592 …)

Поверхность
Формулы площади
В общем, площадь поверхности представляет собой сумму
все области всех форм, покрывающие поверхность объекта.

Cube | прямоугольный
Призма | Призма | сфера
| Цилиндр | Единицы

Примечание: «ab» означает
«а» умножить на «б». «а ² » означает
«в квадрате», что то же самое, что «а» умножить на «а».

Будьте осторожны !! Количество единиц.
Используйте одни и те же единицы для всех измерений. Примеры

Площадь поверхности куба =
6 а ²

(а — длина стороны
каждый край куба)

Проще говоря, площадь поверхности куба — это площадь шести квадратов, которые
накрой это.Площадь одного из них a * a, или ² . Поскольку эти
одинаковы, вы можете умножить одно из них на шесть, так что поверхность
площадь куба в 6 раз больше квадрата одной из сторон.

Площадь поверхности прямоугольника
Призма = 2ab + 2bc + 2ac

(a, b и c —
длины трех сторон)

Проще говоря, площадь поверхности прямоугольной призмы равна площади шести
прямоугольники, которые его покрывают.Но нам не нужно вычислять все шесть, потому что
мы знаем, что верх и низ одинаковы, передняя и задняя — это
то же самое, и левая и правая стороны одинаковы.

Площадь верха и низа (длины сторон a и
в) = а * с. Поскольку их два, вы получаете 2ac. Передняя и задняя
имеют длину стороны b и c. Площадь одного из них b * c, а там
их два, поэтому площадь поверхности этих двух равна 2bc. Левая и
правая сторона имеет длину сторон a и b, поэтому площадь поверхности одного из
их это а * б.Опять же, их два, поэтому их общая площадь поверхности
это 2ab.

(б — форма
концов)

Площадь поверхности = Боковая площадь + Площадь двух концов

(Боковая площадь) = (периметр формы b ) * L

Площадь поверхности = (периметр формы b ) * L + 2 * (Площадь формы b )

Площадь поверхности сферы
= 4 пи r ²

(r — радиус окружности)

Площадь поверхности цилиндра
= 2 pi r ² + 2 pi r h

(h — высота
цилиндра, r — радиус вершины)

Площадь поверхности = области сверху и снизу + площадь сбоку

Площадь поверхности = 2 (Площадь верха) + (периметр верха) * высота

Площадь поверхности = 2 ( pi r ² ) + (2 pi r) * h

На словах проще всего представить банку.Площадь поверхности — это
площади всех частей, необходимых для закрытия банки. Это верх, низ,
и бумажная этикетка, которая оборачивается по центру.

Можно найти область сверху (или снизу). Это формула
для площади круга ( пи р ² ). Так как есть и верх, и
дно, которое умножается на два.

Сторона похожа на этикетку банки. Если отклеить и положить
плоский это будет прямоугольник.Площадь прямоугольника — это произведение
с двух сторон. Одна сторона — это высота банки, другая —
периметр круга, так как этикетка один раз оборачивается вокруг банки. Так
площадь прямоугольника (2 pi r) * h.

Сложите эти две части вместе, и вы получите формулу поверхности.
площадь цилиндра.

Площадь поверхности = 2 ( pi r ² ) + (2 pi r) * h

Совет! Не забывайте единицы.

Эти уравнения дадут вам правильные ответы, если вы будете держать единицы прямо.
Например — найти площадь поверхности куба со стороной 5 дюймов,
уравнение:

Площадь поверхности = 6 * (5 дюймов) ²

= 6 * (25 квадратных дюймов)

= 150 кв. Дюймов

.

Площадь поверхности по формуле куба с решенными примерами и вопросами | BYJU’S

• • Классы
    • Класс 1-3
    • Класс 4-5
    • Класс 6-10
    • Класс 11-12

  • КОНКУРСНЫЙ ЭКЗАМЕН
    • BNAT 000 NC
      • 000 NC Книги
        • Книги NCERT для класса 5
        • Книги NCERT для класса 6
        • Книги NCERT для класса 7
        • Книги NCERT для класса 8
        • Книги NCERT для класса 9
        • Книги NCERT для класса 10
        • Книги NCERT для класса 11
        • Книги NCERT для класса 12

      • NCERT Exemplar
        • NCERT Exemplar Class 8
        • NCERT Exemplar Class 9
        • NCERT Exemplar Class 10
        • NCERT Exemplar Class 11
        • NCERT 9000 9000
        • NCERT Exemplar Class
          • Решения RS Aggarwal, класс 12
          • Решения RS Aggarwal, класс 11
          • Решения RS Aggarwal, класс 10

          90 003 Решения RS Aggarwal класса 9

          • Решения RS Aggarwal класса 8
          • Решения RS Aggarwal класса 7
          • Решения RS Aggarwal класса 6
        • Решения RD Sharma
          • RD Sharma Class 6 Решения
          • Решения RD Sharma

          Решения RD Sharma Class 8

          • Решения RD Sharma Class 9
          • Решения RD Sharma Class 10
          • Решения RD Sharma Class 11
          • Решения RD Sharma Class 12

        • PHYSICS
          • Механика
          • Оптика
          • Термодинамика Электромагнетизм

        • ХИМИЯ
          • Органическая химия
          • Неорганическая химия
          • Периодическая таблица

        • MATHS
          • Теорема Пифагора

          0004

          • 000300030004
          • Простые числа
          • Взаимосвязи и функции
          • Последовательности и серии
          • Таблицы умножения
          • Детерминанты и матрицы
          • Прибыль и убыток
          • Полиномиальные уравнения
          • Деление фракций

        • 000
        • 000
        • 000
        • 000
        • 000
        • 000 Microology
        • 000
        • 000 Microology
        • 000 BIOG3000
          FORMULAS
          • Математические формулы
          • Алгебраические формулы
          • Тригонометрические формулы
          • Геометрические формулы
          • КАЛЬКУЛЯТОРЫ
            • Математические калькуляторы
            • 0003000 PBS4000
            • 000300030002 Примеры калькуляторов химии

            Класс 6

            • Образцы бумаги CBSE для класса 7
            • Образцы бумаги CBSE для класса 8
            • Образцы бумаги CBSE для класса 9
            • Образцы бумаги CBSE для класса 10
            • Образцы бумаги CBSE для класса 11
            • Образцы бумаги CBSE чел для класса 12

          • CBSE Контрольный документ за предыдущий год
            • CBSE Контрольный документ за предыдущий год Класс 10
            • Контрольный документ за предыдущий год CBSE, класс 12

          • HC Verma Solutions
            • HC Verma Solutions Class 11 Physics
            • Решения HC Verma, класс 12, физика

          • Решения Лакмира Сингха
            • Решения Лакмира Сингха, класс 9
            • Решения Лакмира Сингха, класс 10
            • Решения Лакмира Сингха, класс 8

          • Заметки CBSE
          • , класс
            CBSE Notes
            Примечания CBSE класса 7
            • Примечания CBSE класса 8
            • Примечания CBSE класса 9
            • Примечания CBSE класса 10
            • Примечания CBSE класса 11
            • Примечания CBSE класса 12
            • Примечания к редакции CBSE
              • Примечания к редакции
              • CBSE
              • Примечания к редакции класса 10 CBSE
              • Примечания к редакции класса 11 CBSE 9000 4
              • Примечания к редакции класса 12 CBSE

            • Дополнительные вопросы CBSE
              • Дополнительные вопросы по математике класса 8 CBSE
              • Дополнительные вопросы по науке 8 класса CBSE
              • Дополнительные вопросы по математике класса 9 CBSE
              • Дополнительные вопросы по науке класса 9 CBSE

              Дополнительные вопросы по математике для класса 10

              • Дополнительные вопросы по науке, класс 10 по CBSE

            • CBSE, класс
              • , класс 3
              • , класс 4
              • , класс 5
              • , класс 6
              • , класс 7
              • , класс 8
              • , класс 9 Класс 10
              • Класс 11
              • Класс 12

            • Учебные решения

          • Решения NCERT
            • Решения NCERT для класса 11
              • Решения NCERT для класса 11 по физике
              • Решения NCERT для класса 11 Химия

              Решения для биологии класса 11

              • Решения NCERT для математики класса 11

              9 0003 NCERT Solutions Class 11 Accountancy

              • NCERT Solutions Class 11 Business Studies
              • NCERT Solutions Class 11 Economics
              • NCERT Solutions Class 11 Statistics
              • NCERT Solutions Class 11 Commerce

            • NCERT Solutions For Class 12
              • NCERT Solutions For Класс 12 по физике
              • Решения NCERT для химии класса 12
              • Решения NCERT для класса 12 по биологии
              • Решения NCERT для класса 12 по математике
              • Решения NCERT Класс 12 Бухгалтерия
              • Решения NCERT, класс 12, бизнес-исследования
              • Решения NCERT, класс 12 Экономика
              • NCERT Solutions Class 12 Accountancy Part 1
              • NCERT Solutions Class 12 Accountancy Part 2
              • NCERT Solutions Class 12 Micro-Economics
              • NCERT Solutions Class 12 Commerce
              • NCERT Solutions Class 12 Macro-Economics

            • NCERT Solutions For Класс 4
              • Решения NCERT для математики класса 4
              • Решения NCERT для класса 4 EVS

            • Решения NCERT для класса 5
              • Решения NCERT для математики класса 5
              • Решения NCERT для класса 5 EVS

            • Решения NCERT для класса 6
              • Решения NCERT для математики класса 6
              • Решения NCERT для науки класса 6
              • Решения NCERT для социальных наук класса 6
              • Решения NCERT для класса 6 Английский

            • Решения NCERT для класса 7
              • Решения NCERT для класса 7 Математика
              • Решения NCERT для класса 7 Наука
              • Решения NCERT для класса 7 по социальным наукам
              • Решения NCERT для класса 7 Английский

            • Решения NCERT для класса 8
              • Решения NCERT для класса 8 Математика
              • Решения NCERT для класса 8 Science
              • Решения NCERT для социальных наук 8 класса
              • Решение NCERT ns для класса 8 Английский

            • Решения NCERT для класса 9
              • Решения NCERT для социальных наук класса 9

            • Решения NCERT для математики класса 9
              • Решения NCERT для математики класса 9 Глава 1
              • Решения NCERT для Математика класса 9 Глава 2
              • Решения NCERT для математики класса 9 Глава 3
              • Решения NCERT для математики класса 9 Глава 4

              Решения NCERT

              • для математики класса 9 Глава 5
              • Решения NCERT для математики класса 9 Глава 6
              • Решения NCERT для Математика класса 9 Глава 7
              • Решения NCERT для математики класса 9 Глава 8

              Решения NCERT

              • для математики класса 9 Глава 9

              Решения NCERT

              • для математики класса 9 Глава 10
              • Решения NCERT для математики класса 9 Глава 11
              • Решения NCERT для Математика класса 9 Глава 12
              • Решения NCERT для математики класса 9 Глава 13

              Решения

              • NCERT для математики класса 9 Глава 14
              • Решения NCERT для математики класса 9 Глава 15

            • Решения NCERT для науки класса 9
              • Решения NCERT для науки класса 9 Глава 1
              • Решения NCERT для науки класса 9 Глава 2
              • Решения NCERT для класса 9 Наука Глава 3
              • Решения NCERT для Науки Класса 9 Глава 4
              • Решения NCERT для Науки Класса 9 Глава 5
              • Решения NCERT для Науки Класса 9 Глава 6
              • Решения NCERT для Науки Класса 9 Глава 7
              • Решения NCERT для Класса 9 Наука Глава 8
              • Решения NCERT для Науки Класса 9 Глава 9
              • Решения NCERT для Науки Класса 9 Глава 10
              • Решения NCERT для Науки Класса 9 Глава 12
              • Решения NCERT для Науки Класса 9 Глава 11
              • Решения NCERT для Класса 9 Наука Глава 13
              • Решения NCERT для класса 9 Наука Глава 14
              • Решения NCERT для класса 9 по науке Глава 15

            • Решения NCERT для класса 10
              • Решения NCERT для класса 10 по социальным наукам

            • Решения NCERT для математики класса 10
              • Решения NCERT для математики класса 10 Глава 1
              • Решения NCERT для математики класса 10 Глава 2
              • Решения NCERT для математики класса 10 Глава 3
              • Решения NCERT для математики класса 10 Глава 4
              • Решения NCERT для математики класса 10 Глава 5
              • Решения NCERT для математики класса 10 Глава 6
              • Решения NCERT для математики класса 10 Глава 7
              • Решения NCERT для математики класса 10 Глава 8
              • Решения NCERT для математики класса 10 Глава 9

              Решения NCERT

              • для математики класса 10 Глава 10

              Решения

              • NCERT для математики класса 10 Глава 11
              • Решения NCERT для математики класса 10 Глава 12
              • Решения NCERT для математики класса 10 Глава 13
              • NCERT Sol Решения NCERT для математики класса 10 Глава 14
              • Решения NCERT для математики класса 10 Глава 15

            • Решения NCERT для науки класса 10
              • Решения NCERT для науки класса 10 Глава 1
              • Решения NCERT для науки класса 10 Глава 2
              • Решения NCERT для науки класса 10, глава 3
              • Решения NCERT для науки класса 10, глава 4
              • Решения NCERT для науки класса 10, глава 5
              • Решения NCERT для науки класса 10, глава 6
              • Решения NCERT для науки класса 10, глава 7
              • Решения NCERT для науки 10 класса, глава 8
              • Решения NCERT для науки класса 10 Глава 9
              • Решения NCERT для науки класса 10 Глава 10
              • Решения NCERT для науки класса 10 Глава 11
              • Решения NCERT для науки класса 10 Глава 12
              • Решения NCERT для науки 10 класса Глава 13
              • Решения NCERT для науки 10 класса Глава 14
              • Решения NCERT для науки 10 класса Глава 15
              • Решения NCERT для науки 10 класса Глава 16

            • Учебный план NCERT
            • NCERT

          • Commerce
            • Class 11 Commerce Syllabus
              ancy Account
              • Программа бизнес-исследований 11 класса
              • Учебная программа по экономике 11 класса

            • Учебная программа по коммерции 12 класса
              • Учебная программа по бухгалтерии 12 класса
              • Учебная программа по бизнесу 12 класса
              • Учебная программа по экономике
              • 9000 9000
                • Образцы документов по коммерции класса 11
                • Образцы документов по коммерции класса 12
                • TS Grewal Solutions
                  • TS Grewal Solutions Class 12 Accountancy
                  • TS Grewal Solutions Class 11 Accountancy

                • Отчет о движении денежных средств
                • Что такое Entry eurship
                • Защита прав потребителей
                • Что такое основной актив
                • Что такое баланс
                • Формат баланса
                • Что такое акции
                • Разница между продажами и маркетингом

              • ICSE
                • Документы
                • ICSE
                • Вопросы ICSE
                • ML Aggarwal Solutions
                  • ML Aggarwal Solutions Class 10 Maths
                  • ML Aggarwal Solutions Class 9 Maths
                  • ML Aggarwal Solutions Class 8 Maths
                  • ML Aggarwal Solutions Class 7 Maths
                  • ML 6 Maths
                  • ML 6 Maths

                • Selina Solutions
                  • Selina Solutions для класса 8
                  • Selina Solutions для Class 10
                  • Selina Solutions для Class 9

                • Frank Solutions
                  • Frank Solutions для математики класса 10
                  • Frank Solutions для математики класса 9

                • Класс ICSE 9000 2
                • ICSE Class 6
                • ICSE Class 7
                • ICSE Class 8
                • ICSE Class 9
                • ICSE Class 10
                • ISC Class 11
                • ISC Class 12

            • IAS
              Exam
              • IAS
              • Civil
              • Сервисный экзамен
              • Программа UPSC
              • Бесплатная подготовка к IAS
              • Текущие события
              • Список статей IAS
              • Пробный тест IAS 2019
                • Пробный тест IAS 2019 1
                • Пробный тест IAS 2019 2

            • Экзамен KPSC KAS
            • Экзамен UPPSC PCS
            • Экзамен MPSC
            • Экзамен RPSC RAS ​​
            • TNPSC Group 1
            • APPSC Group 1
            • Экзамен BPSC
            • WBPS3000 Экзамен 9000 MPC 9000 9000 MPC4000 Jam
            • Вопросник UPSC 2019
              • Ключ ответов UPSC 2019

            • Коучинг IAS
              • IA S Coaching Бангалор
              • IAS Coaching Дели
              • IAS Coaching Ченнаи
              • IAS Coaching Хайдарабад
              • IAS Coaching Mumbai

          • JEE
            • BYJU’SEE
            • 9000 JEE 9000 Основной документ JEE 9000 JEE 9000
            • Вопросник JEE
            • Биномиальная теорема
            • Статьи JEE
            • Квадратичное уравнение

          • NEET
            • Программа BYJU NEET
            • NEET 2020
            • NEET Приемлемость 9000 Критерии 9000 NEET4 9000 NEET 9000 Пример 9000 9000 NEET
            • Поддержка
              • Разрешение жалоб
              • Служба поддержки
              • Центр поддержки

          • Государственные советы
            • GSEB
              • GSEB Syllabus
              • GSEB4
              • GSEB3 Образец статьи

              GSEB3 004

              • MSBSHSE
                • MSBSHSE Syllabus
                • MSBSHSE Учебники
                • Образцы статей MSBSHSE
                • Вопросники MSBSHSE

              • AP Board
                • APSCERT
                • Syll
                • AP 9000SC4
                • Syll
                • AP
                • Syll 9000SC4
                • Syll
                • Syll

              • MP Board
                • MP Board Syllabus
                • MP Board Образцы документов
                • Учебники MP Board

              • Assam Board
                • Assam Board Syllabus
                • Assam Board Учебники 9000 9000 Board4 BSEB
                  • Bihar Board Syllabus
                  • Bihar Board Учебники
                  • Bihar Board Question Papers
                  • Bihar Board Model Papers

                • BSE Odisha
                  • Odisha Board Syllabus
                  • Odisha Board Syllabus
                  • Odisha Board Syllabus
                  • Программа PSEB
                  • Учебники PSEB
                  • Вопросы PSEB

                • RBSE
                  • Rajasthan Board Syllabus
                  • RBSE Учебники
                  • RBSE Question Papers

                • HPBOSE
                • HPBOSE
                • HPBOSE
                • JKBOSE
                  • Программа обучения JKBOSE
                  • Образцы документов JKBOSE
                  • Шаблон экзамена JKBOSE

                • TN Board
                  • TN Board Syllabus
                  • TN Board 9000 Papers 9000 TN Board 9000 Papers 9000 9000 Paper Papers 9000 TN Board 9000 4 JAC
                    • Программа JAC
                    • Учебники JAC
                    • Вопросники JAC

                  • Telangana Board
                    • Telangana Board Syllabus
                    • Telangana Board Учебники
                    • Papers Telangana Board Учебники
                    • Учебный план KSEEB
                    • Типовой вопросник KSEEB

                  • KBPE
                    • Учебный план KBPE
                    • Учебники KBPE
                    • Документы по KBPE

                  • 9000 Доска UPMSP 9000 Доска UPMSP 9000 Доска UPMSP 9000

                • Совет по Западной Бенгалии
                  • Учебный план Совета по Западной Бенгалии
                  • Учебники для Совета по Западной Бенгалии
                  • Вопросы для Совета по Западной Бенгалии

                • UBSE
                • TBSE
                • Гоа Совет
                • 000
                • NBSE0003 Доска
                • M

          ,
          

Как найти площадь грани куба

Под кубом подразумевается правильный многогранник, у которого все грани образованы правильными четырехугольниками – квадратами. Для того, чтобы найти площадь грани любого куба, не потребуется тяжелых расчетов.

Инструкция

Для начала стоит заострить внимание на само определение куба. Из него видно, что любая из граней куба представляет собой квадрат. Таким образом, задача по нахождению площади грани куба сводится к задаче по нахождению площади любого из квадратов (граней куба). Можно взять именно любую из граней куба, так как длины всех его ребер равны между собой.

Для того, чтобы найти площадь грани куба, требуется перемножить между собой пару любых из его сторон, ведь все они между собой равны. Формулой это можно выразить так:

S = a², где а – сторона квадрата (ребро куба).

Пример: Длина ребра куба 11 см, требуется найти ее площадь.

Решение: зная длину грани, можно найти ее площадь:

S = 11² = 121 см²

Ответ: площадь грани куба с ребром 11 см равна 121 см²

Обратите внимание

Любой куб имеет 8 вершин, 12 ребер, 6 граней и 3 грани при вершине.
Куб – это такая фигура, которая встречается в быту невероятно часто. Достаточно вспомнить игровые кубики, игральные кости, кубики в различны детских и подростковых конструкторах.
Многие элементы архитектуры имеют кубическую форму.
Кубическими метрами принято измерять объемы различных веществ в различных сферах жизни общества.
Говоря научным языком, кубический метр – это мера измерения объема вещества, которое способно поместиться в куб с длиной ребра 1 м
Таким образом, можно ввести и иные единицы измерения объема: кубические миллиметры, сантиметры, дециметры и т.п.
Помимо различных кубических единиц измерения объема, в нефтяной и газовой промышленности возможно применение иной единицы – баррель (1м³ = 6.29 баррелей)

Полезный совет

Если у куба известна длина ее ребра, то, помимо площади грани можно найти и другие параметры данного куба, например:
Площадь поверхности куба: S = 6*a²;
Объем: V = 6*a³;
Радиус вписанной сферы: r = a/2;
Радиус сферы, описанной вокруг куба: R = ((√3)*a))/2;
Диагональ куба (отрезок, соединяющие две противоположные вершины куба, который проходит через его центр): d = a*√3

Источники:

• площадь куба если ребра равны 11 см

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Содержание

• – Как найти площадь грани в кубе?
• – Как решить площадь куба?
• – Где находится грань у куба?
• – Как найти площадь диагонального сечения куба?
• – Как найти площадь куба с ребром 6 см?
• – Как найти периметр и площадь куба?
• – Какая фигура находится в основании куба?
• – Как называется грань куба?
• – Чем грань отличается от стороны?

Площадь каждой грани считается так: S = a ⋅ a = a2. Всего у куба 6 граней, а значит, площадь его поверхности равняется шести площадям одной грани: S = 6 ⋅ a2.

Как найти площадь грани в кубе?

Для того, чтобы найти площадь грани куба, требуется перемножить между собой пару любых из его сторон, ведь все они между собой равны. Формулой это можно выразить так: S = a², где а – сторона квадрата (ребро куба).

Как решить площадь куба?

Площадь поверхности куба равна квадрату длины его грани умноженному на шесть (куб имеет шесть одинаковых граней). где S – площадь куба, a – длина грани куба.

Где находится грань у куба?

Глоссарий по теме: Куб – это многогранник, поверхность которого состоит из шести квадратов. Грани куба – это стороны куба, которые представляют собой квадрат.

Как найти площадь диагонального сечения куба?

Малая диагональ куба по теореме Пифагора. d = √2*a – диагональ – сторона сечения. S = d*a = 2√2 см² – площадь сечения – ответ.

Как найти площадь куба с ребром 6 см?

Из условия задачи нам известно, что длина ребра рассматриваемого куба составляет: a = 6 см. Подставим данное значение в формулу (1) и получим, что площадь поверхности куба составит: S = 6 * a^2 = 6 * 6^2 = 6 * 36 = 216 см. кв.

Как найти периметр и площадь куба?

Чтобы найти периметр куба, определите длину одного из его ребер и умножьте это число на 12. В виде формулы это правило можно записать следующим образом:P. = 12 * a,где:Р – периметр куба,а – длина его стороны. Подобная формула может понадобиться если нужно собрать каркас куба, равного существующему.

Какая фигура находится в основании куба?

Куб является частным случаем параллелепипеда и призмы. Куб или правильный гексаэдр – это правильный многогранник, у которого все грани это квадраты. шестиугольников — это сечения через центр куба перпендикулярно 4-м главным диагоналям.

Как называется грань куба?

Куб (др. … κύβος); иногда гекса́эдр или правильный гекса́эдр — правильный многогранник, каждая грань которого представляет собой квадрат.

Чем грань отличается от стороны?

Поверхности многогранника называют гранями. По-сути грани представляют собой плоскости, ограниченные сторонами многоугольников, из которых состоит многогранник. Сами стороны многоугольников называются ребрами. По-сути они представляют собой отрезки.

Интересные материалы:

Когда котенок перестает мяукать?
Когда ловить карпа?
Когда лучше начинать продавать квартиру по лунному календарю?
Когда лучше наносить тканевые маски?
Когда лучше покупать авто в 2020?
Когда лучше покупать авто в салоне?
Когда лучше покупать автомобиль в автосалоне новый?
Когда лучше покупать летнюю резину для автомобиля?
Когда лучше покупать летнюю резину на авто?
Когда лучше покупать новый автомобиль в салоне?