Одним из фундаментальных объектов в геометрии является многоугольник. Если рассматривать фигуру в трёхмерном пространстве, то с помощью двух таких геометрических тел с шестью углами можно построит правильную шестиугольную призму. При этом боковые грани обязательно будут прямоугольниками. По своему виду такая фигура напоминает пчелиные соты, поэтому она и интересна для изучения архитекторам и математикам.

Общие сведения
Призма представляет собой многогранную объёмную фигуру. Две стороны её всегда конгруэнтные (равные) и расположены относительно друг друга в параллельных плоскостях. Остальные же грани являются параллелограммами и формируют общие боковые основания с параллельными поверхностями. Четырёхугольники состоят из попарно равноудалённых прямых. Называют их боковыми гранями призмы. Оставшиеся же 2 многоугольника — основанием. По сути, фигура — это частный случай некругового цилиндра.
Кроме основания и граней, в состав стереофигуры входит:

- высота — прямая, перпендикулярная плоскостям, лежащим у основания многогранника;
- боковые рёбра — стороны, являющиеся общими для боковых граней;
- вершины — точки, принадлежащие сразу двум отрезкам и формирующим периметр геометрического тела;
- диагонали — отрезки, проходящие через 2 вершины, но при этом несвойственные одной грани;
- диагональные плоскости — пересекающие боковые рёбра и диагональ у основания.
Кроме этого, используются такие понятия, как диагональное и ортогональное сечение. Первое представляет собой параллелограмм, полученный при пересечении призмы и диагональной плоскости. Второе же — пересечение многогранника с плоскостью, перпендикулярной боковому ребру.

В зависимости от расположения стенок и вида основания, призмы разделяют на 3 типа. Прямой называют ту, где все грани — прямоугольники. Если у фигуры в основании находится правильный многоугольник, стереофигура считается правильной. Частным случаем её является полуправильная призма. В ней боковые грани образуют квадраты. Когда же у многогранника основания непараллельные, призму называют усечённой.
Полуправильный многогранник, имеющий 2 параллельных основания в виде правильных n-угольников, равных между собой, чьи грани представляют собой ломаную линию, называют антипризмой. В качестве примера такой фигуры можно привести октаэдр, икосаэдр и восьмиугольный октагон.
Свойства шестигранника
Правильную шестиугольную призму принято обозначать большими латинскими буквами: ABCDEFA1B1C1D1E1F1. Длину основания подписывают маленьким символом a, а длину боковой стороны h. К характеристикам фигуры относят площади основания, боковые грани, полную поверхность, объём многогранника. Всего у геометрического тела 8 граней, 18 рёбер и 12 вершин.
Для успешного вычисления различных параметров фигуры понадобится знать следующие формулы:

Если рассмотреть правильный шестиугольник, лежащий в основе призмы ABCDEF, и провести отрезки AB, CD, EF, у них будет общая точка пересечения. Для удобства обозначить её можно буквой O. Так как, в соответствии со свойствами, треугольники AOB, BOC, COD, DOE, EOF, FOA будут правильными, можно составить равенство: AO = OD = EO = OB = CO = OF = a .

Через точку М можно провести прямую AC и CF. Образованный ранее треугольник AEO будет равнобедренным. В нём отрезок AO равняется по величине OE. Значит, угол EOA будет развёрнутым и равняться 120 градусам. Используя свойства равнобедренного треугольника, можно записать: AE = a * √2 * (1 — cos EOA). То есть: AE = AC = √3 * a.
По аналогии можно найти и стороны: EA1, FB1, AC1, BD1, CE1, DF1. Так как AA1 = h, а из свойств правильной призмы следует, что угол EAA1 — прямой, длины сторон будут равны между собой, и их можно найти, используя формулу: √(AA12 + AE2)= √(h2 + 3 * a) = 2 * a. Грань EB1 = FC1 = AD1 = BE1 = CF1 = DA1 = √(BB12 + BE2) = √(h2 + 4 *a) = √5 *a. Сторона FE1 = √(FE2 + EE2) = √(h2 + a2) = √2 *a.
Длины диагоналей призмы равняются сумме квадратов высоты и длины основания под корнем. Это легко доказать, если принять, что ЕЕ1 = h, а FE = a. Треугольник FEE1 прямоугольный, значит, FE = √(h2 + a2), что и следовало доказать.
Решение простого примера
Такого вида задачи обычно даются в учебниках по геометрии для выпускных классов средней школы. Решить их самостоятельно несложно, нужно только знать формулы и представлять, как выглядит та или иная фигура. При этом часто приходится использовать дополнительные построения. Вот один из таких типовых примеров.

Пусть имеется девятиугольная фигура, в которую вписана правильная шестиугольная призма со стандартным обозначением вершин. Сторона основания в ней составляет 4 см, а длина бокового ребра меньше её в 2 раза, то есть равняется 2. Необходимо вычислить расстояние от точки C1 до прямой, соединяющей вершины EF. По условию задачи в основании лежит геометрическое тело, у которого все стороны и углы равны, то есть фигура правильная.
Чтобы понять, что будет представлять искомая прямая, нужно изобразить призму на рисунке и на нём же начертить отрезок. Фактически это будет перпендикуляр, который и является вычисляемым расстоянием. Проекцией точки С1 будет вершина С. Из неё можно построить перпендикуляр, который ограничится точкой E. Таким образом, поставленная задача сводится к поиску длины отрезка C1E.
Найти длину прямой можно как гипотенузу прямоугольного треугольника С1СE. Треугольная фигура будет с прямым углом C. Из условия задачи отрезок С1С в два раза меньше ребра основания, а значит равен 2. Теперь осталось найти, чему равняется длина CE. Геометрическое тело CDE является равнобедренным. По условию CD = ED. Сумму углов шестиугольника можно найти по формуле е = 180 * (n — 2) = 180 * 4 = 720. Получается, что на каждый угол приходится по 120 градусов.

С вершины D можно опустить перпендикуляр DN на CE. Принимая во внимание свойства равнобедренного треугольника, высота DN будет медианной и биссектрисой. Следовательно, угол C равняется 30 градусов, так как CDH — прямоугольный.
Теперь можно найти СH. Сделать это возможно через косинус угла C: cos 30 = CH / CD. Отсюда: CH = 4 * p/2 = 2 √ 3. Так как CH = HE, сторона CE = 2 * 2 √3. К треугольнику CC1E можно применить теорему Пифагора: C1E2 = C1C2 + CE = 22 + (4 c3) 2. C1E2 = √ 52. Таким образом, искомый ответ можно записать так: C1E = 2√13.
Задача высокого уровня
Решение примеров повышенного уровня сложности предполагает не только хорошее понимание изучаемого материала, но и знание предыдущих тем. Понадобится вспомнить формулы для нахождения площадей и объёмов плоских фигур и их свойства. Вот пример одной из таких задач.
Пусть имеется шестиугольная объёмная фигура, у которой баковая грань равняется 6, а площадь основания 12. Нужно найти объём геометрического тела с вершинами в точках A, B1, C1, D1, E1, F1.

В таких задачах перед тем как непосредственно приступить к вычислениям, желательно использовать вспомогательный рисунок. На нём нужно изобразить фигуру в трёхмерной системе координат и подписать все её вершины.
Согласно условию, площадь основания Sabcde1f1 = 12, отрезок AA1 = 6. Так как фигура правильная, то все ребра у призмы буду равны. Чтобы найти, сколько будет составлять объём, понадобится обозначить многогранник. Для этого следует построить отрезки F1B, F1A, B1, E1A, D1A, C1A. Получившаяся фигура представляет собой пирамиду.
Формула для нахождения объёма пирамиды записывается так: V = h * S / 3. Её можно привести к виду: V = (AA1 * Sb1c1d1e1f1) / 3. Теперь нужно определить, чему же будет равняться площадь шестиугольника. Так как в основании призмы лежит правильная фигура с шестью углами, радиус описанной окружности будет совпадать с боковой стороной.
Таким образом, искомая площадь будет равняться шести поверхностям правильного треугольника. В свою очередь, его занимаемый размер можно определить как Sтр = (a * b) * sin / 2. Значит, площадь основания призмы равна: S = (6 * R * R * sin 60) / 2. Подставив заданное условием значение из формулы, можно выразить радиус: R2 = (12 * 2) / 3 √ 3 = 8 /√3.
Площадь треугольника A1B1F1 находится как произведение сторон, умноженное на синус угла и разделённое на 2: S = (a * a * sin120) / 2 = a2 * sin60 / 2 = (R2 * √ 3/3) / 2. Подставив значение R, можно получить: S = (½) * (8 / √ 3) * (√3 / 2) = 2. Тогда площадь пятиугольника будет равняться разнице поверхностей шестиугольника и треугольника A1B1F1, то есть S = 12 — 2 = 10. Теперь можно будет подсчитать и объём пирамиды: Vab1c1d1e1f1 = (1 / 3) * 6 * 10 = 20. Задача решена.
Предыдущая
ГеометрияТочка пересечения биссектрис – свойства, теорема и соотношения
Следующая
ГеометрияЭлементы треугольника – формулы вычисления основных параметров
Изучением призм занимается пространственная геометрия. Важными их характеристиками являются заключенный в них объем, площадь поверхности и число составляющих элементов. В статье рассмотрим все эти свойства для шестиугольной призмы.
О какой призме пойдет речь?
Призма шестиугольная – это фигура, образованная двумя многоугольниками, имеющими шесть сторон и шесть углов, и шестью параллелограммами, соединяющими отмеченные шестиугольники в единое геометрическое образование.
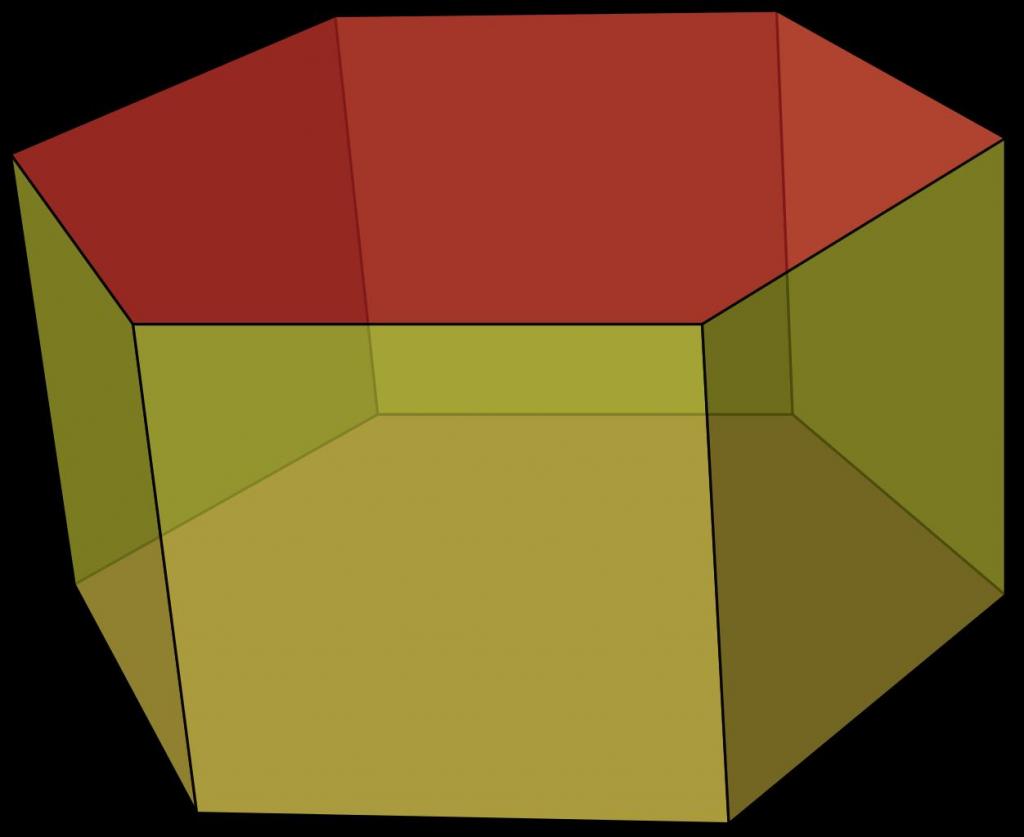
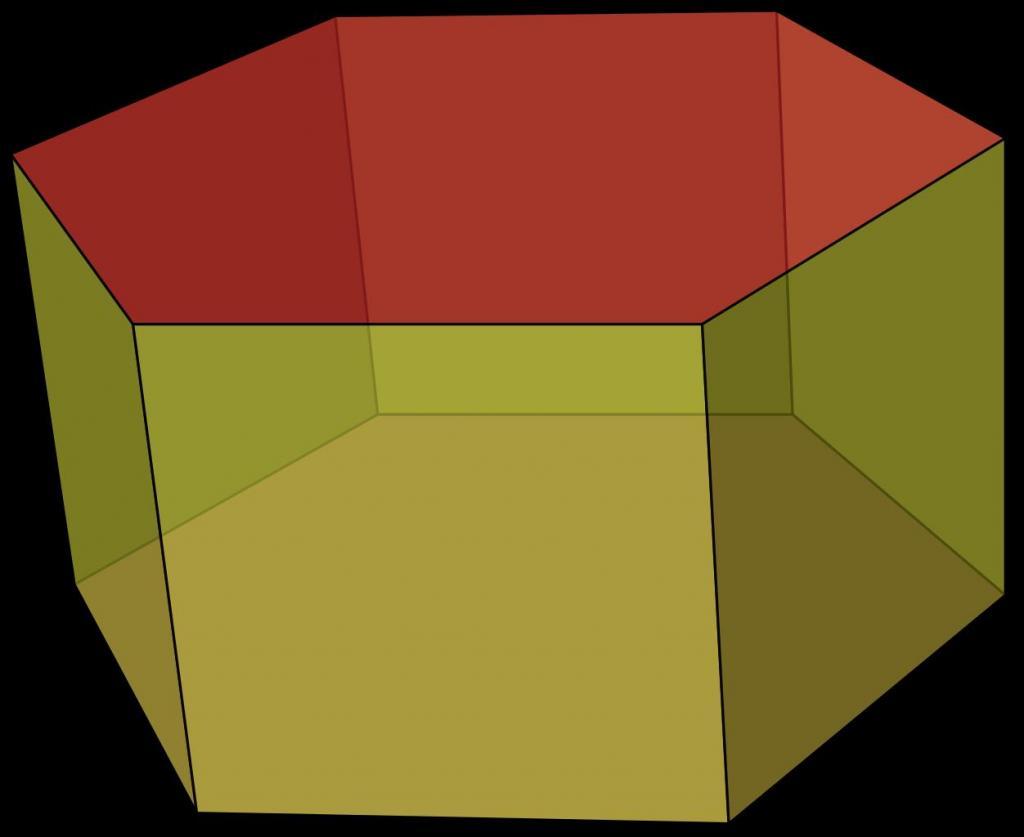
На рисунке изображен пример этой призмы.
Отмеченный красным цветом шестиугольник называется основанием фигуры. Очевидно, что число ее оснований равно двум, причем оба они идентичны. Желто-зеленоватые грани призмы называются ее боковыми сторонами. На рисунке они представлены квадратами, но в общем случае они являются параллелограммами.
Шестиугольная призма может быть наклонной и прямой. В первом случае углы между основанием и боковыми сторонами не являются прямыми, во втором они равны 90o. Также эта призма может быть правильной и неправильной. Правильная шестиугольная призма обязательно должна быть прямой и иметь правильный шестиугольник в основании. Приведенная выше призма на рисунке этим требованиям удовлетворяет, поэтому она называется правильной. Далее в статье будем изучать только ее свойства, как общий случай.
Элементы
Для любой призмы главными ее элементами являются ребра, грани и вершины. Шестиугольная призма не является исключением. Приведенный выше рисунок позволяет посчитать количество этих элементов. Так, граней или сторон мы получаем 8 (два основания и шесть боковых параллелограммов), число вершин составляет 12 (по 6 вершин для каждого основания), количество ребер шестиугольной призмы равно 18 (шесть боковых и 12 для оснований).
В 1750-е годы Леонард Эйлер (швейцарский математик) установил для всех полиэдров, к которым относится призма, математическую связь между числами указанных элементов. Эта связь имеет вид:
число ребер = число граней + число вершин – 2.
Указанные выше цифры удовлетворяют этой формуле.
Диагонали призмы
Все диагонали шестиугольной призмы можно разделить на два типа:
- те, которые лежат в плоскостях ее граней;
- те, которые принадлежат всему объему фигуры.
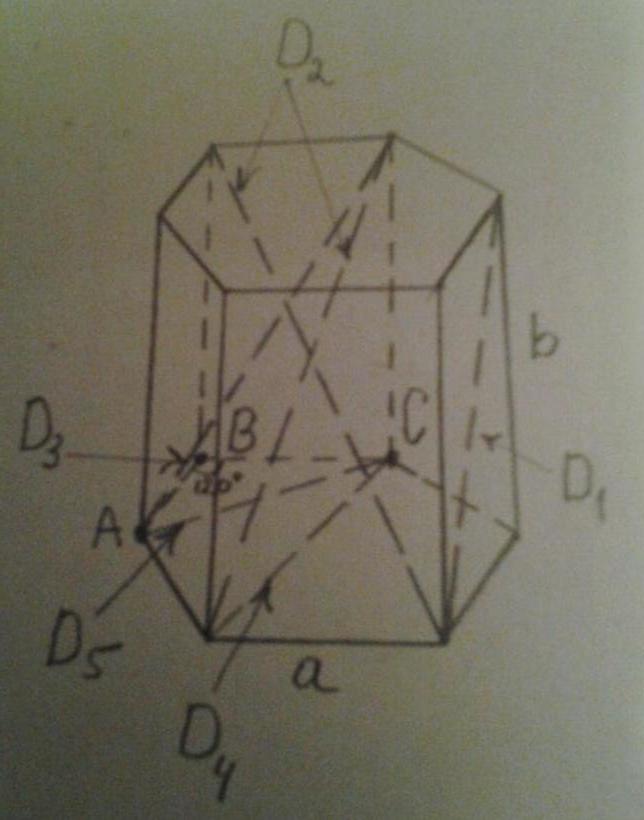
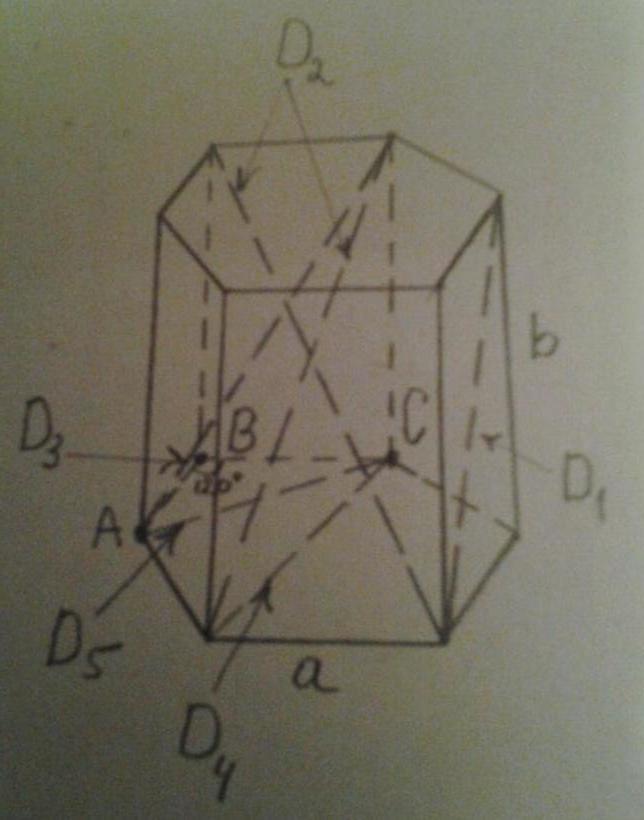
Рисунок ниже показывает все эти диагонали.
Видно, что D1 – это диагональ боковой стороны, D2 и D3 – диагонали всей призмы, D4 и D5 – диагонали основания.
Длины диагоналей боковых сторон между собой равны. Вычислить их легко, используя всем известную теорему Пифагора. Обозначим символом a длину стороны шестиугольника, символом b – длину бокового ребра. Тогда диагональ имеет длину:
D1 = √(a2 + b2).
Диагональ D4 также легко определяется. Если вспомнить, что правильный шестиугольник вписывается в окружность радиусом a, то D4 является диаметром этой окружности, то есть получим следующую формулу:
D4 = 2*a.
Диагональ D5 основания найти несколько сложнее. Для этого следует рассмотреть равносторонний треугольник ABC (см. рис.). Для него AB = BC = a, угол ABC равен 120o. Если из этого угла опустить высоту (она же будет биссектрисой и медианой), тогда половина основания AC будет равно:
AC/2 = AB*sin(60o) = a*√3/2.
Сторона AC является диагональю D5, поэтому получаем:
D5 = AC = √3*a.
Теперь остается найти диагонали D2 и D3 правильной шестиугольной призмы. Для этого нужно увидеть, что они являются гипотенузами соответствующих прямоугольных треугольников. Воспользовавшись теоремой Пифагора, получаем:
D2 = √(D42 + b2) = √(4*a2 + b2);
D3 = √(D52+ b2) = √(3*a2+ b2).
Таким образом, самой большой диагональю для любых значений a и b является D2.
Площадь поверхности
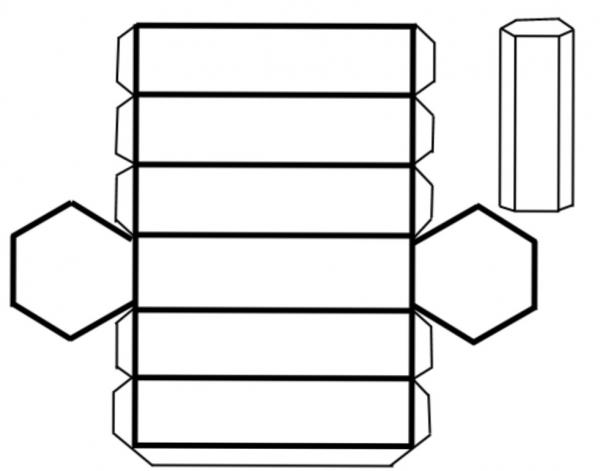
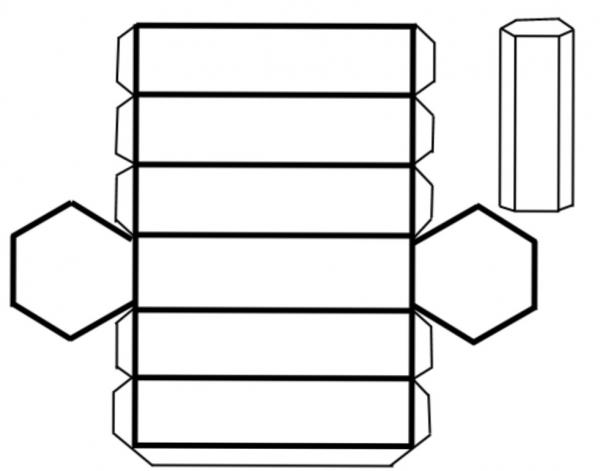
Чтобы понять, о чем идет речь, проще всего рассмотреть развертку этой призмы. Она показана на рисунке.
Видно, что для определения площади всех сторон рассматриваемой фигуры необходимо рассчитать отдельно площадь четырехугольника и площадь шестиугольника, затем умножить их на соответствующие целые числа, равные количеству каждого n-угольника в призме, и сложить полученные результаты. Шестиугольников 2, прямоугольников 6.
Для площади прямоугольника получаем:
S1 = a*b.
Тогда площадь боковой поверхности равна:
S2 = 6*a*b.
Для определения площади шестиугольника проще всего воспользоваться соответствующей формулой, которая имеет вид:
Sn = n/4*a2*ctg(pi/n).
Подставляя в это выражение число n равное 6, получаем площадь одного шестиугольника:
S6 = 6/4*a2*ctg(pi/6) = 3*√3/2*a2.
Это выражение следует умножить на два, чтобы получить площадь оснований призмы:
Sos = 3*√3*a2.
Остается сложить Sos и S2, чтобы получить полную площадь поверхности фигуры:
S = Sos + S2 = 3*√3*a2 + 6*a*b = 3*a*(√3*a + 2*b).
Объем призмы
После того как была получена формула для площади шестиугольного основания, вычислить объем, заключенный в рассматриваемую призму, проще простого. Для этого следует лишь умножить площадь одного основания (шестиугольника) на высоту фигуры, длина которой равна длине бокового ребра. Получаем формулу:
V = S6*b = 3*√3/2*a2*b.
Отметим, что произведение основания на высоту дает значение объема абсолютно любой призмы, включая наклонную. Однако в последнем случае расчет высоты осложняется, поскольку она уже не будет равна длине бокового ребра. Что касается шестиугольной правильной призмы, то значение ее объема является функцией двух переменных: сторон a и b.
-
Вы здесь:
- Главная
- Правильная шестиугольная призма
Правильная шестиугольная призма
Шестиугольная призма — это многогранник, две грани которого являются равными шестиугольниками, лежащими в параллельных плоскостях, а остальные грани (боковые грани) — параллелограммами, имеющими общие стороны с этими треугольниками.
Правильная шестиугольная призма – это шестиугольная призма у которой основания правильные шестиугольники (все стороны которых равны, углы между сторонами основания составляют 120 градусов), а боковые грани прямоугольники.
Основания призмы являются равными правильными шестиугольниками.
Боковые грани призмы являются прямоугольниками.
Боковые рёбра призмы параллельны и равны.
Размеры призмы можно выразить через длину стороны a и высоту h.
Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания.
Формула площади поверхности шестиугольной призмы:
Объём призмы равен произведению её высоты на площадь основания.
Формула объема правильной шестиугольной призмы:
Правильная шестиугольная призма может быть вписана в цилиндр.
Формула радиуса цилиндра вписанной шестиугольной призмы:
Двойственным многогранником прямой призмы является бипирамида.
Исторически понятие “призма” возникло из латыни и означало – нечто отпиленное.
Анимация демонстрирует как две параллельные плоскости отрезая лишнее формируют два основания призмы. Из одной заготовки можно получить как правильную призму, так и наклонную призму.
Геометрические размеры готовой призмы (мм):
Длина = 90
Ширина = 78
Высота = 45
Геометрические размеры готовой призмы (мм):
Длина = 73
Ширина = 64
Высота = 73
Геометрические размеры готовой призмы (мм):
Длина = 62
Ширина = 54
Высота = 93
посмотреть другие призмы
Популярное
Естественные многогранники. Часть 2
В микромире многогранники встречаются в виде молекул, вирусов и бактерий – простейших организмов. Например: фуллерены – шарообразные молекулы углерода С60 (рис.) – “кирпичики”…
Домик для птиц
Студией Артемия Лебедева (https://www.artlebedev.ru/) была предложена форма скворечника в виде многогранника.
В качестве геометрической…
Куб Принца Руперта
В выпуске 25 «Волшебных граней» мы обратили взор читателя на то, что разрезая куб плоскостью, мы получаем в точке разреза сечение, имеющее форму…
Многогранники для Новогодней сказки
Сделать новогодний праздник красивым и необычным, чтобы дети видели в нём сказку, а гости восхищались, можно только своими руками. Бумажные многогранники –…
Миры Ричарда Суини
Молодой британский дизайнер Ричард Суини (Richard Sweeney) создает удивительные скульптуры из…
Многогранники в архитектуре. Часть 5
Архитекторы с древних времен применяли элементы многогранников в создании своих творений. В современно мире этот подход выделяет здания среди тысяч других.
Шестиугольная призма и ее основные характеристики
Изучением призм занимается пространственная геометрия. Важными их характеристиками являются заключенный в них объем, площадь поверхности и число составляющих элементов. В статье рассмотрим все эти свойства для шестиугольной призмы.
О какой призме пойдет речь?
Призма шестиугольная – это фигура, образованная двумя многоугольниками, имеющими шесть сторон и шесть углов, и шестью параллелограммами, соединяющими отмеченные шестиугольники в единое геометрическое образование.
На рисунке изображен пример этой призмы.
Отмеченный красным цветом шестиугольник называется основанием фигуры. Очевидно, что число ее оснований равно двум, причем оба они идентичны. Желто-зеленоватые грани призмы называются ее боковыми сторонами. На рисунке они представлены квадратами, но в общем случае они являются параллелограммами.
Шестиугольная призма может быть наклонной и прямой. В первом случае углы между основанием и боковыми сторонами не являются прямыми, во втором они равны 90 o . Также эта призма может быть правильной и неправильной. Правильная шестиугольная призма обязательно должна быть прямой и иметь правильный шестиугольник в основании. Приведенная выше призма на рисунке этим требованиям удовлетворяет, поэтому она называется правильной. Далее в статье будем изучать только ее свойства, как общий случай.
Элементы
Для любой призмы главными ее элементами являются ребра, грани и вершины. Шестиугольная призма не является исключением. Приведенный выше рисунок позволяет посчитать количество этих элементов. Так, граней или сторон мы получаем 8 (два основания и шесть боковых параллелограммов), число вершин составляет 12 (по 6 вершин для каждого основания), количество ребер шестиугольной призмы равно 18 (шесть боковых и 12 для оснований).
В 1750-е годы Леонард Эйлер (швейцарский математик) установил для всех полиэдров, к которым относится призма, математическую связь между числами указанных элементов. Эта связь имеет вид:
число ребер = число граней + число вершин – 2.
Указанные выше цифры удовлетворяют этой формуле.
Диагонали призмы
Все диагонали шестиугольной призмы можно разделить на два типа:
- те, которые лежат в плоскостях ее граней;
- те, которые принадлежат всему объему фигуры.
Рисунок ниже показывает все эти диагонали.
Видно, что D1 – это диагональ боковой стороны, D2 и D3 – диагонали всей призмы, D4 и D5 – диагонали основания.
Длины диагоналей боковых сторон между собой равны. Вычислить их легко, используя всем известную теорему Пифагора. Обозначим символом a длину стороны шестиугольника, символом b – длину бокового ребра. Тогда диагональ имеет длину:
Диагональ D4 также легко определяется. Если вспомнить, что правильный шестиугольник вписывается в окружность радиусом a, то D4 является диаметром этой окружности, то есть получим следующую формулу:
Диагональ D5 основания найти несколько сложнее. Для этого следует рассмотреть равносторонний треугольник ABC (см. рис.). Для него AB = BC = a, угол ABC равен 120 o . Если из этого угла опустить высоту (она же будет биссектрисой и медианой), тогда половина основания AC будет равно:
Сторона AC является диагональю D5, поэтому получаем:
Теперь остается найти диагонали D2 и D3 правильной шестиугольной призмы. Для этого нужно увидеть, что они являются гипотенузами соответствующих прямоугольных треугольников. Воспользовавшись теоремой Пифагора, получаем:
Таким образом, самой большой диагональю для любых значений a и b является D2.
Площадь поверхности
Чтобы понять, о чем идет речь, проще всего рассмотреть развертку этой призмы. Она показана на рисунке.
Видно, что для определения площади всех сторон рассматриваемой фигуры необходимо рассчитать отдельно площадь четырехугольника и площадь шестиугольника, затем умножить их на соответствующие целые числа, равные количеству каждого n-угольника в призме, и сложить полученные результаты. Шестиугольников 2, прямоугольников 6.
Для площади прямоугольника получаем:
Тогда площадь боковой поверхности равна:
Для определения площади шестиугольника проще всего воспользоваться соответствующей формулой, которая имеет вид:
Подставляя в это выражение число n равное 6, получаем площадь одного шестиугольника:
Это выражение следует умножить на два, чтобы получить площадь оснований призмы:
Остается сложить Sos и S2, чтобы получить полную площадь поверхности фигуры:
Объем призмы
После того как была получена формула для площади шестиугольного основания, вычислить объем, заключенный в рассматриваемую призму, проще простого. Для этого следует лишь умножить площадь одного основания (шестиугольника) на высоту фигуры, длина которой равна длине бокового ребра. Получаем формулу:
Отметим, что произведение основания на высоту дает значение объема абсолютно любой призмы, включая наклонную. Однако в последнем случае расчет высоты осложняется, поскольку она уже не будет равна длине бокового ребра. Что касается шестиугольной правильной призмы, то значение ее объема является функцией двух переменных: сторон a и b.
Правильная шестиугольная призма — свойства, признаки и формулы
Одним из фундаментальных объектов в геометрии является многоугольник. Если рассматривать фигуру в трёхмерном пространстве, то с помощью двух таких геометрических тел с шестью углами можно построит правильную шестиугольную призму. При этом боковые грани обязательно будут прямоугольниками. По своему виду такая фигура напоминает пчелиные соты, поэтому она и интересна для изучения архитекторам и математикам.
Общие сведения
Призма представляет собой многогранную объёмную фигуру. Две стороны её всегда конгруэнтные (равные) и расположены относительно друг друга в параллельных плоскостях. Остальные же грани являются параллелограммами и формируют общие боковые основания с параллельными поверхностями. Четырёхугольники состоят из попарно равноудалённых прямых. Называют их боковыми гранями призмы. Оставшиеся же 2 многоугольника — основанием. По сути, фигура — это частный случай некругового цилиндра.
Кроме основания и граней, в состав стереофигуры входит:
- высота — прямая, перпендикулярная плоскостям, лежащим у основания многогранника;
- боковые рёбра — стороны, являющиеся общими для боковых граней;
- вершины — точки, принадлежащие сразу двум отрезкам и формирующим периметр геометрического тела;
- диагонали — отрезки, проходящие через 2 вершины, но при этом несвойственные одной грани;
- диагональные плоскости — пересекающие боковые рёбра и диагональ у основания.
Кроме этого, используются такие понятия, как диагональное и ортогональное сечение. Первое представляет собой параллелограмм, полученный при пересечении призмы и диагональной плоскости. Второе же — пересечение многогранника с плоскостью, перпендикулярной боковому ребру.
В зависимости от расположения стенок и вида основания, призмы разделяют на 3 типа. Прямой называют ту, где все грани — прямоугольники. Если у фигуры в основании находится правильный многоугольник, стереофигура считается правильной. Частным случаем её является полуправильная призма. В ней боковые грани образуют квадраты. Когда же у многогранника основания непараллельные, призму называют усечённой.
Полуправильный многогранник, имеющий 2 параллельных основания в виде правильных n-угольников, равных между собой, чьи грани представляют собой ломаную линию, называют антипризмой. В качестве примера такой фигуры можно привести октаэдр, икосаэдр и восьмиугольный октагон.
Свойства шестигранника
Правильную шестиугольную призму принято обозначать большими латинскими буквами: ABCDEFA1B1C1D1E1F1. Длину основания подписывают маленьким символом a, а длину боковой стороны h. К характеристикам фигуры относят площади основания, боковые грани, полную поверхность, объём многогранника. Всего у геометрического тела 8 граней, 18 рёбер и 12 вершин.
Для успешного вычисления различных параметров фигуры понадобится знать следующие формулы:
Если рассмотреть правильный шестиугольник, лежащий в основе призмы ABCDEF, и провести отрезки AB, CD, EF, у них будет общая точка пересечения. Для удобства обозначить её можно буквой O. Так как, в соответствии со свойствами, треугольники AOB, BOC, COD, DOE, EOF, FOA будут правильными, можно составить равенство: AO = OD = EO = OB = CO = OF = a .
Через точку М можно провести прямую AC и CF. Образованный ранее треугольник AEO будет равнобедренным. В нём отрезок AO равняется по величине OE. Значит, угол EOA будет развёрнутым и равняться 120 градусам. Используя свойства равнобедренного треугольника, можно записать: AE = a * √2 * (1 — cos EOA). То есть: AE = AC = √3 * a.
По аналогии можно найти и стороны: EA1, FB1, AC1, BD1, CE1, DF1. Так как AA1 = h, а из свойств правильной призмы следует, что угол EAA1 — прямой, длины сторон будут равны между собой, и их можно найти, используя формулу: √(AA1 2 + AE 2 )= √(h 2 + 3 * a) = 2 * a. Грань EB1 = FC1 = AD1 = BE1 = CF1 = DA1 = √(BB1 2 + BE 2 ) = √(h 2 + 4 *a) = √5 *a. Сторона FE1 = √(FE 2 + EE 2 ) = √(h 2 + a 2 ) = √2 *a.
Длины диагоналей призмы равняются сумме квадратов высоты и длины основания под корнем. Это легко доказать, если принять, что ЕЕ1 = h, а FE = a. Треугольник FEE1 прямоугольный, значит, FE = √(h 2 + a 2 ), что и следовало доказать.
Решение простого примера
Такого вида задачи обычно даются в учебниках по геометрии для выпускных классов средней школы. Решить их самостоятельно несложно, нужно только знать формулы и представлять, как выглядит та или иная фигура. При этом часто приходится использовать дополнительные построения. Вот один из таких типовых примеров.
Пусть имеется девятиугольная фигура, в которую вписана правильная шестиугольная призма со стандартным обозначением вершин. Сторона основания в ней составляет 4 см, а длина бокового ребра меньше её в 2 раза, то есть равняется 2. Необходимо вычислить расстояние от точки C1 до прямой, соединяющей вершины EF. По условию задачи в основании лежит геометрическое тело, у которого все стороны и углы равны, то есть фигура правильная.
Чтобы понять, что будет представлять искомая прямая, нужно изобразить призму на рисунке и на нём же начертить отрезок. Фактически это будет перпендикуляр, который и является вычисляемым расстоянием. Проекцией точки С1 будет вершина С. Из неё можно построить перпендикуляр, который ограничится точкой E. Таким образом, поставленная задача сводится к поиску длины отрезка C1E.
Найти длину прямой можно как гипотенузу прямоугольного треугольника С1СE. Треугольная фигура будет с прямым углом C. Из условия задачи отрезок С1С в два раза меньше ребра основания, а значит равен 2. Теперь осталось найти, чему равняется длина CE. Геометрическое тело CDE является равнобедренным. По условию CD = ED. Сумму углов шестиугольника можно найти по формуле е = 180 * (n — 2) = 180 * 4 = 720. Получается, что на каждый угол приходится по 120 градусов.
С вершины D можно опустить перпендикуляр DN на CE. Принимая во внимание свойства равнобедренного треугольника, высота DN будет медианной и биссектрисой. Следовательно, угол C равняется 30 градусов, так как CDH — прямоугольный.
Теперь можно найти СH. Сделать это возможно через косинус угла C: cos 30 = CH / CD. Отсюда: CH = 4 * p/2 = 2 √ 3. Так как CH = HE, сторона CE = 2 * 2 √3. К треугольнику CC1E можно применить теорему Пифагора: C1E 2 = C1C 2 + CE = 2 2 + (4 c3) 2 . C1E 2 = √ 52. Таким образом, искомый ответ можно записать так: C1E = 2√13.
Задача высокого уровня
Решение примеров повышенного уровня сложности предполагает не только хорошее понимание изучаемого материала, но и знание предыдущих тем. Понадобится вспомнить формулы для нахождения площадей и объёмов плоских фигур и их свойства. Вот пример одной из таких задач.
Пусть имеется шестиугольная объёмная фигура, у которой баковая грань равняется 6, а площадь основания 12. Нужно найти объём геометрического тела с вершинами в точках A, B1, C1, D1, E1, F1.
В таких задачах перед тем как непосредственно приступить к вычислениям, желательно использовать вспомогательный рисунок. На нём нужно изобразить фигуру в трёхмерной системе координат и подписать все её вершины.
Согласно условию, площадь основания Sabcde1f1 = 12, отрезок AA1 = 6. Так как фигура правильная, то все ребра у призмы буду равны. Чтобы найти, сколько будет составлять объём, понадобится обозначить многогранник. Для этого следует построить отрезки F1B, F1A, B1, E1A, D1A, C1A. Получившаяся фигура представляет собой пирамиду.
Формула для нахождения объёма пирамиды записывается так: V = h * S / 3. Её можно привести к виду: V = (AA1 * Sb1c1d1e1f1) / 3. Теперь нужно определить, чему же будет равняться площадь шестиугольника. Так как в основании призмы лежит правильная фигура с шестью углами, радиус описанной окружности будет совпадать с боковой стороной.
Таким образом, искомая площадь будет равняться шести поверхностям правильного треугольника. В свою очередь, его занимаемый размер можно определить как Sтр = (a * b) * sin / 2. Значит, площадь основания призмы равна: S = (6 * R * R * sin 60) / 2. Подставив заданное условием значение из формулы, можно выразить радиус: R 2 = (12 * 2) / 3 √ 3 = 8 /√3.
Площадь треугольника A1B1F1 находится как произведение сторон, умноженное на синус угла и разделённое на 2: S = (a * a * sin120) / 2 = a 2 * sin60 / 2 = (R 2 * √ 3/3) / 2. Подставив значение R, можно получить: S = (½) * (8 / √ 3) * (√3 / 2) = 2. Тогда площадь пятиугольника будет равняться разнице поверхностей шестиугольника и треугольника A1B1F1, то есть S = 12 — 2 = 10. Теперь можно будет подсчитать и объём пирамиды: Vab1c1d1e1f1 = (1 / 3) * 6 * 10 = 20. Задача решена.
Шестиугольная призма и ее основные характеристики
Изучением призм занимается пространственная геометрия. Важными их характеристиками являются заключенный в них объем, площадь поверхности и число составляющих элементов. В статье рассмотрим все эти свойства для шестиугольной призмы.
О какой призме пойдет речь?
Призма шестиугольная – это фигура, образованная двумя многоугольниками, имеющими шесть сторон и шесть углов, и шестью параллелограммами, соединяющими отмеченные шестиугольники в единое геометрическое образование.
На рисунке изображен пример этой призмы.

Отмеченный красным цветом шестиугольник называется основанием фигуры. Очевидно, что число ее оснований равно двум, причем оба они идентичны. Желто-зеленоватые грани призмы называются ее боковыми сторонами. На рисунке они представлены квадратами, но в общем случае они являются параллелограммами.
Шестиугольная призма может быть наклонной и прямой. В первом случае углы между основанием и боковыми сторонами не являются прямыми, во втором они равны 90o. Также эта призма может быть правильной и неправильной. Правильная шестиугольная призма обязательно должна быть прямой и иметь правильный шестиугольник в основании. Приведенная выше призма на рисунке этим требованиям удовлетворяет, поэтому она называется правильной. Далее в статье будем изучать только ее свойства, как общий случай.
Элементы
Для любой призмы главными ее элементами являются ребра, грани и вершины. Шестиугольная призма не является исключением. Приведенный выше рисунок позволяет посчитать количество этих элементов. Так, граней или сторон мы получаем 8 (два основания и шесть боковых параллелограммов), число вершин составляет 12 (по 6 вершин для каждого основания), количество ребер шестиугольной призмы равно 18 (шесть боковых и 12 для оснований).
В 1750-е годы Леонард Эйлер (швейцарский математик) установил для всех полиэдров, к которым относится призма, математическую связь между числами указанных элементов. Эта связь имеет вид:
число ребер = число граней + число вершин – 2.
Указанные выше цифры удовлетворяют этой формуле.
Диагонали призмы
Все диагонали шестиугольной призмы можно разделить на два типа:
- те, которые лежат в плоскостях ее граней;
- те, которые принадлежат всему объему фигуры.
Рисунок ниже показывает все эти диагонали.
Видно, что D1 – это диагональ боковой стороны, D2 и D3 – диагонали всей призмы, D4 и D5 – диагонали основания.
Длины диагоналей боковых сторон между собой равны. Вычислить их легко, используя всем известную теорему Пифагора. Обозначим символом a длину стороны шестиугольника, символом b – длину бокового ребра. Тогда диагональ имеет длину:
Диагональ D4 также легко определяется. Если вспомнить, что правильный шестиугольник вписывается в окружность радиусом a, то D4 является диаметром этой окружности, то есть получим следующую формулу:
Диагональ D5 основания найти несколько сложнее. Для этого следует рассмотреть равносторонний треугольник ABC (см. рис.). Для него AB = BC = a, угол ABC равен 120o. Если из этого угла опустить высоту (она же будет биссектрисой и медианой), тогда половина основания AC будет равно:
AC/2 = AB*sin(60o) = a*√3/2.
Сторона AC является диагональю D5, поэтому получаем:
Теперь остается найти диагонали D2 и D3 правильной шестиугольной призмы. Для этого нужно увидеть, что они являются гипотенузами соответствующих прямоугольных треугольников. Воспользовавшись теоремой Пифагора, получаем:
D2 = √(D42 + b2) = √(4*a2 + b2);
D3 = √(D52+ b2) = √(3*a2+ b2).
Таким образом, самой большой диагональю для любых значений a и b является D2.
Площадь поверхности
Чтобы понять, о чем идет речь, проще всего рассмотреть развертку этой призмы. Она показана на рисунке.
Видно, что для определения площади всех сторон рассматриваемой фигуры необходимо рассчитать отдельно площадь четырехугольника и площадь шестиугольника, затем умножить их на соответствующие целые числа, равные количеству каждого n-угольника в призме, и сложить полученные результаты. Шестиугольников 2, прямоугольников 6.
Для площади прямоугольника получаем:
Тогда площадь боковой поверхности равна:
Для определения площади шестиугольника проще всего воспользоваться соответствующей формулой, которая имеет вид:
Подставляя в это выражение число n равное 6, получаем площадь одного шестиугольника:
S6 = 6/4*a2*ctg(pi/6) = 3*√3/2*a2.
Это выражение следует умножить на два, чтобы получить площадь оснований призмы:
Остается сложить Sos и S2, чтобы получить полную площадь поверхности фигуры:
S = Sos + S2 = 3*√3*a2 + 6*a*b = 3*a*(√3*a + 2*b).
Объем призмы
После того как была получена формула для площади шестиугольного основания, вычислить объем, заключенный в рассматриваемую призму, проще простого. Для этого следует лишь умножить площадь одного основания (шестиугольника) на высоту фигуры, длина которой равна длине бокового ребра. Получаем формулу:
Отметим, что произведение основания на высоту дает значение объема абсолютно любой призмы, включая наклонную. Однако в последнем случае расчет высоты осложняется, поскольку она уже не будет равна длине бокового ребра. Что касается шестиугольной правильной призмы, то значение ее объема является функцией двух переменных: сторон a и b.
[spoiler title=”источники:”]
http://sprint-olympic.ru/uroki/geometrija/99823-pravilnaia-shestiygolnaia-prizma-svoistva-priznaki-i-formyly.html
http://1ku.ru/obrazovanie/38524-shestiugolnaja-prizma-i-ee-osnovnye-harakteristiki/
[/spoiler]
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 18 апреля 2020 года; проверки требует 1 правка.
Шестиугольная призма — призма с шестиугольным основанием. У этого многогранника 8 граней, 18 рёбер и 12 вершин[1].
До заточки многие карандаши имеют форму длинной шестиугольной призмы[2].
Полуправильный (или однородный) многогранник[править | править код]
Если все боковые грани одинаковые, шестиугольная призма является полуправильным многогранником, более обще, однородным многогранником и четвёртой призмой в бесконечном множестве призм, образованных прямоугольными боковыми сторонами и двумя правильными основаниями. Призму можно рассматривать как усечённый[en] шестигранный осоэдр, представленный символом Шлефли t{2,6}. С другой стороны, его можно рассматривать как прямое произведение правильного шестиугольника на отрезок, которое представляется как {6}×{}. Двойственным многогранником шестиугольной призмы является шестиугольная бипирамида[en].
Группой симметрии прямой шестиугольной призмы является D6h с порядком 24, а группой вращений является D6 с порядком 12.
Объём[править | править код]
Как и у большинства призм, объём правильной шестигранной призмы можно найти умножением площади основания (с длиной стороны 


Симметрия[править | править код]
Топология однородной шестиугольной призмы могут иметь геометрические вариации с низкой симметрией:
| Симметрия | D6h, [2,6], (*622) | C6v, [6], (*66) | D3h, [2,3], (*322) | D3d, [2+,6], (2*3) | |
|---|---|---|---|---|---|
| Конструкция | {6}×{}, |
t{3}×{}, |
s2{2,6}, |
||
| Рисунок | 
|

|
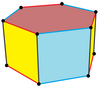
|

|
|
| Нарушение | 
|

|
 
|

|
Как часть пространственных мозаик[править | править код]
Шестигранная призма присутствует как ячейка в четырёх призматических однородных выпуклых сотах[en] в трёхмерном пространстве:
Шестигранные призмы существуют также в качестве трёхмерных граней четырёхмерных однородных многогранников[en]:
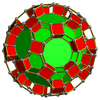
| Усечённая тетраэдральная призма[en] |
Усечённая октаэдральная призма[en] |
Усечённая кубоктаэдрическая призма[en] |
Усечённая икосаэдрическая призма[en] |
Усечённая икосододекаэдрическая призма[en] |
|
|
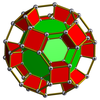
|
|
|
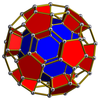
| Усечённая внутрь 5-ячейка[en] |
Рёберно усечённая 5-ячейка[en] |
Усечённая внутрь 16-ячейка[en] |
Рёберно усечённый гиперкуб[en] |
|

|

|

|

|
|
| Усечённая внутрь 24-ячейка[en] |
Рёберно усечённая 24-ячейка[en] |
Усечённая внутрь 600-ячейка[en] |
Рёберно усечённая 120-ячейка[en] |
|

|

|

|

|
Связанные многогранники и мозаики[править | править код]
| Симметрия: [6,2], (*622) | [6,2]+, (622) | [6,2+], (2*3) | ||||||
|---|---|---|---|---|---|---|---|---|

|

|

|

|

|

|

|
||
| {6,2} | t{6,2} | r{6,2} | t{2,6} | {2,6} | rr{2,6} | tr{6,2}[en] | sr{6,2} | s{2,6} |
| Двойственные им многогранники | ||||||||

|

|

|

|

|

|

|

|

|
| V62 | V122 | V62 | V4.4.6[en] | V26 | V4.4.6[en] | V4.4.12 | V3.3.3.6[en] | V3.3.3.3 |
Этот многогранник можно считать членом последовательности однородных многогранников с угловой фигурой (4.6.2p) и диаграммой Коксетера — Дынкина . Для p < 6 членами последовательности являются усечённые во всех углах многогранники (зоноэдры), и они показаны ниже как сферические мозаики. Для p > 6 они являются мозаиками гиперболической плоскости начиная с усечённой трисемиугольной мозаики[en].
| Симметрия *n32[en] n,3[en] |
Сферическая | Евклидова | Компактная гиперболическая | Паракомп. | Некомпактная гиперболическая | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| *232 [2,3] |
*332 [3,3] |
*432 [4,3] |
*532 [5,3] |
*632 [6,3] |
*732 [7,3] |
*832 [8,3] |
*∞32 [∞,3] |
[12i,3] |
[9i,3] |
[6i,3] |
[3i,3] |
|
| Фигуры | 
|

|

|

|

|

|

|

|

|

|

|
|
| Конфигурация | 4.6.4 | 4.6.6 | 4.6.8 | 4.6.10 | 4.6.12[en] | 4.6.14[en] | 4.6.16[en] | 4.6.∞[en] | 4.6.24i | 4.6.18i | 4.6.12i | 4.6.6i |
| Двойственная | 
|

|

|

|

|

|

|

|

|

|

|

|
| Конфигурация грани | V4.6.4[en] | V4.6.6 | V4.6.8[en] | V4.6.10 | V4.6.12[en] | V4.6.14[en] | V4.6.16[en] | V4.6.∞ | V4.6.24i | V4.6.18i | V4.6.12i | V4.6.6i |
См. также[править | править код]
| Многоугольник | 
|
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Мозаика | ||||||||||||
| Конфигурация | 3.4.4 | 4.4.4 | 5.4.4 | 6.4.4 | 7.4.4 | 8.4.4 | 9.4.4 | 10.4.4 | 11.4.4 | 12.4.4 | 17.4.4 | ∞.4.4 |
Примечания[править | править код]
- ↑ 1 2 Anthony Pugh. Polyhedra: A Visual Approach. — University of California Press, 1976. — С. 21, 27, 62. — ISBN 9780520030565.
- ↑ Audrey Simpson. Core Mathematics for Cambridge IGCSE. — Cambridge University Press, 2011. — С. 266–267. — ISBN 9780521727921.
- ↑ Carolyn C. Wheater. Geometry. — Career Press, 2007. — С. 236–237. — ISBN 9781564149367.
Ссылки[править | править код]
- Uniform Honeycombs in 3-Space Модели в формате VRML
- The Uniform Polyhedra
- Virtual Reality Polyhedra The Encyclopedia of Polyhedra
- Prisms and antiprisms
- Weisstein, Eric W. Hexagonal prism (англ.) на сайте Wolfram MathWorld.
- Hexagonal Prism Interactive Model — Просмотр призм в браузере