Как найти границу дроби

Самые старые упоминания о таких математических явлениях, как дробь, учёные обнаружили в древнем Египте. Особенностью их было то, что у них были обозначения только вида 12, 23,13, при этом больше двойки числа, делимого они не использовали, а использовали метод сложения, к примеру, вместо дроби 56, писали 12 +13.

Но применять такие дроби было сложно, поэтому учёные разных областей пытались вывести общую универсальную формулу для удобства. Так появилась шестидесятеричная, но проводить вычисления с ней тоже было очень трудно, однако её довольно долго применяли в Вавилоне и Греции. Существовала также система называемая Асс, её суть в делении на 12, использовали её римляне. Результат такого деления, точнее одну долю, называли унцией. Самой близкой по своей системе исчисления была дробь, которую предложили в Индии, разница от современных была в формате записи, без чёрточки, и такая дробь была перевернута, в верхней части находился делитель, а в нижней делимое. Та запись, которую и по сей день используют в математике была придумана арабами.

Что такое дробь, основные понятия и виды

По сути дробь — это деление одного числа на другое. Выделяют два вида: обыкновенные и десятичные.

Обыкновенная дробь — означает, состоящая из целых чисел. Обыкновенные, имею два типа записи к примеру:

• 15- разделена наклонной линией, читается как одна пятая;
• [frac{1}{5}] — горизонтальной линией.

Определения:

• Числитель — число, находящееся в верхней границе дроби;
• Знаменатель — число которое мы видим в нижней границе дроби.

Например: 15, где 1- числитель, 5- знаменатель. Для того чтобы проще объяснить, что такое дробь приведём простой пример. Торт разрезан на 5 кусков, если мы взяли два и них то это 25 (две пятые части торта).

Обыкновенные дроби имеют два типа правильные и неправильные.

Правильной дробью называется дробь с значениями, в которых числитель меньше знаменателя. Такое название данный тип дроби получил не зря, ведь так логичнее и правильнее, когда часть меньше целого.

Неправильная в свою очередь имеет обратные значения, когда числитель больше знаменателя.

_{Примечание. Дроби, у которых знаменатель и числитель одинаковы, тоже неправильные.}

Смешанная дробь. Существует также такое определение как смешанная дробь, такой вид, представляет собой дробь, состоящую из двух частей целой и дробной. Пример — [4 frac{3}{5}], где четыре это целая часть, а 35 дробная. Такой тип дроби можно получить, только при делении неправильного вида дробей.

Десятичные дроби. К десятичным, относят дроби которые в знаменателе имеют 10 в натуральной степени. К примеру [frac{5}{10},
frac{6}{100}] и тд. Такие, так же могут иметь вид строчной записи, 0,5 и 0,06. При этом в такой записи целая часть отделяется от дробной знаком запятой.

Существуют также понятия сократимой и несократимой дроби. Сократимая дробь, это та, в которой можно произвести деление числителя и знаменателя на одно и то же число.

Несократимая дробь, если такие действия выполнить нельзя.

Составная дробь, многоуровневая или выражение, имеющее несколько черт дроби. Пример [frac{frac{3}{7}}{-31}]

Равные и неравные дроби. Для того чтобы сказать, являются дроби равными или нет, нужно их сравнить.

Равные обыкновенные [frac{a}{d} frac{c}{b}] — можно вывести при помощи такого верного равенства а*b=d*c , если такое равенство не верно то данные дроби будут называться неравными.

Положительные и отрицательные дроби.

Положительные называют обыкновенные дроби, с положительными числами, при необходимость перед такими дробями ставится знак +, пример [+frac{6}{9}].

Отрицательными, считаются дроби со знаком минус, пример [-frac{6}{9}].

Стоит отметить что две дроби вида [-frac{6}{9} text { и }+frac{6}{9}] являются противоположными.

Алгебраическая дробь.

Отличается она тем, что на месте числителя и знаменателя находятся алгебраические значения, числа заменены буквами. Примеры —

[
frac{x+y}{x-y}, frac{x^{3}+1}{x^{2}-x+2}, frac{a^{2}-4}{a+2}, frac{a}{2}, frac{3 a+7}{5}
]

Если в такой дроби буквы заменить числами, то она сразу станет обыкновенной.

Одночлен — это выражение, содержащее числа, степени положительные и их произведение. Пример: в.

Многочлен — это сумма одночленов. Пример: 7а+6в

Дроби на координате прямых.

Если рассматривать координату прямых, то положительные дроби на ней будут расположены справа от нулевого значения, а отрицательные слева.

Действия, которые можно выполнить с дробями

В общем то, действия с дробями это все те же действия, которые можно выполнить с числами:

• Сравнение;
• Сложение;
• Вычитание;
• Умножение;
• Деление.

Свойства дроби

Чтобы сложить или вычесть дроби, дробь обязана иметь равные знаменатели, необходимо просто выполнить это действие с их числителями

Примеры:

[
frac{4}{9}+frac{5}{9}=frac{4+5}{9} ; text { и } frac{4}{9}-frac{5}{9}=frac{5-4}{9}.
]

Что же касается дробей с разной частью делителя (Знаменателя), то тут чтобы выполнить действия сложения и вычитания с ними необходимо привести знаменатели к общему числу.

Примеры: [frac{4}{9}+frac{5}{8}=frac{4+5}{9 cdot 8}], точно так же и для вычитания.

Чтобы выполнить такое действие, как умножение обыкновенных дробей, нужно произвести умножение сначала с их числителями, а после и знаменателями.

Пример: [frac{4}{9} cdot frac{5}{8}=frac{4 cdot 5}{9 cdot 8}].

При умножении дроби на число, в такой вычислении просто умножается числитель на заданное число, а знаменатель остаётся тем же.

Пример: [frac{4}{9} cdot 6=frac{4 cdot 6}{9}];

Что же касается деления, то при делении одной дроби на другую, нужно произвести умножение, при котором первая дробь остаётся в неизменном виде, а вторая переворачивается. То есть получается мы умножаем числитель первой дроби данного примера, на знаменатель второй, и полученное число находится в верхней части дроби, а в нижней умножение знаменателя первой дроби на числитель второй.

Пример: [frac{4}{9} backslash frac{5}{8}=frac{4 cdot 8}{9 cdot 5}].

Сравнение дробей

Чтобы провести сравнение с разными делителями (знаменателями), необходимо сделать так, чтобы знаменатель стал общим только тогда можно будет сравнить числители. Соответственно, где числитель больше там и дробь больше.

Основное свойство дробей

Основным свойством дроби является выражение — «числитель и знаменатель можно делить и умножать на одно и то же число при этом значение всей дроби не поменяется.»

Еще одно определение которое пригодится нам для сокращения дроби это НОД.

НОД — наибольший общий делитель.

Общий делитель — это число, которое может быть делителем каждого из указанных чисел.

Пример: если взять число 3, то оно станет общим делителем для чисел 6 и 9. так как 9=3*3 а 6=3*2.

Алгоритм Евклида для вычисления НОД (наибольшего общего делителя)

Не всегда, сходу, можно понять какое число является наибольшим общим числителем, особенно если числа крупные, поэтому существует специальный алгоритм для выведения такого числа НОД.

Суть алгоритма такова: для нахождения НОД чисел а и b (где они целые и положительные числа, к тому же a больше b), выполняется ряд делений с остатком, получается ряд равенств, где деление останавливается в том случае если r_k+1=0, при этом r_k=НОД(a, b)

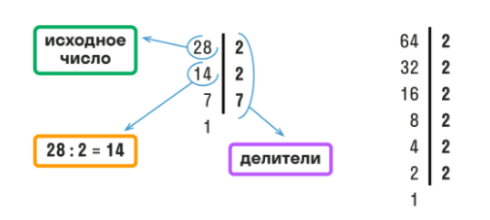
Пример. Рассчитаем НОД для 28 и 64.

Как находим:

Распишем простые множители для каждого числа и подчеркнем одинаковые

Д (28) = 2 * 2 * 7

Д (64) = 2 * 2 * 2 * 2 * 2 * 2

Найдем произведение одинаковых простых множителей и запишем ответ

НОД (28; 64) = 2 * 2 = 4

Ответ: НОД (28; 64) = 4

Оформить поиск НОД можно в строчку, как мы сделали выше или в столбик, как на картинке.

Сокращение дроби

Выражение сократить дробь, фактически означает что необходимо провести деление её числителя и знаменателя на одно и то же число, не равное единице.

Результатом таких действий станет появление новой дроби, значение которой, равно первичной.

Например: возьмём обыкновенную дробь [frac{12}{44}] и произведем сокращение. Для этого разделим и числитель и знаменатель на 2, получится такая дробь [frac{12}{44} backslash 2=frac{12 backslash 2}{44 backslash 2}=frac{6}{22}].

Несократимый вид дроби, приведение к такому виду

Обычно целью таких манипуляций с дробями является получение из исходного вида дроби несократимый. К примеру дробь, которая получилась у нас выше, [frac{6}{22}] при сокращении на два, как мы видим все ещё можно сократить.

Для того чтобы привести дробь к виду несократимой, нужно выполнить манипуляции по делению, числителя и знаменателя на наибольший НОД. В таком случае по свойству НОД в числителе и знаменателе окажутся простые числа, а дробь будет несократимой.

[
frac{a}{d}=frac{a backslash text { НОД }(a, d)}{d backslash text { НОД }(a, d)}
]

Из вышесказанного следует, что приведение дроби к несократимому виду значит, нужно произвести деление числителя и знаменателя на их НОД.

Пример: вернёмся к нашему примеру дроби [frac{12}{44}], для приведения ее к несократимому виду нужной сначала найти наибольший общий делитель чисел 12 и 44. таким числом НОД для них является цифра 4.

Получается: [frac{12}{44}=frac{12 backslash 4}{44 backslash 4}=frac{3}{11}].

Для чего нужно сокращение? Такие манипуляции с дробями необходимо применять, в случаях работы с большими числами.

Стоит вспомнить негласное правило математики, суть его в том, что если что-то можно сделать проще нужно упростить. Поэтому, говоря о сокращении дроби, имеется в виду именно приведение к несократимому виду, а не просто уменьшение числителя и знаменателя.

Правило сокращения

Для того чтобы сократить, необходимо:

• Найти делитель наибольшего значения, который будет общим для знаменателя и числителя;
• Разделить числитель и знаменатель на него.

Примеры:

Дана такая дробь: [frac{182}{195}]. сократим её.

Найдём такой делитель, при помощи применения алгоритма Евклида.

195 = 182 *1+13

182=13*14

Из чего следует, что НОД_(182,195)=13

Поэтому для сокращения дроби [frac{182}{195}], разделим числитель 182 и знаменатель 195 на 13 и получим равенство: [frac{182}{195}=frac{182 backslash 13}{195 backslash 13}=frac{14}{25}]

Таким образом мы и получили несократимую дробь равную исходной.

Второй способ.

Второй способ основан на разложении числителя и знаменателя исходной дроби на простые множители, из которых позже все общие множители убираются.

Пример сокращения: [frac{123}{154}] для сокращения представим числитель и знаменатель дроби в виде простых множителей

[
frac{182}{195}=frac{2 cdot 7 cdot 13}{3 cdot 5 cdot 13}
]

Затем уберём все общие множители, как в числителе так и в знаменателе, [frac{182}{195}=frac{2 cdot 7 cdot 13}{3 cdot 5 cdot 13}=frac{2 cdot 7}{3 cdot 5}=frac{14}{15}]

Третий способ сокращения дроби.

Третий способ — способ последовательного сокращения. Применяя такой способ, сокращение происходит поэтапно, сокращая каждый раз на какой-либо очевидный общий множитель.

Пример: [frac{18000}{22000}]

При сокращении такой дроби сразу можно увидеть, что и числитель и знаменатель деяться на 1000 в результате такого деления получается:

[
frac{18000}{22000}=frac{18000 backslash 1000}{22000 backslash 1000}=frac{18}{22}
]

Следующим этапом мы видим, что оба значения и числителя, и знаменателя делятся на 2, получим несократимую дробь.

[
frac{18}{22}=frac{18000 backslash 2}{22000 backslash 2}=frac{9}{11}
]

Как мы видим сокращение дроби не такой сложный процесс, главное подобрать удобный способ.

Сокращение алгебраической дроби

Так же, как и в примерах выше, сокращение алгебраической дроби, это деление числителя и знаменателя на общий делитель. Отличие в том, что в алгебраической, таким общим множителем является многочлен и одночлен.

Для того чтобы сократить такие дроби нужно пройти три этапа:

• Определение множителя, который будет общим для числителя и знаменателя;
• Сокращение коэффициента;
• Деление числителя и знаменателя на множитель.

Сокращая дробь со степенями, применяется правило деления степеней с равными основаниями.

Формула:

[
a^{n} div a^{m}=a^{n-m}
]

Рассмотрим пример сокращения со степенями:

[
frac{x^{3}}{x^{2}}=frac{x^{3} / x^{2}}{x^{2} / x^{2}}=frac{x^{3-2}}{x^{2-2}}=frac{x^{1}}{x^{0}}=frac{x}{1}=x
]

Исходя из вышеописанной схемы:

• Сокращаем x³ и x^2;
• Производим деление выбирая меньшее значение степени;
• Вычитаем.

В результате получаем сокращенную дробь.

Не забываем, что сократить можно только одинаковые буквенные множители.

Сокращение дробей с одночленами.

Пример: [frac{40 x}{5 x^{2}}=frac{8}{x^{2-1}}=frac{8}{x}]

Решение:

• 8 — тот самый множитель, который является общим

• Х и x2 делим на x и получаем ответ.

Дроби с многочленами: сокращение.

Для сокращения таких видов, существует два правила:

• Сократить многочлен в взятый в скобки, можно только с точно таким же многочленом в скобках;
• Сократится должен весь многочлен, взятый в скобки, нельзя сократить только часть.

Пример: [frac{x-c}{x(x-c)}=frac{1}{x}]

Вынесение общего множителя при сокращении.

Бывают случаи, когда при сокращении алгебраической дроби с многочленами, их нет одинаковых, в таком случае нужно убрать общий множитель за скобки.

Для такого вынесения тоже существуют правила их 4:

1. необходимо найти число, на которое можно разделить числа каждого одночлена;
2. необходимо также найти буквенный множитель, который повторяется, в каждом одночлене, их может быть несколько;
3. выносим буквенный множитель, который был найден, за скобки;
4. производим работу с оставшимися многочленами в скобках.

Для того чтобы умножить многочлен на одночлен, необходимо по очереди умножить каждый член многочлена на одночлен.

Приведём пример:

[frac{6 x+42 a}{7 a+x}=frac{6(x+7 a)}{7 a+x}=frac{6}{7}]

Калькулятор сокращения дробей

Подведём итоги. Для того чтобы не возникло трудностей с сокращением, стоит запомнить:

• Сокращая дробь вам необходимо найти общий множитель для числителя и знаменателя, если речь идет об алгебраических дробях, но и НОД обыкновенных;
• Разделить числитель и знаменатель на общий множительделитель;
• Если дробь алгебраическая, при делении многочлена на множитель необходимо вынести общий множитель за скобки;
• Стоит хорошо выучить все формулы и определения, связанные с дробями.
• Всегда проверять результат сокращения.

Подробности

Категория: Математика 5-6 классы

Равенство дробей

Для любой дроби можно указать сколько угодно ей равных дробей.

Например, или

Это можно объяснить так: если отрезок разделить пополам, а половину также пополам, то ясно, что половина отрезка равна двум его четвертям, т. е. Также  можно показать, что половина равна трем шестым и т. д. (рис. 4.4).

Можно еще сказать, что дроби и определяют одно и то же число; записанное в разных формах. Дроби и так же определяют одно и то же число, записанное в разных формах, и т. д.

Если числитель и знаменатель дроби умножить на одно и то же натуральное число, то получится дробь, равная данной, т. е. выполняется равенство

Это свойство называют основным, свойством дроби. С его помощью можно получать дроби, равные данной дроби.

Например,

Равенство (1) можно записать и в обратном порядке:

В таком виде левая часть равенства есть дробь числитель и знаменатель которой имеют общий множитель n.

Если n > 1, то говорят, что можно дробь сократить на n и получить дробь . Говорят еще, что можно разделить числитель и знаменатель на общий множитель n.

Поэтому основное свойство дробей можно сформулировать по-другому:

Если числитель и знаменатель дроби имеют общий множитель, отличный от 1, то дробь можно сократить на этот множитель. При этом получится дробь, равная данной.

Пример. Сократить дроби

Решение.

Если р—натуральное число, то справедливо равенство

Действительно,

Дробь называется несократимой, если ее числитель и знаменатель не имеют общих простых делителей.

Например, дроби несократимые дроби, так как числа 1 и 2, 3 и 4, б и 7, 11 и 8 не имеют общих простых делителей.

Для каждой дроби существует единственная равная ей несократимая дробь.   

Например,

Левые части равенств—данные дроби, а правые равные им несократимые дроби.

Чтобы получить несократимую дробь, равную данной дроби, надо сократить данную дробь на наибольший общий делитель ее числителя и знаменателя. Часто наибольший общий делитель числителя и знаменателя указать трудно. В этом случае сокращение дроби выполняют постепенно.

Пример. Сократить дробь 

Решение.

Рассмотрение данной темы мы начнем с изучения понятия доли в целом, которое даст нам более полное понимание смысла обыкновенной дроби. Дадим основные термины и их определение, изучим тему в геометрическом толковании, т.е. на координатной прямой, а также определим список основных действий с дробями.

Доли целого

Представим некий предмет, состоящий из нескольких, совершенно равных частей. Например, это может быть апельсин, состоящий из нескольких одинаковых долек.

Доля целого или доля – это каждая из равных частей, составляющих целый предмет.

Очевидно, что доли могут быть разные. Чтобы наглядно пояснить это утверждение, представим два яблока, одно из которых разрезано на две равные части, а второе – на четыре. Ясно, что размеры получившихся долей у разных яблок будут различаться.

Доли имеют свои названия, которые зависят от количества долей, составляющих целый предмет. Если предмет имеет две доли, то каждая из них будет определяться как одна вторая доля этого предмета; когда предмет состоит из трех долей, то каждая из них – одна третья и так далее.

Чтобы сократить запись, ввели следующие обозначения долей: половина – 12 или 1/2; треть – 13 или 1/3; одна четвертая доля – 14 или 1/4 и так далее. Записи с горизонтальной чертой используются чаще.

Понятие доли естественно расширяется с предметов на величины. Так, можно использовать для измерения небольших предметов доли метра (треть или одна сотая), как одной из единиц измерения длины. Аналогичным образом можно применить доли других величин.

Обыкновенные дроби, определение и примеры

Обыкновенные дробиприменяются для описания количества долей. Рассмотрим простой пример, который приблизит нас к определению обыкновенной дроби.

Представим апельсин, состоящий из 12 долек. Каждая доля тогда будет – одна двенадцатая или 1/12. Две доли – 2/12; три доли – 3/12 и т.д. Все 12 долей или целое число будет выглядеть так: 12/12. Каждая из используемых в примере записей является примером обыкновенной дроби.

Обыкновенная дробь – это запись вида mn или m/n, где m и n являются любыми натуральными числами.

Согласно данному определению, примерами обыкновенных дробей могут быть записи: 4/9, 1134, 91754. А такие записи: 115, 1,94,3 не являются обыкновенными дробями.

Числитель и знаменатель

Т.е. числитель – число, расположенное сверху над чертой обыкновенной дроби (или слева от наклонной черты), а знаменатель – число, расположенное под чертой (справа от наклонной черты).

Какой же смысл несут в себе числитель и знаменатель? Знаменатель обыкновенной дроби указывает на то, из скольких долей состоит один предмет, а числитель дает нам информацию о том, каково рассматриваемое количество таких долей. К примеру, обыкновенная дробь 754 указывает нам на то, что некий предмет состоит из 54 долей, и для рассмотрения мы взяли 7 таких долей.

Натуральное число как дробь со знаменателем 1

Знаменатель обыкновенной дроби может быть равен единице. В таком случае возможно говорить, что рассматриваемый предмет (величина) неделим, являет собой нечто целое. Числитель в подобной дроби укажет, какое количество таких предметов взято, т.е. обыкновенная дробь вида m1 имеет смысл натурального числа m. Это утверждение служит обоснованием равенства m1 = m.

Запишем последнее равенство так: m = m1.  Оно даст нам возможность любое натуральное число использовать в виде обыкновенной дроби. К примеру, число 74 – это обыкновенная дробь вида 741.

Черта дроби как знак деления

 Использованное выше представление данного предмета как n долей является не чем иным, как делением на n равных частей. Когда предмет разделен на n частей, мы имеем возможность разделить его поровну между n людьми – каждый получит свою долю.

В случае, когда мы изначально имеем m одинаковых предметов (каждый разделен на n частей), то и эти m предметов возможно поровну разделить между n людьми, дав каждому из них по одной доле от каждого из m предметов. При этом у каждого человека будет m долей 1n, а m долей 1n даст обыкновенную дробь mn. Следовательно, обыкновенную дробь mn можно использовать, чтобы обозначать деление m предметов между n людьми.

Полученное утверждение устанавливает связь между обыкновенными дробями и делением. И эту связь можно выразить следующим образом: черту дроби возможно иметь в виду в качестве знака деления, т.е. m/n = m : n.

При помощи обыкновенной дроби мы можем записать итог деления двух натуральных чисел. К примеру, деление 7 яблок на 10 человек запишем как 710: каждому человеку достанется семь десятых долей.

Равные и неравные обыкновенные дроби

Логичным действием является сравнение обыкновенных дробей, ведь очевидно, что, к примеру, 18 яблока отлична от 78.

Результатом сравнения обыкновенных дробей может быть: равны или неравны.

Пример равных дробей: 13 и 412 – поскольку выполняется равенство 1 ·12 = 3 · 4.

В случае, когда выясняется, что дроби не являются равными, обычно необходимо также узнать, какая из данных дробей меньше, а какая – больше. Чтобы дать ответ на эти вопросы, обыкновенные дроби сравнивают, приводя их к общему знаменателю и затем сравнив числители.

Дробные числа

Каждая дробь – это запись дробного числа, что по сути – просто «оболочка», визуализация смысловой нагрузки. Но все же для удобства мы объединяем понятия дроби и дробного числа, говоря просто – дробь.

Дроби на координатном луче

Все дробные числа, как и любое другое число, имеют свое уникальное месторасположение на координатном луче: существует однозначное соответствие между дробями и точками координатного луча.

Чтобы на координатном луче найти точку, обозначающую дробь mn, необходимо от начала координат отложить в положительном направлении m отрезков, длина каждого из которых составит 1n долю единичного отрезка. Отрезки можно получить, разделив единичный отрезок на n одинаковых частей.

Как пример, обозначим на координатном луче точку М, которая соответствует дроби 1410.  Длина отрезка, концами которого является точка О и ближайшая точка, отмеченная маленьким штрихом, равна 110 доле единичного отрезка. Точка, соответствующая дроби 1410, расположена в удалении от начала координат на расстояние 14 таких отрезков.

Если дроби равны, т.е. им соответствует одно и то же дробное число, тогда эти дроби служат координатами одной и той же точки на координатном луче. К примеру, координатам в виде равных дробей 13, 26, 39, 515, 1133 соответствует одна и та же точка на координатном луче, располагающаяся на расстоянии трети единичного отрезка, отложенного от начала отсчета в положительном направлении.

Здесь работает тот же принцип, что и с целыми числами: на горизонтальном, направленном вправо координатном луче точка, которой соответствует большая дробь, разместится правее точки, которой соответствует меньшая дробь. И наоборот: точка, координата которой – меньшая дробь, будет располагаться левее точки, которой соответствует бОльшая координата.

Правильные и неправильные дроби, определения, примеры

В основе разделения дробей на правильные и неправильные лежит сравнение числителя и знаменателя в пределах одной дроби.

Приведем примеры: – правильные дроби:

5/9, 367, 138514;

– неправильные дроби:

13/13, 573, 901112, 167.

Также возможно дать определение правильных и неправильных дробей, опираясь на сравнение дроби с единицей.

Например, дробь 812 – правильная, т.к. 8 12< 1. Дроби 532 и 1414 являются неправильными, т.к. 532 > 1, а 1414 = 1.

Немного углубимся в размышление, почему дроби, в которых числитель больше или равен знаменателю получили название «неправильных».

Рассмотрим неправильную дробь 88: она сообщает нам, что взято 8 долей предмета, состоящего из 8 долей. Таким образом, из имеющихся восьми долей мы можем составить целый предмет, т.е. заданная дробь 88 по сути представляет целый предмет: 88=1. Дроби, в которых числитель и знаменатель равны, полноценно заменяет натуральное число 1.

Рассмотрим также дроби, в которых числитель превосходит знаменатель: 115 и 363. Понятно, что дробь 115 сообщает о том, что из нее мы можем составить два целых предмета и еще останется одна пятая доля. Т.е. дробь 115 – это 2 предмета и еще 15 от него. В свою очередь, 363 – дробь, означающая по сути 12 целых предметов.

Указанные примеры дают возможность сделать вывод, что неправильные дроби возможно заменить натуральными числами (если числитель без остатка делится на знаменатель: 88 = 1; 363 = 12) или суммой натурального числа и правильной дроби (если числитель не делится на знаменатель без остатка: 115 = 2 + 15). Вероятно, потому такие дроби и получили название «неправильных».

Здесь также мы сталкиваемся с одним из важнейших навыков работы с числами.

Выделение целой части из неправильной дроби – это запись неправильной дроби в виде суммы натурального числа и правильной дроби.

Также отметим, что существует тесная взаимосвязь между неправильными дробями и смешанными числами.

Положительные и отрицательные дроби

Выше мы говорили о том, что каждой обыкновенной дроби соответствует положительное дробное число. Т.е. обыкновенные дроби – это положительные дроби. Например, дроби 517, 698, 6479 – положительные, и, когда необходимо особо подчеркнуть «положительность» дроби, она записывается с использованием знака плюс: +517, +698, +6479.

Если же обыкновенной дроби присвоить знак минус, то полученная запись будет являться записью отрицательного дробного числа, и мы говорим в таком случае об отрицательных дробях. Например, -817, -7814 и т.д.

Положительная и отрицательная дробиmn и -mn – противоположные числа. Например, дроби 78 и -78 являются противоположными.

Положительные дроби, как и любые положительные числа в целом, означают прибавление, изменение в сторону увеличения. В свою очередь, отрицательные дроби соответствуют расходу, изменению в сторону уменьшения.

Если мы рассмотрим координатную прямую, то увидим, что отрицательные дроби расположены левее точки начала отсчета. Точки, которым соответствуют дроби, являющиеся противоположными (mn и -mn), располагаются на одинаковом расстоянии от начала отсчета координат О, но по разные стороны от нее.

Здесь также отдельно скажем о дробях, записанных в виде 0n. Такая дробь равна нулю, т.е. 0n= 0.

Суммируя все вышесказанное, мы подошли к важнейшему понятию рациональных чисел.

Рациональные числа – это множество положительных дробей, отрицательных дробей и дробей вида 0n.

Действия с дробями

Перечислим основные действия с дробями. В общем и целом, суть их та же, что имеют соответствующие действия с натуральными числами

1. Сравнение дробей – данное действие мы рассмотрели выше.
2. Сложение дробей – результатом сложения обыкновенных дробей является обыкновенная дробь (в частном случае сокращаемая до натурального числа).
3. Вычитание дробей – действие, обратно сложению, когда по одной известной дроби и заданной сумме дробей определяется неизвестная дробь.
4. Умножение дробей – это действие можно описать как нахождение дроби от дроби. Результат умножения двух обыкновенных дробей – обыкновенная дробь (в частном случае равная натуральному числу).
5. Деление дробей – действие, обратное умножению, когда мы определяем дробь, на которую необходимо умножить заданную, чтобы получить известное произведение двух дробей.