Алгоритм построения интервального вариационного ряда с равными интервалами
-
Определяем
число интервалов (групп) вариационного
ряда
Число
групп (интервалов)
приближенно определяется по формуле
Стерджесса:
m
= 1 + 3,322 × lg(n)
где n
– общее число единиц наблюдения (общее
количество элементов в совокупности и
т.д.), lg(n)
– десятичный логарифм от n.
Полученную
по
формуле Стерджесса величину округляют
обычно до целого большего числа,
поскольку количество групп не может
быть дробным числом.
Если
ряд интервальный ряд с таким количеством
групп по каким-то критериям не устраивает,
то можно построить другой интервальный
ряд, округлив m
до
целого меньшего числа и выбрать из двух
рядов более подходящий.
Число
групп не должно быть больше 15.
Также
можно пользоваться следующей таблицей,
если совсем нет возможности вычислить
десятичный логарифм.
|
Объем выборки, |
25-40 |
40-60 |
60-100 |
100-200 |
Больше 200 |
|
Число интервалов, |
5-6 |
6-8 |
7-10 |
8-12 |
10-15 |
-
Определяем
ширину интервала
Ширина
интервала
для интервального вариационного ряда
с равными интервалами определяется по
формуле:
где
Xмакс
– максимальное из значений xi,
Xмин
–
минимальное из значений xi;
m
– число групп (интервалов).
Величину
интервала (i)
обычно округляют до целого числа,
исключение составляют лишь случаи,
когда изучаются малейшие колебания
признака (например, при группировке
деталей по величине размера отклонений
от номинала, измеряемого в долях
миллиметра).
Часто
применяется следующее правило:
|
Количество |
Количество |
Пример |
До |
Пример |
|
0 |
3 |
0,375 |
0,01 |
0,38 |
|
0 |
2 |
0,56 |
0,1 |
0,6 |
|
1 |
3 |
4,658 |
0,01 |
4,66 |
|
1 |
2 |
2,54 |
0,1 |
2,5 |
|
2 |
любое |
12,54 |
1,0 |
13 |
|
3 |
любое |
672,54 |
10,00 |
670 |
|
4 |
любое |
3472,45 |
100,00 |
3500 |
|
и |
-
Определяем
границы интервалов
Нижнюю
границу
первого интервала
принимают равной минимальному значению
признака (чаще всего его предварительно
округляют до целого меньшего числа с
таким же разрядом как ширина интервала).
Например, хмин=
15, i=130,
хн
первого интервала = 10.
хн1
≈ хмин
Верхняя
граница
первого интервала соответствует значению
(Хmin
+ i).
Нижняя
граница второго интервала всегда равно
верхней границе первого интервала. Для
последующих групп границы определяются
аналогично, т е. последовательно
прибавляется величина интервала.
xвi
=
xнi
+ i
xнi
= xвi-1
-
Определяем
частоты интервалов.
Считаем,
сколько значений попало в каждый
интервал. При этом помним, что если
единица обладает значением признака,
равным величине верхней границы
интервала, то ее следует относить к
следующему интервалу.
-
Строим
интервальный ряд в виде таблицы. -
Определяем
середины интервалов.
Для
дальнейшего анализа интервального ряда
понадобится выбрать значение признака
для каждого интервала. Это значение
признака будет общим для всех единиц
наблюдения, попавшим в этот интервал.
Т.е. отдельные элементы «теряют» свои
индивидуальные значения признака и им
присваивается одно общее значение
признака. Таким общим значением является
середина
интервала,
которая обозначается x’i
.
Рассмотрим
на примере с ростом детей, как построить
интервальный ряд с равными интервалами.
Имеются
первоначальные данные.
90,
91, 92, 93, 94, 95, 96, 97, 98, 99,
92,
93, 94, 95, 96, 98,
100,
101, 102, 103, 104, 105, 106, 107, 108, 109,
100,
101, 102, 103, 104, 105, 106, 107, 108, 109,
100,
101, 102, 104,
110,
112, 114, 116, 117, 120, 122, 123, 124, 129,
110,
111, 113, 115, 116, 117, 121, 125, 126, 127,
110,
111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124,
125, 126, 127, 128, 129,
111,
113, 116, 127,
123, 122, 130,
131, 132, 133, 134, 136, 137, 138, 139, 140, 141, 142, 143, 144, 145,
146, 147, 148, 149, 150,
131,
133, 135, 136, 138, 139, 140, 141, 142, 143, 145, 146, 147, 148
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
17.02.2016629.11 Кб140308126_71740_lekcii_upravlencheskie_resheniya.rtf
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
В результате статистической обработки материалов, полученных при измерении величины явления, можно подсчитать число единиц, обладающих конкретным значением того или иного признака.
Допустим, что в качестве изучаемого признака взят вес детали. Будем обозначать этот признак X. Измерения веса, например, 50 деталей дали следующие результаты (в г): 83, 85, 81, 82, 84, 82, 79, 84, 80, 81, 82, 82, 80, 82, 80, 82, 83, 84, 79, 79, 83, 82, 83, 85, 82, 82, 81, 80, 82, 82, .83,80, 82, 85, 81, 83, 81, 81, 83, 82, 81, 85, 83, 79, 81, 85, 81, 84, 81, 82.
Условились каждое отдельное значение признака обозначать
Если мы расположим отдельные значения признака (варианты) в возрастающем или убывающем порядке и укажем относительно каждого варианта, как часто он встречался в данной совокупности, то получим распределение признака, или вариационный ряд.
Вариационные ряды и их характеристики
Построим вариационный ряд для приведенного выше примера. Для этого находим наименьший вариант, равный 79 г, и, располагая варианты в возрастающем порядке, подсчитываем их частоту. Так, вариант 79 г встречается 4 раза, вариант 80 г — 5 раз и т. д. Расположим полученные варианты следующим образом (см. табл. 1).
Такой ряд называется вариационным рядом; он характеризует изменение (варьирование) какого-нибудь количественного признака (в нашем примере варьирование веса деталей). Следовательно, вариационный ряд представляет собой две строки (или колонки). В одной из них приводятся варианты, а в другой частоты.
Виды вариации
Вариация признака может быть дискретной и непрерывной. Дискретной вариацией признака называется такая, при которой отдельные значения признака (варианты) отличаются друг от друга на некоторую конечную величину (обычно целое число), т. е. даны в виде прерывных чисел. Непрерывной называется вариация, при которой значения признака могут отличаться одно от другого на сколь угодно малую величину. В качестве примера можно привести: для дискретной вариации признака — число станков, обслуживаемых одним рабочим, число семян в 1 кг и т. д.; для непрерывной вариации признака— процент выполнения рабочим нормы выработки, вес одного семени и т. д.
При непрерывной вариации распределение признака называется интервальным. Частоты относятся не к отдельному значению признака, как это бывает при дискретной вариации, а ко всему интервалу. Часто за значение интервала принимают его середину, т. е. центральное значение. В качестве примера можно привести интервальный вариационный ряд по проценту выполнения норм выработки.
Пример 1.
Распределение рабочих по проценту выполнения норм выработки.
Частость
Нередко вместо абсолютных значений. частот используют относительные величины. Для этой цели можно использовать долю частоты того или иного варианта (а также интервала) в сумме всех частот. Такая величина называется частостью и обозначается
Мы имеем частоты
Для получения суммы всех частот их нужно сложить
В математике используется знак 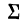
Следовательно, можно записать:
где значки 1=1 и i=n под и над 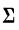
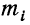
В дальнейшем в подобных случаях (т. е. при суммировании по подстрочному номеру i) мы не будем записывать значения, принимаемые i, но будем помнить смысл записи 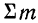
Для получения частости каждого варианта или интервала-нужно его частоту разделить на
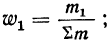
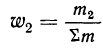
где 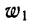
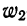
Вычислим частости, используя данные табл. 1:
Сумма всех частостей равна 1:
В нашем примере
0,08+0,1+0,2+0,28+0,16+0,08+0,1 = 1,00.
Частости можно выражать и в процентах (тогда сумма всех частостей равна 100%).
Границы интервалов
В интервальном вариационном ряду в каждом интервале различают нижнюю и верхнюю границы интервала:
- нижняя граница интервала
- верхняя граница интервала
- величина интервала
При построении интервальных вариационных рядов в каждый интервал включаются варианты, числовые значения которых больше нижней границы и меньше или равны верхней грани це. Так, в табл.12 в интервал 95—100% попадают все рабочие, выполнившие нормы выработки от 95 до 100% включительно. Рабочие, выполнившие план на 100,01%, попадают в следующий интервал. Разумеется надо стремиться строить интервалы так, чтобы избегать попадания значительного числа случаев на границы интервалов.
Интервальные вариационные ряды бывают с одинаковыми и неодинаковыми интервалами. В последнем случае чаще всего встречаются интервалы последовательно увеличивающиеся.
Пример 2.
Вариационный ряд с равными интервалами:
Пример 2а.
Вариационный ряд с последовательно увеличивающимися интервалами:
Свойства сумм
Как видно (и из дальнейшего изучения материала), нам приходится иметь дело с суммами. Рассмотрим некоторые свойства сумм.
1) Сумма ограниченного числа слагаемых, имеющих одну и ту же величину (сумма постоянной), равна произведению величины слагаемых на их число:
2) Постоянный множитель может быть вынесен из-под знака суммы и введен под знак суммы:
3) Сумма алгебраической суммы нескольких переменных равна алгебраической сумме сумм каждой переменной:
(легко обобщается на большее число слагаемых).
Величина интервала
Для выбора оптимальной величины интервала, т. е. такой величины интервала, при которой вариационный ряд не будет очень громоздким и в нем не исчезнут особенности явления, можно рекомендовать формулу:
где n — число единиц в совокупности.
Так, если в совокупности 200 единиц наибольший вариант равен 49,961, а наименьший — 49,918, то
Следовательно, в данном случае оптимальной величиной интервала может служить величина 0,005.
Плотность распределения
В качестве характеристики ряда распределения применяют плотность распределения, которую вычисляют как отношение-частот или частостей к величине интервала.
Различают абсолютную плотность распределения:
и относительную плотность распределения:
где 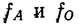
Пример 3.
По данным примера 2 вычислим относительную плотность распределения. Для первого интервала
для второго интервала
Расщепление интервалов
Часто возникает необходимость в расщеплении интервалов. Для этой цели можно воспользоваться следующим методом для интервальных вариационных рядов с равными интервалами.
Расщепление производится при предположении, что плотность вариационного ряда изменяется по параболе второго порядка. Имеется в виду, что весь интервал разбивается на две части: первую, составляющую долю 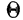
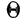
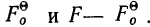
где А — частость интервала, предшествующего расщепляемому;
В — частость расщепляемого интервала;
С — частость интервала, последующего за расщепляемым;
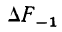
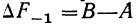
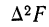
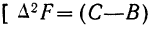
Пример 4.
По данным примера 2 произведем расщепление интервала 100—125% на две части, выделим часть интервала 100—120% и определим удельный вес рабочих, выполняющих норму выработки от 100 до 120%.
Имеем:
Получаем частость по соответствующей формуле:
В случае неравных интервалов вычисление усложняется.
Графические методы изображения вариационных рядов
Большое значение для наглядного представления вариационного ряда имеют графические методы его изображения. Вариационный ряд графически может быть изображен в виде полигона, гистограммы, кумуляты и огивы.
Полигон распределения (Дословно – многоугольник распределения) строится в прямоугольной системе координат. Величина признака откладывается на оси абсцисс, частоты или частости (точнее — плотности распределения) — по оси ординат.
На оси абсцисс отмечаются точки, соответствующие, величине вариантов, и из них восстанавливаются ординаты (перпендикуляры), длина которых соответствует численности этих вариантов. Вершины ординат соединяются прямыми линиями. Чаще всего полигоны применяются для изображения дискретных вариационных рядов, но могут быть применены и для интервальных рядов. В этом случае ординаты, пропорциональные частоте или частости интервала, восстанавливаются перпендикулярно оси абсцисс в точке, соответствующей середине данного интервала. Для замыкания крайние ординаты соединяются с •серединой интервалов, в которых частоты или частости равны нулю.
Пример 5.
По данным примера 1 строим полигон.
Гистограмма распределения строится аналогично полигону в прямоугольной системе координат. В отличие от полигона при построении гистограммы на оси абсцисс берутся не точки, а отрезки, изображающие интервал, а вместо ординат, соответствующих частотам или частостям отдельных вариантов, строят прямоугольники с высотой, пропорциональной частотам или частостям интервала.
В случае неравенства интервалов гистограмма распределения строится не по частотам или частостям, а по плотности интервалов (абсолютной или относительной). При этом общая площадь гистограммы равна численности совокупности, если построение производится по абсолютной плотности, или единице, если гистограмма построена по относительной плотности.
Если соединить прямыми линиями середины верхних сторон прямоугольников, то получим полигоны распределения.
Разбивая интервалы на несколько частей и исходя из того, что вся площадь гистограммы должна остаться при этом неизменной, можно получить мелкоступенчатую гистограмму, которая в пределе (за счет уменьшения величины интервала) перейдет в плавную кривую, называемую кривой распределения.
Пример 6.
Имеются данные о диаметре 200 валиков (см. табл. 4).
Чтобы по этим данным построить вариационный ряд с равными интервалами, изобразить его с помощью гистограммы, а затем превратить ее в мелкоступенчатую, производим следующие действия:
а) Выбираем наименьший вариант, а затем наибольший и находим между ними разность. Делим полученную разность на число проектируемых интервалов и получаем величину каждого интервала.
Так, наименьший интервал 49,918, наибольший — 49,961. Разность 49,961—49,918=0,043.
Допустим, мы хотим получить пять интервалов, тогда величина каждого интервала равна
Следовательно, будем иметь такие интервалы:
49,918—49,928; 49,928—49,938 и т. д.
Строим рабочую таблицу, в которой подсчитываем численность каждого интервала путём . разноски данных из табл. 4 в рабочую табл. 5 и проставления черточек, соответствующих единице счета. По мере накопления четырех черточек перечеркиваем их одной чертой и ведем счет пятками (см. табл. 5).
На основании рабочей таблицы получаем следующий вариационный ряд (см. табл. 6).
б) По полученному вариационному ряду строим гистограмму распределения: на оси абсцисс откладываем диаметры валиков, начиная с 49,918 до 49,968, а на оси ординат проставляем масштаб; далее строим прямоугольники с высотой, пропорциональной количеству валиков в каждом интервале.
Соединяем прямыми линиями середины верхних сторон прямоугольников и получаем полигон (см. график 2).
Для получения мелкоступенчатой гистограммы разбиваем интервалы на две равные части и получаем:
Если построить гистограмму по новому вариационному ряду, с уменьшенными интервалами, то получим гистограмму с более мелкими ступенями. Учет требования о неизменности площади гистограммы приводит к необходимости увеличить масштаб оси ординат вдвое.
Можно продолжить процесс расчленения интервалов и дальше, получая все более и более мелкоступенчатую гистограмму.
Кумулятивная кривая (кривая сумм — кумулята) получается при изображении вариационного ряда с накопленными частотами или частостями в прямоугольной системе координат. При построении кумуляты дискретного признака на ось абсцисс наносятся значения признака (варианты). Ординатами служат вертикальные отрезки, длина которых пропорциональна накопленной частоте или частости того или иного варианта. Соединением вершин ординат прямыми линиями получаем ломаную (кривую) кумуляту.
Пример 7.
По данным табл. 4 построить кумуляту.
Составляем дискретный вариационный ряд с накопленными частотами (при наличии частостей можно для построения кумуляты пользоваться ими; см. табл. 8).
Накопленная частота определенного варианта получается суммированием всех частот вариантов, предшествующих данному, с частотой этого варианта.
Используя накопленные частоты, строим кумуляту.
При построении кумуляты- интервального вариационного ряда нижней границе первого интервала соответствует частота, равная нулю, а верхней границе — вся частота интервала. Верхней границе второго интервала соответствует накопленная частота первых двух интервалов (т. е. сумма частот этих интервалов) и т. д. Верхней границе последнего (максимального) интервала соответствует накопленная частота, равная сумме всех частот.
Пример 8.
По данным табл. 7 построить кумуляту.
Составляем интервальный вариационный ряд с накопленными частотами (см. табл. 9). По полученным накопленным частотам строим кумуляту (см. график 5).
Огива строится аналогично кумуляте с той лишь разницей, что на ось абсцисс наносят накопленные частоты, а на ось ординат — значения признака. Если лист бумаги, на котором изображена кумулята, повернуть на 90° и посмотреть на него с обратной стороны на свет, то можно увидеть огиву.
График 5. Кумулята интервального вариационного ряда
Пример 9. По данным табл. 9 построим огиву (см. график 6)-
Накопленные частоты можно получать не только в восходящем порядке, но и в нисходящем, тогда частоты вариантов суммируются снизу вверх.
Пример 10.
По данным табл. 7. вычислить накопленные частоты в нисходящем порядке.
Средние величины
В качестве одной из важнейших характеристик вариационного ряда применяют среднюю величину. Математическая статистика различает ряд типов средних величин: арифметическую, геометрическую, гармоническую, квадратическую, кубическую и др. Все перечисленные типы средних могут быть исчислены для случаев, когда каждый из вариантов вариационного ряда встречается только один раз, — тогда средняя называется простой или невзвешенной, — и для случаев, когда варианты или интервалы повторяются различное число раз. При этом число повторений вариантов или интервалов называют частотой или статистическим весом, а среднюю, вычисленную с учетом статистического веса, —взвешенной средней.
Выбор одного из перечисленных типов средних для характеристики вариационного ряда производится не произвольно, а в зависимости от особенностей изучаемого явления и цели, для которой средняя исчисляется.
Практически при выборе того или другого типа средней следует исходить из принципа осмысленности результата при суммировании или при взвешивании. Только тогда средняя применена правильно, когда в результате взвешивания или суммирования получаются величины, имеющие реальный смысл.
Обычно затруднения при выборе типа средней возникают лишь в использовании средней арифметической или гармонической. Что же касается геометрической и квадратической средних, то их применение ограничено особыми случаями (см. далее).
Следует иметь в виду, что средняя только в том случае является обобщающей характеристикой, если она применяется к однородной совокупности., В случае использования средней для неоднородных совокупностей можно прийти к неверным выводам. Научной – основой статистического анализа является метод статистических группировок, т. е. расчленения совокупности на качественно однородные группы.
Степенная средняя
Все указанные типы средних величин могут быть получены из формул степенной средней. Если имеются варианты 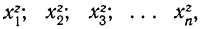
При наличии соответствующих частот 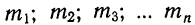
где 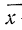
z — показатель степени, определяющий тип средней;
х — варианты;
m — частоты или статистические веса вариантов.
Средняя арифметическая получается из формулы степенной средней при подстановке z=1
средняя арифметическая невзвешенная и
средняя арифметическая взвешенная.
Пример 11.
Измерения 20 единиц продукции дали следующие результаты (колонки 1 и 2):
Вычислить средний размер единицы продукции.
Находим среднюю арифметическую. Для этого исчисляем в табл. 11 колонку 3
Здесь умножение значения признака на вес и суммирование этих произведений дает общий размер продукции, т. е. имеет реальный смысл.
Средняя гармоническая получается при подстановке в формулу степенной средней значения z =—1.
Средняя гармоническая простая
Средняя гармоническая взвешенная
Средняя гармоническая вычисляется в тех случаях, когда средняя предназначается для расчета сумм слагаемых, обратно пропорциональных величине данного признака, т. е. когда суммированию подлежат не сами варианты, а обратные им величины
или
Пример 12.
По следующим данным о работе 22 рабочих в течение 6 часов вычислить среднюю гармоническую взвешенную.
В данном случае взвешивание состоит в делении по каждой группе количества рабочих (m) на затраты времени по изготовлению одной детали (х). Для проверки правильности выбора типа средней осмыслим результат взвешивания. Исходя из того, что все рабочие работали по 6 часов, количество рабочих можно рассматривать как величину, определяющую общие затраты времени. Тогда результат деления представит вполне осмысленную величину:
Таким образом, средняя гармоническая в данном примере применена правильно. При использовании средней гармонической для упрощения расчетов целесообразно пользоваться таблицами обратных чисел (см. приложение VIII).
Средняя квадратическая получается из формулы степенной средней при подстановке z=2
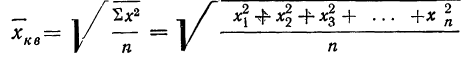
средняя квадратическая невзвешенная и
средняя квадратическая взвешенная.
Средняя квадратическая используется только в тех случаях, когда варианты представляют собой отклонения фактических величин от их средней арифметической или от заданной нормы.
Пример 13.
Имеются результаты измерения отклонений фактической длины изделий от заданной нормы.
Вычислим среднюю величину отклонений.
Находим среднюю квадратическую взвешенную; для этого исчисляем в табл. 13 колонки 3 и 4:
Значит, средняя величина отклонений фактической длины изделий от заданной нормы составляет 1,08 мм. В данном случае средняя арифметическая была бы непригодна, так как в результате мы получили бы нуль
Средняя геометрическая получается из формулы степенной средней при подстановке z=0:
Для раскрытия неопределенности этого вида прологарифмируем обе части равенства:
Теперь при подстановке z в правую часть равенства получаем неопределенность вида 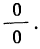
Таким образом:
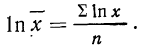
Потенцируя, находим среднюю:
Это и есть формула средней геометрической невзвешенной, которая записывается сокращенно так:
где П — знак произведения;
n — число вариантов.
Если использовать частоты (m), то средняя геометрическая взвешенная примет следующий вид:
Вычисления средней геометрической в значительной мере упрощаются применением логарифмирования. Для невзвешенной средней геометрической 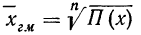
Для взвешенной средней геометрической:
Таким образом, логарифм средней геометрической есть средняя арифметическая, из логарифмов вариантов (см. формулы средней арифметической).
Средняя геометрическая используется главным образом при изучении динамики (см. раздел II).
Расчет средних коэффициентов и темпов. роста производится по формулам средней геометрической.
Пример 14.
Выпуск промышленной продукции производился предприятием в следующих размерах:
Чтобы найти средний месячный коэффициент и темп роста промышленной продукции, определяем помесячные коэффициенты роста 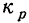
Из найденных трех помесячных коэффициентов роста (вариантов) определяем средний месячный коэффициент роста 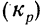
Из разобранного примера можно сделать два вывода: во-первых, что произведение трех найденных коэффициентов роста можно получить без их предварительного исчисления путем деления апрельского объема продукции (12,0) на январский объем (10,2):
и, во-вторых, что показатель степени корня, равный трем (число коэффициентов роста), можно получить вычитанием единицы из числа приведенных в примере месяцев (четыре).
Таким образом, наиболее удобной для исчисления среднего коэффициента роста следует считать формулу:
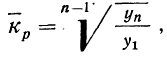
где n — число приведенных дат или периодов;
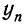
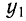
Математические свойства средней арифметической
Из вышеуказанных средних наиболее часто применяется средняя арифметическая. Знание свойств средней арифметической позволяет упрощенно ее вычислять.
Математические свойства средней арифметической:
1) Средняя постоянной величины равна этой же постоянной
величине.
2) Сумма отклонений от средней, умноженных на веса (частоты), равна нулю:
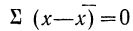
или
Докажем это свойство для средней взвешенной.
Имеем: варианты
частоты
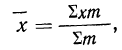
и
Подводя под общий знак суммы, получаем:
Следовательно,
Пример 15.
Вычислить среднюю (по колонкам 1 и 2) и убедиться в правильности выведенной формулы.
3) Если у всех вариантов х частоты m равны друг другу, то средняя арифметическая взвешенная равна средней арифметической невзвешенной.
Имеем
Тогда:
4) Если из всех вариантов (х) вычесть постоянную величину 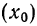
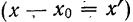
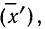
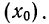
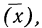
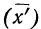
если
Доказательство.
Имеем отклонения от постоянной величины 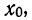
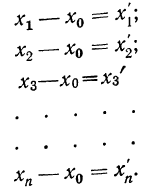
Находим среднюю из 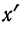
Откуда
Пример 16.
Вычислить среднюю путем вычитания 1000 из всех вариантов по следующим данным (колонки 1 и 2).
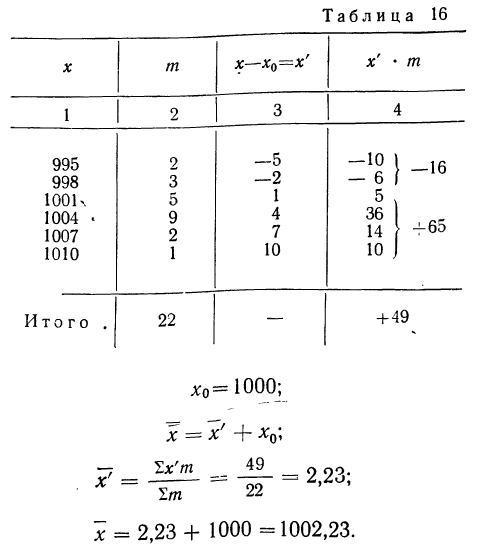
Пример 17.
Используя данные прёдыдущего примера, можно убедиться, что если за 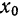
5) Если все варианты (х) уменьшить в одно и то же число раз, т. е. разделить на постоянную величину (k), и из частных 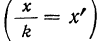
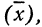
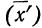
Доказательство.
Имеем частные от деления вариантов х на постоянную величину k, обозначенные х’:
Находим среднюю из
откуда
Пример 18.
Вычислить среднюю путем деления всех вариантов на 100 по следующим данным (колонки 1 и 2):
6) При вычислении средней вместо абсолютных значений весов (m) можно использовать относительные величины структуры (частости), т. е. удельные веса отдельных частот в общей сумме всех частот (см. § 4), или относительные величины координации, которые получаются путем отношения частот всех вариантов к одной из частот, принятой за единицу
Если же удельные веса частот выражены в процентах, то
где 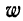
Доказательство.
Значит
Пример 19.
Вычислить средний размер детали по следующим данным (колонки 1 и 2):
Предварительно найдем относительные величины структуры (колонка 3), а затем вычислим средний размер детали, используя их в качестве весов:
Если теперь вычислить средний размер детали, используя в качестве весов частоты, то получим:
что согласуется с результатом, полученным ранее.
Для вычисления средней можно было использовать колонку 4 :
7) Если в частотах (m) имеется общий множитель (A), то его можно при вычислении средней не принимать во внимание т. е. взвешивание производить по сокращенным частотам 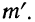
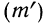
Доказательство.
Имеем:
Разделим частоты на общий множитель А, содержащийся в них:
Тогда
Пример 20.
Вычислить среднюю по данным табл. 20 (колонки 1 и 2), произведя взвешивание вариантов по сокращенным весам.
Вычисляем среднюю по указанной формуле, предварительно сократив веса и заполнив колонки 3 и 4.
8) Общая средняя равна-.-взвешенной средней из частных средних:
где 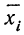
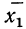
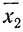
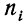
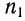
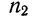
Доказательство.
Пусть имеются частные средние:
Найдем среднюю для всей совокупности:
Пример 21.
В трех, партиях продукции численностью 1000, 2000 и 500 единиц найден средний вес детали (в кг): 3,3; 3,1; 3,7. Вычислить средний вес детали во всех трех партиях
9) Сумма квадратов отклонений от средней меньше суммы квадратов отклонений от произвольной величины (В) на величину поправки С, равной произведению объема совокупности на квадрат разности между средней и данной произвольной величиной:
для случая невзвешенной средней или
для случая взвешенной средней.
Доказательство для случая невзвешенной средней.
Имеем:
Пользуясь свойствами сумм (см. стр. 11), производим преобразования:
На основании второго свойства средней арифметической 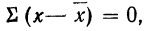
откуда
Пример 22.
По данным табл. 21 (колонки 1 и 2) убедиться в правильности указанных соотношений.
Вычисляем колонки 3, 4, 5, 6, 7, 8, 9 и находим:
Подставляя полученные результаты в формулу
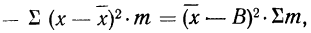
Метод отсчета от условного нуля
Упрощенное вычисление средней, состоящее в использовании ряда ее свойств, называется методом отсчета от условного нуля и предполагает:
- вычитание из всех вариантов начала отсчета или «ложного нуля»
- деление всех вариантов или отклонений вариантов от начала отсчета на общий множитель, содержащийся в них (k);
- условное принятие центра интервала за значение признака всех единиц в данном интервале.
Кроме того, в качестве весов используют сокращенные частоты 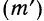
Формула исчисления средней методом отсчета от условного нуля:
где 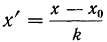
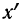
где 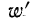
Пример 23.
Вычислить средний вес зерен (на 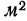
Используем формулу 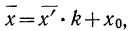
Метод стандартизации средних
Часто сравниваемые совокупности неоднородны по своему составу, и выводы при использовании средних для подобных сравнений могут оказаться неправильными. Чтобы .этого избежать, используют метод стандартизации.
Метод стандартизации средних наиболее разработан в статистике населения (демографической) и медицинской статистике, когда производится сравнение совокупностей с различными Структурами. Стандартизация достигается элиминированием (устранением) влияния различия в структурах совокупностей. Результат сравнения характеризует различие в средних при условии, что структура сравниваемых совокупностей одинакова.
Рассмотрим применение метода стандартизации на примере из медицинской статистики. Имеются данные о двух больницах А и Б по отделениям и в целом.
Получается парадоксальное положение, при котором по больнице Б итоговая (общая) летальность (8,4%) ниже, чем в больнице А (9,2%), хотя по всем отделениям летальность в больнице Б выше (см. последние две колонки).
Причиной этого парадокса является отличие удельных весов разных отделений в больницах. Доля терапевтического отделения (по числу больных) с самой высокой летальностью составляет в больнице А 60%„ а в больнице Б — 20%, а доля хирургического отделения, с самой низкой летальностью, в больнице А — 20%, а в больнице Б — 60%.
Устраним влияние различия в структурах и стандартизуем распределение больных по отделениям. В качестве стандарта можно взять распределение больных по отделениям в любой больнице или привлечь данные о распределении больных нескольких других больниц. Возьмем за стандарт распределение больных в больнице А. Тогда по больнице А общая летальность (9,2%) останется без изменения. По больнице Б произведем пересчет.
Находим среднюю стандартизованную летальность больных больницы Б:
Таким образом, после стандартизации летальность в больнице Б оказалась значительно выше,, чем в больнице А:
Следует иметь в виду, что полученное значение стандартизованной средней может служить только для сравнительных целей, абсолютное же ее значение принимать во внимание не следует.
Если за стандарт принять распределение больных в больнице Б, то получим следующую стандартизованную летальность для больницы А:
а отношение стандартизованных средних почти не изменится:
Мажорантность средних
Если вычислить различные типы средних для одного и того же вариационного ряда, то численные их значения будут отличаться друг от друга. При этом средние по своей величине расположатся в определенном порядке. Наименьшей из перечисленных средних окажется средняя гармоническая, затем геометрическая и т. д., наибольшей — средняя квадратическая. Порядок возрастания средних при этом определяется показателем степени z в формуле степенной средней и вытекает из «правила мажорантности».
Так,
при z= —1 получаем среднюю гармоническую,
при z= 0 »» геометрическую,
при z= 1 »» арифметическую,
при z= 2 »» квадратическую:
Подробное выяснение общего условия мажорантности впервые было произведено А. Я. Боярским, доказавшим, что если две средние должны удовлетворять соответственно уравнениям
и
то первая из них 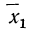
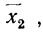
Для степенной средней порядка z имеем:
Это отношение для положительных значений с показателем x растет вместе с показателем z.
Пример 24.
Вычислить различные типы средних,по следующим данным (колонки 1 и 2) и убедиться в правильности порядка возрастания средних:
Заполняем колонки с 3-й по 8-ю и по соответствующим формулам исчисляем средние взвешенные:
Порядок средних определился в соответствии с правилом мажорантности:
17,41 < 18,14 < 18,8< 19,37.
Медиана
В качестве характеристики вариационного ряда применяется медиана (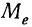
Формулы для исчисления медианы при нечетном и четном числе вариантов:
Пример 25.
Дано девять вариантов признака х, расположенных в возрастающем порядке:
Вычислить медиану.
Имеем нёчетное число вариантов:
Находим медиану
Пример 26.
Дано 12 вариантов признака х, расположенных в возрастающем порядке:
Ищем медиану.
Имеем четное число вариантов:
При исчислении медианы интервального вариационного ряда сначала находят интервал, содержащий медиану, путем использования накопленных частот или частостей. Медианному интервалу соответствует первая из накопленных частот или частостей, превышающая половину всего объема совокупности.
Для нахождения медианы при постоянстве плотности внутри интервала, содержащего медиану, используют следующую формулу:
где 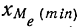
k — интервальная разность;
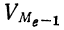
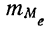
Пример 27.
По данным табл. 7 вычислить медиану.
Используем табл. 9, в которой дана колонка накопленных частот. Так как вариационный ряд содержит 200 единиц, то медиана будет 100-й единицей, входящей в интервал 49,938— 49,943 (определяется из колонки 3 табл. 9 по накопленной частоте 121, первой из накопленных частот, которая превышает половину всего объема вариационного ряда). Следовательно:
Вычислим медиану:
Медиана может быть определена и графически по кумуляте или огиве. Для определения медианы по кумуляте последнюю ординату, пропорциональную сумме всех частот или частостей, делят пополам. Из полученной точки восстанавливают перпендикуляр до пересечения с кумулятой. Абсцисса точки пересечения и дает значение медианы.
П р и м е р 28. По графику 5 определить медиану.
Последняя ордината, как видно из графика, равна 200. Деление этой ординаты пополам дает точку А (100). Перпендикуляр из точки А до пересечения с кумулятой дает точку В. Абсцисса точки В, равная 49,941, и будет медианой.
Медиана обладает тем свойством, что сумма абсолютных величин отклонений вариантов от медианы меньше, чем от любой другой величины (в том числе и от средней арифметической).
Доказательство. Допустим, что в упорядоченном вариационном ряду, состоящем из n вариантов, в качестве начала отсчета отклонений взят вариант, расположенный так, что число вариантов меньше его m, а больше n—m.
Найденную сумму абсолютных величин отклонений от этого варианта обозначим
Если теперь передвинуть начало отсчета на один вариант вверх так, чтобы вариантов, величина которых меньше начала отсчета, было m—1, а больше n—m+1, то при этом сумма абсолютных величин отклонений вариантов меньших, чем начало отсчета, от начала отсчета уменьшится на m • с, где с — разность между старым и новым началами отсчета.
В то же время сумма абсолютных величин отклонений больших вариантов от нового начала отсчета отклонений увеличится на (n—m) • с. Новая сумма абсолютных отклонений окажется равной
Следовательно, при таком передвижении начала отсчета вверх новая сумма абсолютных отклонений будет уменьшаться до тех пор, пока 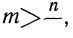
При 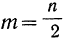
Теперь следует учесть, что n-й вариант, расположенный в середине вариационного ряда, и есть медиана.
Таким образом, минимальное свойство медианы будет доказано.
Это свойство медианы может быть использовано при проектировке расположения трамвайных и троллейбусных остановок, бензоколонок, ссыпных пунктов и т. д.
Например, на шоссе длиной 100 км имеется 10 гаражей. Для проектирования строительства бензоколонки были собраны данные о числе предполагаемых ездок на заправку с каждого гаража. Результаты обследования представлены в табл, на стр. 45.
Нужно поставить бензоколонку так, чтобы общий пробег автомашин на заправку был наименьшим.
Решение: Вариант 1. Если бензоколонку поставить на середине шоссе, т. е. на 50-м километре, то пробеги с учетом числа ездок составят:
а) в одном направлении: 43 • 10 + 24 • 15 + 22 • 5 + 13 • 20 +
+ 10-5 + 4-25 = 1310 км;
б) в противоположном направлении: 10-15 + 28-30 + 36-10 +
+ 42-65 = 4080 км.
Общий пробег в оба направления окажется равным 5390 км.
Вариант 2. Уменьшения пробега можно достигнуть, если бензоколонку поставить на 63,85-м километре (средний участок шоссе с учетом числа ездок).
В этом случае пробеги составят:
а) в одном направлении: 56,85-10 + 37,85-15 + 35,85-5 + 26,85 -20 + 23,85-5+17,85 • 25 + 3,85 -15 = 2475,75 км;
б) в противоположном направлении: 14,15-30 + 22,15-10 + 28,15-65 = 2475,75 км.
Общий пробег в оба направления составит 4951,5 км и окажется меньше, чем при первом варианте, на 438,5 км.
Вариант 3. Наилучший результат, т. е. минимальный общий пробег, будет получен в том случае, если мы поставим бензоколонку на 78-м километре, что будет соответствовать медиане.
Тогда пробеги составят:
а) в одном направлении: 71 • 10 + 52 • 15 + 50 • 5 + 41 • 20 + 38-5 + 32-25+ 18-15 = 3820 км;
б) в противоположном направлении: 8 • 10+14 • 65 = 990 км.
Общий пробег равен 4810 км, т. е. он оказался меньше общих пробегов, рассчитанных по предыдущим вариантам.
Мода
Модой (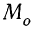
В случае интервального распределения с равными интервалами модальный интервал (т. е. содержащий моду) определяется пр наибольшей частоте, а при неравных интервалах — по наибольшей плотности.
Вычисление моды производится по следующей формуле:
где
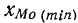
k—интервальная разность;
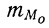
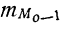
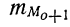
Пример 29.
По данным табл. 7 находим моду.
Наибольшая частота, равная 49 (колонка 2, табл. 7), соответствует интервалу 49,938—49,943, который и будет модальным.
Следовательно:
Подставляя в формулу найденные значения, вычислим моду
Как видно из разобранного примера и примера 27, для данного вариационного ряда мода и медиана очень близки друг к другу.
Симметричные вариационные ряды
Вариационные ряды, в которых частоты вариантов, равно отстоящих от средней, равны между собой, называются симметричными. Особенностью симметричных вариационных рядов является равенство трех характеристик: средней арифметической, моды и медианы:
Этим пользуются для распознания симметричности вариации в тех случаях, когда она затушевана тем, что средняя приходится не на середину интервала и не на границу между двумя интервалами, т. е. в результате сдвига интервалов группировки ряд частот как таковых оказывается не вполне симметричным.
Пример 30.
По данным табл. 7 определить среднюю и сопоставить с модой и медианой, вычисленными по этим же данным в примерах 27 и 29.
Вычисляем среднюю (см. табл. 26):
Найденную среднюю сопоставляем с модой и медианой, вычисленными ранее:
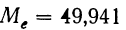
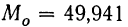
Полученные характеристики по своей величине близки друг к другу, что дает нам основание считать данный вариационный ряд не очень отклоняющимся от симметричного.
Асимметричные вариационные ряды
Вариационные ряды, в которых расположение вариантов вокруг средней неодинаково, т. е. частоты по обе стороны от средней изменяются по-разному, называются асимметричными или скошенными. Различают левостороннюю и правостороннюю асимметрию.
Меры колеблемости (вариации) признака
Средние величины, характеризуя вариационный ряд одним числом, не учитывают вариацию признака, между тем эта вариация существует. Для измерения вариации признака математическая статистика применяет ряд способов.
Вариационный размах (R) (или широта распределения) есть разность между экстремальными (крайними) значениями вариационного ряда. Он представляет собой величину неустойчивую, чрезвычайно зависящую от случайных обстоятельств; применяется в качестве приблизительной оценки вариации.
В последнее время вариационный размах стал применяться в ряде отраслей промышленности при статистическом изучении качества продукции.
где 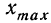
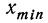
Среднее линейное отклонение или простое среднее отклонение (р —ро) представляет собой среднюю арифметическую из абсолютных значений отклонений вариантов от средней.
В зависимости от отсутствия или наличия частот вычисляют среднее линейное отклонение невзвешенное или взвешенное:
где прямые скобки, в которых заключены разности между вариантами и средней, показывают, что непосредственное суммирование и суммирование после взвешивания производится без учета знаков.
Средний квадрат отклонения — дисперсия (обычно обозначаемый 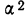
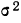
Дисперсия невзвешенная
Дисперсия взвешенная
Таким образом, общая дисперсия есть средняя арифметическая из квадратов отклонений вариантов от их средней арифметической.
Среднее квадратическое отклонение (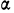
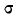
Среднее квадратическое отклонение невзвешенное
Среднее квадратическое отклонение взвешенное
Достоинством этого показателя по сравнению со средним линейным отклонением (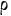
Учитывая, что среднее линейное отклонение и среднее квадратическое отклонение представляют собой абсолютные величины, выраженные в тех же единицах измерения, что и варианты, для характеристики колеблемости признака используют относительные показатели – коэффициенты вариации (V), представляющие собой отношение среднего линейного отклонения или среднего квадратического отклонения к средней, выраженное в процентах (или в долях единицы):
Коэффициент вариации по среднему линейному отклонению
Коэффициент вариации по среднему квадратическому отклонению
Видоизмененный показатель коэффициента вариации по среднему линейному отклонению (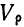
Показатель неровноты невзвешенный
Показатель неровноты взвешенный
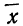
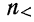
n — объем вариационного ряда;
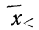
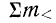
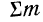
Доказательство (для показателя неровноты невзвешенного) .
Подставляя в формулу 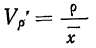
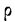
получаем:
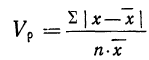
Разделим весь вариационный ряд на две части. Пусть в первую часть включены варианты меньшие, чем общая средняя, а во вторую — большие, чем общая средняя.
Тогда
где
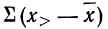
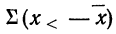
Но так как 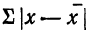
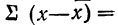
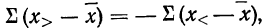
Учитывая, что под знаком суммы слагаемых будет 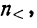
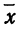
Делим и умножаем числитель на
Пример 31.
По данным табл. 27 о крепости одиночной нити (в г) вычислим показатели вариации признака: вариационный размах, показатель неровноты, коэффициенты вариации по среднему линейному отклонению и среднему квадратическому отклонению.
Вычисляем R:
Находим среднюю:
Находим Н. Интервал 190—200 расчленяем на две части: 190—192,16 и 192,16—200.
Аналогично поступаем с частотами: так как вся частота данного интервала равна 69, то, предполагая равномерное распределение признака внутри интервала, получим, что на величину, равную единице интервала, приходится 6,9 единицы частот (абсолютная плотность); на новый интервал (190—192,16), в котором интервальная разность равна 2,16, придется 6,9*2,16 = 14,9 единицы частот. Для простоты возьмем 15. Суммируя частоты вариантов, меньших общей средней, получим 255 (см. колонку 5 табл. 27). Суммируя произведения х
Вычисляем 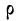
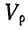
Учитывая одно из свойств средней, а именно, что сумма отклонений от средней, соответствующим образом взвешенных, равна нулю, практически поступают следующим образом. В колонке 7 табл. 27, несмотря на знак прямых скобок, указывающих на абсолютную величину отклонений, для отрицательных отклонений от средней знак минус оставляют и ведут вычисление только до перемены знака на плюс. Взвешивают отрицательные отклонения от средней (колонка 8 табл. 27) и, так как сумма взвешенных положительных отклонений от средней должна быть равна сумме взвешенных отрицательных отклонений от средней, для определения общей суммы взвешенных отклонений найденную сумму удваивают.
Получаем:
Вычисляем
Между средним квадратическим отклонением 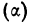
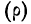
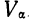
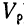
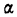
Если объем совокупности достаточно большой и распределение признака в вариационном ряде близко к нормальному (см. раздел IV), то связь между 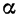
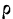
Отклонения 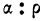
Пример 32.
По данным примера 31. найти соотношение между 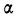
Имеем:
Это отношение не намного отличается от теоретического (1,25), что косвенно свидетельствует о близости взятого распределения к нормальному.
Свойства дисперсии
Средний квадрат отклонения — дисперсия — обладает рядом свойств, которые позволяют упростить вычисления.
1) Дисперсия постоянной величины равна нулю:
где с — постоянная величина;
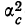
2) Если все значения вариантов признака х уменьшить на постоянную величину, то дисперсия не изменится. Это позволяет вычислить дисперсию вариационного ряда путем вычитания из вариантов начала отсчета
где 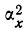
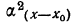
Доказательство для невзвешенной дисперсии
Имеем: 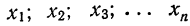
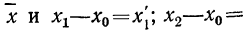
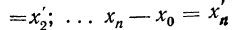
Тогда
3) Дисперсия алгебраической суммы независимых случайных величин (см. стр. 115 и далее) равна сумме их дисперсий:
4) Если все значения вариантов х уменьшить в k раз, то дисперсия уменьшится в 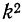
где 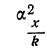
Доказательство для невзвешенной дисперсии
Имеем: 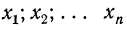
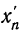
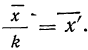
Отсюда:
5) Дисперсия суммы двух случайных величин, связанных корреляционной зависимостью, равна сумме их дисперсий плюс удвоенное произведение среднеквадратических отклонений на коэффициент корреляции между этими случайными величинами
где 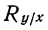
(Значение его как меры тесноты связи см. раздел «Корреляция».)
Пример 33.
Даны случайные величины у и х, связанные корреляционной зависимостью так, что 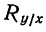
Найти дисперсию суммы этих случайных величин (для простоты дан пример без взвешивания).
Находим средние:
Определяем дисперсии:
Используя рассматриваемую формулу, имеем:
Убедимся, что если х + у = z, то получаем три значения z: 4, 8 и 9.
Находим: среднюю
дисперсию
т. е.
Результаты вычисления, произведенные по непосредственным данным и суммированным, совпадают.
6) Дисперсия суммы двух случайных величин, связанных Линейной функциональной зависимостью (см. раздел «Корреляция»), равна сумме их дисперсий плюс или минус удвоенное произведение среднеквадратических отклонений:
В данной формуле знак плюс или минус определяется характером связи. При прямолинейной связи у с х 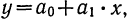
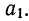
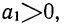
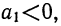
Пример 34.
Даны две случайные величины х и у, связанные уравнением у=2+Зх.
Найти дисперсию суммы этих случайных величин. Находим средние:
Определяем дисперсии по формуле:
Используем рассматриваемую формулу. В данном случае берем знак плюс:
Убеждаемся, что если х + у = z, то получаем три значения z: 6, 14 и 22.
Находим: среднюю
дисперсию
т. е.
Вычисление дисперсии методом отсчета от условного нуля
Практически расчет дисперсии производят по формуле, упрощающей вычисления. Эта формула получена с учетом свойств дисперсии, а расчет по ней называется отсчетом от условного нуля:
Доказательство. Возьмем выражение 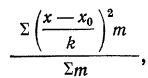
Так как второе слагаемое в фигурной скобке равно нулю: 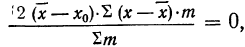
Отсюда:
и
Пример 35.
По данным табл. 27 (колонки 2 и 3) рассчитать дисперсию, используя формулу, упрощающую вычисления. Располагаем данные, необходимые для ее вычисления, в таблице (см. табл. 30).
Величина дисперсии совпадает с величиной, полученной в примере 31, но в данном случае вычисления в значительной мере упрощены.
Из формулы 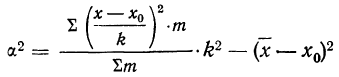
При 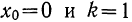
или
где 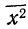
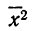
Так, если вычислить дисперсию по данным табл. 27, пользуясь этой формулой, то получим:
Результат совпадает с дисперсией, полученной по этим данным в примере 31.
Частные дисперсии
Для каждой группы вариантов вариационного ряда может быть исчислена наряду с частной средней и дисперсия, которая называется частной дисперсией или внутригрупповой,
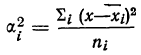
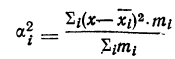
Где 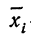
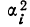
(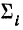
Средняя из частных дисперсий
Из частных, т. е.
внутригрупповых, дисперсий может быть найдена средняя, которая обозначается
Средняя из частных дисперсий служит для характеристики среднего рассеяния признака внутри групп.
Межгрупповая дисперсия
Частные средние по группам 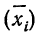
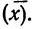
групповая дисперсия 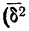
Правило сложения вариаций
Между общей дисперсией, средней из частных дисперсий и межгрупповой дисперсией “существует такая связь:
Это — правило сложения вариации (или дисперсий).
Доказательство.
Пусть общая совокупность состоит из t групп численностью 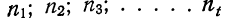
Частные средние 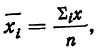
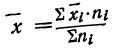
Частные дисперсии можно записать следующим образом.
откуда
Суммируя 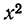
Умножим обе части этого равенства на 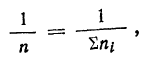
Вычитая из обеих частей равенства 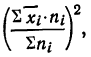
Левая часть равенства представляет собой общую дисперсию, т. е. 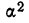
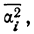
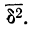
Пример 36.
Используя данные табл. 27 и расчленяя вариационный ряд на две группы (1-я группа с интервала 120—130 до интервала 190—200 включительно, а 2-я группа с •интервала 200—210 до интервала 260—270), исчислить частные дисперсии, среднюю из частных дисперсий и межгрупповую дисперсию.
Начинаем расчет с 1-й группы (см. табл. 33):
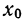
Для 2-й группы получаем (по тем же формулам):
Вычисляем среднюю из частных дисперсий:
Находим межгрупповую дисперсию, используя общую среднюю для всего вариационного ряда, найденную в примере 31 и равную 192,16
Для получения общей дисперсии используем правило сложения вариации:
Результат совпадает с дисперсией, вычисленной в примере 31 по табл. 27 без расчленения вариационного ряда на две группы.
Вариация альтернативного признака
Наряду с количественной вариацией признака может иметь место и качественная вариация. Если, имеются два взаимно исключающих друг друга варианта, то вариация признака называется альтернативной.
Так, например, рассмотрение выпущенной продукции с точки зрения ее качества, т. е. пригодности к дальнейшему использованию, дает альтернативный признак. Обозначая наличие признака 1, а отсутствие — 0 и долю вариантов, обладающих данным признаком, — р, а долю вариантов, не обладающий им, — q
и замечая, что p + q=1, получаем сначала среднюю:
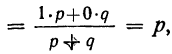
Следовательно,
§ 35. Из дисперсии альтернативного признака извлечением корня находится среднее квадратическое отклонение:
Пример 37.
Совокупность состоит из 10000 электрических, лампочек, включающих в свой состав 20 бракованных. Найти дисперсию признака и среднее квадратическое отклонение.
Находим долю брака и долю доброкачественных лампочек:
По формуле 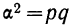
а затем среднее квадратическое отклонение:
Попытки измерить колеблемость признака путем нахождения средней арифметической из квадратов разностей вариантов во всех возможных их попарных сочетаниях не вносят-ничего принципиально нового.
Можно доказать, что этот показатель 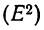
Пусть, например, имеются варианты:
1; 3; 5; 6; 10.
Исчислим среднюю и дисперсию:
Вычислим абсолютные разности всех возможных попарных сочетаний, включая и сочетания каждого варианта с ним же:
1) Разности попарных сочетаний с первым вариантом
1 — 1=0; 3—1=2; 5—1=4; 6—1 = 5; 10—1=9.
2) Разности попарных сочетаний со вторым вариантом
3 — 3 = 0; 3—1 =2; 3 —5 = 2; 3 — 6 = 3; 3—10 = 7
и далее:
5 —5 = 0; 5—1 =4; 5 —3 = 2; 5 —6= 1; 5—10 = 5;
6 — 6 = 0; 6—1 =5; 6 — 3 = 3; 6 — 5= 1; 6—10 = 4;
10 — 10 = 0; 10 — 1 = 9; 10 —3 = 7; 10 —5 = 5; 10 —6 = 4.
Находим сумму квадратов 25 разностей и делением на 25 — среднюю арифметическую из квадратов разностей:
Замечаем, что этот же результат можно получить умножением дисперсии (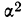
9,2*2=18,4.
Квартили и децили
Как уже было показано, медиана — это вариант, который делит упорядоченный вариационный ряд на две равные по объему группы. В каждой группе аналогично можно найти также вариант, делящий ее на две подгруппы. Такие варианты называются квартилями.
Различают нижний и верхний квартили. Иногда вычисляют и децили, т.е. такие варианты, которые делят вариационный ряд на 10 равных по объему групп.
При отношении объема двух подгрупп, как 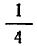
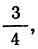
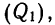
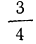
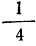
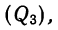
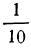
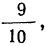
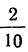
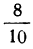
Формулы для расчетов в интервальном ряду:
нижнего квартиля
верхнего квартиля
где 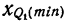
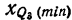
k — интервальная разность;
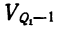
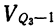
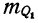
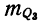
Вычисление децилей ничем принципиально не отличается от вычисления медианы и квартилей. Так, первый и второй децили могут быть вычислены по формулам:
и т.д.
Пример 38.
По данным табл. 7 вычислить нижний и верхний квартили (рекомендуется предварительно вспомнить вычисление медианы).
Используем табл. 9, в которой дана колонка накопленных частот. Нижний квартиль рассчитывается по соответствующей формуле 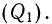
Следовательно:
Находим нижний квартиль:
Верхний квартиль отвечает 150-й единице и содержится в интервале 49,943-49,948 (так как первая из накопленных частот, превышающая 150, равна 164 и соответствует данному интервалу).
Находим верхний квартиль:
Квартиль
В качестве характеристики колеблемости вариационного ряда применяется относительный показатель, подобный коэффициенту вариации, но для вычисления которого используются нижний и верхний квартили и медиана. Этот показатель называют квартилем 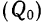
где 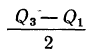
Пример 39.
По результатам исчисления медианы, а также нижнего и верхнего квартилей по табл. 7 (см. примеры 27 и 38) найти квартиль.
Имеем:
Интересно, что величина коэффициента вариации, по данным табл. 7, довольно близка к полученной величине квартиля:
Моменты распределения
Обобщающими характеристиками вариационных рядов являются моменты распределения. Характер распределения может быть определен с помощью небольшого числа моментов. Способ моментов был разработан русским математиком П. Л. Чебышевым и успешно применен А. А. Марковым для рассмотрения возможностей использования закона нормального распределения при изучении сумм: большого, но конечного числа независимых случайных величин.
Средняя из k-x степеней-отклонений вариантов х от некоторой постоянной величины А называется моментом k-гo порядка:
При исчислении средней в качестве весов могут быть использованы частоты, частости или вероятности (см. раздел II). При использовании в качестве весов частот или частостей моменты называются эмпирическими, а при использовании вероятностей — теоретическими.
Порядок момента определяется величиной k. Эмпирический момент k-гo порядка находится как отношение суммы произведений k-x степеней отклонений вариантов от постоянной величины А на частоты к сумме частот:
В зависимости от выбора постоянной величины А различают следующие моменты:
1) Если постоянная величина А равна нулю (А=0), то моменты называются начальными. Приводим формулу всех начальных моментов:
Тогда:
при k = 0 получаем
при k=1
при k=2
при k = 3
при k = 4
и т. д. Практически используют моменты первых четырех порядков.
Пример 40.
Вычислить начальные моменты первых четырех порядков, если варианты х имеют как отрицательные, так и положительные значения.
Располагаем все расчеты в таблицу:
Вычисляем моменты:
2) Если А не равно нулю, а некоторой произвольной величине 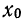
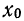
При подстановке различных значений k получаем начальные моменты относительно
при k=0
при k=1
при k=2
при k=3
при k=4
и т.д.
Из формулы момента первого порядка вытекает, что 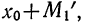
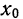
Отсюда следует, что
При сравнении с вычислением средней методом отсчета от условного нуля видно, что 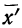
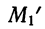
Пример 41.
Вычислить начальные моменты относительно 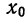
Располагаем все расчеты в таблицу:
Таблица 35
Возьмем в качестве 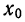
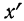
Для получения 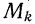
Практически при нахождении начальных моментов относительно 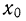
из всех вариантов вычитают начало отсчета и находят отклонения
делят эти отклонения на общий множитель
находят начальные моменты для
путем умножения найденных начальных моментов на 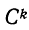
3) Если за постоянную величину А взять среднюю 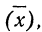
Тогда:
при k = 0
центральный момент нулевого порядка равен единице
при k=1
центральный момент первого порядка равен нулю
при k = 2
центральный момент второго порядка равен дисперсии и служит мерой колеблемости признака
при k = 3
центральный момент третьего порядка служит мерой асимметрии распределения признака. Если распределение симметрично, то
При k = 4
центральный момент четвертого порядка
Пример 42.
Вычислим центральные,моменты первых четырех порядков по данным табл. 36 (колонки 1, 2).
Располагаем все расчеты в таблицу (см. табл. 36). Получаем:
§ 40. Существует связь между начальными моментами первых четырех порядков вариантов 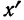
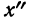
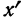
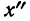
где 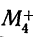
В правой части формулы все начальные моменты (от нулевого порядка до четвертого порядка) вариантов 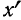
Практически данная формула используется для проверки
вычисления начальных моментов первых четырех порядков вариантов 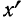
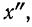
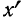
Если исчисления 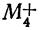
и по формуле связи между моментами дают тождественные результаты, то это свидетельствует о правильности всех начальных моментов первых четырех порядков, вычисленных для вариантов
Пример 43.
Проверим правильность начальных моментов первых четырех порядков, вычисленных в примере 40.
Располагаем все расчеты в таблицу:
В колонке 3 записываем новые варианты 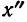
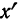
Получаем по формуле:
Для расчетов 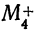
Получаем:
Результаты совпадают, следовательно, начальные моменты первых четырех порядков в примере 40 вычислены правильно.
Вычисление центральных моментов, привлекаемых в качестве характеристик вариационного ряда, по формуле
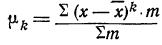
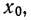
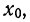
Знаки в формуле чередуются.
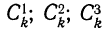
Полагая в этой формуле k равным 0, 1, 2, 3, 4 и т. д., можем получить центральные моменты различных порядков:
Для вычисления центральных моментов высших порядков по найденным центральным моментам низших порядков и начальным моментам относительно 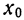
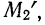
т. е.
Пример 44.
Используя данные примера 41, где вычислены начальные моменты относительно 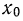
Из примера 41 имеем:
По формулам центральных моментов получаем, используя начальные моменты:
Сравнивая центральные моменты первых четырех порядков, вычисленные по указанным формулам, с центральными моментами, вычисленными в примере 42 непосредственно по формуле 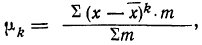
Аналогично используются и формулы центральных моментов высших порядков по центральным моментам низших порядков.
Вычислим третий центральный момент по второму центральному моменту и начальным относительно 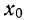
Вычислим и четвертый центральный момент по третьему и второму центральным моментам и начальным относительно 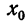
Исчисление центральных моментов сводится к:
- нахождению начальных моментов
и их проверке:
- нахождению начальных моментов относительно произвольно выбранного начала отсчета
- использованию формул перехода от начальных моментов относительно произвольно выбранного начала отсчета к центральным моментам
Пример 45.
По данным табл. 38 (колонки 1, 2 и 3) вычислить центральные моменты первых четырех порядков:
Начнем с вычисления начальных моментов. Для этого выбираем 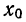
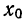
Все действия производим в табл. 38 и получаем колонку 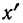
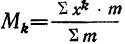
Для простоты расчета числа колонки 5 получают перемножением чисел, расположенных в колонках 2 и 4, числа колонки 6 получают перемножением чисел колонок 4 и 5, числа колонки 7— перемножением чисел колонок 4 и 6 и т. д.
Проверяем вычисление начальных моментов первых четырех порядков. Для этого вычисляем колонки 9 и 10.
Числа колонки 9 получают прибавлением к числам колонки 4 единицы. Числа колонки 10 (а можно и 8) получают, используя таблицу, имеющую следующий вид:
В колонке 1 таблицы указаны частоты (m) от 1 до 50, а в верхнем заголовке — числа х’ или х”. Произведения 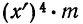
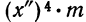
Так, если
если
и т. д. (см. приложение VII).
Используя формулу 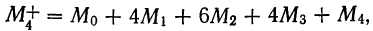
Исчисляя 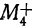
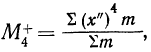
Результаты вычисления 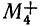
Находим начальные моменты первых четырех порядков относительно выбранного начала отсчета 44,5 по формуле
Находим центральные моменты, используя формулы перехода от начальных моментов, вычисленных относительно
Вычисление моментов способом сумм
Вычисление моментов при равно отстоящих значениях признака может производиться двумя способами: 1) способом произведений, использованным нами ранее во всех случаях вычислений моментов, и 2) способом сумм, являющимся более упрощенным.
Таблица, в которой производятся все подготовительные расчеты для вычисления начальных четырех моментов, включает в себя колонки х и m и, кроме этого, 4 нумерованные колонки.
Рассмотрим пример вычисления начальных моментов способом сумм по данным табл. 38 (см. табл. 40).
Вся таблица делится на две части чертой, проведенной против частости, соответствующей 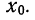
Для получения 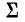
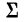
Величины S и D получаются сложением и вычитанием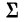
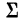
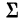
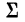
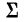
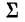
Для вычисления начальных моментов по способу сумм используют следующие формулы:
Как видим, результаты вычислений по способу сумм совпадают с результатами примера 45.
Нормированные моменты
Второй центральный момент равен дисперсии, т. е. 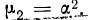
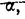
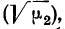
Пример 46. По найденным в примере 45 центральным моментам найти нормированные моменты первых четырех порядков.
Из примера 45 имеем:
Находим сначала стандарт:
а затем нормированные моменты:
Использование нормированных моментов
Нормированные моменты используются при изучении вариационных рядов. Третий нормированный момент 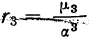
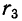

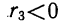
Четвертый нормированный момент 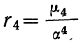
Если 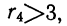
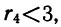
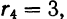
По результатам вычисления нормированных моментов в примере 46 видно, что 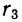
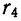
Коэффициент асимметрии
В качестве показателя отклонения вариационного ряда от симметрии применяется простой эмпирический коэффициент асимметрии 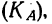
Если 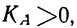
если 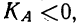
если 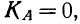
Пример 47.
По данным примера 31 (табл. 27) вычислим коэффициент асимметрии.
Имеем:
Вычислим моду по формуле
В данном случае асимметрия небольшая и скошенность левосторонняя.
- Законы распределения случайных величин
- Дисперсионный анализ
- Математическая обработка динамических рядов
- Корреляция – определение и вычисление
- Статистическая проверка гипотез
- Статистические оценки
- Теория статистической проверки гипотез
- Линейный регрессионный анализ
3) определяют границы всех интервалов. Нижняя граница первого интервала принимается за хmin, верхняя граница первого интервала находится по формуле: xmin + h.
В качестве нижней границы второго интервала принимается верхняя граница первого, а верхнюю границу второго интервала получают прибавлением к верхней границе шага h. Процедуру повторяют до тех пор, пока не будут определены границы последней группы;
4) разносят единицы совокупности по интервалам;
5) подсчитывают единицы совокупности в каждом интервале.
Если полученные указанными выше способами группировки не удовлетворяют требованиям анализа, то производят перегруппировку. Ряды распределения используются в статистике как средство систематизации и упорядочивания материалов наблюдения, как метод изучения структуры явлений, анализа самих распределений и вариативности группировочного признака.
13. Графическое изображение вариационных рядов
Табличное распределение частот вариационного ряда обычно дополняют его графическим представлением. Схематически все множество графических представлений статистических данных разделяют на два класса: диаграммы и линейные изображения. К классу линейных графиков относятся полигон распределения, кумулятивная кривая, кривая концентрации, огива. К классу диаграмм относится гистограмма.
Вариационные ряды могут изображаться графически путем построения полигона распределения, гистограммы, кумуляты.
Для графического изображения дискретного вариационного ряда строится xmin полигон распределения xmin в прямоугольной системе координат. На оси абсцисс проставляются варианты, на оси ординат — частоты. На пересечении каждой абсциссы и ординаты строятся точки, которые затем соединяются отрезками прямой. Крайние точки соединяются с осью абсцисс в точках, отстоящих от минимального и максимального варианта на одно деление. Полигоном частот называют ломаную, отрезки которой соединяют точки (x1, f1, …,(xnfn). Иногда крайние точки соединяют с точками, имеющими нулевую ординату. Полигоном относительных частот называют ломаную, отрезки которой соединяют точки ( x 1, w 1), …, ( xn , wn ), где
Интервальные вариационные ряды изображаются в виде гистограммы. На оси абсцисс откладываются отрезки, соответствующие длине интервала h. На каждом отрезке строятся прямоугольники, одна сторона каждого из них лежит на оси абсцисс, длина второй стороны соответствует частоте fi или плотности
. Гистограммой частот называют ступенчатую фигуру, состоящую из полученных прямоугольников. Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых случат интервалы длиной h, а высоты которых равны .
Любой вариационный ряд можно изобразить графически в виде кривой накопленных частот — кумуляты. На оси абсцисс откладываются либо варианты, либо границы интервалов. Наоси ординат— накопленная частота. Получают точки при пересечении каждой пары абсциссы и ординаты, которые соединяют плавной кривой.
Кумулятивная кривая (кривая сумм) — ломаная, составленная по последовательно суммированным, т.е. накопленным частотам или относительным частотам. При построении кумулятивной кривой дискретного признака на ось абсцисс наносятся значения признака, а ординатами служат нарастающие итоги частот. Соединением вершин ординат прямыми линиями получают кумуляту. При построении кумуляты интервального признака на ось абсцисс откладываются границы интервалов и верхним значениям присваивают накопленные частоты. Кумулятивную кривую называют полигоном накопленных частот.
Если на ось ординат нанести значение признака, а на ось абсцисс — накопленные частоты, то получим кривую, называемую огивой.
14. Показатели, характеризующие вариационные ряды
Вариацией признака называется различие индивидуальных значений признака внутри изучаемой совокупности. Вариация возникает в результа-те того, что индивидуальные значения признака складываются под совокупным влиянием разнообразных факторов. Средняя величина дает обобщающую характеристику признака изучаемой совокупности, но не показывает строения совокупности, которое весьма существенно для ее познания.
Варианты для выполнения работы
I. Установление закономерностей, которым подчинены массовые случайные явления, основано на изучении методами теории вероятностей статистических данных — результатов наблюдений.
Почти все встречающиеся в жизни величины (урожайность сельскохозяйственных растений, продуктивности скота, производительность труда и заработная плата рабочих, объем производства продукции и т.д.) принимают неодинаковые значения у различных членов совокупности. Поэтому возникает необходимость в изучении их изменяемости. Это изучение начинается с проведения соответствующих наблюдений, обследований.
В результате наблюдений получают сведения о численной величине изучаемого признака у каждого члена данной совокупности.
Пример. Имеются данные о размере прибыли 100 коммерческих банков. Прибыль, млн. рублей.
| 30,2 | 51,9 | 43,1 | 58,9 | 34,1 | 55,2 | 47,9 | 43,7 | 53,2 | 34,9 |
| 47,8 | 65,7 | 37,8 | 68,6 | 48,4 | 67,5 | 27,3 | 66,1 | 52,0 | 55,6 |
| 54,1 | 26,9 | 53,6 | 42,5 | 59,3 | 44,8 | 52,8 | 42,3 | 55,9 | 48,1 |
| 44,5 | 69,8 | 47,3 | 35,6 | 70,1 | 39,5 | 70,3 | 33,7 | 51,8 | 56,1 |
| 28,4 | 48,7 | 41,9 | 58,1 | 20,4 | 56,3 | 46,5 | 41,8 | 59,5 | 38,1 |
| 41,4 | 70,4 | 31,4 | 52,5 | 45,2 | 52,3 | 40,2 | 60,4 | 27,6 | 57,4 |
| 29,3 | 53,8 | 46,3 | 40,1 | 50,3 | 48,9 | 35,8 | 61,7 | 49,2 | 45,8 |
| 45,3 | 71,5 | 35,1 | 57,8 | 28,1 | 57,6 | 49,6 | 45,5 | 36,2 | 63,2 |
| 61,9 | 25,1 | 65,1 | 49,7 | 62,1 | 46,1 | 39,9 | 62,4 | 50,1 | 33,1 |
| 33,3 | 49,8 | 39,8 | 45,9 | 37,3 | 78,0 | 64,9 | 28,8 | 62,5 | 58,7 |
Из данной таблицы видно, что интересующий нас признак (прибыль банков) меняется от одного члена совокупности к другому, варьирует. Варьирование есть изменяемость признака у отдельных членов совокупности.
Вариационным рядом называется последовательность вариант, записанных в возрастающем порядке и соответствующих им частот.
Число, показывающее, сколько раз повторяется в данной совокупности каждое значение признака, называется частотой.
Составим ранжированный вариационный ряд (выпишем варианты в порядке возрастания):
| 20,4 | 25,1 | 26,9 | 27,3 | 27,6 | 28,1 | 28,4 | 28,8 | 29,3 | 30,2 |
| 31,4 | 33,1 | 33,3 | 33,7 | 34,1 | 34,9 | 35,1 | 35,6 | 35,8 | 36,2 |
| 37,3 | 37,8 | 38,1 | 39,5 | 39,8 | 39,9 | 40,1 | 40,2 | 41,4 | 41,8 |
| 41,9 | 42,3 | 42,5 | 43,1 | 43,7 | 44,5 | 44,8 | 45,2 | 45,3 | 45,5 |
| 45,8 | 45,9 | 46,1 | 46,3 | 46,5 | 47,3 | 47,8 | 47,9 | 48,1 | 48,4 |
| 48,7 | 48,9 | 49,2 | 49,6 | 49,7 | 49,8 | 50,1 | 50,3 | 51,8 | 51,9 |
| 52,0 | 52,3 | 52,5 | 52,8 | 53,2 | 53,6 | 53,8 | 54,1 | 55,2 | 55,6 |
| 55,9 | 56,1 | 56,3 | 57,4 | 57,6 | 57,8 | 58,1 | 58,7 | 58,9 | 59,3 |
| 59,5 | 60,4 | 61,7 | 61,9 | 62,1 | 62,4 | 62,5 | 63,2 | 64,9 | 65,1 |
| 65,7 | 66,1 | 67,5 | 68,6 | 69,8 | 70,1 | 70,3 | 70,4 | 71,5 | 78,0 |
В нашем случае каждое значение признака (варианта вариационного ряда) повторилось только один раз, т.е. значение частоты для всех вариант равно единице. Перейдем к интервальному вариационному ряду, так как интересующий нас признак принимает дробные, практически не повторяющиеся значения.
Для этого необходимо определить число интервалов (классов) и длину интервала (классного промежутка), после чего произвести разноску, т.е. подсчитать для каждого интервала число вариант, попавших в него.
Количество классов устанавливают в зависимости от степени точности, с которой ведется обработка, и количества объектов в выборке. Считается удобным при объеме выборки (n) в пределах от 30 до 60 вариант распределять их на 6-7 классов, при n от 60 до 100 вариант — на 7-8 классов, при n от 100 и более вариант — на 9-17 классов.
Нужное количество групп также может быть ориентировочно вычислено по формуле Стерджесса:
где — число групп (классов, интервалов) ряда распределения; n — объем выборки.
Можно также использовать выражение:
При они дают примерно одинаковые результаты.
В рассматриваемом примере о размере прибыли коммерческих банков, n=100. Применяя формулу Стерджесса, получим:
Однако Таким образом, число интервалов может быть равно 8, 9, 10 и т.д.
Нахождение нужного количества групп и их размеров часто бывает взаимообусловлено. Для того, чтобы как-то определиться с числом интервалов, найдем размах вариации — разность между наибольшей и наименьшей вариантой:
где — размах вариации,
— наибольшее значение варьирующего признака,
— наименьшее значение варьирующего признака.
Найдем размах вариации для рассматриваемой задачи:
Для того, чтобы найти длину интервала (величину классового промежутка) необходимо разделить размах вариации на число классов и полученную величину округлить таким образом, чтобы было удобно производить сначала разноску, а затем и различные вычисления. Рекомендую округлять до единиц, до которых округлены варианты в исходной таблице, в нашем случае до десятых.
Согласно формуле получаем
Теперь необходимо определиться с началом первого интервала. Для этого можно использовать формулу:
Замечание. За начало первого интервала можно принять некоторое значение, несколько меньшее или само значение
. Далее в табличном виде я покажу оба варианта.
Прибавив к началу первого интервала (нижней границе) шаг, получим верхнюю границу первого интервала и одновременно нижнюю границу второго интервала. Выполняя последовательно указанные действия, будем находить границы последующих интервалов до тех пор, пока не будет получено или перекрыто .
Таким образом, верхняя граница одного интервала одновременно является нижней границей другого интервала. Чтобы не возникало сомнений, в какой интервал отнести варианту, попавшую на границу, условимся относить ее к верхнему интервалу.
Составим теперь рабочую таблицу для построения интервального вариационного ряда и произведем подсчет частот вариант, попавших в тот или иной интервал.
Как и обещал покажу две таблицы построения ряда:
1. Отсчет ведем от , т.е. нижняя граница первого интервала совпадает с
.
|
Группы банков по размеру прибыли (границы интервалов) |
Количество банков, принадлежащих данной группе (частоты, |
Накопленные частоты, |
| 20,4 — 27,6 | 4 | 4 |
| 27,6 — 34,8 | 11 | 15 |
| 34,8 — 42 | 16 | 31 |
| 42 — 49,2 | 21 | 52 |
| 49,2 — 56,4 | 21 | 73 |
| 56,4 — 63,6 | 15 | 88 |
| 63,6 — 70,8 | 10 | 98 |
| 70,8 — 78 | 2 | 100 |
2. Начало первого интервала определяем с помощью формулы: .
|
Группы банков по размеру прибыли (границы интервалов) |
Количество банков, принадлежащих данной группе (частоты, |
Накопленные частоты, |
| 16,8 — 24 | 1 | 1 |
| 24 — 31,2 | 9 | 10 |
| 31,2 — 38,4 | 13 | 23 |
| 38,4 — 45,6 | 17 | 40 |
| 45,6 — 52,8 | 23 | 63 |
| 52,8 — 60 | 18 | 81 |
| 60 — 67,2 | 11 | 92 |
| 67,2 — 74,4 | 7 | 99 |
| 74,4 — 81,6 | 1 | 100 |
Как мы видим в 1-м случае у нас получилось восемь интервалов, что полностью совпадает с результатом, который нам дала формула Стерджесса. Во втором случае у нас получилось девять интервалов, так как при поиске начала первого интервала пользовались специальной формулой.
Для дальнейшего исследования я буду пользоваться результатами второй таблицы, так как там ярко выражен модальный интервал (одна мода) и медиана практически точно попадает на середину вариационного ряда.
Мы получили интервальный вариационный ряд — упорядоченную совокупность интервалов варьирования значений случайной величины с соответствующими частотами попаданий в каждый из них значений величины.
II. Графическая интерпретация вариационных рядов.
| № п/п |
Границы интервалов, |
Середины интервалов, |
Частоты интервалов, |
Относительные частоты |
Плотность относит. частоты |
Плотность частоты |
| 1 | 16,8 — 24 | 20,4 | 1 | 0,01 | 0,001 | 0,139 |
| 2 | 24 — 31,2 | 27,6 | 9 | 0,09 | 0,013 | 1,250 |
| 3 | 31,2 — 38,4 | 34,8 | 13 | 0,13 | 0,018 | 1,806 |
| 4 | 38,4 — 45,6 | 42 | 17 | 0,17 | 0,024 | 2,361 |
| 5 | 45,6 — 52,8 | 49,2 | 23 | 0,23 | 0,032 | 3,194 |
| 6 | 52,8 — 60 | 56,4 | 18 | 0,18 | 0,025 | 2,500 |
| 7 | 60 — 67,2 | 63,6 | 11 | 0,11 | 0,015 | 1,528 |
| 8 | 67,2 — 74,4 | 70,8 | 7 | 0,07 | 0,010 | 0,972 |
| 9 | 74,4 — 81,6 | 78 | 1 | 0,01 | 0,001 | 0,139 |
Строим графики:
Далее найдем моду вариационного ряда:
где
— начало модального интервала;
— длина частичного интервала (шаг);


— частота послемодального интервала.
Определим модальный интервал — интервал, имеющий наибольшую частоту. Из таблицы видно, что модальным является интервал (45,6 — 52,8).
Медиана
Для интервального ряда медиана находится по формуле:
где
— начало медианного интервала;
— длина частичного интервала (шаг);
— объем совокупности;
— накопленная частота интервала, предшествующая медианному;
— частота медианного интервала.
Определим медианный интервал — интервал, в котором впервые накопленная частота превышает половину объема выборки.Так как объем выборки n=100, то n/2=50. По таблице найдем интервал, где впервые накопленные частоты превысят это значение. Таким является интервал (45,6 — 52,8).
Получаем,
III. Расчет сводных характеристик выборки.
Для определения составим расчетную таблицу. Для начала определимся с ложным нулем С. В качестве ложного нуля можно принять любую варианту. Максимальная простота вычислений достигается, если выбрать в качестве ложного нуля варианту, которая расположена примерно в середине вариационного ряда (часто такая варианта имеет наибольшую частоту).
Варианте, которая принята в качестве ложного нуля, соответствует условная варианта, равная нулю. В нашем случае С=49,2.
Равноотстоящими называют варианты, которые образуют арифметическую прогрессию с разностью h.
Условными называют варианты, определяемые равенством:
Произведем расчет условных вариант согласно формуле:
| N п/п |
Середины интервалов, |
Частоты интервалов, |
Условные варианты, |
Произведения частот и условных вариант, |
Произведения частот и условных вариант, |
Произведения частот и условных вариант, |
Произведения частот и условных вариант, |
Произведения частот и условных вариант, |
Произведения частот и условных вариант, |
| 1 | 20,4 | 1 | -4 | -4 | 16 | -64 | 256 | 9 | 81 |
| 2 | 27,6 | 9 | -3 | -27 | 81 | -243 | 729 | 36 | 144 |
| 3 | 34,8 | 13 | -2 | -26 | 52 | -104 | 208 | 13 | 13 |
| 4 | 42 | 17 | -1 | -17 | 17 | -17 | 17 | 0 | 0 |
| 5 | 49,2 | 23 | 0 | 0 | 0 | 0 | 0 | 23 | 23 |
| 6 | 56,4 | 18 | 1 | 18 | 18 | 18 | 18 | 72 | 288 |
| 7 | 63,6 | 11 | 2 | 22 | 44 | 88 | 176 | 99 | 891 |
| 8 | 70,8 | 7 | 3 | 21 | 63 | 189 | 567 | 112 | 1792 |
| 9 | 78 | 1 | 4 | 4 | 16 | 64 | 256 | 25 | 625 |
Контроль:
Контроль:
Равенство выполнено, следовательно вычисления произведены верно.
Вычислим условные моменты 1-го, 2-го, 3-го и 4-го порядков:
Найдем выборочные среднюю, дисперсию и среднее квадратическое отклонение :
Также для оценки отклонения эмпирического распределения от нормального используют такие характеристики, как асимметрия и эксцесс.
Асимметрией теоретического распределения называют отношение центрального момента третьего порядка к кубу среднего квадратического отклонения:
Асимметрия положительна, если «длинная часть» кривой распределения расположена справа от математического ожидания; асимметрия отрицательна, если «длинная часть» кривой расположена слева от математического ожидания. Практически определяют знак асимметрии по расположению кривой распределения относительно моды (точки максимума дифференциальной функции): если «длинная часть» кривой расположена правее моды, то асимметрия положительна, если слева — отрицательна.
Эксцесс эмпирического распределения определяется равенством:
где — центральный эмпирический момент четвертого порядка.
Для нормального распределения эксцесс равен нулю. Поэтому если эксцесс некоторого распределения отличен от нуля, то кривая этого распределения отличается от нормальной кривой: если эксцесс положительный, то кривая имеет более высокую и «острую» вершину, чем нормальная кривая; если эксцесс отрицательный, то сравниваемая кривая имеет более низкую и «плоскую» вершину, чем нормальная кривая. При этом предполагается, что нормальное и теоретическое распределения имеют одинаковые математические ожидания и дисперсии.
Вычисляем центральные эмпирические моменты третьего и четвертого порядков:
Найдем асимметрию и эксцесс:
IV. Проверка гипотезы о нормальном распределении генеральной совокупности. Критерий согласия Пирсона.
Проверим генеральную совокупность значений размера прибыли банков по критерию Пирсона
Правило. Для того, чтобы при заданном уровне значимости проверить нулевую гипотезу : генеральная совокупность распределена нормально, надо сначала вычислить теоретические частоты, а затем наблюдаемое значение критерия:
и по таблице критических точек распределения , по заданному уровню значимости
и числу степеней свободы
найти критическую точку
, где s — количество интервалов.
Если — нет оснований отвергнуть нулевую гипотезу.
Если — нулевую гипотезу отвергают.
Найдем теоретические частоты , для этого составим следующую таблицу.
|
Середины интервалов, |
Частоты интервалов, |
Произведем расчет, |
Произведем расчет, |
Значения функции Гаусса, |
Произведем расчет, |
Теоретические частоты, |
| 20,4 | 1 | -28,152 | -2,23 | 0,0332 | 57 | 2 |
| 27,6 | 9 | -20,952 | -1,66 | 0,1006 | 57 | 6 |
| 34,8 | 13 | -13,752 | -1,09 | 0,2203 | 57 | 13 |
| 42 | 17 | -6,552 | -0,52 | 0,3485 | 57 | 20 |
| 49,2 | 23 | 0,648 | 0,05 | 0,3984 | 57 | 23 |
| 56,4 | 18 | 7,848 | 0,62 | 0,3292 | 57 | 19 |
| 63,6 | 11 | 15,048 | 1,19 | 0,1965 | 57 | 11 |
| 70,8 | 7 | 22,248 | 1,77 | 0,0833 | 57 | 5 |
| 78 | 1 | 29,448 | 2,34 | 0,0258 | 57 | 1 |
Вычислим , для чего составим расчетную таблицу.
| 1 | 1 | 2 | -1 | 1 | 0,5 | 1 | 0,5 |
| 2 | 9 | 6 | 3 | 9 | 1,5 | 81 | 13,5 |
| 3 | 13 | 13 | 0 | 0 | 0 | 169 | 13 |
| 4 | 17 | 20 | -3 | 9 | 0,45 | 289 | 14,45 |
| 5 | 23 | 23 | 0 | 0 | 0 | 529 | 23 |
| 6 | 18 | 19 | -1 | 1 | 0,05 | 324 | 17,05 |
| 7 | 11 | 11 | 0 | 0 | 0 | 121 | 11 |
| 8 | 7 | 5 | 2 | 4 | 0,8 | 49 | 9,8 |
| 9 | 1 | 1 | 0 | 0 | 0 | 1 | 1 |
| 100 | 100 |
Наблюдаемое значение критерия, |
103,30 |
Контроль:
Вычисления произведены правильно.
Найдем число степеней свободы, учитывая, что число групп выборки (число различных вариант) s=9;
По таблице критических точек распределения по уровню значимости
и числу степеней свободы k=6 находим
Так как — нет оснований отвергнуть нулевую гипотезу. Другими словами, расхождение эмпирических и теоретических частот незначительное. Следовательно, данные наблюдений согласуются с гипотезой о нормальном распределении генеральной совокупности.
На рисунке построены нормальная (теоретическая) кривая по теоретическим частотам (зеленый график) и полигон наблюдаемых частот (коричневый график). Сравнение графиков наглядно показывает, что построенная теоретическая кривая удовлетворительно отражает данные наблюдений.
V. Интервальные оценки.
Интервальной называют оценку, которая определяется двумя числами — концами интервала, покрывающего оцениваемый параметр.
Доверительным называют интервал, который с заданной надежностью покрывает заданный параметр.
Интервальной оценкой (с надежностью ) математического ожидания (а) нормально распределенного количественного признака Х по выборочной средней
при известном среднем квадратическом отклонении

где — точность оценки, n — объем выборки, t — значение аргумента функции Лапласа
(см. приложение 2), при котором
;
при неизвестном среднем квадратическом отклонении 
где S — исправленное выборочное среднее квадратическое отклонение, находят по таблице приложения по заданным n и
.
В нашем примере среднее квадратическое отклонение известно, . А также
,
,
. Поэтому для поиска доверительного интервала используем первую формулу:
Все величины, кроме t, известны. Найдем t из соотношения По таблице приложения находим t=1,96. Подставив t=1,96,
,
,
в формулу, окончательно получим искомый доверительный интервал:
Интервальной оценкой (с надежностью ) среднего квадратического отклонения

(при q<1), (*)
(при q>1),
где q — находят по таблице приложения по заданным n и .
По данным и n=100 по таблице приложения 4 найдем q=0,143. Так как q<1, то, подставив
в соотношение (*), получим доверительный интервал:
Содержание курса лекций «Статистика»
Статистическая сводка и группировка. В результате проведения статистического наблюдения получают данные о признаках каждой обследованной единицы статистической совокупности. Однако эти массивы данных, содержащие подробные сведения о каждой единице совокупности, собирают не для того, чтобы получить характеристики каждой из них, а с целью изучить совокупность в целом, выявить ее характерные группы и закономерности. Для этого необходимо обобщить и систематизировать сведения, полученные в ходе статистического наблюдения.
Обобщение и систематизация первичных статистических данных – это самостоятельный этап статистического исследования, основная задача которого получить полную и всестороннюю характеристику как совокупности в целом, так и отдельных ее частей и представить полученную информацию об изучаемой совокупности в наиболее удобной для пользователей форме. В статистической практике данный этап статистического исследования называют этапом сводки и группировки статистических данных.
Статистическая сводка
Сводка – это научная обработка первичных данных с целью получения обобщенных характеристик изучаемого социально-экономического явления по ряду существенных для него признаков с целью выявления типичных черт и закономерностей, присущих изучаемому явлению в целом.
По глубине и точности обработки материала различают простую сводку и сложную сводку.
Простая сводка – это операция по подсчету общих итогов по совокупности единиц наблюдения и оформление этого материала в статистических таблицах.
Сложная сводка – это комплекс последовательных операций, включающих группировку полученных при наблюдении материалов, составление системы показателей для характеристики типичных групп и подгрупп изучаемой совокупности явлений, подсчет числа единиц и итогов по каждой группе и подгруппе, и по всему объекту и представление результатов в виде статистических таблиц.
Этапы проведение сводки
- Выбор группировочного признака.
- Определение порядка формирования групп.
- Разработка системы статистических показателей для характеристики групп и объекта в целом
- Разработка макетов статистических таблиц для представления результатов сводки.
Статистическая группировка
Группировка – разбиение общей совокупности единиц объекта наблюдения по одному или нескольким существенным признакам на однородные группы, различающиеся между собой в количественном и качественном отношении и позволяющие выделить социально-экономические типы, изучить структуру совокупности и проанализировать связи между отдельными признаками.
Задачи, решаемые с помощью метода группировок:
- выделение социально-экономических типов явлений;
- изучение структуры явления и структурных сдвигов, происходящих в нем;
- выявление взаимосвязи и взаимозависимости между явлениями.
Виды группировок. В соответствии с познавательными задачами, решаемыми в ходе построения статистических группировок, различают следующие их виды: типологические, структурные, аналитические.
Типологическая группировка – это разбиение разнородной совокупности единиц наблюдения на отдельные качественно однородные группы и выявление на этой основе социально-экономических типов явлений. При построении группировки этого вида основное внимание должно быть уделено идентификации типов и выбору группировочного признака. Решение вопроса об основании группировки должно осуществляться на основе анализа сущности изучаемого социально-экономического явления.
Структурная группировка – предназначена для изучения состава однородной совокупности по какому-либо варьирующему признаку, а также структуры и структурных сдвигов, происходящих в нем.
Аналитическая группировка – выявляет взаимосвязи между изучаемыми явлениями и признаками, их характеризующими.
!!!В статистике при изучении связей социально-экономических явлений признаки подразделяют на факторные и результативные.
Факторные признаки, под их воздействием изменяются результативные признаки. Взаимосвязь проявляется в том, что с возрастанием или убыванием значения факторного признака систематически возрастает или убывает значение признака результативного и наоборот.!!!
Особенности построения аналитической группировки:
- единицы статистической совокупности группируются по факторному признаку;
- каждая выделенная группа характеризуется средними величинами результативного признака.
По способу построения группировки бывают простые и комбинационные.
Простая группировка – группы образованы только по одному признаку.
Комбинационная группировка – разбиение совокупности на группы производится по двум и более признакам, взятым в сочетании (комбинации).
Сначала группы формируются по одному признаку, затем группы делятся на подгруппы по другому признаку, а эти в свою очередь делятся по третьему и так далее. Таким образом, комбинационные группировки дают возможность изучить единицы совокупности одновременно по нескольким взаимосвязанным признакам.
При построении комбинационной группировки возникает вопрос о последовательности разбиения единиц объекта по признакам. Как правило, рекомендуется сначала производить группировку по атрибутивным признакам, значения которых имеют ярко выраженные качественные различия.
Этапы построения статистических группировок
- Определение группировочного признака.
- Определение размаха вариации.
- Определение числа групп.
- Расчет ширины интервала группировки.
- Определение признаков, которые в комбинации друг с другом будут характеризовать каждую выделенную группу.
При небольшом объеме совокупности (n<50) не следует образовывать большого количества групп, так как группы будут включать недостаточное число единиц объекта. Показатели, рассчитанные для таких групп, не будут представительными и не позволят получить адекватную характеристику исследуемого явления.
Часто группировка по количественному признаку имеет задачу отразить распределение единиц совокупности по этому признаку. В этом случае количество групп зависит, в первую очередь, от степени колеблемости группировочного признака: чем больше его колеблемость, тем больше можно образовать групп.
При определении числа групп необходимо принять во внимание размах вариации признака (R), который позволяет оценить вариацию признака между крайними значениями признака – максимальным (Хmax) и минимальным (Xmin) и определяется по формуле 5.1): 
Чем больше размах вариации признака, положенного в основание группировки, тем, как правило, может быть образовано большее число групп. При этом может возникнуть проблема получения пустых групп, т.е. групп, не содержащих ни одной единицы наблюдения.
Определение числа групп можно осуществить несколькими способами. Формально-математический способ предполагает использование формулы Стерджесса (формула 5.2): 
где n – число групп; N – число единиц совокупности.
Согласно этой формуле выбор числа групп зависит только от объема изучаемой совокупности.
Применение данной формулы дает хорошие результаты в том случае, если совокупность состоит из большого числа единиц наблюдения (n>50).
Другой способ определения числа групп основан на применении показателя среднего квадратического отклонения (σ). Если величина интервала равна 0,5σ, то совокупность разбивается на 12 групп, а когда величина интервала равна 2/3σ и σ, то совокупность делится, собственно, на 9 и 6 групп. Однако при определении групп данными методами существует большая вероятность получения «пустых» или малочисленных групп, характеристики изучаемого явления на основе которых будут недостаточно типичными для выделенной группы и изучаемой совокупности в целом.
Когда определено число групп, то следует определить интервалы группировки.
Интервал – это значения варьирующего признака, лежащие в определенных границах. Каждый интервал имеет верхнюю и нижнюю границы или одну из них. Нижней границей интервала называется наименьшее значение признака в интервале. Верхней границей интервала называется наибольшее значение признака в интервале. Величина интервала представляет собой разность между верхней и нижней границами интервала.
Интервалы группировки бывают: равные и неравные; открытые и закрытые.
Ширина равного интервала определяется по (формуле 5.3):

Если максимальные или минимальные значения сильно отличаются от смежных с ними значений вариантов в упорядоченном ряду значений группировочного признака, то для определения величины интервала следует использовать не максимальное или минимальное значения, а значения, несколько превышающие минимум, и несколько меньше, чем максимум.
Полученную по формуле (5.3) величину округляют и она будет являться шириной интервала.
Существуют следующие правила определения ширины интервала.
Если величина интервала, рассчитанная по формуле (5.3) представляет собой величину, которая имеет один знак до запятой (например: 0,67; 1,487; 3,82), то в этом случае полученные значения целесообразно округлить до десятых и их использовать в качестве ширины интервала. В приведенном выше примере это будут соответственно значения: 0,7; 1,5; 3,8.
Если рассчитанная величина интервала имеет две значащие цифры до запятой и несколько после запятой (например, 14,876), то это значение необходимо округлит до целого числа (15).
В случае, когда рассчитанная величина интервала представляет собой трехзначное, четырехзначное и так далее число, то эту величину следует округлить до ближайшего числа, кратного 100 или 50. Например, 652 следует округлить до 650 или до 700.
Если размах вариации признака в совокупности велик и значения признака варьируют неравномерно, то надо использовать группировку с неравными интервалами.
Неравные интервалы могут быть получены в процессе объединения пустых, не содержащих ни одной единицы совокупности, равных интервалов. Это происходит в том случае, если после построения равных интервалов по изучаемому признаку образуются группы, содержащие мало или не содержащие вообще ни одной единицы, т.е. группы, не отражающие определенных типов изучаемого явления по признаку. В этом случае возникает необходимость в увеличении интервалов группировки.
Также неравные интервалы могут быть прогрессивно-возрастающие или прогрессивно-убывающие в арифметической или геометрической прогрессии. Величина интервалов, изменяющихся в арифметической и геометрической прогрессии, определяется следующим образом:hi+1=hi+а,
а в геометрической прогрессии: hi +1= hi ×q, где:
а – константа: для прогрессивно-возрастающих интервалов имеет знак «+», а при прогрессивно-убывающих – знак «-».
q — константа: для прогрессивно-возрастающих – больше «1»; для прогрессивно-убывающих ‑ меньше «1».
Применение неравных интервалов обусловлено тем, что в первых группах небольшая разница в показателях имеет большое значение, а в последних группах эта разница не существенна.
Например, при построении группировки строительных компаний города по показателю численности работающих, который варьирует от 500 человек до 3500 человек, нецелесообразно рассматривать равные интервалы, т. к. учитываются как малые, так и крупнейшие строительные фирмы города. Поэтому следует образовывать неравные интервалы: 500–1000, 1000–2000, 2000–3500, т.е. величина каждого последующего интервала больше предыдущего на 500 человек и увеличивается в арифметической прогрессии. Выбор исследователя в построении равных или неравных интервалов зависит от степени заполнения каждой выделенной группы, т.е. от числа единиц в них. Если величина интервала существенна и содержит большое число единиц совокупности, то эти интервалы необходимо дробить, а в противном случае – объединять.
Интервалы статистической группировки
Интервалы группировок могут быть закрытыми и открытыми.
Закрытые интервалы – это интервалы, у которых есть и верхняя и нижняя границы.
Открытые интервалы – это интервалы, у которых указана только одна граница: как правило, верхняя – у первого интервала и нижняя – у последнего.
Например, группы страховых компаний по числу работающих в них сотрудников (чел.): до 50, 50–100, 100–150, 150 и более. Применение открытых интервалов целесообразно в тех случаях, когда в совокупности встречается незначительное число единиц наблюдения с очень малыми или очень большими значениями вариантов, которые резко, в несколько раз, отличаются от всех остальных значений изучаемого признака.
Если основанием группировки служит непрерывный признак (например, группы строительных фирм по объему строительно-монтажных работ, выполненных собственными силами (тыс. руб.): 1200–1400, 1400–1600, 1600–1800, 1800–2000), то одно и то же значение признака выступает и верхней и нижней границами двух смежных интервалов. В данном случае объем работ 1400 тыс. руб. составляет верхнюю границу первого интервала и нижнюю границу второго, 1600 тыс. руб. ‑ соответственно второго и третьего и т.д., т.е. верхняя граница i-го интервала равна нижней границе (i+1)-го интервала.
При таком обозначении границ может возникнуть вопрос, в какую группу включать единицы наблюдения, значения признака у которых совпадают с границами интервалов.
Например, во вторую или третью группу должна войти строительная фирма с объемом строительно-монтажных работ 1600 тыс. рублей? Если верхняя граница формируется по принципу «исключительно», то фирма должна быть отнесена к третьей группе, в противном случае – ко второй. Для того, чтобы правильно отнести к той или иной группе единицу совокупности, значение признака которой совпадает с границами интервалов, можно ориентироваться на открытые интервалы (по нашему примеру группы строительных фирм по объему строительно-монтажных работ преобразуются в следующие: до 1400, 1400–1600, 1600–1800, 1800 и более). В данном случае, вопрос отнесения отдельных единиц совокупности, значения которых являются граничными, к той или иной группе решается на основе анализа последнего открытого интервала. Возможны два случая обозначения последнего открытого интервала: 1) 1800 тыс. руб. и более; 2) более 1800 тыс. руб. В первом случае, строительные фирмы с объемом строительно-монтажных работ 1600 тыс. руб. попадут в третью группу; во втором случае – во вторую группу.
Если в основании группировки лежит дискретный признак, то нижняя граница 1-го интервала равна верхней границе i-1-го интервала, увеличенной на 1.
Например, группы строительных фирм по числу занятого персонала (чел.) будут иметь вид: 100–150, 151–200, 201–300.
Строя такую группировку, следует дифференцированно устанавливать границы интервалов для разных отраслей народного хозяйства. Это достигается путем использования группировок со специализированными интервалами.
Специализированные интервалы – применяются дли выделения из совокупности одних и тех же типов по одному и тому же признаку для явлений, находящихся в различных условиях.
При изучении социально-экономических явлений на макроуровне часто применяют группировки, интервалы которых не будут ни прогрессивно-возрастающими, ни прогрессивно-убывающими. Такие интервалы называются произвольными и, как правило, используются при группировке предприятий, например, по уровню рентабельности.
Пример. Далее на примере данных приведенных в табл. 5.1. произведем аналитическую группировку совокупности, включающей 30 банков.
Таблица 5.1 ‑ Совокупность 30 банков Российской Федерации
(на 01.01.19 г., цифры условные)
| Номер банка | Капитал, млн. руб. | Активы, млн. руб. |
Работающие активы, млн. руб |
| 1 | 2 | 3 | 4 |
| 1 | 207,7 | 2,48 | 1,14 |
| 2 | 200,3 | 2,40 | 1,10 |
| 3 | 190,2 | 2,28 | 1,05 |
| 4 | 323,2 | 3,88 | 1,88 |
| 5 | 247,1 | 2,96 | 1,36 |
| 6 | 177,7 | 2,12 | 0,97 |
| 7 | 242,5 | 2,90 | 1,33 |
| 8 | 182,9 | 2,18 | 0,99 |
| 9 | 315,6 | 3,78 | 1,73 |
| 10 | 183,2 | 2,20 | 1,01 |
| 11 | 320,2 | 3,84 | 1,76 |
| 12 | 207,3 | 2,48 | 1,14 |
| 13 | 181,0 | 2,17 | 0,99 |
| 14 | 172,4 | 2,06 | 0,94 |
| 15 | 234,3 | 2,81 | 1,29 |
| 16 | 189,5 | 2,27 | 1,04 |
| 17 | 187,8 | 2,24 | 1,03 |
| 18 | 166,9 | 1,99 | 0,91 |
| 19 | 157,7 | 1,88 | 0,86 |
| 20 | 168,3 | 2,02 | 0,93 |
| 21 | 224,4 | 2,69 | 1,23 |
| 22 | 166,5 | 1,99 | 0,91 |
| 23 | 198,5 | 2,38 | 1,09 |
| 24 | 240,4 | 2,88 | 1,32 |
| 25 | 229,3 | 2,75 | 1,26 |
| 26 | 175,2 | 2,10 | 0,96 |
| 27 | 156,0 | 1,87 | 0,86 |
| 28 | 160,1 | 1,92 | 0,88 |
| 29 | 178,7 | 2,14 | 0,98 |
| 30 | 171,6 | 2,05 | 0,94 |
По данным табл.5.1 группировочным (факторным) признаком является капитал, результативным – прибыль. Группировку производим по факторному признаку. Зададим количество групп (условно) – 4, а величину интервала определим по формуле (5.3).
Обозначим границы групп:
1-я группа – 156,0-197,8;
2-я группа – 197,8-239,6;
3-я группа – 239,6-281,4;
4-я группа – 281,4-323,2.
После того, как определен группировочный признак – капитал, задано число групп – 4 и образованы сами группы, необходимо отобрать показатели, которые характеризуют группы, и определить их величины по каждой группе.
Далее показатели, характеризующие банки, разносятся по четырем указанным группам и подсчитываются групповые итоги. Результаты группировки заносятся в таблицу и определяются общие итоги по совокупности единиц наблюдения по каждому показателю.
Таблица 5.2 ‑ Группировка коммерческих банков по величине капитала
| Группы банков
по величине капитала, млн. руб |
Число
банков |
Капитал,
млн. руб |
Активы,
млн. руб |
Работающие
активы, млн. руб |
| 156,0-197,8
197,8-239,6 239,6-281,4 281,4-323,2 |
17
7 3 3 |
2966,5
1501,8 730,0 958,8 |
35,48
17,99 8,74 11,5 |
16,25
8,25 4,01 5,37 |
| Итого | 30 | 6157,1 | 73,71 | 33,88 |
Структурная группировка коммерческих банков на основе данных таблицы 5.2 будет иметь вид:
Таблица 5.3 ‑ Группировка коммерческих банков по величине капитала (в % к итогу)
| Группы банков по величине капитала, млн. руб. | Число банков в % к итогу | Капитал | Активы | Работающие активы |
| 156,0-197,8 | 56,7 | 48,2 | 48,1 | 48,0 |
| 197,8-239,6 | 23,3 | 24,4 | 24,4 | 24,3 |
| 239,6-281,4 | 10,0 | 11,9 | 11,9 | 11,8 |
| 281,4-323,2 | 10,0 | 15,5 | 15,6 | 15,9 |
| Итого | 100,0 | 100,0 | 100,0 | 100,0 |
Из таблицы 5.3 видно, что в основном преобладают малые банки ‑ 56,7%, на долю которых приходится 48,2% всего капитала. Более конкретный анализ взаимосвязи показателей можно сделать на основе аналитической группировки.
Таблица 5.4 ‑ Группировка коммерческих банков по величине капитала
|
Группы банков по величине капитала, млн. руб. |
Число банков | Капитал, млн. руб. | Активы, млн. руб. | Работающие активы, млн. руб. | |||
| всего | в среднем на один банк | всего | в среднем на один банк | всего | в среднем на один банк | ||
| 156,0-197,8 | 17 | 2966,5 | 174,5 | 35,48 | 2,09 | 16,25 | 0,96 |
| 197,8-239,6 | 7 | 1501,8 | 214,5 | 17,99 | 2,57 | 8,25 | 1,18 |
| 239,6-281,4 | 3 | 730,0 | 243,3 | 8,74 | 2,91 | 4,01 | 1,34 |
| 281,4-323,2 | 3 | 958,8 | 319,6 | 11,5 | 3,83 | 5,37 | 1,79 |
| Итого | 30 | 6157,1 | 205,2 | 73,71 | 2,46 | 33,88 | 1,13 |
Величина капитала, все активы банка и работающие активы прямо зависят между собой, и чем крупнее банк, тем эффективнее управление работающими активами.
Мы рассмотрели примеры группировок по одному признаку. Однако в ряде случаев для решения поставленных задач такая группировка является недостаточной. В этих случаях переходят к группировке исследуемой совокупности по двум и более существенным признакам во взаимосвязи (комбинационной группировке).
От группировок следует отличать классификацию. Классификацией называется систематизированное распределение явлений и объектов на определенные группы, классы, разряды на основании их сходства и различия.
Ряды распределения представляют собой простейшую группировку, в которой каждая выделенная группа характеризуется только частотой.
В зависимости от признака, положенного в основу образования ряда распределения, различают атрибутивные и вариационные ряды распределения.
Атрибутивными называют ряды распределения, построенные по качественным признакам, то есть признакам, характеризующим состояние изучаемого явления и не имеющим числового выражения.
Атрибутивные ряды распределения характеризуют состав совокупности по тем или иным существенным признакам. Взятые за несколько периодов, эти данные позволяют исследовать изменение структуры.
Вариационными рядами называют ряды распределения, построенные по количественному признаку, т.е. признаку, имеющему числовое выражение у отдельных единиц совокупности. Вариационный ряд состоит из двух элементов: вариантов и частот.
Вариантами называются отдельные значения признака, которые он принимает в вариационном ряду, то есть конкретное значение варьирующего признака.
Частотами называются численности отдельных вариант, или каждой группы вариационного ряда. Частоты показывают, как часто встречаются те или иные значения признака в изучаемой совокупности. Сумма всех частот определяет численность всей совокупности, ее объем.
Частостями называются частоты, выраженные в долях единицы или в процентах к итогу. Соответственно сумма частостей равна 1 или 100%.
В зависимости от характера вариации признака различают дискретные и интервальные вариационные ряды.
Дискретный вариационный ряд ‑ это ряд распределения в котором группы составлены по признаку, изменяющемуся прерывно, т.е. через определенное число единиц и характеризуют распределение единиц совокупности по дискретному признаку, принимающему только целые значения.
Например, группы студентов по баллу в сессию по предмету: 5,4,3,2.
Интервальный вариационный ряд распределения – это ряд распределения, в котором группировочный признак, составляющий основание группировки, может принимать в интервале любые значения, отличающиеся друг от друга на сколь угодную малую величину
Построение интервальных вариационных рядов целесообразно прежде всего при непрерывной вариации признака, а также если дискретная вариация признака проявляется в широких пределах, то есть число вариантов дискретного признака достаточно велико.
Правила построения рядов распределения аналогичны правилам построения группировки.
Анализ рядов распределения наглядно можно проводить на основе их графического изображения. Для этой цели строят полигон, гистограмму, огиву и кумуляту распределения.
Полигон используется при изображении дискретных вариационных рядов. Для его построения в прямоугольной системе координат по оси абсцисс в одинаковом масштабе откладываются ранжированные значения варьирующего признака, а по оси ординат наносится шкала для выражения величины частот. Полученные на пересечении оси абсцисс (х) и оси ординат (у) точки соединяются прямыми линиями, в результате чего получают ломаную линию, называемую полигоном частот. Иногда для замыкания полигона предлагается крайние точки (слева и справа на ломаной линии) соединить с точками на оси абсцисс, в результате чего получается многоугольник.
Гистограмма применяется для изображения интервального вариационного ряда. При построении гистограммы на оси абсцисс откладываются величины интервалов, а частоты изображаются прямоугольниками, построенным на соответствующих интервалах. Высота столбиков должна быть пропорциональна частотам. В результате получается график, на котором ряд распределения изображен в виде смежных друг с другом столбиков.
Гистограмма может быть преобразована в полигон распределения, если середины верхних сторон прямоугольников соединить прямыми линиями.
При построении гистограммы распределения вариационного ряда с неравными интервалами по оси ординат наносят не частоты, а плотность распределения признака в соответствующих интервалах. Это необходимо сделать для устранения влияния величины интервала на распределение интервала и получения возможности сравнивать частоты.
Плотность распределения – это частота, рассчитанная на единицу ширины интервалу то есть, сколько единиц в каждой группе приходится на единицу величины интервала.
Для графического изображения вариационных рядов может использоваться кумулятивная кривая. При помощи кумуляты изображается ряд накопленных частот. Накопленные частоты определяются путем последовательного суммирования частот по группам. Накопленные частоты показывают, сколько единиц совокупности имеют значения признака не больше, чем рассматриваемое значение.
При построении кумуляты интервального вариационного ряда по оси абсцисс (х) откладываются варианты ряда, а по оси ординат (у) накопленные частоты, которые наносят на поле графика в виде перпендикуляров к оси абсцисс в верхних границах интервалов. Затем эти перпендикуляры соединяют и получают ломаную линию, то есть кумуляту.
Если при графическом изображении вариационного ряда в виде кумуляты оси х и у поменять местами, то получим огиву.
Контрольные задания
- В чем суть и каково значение сводки как второго этапа статистического исследования?
- Какова роль группировок в статистике?
- Что такое ряды распределения?
- Дайте характеристику вариационному ряду.
- Пользуясь формулой Стерджесса, определите интервал группировки сотрудников фирмы по уровню доходов, если общая численность сотрудников составляет 50 человек, а минимальный и максимальный доход соответственно равен 50000 и 300000 рублей.
- По данным статистических сборников, постройте группировку численности безработных двух регионов по полу и возрасту (% к итогу) с целью приведения их к сопоставимому виду. Сделайте сравнительный анализ результатов.
- Имеются следующие данные об успеваемости в летнюю сессию 2019 г.: 5, 4, 4, 4. 3. 2, 5, 3, 4, 4, 4, 3, 2, 5, 2, 5, 5, 2, 3, 3. Постройте по этим данным: а) ряд распределения студентов по баллам оценок, полученных в сессию; б) ряд распределения студентов по уровню успеваемости, выделив в нем 2 группы студентов: не успевающие (2 балла), успевающие (3 балла и выше); в) каким видом ряда распределения (вариационным или атрибутивным) является каждый из этих двух рядов?
- Какие из указанных ниже группировок являются типологическими: а) группировка населения по полу; б) группировка населения по отраслям, занятого в народном хозяйстве; в) группировка вложений на строительство объектов производственного и непроизводственного назначения; г) группировка предприятий общественного питания по формам собственности.
Содержание курса лекций «Статистика»
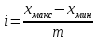
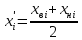
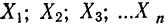
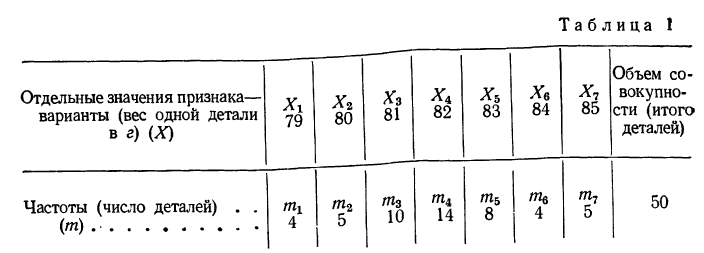
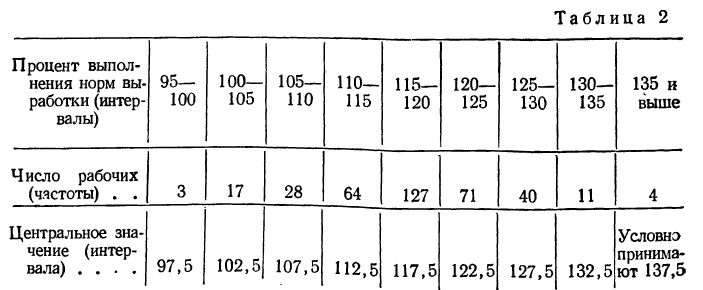
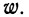
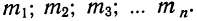
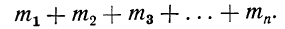
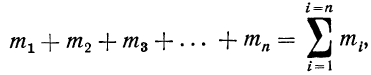
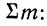
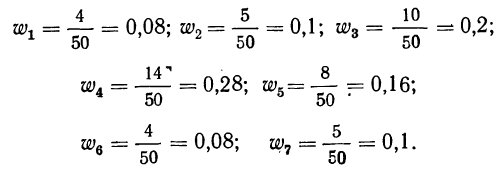
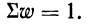
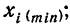
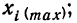
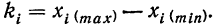
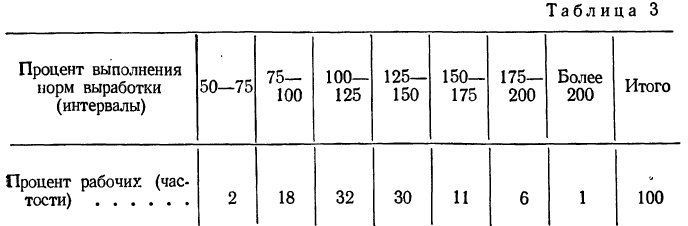
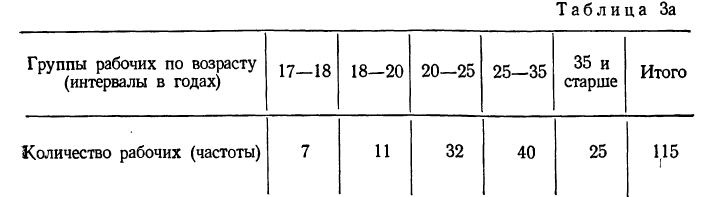
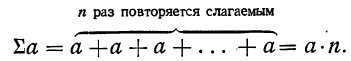
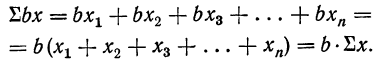
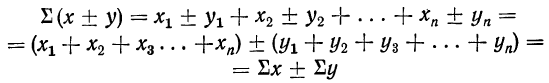
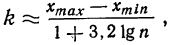
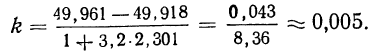
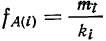
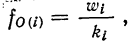
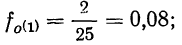
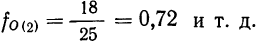
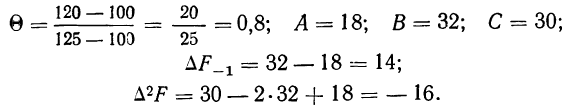
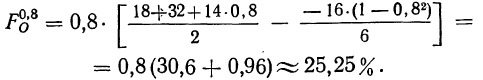
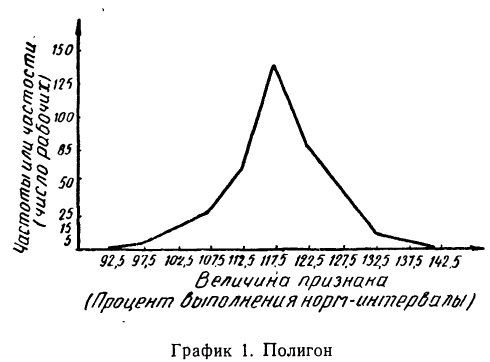
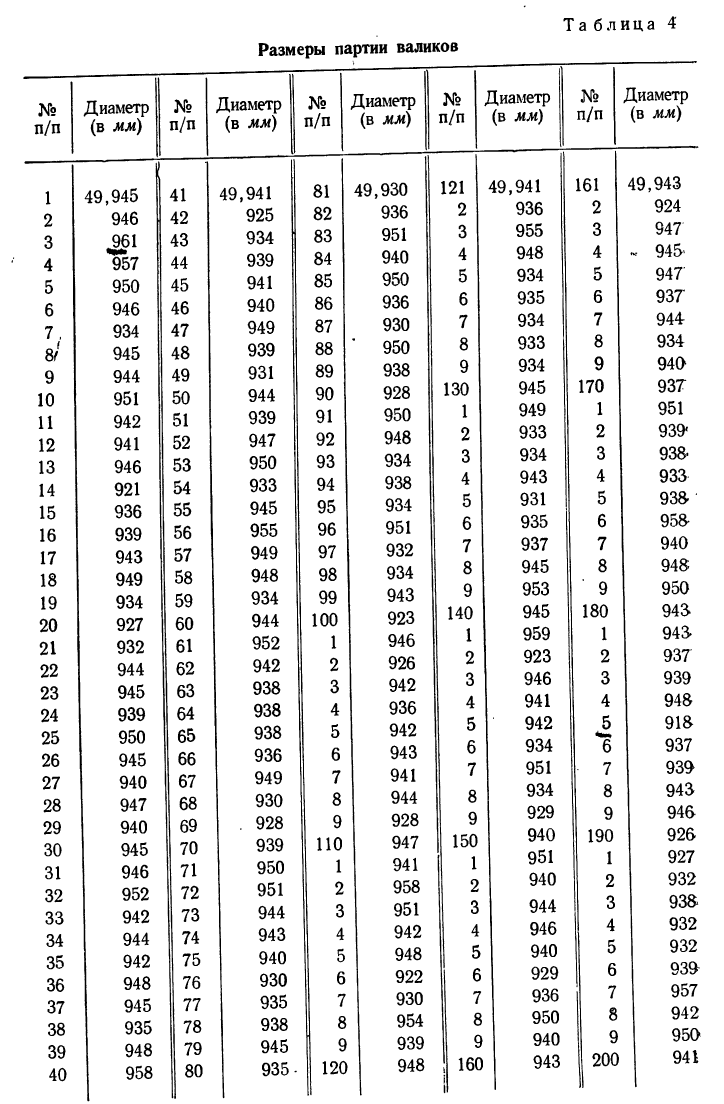
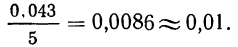
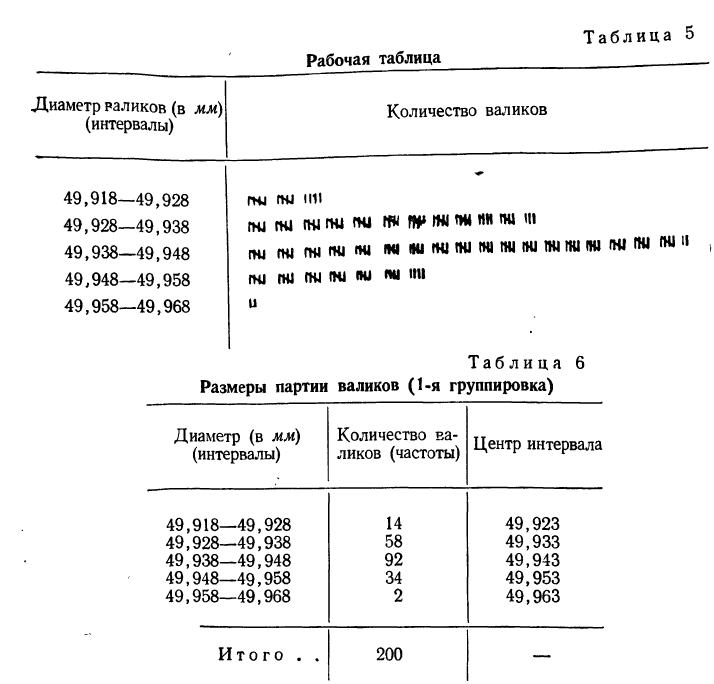
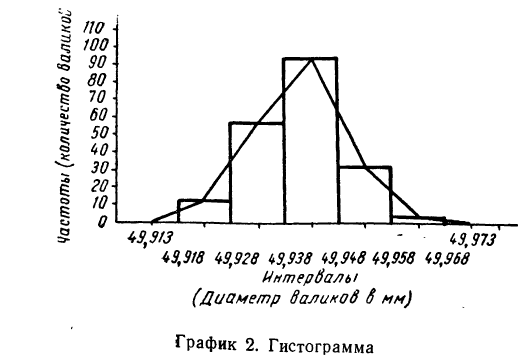
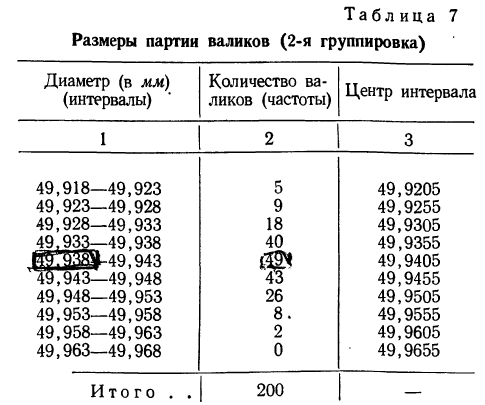
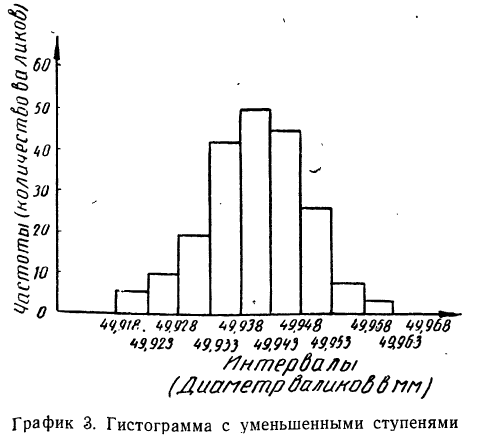
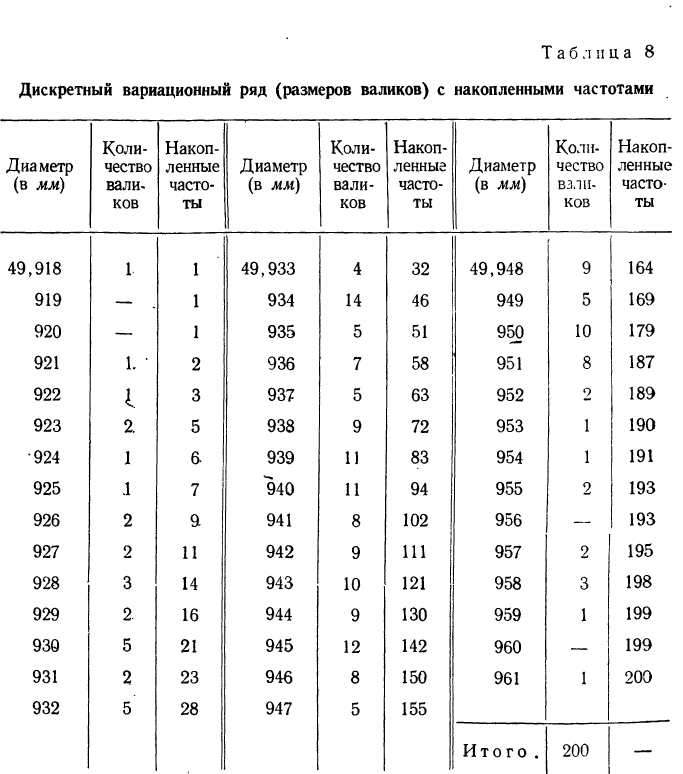
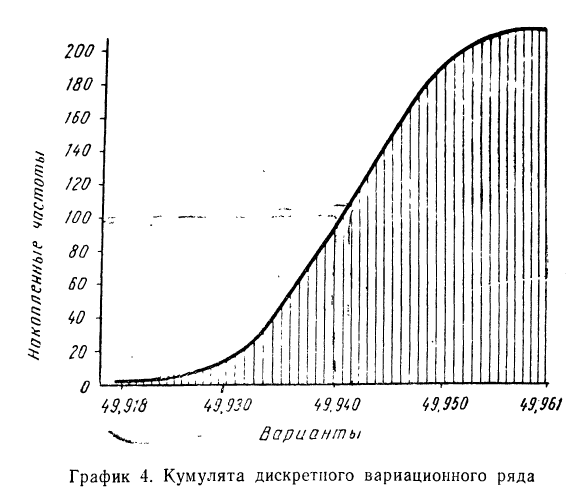
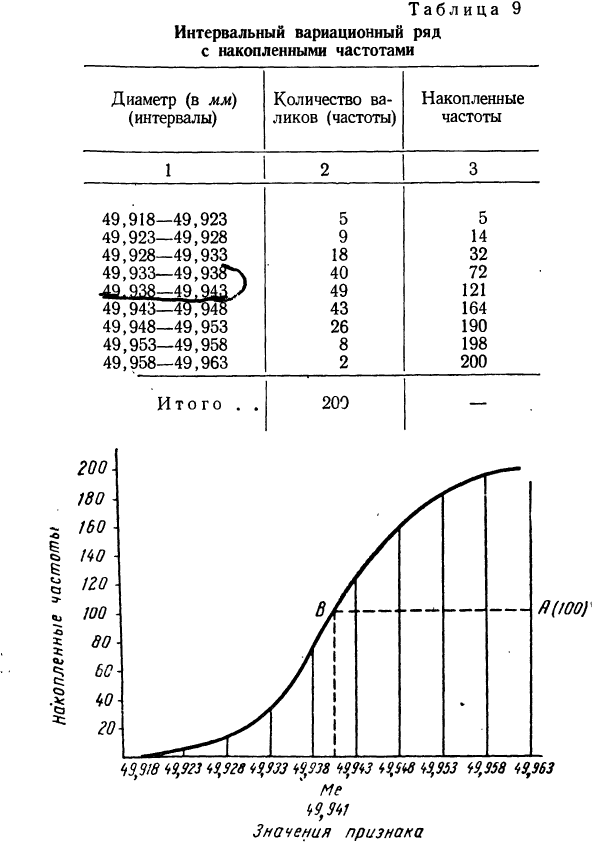
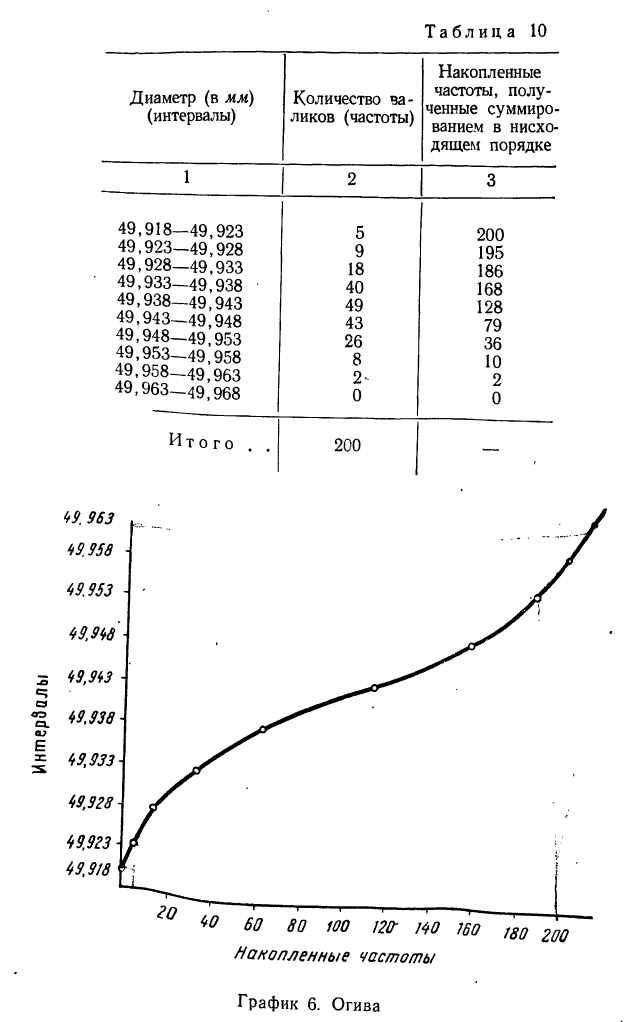
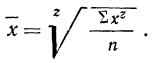
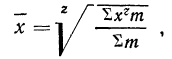
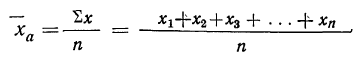
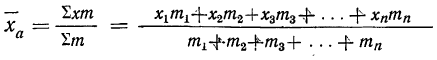
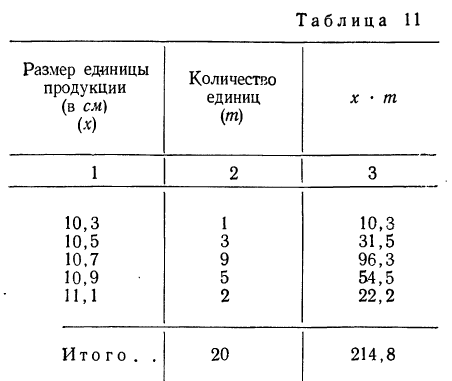
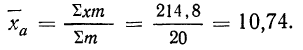
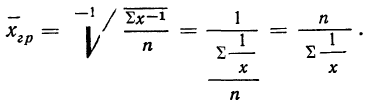
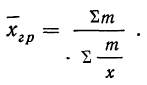
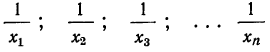
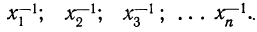

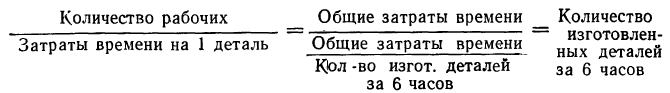
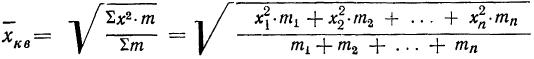

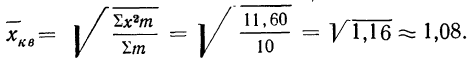
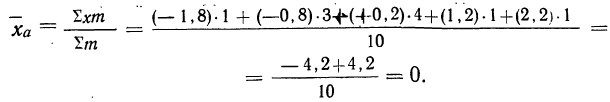
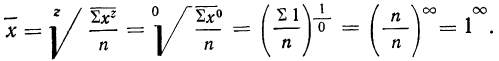
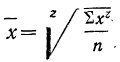
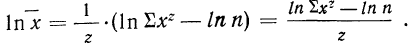
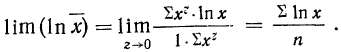
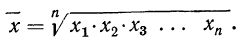
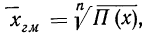
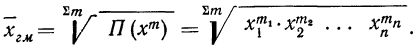
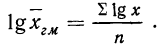
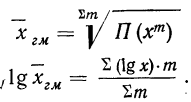

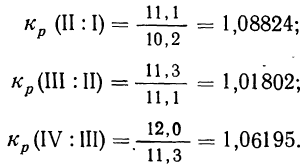
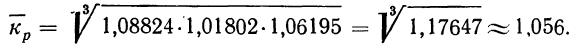
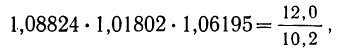
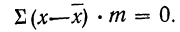
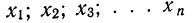
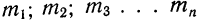
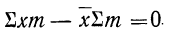
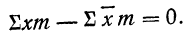
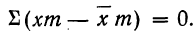
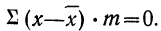
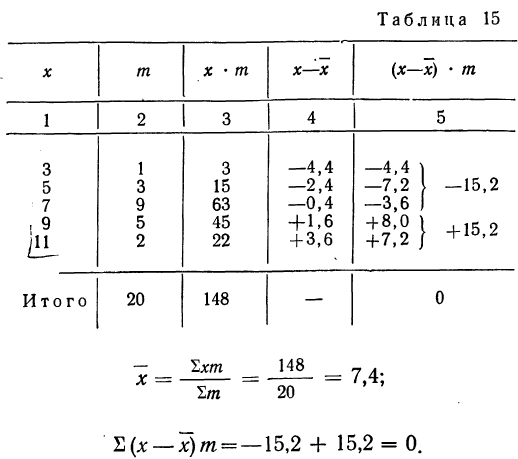

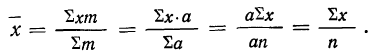
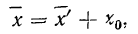
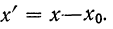
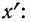
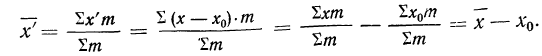
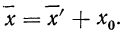
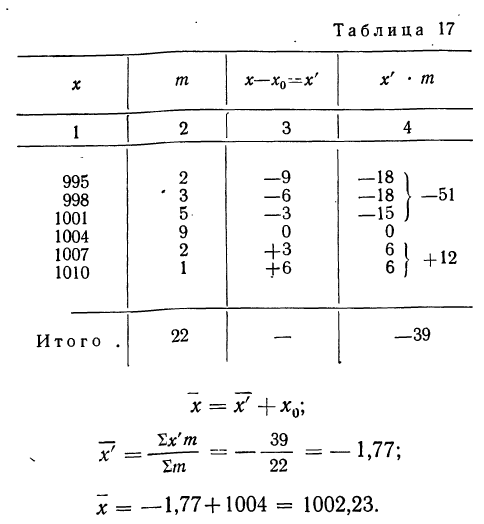
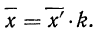
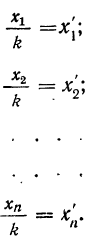
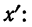
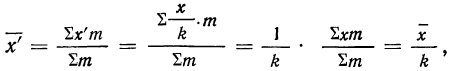
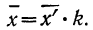
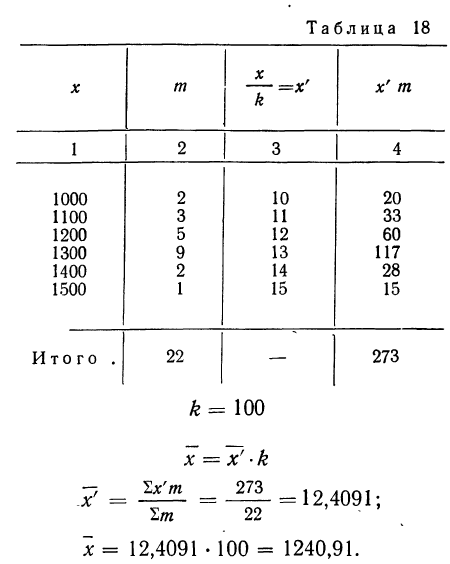
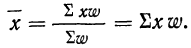
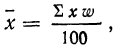
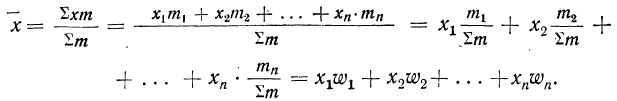
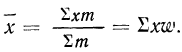
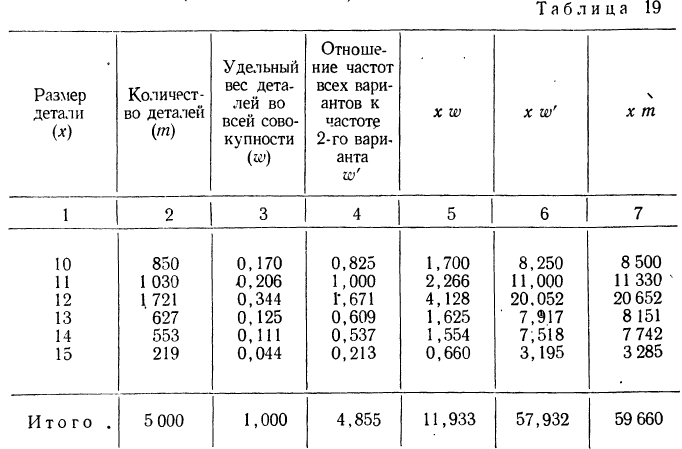
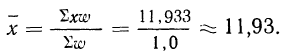
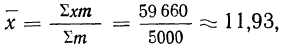
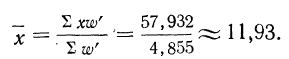
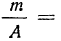
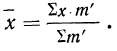
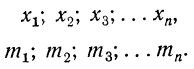
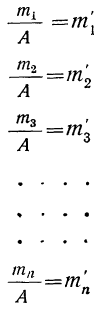

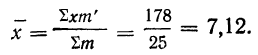
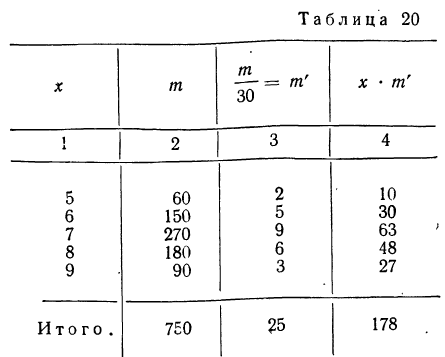
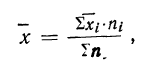
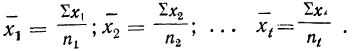
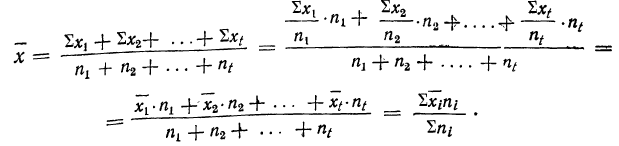
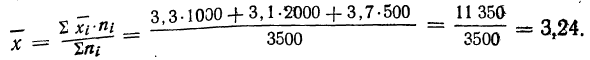
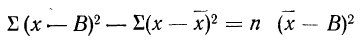
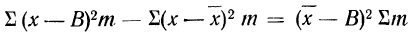
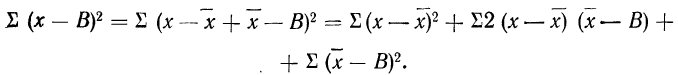
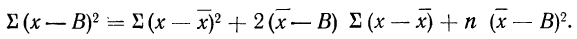
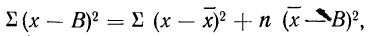
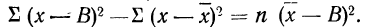

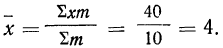
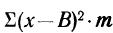
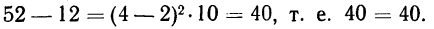
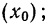
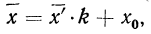
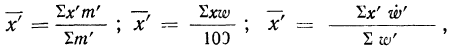
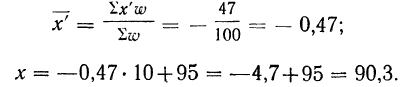

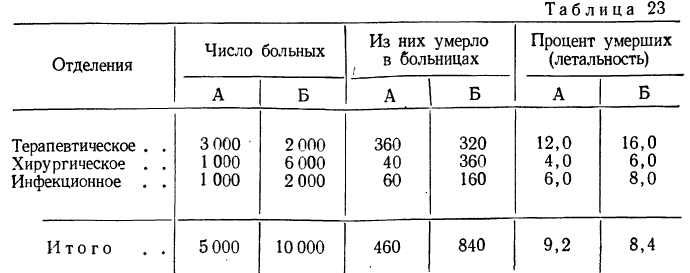

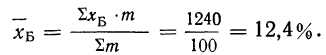
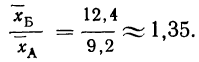
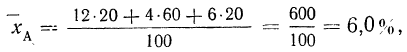
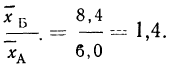
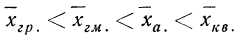
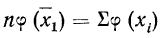
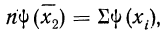
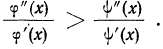
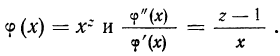
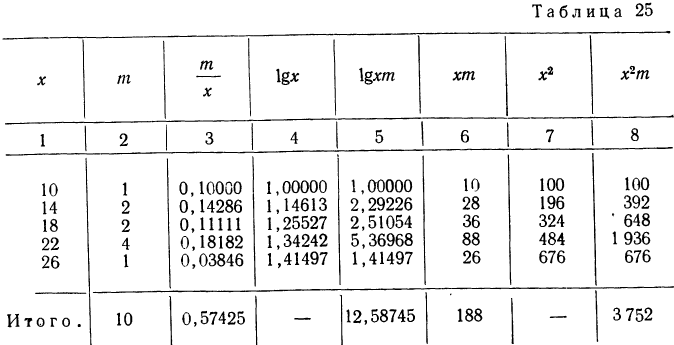

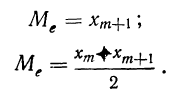
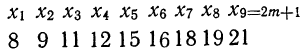
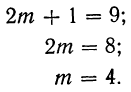
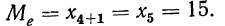
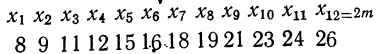
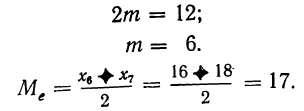
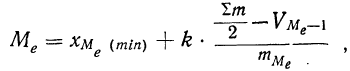
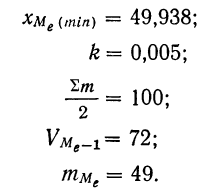
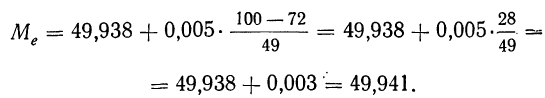
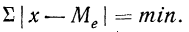
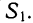
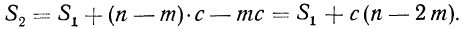
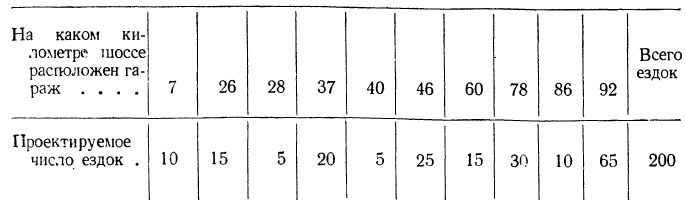
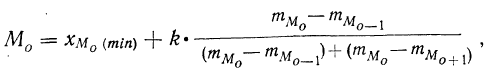
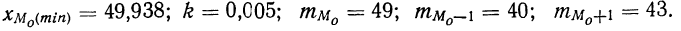
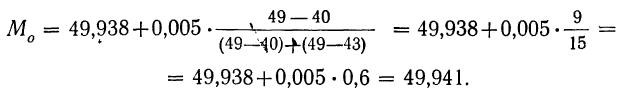
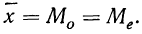
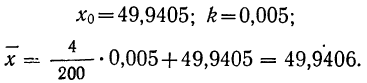

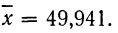
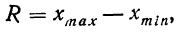
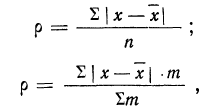
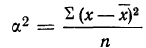
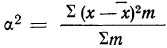
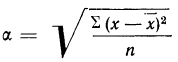
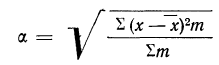
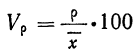
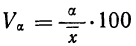
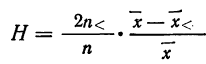
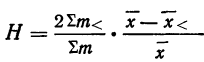
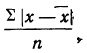
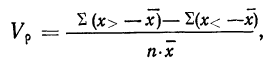
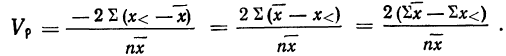
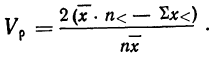
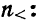
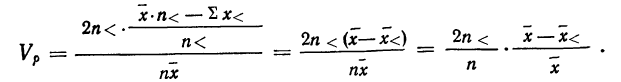
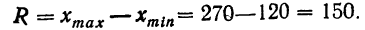
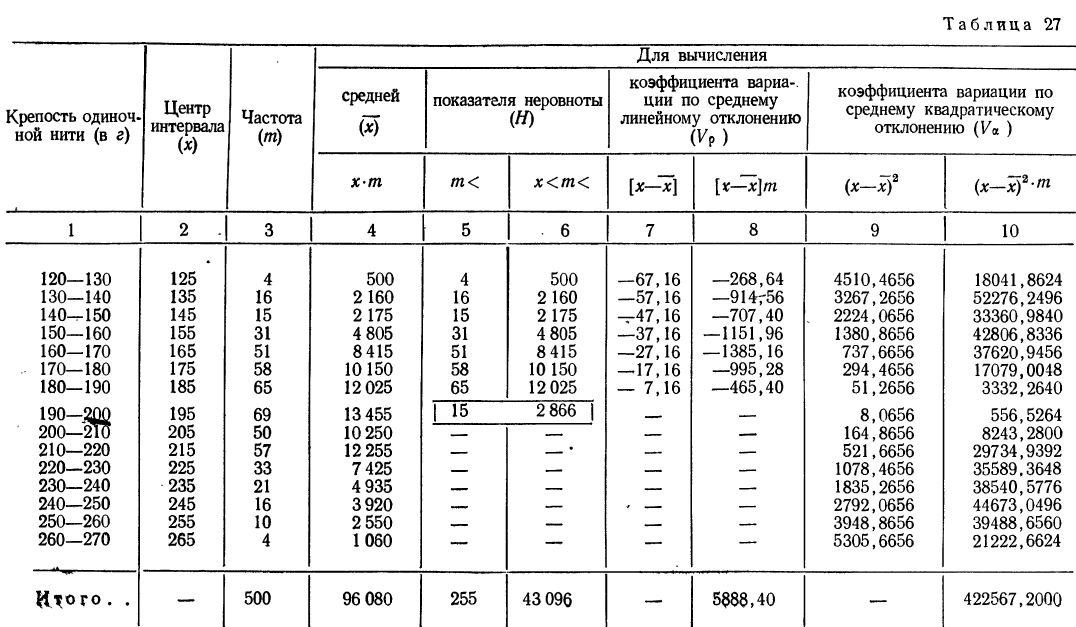
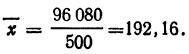
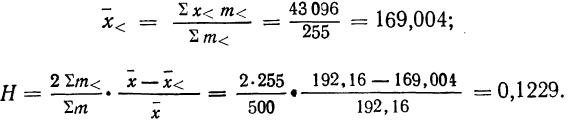
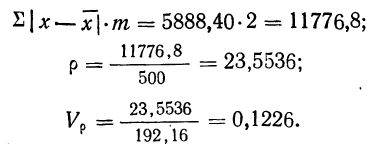
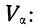
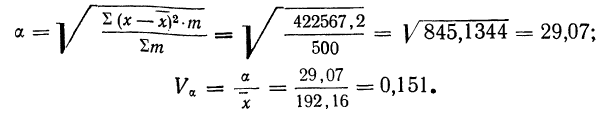
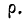
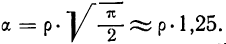
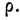
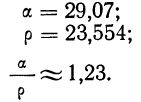
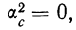
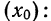
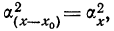
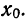
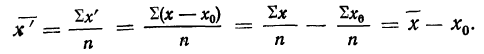
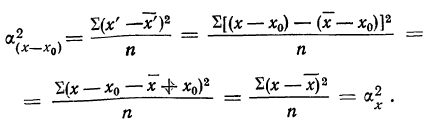
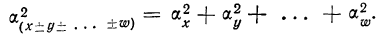
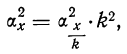
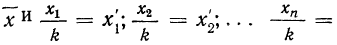
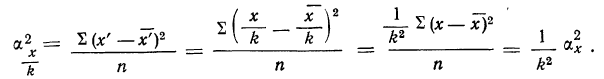
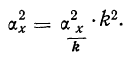
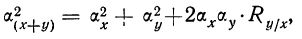
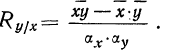
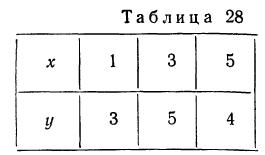
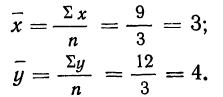
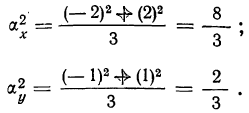
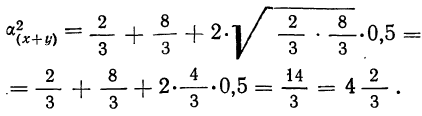
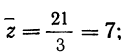
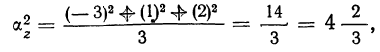
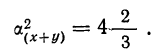
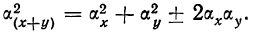
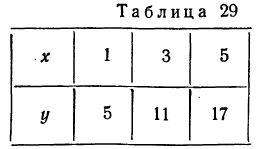
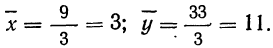
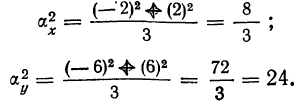
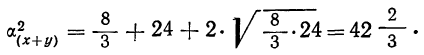
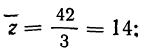
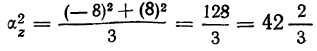
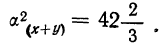
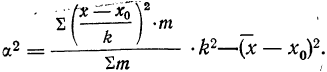
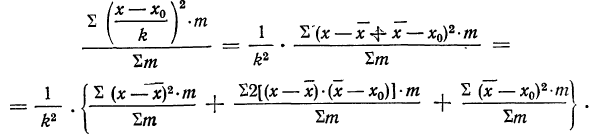
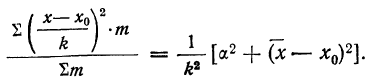
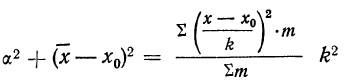
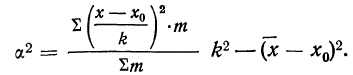
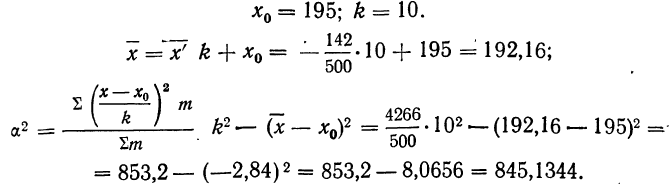
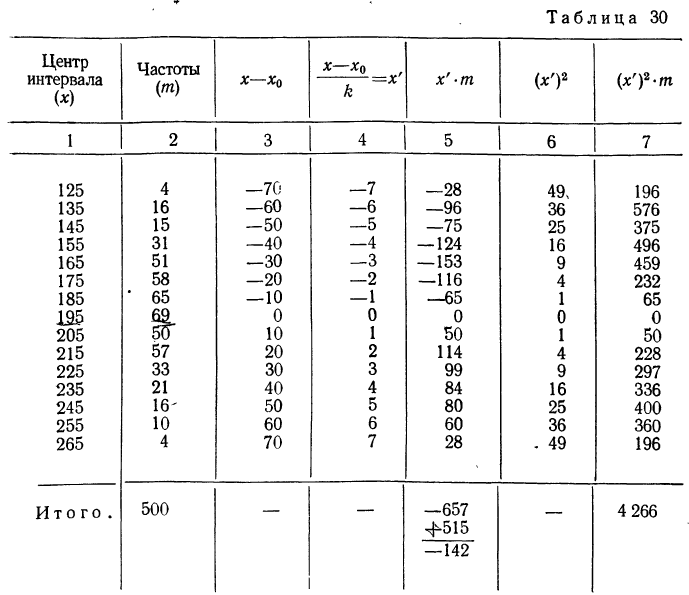
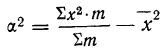
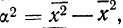
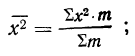
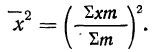
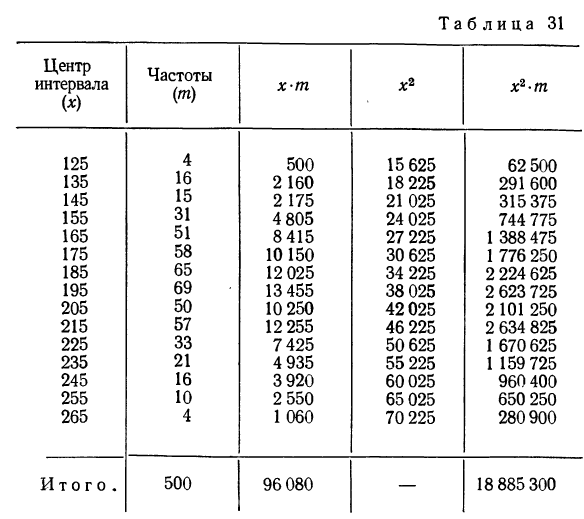
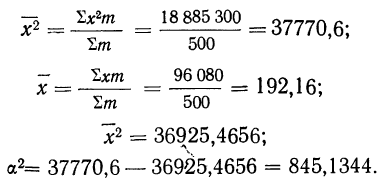
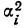
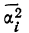
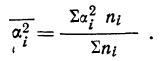
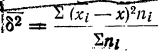
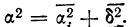
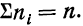
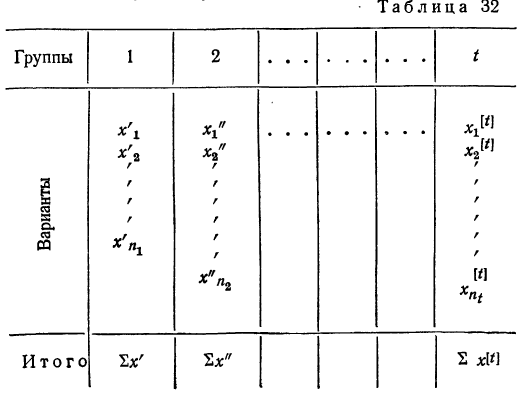
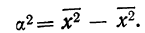
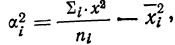
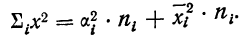
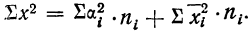
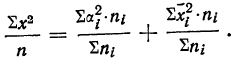
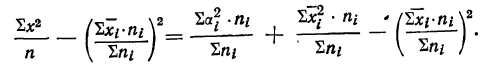
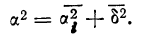
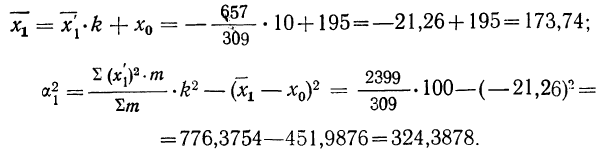

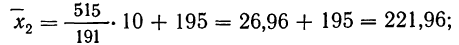
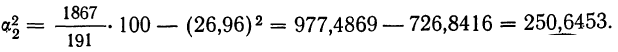
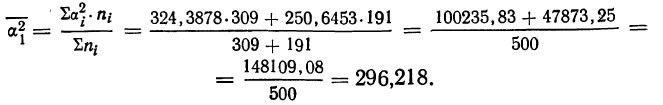
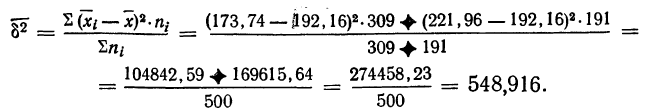
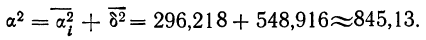
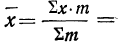
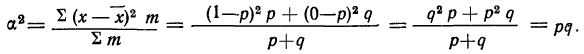
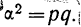
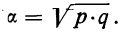
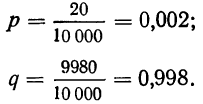
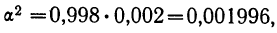
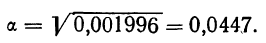
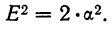
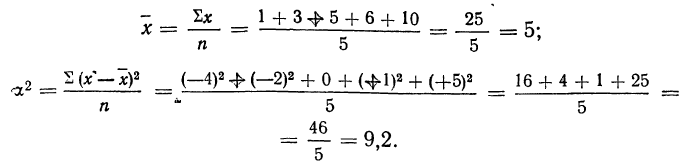
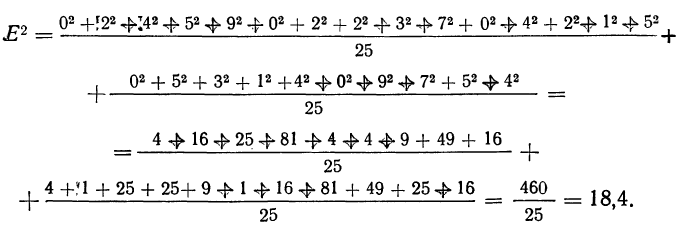
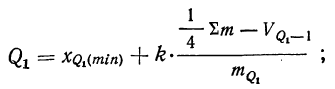
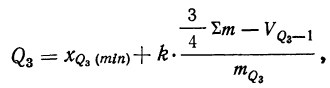
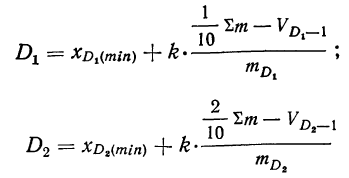
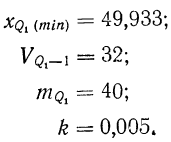
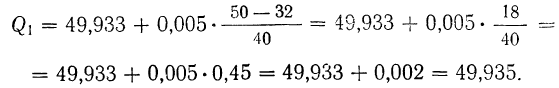
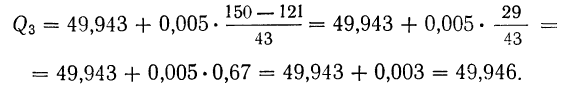
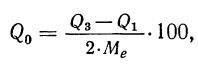
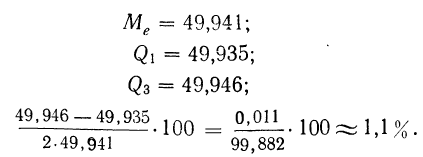
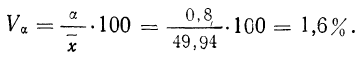
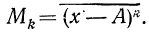
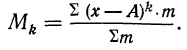
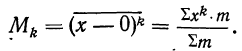
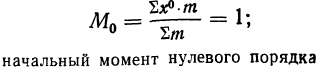
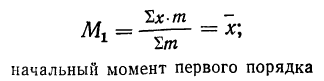
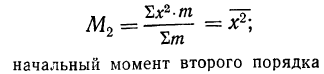
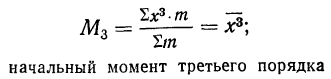
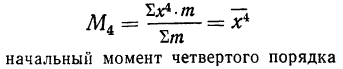

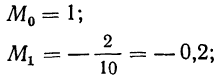
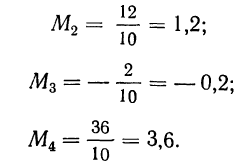
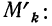
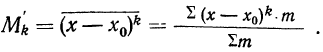
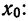
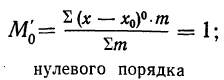
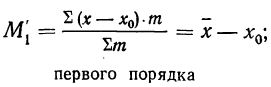
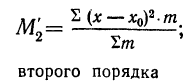
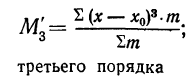
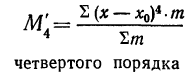
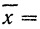
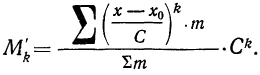
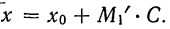

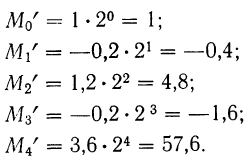
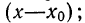
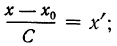
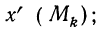
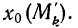
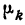
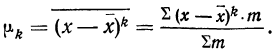
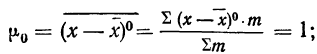
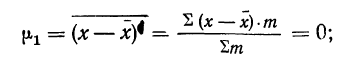
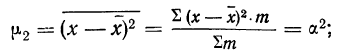
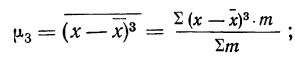
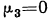
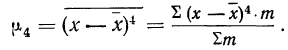

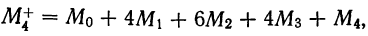
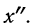
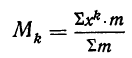
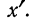
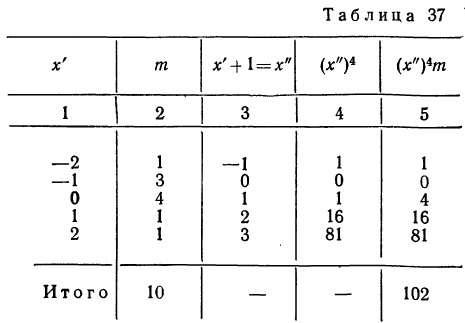
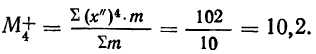
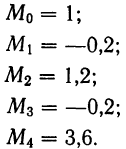
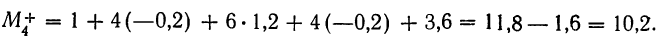
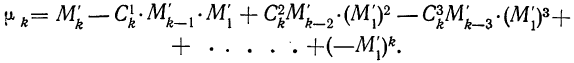
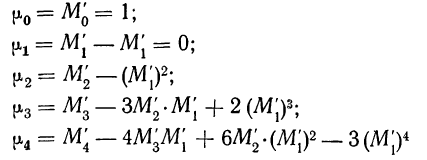
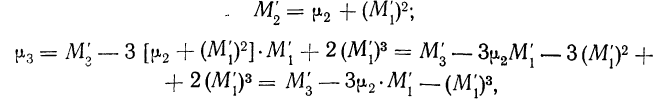
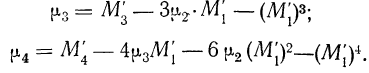
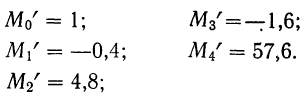
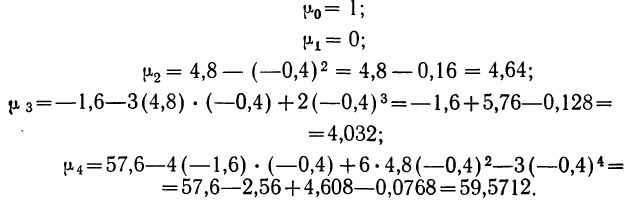
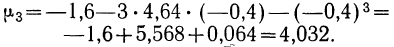
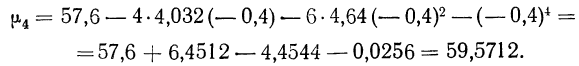
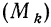 и их проверке:
и их проверке: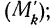
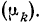
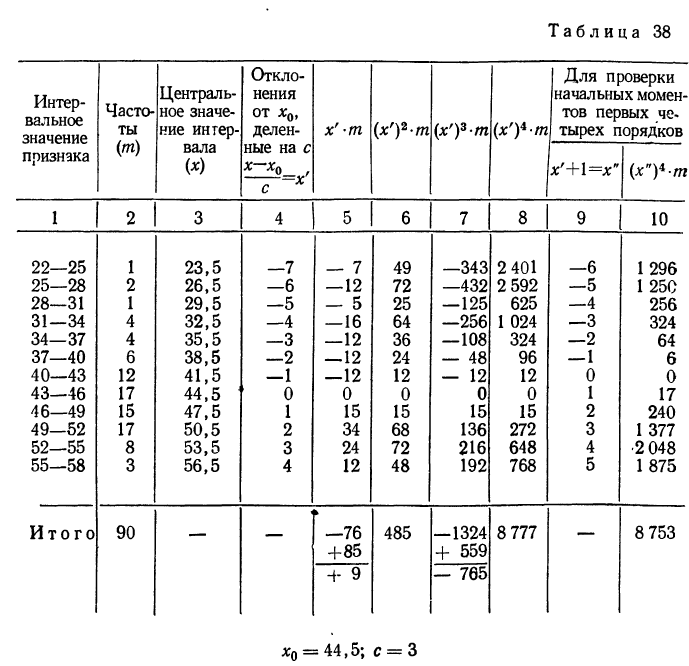
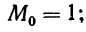
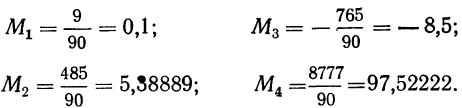
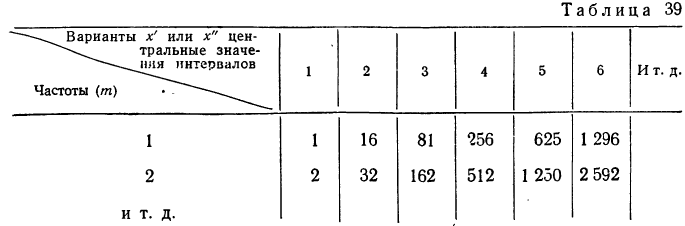
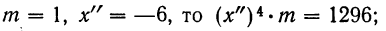
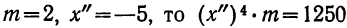
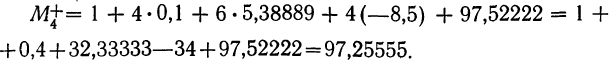
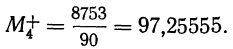
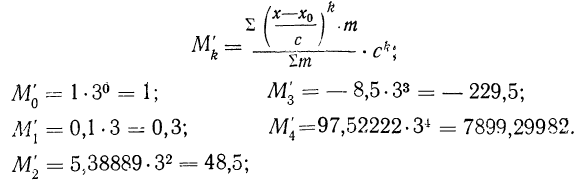
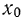
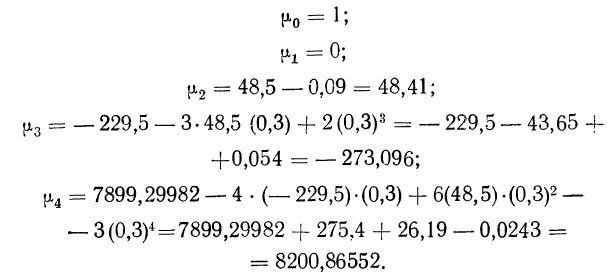
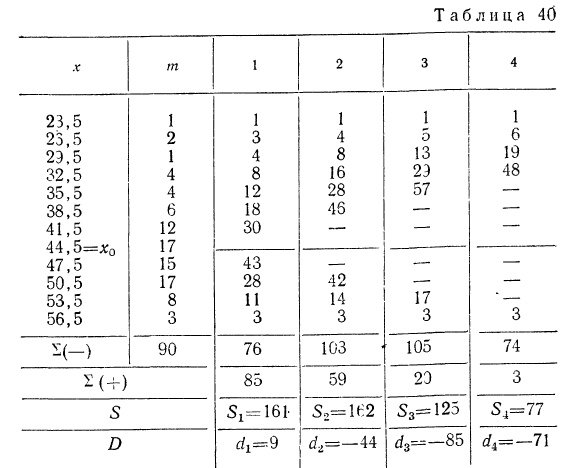
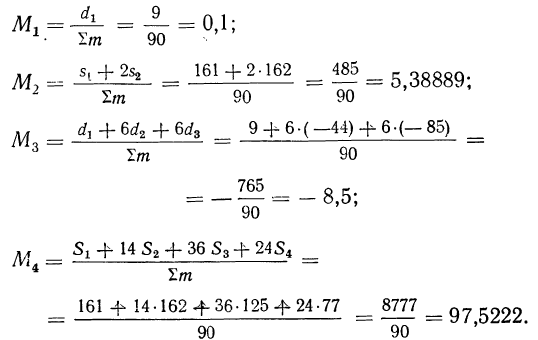
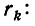
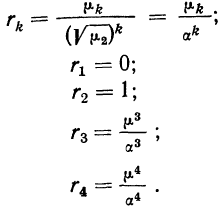
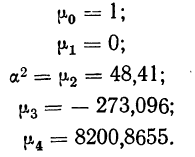
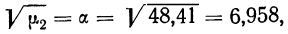
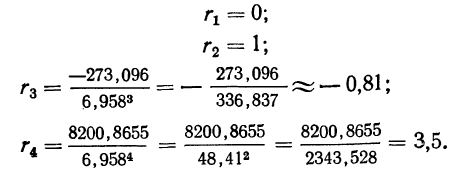
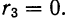
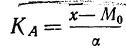
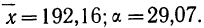
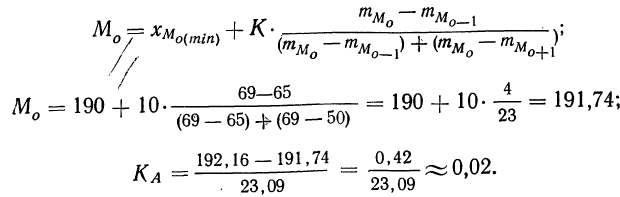





![Rendered by QuickLaTeX.com [chi^2_{nabl}=sum frac{ {(n_i-n_i^{'})}^2}{n_i^{'}}]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-43685ed67e69272b6c950828a97acd89_l3.png)
![Rendered by QuickLaTeX.com [sumfrac{n_i^2}{n_i^{'}}-n=sum frac{{(n_i-n_i^{'})}^2}{n_i^'}]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-6c32fcc2a5c6b3b4b603ae3d99533b4a_l3.png)


