Как найти границы приближенного числа

Как найти границы приближенного числа

ПРИБЛИЖЕННЫЕ ЧИСЛА И ДЕЙСТВИЯ НАД НИМИ

  1. Приближенное значение величины. Абсолютная и относительная погрешности
  2. Верные и значащие цифры. Запись приближенных значений.
  3. Вычисление погрешностей величин и арифметических действий
  4. Методы оценки погрешности приближенных вычислений
  1. Приближенное значение величины. Абсолютная и относительная погрешности

Решение практических задач, как правило, связано с числовыми значениями величин. Эти значения получаются либо в результате измерения, либо в результате вычислений. В большинстве случаев значения величин, которыми приходится оперировать, являются приближенными.

Пусть X – точное значение некоторой величины, а х – наилучшее из известных ее приближенных значений. В этом случае погрешность (или ошибка) приближения х определяется разностью Х-х. Обычно знак этой ошибки не имеет решающего значения, поэтому рассматривают ее абсолютную величину:

Величина ех, называемая абсолютной погрешностью приближенного значения х, в большинстве случаев остается неизвестной, так как для ее вычисления нужно точное значение X. Вместе с тем, на практике обычно удается установить верхнюю границу абсолютной погрешности, т.е. такое (по возможности наименьшее) число  для которого справедливо неравенство

Число  в этом случае называется предельной абсолютной погрешностью, или границей абсолютной погрешности приближения х.

Таким образом, предельная абсолютная погрешность приближенного числа х – это всякое число , не меньшее абсолютной погрешности ех этого числа.

Пример: Возьмем число . Если же вызвать  на индикатор 8-разрядного МК, получим приближение этого числа: Попытаемся выразить абсолютную погрешность значения . Получили бесконечную дробь, не пригодную для практических расчетов. Очевидно, однако, что  следовательно, число 0,00000006 = 0,6 * 10-7 можно считать предельной абсолютной погрешностью приближения , используемого МК вместо числа

Неравенство (2) позволяет установить приближения к точному значению X по недостатку и избытку:

которые могут рассматриваться как одна из возможных пар значений соответственно нижней границы (НГ) и верхней границы (ВГ) приближения х:

Во многих случаях значения границы абсолютной ошибки  так же как и наилучшие значения приближения х, получаются на практике в результате измерений. Пусть, например, в результате повторных измерений одной и той же величины х получены значения: 5,2; 5,3; 5,4; 5,3. В этом случае естественно принять за наилучшее приближение измеряемой величины среднее значение х=5,3. Очевидно также, что граничными значениями величины х в данном случае будут НГХ= 5,2, ВГХ = 5,4, а граница абсолютной погрешности х может быть определена как половина длины интервала, образуемого граничными значениями НГХ и ВГХ,

т.е.

По абсолютной погрешности нельзя в полной мере судить о точности измерений или вычислений. Качество приближения характеризуется величиной относительной погрешности, которая определяется как отношение ошибки ех к модулю значения X(когда оно неизвестно, то к модулю приближения х).

 Предельной относительной погрешностью (или границей относительной погрешности)  приближенного числа называется отношение предельной абсолютной погрешности к абсолютному значению приближения х:

Формула (5) позволяет при необходимости выражать абсолютную погрешность через относительную:

Относительную погрешность выражают обычно в процентах.

Пример  Определим предельные погрешности числа х=3,14 как приближенного значения π. Так как π=3,1415926…., то  |π-3,14|<0,0015927<0,0016=по формуле связи получаем таким образом

  1. Верные и значащие цифры. Запись приближенных значений

Цифра числа называется верной (в широком смысле), если ее абсолютная погрешность не превосходит единицы разряда, в котором стоит эта цифра.

Пример. Х=6,328 Х=0,0007 X<0,001 следовательно цифра 8-верная

Пример: А). Пусть 0 = 2,91385,  В числе а верны в широком смысле цифры 2, 9, 1.

Б) Возьмем в качестве приближения к числу = 3,141592… число = 3,142. Тогда  (рис.) откуда следует, что в приближенном значении = 3,142 все цифры являются верными.

В) Вычислим на 8-разрядном МК частное точных чисел 3,2 и 2,3, получим ответ: 1,3913043. Ответ содержит ошибку, поскольку

Рис.  Приближение числа π

разрядная сетка МК не вместила всех цифр результата и все разряды начиная с восьмого были опущены. (В том, что ответ неточен, легко убедиться, проверив деление умножением: 1,3913043 2,3 = 3,9999998.) Не зная истинного значения допущенной ошибки, вычислитель в подобной ситуации всегда может быть уверен, что ее величина не превышает единицы самого младшего из изображенных на индикаторе разряда результата. Следовательно, в полученном результате все цифры верны.

Первая отброшенная (неверная) цифра часто называется сомнительной.

Говорят, что приближенное данное записано правильно, если в его записи все цифры верные. Если число записано правильно, то по одной только его записи в виде десятичной дроби можно судить о точности этого числа. Пусть, например, записано приближенное число а = 16,784, в котором все цифры верны. Из того, что верна последняя цифра 4, которая стоит в разряде тысячных, следует, что абсолютная погрешность значения а не превышает 0,001. Это значит, что можно принять  т.е. а = 16,784±0,001.

Очевидно, что правильная запись приближенных данных не только допускает, но и обязывает выписывать нули в последних разрядах, если эти нули являются выражением верных цифр. Например, в записи = 109,070 нуль в конце означает, что цифра в разряде тысячных верна и она равна нулю. Предельной абсолютной погрешностью значения , как следует из записи, можно считать  Для сравнения можно заметить, что значение с = 109,07 является менее точным, так как из его записи приходится принять, что

Значащими цифрами в записи числа называются все цифры в его десятичном изображении, отличные от нуля, и нули, если они расположены между значащими цифрами или стоят в конце для выражения верных знаков.

Пример  а) 0,2409 – четыре значащие цифры; б) 24,09 – четыре значащие цифры; в) 100,700 – шесть значащих цифр.

Выдача числовых значений в ЭВМ, как правило, устроена таким образом, что нули в конце записи числа, даже если они верные, не сообщаются. Это означает, что если, например, ЭВМ показывает результат 247,064 и в то же время известно, что в этом результате верными должны быть восемь значащих цифр, то полученный ответ следует дополнить нулями: 247,06400.

В процессе вычислений часто происходит округление чисел, т.е. замена чисел их значениями с меньшим количеством значащих цифр. При округлении возникает погрешность, называемая погрешностью округления. Пусть х – данное число, а х1 – результат округления. Погрешность округления определяется как модуль разности прежнего и нового значений числа:

В отдельных случаях вместо ∆окр приходится использовать его верхнюю оценку.

Пример  Выполним на 8-разрядном МК действие 1/6. На индикаторе высветится число 0,1666666. Произошло автоматическое округление бесконечной десятичной дроби 0,1(6) до числа разрядов, вмещающихся в регистре МК. При этом можно принять

Цифра числа называется верной в строгом смысле, если абсолютная погрешность этого числа не превосходит половины единицы разряда, в котором стоит эта цифра.

Правила записи приближенных чисел.

  1. Приближенные числа записываются в форме х ± х. Запись X = х ± x означает, что неизвестная величина X удовлетворяет следующим неравенствам:     x-x <= X <= x+x

При этом погрешность х рекомендуется подбирать так, чтобы

а) в записи х было не более 1-2 значащих цифр;

б) младшие разряды в записи чисел х и х соответствовали друг другу.

Примеры:  23,4±0,2 ;   2,730±0,017 ;   -6,970,10.

  1. Приближенное число может быть записано без явного указания  его  предельной абсолютной погрешности. В этом случае в его  записи  (мантиссе)  должны  присутствовать только верные цифры (в широком смысле, если не сказано обратное). Тогда по самой записи числа можно судить о его точности.

Примеры. Если в числе А=5,83 все цифры верны в строгом смысле, то А=0,005. Запись В=3,2 подразумевает, что В=0,1. А по записи С=3,200 мы можем заключить, что С=0,001. Таким образом, записи 3,2 и 3,200  в теории приближенных вычислений означают не одно и то же.

 Цифры в записи приближенного числа, о которых нам неизвестно, верны они или нет, называются сомнительными. Сомнительные цифры (одну-две) оставляют в  записи чисел промежуточных результатов для сохранения  точности  вычислений.  В окончательном результате сомнительные цифры отбрасываются.

Округление чисел.

  1. Правило округления. Если в старшем из отбрасываемых  разрядов  стоит  цифра меньше пяти, то содержимое сохраняемых разрядов числа не изменяется. В противном случае в младший сохраняемый разряд добавляется единица с тем же знаком, что и у самого числа.
  2. При округлении числа, записанного в форме х±х, его  предельная  абсолютная погрешность увеличивается с учетом погрешности округления.

Пример: Округлим до сотых число 4,5371±0,0482. Неправильно было бы записать 4,54±0,05 ,  так как погрешность  округленного числа складывается из погрешности исходного числа и погрешности округления.  В данном случае она равна 0,0482 + 0,0029 = 0,0511 .  Округлять погрешности всегда следует с избытком, поэтому окончательный ответ:  4,54±0,06.

Пример  Пусть в приближенном значении а = 16,395 все цифры верны в широком смысле. Округлим а до сотых: a1 = 16,40. Погрешность округления  Для нахождения полной погрешности , нужно сложить c погрешностью исходного значения а1 которая в данном случае может быть найдена из условия, что все цифры в записи а верны: = 0,001. Таким образом, . Отсюда следует, что в значении a1 = 16,40 цифра 0 не верна в строгом смысле.

  1. Вычисление погрешностей арифметических действий

1. Сложение и вычитание. Предельной абсолютной погрешностью алгебраической суммы является сумма соответствующих погрешностей слагаемых:

Ф.1                               (X+Y) = Х + Y ,       (X-Y) = Х + Y .

Пример.  Даны приближенные числа Х = 34,38 и Y = 15,23 , все цифры верны в строгом смысле. Найти (X-Y) и (X-Y). По формуле Ф.1 получаем:

(X-Y) = 0,005 + 0,005 = 0,01.

Относительную погрешность получим по формуле связи:

2. Умножение и деление. Если   Х << |Х| и Y << |Y|,   то имеет место следующая формула:

Ф.2                                     (X · Y) = (X/Y) = X + Y.

Пример. Найти (X·Y) и (X·Y) для чисел из предыдущего примера. Сначала с помощью формулы Ф.2 найдем (X·Y):

(X·Y)= X + Y=0,00015+0,00033=0,00048

Теперь (X·Y) найдем с помощью формулы связи:

(X·Y) = |X·Y|·(X·Y) = |34,38 -15,23|·0,00048  0,26 .

3. Возведение в степень и извлечение корня. Если   Х << |Х| , то справедливы формулы

Ф.З

4. Функция одной переменной. 

Пусть даны аналитическая функция f(x) и приближенное число с ± с. Тогда, обозначая через  малое приращение аргумента, можно написать

Если f ‘(с)  0, то приращение функции f(с+) – f(c) можно оценить ее дифференциалом:

f(c+) – f(c)  f ‘(c) ·.

Если погрешность с достаточно мала, получаем окончательно следующую формулу:

Ф.4                                               f(c) = |f ‘(с)|· с .

Пример.  Даны   f(x) = arcsin x , с = 0,5 , с = 0,05 . Вычислить f(с).

Применим формулу Ф.4:    

5. Функция нескольких переменных.

Для функции нескольких переменных f(x1, … , хn) при xk= ck ± ck справедлива формула, аналогичная Ф.4:

Ф.5             f(c1, … ,сn)  l df(c1, … ,сn) | = |f ‘x1 (с1)|·с1+… + |f ‘xn (сn)|· сn.

Пример  Пусть х = 1,5, причем  т.е. все цифры в числе х верны в строгом смысле. Вычислим значение tg x. С помощью МК получаем: tgl,5= 14,10141994. Для определения верных цифр в результате оценим его абсолютную погрешность:  отсюда следует, что в полученном значении tgl,5 ни одну цифру нельзя считать верной.

  1. Методы оценки погрешности приближенных вычислений

Существуют строгие и нестрогие методы оценки точности результатов вычислений.

1.   Строгий метод итоговой оценки. Если приближенные вычисления выполняются по сравнительно простой формуле, то с помощью формул Ф.1-Ф.5 и формул связи погрешностей можно вывести формулу итоговой погрешности вычислений. Вывод формулы и оценка погрешности вычислений с ее помощью составляют суть данного метода.

Пример Значения a = 23,1 и b = 5,24 даны цифрами, верными в строгом смысле. Вычислить значение выражения

С помощью МК получаем В = 0,2921247. Используя формулы относительных погрешностей частного и произведения, запишем:

 т.е.

Пользуясь МК, получим 5, что дает . Это означает, что в результате две цифры после запятой верны в строгом смысле: В=0,29±0,001.

2.   Метод строгого пооперационного учета погрешностей. Иногда попытка применения метода итоговой оценки приводит к слишком громоздкой формуле. В этом случае более целесообразным может оказаться применение данного метода. Он заключается в том, что оценивается точность каждой операции вычислений отдельно с помощью тех же формул Ф.1-Ф.5 и формул связи.        

3.   Метод подсчета верных цифр. Данный метод относится к нестрогим. Оценка точности вычислений, которую он дает, в принципе не гарантирована (в отличие  от строгих методов), но на практике является довольно надежной. Суть метода заключается в том, что после каждой операции вычислений в полученном числе определяется количество верных цифр с помощью нижеследующие правил.

П.1. При сложении и вычитании приближенных чисел в результате верными следует считать, те цифры, десятичным разрядам которых соответствуют верные цифры во всех слагаемых. Цифры всех других разрядов кроме самого старшего из них перед выполнением сложения или вычитания должны быть округлены во всех слагаемых.

П.2. При умножении и делении приближенных чисел в результате верными следует считать столько значащих цифр, сколько их имеет приближенное данное с наименьшим количеством верных значащих цифр. Перед  выполнением  этих  действий среди приближенных данных нужно выбрать число с наименьшим количеством значащих цифр и округлить остальные числа так, чтобы они имели лишь на одну значащую цифру больше него.

П.З. При возведении в квадрат или в куб, а также при извлечении квадратного или кубического корня в результате следует считать верными столько значащих цифр, сколько имелось верных значащих цифр в исходном числе.

П.4. Количество верных цифр в результате вычисления функции зависит от величины модуля производной и от количества верных цифр в аргументе. Если модуль производной близок к числу 10k  (k – целое), то в результате количество верных цифр относительно запятой на k меньше (если k отрицательно, то – больше), чем их было в аргументе. В данной лабораторной работе для  определенности  примем соглашение считать модуль, производной близким к 10k , если имеет  место  неравенство:

0,2·10K  < |f ‘(X) |  2·10k  .

П.5. В промежуточных результатах помимо верных цифр следует оставлять одну  сомнительную цифру (остальные сомнительные цифры можно округлять) для сохранения точности вычислений. В окончательном результате оставляют только верные цифры.

Вычисления по методу границ

Если нужно иметь абсолютно гарантированные границы возможных значений вычисляемой величины, используют специальный метод вычислений – метод границ.

Пусть f(x, у) – функция, непрерывная и монотонная в некоторой области допустимых значений аргументов х и у. Нужно получить ее значение f(a, b), где а и b – приближенные значения аргументов, причем достоверно известно, что

Здесь НГ, ВГ – обозначения соответственно нижней и верхней границ значений параметров. Итак, вопрос состоит в том, чтобы найти строгие границы значения f(a, b), при известных границах значений а и b.

Допустим, что функция f(x, у) возрастает по каждому из аргументов x и y. Тогда

f(НГа, НГb< f(a, b)<f(ВГa ВГb).

Пусть f(x, у) возрастает по аргументу х и убывает по аргументу у. Тогда будет строго гарантировано неравенство

f(НГa ВГb)< f(a, b)< f(ВГa, НГb).

Указанный принцип особенно очевиден для основных арифметических действий. Пусть, например, f(x, у)=х + у. Тогда очевидно, что

Точно так же для функции f2(x, у) = х–у (она по х возрастает, а по у убывает) имеем

Аналогично для умножения и деления:

НГа*НГb<а * b<ВГa*ВГb.

НГа/ВГb<а / b<ВГa/НГb.

Пример. Вычислите значение где 2,57<=x<=2,58;  1,45<=y<=1,46;  8,33<=z<=8,34

Действие

Содержимое

НГ

ВГ

1

X

2.57

2.58

2

Y

1.45

1.46

3

Z

8.33

8.34

4

x+y

4.02

4.04

5

x-y

1.11

1.13

6

(x-y)z

9.24

9.43

7

2.28

2.35

Пример. В табл.  приведены вычисления по формуле  методом границ. Нижняя и верхняя границы значений a и b определены из условия, что в исходных данных а = 2,156 и b = 0,927 все цифры верны в строгом смысле (∆a = ∆b = 0,0005), т.е. 2,1555<а<2,1565; 0,92650,9275.

a

b

ea

b2

a+b2

A

НГ

2,1555

0,9265

8,63220

0,96255

9,59475

0,85840

3,01434

1,10338

8,6894

ВГ

2,15,65

0,9275

8,64084

0,96307

9,60391

0,86026

3,01676

1,10419

8,7041

Рис. Связь между абсолютной погрешностью и границами

Таким образом, результат вычислений значения А по методу границ имеет следующий вид:

8,6894 <А< 8,7041.

Источник

АБСОЛЮТНАЯ ПОГРЕШНОСТЬ И ЕЕ ГРАНИЦА.

ЗАПИСЬ ПРИБЛИЖЕННОГО ЧИСЛА.

ВЕРНЫЕ И ЗНАЧАЩИЕ ЦИФРЫ ЧИСЛА

х – точное число

а – приближенное число

Разность   х – а    между точным числом х и приближенным числом а называется погрешностью приближения.

Модуль погрешности называется абсолютной погрешностью и обозначается ∆:

| х – а | = ∆

Погрешность и абсолютная погрешность имеют ту же размерность, что и рассматриваемая величина

Граница абсолютной погрешности ∆а – положительное число, которое больше или равно абсолютной погрешности или:

| х – а | ≤ ∆а

Если задана граница абсолютной погрешности ∆а, то число а есть приближенное значение числа х с точностью до ∆а и записывают

х = а ± ∆а, например: 94,5 ± 0,3

В отличие от абсолютной погрешности, граница абсолютной погрешности не определяется однозначно, поэтому на практике выбирается такое значение границы абсолютной погрешности, которое удобно для вычислений и обеспечивает максимальную точность.

Цифра приближенного числа а, записанного в виде десятичной дроби, называется верной (точной), если граница абсолютной погрешности числа не превышает (меньше или равно) единицы того разряда, в котором стоит эта цифра. В противном случае она называется сомнительной, например:

25,63 ± 0,2

Граница погрешности 0,2 , поэтому рассмотрим

цифру 5, разряд единицы, единица разряда 1 и 0,2 < 1 (граница погрешности не превышает единицу разряда), значит цифра 5 – верная, тогда цифра десятков – 2  данного числа тоже верная.

Цифра 6, разряд десятые, единица разряда 0,1 и 0,2 > 0,1  (граница погрешности превышает единицу разряда), значит цифра 6 – сомнительная. Значит и цифра 3 (сотые) будет также сомнительной

2 и 5 – верные цифры, 6 и 3 – сомнительные цифры числа

Запись чисел с сохранением только верных цифр широко используется во всех математических таблицах, в справочниках (физика, астрономия, техника). При этом, по записи приближенного числа можно оценить погрешность приближения, например:

табличные данные: температура кипения золота – 2700 ºС, значит граница абсолютной погрешности 1 ºС, температура кипения йода – 182,8 ºС, значит граница абсолютной погрешности 0,1 ºС.

Записи приближенных чисел 0,3; 0,30; 0,300 – неравносильны, т.к. приближенное число 0,3 имеет погрешность не более 0,1;

приближенное число 0,30 имеет погрешность не более 0,01;

приближенное число 0,300 имеет погрешность не более 0,001.

Если целое число содержит в конце нули, не являющиеся верными цифрами, то их заменяют множителем 10р, где р – число таких нулей.

В записи приближенных чисел принято соблюдать следующие правила:

  • Оставлять в записи приближенного числа только верные цифры;
  • Если в десятичной дроби последние верные цифры нули, то их надо выписать;
  • Если число содержит в конце нули, не являющиеся верными цифрами, то они должны быть заменены на 10р , где р – число нулей, которые надо заменить

Например,

Записать правильно следующие приближенные числа:  

  1. а = 0,075 ± 0,000005 – здесь погрешность меньше, чем 0,00001 (0,000005<0,00001), значит а = 0,07500 (последние верные цифры нули и их надо выписать, см. правило)
  2. а = 746000000 ± 5000 здесь погрешность меньше, чем 10000 (5000<10000), значит последние четыре нуля не являются верными цифрами и их надо заменить на  10р  а = 74600·104
  3. а = 0,35  ∆а = 0,00005 – здесь погрешность меньше, чем 0,0001 значит

а = 0,3500 (последние верные цифры нули)

  1. а = 765000  ∆а = 5 – здесь погрешность  5<10  значит а = 76500·10, т.к. последний нуль не является верной цифрой
  2. а = 0,3700  ∆а = 0,05 – здесь погрешность 0,05<0,1 и цифра 7 не является верной, она отбрасывается, значит а = 0,4

В некоторых заданиях необходимо наоборот определить абсолютную погрешность по записи приближенного числа, например,

Указать абсолютную погрешность приближенных чисел:

  1. а = 14,5 ·10, значит ∆а = 10
  2. а = 34,20 т.к. последний нуль является верной цифрой, то ∆а = 0,01
  3. а = 263·104 , значит ∆а = 10000

Число в стандартном виде записывают так:

а = а0, а1 а2 … аk  ·10m , где 1 ≤ а0 ≤ 10,

а0, а1 а2 … аk  –  все верные цифры числа,

показатель m – называется порядком числа.

Если число, записанное в виде десятичной дроби содержит все верные цифры, то все его цифры, начиная с первой слева отличной от нуля, называют значащими, например:

7,03 – три значащие цифры

4400 – четыре значащие цифры

0,000270 – три значащие цифры (нули, расположенные левее первой, отличной   от нуля цифры, не считаются значащими  0,000270).

Округление числа – это замена его числом с меньшим количеством значащих цифр. При округлении числа до m значащих цифр отбрасывают все цифры, стоящие правее m-ой значащей цифры, заменяя их на нули (при сохранении разряда). При этом, если первая из отбрасываемых цифр ≥ 5, то последнюю оставшуюся цифру увеличивают на единицу,

например:

Округлить число с заданной точностью:

  • с точностью до 10-3   (10-3  = 0,001)

1,5783

Значащие цифры – 1, 5, 7  и 8, цифра 3 – сомнительная, т.к. 0,001 > 0,0001 (единицы разряда)

1,5783 ≈ 1,578 (последняя из отбрасываемых цифр 3<5, значит предыдущую оставляем без изменений)

23,4997

Значащие цифры – 2, 3, 4, 9 и 9, цифра 7 – сомнительная

7>5, значит предыдущую увеличиваем на 1, получим

23,4997 ≈ 23,500

  • с точностью до 10-2  (10-2  = 0,01)

4,761 ≈ 4,76

31,009 ≈ 31,01

  • с точностью до 103  (103 = 1000)

159734 ≈ 160000 = 160·103

28,34 ≈ 0 – ни одна из цифр не является значащей 1000 > 10, т.к. задана точность 1000, а заданное число меньше, чем погрешность.

Лисичкин В.Т., Соловейчик И.Л. Сборник задач по математике с решениями для техникумов (учебное пособие)

Источник

Наилучшим в смысле
строгости из известных способов
приближенных вычислений является способ
границ. Пользуясь этим способом, по
известным нижним и верхним границам
данных чисел, находят отдельно нижнюю
и верхнюю границы результата.

Пусть, например, надо
сложить два числа:

х ≈ 3,2 (±0,05) иy ≈
7.9 (±0,05).

Имеем: 3,15< х <
3,25, 7,85<у < 7,95, откуда 11,00<х +у < 11,20.

Итак, х +у ≈
11,1 (±0,1).

Вообще, нижняя граница
суммы приближенных чисел равна сумме
нижних границ слагаемых, а верхняя –
сумме верхних границ слагаемых.
Символически это можно записать так:

НГ ( x +у ) = НГх + HГy ; ВГ (х +у ) = ВГх
+ ВГy .

Аналогичные правила
справедливы для умножения:

НГ ( ху ) = НГх ·
НГу ; ВГ (х у) = ВГх · ВГy .

Для обратных действий
– вычитания и деления – соответствующие
правила имеют такой вид:

НГ ( х –у ) = НГх – ВГу ; ВГ (х –у ) = ВГх
– НГу .

Из определения НГ и
ВГ вытекают также следующие правила:

1) округлять НГ можно
только по недостатку, а ВГ – по избытку;

2) чем меньше разность
ВГ х – НГх , тем точнее определяетсях ;

3) в качестве приближенного
значения х рекомендуется брать
среднее арифметическое чисел НГх и
ВГх или число, близкое к нему.

Применение способа
границ при вычислениях рассмотрим на
примере.

Пример. Найти значение

если а ≈ 9,21 (±0,01);b ≈ 3,05 (±0,02),с ≈ 2,33 (±0,01).

Решение. Определяем
НГ и В Г каждого из чисел а ,b ,c
и, выполнив над ними соответствующие
действия, находим НГ и ВГ числах .

Запись удобно оформить
в виде такой таблицы.

Компоненты
а b с
а –b (а –b )с а
+b x

НГ
9,20
3,03
2,32
6,13
14,22
12,23
1,15

ВГ
9,22
3,07
2,34
6,19
14,49
12,29
1,19

1,15< x < 1,19

2,34 : 2 = 1,17; 0,04 : 2 = 0,02

x ≈ 1,17 (±0,02).

Литература. Энциклопедия
элементарной математики, I, М, 1951.

В.М. Брадис, Средства
и способы элементарных вычислений,
Учпедгиз, М., 1954.

А.Н. Крылов, Лекции о
приближенных вычислениях, Изд-во АН
СССР, Л., 1933.

ВЕЛИЧИНЫ
И ПРОПОРЦИИ

27. Измерение величин

1. Величины и их
измерения. Дать строгое определение
понятию “величина” нельзя. Это одно
из основных (неопределяемых) понятий,
смысл которого раскрывают при помощи
различных описаний. В старых книгах
величинами называли все то, что способно
увеличиваться или уменьшаться. Однако
это нельзя считать строгим определением,
так как говорят, например, об увеличении
аппетита, прав, обязанностей и других
понятий, которых не принято считать
величинами.

Примерами величин
есть: длина, площадь, объем, вес, скорость,
время и др.

Характерное свойство
величины состоит в том, что наряду с
другими свойствами она имеет и числовую
характеристику. Поэтому говорят о том
или ином числовом значении величины.
Величины можно измерять.

Измерить какую-нибудь
величину – значит сравнить ее значение
со значением другой величины такого же
рода, принятой за единицу.

В каждом государстве
установлены определенные единицы для
измерения основных величин. Единицы
измерения, вошедшие в употребление,
называются мерами. Так, сейчас у нас
приняты: за единицу длины метр, за единицу
веса – грамм, за единицу времени – секунда
и т.д.**

Однако не всегда у нас
пользовались такими мерами, а в некоторых
странах и теперь приняты другие меры.

*Абсолютная
погрешность бывает и положительной и
отрицательной. Например, 1,68 ≈ 1,7.
Абсолютная погрешность равна 1,68 – 1,7 ≈
–0,02. Граничная абсолютная погрешность
всегда положительна
**Для
каждого рода величин выбирают несколько
единиц: одни более крупные (кратные),
другие более мелкие (дольные)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Практическая работа № 1: «Приближенные вычисления»

Цель:

– научиться определять абсолютную и относительную погрешности числа;

– научиться определять верные значащие цифры числа;

– научиться определять погрешности функций.

Указания:

Практическая работа состоит из двух частей – теоретической и практической. После изучения теоретического материала можно приступать к выполнению практической части. Она состоит из одной или более задач для самостоятельного выполнения. Не забывайте о правильном оформлении решения.

Порядок выполнения работы:

  1. Рассмотрите теоретический материал по теме и примеры решения задач.

  2. Решите самостоятельную работу. Оформите решение письменно в тетради.

Ход работы

Теоретический материал

Разность точного и приближенного значений величины называется погрешностью приближения (обозначается х), т.е. х=х-а – погрешность приближения, откуда х=а+ х, т.е. истинное значение равно сумме приближенного значения и погрешности приближения.

Модуль разности точного и приближенного значений величины называется абсолютной погрешностью приближенного значения числа х.

т.е. –абсолютная погрешность приближения.

Запись х= а h означает, что истинное значение величины х заключено между границами, т.е. а – h х а + h

Пример 1. На предприятии 1284 рабочих и служащих. При округлении этого числа до 1300 абсолютная погрешность составляет 1300 -1284 = 16. При округлении до 1280 абсолютная погрешность состав­ляет 1284 – 1280 = 4.

Пример 2. Даны приближенные значения числа х = ; Какое из этих трех приближений является лучшим?

Решение: Находим 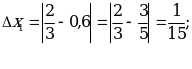; 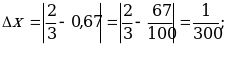Лучшим приближением числа х является

Пример 3. Длина детали х (см) заключена в границах 33 х 34. Найти границу абсолютной погрешности измерения детали.

Решение: Примем за приближенное значение длины детали среднее арифметическое границ: а=(33+34)/2 = 33,5 (см). Тогда граница абсолютной погрешности приближенного значения длины детали не превзойдет 0,5 (см). Величину можно найти и как полуразность верхней и нижней границ, т.е. = (34-33)/2 = 0,5 (см). Длина детали х, найденная с точностью до =0,5 (см), заключена между приближенными значениями числа х: 33,5-0,5 х 33,5+0,5; х=33,5 0,5 (см). Отношение абсолютной погрешности приближения к модулю приближенного значения величины называется относительной погрешностью приближения и обозначается .

Т.е. 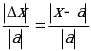= является относительной погрешностью приближения.

Пример 4. При измерении длины L и диаметра проводника получили L=(10,0 0,1) м, d = (2,5 0,1) мм. Какое из этих измерений точнее?

Решение: Измерение длины проводника производилось с точностью до 0,1м=100мм, а измерение диаметра проводника – с точностью до 0,1мм.

При измерении длины проводника допускается абсолютная погрешность в 100мм на 10000мм, и, следовательно, допустимая абсолютная погрешность составляет измеряемой величины.

При измерении диаметра допустимая абсолютная погрешность составляет

измеряемой величины. Следовательно, измерение длины проводника выполнено точнее.

Пример 5. Известно, что 0,111 является приближенным значением для Найти абсолютную и относительную погрешности этого приближения.

Решение: Здесь х= , а=0,111. Тогда = х-а = 1/9 – 0,111 = 1/9000-а.п.п,

-о.п.п

Пример 6. В школе 197 учащихся. Округляем это число до 200. Абсолютная погрешность составляет 200-197 = 3. Относительная погрешность равна или, округленно, %. В большинстве случаев невозможно узнать точное значение приближенного числа, а значит, и точную величину погрешности. Однако почти всегда можно установить, что погрешность (абсолютная или относи­тельная) не превосходит некоторого числа.

Пример 7. Продавец взвешивает арбуз на чашечных весах. В наборе гирь наименьшая— 50 г. Взвешивание дало 3600 г. Это число — приближенное. Точная масса арбуза неизвестна. Но абсолютная погрешность не превышает 50 г. Относительная погреш­ность не превосходит %.

Самостоятельная работа

1 вариант

2 вариант

1

Найдите абсолютную погрешность округления до единиц следующих чисел:

1) 0,8; 2) 7,6;

(1 балл) (1 балл)

1) 19,3; 2) 563,58.

(1 балл) (1 балл)

2

Граница абсолютной погрешности приближенного значения 386 числа х = 0,5. Укажите границы, в которых заключено число х. (2 балла)

Найдите границу абсолютной погрешности измерений, полученных в виде неравенства 37 .

(2 балла)

3

Амперметр дает точность 0,02 А. При измерении силы тока получили 10,63 А. Укажите границы этого числа. (2 балла)

Атомная масса водорода 1,0082 0,0005, а меди 63,44 0,15. Укажите границы приближенных значений этих чисел. (2 балла)

4

Шоколадка стоит 40 рублей. В воскресенье в супермаркете действует специальное предложение: заплатив за две шоколадки, покупатель получает три (одну в подарок). Сколько шоколадок можно получить на 320 рублей в воскресенье? (2 балла)

В университетскую библиотеку привезли новые учебники по геометрии для 2—3 курсов, по 280 штук для каждого курса. Все книги одинаковы по размеру. В книжном шкафу 7 полок, на каждой полке помещается 30 учебников. Сколько шкафов можно полностью заполнить новыми учебниками? (2 балла)

5

Больному прописано лекарство, которое нужно пить по 0,5 г 3 раза в день в течение 21 дня. В одной упаковке 10 таблеток лекарства по 0,5 г. Какого наименьшего количества упаковок хватит на весь курс лечения? (2 балла)

Больному прописано лекарство, которое нужно пить по 0,5 г 3 раза в день в течение 21 дня. В одной упаковке 10 таблеток лекарства по 0,5 г. Какого наименьшего количества упаковок хватит на весь курс лечения? (2 балла)

6

Граница абсолютной погрешности приближенного значения a равна h. Найдите границы, в которых заключено число x, если:

a=23; h=0.5; (2 балла)

a=1.5; h=0.01; (2 балла)

Критерии оценки

количество набранных баллов

оценка

6-8

3

9-10

4

11-14

5

Форма контроля: Проверка письменных работ.

Источник

Добавить комментарий