Макеты страниц
Для алгебраического уравнения

задача отделения корней решается более просто и точно. Прежде чем отделять корни уравнения, естественно найти границы области, в которой расположены все корни уравнения, поэтому мы сначала приведем ряд способов отыскания этих границ. Пусть

Теорема 1. Все корни уравнения (1) расположены в кольце

Доказательство. Действительно, 


Следовательно, 


т. е. при 

Далее, уравнение

имеет корнями величины, обратные корням исходного уравнения. По доказанному все корни этого уравнения находятся внутри круга
радиуса 


Объединяя результаты, получим неравенство (2).
Предположим, что все коэффициенты уравнений действительные числа и 

Теорема 2. Обозначим через а максимум абсолютных вели 



Доказательство. Заменим положительные коэффициенты 

Тогда при 

Отсюда при 


а это и означает, что все положительные корни меньше 
Пусть в уравнении коэффициенты 



Тогда

Первое слагаемое в скобках содержит только положительные степени х, а второе только отрицательные. Следовательно, при 



В общем случае представим 

где 










Хороший способ отыскания верхней границы положительных корней указал Ньютон. Этот способ основан на утверждении: если при 

то уравнение 

при всех 
Таким образом, способ Ньютона заключается в отыскании значения 

Замечание. Нижняя граница положительных корней может быть найдена из уравнения 

Пример. Найти границы действительных корней уравнения

1-й способ (использование теоремы 2). В данном случае

Следовательно, все положительные корни уравнения меньше

Для отыскания нижней границы положительных корней уравнения рассмотрим уравнение

Так как 

а следовательно, нижняя граница корней исходного уравнения

Итак, все положительные корни уравнения находятся на отрезке [0,57; 1351].
Для отыскания границ отрицательных корней рассмотрим уравнение

получающееся заменой х на — z. Это уравнение, очевидно, не имеет положительных корней, а следовательно, исходное уравнение не имеет отрицательных корней. 2-й способ. Представим

в виде

где

При 
Для отыскания нижней границы снова заменим х на у. Получим:

где



уравнения больше Следовательно, корни уравнения 
Способом Ньютона можно показать, что корни уравнения расположены на отрезке [0,74; 22], т. е. удается еще улучшить результат.
Рассмотрим еще одну задачу связаннуюс полиномами. Когда мы пытаемся решить такое уравнение численно, то нам необходимо знать, в каких пределах могут находится действительные корни этого полинома.
Эти знания позволят нам быстрее обеспечить сходимость при компьютерных вычислениях. Это позволит при прорисовке полинома в виде графика, выбрать такой масштаб, что бы мы увидели все пересечения функции с осью абсцисс.
Итак, как же формулы мы будем использовать для решения задачи?
Если нам известен полином вида
То разделив его на a0 мы получаем
Правило утверждает, что если среди коэффицентов есть отрицательные числа и -первое из них, и также есть отрицательный коэффицент A который является самым большим (в абсолютном значении), то действительные корни этого полинома не превышают число
Нижнюю границу можно определить по аналогичной формуле, вычислив значения функции коэффицентов при -x
Давайте рассмотрим пример
Разделим на 3 , что бы первый член полинома был равен единице.
Первый отрицательный коэффициент который мы встречаем это он стоит на второй позиции ( )
Значение А=9, так как 9 явлется максимальном в абсолютном выражении числом из всех отрицательных коэффициентов полинома.
Таким образом верхняя граница действительных корней
Теперь определяем нижнюю границу
Разделим полином на -3, что бы первый член полинома был равен единице.
Первый отрицательный коэффициент который мы встречаем это он стоит на первой позиции ( )
Таким образом нижняя граница действительных корней
Следовательно, все действительные корни заданного многочлена находятся в пределах
Бот позволяет выполнять эти вычисления автоматически и при заданных действительных коэффициентах давать правильные результаты.
Единственное замечание, не стоит вводить в качестве коэффициентов комплексные числа. Результат будет непредсказуем.
Алгебраические уравнения в математике с примерами решения и образцами выполнения
Алгебраическое уравнение — это уравнение вида. где. — многочлен от переменных. , которые называются неизвестными.
Делимость многочлена
Делимость многочлена, целого относительно х, на разность x— а.
Теорема Безу:
Многочлен, целый относительно х: 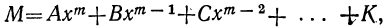
при делении на разность х — а (где а есть произвольное число, положительное или отрицательное) даёт остаток
равный тому значению делимого, которое оно получает при х=а.
Доказательство:
Из процесса деления многочлена, расположенного по убывающим степеням буквы х, видно, что деление такого многочлена на х — а можно продолжать до тех пор, пока высший член остатка R не будет содержать в себе буквы х. Пусть при этом частное будет некоторый многочлен Q. Тогда мы можем написать равенство:
M=(x- a)Q+R.
Равенство это есть тождество, т. е. оно верно при всевозможных значениях буквы х, а потому оно должно быть верно и при х-а. Но при x=а оно даёт
M’ = (α — α) Q’ + R
если буквами М‘ и Q‘ обозначим те значения M и Q, которые эти многочлены принимают при х=а (остаток R, как не содержащий вовсе x, не изменится от подстановки а на место х). Так как a — α=0, то и произведение (а — a) Q‘ равно 0; значит, последнее равенство даёт M‘= R, т. е.
что и требовалось доказать.
Следствие:
Так как x+α=x— (—а), то, применяя доказанную теорему к сумме х+а, найдём:
многочлен
при делении на сумму x+α даёт в остатке число, равное
т. е. число, равное тому значению делимого, которое оно получает при x= —а.
Примеры:
1) Многочлен x⁵—3x²+5x—1 при делении на х—2 даёт остаток, равный
2⁵-3 ∙ 2²+5 ∙ 2—1=29.
2) Многочлен x⁵—3x²+5x—1 при делении на x+2 даёт остаток
(-2)⁵-3 (- 2)²+5 (-2)—1=-55.
Следствие:
Для того чтобы многочлен
делился на разность х—а, необходимо и достаточно, чтобы при х=а он обращался в нуль.
Это необходимо, так как если указанный многочлен делится на x—а, то остаток от деления должен быть нуль, а этот остаток, по доказанному выше, есть то значение делимого, которое оно принимает при x=а. Это и достаточно, так как если многочлен обращается в нуль при x=a, то это значит, что остаток от деления этого многочлена на х—а равен нулю.
Следствие:
Для того чтобы многочлен
делился на сумму х+а, необходимо и достаточно, чтобы при х = —а он обращался в нуль, так как сумма х+а есть разность x—(— а).
Примеры:
1) Многочлен x³-4x²+9 делится на х—3, потому что
З³ — 4∙3²+9=0.
2) Многочлен 2x²+x-45 делится на x+5, так как
2 (-5)²+(-5)—45=0.
Делимость двучлена 
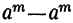
2) Сумма одинаковых степеней двух чисел не делится на разность этих чисел, так как 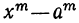
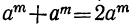
3) Разность одинаковых чётных степеней двух чисел делится, а нечётных не делится на сумму этих чисел, так как при делении разности 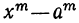
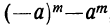
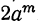
4) Сумма одинаковых нечётных степеней двух чисел делится, а чётных не делится на сумму этих чисел, так как. при делении суммы 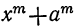
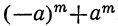
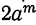
Примеры:
1) x¹+α¹ делится на x+α, но не делится на х—а.
2) x²- α² делится и на х—а, и на x+a.
3) x²+α² не делится ни на х—а, ни на x+a.
4) x³- α³ делится на х—а, но не делится на x+α.
5) x³+α³ делится на x+a, но не делится на х—а.
Частные, получаемые при делении 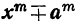
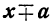
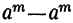
(остатки при этом делении идут в такой последовательности: 1-й остаток 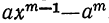
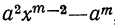
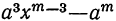
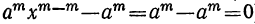
Очевидно, что многочлен, получившийся в частном, содержит m членов; сумма показателей в каждом члене при а и х одна и та же, именно: m—1; показатели х идут, уменьшаясь на 1,от m—1 до 0, показатели же а идут, увеличиваясь на 1, от 0 до m—1; коэффициенты у всех членов равны 1; знаки все +; число членов в частном m.
Заметив это, можем прямо писать:
x³- α³=(x-a) (x²+αx+α²);
x⁴- α⁴=(x-α) (x³+αx²+α²x+ α³);
x⁵ — α⁵=(x-a) (x⁴+αx3+α²x²+α³x+α⁴) и т. п.
Чтобы получить частное от деления 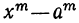
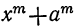
x³+α³=(x+α) (x²-αx+α²);
x⁴—α⁴=(x+α) (х³-αx²+α²x-α³);
x⁵+a⁵=(x+α) (х⁴ — αx³+α²x² — a³x+a⁴) и т.п.
Общий вид алгебраического уравнения
Мы ранее видели, что уравнение, содержащее неизвестное в знаменателях, может быть приведено к целому виду. Далее мы знаем, что уравнение, содержащее неизвестное под знаком радикала, может быть приведено к рациональному виду. Вследствие этого можем сказать, что всякое уравнение, в котором неизвестное связано с данными числами посредством конечного числа шести алгебраических действий (сложения, вычитания, умножения, деления, возвышения в степень и извлечения корня), может быть приведено к такому целому и рациональному виду:
где коэффициенты А, В, С, … , K и L суть постоянные вещественные или комплексные числа, а m есть показатель степени уравнения. Некоторые коэффициенты, кроме первого, в частных случаях могут равняться нулю.
Уравнение такого вида называется алгебраическим. Алгебраические уравнения степени выше второй называются уравнениями высших степеней.
Некоторые свойства алгебраического уравнения
Уравнения высших степеней составляют предмет высшей алгебры. Элементарная же рассматривает только некоторые частные виды этих уравнений.
Высшая алгебра устанавливает следующую важную теорему:
Всякое алгебраическое уравнение имеет вещественный или комплексный корень (теорема Гаусса 2), 1799 г.).
Допустив эту истину (доказательство которой в элементарной алгебре было бы затруднительно), нетрудно показать, что:
Алгебраическое уравнение имеет столько корней, вещественных или комплексных, сколько единиц в показателе его степени.
Действительно, согласно теореме Гаусса, уравнение
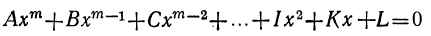
имеет вещественный или комплексный корень; пусть этот корень будет а. Тогда многочлен, стоящий в левой части уравнения (1), должен делиться на х—а. Если произвести это деление, то в частном получим многочлен степени m—1, у которого первый коэффициент будет А. Обозначив другие его коэффициенты соответственно буквами B₁, C₁ ,…, K₁ и приняв во внимание, что делимое равно делителю, умноженному на частное, можем представить уравнение (1) так:
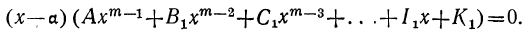
Приравняв нулю многочлен, стоящий во вторых скобках, получим новое уравнение, которое по той же теореме должно иметь некоторый корень β; вследствие этого левая его часть может быть разложена на два множителя: х—β и многочлен степени m—2, у которого первый коэффициент по-прежнему будет А. Поэтому уравнение (1) можно переписать так:
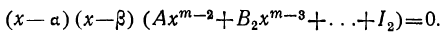
Продолжая эти рассуждения далее, дойдём, наконец, до того, что многочлен, заключённый в последних скобках, будет второй степени, причём первый его коэффициент останется А. Разложив этот трёхчлен на множители, приведём уравнение (1) к виду:
A(x- а) (х—β) (х— γ) . .. (х—λ)=0, (4)
где всех разностей: x-a, х- β,…, будет m. Очевидно, что уравнение (4) обращается в тождество при каждом из значений: x=α, x=β, x=γ, . x=λ и не удовлетворяется никакими иными значениями x (если A≠0); значит, уравнение (1) имеет m корней: a, β, γ ,…, λ. В частных случаях некоторые корни могут оказаться одинаковыми.
Полезно заметить ещё следующие истины, доказываемые в высшей алгебре.
Сумма корней всякого алгебраического уравнения 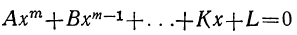
равна 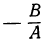
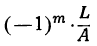
Если алгебраическое уравнение с вещественными коэффициентами имеет комплексные корни, то число этих корней — чётное (примером может служить биквадратное уравнение).
Если алгебраическое уравнение с вещественными коэффициентами имеет n корней вида p+qi, оно имеет ещё n корней вида p—qi (примером может служить биквадратное уравнение, комплексные корни которого всегда сопряжённые), и так как
[х—(p+qi)][x-(р— qi)]=[(x-p)- qi] (x-p)+qi] =
=(х—р)²—q²i²=(x-p)²+q²=x²-2 +(p²+q²),
то левая часть уравнения содержит в этом случае n вещественных множителей вида ax²+bx+c.
Алгебраическое уравнение нечётной степени с вещественными коэффициентами имеет, по крайней мере, один вещественный корень.
Уравнения с произвольными буквенными коэффициентами степени не выше четвёртой разрешены алгебраически, т. е. для корней этих уравнений найдены общие формулы, составленные из коэффициентов уравнения посредством алгебраических действий.
В этом смысле уравнения с произвольными коэффициентами степени выше четвёртой не могут быть разрешены алгебраически (теорема Абеля); однако, если коэффициенты уравнения какой угодно степени выражены числами, всегда есть возможность вычислить с желаемой степенью приближения все его корни как вещественные, так и мнимые. Способы такого вычисления излагаются в высшей алгебре.
Методы решения целых алгебраических уравнений
Разложение на множители
Часть целых алгебраических уравнений 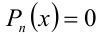
Если разложение на множители удалось выполнить, то решение алгебраического уравнения сводится к решению совокупности нескольких уравнений, но более низкой степени. Неравенство после разложения на множители можно решать методом интервалов.
Пример:
Решить уравнение
Решение:
Из 1-го уравнения находим корни 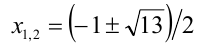
Пример:
Найти все положительные корни уравнения
Решение:
Покажем, что второе уравнение в совокупности не имеет положительных решений. Действительно, рассмотрим функцию 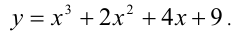
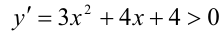
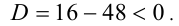
Ответ:
Подбор корня с последующим понижением степени уравнения
При решении алгебраических уравнений и неравенств степени выше второй можно использовать общий принцип последовательного понижения степени уравнения (неравенства).
Пусть требуется решить уравнение n -й степени
где 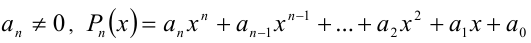
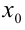

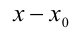
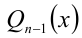
Пример:
Решить уравнение
Решение:
Заметим, что x = 2 является корнем данного уравнения. Найдём другие корни этого уравнения:
Решая уравнение 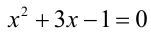
Эта ссылка возможно вам будет полезна:
Пример:
Решить уравнение
Решение:
Легко заметить, проанализировав структуру уравнения, что числа x = 0 и x = -10 являются решениями данного уравнения. С другой стороны, ясно, что это квадратное уравнение, а поэтому может иметь не более двух корней. Так как два корня уравнения уже подобраны, то других корней нет.
В некоторых случаях, для того чтобы не подбирать корень «вслепую», можно воспользоваться следующим методом.
Метод поиска рациональных корней у многочленов с целыми коэффициентами
Для решения такого рода уравнений и неравенств используется метод, в основе которого лежит Теорема 9 из предыдущего пункта. Рассмотрим подробнее суть этого метода. Пусть требуется найти рациональные корни уравнения n -й степени
причём все коэффициенты 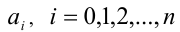

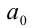
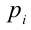
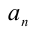
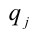
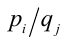
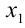
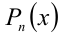
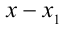

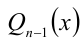
Пример:
При каких натуральных n уравнение 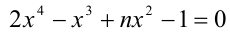
Решение:
Воспользуемся приведённым выше методом. Свободный член имеет два целочисленных делителя: ± 1, а старший коэффициент — два натуральных делителя: 1,2. Поэтому рациональные корни следует искать среди чисел 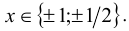
Ответ:
Метод неопределённых коэффициентов
Иногда для решения целых алгебраических уравнений (неравенств) с одной или несколькими неизвестными используют метод неопределённых коэффициентов. Пусть, например, решается уравнение
Суть метода состоит в том, что многочлен 
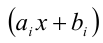
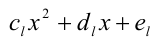
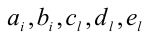
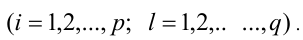
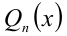
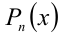
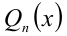
когда равны коэффициенты при одинаковых степенях переменной x, то, приравнивая эти коэффициенты, получают систему уравнений относительно неизвестных коэффициентов. Эту систему решают (или подбирают любое решение). Найденные таким способом коэффи-циенты 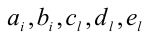
Рассмотрим применение этого метода на примере решения кубического уравнения. Допустим, требуется решить уравнение
Известно, что многочлен третьей степени всегда можно представить в виде произведения многочленов первой и второй степеней. Таким образом, сразу для всех действительных значений переменной x должно выполняться равенство
где числа а,b,c являются в данном случае искомыми неопределён-ными коэффициентами. Найдём их значения. После этого останется подставить их в правую часть (1) и, приравняв её к нулю, решить уравнение 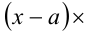
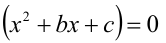
Чтобы найти коэффициенты а,b,c, раскроем скобки в правой части тождества (1) и приведём образовавшийся при этом многочлен к стандартному виду
Многочлены третьей степени тождественно равны тогда и только тогда, когда равны коэффициенты при одинаковых степенях x . Приравнивая коэффициенты при 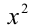
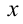
решая которую (можно даже просто подобрать любое решение этой системы) находим коэффициенты.
Пример:
Решить уравнение
Решение:
Воспользуемся для решения методом неопределённых коэффициентов. Будем искать разложение многочлена, стоящего в левой части уравнения, в виде
Раскрыв скобки, приведём многочлен в правой части к стандартному виду
Приравнивая коэффициенты слева и справа при 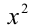
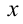
Найдя подбором решение 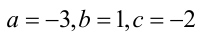
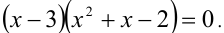
Пример:
При каких значениях а все корни уравнения 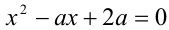
Решение:
Чтобы первое из уравнений имело корни, необходимо, чтобы его дискриминант был неотрицателен, т.е.
Далее, второй многочлен в силу теоремы Безу должен делиться нацело на первый многочлен. Иными словами, должно найтись такое b , что при всех действительных x справедливо тождество
Для нахождения неопределённых коэффициентов (в данном случае в их роли выступают а и b ) воспользуемся известным фактом, что два кубических многочлена, стоящие по разные стороны от знака равенства, тождественно равны тогда и только тогда, когда равны коэффициенты при одинаковых степенях переменной x . Приравнивая эти коэффициенты, получаем систему уравнений
Метод умножения на функцию
Иногда, применяя приём умножения обеих частей уравнения (неравенства) на некоторую функцию, удаётся упростить уравнение (неравенство).
Пример:
Решить уравнение
Решение:
Заметим, что x = — 1 (и вообще никакое отрицательное число) не является корнем данного уравнения. Домножим обе части данного уравнения на выражение (х +1). Получаем уравнение-следствие
множество решений которого состоит из всех решений исходного уравнения и числа x = -1. Это число является посторонним корнем, возникшем как раз в результате умножения уравнения на функцию, имеющую действительный нуль. Применяя известную формулу сокращенного умножения, получаем существенно более простое уравнение 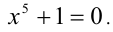
Ответ: уравнение не имеет решений.
Рассмотрим некоторые виды целых алгебраических уравнений, решаемые в основном при помощи специально подобранных подстановок.
Понятие алгебраического и трансцендентного уравнения и методов их приближенного решения
Введем понятия алгебраического и трансцендентного уравнения.
Алгебраическое уравнение — уравнение, в котором переменная 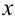
Примерами алгебраических уравнений могут служить уравнения вида: 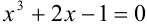
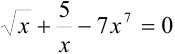
Уравнение, содержащее неизвестную переменную под знаком логарифма, тригонометрических функций, обратных тригонометрических функций или в показателе степени некоторого числа, называется трансцендентным.
Примерами трансцендентных уравнений могут служить уравнения вида:
Решить предложенное уравнение — значит найти все значения переменной 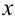
Из курса алгебры нам известны методы и приемы решения некоторых видов алгебраических и трансцендентных уравнений: например, квадратных уравнений; уравнений, решаемых методом группировки и вынесения за скобки общего множителя. Но даже решение несложного кубического уравнения вызовет у нас определенные сложности. Если нс удастся решить заданное уравнение привычными способами, существуют методы приближенного решения уравнений, состоящие из двух этапов:
1. отделение корней;
2. уточнение корней до заданной степени точности с помощью одного из следующих методов:
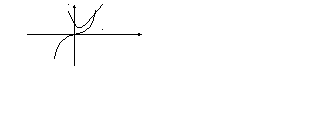
Этап отделения корней необходим для того, чтобы определить, какому промежутку принадлежат корни уравнения. На этом этапе обычно используется графический способ.
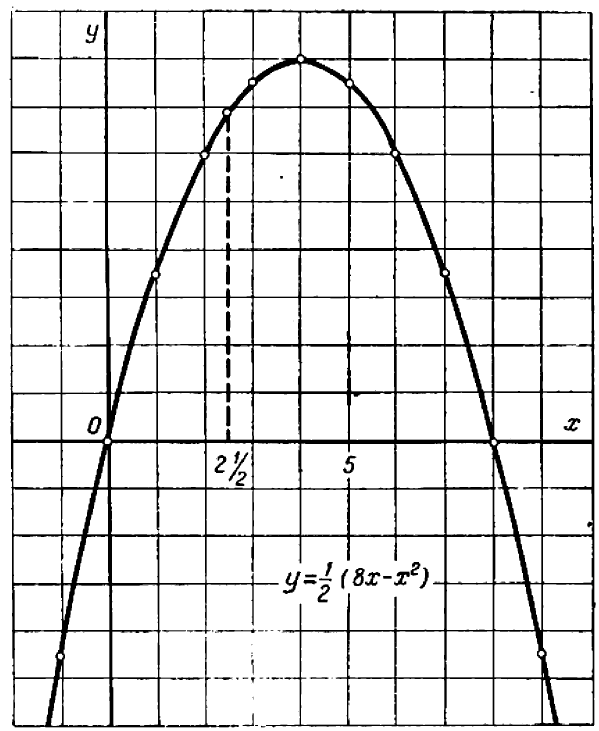
Пример:
Определить промежуток, которому принадлежат корни уравнения 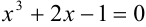
Решение:
Преобразуем данное уравнение к виду: 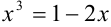
Построим графики функций 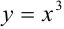
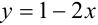
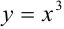
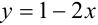
По рисунку видим, что графики функций 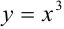
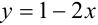
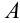
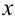
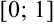
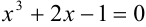
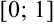
Ответ: 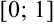
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
Алгебраические уравнения и их геометрическое истолкование
Уравнение с одной буквой (неизвестным)
Один из основных вопросов, которыми занимается алгебра, заключается в решении уравнений нормального вида. Так называются уравнения, у которых в левой части стоит многочлен, расположенный по степеням неизвестной буквы, а в правой части — нуль.
Степень многочлена в левой части носит название степени уравнения.
Мы встречались не раз с уравнениями, которые не имели нормального вида: таковы, например, уравнения 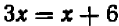
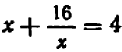
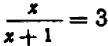
Подобного рода уравнения могут быть приведены к уравнениям нормального вида. Для этого до статочно освободиться от дробей, затем перенести на лево члены, стоящие в правой части, сделать приведение подобных членов и, наконец, правильно расположить члены.
Таким образом, привести заданное уравнение к уравнению нормального вида удается по большей части несложными приемами.
Напротив, нахождение всех корней уравнения представляет собою более трудную задачу, в особенности в том случае, если уравнение высокой степени.
Уравнение первой степени (линейное) имеет вид 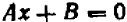
Уравнение второй степени (иначе квадратное) имеет вид 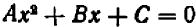
Уравнение третьей степени (иначе кубическое) имеет вид 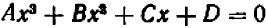
Так можно продолжать и дальше. Ради единообразия неизвестное здесь обозначено буквой 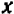
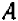
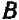
Уравнение первой степени мы решаем (см. гл. 6) следующим образом: свободный член переносим направо 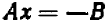
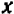
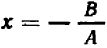
В случае уравнений второй степени или высших степеней решение уравнения тесно связано с разложением левой части на линейные множители. Так, например, уравнение 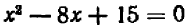
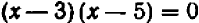
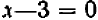
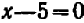
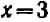
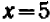
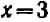
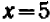
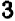
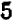
В отдельных примерах нам удавалось разлагать трехчлен второй степени на линейные множители; более полно общий прием разложения (по средствам «выделения квадрата») будет рассмотрен в главе 12.
Что касается уравнений третьей, четвертой и высших степеней, то, не говоря об отдельных частных случаях, разложить их левую часть на множители весьма трудно. С другой стороны, очень просто можно составить уравнение, имеющее наперед заданные корни; при этом степень уравнения в точности будет равняться числу корней.
Например, пусть заданы три числа: 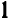
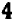
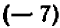
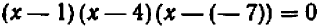
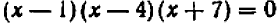
Производя умножение, получаем окончательно: 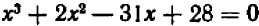
Можно доказать, что число корней уравнения никогда не превышает его степени. Но иногда оно бывает меньше степени уравнения.
Например, уравнение 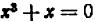

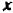
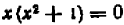
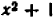
Совокупность точек на числовой оси, являющихся корнями уравнения (иначе, удовлетворяющих этому уравнению), дает нам геометрическое представление этого уравнения.
Уравнение с двумя буквами (переменными)
Нам хорошо известно, что решением (корнем) уравнения с одной неизвестной буквой называется всякое значение входящей буквы, удовлетворяющее уравнению.
Если уравнение содержит две неизвестные буквы, понятие решения должно быть обобщено и именно следующим образом: решением уравнения с двумя неизвестными буквами называется пара значений двух неизвестных, удовлетворяющая уравнению.
Так, пара чисел 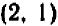
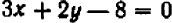

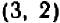
В случае уравнения с двумя неизвестными найти и перечислить все решения, как правило, невозможно. Уже простейшие примеры, вроде 
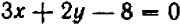
Поэтому, если в уравнение входят две (или более) неизвестных буквы, их называют обыкновенно не неизвестными, а переменными (переменными величинами).
Алгебраическое уравнение с двумя буквами считается нормальным, если в правой части стоит нуль, а в левой — многочлен, расположенный по обеим буквам.
Уравнения с двумя буквами (как и уравнения с одной буквой) классифицируются по степеням: степенью уравнения называется степень многочлена, стоящего в его левой части, причем обе буквы считаются главными.
Уравнения первой степени (линейные) имеют вид 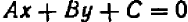
Уравнения второй степени (квадратные) имеют вид 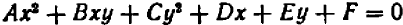
Отдать себе отчет в том, какова совокупность решений данного уравнения, нам помогает геометрическое представление уравнения: оно делает наглядной ту зависимость, которая существует между значениями букв, удовлетворяющими уравнению. Познакомимся ближе с этим геометрическим представлением.
Так как у нас имеется не одна, а две буквы, допустим, 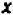
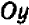
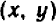
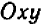
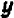
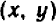
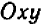
Пример:
Рассмотрим уравнение 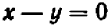
Его графиком является совокупность точек 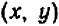
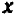
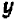
Пример:
Второй пример возьмем более сложный. Пусть нам дано уравнение второй степени: 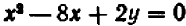
Посмотрим, как можно наметить его график.
Ничего не стоит решить уравнение относительно буквы 
Дальше можно составить табличку числовых значений переменной 
Каждую полученную точку сейчас же отмечают на черте же. Точки располагаются с известной правильностью.
Чертеж 39 показывает, что при возрастании значений 
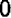
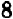
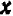
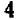
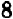
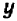
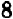
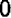
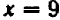
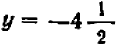
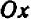
При 
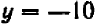
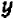
Можно букве 
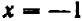
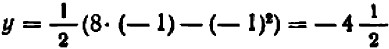
Полезло убедиться, что точки, получающиеся при подстановке дробных значений 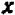
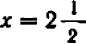
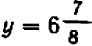
Поставим себе еще и такой вопрос: имеет ли наш график какие-нибудь точки на оси 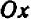
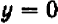

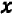

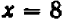
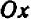
Хотя мы отметили на чертеже не свыше десятка точек, положение которых нам известно вполне точно, тем не менее правильность их расположения не оставляет сомнений в том, что все остальные, не отмеченные нами, точки графика лежат на некоторой плавной кривой, проходящей через отмеченные точки.
Эта кривая и есть график нашего уравнения. Провести ее от руки не представит труда.
Правда, полученная таким образом кривая даст возможность лишь приближенно судить о положении тех точек графика, координаты которых не были вычислены.
Использованный нами прием получения графика носит название построения графика по точкам.
Постараемся дать описание этого приема, не связывая его с каким-либо определенным примером. Пусть дано некоторое уравнение, содержащее буквы 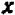
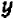
Посмотрим, существуют ли такие точки графика, которые имеют заранее назначенную абсциссу, скажем, 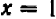
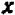

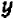
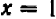

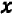
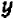
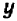
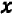
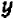
Разумеется, можно было бы также решить данное уравнение относительно буквы 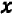
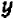
Примечание:
Иные уравнения — таковы, что не существует ни одной точки, координаты которой удовлетворяли бы уравнению.
Тогда график отсутствует или представляет собою «пустое место».
Этим свойством обладает, например, уравнение 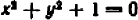
В редких случаях график может оказаться состоящим из одной точки или нескольких точек (в конечном числе). Так, уравнение 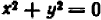

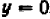
Действительно, каждый из квадратов 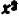
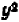
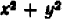
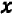
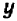
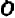
Линейное уравнение с двумя переменными
На чертеже 40 изображен график уравнения 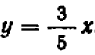
Это — прямая линия, проходящая через начало координат и расположенная в первой и третьей четвертях.
Уравнение показывает, что величина у прямо пропорциональна величине . Желая найти все точки графика с целыми координатами, мы даем букве значения, кратные , и получаем точки: , 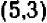
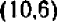
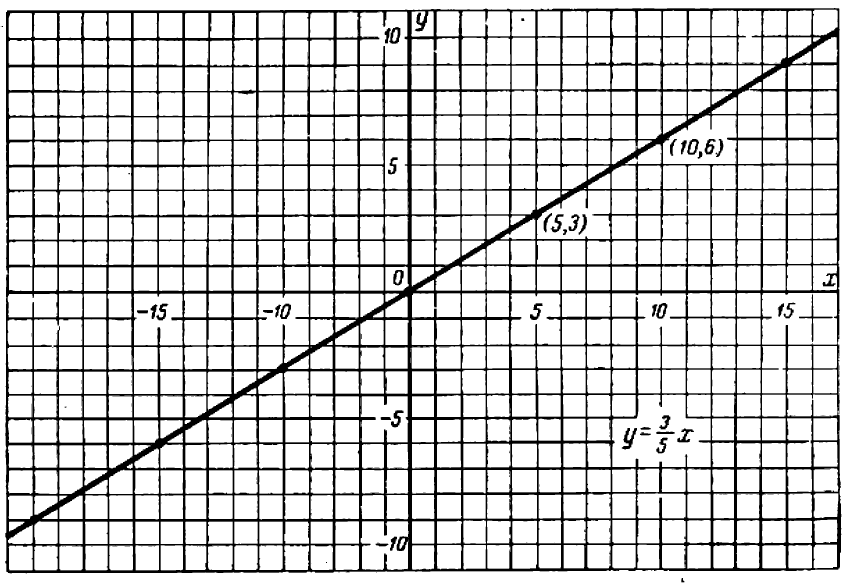
Эти точки отмечены на чертеже. Чтобы перейти от одной такой точки к следующей (считая вправо), достаточно отсчитать « клеточек вправо и 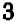
Коэффициент пропорциональности 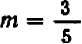
таким образом, определить направление нашей прямой.
Если бы вместо уравнения (I) было задано, например, уравнение 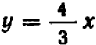
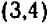
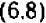
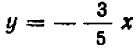
При значениях , кратных , получаем точки: , , и т. д.
Отсчитывать нужно « клеток вправо и — вниз». Прямая, являющаяся графиком этого уравнения, расположена во второй и в четвертой четвертях. Из наших примеров можно сделать следующие общие заключения. Графиком уравнения вида (4) является прямая линия, проходящая через начало . Придавая уравнению вид , мы убеждаемся, что коэффициент пропорциональности представляет собою отношение ординаты любой точки графика к ее абсциссе. Если , то прямая проходит в первой и третьей четвертях; если , то во второй и четвертой. При уравнение принимает вид , и графиком тогда является ось .
Чем меньше по абсолютному значению, тем более полого расположена прямая (т. е. тем меньше острый угол, образованный ею с горизонтальной осью); напротив, чем больше по абсолютному значению, тем более круто расположена прямая (тем упомянутый острый угол ближе к прямому).
Коэффициент в уравнении (4) называется наклоном прямой, являющейся графиком этого уравнения.
Обратим внимание на то, чем график уравнения отличается от графика уравнения . При каждом данном значении абсциссы соответствующая ордината увеличена на единиц (, или ); значит, получается снова прямая линия, но «сдвинутая» на единиц в направлении оси : она уже не проходит через начало , а пересекает ось в точке .
Таким образом, направление прямой то же, что и направление прямой : оно зависит от коэффициента при в уравнении прямой, решенном относительно (называемого и в этом случае наклоном прямой).
Другими словами, прямые и параллельны.
На черт. 41 изображен график уравнения . Это — прямая, параллельная прямой , но образующая на оси отрезок, равный .
Черт. 41
Пусть буква обозначает какое угодно число. Постараемся уяснить себе, каков график уравнения .
Нам нужно установить, какова совокупность точек на плоскости , координаты которых удовлетворяют уравнению. Уравнение не удовлетворяется, если значение абсциссы не равно ; если же оно равно , то, како во бы ни было значение ординаты , уравнение удовлетворяется. Это значит, что уравнению удовлетворяют координаты любой точки на прямой, параллельной оси и отстоящей от этой оси вправо на расстоянии .
Итак, уравнение вида имеет графиком прямую, параллельную оси . Точно так же уравнение вида имеет графиком прямую, параллельную оси .
Из предыдущего следует весьма важное заключение: всякое уравнение, линейное относительно буквы и именно, уравнение вида (где , и — постоянные числа, причем и не равны нулю одновременно), имеет своим графиком прямую линию .
Действительно, если буква на самом деле входит в уравнение (это значит, что не равно нулю), то не представляет труда решить уравнение относительно . Мы получим: и далее, деля все уравнение на , полагая затем
приходим к уравнению вида
, которое, как нам уже известно, изображается прямой линией.
Если же буква отсутствует в уравнении (т. е., если ), то тогда уравнение можно решить относительно буквы (раз , то, по предположению, ), и мы получим: или (где для краткости положено ). Графиком такого уравнения является совокупность точек, имеющих абсциссу ; это также прямая, но уже параллельная оси .
Рассматривать случай, когда не представляет интереса. В этом случае, если , заданное уравнение не удовлетворяется ни при каких значениях и и, значит, график этого уравнения представляет собою «пустое место»; если же , то напротив, уравнение удовлетворяется при всех значениях и тогда его «график» — вся плоскость.
Раз известно, что линейное уравнение изображается прямой линией, то для того, чтобы начертить эту линию на координатной плоскости (на листе клетчатой бумаги), нет необходимости в больших вычислениях.
В самом деле, прямая определяется двумя точками: значит, достаточно сделать две числовые подстановки.
Проще всего установить точки пересечения прямой с осями и . Пусть, например, дано уравнение . Полагая , получим уравнение относительно : , из которого следует, что . Таким образом, найдена точка графика , лежащая на оси . Полагая , получим таким же образом: , откуда следует, что . Итак, найдена точка графика , лежащая на оси . Затем остается провести прямую через точки и .
Указанный прием неудобен только в том случае, если точки и находятся очень близко одна от другой, т. е. близки к началу ; он непригоден вовсе, если график проходит через начала . В этих случаях следует делать какие-нибудь другие подстановки.
Например, чтобы построить график прямой , заметим прежде всего, что она проходит через начало ; чтобы получить еще одну точку, положим и получим ; итак, прямая проходит через точку .
Нелинейные уравнения с двумя переменными
Мы видели, что если заданное уравнение — линейное (т. е. первой степени) относительно букв и , то его график — прямая линия.
Дальнейшие примеры покажут, что если заданное уравнение — не линейное (т. е. степени второй или выше) относительно букв и , то его графиком являются кривые линии.
Степень уравнения относительно букв и называется порядком соответствующей кривой.
Мы рассмотрим здесь только несколько наиболее простых и важных примеров кривых, преимущественно второго порядка.
Пример:
С этим уравнением мы уже встречались. Оно говорит о том, что переменные величины и обратно пропорциональны.
Можно ли решить уравнение относительно ? Ответ — утвердительный, если только имеет значение, не равное нулю. Но легко понять, что при никакое значение не может удовлетворить уравнению: это значит геометрически, что на оси нет ни одной точки графика.
Итак, пусть теперь . Решим уравнение относительно у: .
Это равенство свидетельствует, что есть «величина, обратная величине ». Посмотрим, как изменится величина, обратная , при изменении самого .
Ограничиваясь пока положительными значениями величины , станем составлять табличку и одновременно отмечать точки на чертеже. Ясно, что с увеличением величина убывает, приближаясь к нулю. Но значения она не принимает.
Попробуем взять и дробные значения :
Получающиеся на чертеже точки имеют правильное расположение: через них можно с уверенностью про вести плавную кривую. Менее ясно пока, как вести кривую влево, в промежутке от до . Продолжим табличку:
и станем отмечать новые точки. Теперь становится ясно, что с убыванием положительных значений величина возрастает и притом не ограничено. Именно, примет какое угодно большое значение, если только значение будет достаточно малым. Кривая (при движении справа налево) поднимается вверх, примыкая к оси , хотя, как мы видели, с этой осью общих точек не имеет (см. черт. 42).
Черт. 42
Вся полученная кривая расположена в первой четверти. Если бы мы пожелали давать букве отрицательные значения, то, составляя соответствующую таблицу и при этом производя деление по известным правилам, получили бы в третьей четверти другую «ветвь» кривой.
Обе «ветви». рассматриваемые совместно, образуют кривую, называемую «гиперболой».
Гипербола — кривая второго порядка.
Пример:
Подставляя положительные значения , получаем таблицу:
Отметив соответствующие точки на чертеже, мы видим, что при увеличении абсциссы ордината очень быстро возрастает, причем сам график (если попробовать его провести) все больше выпрямляется. Напротив, ближе к началу он довольно сильно искривлен. Подставляя еще значения , , , мы получим:
В первой клеточке сделаем подстановки даже через одну десятую:
Последняя табличка позволяет заключить, что. под ходя к началу . график тесно примыкает к оси , касается ее.
Обращаясь к отрицательным значениям , мы видим, что при возведении в квадрат отрицательного числа знак минус будет уничтожаться. Отсюда ясно, что кривая продолжается из первой четверти во вторую симметрично относительно вертикальной оси.
Черт. 43
Полученная кривая носит название параболы(см. черт. 43).
Парабола — кривая также второго порядка.
Пример:
При подстановке больших значений , как показывает следующая таблица, кубы возрастают гораздо быстрее, чем квадраты:
Напротив, при подстановке значений, близких к нулю, кубы убывают быстрее, чем квадраты:
Поэтому кривая с возрастанием поднимается вверх гораздо круче, чем парабола ; и при убывании до нуля гораздо теснее примыкает к оси .
На параболу эта кривая не похожа еще и в том отношении, что у нее отсутствует вертикальная ось симметрии; но имеется центр симметрии в начале . Это зависит от того, что при возведении в куб отрицательного числа его абсолютное значение возводится в куб, но знак остается отрицательный.
Общий вид кривой (кубической параболы) показан на черт. 44.
Черт. 44
Это — кривая третьего порядка.
Алгебраические уравнения и алгоритм их решения
Общая теория уравнений
Тождества:
Введем понятие тождественного равенства функций на числовом множестве X.
Пусть функции у = f(х) и у = F(х) имеют области определения А и В соответственно, и X является подмножеством как A, так и В (но не обязательно совпадает с пересечением А и В). Тогда функции у = f(х) и у = F(х) определены на X.
Функции у=f(х) и у=F(х) называются тождественно равными на числовом множестве X, если для любого числа х из X выполняется равенство f(х)=F(х). В этом случае говорят, что равенство f(х)=F(х) является тождеством на множестве X.
Разумеется, равенство f(х)=F(х) может быть тождеством на некотором множестве X, но не быть тождеством на каком-нибудь другом множестве Y . Рассмотрим, например, функции у=х и у =|x|. На множестве X положительных чисел эти функции тождественно равны: если х — положительное число, то |х|=х. На множестве же Y всех действительных чисел эти функции не являются тождественно равными: при отрицательных значениях х равенство
не имеет места, так как при этих значениях |x|= — х.
Совершенно так же определяется понятие тождественного равенства для функций нескольких переменных. Например, функции переменных х и у тождественно равны на множестве всех значений этих переменных: для любых значений х и у выполняется равенство
Функции же z=х+у и z =|х+у | тождественно равны лишь на множестве пар чисел х, у , для которых или, что то же самое,
Область допустимых значений
Тождественные преобразования многочленов и алгебраических дробей изучались в начальной алгебре, и мы не будем подробно останавливаться на этом вопросе. Разберем лишь вопрос об области допустимых значений функционального равенства. Пусть дано равенство вида
Может случиться, что функции у=f(x) и у=F(x) определены не для всех значений х . Областью допустимых значений аргумента х для равенства (1) мы будем называть множество всех значений х, при которых определены и левая и правая части этого равенства.
Например, для тождества
областью допустимых значений является совокупность всех действительных чисел, из которой исключены числа 2 и 4 (при х=2 не определена функция , а при х=4 — функция ).
Следует иметь в виду, что такие преобразования, как приведение подобных членов, могут привести к изменению области допустимых значений. Например, тождество (2) справедливо для всех значений х , кроме х=2 и х=4. Если же мы приведем подобные члены, то получим тождество
справедливое для всех без исключения значений х.
Уравнения
Обычно когда даны две функции у=f(х) и у=F(х), то неизвестно, каково множество, на котором эти функции тождественно равны. Поэтому возникает следующая задача: найти все значения х, для которых выполняется равенство
При такой постановке задачи (*) называют уравнением с неизвестным х , а все х , при которых функции у=f(х) и у=F(х) принимают одинаковые значения, — корнями или решениями этого уравнения.
Итак, уравнение f(x) =F(х) выражает задачу об отыскании таких значений переменного х, при которых функции f(x) и F(x) имеют одинаковые значения. Решить уравнение — это значит найти все такие значения х, т. е. все корни (решения) уравнения.
Областью допустимых значений для уравнения (1) называют множество всех х у при которых определены обе функции у=f(х) и у=F(х). Например, для уравнения
область допустимых значений определяется условиями:
Область допустимых значений может заранее ограничиваться некоторыми условиями. Например, могут иметь смысл лишь положительные или лишь целые корни. В этом случае надо рассматривать уравнение лишь для положительных (или целых) значений х.
Тогда мы считаем, что функции f(x) и F(х) заданы на некотором множестве X, и рассматриваем уравнение лишь на этом множестве.
Пусть даны два уравнения
Обозначим множество корней уравнения (1) через M, а множество корней уравнения (2) через N. Если (то есть, если всякий корень уравнения (1) является корнем уравнения (2)), то уравнение (2) называют следствием уравнения (1). Например, уравнение является следствием уравнения 2х—6= 0. В самом деле, корнем уравнения 2х — 6=0 является х=3, а при этом значении многочлен обращается в нуль.
Если множества М и N корней уравнений (1) и (2) совпадают, то эти уравнения называются равносильными. Иными словами, уравнения
равносильны, если всякий корень уравнения (2) является корнем уравнения (3) и, обратно, всякий корень уравнения (3) является корнем уравнения (2).
В частности, уравнения равносильны, если множества М и N — пусты, то есть если каждое из уравнений не имеет решений.
Если уравнения (2) и (3) равносильны, то каждое из них является следствием другого.
Следует отметить, что понятие равносильности уравнений существенно зависит от того, какие значения корней считаются допустимыми. Рассмотрим, например, уравнения:
Корнями первого уравнения является число х=3, а второго — числа Так как эти множества различны, то уравнения (4) и (5) не являются равносильными. Но если рассматривать лишь рациональные значения корней уравнения, то уравнения (4) и (5) оказываются равносильными — ибо они имеют по единственному рациональному корню х = 3. Как правило, мы будем в дальнейшем рассматривать равносильность относительно множества всех действительных чисел. Иными словами, уравнения будут считаться равносильными, если они имеют одни и те же действительные корни.
Совокупности уравнений
Пусть задано несколько уравнений
и требуется найти все значения х, которые удовлетворяют хотя бы одному из этих уравнений. Тогда говорят, что задана совокупность уравнений, а такие значения х называют решениями или корнями этой совокупности. Следует различать совокупность уравнений и систему уравнений — для системы уравнений требуется искать значения неизвестных, которые удовлетворяют всем уравнениям, а для совокупности — хотя бы одному из уравнений.
Чтобы отличать совокупность уравнений от системы уравнений, мы будем обозначать совокупность квадратными скобками, а систему — фигурными скобками.
имеет одно решение , а совокупность тех же уравнений
имеет три решения
Обозначим множество решений уравнения через а множество решений совокупности уравнений (1) через N. Тогда Например, множество решений совокупности
состоит из чисел 2, 3 (решений уравнения 1, —1 (решений уравнения ) и —7 (решения уравнения Число х=3 является решением, хотя при этом значении не определена функция
Две совокупности уравнений
называются равносильными, если они имеют одно и то же множество корней.
Например, совокупности уравнений
равносильны — их корнями являются числа 2, —2 и —3.
Преобразования уравнений
При решении уравнений мы переходим от одного уравнения к другому, пока не придем к уравнению вида х = а или совокупности уравнений такого вида. Возьмем, например, уравнение
Прибавляя к обеим частям этого уравнения (—Зх+3) и приводя подобные члены, получаем уравнение
А теперь умножим обе части уравнения (2) на и получим, что
В процессе решения этого уравнения мы прибавляли к обеим частям уравнения некоторое алгебраическое выражение (а именно, —Зх+3), умножали обе части уравнения на одно и то же число (а именно, на). Кроме того, мы выполняли тождественные преобразования. Заметим, что уравнения (1), (2) и (3) имели одно и только одно решение х = 2. Таким образом, все проведенные преобразования приводили к уравнениям, равносильным первоначальному уравнению (1), имевшим с ним одно и то же решение.
Однако не всегда одинаковые преобразования обеих частей уравнения приводят к уравнению, равносильному первоначальному. Рассмотрим уравнение:
Его решением является х = 3. Если же мы умножим обе части уравнения на х — 2, то получим уравнение:
Это уравнение, кроме решения х=3, имеет еще решение х= 2— оно имеет лишний корень по сравнению с (4).
С другой стороны, если мы возьмем уравнение (5), имеющее решения х=2, х=3, и «сократим» его на х — 2 (то есть разделим обе части уравнения на х — 2), то получим уравнение 2х+1= =х+4 с единственным решением х=3. Значит, здесь мы в процессе решения потеряли корень х=2.
Не является «безобидным» и прибавление к обеим частям уравнения одного и того же алгебраического выражения. Например, уравнение
имеет решение х =2. Но если прибавить к обеим частям этого уравнения выражение , то получим уравнение
для которого х =2 не является решением — обе части этого уравнения не имеют смысла при х=2. Таким образом, произошла потеря решения.
Эти примеры наглядно показывают, что при преобразовании уравнений необходима осторожносгь — неправильно преобразуя уравнение, мы можем как приобрести лишние решения, так и потерять решения данного уравнения. При этом надо иметь в виду, что приобретение лишних решений не столь опасно, как потеря существующих. Ведь после того, как уравнение решено, можно подставить все найденные решения в заданное уравнение и отобрать те из решений, которые ему удовлетворяют. А потерянные решения восстановить уже нельзя.
Из изложенного видно, что, прежде чем решать конкретные виды уравнений, надо познакомиться с общей теорией уравнений, выяснить, какие преобразования приводят к равносильным уравнениям, какие дают посторонние решения, а при каких решения могут быть потеряны. Только после этого мы сможем решать уравнения «с открытыми глазами».
Теоремы о равносильности уравнений
Сформулируем сначала условия, при которых одно уравнение является следствием другого уравнения. Потом из этих условий будут получены условия равносильности уравнений.
Теорема:
Если к обеим частям уравнения
прибавить функцию имеющую смысл при всех допустимых значениях неизвестного х, то получится новое уравнение
являющееся следствием данного.
Доказательство:
В самом деле, пусть а—корень уравнения (1). Тогда f(а)=F(а). Но является некоторым числом, так как по условию функция определена для всех допустимых значений х и, в частности, при х=а. Прибавим к обеим частям числового равенства f(a)=F(а) число . Получим равенство
которое показывает, что число а является корнем уравнения (2). Таким образом, всякий корень уравнения (1) является корнем уравнения (2), то есть уравнение (2) является следствием уравнения (1).
Условие, что функция определена при всех допустимых значениях х, существенно. Если не определено при х=а, где а — решение уравния (1), то уравнение (2) не является следствием уравнения (1) и уравнения (1) и (2) неравносильны: х = а является решением для (1), но не является решением для уравнения (2). Примером могут служить уравнения (6) и (7) из п. 5.
Прибавление к обеим частям уравнения одного и того же выражения не может привести к приобретению посторонних корней, если это прибавление не сопровождается приведением подобных членов или иными преобразованиями, меняющими область определения уравнения (например, сокращением дробей). Рассмотрим, например, уравнение
Если прибавить к обеим частям — и привести подобные члены, то получим уравнение Зх +1= 9 — х, имеющее решение х = 2. Это решение не принадлежит области определения исходного уравнения и потому не удовлетворяет ему.
Перейдем к вопросу об умножении обеих частей уравнения на одно и то же выражение.
Теорема:
Если обе части уравнения
умножить на функцию , имеющую смысл при всех допустимых значениях х, то получится новое уравнение
являющееся следствием уравнения (3).
Доказательство.
Пусть а — корень уравнения (3). Тогда справедливо равенство f(а)=F(а). Умножим обе части этого равенства на число . Мы получим числовое равенство Оно показывает, что а является корнем и уравнения (4). Таким образом, всякий корень уравнения (3) является корнем уравнения (4), то есть (4) — следствие (3).
Из доказанных теорем следует, например, что уравнение
является следствием уравнения
Действительно, уравнение (5) получается из уравнения (6) прибавлением к обеим частям функции Зх+2 и умножением полученного уравнения на х + 2.
Многочлены определены при всех значениях х. Поэтому прибавление к обеим частям уравнения многочлена, равно как и умножение обеих частей
уравнения на многочлен, приводит к уравнению, являющемуся следствием исходного.
Оговорка о том, что должно иметь смысл при всех допустимых значениях х, существенна для справедливости теоремы 2. Рассмотрим, например, уравнение
и умножим обе части этого уравнения на Мы получим уравнение Оно уже не является следствием исходного: уравнение (7) имеет корни 2 и 3, а уравнение — лишь корень 3. Причиной потери корня явилось то, что функция не определена при х = 2, а это значение как раз является корнем заданного уравнения.
Докажем теперь теоремы о равносильности уравнений. Чтобы доказать равносильность двух уравнений, надо показать, что пер вое из них является следствием второго, а второе — следствием первого.
Теорема:
Если функция определена при всех допустимых значениях неизвестного х, то уравнения
Доказательство:
Мы уже видели, что при условии теоремы уравнение (9) является следствием уравнения (8). Но уравнение (8) в свою очередь получается из уравнения (9) прибавлением к обеим частям функции — и приведением подобных членов.
Так как функция определена при всех допустимых значениях х, то уравнение (8) является следствием уравнения (9). Тем самым доказано, что уравнения (8) и (9) равносильны.
Из доказанной теоремы вытекает правило перенесения слагаемых из одной части уравнения в другую: если некоторое слагаемое данного уравнения перенести из одной части в другую, изменив знак этого слагаемого на противоположный, то получится уравнение, равносильное данному.
В самом деле, в силу теоремы 3 уравнения
равносильны: уравнение (11) получается путем прибавления функции — к обеим частям уравнения (10) и приведения подобных членов.
Кратко правило перенесения слагаемых формулируют так: всякое слагаемое можно перенести из одной части уравнения в другую, изменив при этом его знак на противоположный.
Из доказанной теоремы вытекает, что всякое уравнение f(х) =F(х) можно заменить равносильным ему уравнением вида Ф(х) = 0. Для этого достаточно перенести F(х) в левую часть уравнения, заменив знак на противоположный, и положить f(х)— F(х) =Ф (х).
Теорема:
Если функция определена для всех допустимых значений х и ни при одном допустимом значении х не обращается в нуль, то уравнения
Доказательство:
Мы уже видели (теорема 2), что уравнение (13) является следствием уравнения (12). Докажем, что уравнение (12) в свою очередь является следствием уравнения (13). Уравнение (12) получается из уравнения (13) умножением обеих частей на функцию Так как по условию функция определена для всех допустимых значений х и не обращается при этих значениях в нуль, то функция также определена при всех допустимых значениях х. Поэтому уравнение (12) является следствием уравнения (13), а значит, эти уравнения равносильны.
Из доказанной теоремы вытекает, например, что уравнения
равносильны в области действительных чисел. В самом деле, уравнение (15) получается из уравнения (14) умножением на функцию , а эта функция всюду определена и не обращается в нуль при действительных значениях х.
не являются равносильными — второе получается из первого умножением на функцию , а эта функция обращается в нуль при х = ± 1. Поэтому второе уравнение, кроме корня удовлетворяющего и первому уравнению, имеет еще и корни
Уравнения (12) и (13) могут быть неравносильными и в том случае, когда множитель теряет смысл при некоторых допустимых значениях неизвестного. Например, уравнения
неравносильны: множитель теряет смысл при х = 2, а x = 2 как раз является корнем уравнения
Если в ходе решения уравнения приходилось умножать обе части этого уравнения на выражение , содержащее неизвестное, то надо проверить две вещи: а) Не обращается ли в нуль при допустимых значениях не известного? б) Не теряет ли смысл при некоторых допустимых значениях неизвестного?
В первом случае среди найденных корней могут оказаться посторонние корни, и надо проверить все найденные корни, удовлетворяют ли они первоначально заданному уравнению. Во втором же случае возможна потеря корней, и мы должны подставить в заданное уравнение значения неизвестного, при которых теряет смысл — среди этих значений могут оказаться потерянные в ходе решения корни уравнения.
Из теоремы 4 непосредственно вытекает справедливость утверждения: если обе части уравнения умножить на произвольное отличное от нуля число, то получим уравнение, равносильное данному.
Это утверждение кратко формулируют так: обе части уравнения можно умножать на произвольное отличное от нуля число.
Уравнения с одним неизвестным
Алгебраические уравнения с одним неизвестным:
Рациональным алгебраическим уравнением с одним неизвестным называют уравнение вида
где R(х) — алгебраическая дробь относительно х. К такому виду можно в силу теорем 3 и 5, привести любое уравнение — алгебраические дроби. Например, уравнение
является рациональным алгебраическим. В дальнейшем мы будем называть такие уравнения просто алгебраическими.
Применяя теоремы о равносильности уравнений, можно заменить каждое уравнение вида (1) равносильным ему уравнением вида:
где f(x)— многочлен от х. Для этого надо записать дробь R(x) в виде отношения двух многочленов. Мы получим уравнение:
где f(х) и — многочлены от х. Но дробь может равняться нулю лишь в случае, когда равен нулю ее числитель. Поэтому решение уравнения (1) сводится к решению уравнения f(x)=0, где f(х) — многочлен от х. При этом нужно иметь в виду, что решениями уравнения (1) являются лишь те корни уравнения (2), при которых дробь R(x) имеет смысл (то есть отлично от нуля).
Пример:
Перенесем в левую часть уравнения и приведем получившуюся сумму к общему знаменателю. Получим уравнение:
Приравнивая нулю числитель этой дроби, получаем уравнение х—2=0, корнем которого является число х=2. Однако при x=2 дробь не определена. Поэтому заданное уравнение корней не имеет.
Метод разложения на множители
Рассмотрим некоторые методы решения алгебраических уравнений, а также отдельные виды таких уравнений.
Выше было сказано, что при решении уравнения его заменяют другими уравнениями или совокупностями уравнений, равносильными заданному, но более простыми
Рассмотрим следующий пример. Пусть надо решить уравнение:
Мы знаем, что произведение может равняться нулю тогда и только тогда, когда хоть один из его сомножителей равен нулю. Поэтому, чтобы решить уравнение (1), надо найти все значения, при кототых хоть один из сомножителей равен нулю. А это все равно, что решить совокупность уравнений
Решая ее, находим для х значения и 6. Они и дают корни уравнения (1).
Метод, примененный для решения уравнения (1), в общем виде формулируется так.
Теорема:
Если функции определены на некотором множестве М, то на этом множестве уравнение
равносильно совокупности уравнений
Доказательство:
Пусть а — одно из решений совокупности (3). Это означает, что а является корнем одного из уравнений этой совокупности, например, уравнения а все остальные функции определены при х = а. Но тогда
так как один из сомножителей равен нулю. Следовательно, любое решение совокупности (3) является корнем уравнения (2).
Наоборот, пусть а — корень уравнения (2). Тогда f (а)=0, то есть Но произведение равно нулю лишь в случае, когда хоть один из сомножителей равен нулю. Поэтому хотя бы одно из чисел равно нулю. Это означает, что а является корнем хотя бы одного из уравнений то есть одним из решений совокупности уравнений (3).
Пример:
Левая часть этого уравнения разлагается на множители следующим образом:
Отсюда следует, что уравнение (4) равносильно совокупности уравнений:
Решая уравнения этой совокупности, получаем корни уравнения (4):
не равносильны, так как при х = 0 функция не определена. На множестве же они равносильны.
В некоторых случаях разложение на множители связано с искусственными преобразованиями. Рассмотрим, например, уравнение:
Нетрудно заметить, что
Поэтому уравнение (б) можно записать в виде:
Таким образом, все свелось к решению совокупности двух квадратных уравнений:
Решая их, находим корни уравнения (6):
Метод введения нового неизвестного
Наряду с методом разложения на множители часто применяется другой метод — введение нового неизвестного.
Рассмотрим следующий пример:
Если раскрыть скобки, то получится уравнение четвертой степени, решить которое довольно сложно. Мы поступим иначе. Обозначим через r. Тогда
Поэтому уравнение (1) после введения нового неизвестного z принимает вид
Решая это квадратное уравнение, получаем, что его корни равны:
Но Поэтому х удовлетворяет или уравнению или уравнению то есть совокупности уравнений:
Решая ее, получаем:
Метод, примененный для решения уравнения (1), в общем виде заключается в следующем.
Пусть дано уравнение F(х)=0 и пусть функцию F(х) можно представить в виде так что уравнение F (х)=0 записывается в виде
Введем новое неизвестное z, положив Тогда вместо уравнения (1) получаем уравнение относительно Докажем следующую теорему.
Теорема:
Если а — один из корней уравнения f(z) = 0, а b — один из корней уравнения то b является одним из корней уравнения F(х)=0, где . Обратно, если b — корень уравнения F(х)=0, то — один из корней уравнения f(z)= 0 .
Доказательство. Пусть b — корень уравнения где а — корень уравнения f (z)=0; f(а) =0. Тогда и потому
Таким образом, b удовлетворяет уравнению F (х) = 0.
Обратно, пусть b — корень уравнения F(х)=0 и Тогда
Следовательно, а — корень уравнения f(z)=0. Теорема доказана.
Из доказанной теоремы следует, что решение уравнения вида сводится к следующему: сначала находят корни уравнения f(z) =0; после этого надо решить все уравнения Совокупность корней этих уравнений и дает решение уравнения (2).
Биквадратные уравнения
Метод замены неизвестного при меняется для решения уравнений вида
Такие уравнения называют биквадратными. Чтобы решить уравнение (1), положим Тогда получим квадратное уравнение:
Его корнями являются числа:
Поэтому корни уравнения (1) получаются путем решения уравнений Значит, мы получаем четыре корня для уравнения (1)
Четыре корня возникают при различных комбинациях знаков:
При решении биквадратных уравнений (как и при решении квадратных уравнений) иногда приходится извлекать квадратные корни из отрицательных чисел. Это приводит к так называемым комплексным числам, которые будут изучены в главе V.
Пример. Решить уравнение
Полагая получаем квадратное уравнение:
Его корнями являются числа Значит, корни уравнения (8) имеют вид:
Возвратные уравнения 3-й и 4-й степеней
Многочлен n-й степени
называется возвратным, если его коэффициенты, одинаково уда ленные от начала и от конца, равны между собой. Иными словами, коэффициенты возвратного многочлена n-й степени удовлетворяют условию
Алгебраическое уравнение вида f(х)=0, где f(х) — возвратный многочлен, называют возвратным уравнением. Примерами таких уравнений являются:
Рассмотрим решение возвратных уравнений третьей и четвертой степеней. Возвратное уравнение третьей степени имеет вид:
Группируя члены, разложим выражение в левой части уравнения на множители:
Отсюда видно, что одним из корней уравнения (1) является х=—1 . Два других корня получаются путем решения квадратного уравнения
Пример:
Разлагая левую часть уравнения на множители, получаем:
Корни квадратного уравнения равны Поэтому корнями заданного уравнения являются числа
Приведем пример задачи, сводящейся к разобранному типу уравнений.
Задача:
Из квадратного листа жести со стороной а см вырезают по углам четыре квадратика со стороной х см и делают из получившейся фигуры коробку. При каком значении х объем коробки равен ?
Решение:
Основанием коробки является квадрат со стороной а-2x, а ее высота равна х. Значит, объем коробки равен По условию имеем уравнение:
Положим . Мы получим для z уравнение
Разлагая на множители, получаем
Поэтому корни нашего уравнения равны
Из условия задачи следует, что Поэтому не удовлетворяет условию. Итак, либо , либо
Теперь рассмотрим возвратное уравнение 4-й степени:
Так как то х=0 не является корнем этого уравнения. Поэтому если разделить обе части уравнения (2) на то получим равносильное уравнение:
Введем новое неизвестное z, положив . Так как
Следовательно, уравнение (3) превращается в квадратное уравнение относительно z
Решив это уравнение, найдем его корни Чтобы найти х, остается решить совокупность уравнений:
Она сводится к совокупности квадратных уравнений:
Пример. Решить уравнение
Перепишем это уравнение в виде
и введем новое неизвестное . Получим уравнение:
Решая его, находим: . Чтобы найти корни уравнения (4), надо решить уравнения:
Из них получаем:
Наряду с уравнениями вида (1) и (2) рассматривают так называемые кососимметричные уравнения, или, иначе, возвратные уравнения второго рода. При n=4 они имеют вид:
Это уравнение сводится к
После этого вводят новое неизвестное по формуле . Так как то уравнение (6) сводится к квадратному уравнению Дальнейшее решение ведется так же, как и для обычных возвратных уравнений.
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
[spoiler title=”источники:”]
http://abakbot.ru/online-16/274-limit-root-polynom
http://lfirmal.com/ponyatie-algebraicheskogo-i-transtsendentnogo-uravneniya-i-metodov-ih-priblizhennogo-resheniya/
[/spoiler]
Если
–
верхняя граница положительных корней
функции,
–
верхняя граница положительных коней,
-верхняя
граница положительных корней,
-верхняя
граница положительных корней,
то все отличные от нуля действительные
корни уравнения(если они существуют) лежат внутри
интервалов.
При
этом: если коэффициенты полинома
удовлетворяют условию
,
то верхняя граница положительных корней
уравнениянаходится по формуле:
,
гдеm-
номер первого отрицательного коэффициента
;B-
наибольший по модулю отрицательный
коэффициент уравнения
.
Пример:
Методом Лагранжа определить границы
корней уравнения:
Решение:
Здесь
Следовательно,
Для
полинома:
и
поэтому:
Для
многочлена:
имеем
и
значит
Наконец,
для полинома
Имеем:
Поэтому,
Итак, корни исходного
уравнения лежат в интервалах (-2;-1/3.828) и
(1/33;3)
3.Метод Ньютона.
Если
при х = с полином
и все его производные принимают
положительные значения, то «с» является
верхней границей положительных корней
уравнения=0.
Пример:
Определить
верхнюю границу положительных корней
уравнения
методом Ньютона.
Решение:
Проверке подлежат только c=x>0.
Пусть
с=1, тогда
Дальнейшая проверка
для с=1 не нужна.
Пусть
с=2, тогда
.
Таким образом верхней границей
положительных корней является число
2, то естьR=2.
Пример:
Определить
верхнюю границу положительных корней
уравнения
методом Ньютона.
Решение:
Проверке
подлежат только с=х>0.
Пусть с=1,
тогда
Дальнейшая
проверка для с=1 не нужна.
Пусть
с=2, тогда
,
.
Таким
образом, верхней границей положительных
корней является число 2, то есть R=2.
Графические
методы решения уравнений и систем
Графический
метод решения конечных уравнений с
одной переменной – один из приближенных
методов, позволяющий выбрать первое
приближение, с которого начинается
уточнение решения уравнения.
Выделяют
два способа графического решения
уравнения:
В
первом способе все члены уравнения
переносят в левую часть, то есть
представляют его в виде.
После этого строят график функции,
где–
левая часть уравнения. Абсциссы точек
пересечения графика функциис
осью Ох и являются корнями уравнения,
так как в этих точках у=0:

x
Во
втором способе все члены уравнения
разбивают на две группы: одну из них
записывают в левой части уравнения, а
другую – в правой, то есть представляют
его в виде
.
После этого строят графики двух функцийи
.
Абсциссы точек пересечения графиков
этих двух функций и служат корнями
данного уравнения.
Так
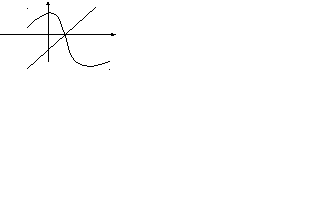
x
Из
равенства
следует, что
–
корень уравнения.
Пример:
Решить графически уравнение:
Решение:
Согласно первому способу решения
уравнения строим график функции

1
x
-1
Абсцисса
точек пересечения этого графика с осью
Ох равна 1. Это означает, что заданное
алгебраическое уравнение имеет один
действительный корень х=1 (два других
корня – комплексные)
Согласно
второму способу заданное уравнение
можно переписать в виде:
и построить графики функций
и
.
Абсцисса точек пересечения этих графиков
х=1
1
x
Пример:
Найти графическим способом корни
трансцендентного уравнения:
Решение:
Перепишем это уравнение в виде
.
Так как функция левой и правой частей
уравнения имеют общую область определения
(интервал 0<x<+∞),
то будем искать корни в интервале ]0,+
∞[.
Построив
графики функций
и

1
x
Находим
корни уравнения: прямая пересекает в
двух точках с абсциссами
0,00001
и1,75.
Пример:
Найти графически корни трансцендентного
уравнения
Решение:
Строим
функции
и
y
1
2
Корнями
уравнения являются абсциссы точек
пересечения графиков, то есть
=1,
=2
Графические
методы решения систем уравнений
Рассмотрим
на примере системы двух нелинейных
уравнений с двумя переменными. При этом
если в заданной системе:
Оба
уравнения можно разрешить относительно
одной из двух переменных, то система
может принять вид:
то
есть получаем уравнение:
.
В
общем же случае строят кривые
и
,
и находят их точки пересечения.
Пример:
Считая x>0
, найти графически решения системы
уравнений:
Решение:
Разрешив
заданные уравнения относительно y,
то есть
,
,
получим
уравнение
.
С
графикии
:
Y
-0.28
1 x
Абсцисса
и ордината точек пересечения графиков
этих функций есть решение заданной
системы, то есть х=1,22; у=-0,28
П
графически решения системы уравнений:
Решение:
Перепишем заданную систему в виде:
Здесь
первое уравнение задает эллипс, а
второе-гиперболу:
y
x
Эти
кривые второго порядка пересекаются в
двух точках
=0,55
;=-0,46;
=1,7;
=1,6.
Отделение
корней конечных уравнений.
Отделить
корни уравнения – это значит разбить
всю его область допустимых значений на
отрезки, в каждом из которых содержится
один корень. Итак, корень
уравнения
не имеет других корней.
Отделение
корней является первым шагом в нахождении
приближенных значений корней уравнения
с заданной степенью точности. Этот шаг
может проводиться как графически, так
и аналитически.
Аналитические
методы отделения корней уравнения
строятся на базе математического анализа
функций.
Примечание:
1.
Если кривая к-раз
пересекает ось абсцисс, то функция
имеетк
простых корня. Так если график функции
имеет вид
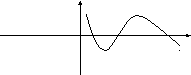
Соседние файлы в папке Лекции Маркина
- #
- #
- #
- #
- #
- #
- #
Верхняя и нижняя граница корней полинома
| Коэффициенты многочлена разделенные пробелами |
| Заданный многочлен имеет вид |
| Нижняя граница действительных корней многочлена |
| Верхняя граница действительных корней многочлена |
Рассмотрим еще одну задачу связаннуюс полиномами. Когда мы пытаемся решить такое уравнение численно, то нам необходимо знать, в каких пределах могут находится действительные корни этого полинома.
Эти знания позволят нам быстрее обеспечить сходимость при компьютерных вычислениях. Это позволит при прорисовке полинома в виде графика, выбрать такой масштаб, что бы мы увидели все пересечения функции с осью абсцисс.
Итак, как же формулы мы будем использовать для решения задачи?
Если нам известен полином вида
То разделив его на a0 мы получаем
Правило утверждает, что если среди коэффицентов 
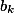
Нижнюю границу можно определить по аналогичной формуле, вычислив значения функции коэффицентов при -x
Давайте рассмотрим пример
Разделим на 3 , что бы первый член полинома был равен единице.
Первый отрицательный коэффициент который мы встречаем это 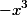
Значение А=9, так как 9 явлется максимальном в абсолютном выражении числом из всех отрицательных коэффициентов полинома.
Таким образом верхняя граница действительных корней
Теперь определяем нижнюю границу
Разделим полином на -3, что бы первый член полинома был равен единице.
Первый отрицательный коэффициент который мы встречаем это 

Значение
Таким образом нижняя граница действительных корней
Следовательно, все действительные корни заданного многочлена находятся в пределах
Бот позволяет выполнять эти вычисления автоматически и при заданных действительных коэффициентах давать правильные результаты.
Единственное замечание, не стоит вводить в качестве коэффициентов комплексные числа. Результат будет непредсказуем.
Удачных расчетов!
Численные методы решения нелинейных уравнений
Корни нелинейных уравнений
Пусть дано нелинейное уравнение
где — функция, определенная и непрерывная на некотором промежутке. В некоторых случаях на функцию
могут быть наложены дополнительные ограничения, например, непрерывность первой и второй производных, что специально оговаривается. Функция
может быть задана в виде алгебраического многочлена или трансцендентной функции (тогда ей соответствует алгебраическое или трансцендентное уравнение).
Требуется найти корни нелинейного уравнения (3.1), т.е. числа которые путем подстановки их в (3.1) превращают уравнение в верное числовое равенство. Числа
называются также нулями функции
.
На практике часто бывает выгодно уравнение (3.1) заменить равносильным ему уравнением (уравнения равносильны, если имеют одинаковые корни):
(3.2)
где функции — более простые, чем функция
. Тогда при задании уравнения в виде (3.1) нулями функции
являются точки пересечения
с осью
(рис. 3.1,д), а при задании в виде (3.2) — абсциссы точек пересечения функций
и
(рис. 3.1,б).
Замечания
1. Если — алгебраический многочлен, то уравнение (3.1) называется также алгебраическим n-й степени:
(3.3)
где — действительные числа, коэффициенты уравнения.
2. На практике встречаются задачи нахождения корней уравнения , левая часть которого задана сеточной функцией
(рис. 3.2).
Число есть корень уравнения (3.1) кратности
, если при
вместе с функцией
обращаются в нуль ее производные до (k-1)-го порядка включительно, т.е.
, а
. Корень кратности к = 1 называется простым. На рис 3.1,с простыми корнями являются
, a корни
— кратные.
В соответствии с классическим результатом Галуа алгебраическое уравнение (3.1) при не имеет решения в замкнутом (формульном) виде. Сеточные уравнения вообще не имеют формульных решений. Поэтому корни алгебраических
, трансцендентных и сеточных уравнений, как правило, определяются приближенно с заданной точностью.
Решение осуществляется в два этапа:
Первый этап. Находятся отрезки , внутри каждого из которых содержится один простой или кратный корень
(см. рис. 3.1). Этот этап называется процедурой отделения корней. По сути на нем осуществляется грубое нахождение корней
.
Второй этап. Грубое значение каждого корня уточняется до заданной точности одним из численных методов, в которых реализуются последовательные приближения. Порядок (скорость) сходимости метода определяется так же, как в методе простых итераций.
Отделение корней уравнения
Для отделения действительных корней полезно определять заранее число корней, а также верхнюю и нижнюю границы их расположения. Для этого используется ряд теорем.
Теорема 3.1 (о числе корней алгебраического уравнения (3.3)). Алгебраическое уравнение (3.3) n-й степени имеет ровно корней, действительных или комплексных, при условии, что каждый корень считается столько раз, какова его кратность.
Теорема 3.2 (о свойстве парной сопряженности комплексных корней уравнения (3.3)). Если — корень алгебраического уравнения (3.3) кратности
, то число
также является корнем той же кратности.
Следствие. Алгебраическое уравнение нечетной степени имеет по крайней мере один действительный корень.
Теорема 3.3 (об оценке модулей корней уравнения (3.3)). Пусть
где — коэффициенты уравнения
. Тогда модули всех корней
уравнения удовлетворяют неравенству
(3.4)
т.е. корни уравнения расположены в кольце.
Следствие. Числа и
являются соответственно нижней и верхней границами положительных корней алгебраического уравнения:
. Аналогично числа
и
служат нижней и верхней границами отрицательных корней уравнения:
.
Приведем полезные теоремы, используемые для более точного установления границ действительных корней алгебраических уравнений.
Теорема 3.4 (теорема Лагранжа о верхней границе положительных корней уравнения (3.3)). Пусть и
— первый отрицательный коэффициент в последовательности
— наибольшая из абсолютных величин отрицательных коэффициентов. Тогда за верхнюю границу положительных корней уравнения (3.3) может быть принято число
(3.5)
Теорема 3.5 (о нижних и верхних границах положительных и отрицательных корней алгебраического уравнения). Пусть — верхняя граница положительных корней уравнения
,
— верхняя граница положительных корней уравнения
,
— верхняя граница положительных корней уравнения
,
— верхняя граница положительных корней уравнения
.
Тогда положительные корни и отрицательные корни
уравнения (3.3) удовлетворяют неравенствам
(3.6)
Теорема 3.6 (теорема Декарта о количестве действительных корней алгебраических уравнений). Число положительных корней (с учетом их кратностей) алгебраического уравнения
равно числу перемен знаков в последовательности коэффициентов
(коэффициенты, равные нулю, не учитываются) многочлена
или меньше этого числа на четное число. Число
отрицательных корней (с учетом их кратностей) алгебраического уравнения
равно числу перемен знаков в последовательности
многочлена
или меньше этого числа на четное число.
Теорема 3.7 (теорема Гюа о необходимом условии действительности всех корней алгебраического уравнения). Если алгебраическое уравнение (3.3) имеет все действительные корни, то квадрат каждого некрайнего коэффициента больше произведения двух его соседних коэффициентов.
Следствие. Если при каком-нибудь выполнено неравенство
, то уравнение (3.3) имеет по крайней мере одну пару комплексных корней.
Для отделения корней применяется следующая теорема.
Теорема 3.8. Если функция , определяющая уравнение
, на концах отрезка
принимает значения разных знаков, т.е.
, то на этом отрезке содержится по крайней мере один корень уравнения. Если же
непрерывна и дифференцируема и ее первая производная сохраняет знак внутри отрезка
, то на
находится только один корень уравнения.
Способы отделения корней
В вычислительной практике обычно используются следующие способы отделения корней:
1) средствами машинной графики: функция представляется на дисплее и приближенно определяются отрезки, которым принадлежат точки
;
2) средствами математического анализа с помощью исследования функций и построения графиков (см. рис. 3.1,д);
3) формированием простых функций и
таких, что получается равносильное уравнение в виде (3.2), и дальнейшим построением графиков этих функций (см. рис. 3.1,б).
▼ Примеры 3.1-3.3
Пример 3.1. Определить число положительных и отрицательных корней, а также их границы для уравнения
Решение
В данной задаче . Согласно теореме 3.1 уравнение имеет пять корней. Поскольку
, то по следствию из теоремы 3.2 уравнение имеет по крайней мере один действительный корень.
Оценим модули корней по теореме 3.3. Так как
то или
, т.е. все корни лежат внутри данного кольца. По следствию из теоремы 3.3 это означает, что положительные корни удовлетворяют неравенству
, а отрицательные — неравенству
.
Применим теоремы 3.4 и 3.5 для уточнения приведенных результатов. Найдем верхнюю границу положительных корней. Так как — первый отрицательный коэффициент в последовательности
, то
, а
— наибольшая из абсолютных величин отрицательных коэффициентов. Следовательно,
.
Найдем нижнюю границу положительных корней. Составим уравнение:
или (старший коэффициент должен быть положительным). Для этого уравнения
, поэтому
. Отсюда
.
Уточним границы отрицательных корней. Составим уравнение:
или
.
Для этого уравнения , поэтому
. Составим уравнение
или . Для этого уравнения
, поэтому
. Отсюда находим:
. Заметим, что данный результат совпадает с полученным ранее.
Исследуем структуру корней уравнения. Так как квадрат каждого некрайнего коэффициента больше произведения двух его соседних коэффициентов, то по теореме 3.7 необходимое условие действительности всех корней уравнения выполняется.
На основе теоремы 3.6 определим число положительных и отрицательных корней. Выписываем коэффициенты многочлена . Так как число перемен знака
, то число положительных корней равно трем или меньше на четное число, т.е. равно 1. Далее выписываем коэффициенты многочлена
. Так как число перемен знаков
, то число отрицательных корней равно двум или меньше на четное число, т.е. их вообще нет.
Пример 3.2. Отделить корни кубического уравнения .
Решение
Согласно теореме 3.1 уравнение имеет три корня, среди которых по крайней мере один действительный (следствие из теоремы 3.2, поскольку это уравнение нечетной степени).
Оценим модули корней уравнения по теореме 3.3. Так как
, то
или
.
Отсюда и
.
Определим число положительных и отрицательных корней. Выписываем коэффициенты многочлена . Так как число перемен знака
(нулевой коэффициент не учитывается), то число положительных корней равно двум или меньше на четное число, т.е. они отсутствуют. Далее выписываем коэффициенты многочлена
. Так как число перемен знака
(нулевой коэффициент не учитывается), то число отрицательных корней равно единице.
Отделим корни третьим способом. Для этого преобразуем уравнение к равносильному виду (3.2): и найдем точки пересечения фафиков
и
(рис. 3.3).
Очевидно, корень уравнения .
Пример 3.3. Отделить корни уравнения третьего порядка .
Решение
Метод половинного деления
Пусть дано уравнение и отделен простой корень
, т.е. найден такой отрезок
, что
и на концах отрезка функция имеет значения, противоположные по знаку
. Отрезок
называется начальным интервалом неопределенности, потому что известно, что корень ему принадлежит, но его местоположение с требуемой точностью не определено.
Процедура уточнения положения корня заключается в построении последовательности вложенных друг в друга отрезков, каждый из которых содержит корень уравнения. Для этого находится середина текущего интервала неопределенности , и в качестве следующего интервала неопределенности из двух возможных выбирается тот, на концах которого функция
имеет разные знаки (рис. 3.5).
Процесс завершается, когда длина текущего интервала неопределенности становится меньше заданной величины , задающей точность нахождения корня. В качестве приближенного значения корня берется середина последнего интервала неопределенности.
Алгоритм метода половинного деления
1. Найти начальный интервал неопределенности одним из методов отделения корней, задать малое положительное число
. Положить
.
2. Найти середину текущего интервала неопределенности: .
3. Если , то положить
, а если
, то принять
. В результате находится текущий интервал неопределенности
.
4. Если , то процесс завершить:
. Приближенное значение корня можно найти по формуле
.
Если , положить
и перейти к п.2.
Замечания
1. Метод имеет линейную, но безусловную сходимость, и его погрешность за каждую итерацию уменьшается в два раза:
Из последнего соотношения можно оценить число итераций для достижения заданной точности
Отсюда видно, что, например, для достижения точности при
необходимо выполнить примерно десять итераций.
2. К достоинствам метода следует отнести то, что он позволяет найти простой корень уравнения любых непрерывных функций
при любых значениях
таких, что
. Недостатки метода — он не обобщается на системы нелинейных уравнений и не может использоваться для нахождения корней четной кратности.
▼ Примеры 3.4-3.6
Пример 3.4. Найти корень уравнения методом половинного деления с точностью
и
.
Решение
Пример 3.5. Найти корень уравнения методом половинного деления с точностью
.
Решение
В примере 3.3 были отделены корни уравнения. Уточним корень, лежащий на отрезке . Результаты расчетов поместим в табл. 3.2.
В результате найден интервал и приближенное значение корня
.
Пример 3.6. Отделить корни трансцендентного уравнения и найти один из корней с точностью
.
Решение
1. Можно отделить корни уравнения, преобразовав его к равносильному виду и определив абсциссу точек пересечения графиков функций
и
. При этом
.
2. Уточним корень. Результаты расчетов приведем в табл. 3.3.
Вычисления показывают, что .
Поэтому .
Метод хорд
Этот метод при тех же предположениях обеспечивает более быстрое нахождение корня, чем метод половинного деления. Для этого отрезок делится не пополам, а в отношении
.
Геометрически метод хорд эквивалентен замене кривой хордой, проходящей через точки
и
(рис. 3.6).
Уравнение хорды имеет вид
. Полагая
и
, получаем
Предположим, что вторая производная сохраняет постоянный знак, и рассмотрим два случая:
(рис. 3.7,д) и
(рис. 3.7,б). Случай
сводится к рассматриваемому, если уравнение записать в форме:
. Первому случаю (см. рис. 3.7,д) соответствует формула (3.7), а второму случаю (3.8) (см. рис. 3.7,б):
(3.7)
(3.8)
В первом случае остается неподвижным конец , а во втором случае конец
.
Замечание. Для выявления неподвижного конца используется условие , где
или
. Если неподвижен конец
, применяется формула (3.7), а если конец
, — формула (3.8).
Пример 3.7. Найти корень уравнения методом хорд с точностью
.
Решение
Рассмотрим задачу нахождения корня на отрезке (см. пример 3.2). Так как
, a
на отрезке
, то
и, следовательно, имеем второй случай (см. рис. 3.7,б).
Положим . Тогда по формуле (3.8) получаем
Так как , то положим
и продолжим процесс:
Так как , то положим
и продолжим процесс:
Поскольку , положим
Так как , положим
Поскольку , положим
Так как , положим
Поскольку , положим
Так как , то корень уравнения
. Из анализа поведения
следует, что сходимость метода хорд линейная, однако более быстрая, чем сходимость метода половинного деления.
Метод простых итераций
Пусть известно, что корень уравнения
лежит на отрезке
.
Методика решения задачи
1. Уравнение равносильным преобразованием привести к виду
. Это преобразование может быть осуществлено различными путями, но для сходимости нужно обеспечить выполнение условия
(
— некоторая константа). При этом задача сводится к нахождению абсциссы точки пересечения прямой
и кривой
(рис. 3.8).
2. Задать начальное приближение и малое положительное число
. Положить
.
3. Вычислить следующее приближение:
(3.9)
4. Если , итерации завершаются и
. Если
, положить
и перейти к п.3.
Замечание. В качестве условия завершения итераций при известном значении может быть использовано неравенство
Проблемы сходимости и единственности численного решения, являющиеся главными при использовании этого метода, решаются и исследуются с помощью понятия о сжимающем отображении и теоремы о достаточном условии сходимости метода.
Отображение (функция) называется сжимающим в области
с коэффициентом
, если для любых двух
из
выполнено неравенство
(3.10)
Теорема 3.9 (о сходимости метода простых итераций и единственности получаемого численного решения)
Пусть выполнены условия:
1. Нелинейное уравнение имеет решение
.
2. Отображение является сжимающим в области
с некоторым коэффициентом
.
Тогда:
а) решение является единственным решением в области
;
б) последовательность , определяемая по отображению на основе итерационного процесса, сходится к решению
со скоростью геометрической прогрессии, т.е. при выборе
из условия
, где
— некоторое малое число, справедливо неравенство
Теорема 3.9 утверждает, что при выполнении условий 1,2 существует окрестность такая, что если взять
в этой окрестности и вычислять
по формуле (3.9), то в результате с любой наперед заданной точностью можно вычислить
, соответствующее искомому (единственному) корню. Но так как эта окрестность неизвестна, то можно взять произвольное
. Если при этом вычисляется последовательность
, сходящаяся к некоторому значению
, то в силу теоремы
. Если сходимость отсутствует, то надо взять другое
и повторить расчет.
Теорема 3.10 (о достаточном условии сходимости метода простых итераций). Пусть выполнены условия:
1. Функция имеет производные для всех
.
2. Существует число , такое, что
для всех
.
Тогда отображение является сжимающим в
с коэффициентом сжатия х и последовательность
, определяемая на основе итерационного процесса, сходится к решению
, то есть
при
.
▼ Доказательство
В силу условия 1 справедлива теорема Лагранжа о конечных приращениях:
для
,
где — точка, лежащая между
и
. Но тогда с учетом условия 2 и замены
ее мажорантой
получим
т.е. отображение — сжимающее, и, таким образом, последовательность
сходится к некоторому
. Но тогда в силу непрерывности
в
имеет место равенство
.
Геометрическая интерпретация процесса сходимости и расходимости в зависимости от выполнения или невыполнения достаточного условия сходимости представлена на рис. 3.9.
Из рис. 3.9 видно, что при и при
(см.рис. 3.9,д,б) итерационные последовательности
сходятся к
. Причем в первом случае реализуется односторонняя (монотонная) сходимость, а во втором — двусторонняя (немонотонная). При
(см.рис. 3.9,в,г) процесс расходится несмотря на то, что точка
очень близка к
. Процессы на рис. 3.9,а,б соответствуют сжимающему отображению.
Преобразование уравнения к равносильному виду
может быть выполнено неоднозначно. Рассмотрим универсальные практические приемы равносильного преобразования
, дающие сжимающие отображения.
1. Можно заменить уравнение на равносильное
, где
. Тогда, принимая правую часть этого уравнения за
и раскрывая
, получаем условие
(3.11)
Таким образом, можно найти константу на отрезке
так, чтобы удовлетворялись неравенства (3.11). При этом надо стремиться получить такую постоянную
, которая бы больше отличалась от нуля, и тогда будет реализовы-ваться более быстрая сходимость.
Можно показать, что абсолютная погрешность метода оценивается по формуле (эта оценка выражается через два последовательных приближения)
(3.12)
или по формуле (эта оценка выражается через два приближения и
)
(3.13)
Из оценки следует условие выхода из итерационного процесса. Если значение неизвестно, то выход осуществляется по условию
2. Уравнение заменяется равносильным (где знак в правой части выбирается из условия
):
при
,
3. Можно выразить из уравнения
так, чтобы для полученного уравнения
выполнялось условие сходимости
в окрестности искомого корня.
Замечание к доказательству. Выполнение условия не гарантирует близости к точному решению (на рис. 3.10 достигается область, где условие окончания выполняется, но корень
расположен достаточно далеко от этой области).
▼ Примеры 3.8-3.10
Пример 3.8. Методом простых итераций с точностью уточнить корень трансцендентного уравнения
, причем искомый корень
.
Решение
Пример 3.9. Найти решение уравнения методом простых итераций с точностью
и
.
Решение
Пример 3.10. Найти корни уравнения методом простых итераций с точностью
.
Решение
1. Преобразуем уравнение к виду .
В примере 3.3 была выполнена операция отделения корней и получены отрезки .
Можно показать, что на отрезках функция
удовлетворяет условию
.
На отрезке используем другой вид уравнения:
. Также легко проверить, что функция
удовлетворяет достаточному условию сходимости на отрезке
.
2. В качестве начальных приближений выберем:
– точку на отрезке
;
– точку на отрезке
;
– точку на отрезке
;.
В поставленной задаче .
3,4. Выполним расчеты по формуле
с начальными значениями и
и по формуле
с начальным значением .
Результаты расчетов занесены в табл. 3.6–3.8.
В результате получены приближенные значения корней:
Обратим внимание на сильное различие в числе итераций, потребовавшихся для нахождения корней (табл. 3.6) и
(табл. 3.7), с помощью одной и той же формулы. Заметим, что в окрестности корня
значения модуля производной функции
равны:
С другой стороны, в окрестности корня имеем:
Анализ результатов показывает, что чем меньше значения модуля производной , тем быстрее сходимость.
Метод Ньютона для решения нелинейных уравнений
Метод Ньютона (метод касательных, или метод линеаризации) является одним из наиболее популярных численных методов. Он быстро сходится (имеет квадратичную сходимость) и допускает различные модификации, приспособленные для решения векторных задач и сеточных уравнений. Однако этот метод эффективен при весьма жестких ограничениях на характер функции
1) существование второй производной функции на множестве
;
2) удовлетворение первой производной условию для всех
;
3) знакопостоянство для всех
.
Поэтому его желательно использовать совместно с другими методами, например методом половинного деления, чтобы достигнуть диапазона , где указанные условия начинают выполняться.
Геометрическая интерпретация метода Ньютона состоит в следующем. Задается начальное приближение . Далее проводится касательная к кривой
в точке
(рис. 3.11), т.е. кривая заменяется прямой линией. В качестве следующего приближения выбирается точка пересечения этой касательной с осью абсцисс. Процесс построения касательных и нахождения точек пересечения с осью абсцисс повторяется до тех пор, пока приращение не станет меньше заданной величины
.
Получим расчетную формулу метода Ньютона. Вместо участка кривой (точка
соответствует
) возьмем участок
— касательную, проведенную в точке
). Для этого отрезка справедливо конечное соотношение:
где — угол наклона касательной в точке
к оси абсцисс. Разрешая это соотношение относительно
, получаем
. Повторяя процесс, находим общую формулу:
(3.14)
Подчеркнем, что если отбросить итерационный индекс, то (3.14) записывается в виде нелинейного уравнения
(3.15)
которое, однако, на не равносильно исходному, а является таковым только в одной точке при
. Поэтому данный метод не служит разновидностью метода простых итераций.
Применим теперь для вывода формулы (3.14) метод линеаризации. Положим, что итерационный процесс имеет вид
(3.16)
где — поправка к k-му приближению, которую необходимо найти. Предполагая, что
имеет непрерывную вторую производную, разложим
по формуле Тейлора относительно точки
где . Учитывая, что
(это соответствует нахождению точки пересечения с осью абсцисс), и оставляя только линейную (относительно
) часть разложения (отсюда и название — метод линеаризации), записываем линейное относительно
уравнение
Отсюда выражается поправка . Подставляя
в (3.16), получаем (3.14).
Теорема 3.11 (о достаточных условиях сходимости метода Ньютона). Пусть выполняются следующие условия:
1. Функция определена и дважды дифференцируема на
.
2. Отрезку принадлежит только один простой корень
, так что
.
3. Производные на
сохраняют знак, и
.
4. Начальное приближение удовлетворяет неравенству
(знаки функций
и
в точке
совпадают).
Тогда с помощью метода Ньютона (3.14) можно вычислить корень уравнения с любой точностью.
Замечания
1. Метод Ньютона характеризуется вторым порядком сходимости вблизи корня и первым порядком — вдали от него. Данную оценку проверяем для двух случаев, когда находится далеко от корня
(это возможно на первых итерациях) и когда
располагается вблизи
.
Первый случай. Пусть отрезок не мал. Тогда на основе теоремы Лагранжа получим (где
)
(3.17)
Преобразуем с использованием (3.17) итерационную формулу (3.14) (где ):
В силу монотонности последовательности имеем
Таким образом, вдали от корня получаем линейную сходимость
, где
.
Второй случай. Пусть теперь отрезок мал, т.е. итерации выполняются вблизи корня. Тогда, полагая, что указанные выше предположения 1–4 теоремы 3.10 выполнены, разложим функцию
в окрестности корня
относительно точки
, учитывая члены до второго порядка. Получим
где (
— малая величина). Из данного соотношения выражаем
Но первые два слагаемых в правой части в соответствии с (3.14) равны . Тогда будем иметь
Из последнего соотношения следует оценка погрешности (k+1)-го приближения через погрешность k-го приближения:
(3.18)
где принято . Оценка (3.18) свидетельствует о квадратичной сходимости метода касательных вблизи корня. С вычислительной точки зрения это означает, что на каждом приближении количество верных цифр результата удваивается.
2. Для нахождения комплексных корней уравнения можно также использовать (3.14) в форме (где
— комплексная переменная)
Метод Ньютона может применяться не только для нахождения простых корней, но для определения кратных корней, т.е. когда на отрезке содержащем корень, не выполняется условие
(условие 2 теоремы 3.11). Наряду с теоремой 3.11 удобно также пользоваться следующей теоремой.
Достаточные условия сходимости метода Ньютона
Теорема 3.12 (достаточные условия сходимости метода Ньютона). Пусть:
а) дана функция , где
— открытый интервал, и
;
б) для некоторого выполняется условие
при всех
из
.
Если уравнение имеет решение
, то существует некоторое
, такое, что если
, то последовательность
, задаваемая формулой (3.14), существует и сходится к
. Более того, справедлива оценка
Здесь обозначение означает, что функция
непрерывна по Липшицу с константой
на множестве
, то есть
для любых
из
.
Замечания
1. Требование теоремы 3.12, чтобы производная имела ненулевую нижнюю границу в
, определяет, что значение
должно быть ненулевым для квадратичной сходимости метода Ньютона. Если же
, то
является кратным корнем, а метод Ньютона сходится лишь линейно.
2. Выполнение условий теоремы 3.12 гарантирует сходимость метода Ньютона только из “хорошего” начального приближения .
3. Метод Ньютона является локально сходящимся, так как он сходится с определенной скоростью к истинному решению при условии, что стартует в достаточной близости от этого решения.
Методика решения задачи
1. Задать начальное приближение так, чтобы выполнялось неравенство
, а также малое положительное число
. Положить
.
2. Вычислить по формуле
.
3. Если , процесс завершить и положить
.
Если , положить
и перейти к п.2.
▼ Примеры 3.11-3.14
Пример 3.11. Методом Ньютона с точностью уточнить корень трансцендентного уравнения
, причем искомый корень
.
Решение
Можно проверить, что на множестве удовлетворяются условия 1, 2, 3 теоремы 3.11, обеспечивающие сходимость метода касательных.
1. Зададим начальное приближение из условия 4. Так как для справедливо
на множестве
, то
, поэтому
.
2,3. Результаты расчетов по формуле (3.14) помещены в табл. 3.9.
Из табл. 3.9 можно сделать следующие выводы:
1. Для достижения заданной точности, проверяемой по модулю разности , потребовалось выполнить три приближения. Если же выход организовать по условию
, то достаточно двух приближений.
2. Вблизи корня количество верных цифр в результатах
удваивается, так что все цифры в
являются верными, тогда как в
верными являются первые три цифры после запятой.
3. Скорость сходимости метода Ньютона выше скорости сходимости метода простых итераций (та же точность была достигнута за пять итераций).
Пример 3.12. Методом Ньютона найти корень уравнения .
Решение
Пример 3.13. Найти корни уравнения методом Ньютона с точностью
.
Решение
Процедура отделения корней была выполнена в примере 3.3. В качестве отрезков , которым принадлежат корни уравнения, выберем
.
Так как , то есть
, производные
сохраняют знак при
, то условия сходимости выполняются.
Так как , то есть
, и производные
сохраняют знак при
, то условия сходимости на этом отрезке тоже выполняются.
Так как , то есть
, и производные
сохраняют знак при
, то условия сходимости выполняются.
1. Зададим начальные приближения: на отрезке выберем
, так как
; на отрезке
выберем
, так как
; аналогично на отрезке
выберем
. В поставленной задаче
.
2,3. Результаты расчетов по формуле (3.14) приведены в табл. 3.11–3.13.
В результате получены приближенные значения корней:
Пример 3.14. Найти корень уравнения методом Ньютона с точностью
.
Решение
Очевидно, уравнение имеет один кратный корень . Согласно замечанию к теореме 3.12 применение метода Ньютона для решения поставленной задачи сопровождается линейной сходимостью (табл. 3.14).
Полученное приближенное решение .
Метод касательных
Метод касательных, являясь весьма эффективным средством численного анализа, к сожалению, имеет достаточно жесткие ограничения. Действительно, он не может применяться для сеточных уравнений (см. рис. 3.2); при нарушении знакопостоянства производных (рис. 3.12); при существовании неограниченных вторых производных и др. Так, если даже условие знакопостоянства нарушено вдали от корня, где выбрано , а вблизи корня выполняется, то все равно метод касательных неприменим (см. рис. 3.12), если не произвести сужения начального отрезка.
Кроме того, если функция очень сложная, то будет сложной и ее производная, и поэтому на каждой итерации приходится рассчитывать две функции, что снижает эффективность метода касательных.
В силу этого в ряде случаев могут оказаться более предпочтительными модификации метода касательных. Рассмотрим три из них.
Упрощенный метод Ньютона. Методика его применения совпадает с изложенной ранее, но вместо формулы (3.14) используется
Отличие от метода Ньютона заключается в том, что производная функции подсчитывается только в точке начального приближения, а на последующих итерациях не уточняется. Процесс последовательных приближений отражен на рис. 3.13. Первая итерация совпадает с первой итерацией метода Ньютона. На последующих итерациях соответствующие отрезки параллельны касательной, проведенной в начальной точке.
Для этой модификации снимаются некоторые ограничения метода касательных, например условие знакопостоянства производных. Сходимость упрощенного метода Ньютона линейная.
Пример 3.15. Найти корень уравнения упрощенным методом Ньютона.
Решение
Корень уравнения отделен в примере 3.2: .
1. Выберем начальное приближение и зададим
и
.
2,3. Выполним расчеты по формуле (3.19):
Результаты расчетов приведены в табл. 3.15.
При получено решение
, а при
— решение
. Очевидно, по сравнению с методом Ньютона сходимость замедляется (см. пример 3.12).
Метод Ньютона-Бройдена
Этот метод позволяет увеличить скорость сходимости последовательных приближений благодаря использованию формулы
(3.20)
где — число, которое выбирается на каждой итерации так, чтобы уменьшить значение
по сравнению с
. При
метод Ньютона-Бройдена совпадает с методом Ньютона.
Как правило, при плохой сходимости или ее отсутствии полагают (рис. 3.14,д), а при хорошей сходимости для
полагают
(это ускоряет сходимость (рис. 3.14,б)).
На рис. 3.14 прямоугольниками отмечены точки , полученные при
, — поправка, соответствующая методу Ньютона, а точки
получены по методу Ньютона-Бройдена.
Метод секущих
В этом методе производная функции подсчитывается с помощью конечно-разностных соотношений:
– в точке используется формула
, где
— малая положительная величина;
– в точках , используется формула
.
Вычисленное значение определяет тангенс угла наклона секущей (рис. 3.15).
Методика применения метода секущих совпадает с описанной ранее, но вместо (3.14) используется формула
(3.21)
Замечания
1. Метод секущих является более экономичным по сравнению с методом Ньютона по количеству функций, подлежащих расчету: на каждой итерации в методе секущих необходимо рассчитать только значение , так как величина
уже подсчитана на предыдущей итерации.
2. Метод секущих может применяться и для решения сеточных уравнений. Для сеточной функции производные в методе секущих определяются так же, но для определения в промежуточных точках осуществляется аппроксимация (как правило, интерполяция) функции
(рис. 3.16). На этом рисунке штриховой линией показана аппроксимационная кривая.
3. Для всех описанных модификаций скорость сходимости по сравнению с методом касательных снижается:
. Однако для некоторых из них (метод секущих) значение
и может достигать
.
Пример 3.16. Методом секущих найти корень уравнения с точностью
.
Решение
1. Зададим начальное приближение (см. пример 3.12).
2. Для вычисления зададим
. Тогда
Отсюда .
Дальнейшие расчеты выполняются по формуле (3.21):
Результаты расчетов приведены в табл. 3.16.
Очевидно, метод сходится чуть хуже метода Ньютона (см. пример 3.12), однако скорость сходимости выше линейной.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

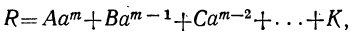
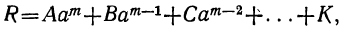
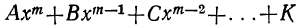
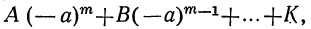
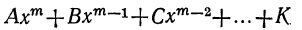
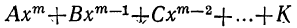
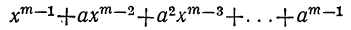
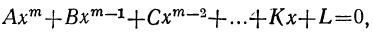
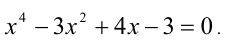
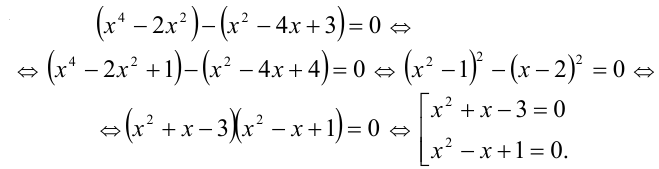
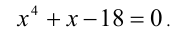
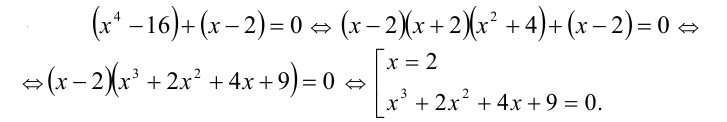
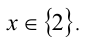
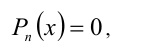
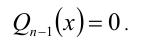
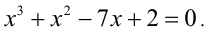
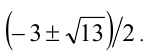
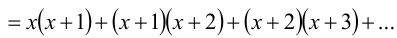
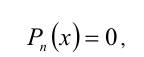
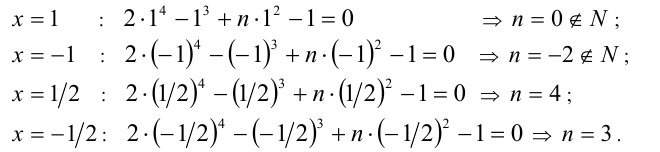
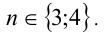
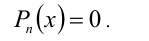
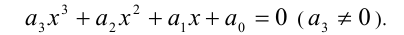
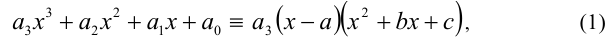
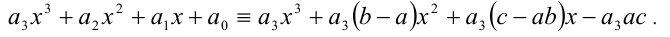
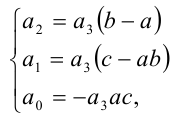
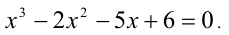
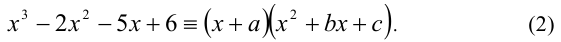
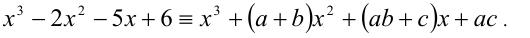
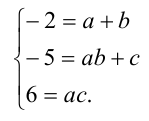
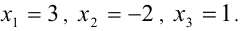
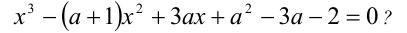
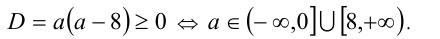
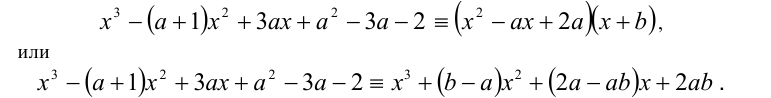

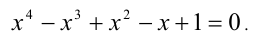
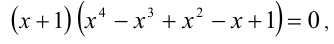
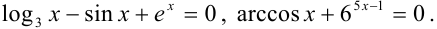
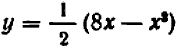






=a_0x^{n}+a_1x^{n-1}+a_2x^{n-2}+.....+a_{n-1}x+a_n)
=x^{n}+b_1x^{n-1}+b_2x^{n-2}+.....+b_{n-1}x+b_n)
![max=1+sqrt[k]{A}](https://img.abakbot.ru/cgi-bin/mathtex.cgi?max=1+sqrt[k]{A})
=3x^{5}+7x^{4}-3x^{3}+x^{2}+5x-27)
=x^{5}+frac{7}{3}x^{4}-x^{3}+frac{1}{3}x^{2}+frac{5}{3}x-9)
![max=1+sqrt[2]{9}=4](https://img.abakbot.ru/cgi-bin/mathtex.cgi?max=1+sqrt[2]{9}=4)
=-3x^{5}+7x^{4}+3x^{3}+x^{2}-5x-27)
=x^{5}-frac{7}{3}x^{4}-x^{3}-frac{1}{3}x^{2}+frac{5}{3}x+9)



![[-frac{10}{3};4]](https://img.abakbot.ru/cgi-bin/mathtex.cgi?[-frac{10}{3};4])
