|
Как посчитать границы прямоугольника?ДЕВОЧКА – РОМАШКА 5 лет назад
Ксения-М-1994 5 лет назад Для начала нужно вспомнить, что такое прямоугольник? Это геометрическая фигура из четырёх углов, у которой все углы прямые. Размеры прямоугольника определяются длинами его сторон, обозначаемых обычно a и b. Прямоугольник, все стороны которого равны (a = b) называется квадратом. Периметр прямоугольника – это сложение 2 сторон, умноженное на 2. Проще описать формулой: Р = 2*(a + b). Площадь прямоугольника – это умножение одной стороны на другую. S = a*b. комментировать
в избранное
ссылка
отблагодарить Знаете ответ? |
Все категории
- Фотография и видеосъемка
- Знания
- Другое
- Гороскопы, магия, гадания
- Общество и политика
- Образование
- Путешествия и туризм
- Искусство и культура
- Города и страны
- Строительство и ремонт
- Работа и карьера
- Спорт
- Стиль и красота
- Юридическая консультация
- Компьютеры и интернет
- Товары и услуги
- Темы для взрослых
- Семья и дом
- Животные и растения
- Еда и кулинария
- Здоровье и медицина
- Авто и мото
- Бизнес и финансы
- Философия, непознанное
- Досуг и развлечения
- Знакомства, любовь, отношения
- Наука и техника
![]()
0
Как посчитать границы прямоугольника?
1 ответ:
![]()
1
0
Для начала нужно вспомнить, что такое прямоугольник? Это геометрическая фигура из четырёх углов, у которой все углы прямые. Размеры прямоугольника определяются длинами его сторон, обозначаемых обычно a и b. Прямоугольник, все стороны которого равны (a = b) называется квадратом.
Периметр прямоугольника – это сложение 2 сторон, умноженное на 2.
Проще описать формулой:
Р = 2*(a + b).
Площадь прямоугольника – это умножение одной стороны на другую.
S = a*b.
Читайте также
![]()
Задачку я решил, конечно не сразу. Потребовалось перенести рисунок на внешний листик, так как в уме ход решения не удавалось сохранять.
Верхняя строчка читается : 2, 0, 1, 3, 4
средняя строчка читается : 4, 2, 0, 1, 3
нижняя строчка читается : 1, 3, 2, 0, 4
Как видим из предложенного решения, в клетке со знаком вопроса должна быть 1.
Ответ на вопрос задания вариант Б { 1 }
![]()
Наиболее рациональным решением этой задачи является такое решение. Боковые стены бассейна – это фактически боковая поверхность прямой призмы (только с внутренней стороны). А площадь боковой поверхности такой призмы (параллелепипеда) умеют находит даже пятиклассники по формуле S = P*h, P = 2*(а+в) – периметр. Далее находим площадь дна (прямоугольник) по известной формуле S = а*в и суммируем их. а=10 м, в=25 м, h= 2 м.
Получаем площадь дна бассейна равна 2*(10+25)*2 + 10*25 = 140 м2 + 250 м2 = 390 м2.
![]()
Эта задача сначала кажется ужасно сложной, я даже хотела ее оставить “на потом”, но ее нужно просто внимательно прочитать и понять, что пчел то всего четыре и сидят они не внутри прямоугольника, а на его контуре, и капля меда тоже падает на контур. Просто вначале сбивает вот это: 10х25, но нам эти данные показывают просто длину сторон прямоугольника. На какую бы сторону не упала капля, две пчелы с вершин этой стороны проползут путь до капли равный длине этой стороны, а две другие проползут путь равный периметру, если из него вычесть длину противоположной стороны, равную той стороне по которой ползут первые две пчелы, то есть общий путь будет как раз равен периметру прямоугольника: 10 + 10 + 25 + 25 = 70.
![]()
У нас есть условие, что клетки закрашены некоторые, если бы этого не было, то минимальный прямоугольник был бы 5 х 6, а его площадь была бы равна 30, но в нем не соблюдалось бы это условие, поэтому прямоугольник придется удлинить или расширить, допустим, мы добавим с этой целью одну строку, по условию задачи в ней нам тоже придется закрасить пять клеток, но тогда нарушится другое условие задачи, в столбцах уже будет не шесть клеток, а больше закрашено. Тогда, чтобы условия все же были выполнены в полном объеме мы будем вынуждены добавить пять столбцов, чтобы закрасить в них клетки этой дополнительной добавленной строки. А еще мы должны будем добавить в дополнение к той первой еще пять строк для закрашивания клеток, чтобы в столбцах было по 6 клеток закрашено. В итоге у нас получится прямоугольник 10 х 12 с площадью 120, такой вариант ответа у нас как раз есть и он правильный.
![]()
Зная, что периметр прямоугольника равен P=2(a+b). Подставим наше значение периметра в формулу: 28=2(a+b). Тогда
a+b=14. Далее по тереме Пифагора имеем a*a+b*b=10*10. Тогда имеем a*a+b*b=100. Далее выразим а=14-b. Получим (14-b)*(14-b)+b*b=10<wbr />0.
196-28b+b*b+b*b=100. 2b*b-28b+96=0. b*b-14b+48=0. Отсюда b1=8. b2=6. Тогда a1=14-8=6. a2=14-6=8. В общем, получилось, что длина прямоугольника равна 8, а ширина равна 6.
Длина прямоугольного участка земли 8 м, а ширина − в 2 раза меньше длины. Какова площадь участка? Какова длина границы этого участка?

reshalka.com
ГДЗ учебник по математике 3 класс (часть 2) Рудницкая. Прямая. Номер №16
Решение
Длина – 8 м
Ширина – ?, в 2 раза меньше
↰
Площадь − ?
Длина границы − ?
Решение:
1) 8 : 2 = 4 (м) − ширина прямоугольного участка.
2) 8 * 4 = 32 (
с
м
2
) − площадь прямоугольного участка.
3) (8 + 4) * 2 = 12 * 2 = 24 (м) − длина границы участка.
Ответ:
32
с
м
2
− площадь прямоугольного участка; 24 метра − длина границы этого участка.
Что такое прямоугольник — это одна из основ геометрии
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru.
Сегодня мы расскажем об одной из основных геометрических фигур – ПРЯМОУГОЛЬНИКЕ.
Название это весьма говорящее, и в нем скрыто официальное определение.

Прямоугольник — это…
Прямоугольник – это четырехугольник, у которого все углы прямые, то есть равны 90 градусам.
Впервые описание этой фигуры встречается еще в Древнем Египте. Но в те времена все геометрические правила давались как неопровержимые истины, не предоставляя доказательств.
Более правильный подход появился в Древней Греции. И естественно, автором стал самый знаменитый математик той эпохи — Евклид. А прямоугольник, как и многие другие фигуры и термины, был подробно описан в его произведении «Начала».
Все тот же Евклид разделил все четырехугольники на два вида – параллелограммы (что это?) и трапеции (что это?).
У первых противоположные стороны равны и параллельны, а у вторых параллельна только одна пара сторон, и они при этом не равны.
То есть выглядит это так:
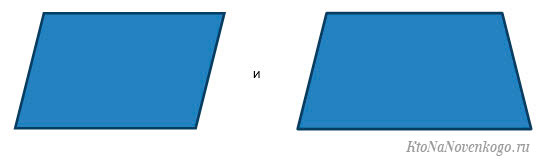
Так вот, прямоугольник в данном случае является частным случаем параллелограмма.
Судите сами:

У этой фигуры противоположные стороны параллельны. Это первое условие по Евклиду. И к тому же они равны, что является условием номер два.
У прямоугольника есть и собственный частный случай. Когда равны не только противоположные стороны, а все. И как нетрудно догадаться, фигура эта называется квадрат.

Ну, и логично предположить, что квадрат является частным случаем параллелограмма.
Признаки прямоугольника
Признаки геометрической фигуры – это совокупность отличий, по которым ее можно выделить среди других.
В нашем случае их всего три:
- Если один из углов параллелограмма прямой, то данный параллелограмм является прямоугольником.
- Если три угла четырехугольника являются прямыми, то перед нами опять же прямоугольник. При этом нет необходимости доказывать, что четырехугольник является параллелограммом. Это промежуточное звено становится верно само по себе.
- Если диагонали параллелограмма равны между собой, то фигура точно является прямоугольником.
Диагонали
Как мы уже упомянули выше, диагонали прямоугольника (отрезки, соединяющие его противоположные углы) равны между собой.
Доказать это можно с помощью известной теоремы Пифагора. Она гласит, что «Сумма квадратов катетов прямоугольного треугольника равна квадрату гипотенузы».
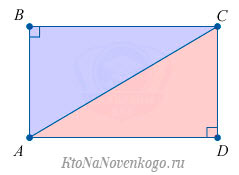
В нашем случае гипотенузой является диагональ прямоугольника, которая делит его на два равных прямоугольных треугольника. И теорема Пифагора выглядит следующим образом:
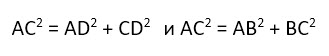
Свойства прямоугольника
К свойствам относятся следующие утверждения:
- Прямоугольник является параллелограммом, а значит имеет все присущие ему свойства.
- У него равны противоположные стороны.
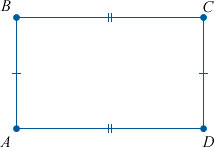
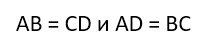
- У него противоположные стороны параллельны.
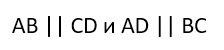
- У него равны противоположные стороны.
- У прямоугольников все прилегающие друг к другу стороны пересекаются под прямыми углами. А в сумме они дают 360 градусов.

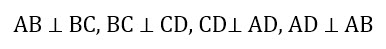
- У прямоугольников обе диагонали равны между собой.
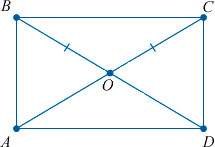
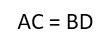
- Диагональ делит фигуру ровно пополам, и в результате получаются два одинаковых прямоугольных треугольника.
- Диагонали прямоугольника пересекаются в его геометрическом центре. А их точка пересечения делит каждую диагональ на два равных отрезка. Более того, все четыре отрезка равны между собой.
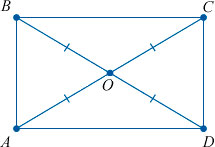
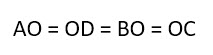
- У прямоугольника точка пересечения диагоналей является еще и центром описанной вокруг окружности. Причем длина диагонали одновременна является диаметром (что это такое?) этой окружности.
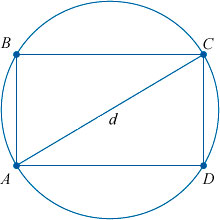
Периметр и площадь
Для того чтобы определить периметр прямоугольника, надо просто сложить длины всех его четырех сторон.

Но с учетом того, что попарно они равны, то конечная формула может выглядеть более просто:
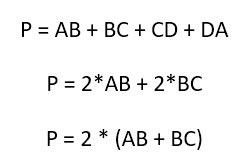
Площадь прямоугольника вычисляется также весьма просто. Надо лишь перемножить две его стороны:
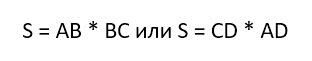
К слову, это не единственная формула для вычисления площади. Площадь также можно получить, имея значение периметра фигуры или длину его диагонали. Но эти формулы гораздо сложнее.

Вот и все, что мы хотели рассказать о геометрической фигуре ПРЯМОУГОЛЬНИК. До новых встреч на страницах нашего блога.
Задача нахождения границ повернутого прямоугольника одинаково востребована, как в векторной, так и в растровой графике. При создании разного рода редакторов необходима область, описывающая фигуру, к которой применена трансформация. При обработке изображений, фото, для достижения каких-то художественных эффектов или решения сугубо технических проблем, например, для «выравнивания горизонта».
Возможно, Вы попали на эту страницу по запросу: «Поворот прямоугольника и нахождение вершин онлайн«. В этом случае имеет смысл посмотреть эту ссылку. Там прямой ответ на этот вопрос. Если требуется поворот вокруг центра прямоугольника, не забудьте установить переключатель «Вращать вокруг центра прямоугольника«.
Подобные задачи можно разделить на три группы:
- Нахождение описывающего прямоугольника для повернутого прямоугольника.
- Нахождение ширины и высоты повернутого прямоугольника, вписанного в некий прямоугольник.
- Нахождение вписанного прямоугольника в повернутый прямоугольник.
Повернуть прямоугольник
Чтобы повернуть прямоугольник необходимо воспользоваться аффинным преобразованием поворота, или просто применить формулы преобразования ко всем четырем вершинам прямоугольника.
Формулы преобразования поворота доказываются тут.
Давайте создадим прямоугольник и зададим угол поворота. Можно менять угол поворота зажав и перетаскивая оранжевую вершину.
Угол поворота:
Ширина:
Высота:
Get a better browser, bro…
Рис.1. Поворот прямоугольника. O(x,y) — координаты центра вращения. За оранжевую вершину можно тащить.
Чтобы посчитать координаты вершин повернутого прямоугольника, используются следующие формулы:
Если вращение происходит не вокруг центра координат, необходимо добавить координаты центра вращения, как на рисунке.1.
Немного кода:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
type T4PointF = array [0..3] of TPointF; //********************************************************************* // Посчитать координаты массива точек повернутых на Angle радиан //********************************************************************* function CalcAnglePoints(const APoints: T4PointF; const ACenter: TPointF; const Angle: single): T4PointF; var i: Integer; sn,cs: single; begin SinCos(Angle, sn, cs); for i := 0 to Length(APoints)–1 do begin Result[i].X := (APoints[i].X–ACenter.X) * cs – (APoints[i].Y–ACenter.Y) * sn + ACenter.X; Result[i].Y := (APoints[i].X–ACenter.X) * sn + (APoints[i].Y–ACenter.Y) * cs + ACenter.Y; end; end; |
Описывающий прямоугольник повернутого прямоугольника
Краткая формулировка задачи:
Есть некий прямоугольник (a b c d), с шириной w и высотой h. К нему применен поворот на α градусов. Необходимо найти ширину W и высоту H описывающего прямоугольника.
Get a better browser, bro…
Рис.2. Описывающий прямоугольник для повернутого прямоугольника. За оранжевую вершину можно тащить.
На рисунке синий цвет угла означает направление против часовой и положительный знак угла, красный — по часовой и отрицательный.
В качестве поворачиваемого прямоугольника может выступать, допустим, картинка. Чтобы получить на выходе «необрезанное» по краям изображение, необходимо посчитать размер будущей картинки, чтобы повернутое изображение полностью входило в область.

Можно решить задачу следующим образом: пройтись по вершинам, найти минимальные и максимальные значения координат:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
//************************************************************** // Получить описывающий прямоугольник массива вершин //************************************************************** function GetPointsRect(const APoints: T4PointF): TRect; var i: Integer; begin Result := Rect(MaxInt, MaxInt, –MaxInt, –MaxInt); for i := 0 to Length(APoints)–1 do begin if APoints[i].X < Result.Left then Result.Left := Trunc(APoints[i].X); if APoints[i].X > Result.Right then Result.Right := Round(APoints[i].X); if APoints[i].Y < Result.Top then Result.Top := Trunc(APoints[i].Y); if APoints[i].Y > Result.Bottom then Result.Bottom := Round(APoints[i].Y); end; end; |
Это способ хороший, не особо затратный и универсальный. Если у нас число таких вершин непредсказуемо большое и отличается таким же непредсказуемым многообразием, это пожалуй, единственный способ. Но для прямоугольника есть способ лучше и проще.
Вспомним свойства прямоугольника.
— Прямоугольник является параллелограммом — его противоположные стороны попарно параллельны.
— Стороны прямоугольника являются его высотами. Середины сторон прямоугольника образуют ромб.
— Квадрат диагонали прямоугольника равен сумме квадратов двух его смежных сторон (по теореме Пифагора).
— Около любого прямоугольника можно описать окружность, причём диагональ прямоугольника равна диаметру описанной окружности (радиус равен полудиагонали).
Википедия
По теме прямоугольника можно заглянуть сюда (не реклама, просто симпатично, кратко, емко).
Сейчас нас интересует попарная параллельность сторон и то, что все углы прямоугольника — прямые. На основании этого и будет строится дальнейшее рассуждение. Предполагается, что про углы у параллельных прямых все в курсе.
Get a better browser, bro…
Рис.4. Расчет ширины W и высоты H описывающего прямоугольника. За оранжевую вершину можно тащить.
Рассмотрим рисунок 4.
- Угол β — интересующая нас часть угла α, остаток от деления на π / 2.
- Угол γ — это дополнение угла β до π / 2, т.е. γ = π / 2 — β.
Цвет в данном случае означает попадание β в один из квадрантов. Синий — квадранты 1 и 3, красный — 2 и 4.
Внимание! Следующий текст генерируется автоматически в зависимости от угла на рисунках.
Поставив галочку ниже, в рисунках 2 и 4 будет отображаться решение. Не стал сразу выводить, ну чтоб не нарушать интригу.
Показать решение
В качестве итога. Чтобы найти высоту и ширину описывающего прямоугольника для повернутого прямоугольника всегда работают эти красивые формулы:
Где:
- W’ — ширина описывающего прямоугольника
- H’ — высота описывающего прямоугольника
- w — ширина исходного прямоугольника
- h — высота исходного прямоугольника
- α — угол поворота
Зная координаты центра трансформации, высоту и ширину границ, нетрудно рассчитать координаты описывающего прямоугольника.
Друзья, спасибо за внимание!
Подписывайтесь на телеграм-канал.
Жду ваших комментариев. Надо ли рассказывать, как вписать повернутый прямоугольник в заданный прямоугольник? Или может про «выравнивание горизонта»?
