На чтение 8 мин Просмотров 2.2к.
Наблюдая за перемещением небесных объектов, люди пытались найти объяснение происходящим на небе событиям. У древних людей преобладали версии мистического характера. Но в 17-м веке Исааком Ньютоном было предложено первое научное объяснение перемещению астрономических тел. Теория гравитации совершенствовалась еще несколько столетий, пока не приобрела современный вид.

Однако, несмотря на наблюдения и опыт, в современной астрофизике есть много пробелов и нестыковок, которые ученые затрудняются объяснить. Например, гравитационная константа, значение которой до сих пор не получается определить с достаточной степенью точности. А в последнее время появились предположения, что эта величина не совсем и константа. В этой статье мы и рассмотрим данный вопрос.
Содержание
- Что такое гравитационная постоянная
- Единица измерения гравитационной постоянной
- Как найти гравитационную постоянную, история открытия
- Работы Ньютона
- Экспериментальное определение гравитационной постоянной, эксперимент Кавендиша
- Измерение гравитационной постоянной
- Современная история изменений гравитационной постоянной
Что такое гравитационная постоянная
Гравитационной постоянной (постоянной Ньютона) называют коэффициент, входящий в формулу закона всемирного тяготения. Численное значение константы гравитации (G, GN или g) равно:

Постоянная Ньютона не зависит от характеристик взаимодействующих объектов и внешних критериев. Данный показатель активно используется практиками при вычислении орбит небесных объектов, в геолого-разведывательных процессах, в геодезии и геофизике.
Единица измерения гравитационной постоянной
Сила в физике сила измеряется в ньютонах:

Гравитационная постоянная численно равна силе, но при этом имеет другую размерность:

Данная единица измерения выводится при помощи несложных расчетов. Два тела весом по 1кг будут взаимно притягиваться с силой, обратно пропорциональной квадрату расстояния между ними:

Коэффициент, уравнивающий Н и единицу измерения гравитационной постоянной, вычисляется следующим образом:

Как найти гравитационную постоянную, история открытия
Открытию явления гравитации предшествовали труды многих исследователей. Еще в древней Греции были предложены гипотезы, которые пытались объяснить, почему материальные тела падают на землю, а не летят в произвольном направлении. История открытия гравитации представлена в таблице.
| Николай Коперник | Обосновал модель мира, в которой Солнце занимает центральное место, а остальные объекты вращаются вокруг него (гелиоцентрическая модель). |
| Уильям Гилберт | Высказал предположение, что наша планета и ее спутник являются магнитами друг для друга, при этом магнитная сила Земли больше из-за того, что больше ее масса. |
| Иоганн Кеплер | Сформулировал ряд законов, в том числе 3-й, который был использован при разработке теории гравитации: период обращения планет в квадрате соотносится как большие полуоси орбит в кубе. |
| Галилео Галилей | Обосновал, что если на тело не оказывать никаких воздействий, то оно будет оставаться в бездействии. Сформулировал закон, смысл которого заключался в том, что все тела, независимо от их тяжести, падают вниз с одинаковой скоростью, при этом пройденный путь пропорционален квадрату времени, за которое тело достигло поверхности Земли. |
| Роберт Гук | Сформулировал закон всемирного тяготения для некруговых орбит и предложил Ньютону обосновать его математически. Создал теорию об универсальной силе тяжести. |
| Эдмунд Галлей | Просчитал обратно пропорциональную зависимость силы тяжести и квадрата расстояния. |
| Исаак Ньютон | На основании работ предшественников вывел закон всемирного тяготения. |
| Генри Кавендиш | Собрал приспособление, с помощью которого можно определить величину константы гравитации. |
| Симеон Дени Пуассон | В его трудах впервые появляется понятие гравитационной константы. |
Ньютона интересовало выведение научных правил, а не чистота искомых значений. Экспериментаторы, которые применяли формулу Ньютона на практике, столкнулись с необходимостью введения поправочного коэффициента, который позже получил название ньютоновская константа. Возник вопрос, чему равна гравитационная постоянная. Последовавшие в данном направлении работы показали, что найти гравитационную постоянную можно только опытным путем.
Работы Ньютона
Научная почва для обоснования закона всемирного тяготения была основательно подготовлена предшественниками Ньютона. Большая часть расчетов базировалась на 3-м законе Кеплера. Сила, благодаря которой планеты удерживаются на орбитах, соизмерима с центростремительным ускорением, и должна быть обратно пропорциональна квадрату расстояния от центра планеты до центра Солнца. Сила, вызывающая падение предметов (пресловутого яблока) на землю, была сопоставлена ученым с силой, удерживающей Луну на ее орбите. Кроме того, физик установил центростремительное ускорение Луны относительно Земли.
Ранее опытным путем было установлено значение ускорения свободного падения объектов. Ученый применил удобные для вычислений цифры: дистанция от Луны до центра Земли в 60 раз больше, чем дистанция от объекта, находящегося на поверхности Земли. Если объект направить к центру Земли, то он за 1 секунду пролетит такой же путь, который пройдет Луна за 1 минуту. Эксперименты подтвердили точность теоретических выкладок с погрешностью около 1%. Это указывало на общность природы происхождения сил тяготения.
Из этого можно заключить, что сила обоюдного притяжения должна соответствовать каждой из масс. Также было подтверждено, что гравитация обратно пропорциональна квадрату расстояния между объектами. Исходя из вышесказанного, формула закона всемирного тяготения будет иметь следующий вид:

где F – сила гравитационного тяготения, g – гравитационная постоянная, m1 и m2 – массы объектов, R – расстояние между объектами.
Работы Ньютона внесли вклад в решение следующих вопросов:
- перемещения тел по космическим орбитам;
- ускорение свободного падения;
- приливы океанических вод;
- причины экваториальной выпуклости.
Эйнштейн использовал закон всемирного тяготения при разработке теории относительности. Постоянная гравитационная показывает соотношение между такими характеристиками уравнений поля, как геометрия пространства-времени и тензор энергии-импульса.
Вместо G Ньютон применял в расчетах «гравитационный параметр» µ. Практические наблюдения за космическими телами позволили определить для ряда небесных объектов значение µ с минимальной погрешностью. Рассчитывают µ по формуле:
µ=GM;
где G – константа гравитации, M – масса объекта

В трудах Кеплера также фигурирует гравитационный параметр. В физике с его помощью упрощают некоторые громоздкие формулы.
Экспериментальное определение гравитационной постоянной, эксперимент Кавендиша
Британец Джон Мичелл увековечил свое имя как создатель крутильных весов, с помощью которых впервые смогли определить величину g. Экспериментальное определение гравитационной постоянной не входило в планы исследователя. Он хотел «взвесить» нашу планету. Однако воплотить свои планы Мичелл не успел, и сконструированное им устройство после его кончины досталось Генри Кавендишу.

Кавендиш доработал установку. Конструкция включала шестифутовый стержень, закрепленный на медном волокне длиной 1 м. К плечам коромысла ученый прикрепил два шара из свинца по 775 грамм каждый, соорудив таким образом гантельку. Затем рядом с маленькими шариками он разместил крупные шары по 49,5 кг, что привело к возникновению явления гравитации между объектами. Стержень конструкции отклонился от первоначального положения, что дало возможность найти величину угла поворота гантельки. Опыт Кавендиша оказался успешным: увязав упругие свойства волокна, массу шаров, размер установки и значение угла, он определил массу Земли и ее среднюю плотность. Сегодня эксперимент Кавендиша по-прежнему актуален, исследователями разрабатываются инновационные модификации прибора.
Измерение гравитационной постоянной
С измерением степени точности гравитационной постоянной g сложилась парадоксальная ситуация. Последние многочисленные эксперименты определяют отклонение с точностью 10-4. Это хуже на несколько порядков по сравнению с точностью определения прочих базисных величин. Сравнительно аккуратные результаты можно получить в условиях лаборатории, измеряя силу гравитации между двумя телами с известной массой (модификации эксперимента Кавендиша). Новые атомно-интерферометрические устройства оказались непригодными в измерении гравитационной постоянной в связи с гораздо большей величиной погрешности, чем при эксперименте на механических устройствах.
Современная история изменений гравитационной постоянной
Неординарность ситуации с нахождением точного значения гравитационной константы привела к возникновению догадки, что G не является постоянной в классическом понимании и может с течением времени изменяться. В уравнениях общей теории относительности Эйнштейн увязал гравитационную постоянную и космологическую константу – параметр, который влияет на устойчивость Вселенной.
Хаббл и Фридман обосновали опытным путем модель расширяющейся Вселенной, что противоречило теории стационарной Вселенной Эйнштейна. На долгое время ученые прекратили учитывать при вычислениях космологическую постоянную. В конце 1990-х годов было выявлено и подтверждено ускорение расширения Вселенной. Вновь открытые результаты не вписывались в теорию Хаббла-Фридмана, концепцию пришлось пересматривать, и космологическая постоянная вернулась в физику.
Современная Лямбда-CDM модель Вселенной учитывает космологическую постоянную. Данная концепция объясняет наличие антигравитации, «темной материи», реликтового излучения, и является стандартом в астрофизике с 1998-го года.
Интересно, что Лямбда-CDM модель хорошо коррелирует с космологией черной дыры. Все больше ученых склонны отказываться от Теории большого взрыва, поскольку накопившиеся научные данные противоречат общепринятому взгляду на образование Вселенной. В гипотезу, что видимое нами пространство-время (и мы вместе с ним) бесконечно «падает» в гигантскую черную дыру, отлично вписывается явление ускорения расширения Вселенной, «странности» реликтового излучения, наличие темной материи.
Современная история изменений гравитационной постоянной привела к попыткам астрономов переосмыслить данный физический параметр. Так, Филипп Мангейм считает, что константа g в зависимости от условий ее измерения может менять свое значение. В условиях нашей планеты постоянная g будет иметь известную ученым величину, а вот в космосе значение G будет гораздо меньше.
Космологическая постоянная, описывающая скорость расширения Вселенной, имеет расчетное значение в 10120 раз превосходящее наблюдаемое. Если бы значение g было верным, то галактики не успели бы образоваться. По мнению Мангейма, в расчеты следует ввести новую величину, которая будет пропорциональна произведению космологической и гравитационной констант.
Такой подход позволит устранить существующие противоречия, но у него есть и свои недостатки: подвергаются сомнению основы теории относительности, не объясняется существование реликтового излучения и двойных пульсаров. Преимуществом идеи Мангейма является возможность синтеза теории гравитации и физики элементарных частиц в одну универсальную доктрину.
По вашему мнению, ньютоновская константа – это объективный параметр, или мы просто не все знаем о физических феноменах?
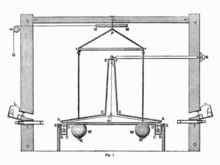
Вертикальный разрез крутильных весов (рисунок 1 из статьи Кавендиша) с защищающей их конструкцией GGGG. ABCDDCBAEFFEA — неподвижный деревянный кожух, внутри которого подвешены крутильные весы, m — тонкий деревянный стержень коромысла, g — растяжка из тонкой серебряной проволоки, сообщающая жёсткость коромыслу, X — малые шары, подвешенные к коромыслу на проволоке, K — рукоятка механизма первоначальной установки коромысла, RrPrR — поворотная ферма, с закреплёнными на ней большими шарами W, MM — шкив поворотного механизма фермы, L — осветительные приборы, T — телескопы для наблюдения за отклонением коромысла через остеклённые отверстия в торцевых стенках кожуха, напротив концов коромысла[1].
Эксперимент Кавендиша — опыт, проведённый в 1797—1798 годах британским учёным Генри Кавендишем с целью определения средней плотности Земли, что впоследствии позволило вычислить её массу из радиуса Земли, определить массы Луны, Солнца и остальных планет Солнечной системы. Измерения плотности Земли с использованием маятников выполнялись до Кавендиша, но точность этих измерений была недостаточной[⇨]. Хотя значение универсальной гравитационной постоянной также можно было определить по плотности Земли и в некоторых источниках оно приводится со ссылкой на Кавендиша, но в его статье значение указано не было[⇨].
Кавендиш усовершенствовал устройство, названное крутильными весами, разработанное примерно в 1783 году Джоном Мичеллом, который умер, не сумев завершить предложенный им эксперимент[⇨]. Результат, полученный Кавендишем, заключался в том, что средняя плотность Земли составляла 5,437 г/см3, что всего на 1,4 % ниже принятого в настоящее время значения 5,515 г/см3[⇨]. Использование крутильных весов для определения гравитационной постоянной или тестирования закона всемирного тяготения на малых расстояниях происходит и в современной истории, но с использованием всё более точных измерений[⇨].
Предыстория[править | править код]


Отклонение отвеса в районе горы.
Одна из первых попыток определения плотности Земли была предпринята профессором гидрографии Гавра французом Пьером Бугером во время геодезической миссии в Перу в 1735—1739 годы. Бугер провёл несколько экспериментов, чтобы определить взаимосвязь между плотностью вулкана Чимборасо и средней плотностью Земли, на основании отклонения от вертикали отвеса вблизи этой большой горы. Исаак Ньютон ранее рассматривал проведение эксперимента как практическую демонстрацию созданной им теории гравитации в своём сочинении «Начала», но в конце концов отверг эту идею. Результаты Бугера были не очень хорошими, так как одно измерение давало плотность Земли в четыре раза больше плотности горы, а другое в двенадцать раз больше[2][3].

Второй эксперимент по определению плотности Земли — это эксперимент Шихаллона середины 1774 года. В 1772 году комитет учёных из Лондонского королевского общества, в который входили Королевский астроном, преподобный Невил Маскелайн, Генри Кавендиш, Бенджамин Франклин, Дэйнс Баррингтон и преподобный Сэмюэл Хорсли[en], был убеждён, что они могут определить притяжение горы по отклонению отвеса, и летом 1773 года астроному Чарльзу Мейсону[en] было поручено выбрать гору. Мейсон выбрал шотландскую гору Шихаллион в графстве Пертшир из-за её симметрии и изолированности. Эксперимент проводил Маскелайн, а данные обрабатывал Чарльз Хаттон[en]. Окончательные результаты показали, что плотность Земли соответствует 4,500 г/см³, что на 20 % ниже принятого в настоящее время значения 5,515 г/см³[4][3].
Примерно в 1768 году преподобный Джон Мичелл, британский физик и геолог, также спроектировал и построил крутильные весы с целью определения средней плотности Земли. Этот прибор был похож на тот, который разработал француз Шарль Огюстен де Кулон, который использовал его для измерения небольших притяжений и отталкиваний электрических зарядов в 1784 году[5]. Мичелл, похоже, не знал о работе Кулона, когда разрабатывал свои крутильные весы[6]. Однако он умер, так и не сумев завершить придуманный им эксперимент, а построенный инструмент унаследовал преподобный Фрэнсис Джон Хайд Волластон, профессор натурфилософии Кембриджского университета, который передал его Генри Кавендишу; оба были членами Королевского общества[6][7].
Определение плотности Земли было важно в то время по нескольким причинам:
- Оно бы усилило ньютоновскую физику, соединив принцип всемирного тяготения, объединивший небесную и земную механику, с геологией[2].
- В области геологии, в конце XVIII века возникла полемика между двумя представлениями о внутреннем составе Земли: нептунианской теорией немца Авраама Готлоба Вернера, считавшего океан, воду, ответственными за образование минерального царства, и плутоновской теорией шотландца Джеймса Геттона, который приписывает основные земные геологические образования внутреннему теплу Земли. Следовательно, определение средней земной плотности позволило бы выяснить твёрдость или текучесть недр планеты[2].
- Плотность Земли позволяла вычислить её массу, а это требовалось в астрономии восемнадцатого века, поскольку уже известные соотношения масс Луны, Солнца и остальных планет Солнечной системы можно было опеределить из этого значения[2].
Эксперимент[править | править код]

Генри Кавендиш начал свои эксперименты летом 1797 года в возрасте 67 лет в саду своего дома в Клэфэм-Коммон[en], ныне жилом районе на юге Лондона, где он поместил крутильные весы внутри комнаты здания размером 17,7×7,9 м[8]. Первый эксперимент он провёл 5 августа 1797 года, и до 23 сентября провёл ещё семь опытов. Семь месяцев спустя, между 29 апреля и 30 мая 1798 года, он сделал ещё девять серий наблюдений, и последние два эксперимента — с помощью своего секретаря Джорджа Гилпина[9].
Обычно можно найти много книг[10][11], в которых ошибочно утверждается, что целью Кавендиша было определение гравитационной постоянной 


Крутильные весы[править | править код]

Вид сверху на крутильные весы (рисунок 2 статьи Кавендиша). Схема горизонтального рычага с двумя маленькими сферами b и большими сферами в двух разных положениях (WW и ww)[13].
Крутильные весы Мичелла, перестроенные и улучшенные Кавендишем, состояли из нескольких частей:

Деталь крутильных весов (рисунок 1 статьи Кавендиша). W — толстая сфера, x — маленькая сфера. Деревянный ящик, закрывающий коромысло, — это ABCD. n представляет собой апертуру, через которую можно наблюдать градуированную шкалу h.
- Горизонтальное деревянное коромысло незначительной массы и длиной 183 см (6 футов) было подвешено на тонкой проволоке длинной 102 см (40 дюймов) прямо посередине. На каждом конце коромысла находилась небольшая свинцовая сфера диаметром 5,08 см (2 дюйма) с массой 0,73 кг (b на рисунках)[7]. Всё заключено в ящик из красного дерева, АААА, для предотвращения сквозняков и перепадов температуры, с небольшими отверстиями на торцах, закрытыми стеклом, что позволяло наблюдать за положением этих сфер. Небольшая сила позволяла этому горизонтальному коромыслу вращаться вокруг оси вращения, отмеченной проволокой, если та была достаточно тонкой[8][6].
- Рядом с каждой из вышеупомянутых сфер b у Кавендиша была ещё одна неподвижная сфера, также сделанная из свинца, но гораздо более тяжёлая, 158 кг[14] (диаметром около 1 фута). Они указаны на рисунках в двух разных позициях, WW и ww. Чтобы разместить их очень близко к маленьким сферам, Кавендиш разработал механизм, который активирует их перемещение на расстоянии, чтобы избежать помех — отмечено как ММ. Гравитационное действие этих сфер должно было притягивать маленькие сферы к шарам на коромысле, производя небольшое закручивание проволоки[6][15].
- Чтобы измерить отклонение малых сфер, Кавендиш расположил градуированную шкалу из слоновой кости внутри деревянного ящика, защищающего коромысло, расположенную рядом с маленькими сферами и освещённую лучом света снаружи. Шкала имела отдельные деления на расстоянии 0,13 см (1/20 дюйма). На конце коромысла находился небольшой кусочек слоновой кости, выполнявший роль шкалы нониуса и разделявший деления шкалы на 5 частей, то есть величиной около 0,25 мм[6][1]. На многих схемах крутильных весов, встречающихся в литературе, указано, что несущая проволока имела зеркало, позволяющее наблюдать за производимым отклонением. Эта система является усовершенствованием, сделанным после эксперимента Кавендиша другими исследователями. Кавендиш измерял отклонение прямо на шкале возле маленьких сфер[2].
- Для предотвращения возмущений, вызванных сквозняками и колебаниями температуры, Кавендиш поместил весы в закрытой комнате, на рисунке обозначенном вершинами GGGG. Большие сферы можно было перемещать из другой соседней комнаты с помощью механизма, обозначенного PRR, активируемого в точке m. И он мог также измерить небольшое кручение весов с помощью телескопа, отмеченного буквой Т, чтобы наблюдать отклонения на шкале из слоновой кости, освещённой светом от свечей, отмеченной буквой l[2].
Крутильные весы были удивительно точны для своего времени. Сила кручения, создаваемая притяжением шаров, была очень мала, 1,74 · 10−7 Н, что примерно равно 24 · 10−9 веса маленьких шаров. Эквивалентно силе, необходимой для удержания 0,0155 мг вещества. При подъёме песчинки диаметром 1 мм требуется усилие, примерно в 90 раз превышающее силу, измеренную по шкале Кавендиша[2].
Метод Кавендиша[править | править код]

Один конец современных крутильных весов, предназначенных для демонстрации эксперимента Кавендиша

Закон всемирного тяготения Ньютона гласит, что масса M притягивает другую массу m с силой F, пропорциональной произведению M · m и обратно пропорциональной квадрату расстояния r, разделяющего их.
Метод Кавендиша, используемый для расчёта плотности Земли, заключался в измерении периода колебаний горизонтального коромысла, которое колеблется, приближаясь к большой сфере и удаляясь от неё[13].
Когда большая сфера приближается на небольшое расстояние (9 дюймов или 22,9 см) к маленькой сфере, то сила гравитационного притяжения становится чувствительной и коромысло с маленькими сферами начинает вращаться в сторону больших сфер. По мере приближения малых сфер к более крупным сила притяжения увеличивается, так как она обратно пропорциональна расстоянию между их центрами, 
Период колебаний, измеренный Кавендишем, составил около 15 минут, что даёт представление о медленном движении коромысла. Кавендиш измерил время трёх полных колебаний, а затем определил период, разделив общее время на количество колебаний[16]. Можно показать, что период связан с силой тяжести и силой восстановления проволоки. Колебание затухает и его амплитуда, не превышающая 2 см, несколько уменьшается при каждом колебании, хотя это и не влияет на не зависящий от него период. Чтобы полностью прекратить колебательное движение, потребовалось много часов, но вскоре Кавендиш изменил положение больших сфер на другой стороне и сумел реактивировать колебания и провести новые измерения[2].
Определив период этих малых колебаний, можно вычислить силу гравитационного притяжения малого шара со стороны большого шара известной массы М и сравнить её с силой притяжения такого же малого шара к Земле. Таким образом, Земля может быть описана как в N раз более массивная, чем толстая сфера[9]. Все это основано на теории всемирного тяготения Исаака Ньютона, согласно которой сила притяжения пропорциональна произведению масс M и m и обратно пропорциональна квадрату расстояния r между ними
После того как были произведены расчёты и сделан ряд поправок, результат, полученный Кавендишем, состоял в том, что средняя плотность Земли в 5,448 раз превышала плотность воды при температуре от 19°С до 21°С (0,998 г/см3). Эта величина отличается всего на 1,4 % от принятого в настоящее время значения, что в 5,526 раз больше плотности воды, или 5,515 г/см3[2].

CAVENDISH, H. Experiments to Determine the Density of the Earth. Phil. Trans. R. Soc. Lond. 1 Gener 1798, 88:469-526
Несмотря на то, что опыт Кавендиша считается первым определением гравитационной постоянной, он не только не приводил её значение, но и не мог сослаться на закон всемирного тяготения в современной форме, потому, что до конца XIX века его так не записывали[17]. В его время не существовало единства среди учёных в определении силы, периода колебаний и рассуждения велись используя сравнения и аналогии[2][18]. Для математического анализа Кавендиш использовал аналогию крутильных весов с математическим маятником, период которого известен[17]. Для математического маятника в крайнем положении возвращающая сила 

















Математическая формулировка[править | править код]

Определения терминов, используемых в формулах, приведены в подписи в конце этого раздела.
Приведённый ниже вывод формулы[21] для определения плотности Земли использует современную терминологию. Он не соответствует методу, которому следовал Кавендиш[22][18].
Момент силы 




Сила гравитационного притяжения F между маленькой сферой массы m и большой сферой массы M, расстояние между центрами которых равно r, определяется выражением закона всемирного тяготения Исаака Ньютона:
Подставив это выражение для F в уравнение (1), получается[22]
Для определения коэффициента крутящего момента 

Учитывая, что масса деревянного коромысла пренебрежимо мала по сравнению с массами маленьких сфер, момент инерции весов обусловлен только двумя маленькими сферами и справедливо равенство[24]:
где выражение (3) можно заменить и период примет вид
Выразив из предыдущей формулы 
в выражении (2) можно произвести замену и перестановку, выделив константу G[25]:
Притяжение, оказываемое Землёй на массу m (массу маленьких сфер), находящуюся вблизи её поверхности, то есть на её вес, составляет:
Выделяя массу Земли, получается выражение
Подставляя значение G из периода колебаний, получаем массу Земли
Плотность Земли, 

Легенда[править | править код]
| Символ | Размерность | Определение |

|

|
Угловое отклонение положения малых сфер относительно их положения равновесия |

|

|
Гравитационная сила между массами M и m |

|

|
Гравитационная постоянная |

|

|
Масса маленьких сфер |

|

|
Масса больших сфер |

|

|
Расстояние между центрами малых и больших сфер |

|

|
Расстояние между центрами двух маленьких сфер |

|

|
Коэффициент кручения проволоки |

|

|
Момент инерции коромысла |

|

|
Период колебаний коромысла |

|

|
Ускорение силы тяжести на поверхности Земли |

|

|
Масса Земли |

|

|
Радиус Земли |

|

|
Плотность Земли |
Последующие эксперименты[править | править код]
После эксперимента Кавендиша другие учёные повторили эксперимент с той же сборкой, внося улучшения. С середины XIX века и далее проводились опыты с целью определения гравитационной постоянной 
- Немец Фердинанд Райх повторил измерение плотности Земли с помощью весов, очень похожих на те, которыми пользовался Кавендиш[26], и получил новые значения средней плотности Земли, ρ = 5,49 г/см³[27] в 1837 году и ρ = 5,58 г/см³ в 1852 году[28].
- Фрэнсис Бейли повторил эксперимент с крутильными весами и в 1842 году получил значение ρ = 5,67 г/см³[29]. Его опыты финансировались правительством с целью улучшить измерения Кавендиша. Теория была построена Джорджем Эйри. В его опытах размеры, вес шаров и способ их подвеса варьировались[30].
- Французы Мари Альфред Корню и Баптистин Бай[en] нашли в 1873 г.[31] значения ρ в пределах от 5,50 до 5,56 г/см³[12].
- В 1895 году Чарльз Вернон Бойз модифицировал оригинальный инструмент Мичелла и Кавендиша, уменьшив его до 1/18 части, заменив торсионную проволоку, первоначально сделанную из железа, тонкими кварцевыми волокнами диаметром 0,002 мм. Это нововведение позволяет использовать меньшие массы золота (m = 2,7 г, M = 7,5 кг) и меньшее расстояние 15 см[32] при лучшем контроле температурных колебаний и отклонений от уклона земли. Он также разделяет положение пар сфер на 6 дюймов по вертикали, чтобы уменьшить влияние толстой сферы другой пары, и имеет зеркало на плече, отражающее луч света, что позволило определить с помощью телескопа малый угол отклонения[33]. Его измерения дали значение ρ = 5,527 г/см³[34].
- В 1897 году немецкий физик Карл Фердинанд Браун усовершенствовал крутильные весы, поместив их в контейнер, откуда он откачивал воздух, избегая таким образом сквозняков, влияющих на колебания. Он также использовал новый метод. Он расположил большие массы на одной линии с малыми массами коромысла, а затем изменил их расположение на 90°, способ, названный периодом колебаний. В положениях с четырьмя выровненными сферами гравитационное притяжение сокращает период колебаний и удлиняет массы в скрещённых, более удалённых положениях. У него получилось значение ρ = 5,527 г/см³, как и у Бойза[35].
- Метод Брауна также был использован в 1930 году Паулем Ренно Хейлом с различными материалами (золото, платина и стекло) и получил среднее значение плотности Земли ρ = 5,517 г/см³[36]. Он повторил эксперимент в 1942 году вместе с Петером Хшановски, и получили значение ρ = 5,514 г/см³, проводя эксперимент с разными проволоками[37]. Наконец, Габриэль Г. Лютер и Уильям Р. Таулер в 1982 г. использовали вольфрамовые сферы массой 10,5 кг и получили очень точное значение[38][39].
- В 2008—2010 годах были опубликованы результаты ещё трёх экспериментов. Хотя авторы каждого из них заявляют о высокой точности полученного значения, их результаты различаются на величину больше заявленных экспериментальных погрешностей[40].
- В 2021 году эксперимент был повторён на золотых шариках диаметром 2 мм и массой всего 90 мг. Сила, действующая между ними, не превышала 10−13 Н[41].
| Год | Экспериментаторы[42] | Описание | Плотность Земли, г/см³ | Гравитационная постоянная, 10−11 м³/(кг·с²) |
|---|---|---|---|---|
| 1837—1847, 1852 | Ф. Райх | Провёл две серии опытов. | 5,58[28] | 6,70±0,04[43] |
| 1843 | Ф. Бейли[44][45] | Было проведено 2000 опытов[46] | 5,6747±0,0038[46]. | 6,63±0,07[43] |
| 1873 | А. Корню и Ф. Бейли | При помощи более совершенного прибора, составленного из алюминиевого стержня, маленьких платиновых шариков и больших стеклянных шаров, наполненных ртутью | 5,50—5,58[47]. | 6,64±0,017[43] |
| 1880 | Ф. Йолли | Использовал обыкновенные рычажные весы. | 5,692 ± 0,068[48] | 6,58 |
| 1887 | И. Вильзинг | Вместо горизонтального стержня, отклоняемого тяжёлыми шарами в опытах Кавендиша, он использовал вертикальный. | 5,594 ± 0,032[49] | 6,71 |
| 1895 | Ч. Бойс[50] | Улучшил измерения уменьшив размер установки. | 5,5270[31] | 6,66 ± 0,007[43] |
| 1930 | П. Хейл[51] | 5,517 | 6,670 ± 0,005[52] | |
| 1942 | П. Хейл и П. Хржановский[53] | 5,514 | 6,673 ± 0,003[52] | |
| 1982 | G. Luther и W. Towler[54] | 5,617 | 6,6726 ± 0,0005[52] | |
| 2000 | Университет Вашингтона в Сиэтле[55] | 5,6154 | 6,67390 | |
| 2018 | CODATA | 6,674 30(15)[56] |
Примечания[править | править код]
- ↑ 1 2 Голин, Филонович, 1989, с. 257.
- ↑ 1 2 3 4 5 6 7 8 9 10 11 F. Moreno. Un Experimento Para Pesar El Mundo (исп.). Los Lagartos terribles. Apuntes, escritos y ensayos científicos (15 июля 2011). Дата обращения: 22 января 2022.Архивировано 21 декабря 2021 года.
- ↑ 1 2 3 4 Moreno González, Antonio. «Pesar» la tierra : test newtoniano y origen de un anacronismo (исп.) // Enseñanza de las ciencias. — València: Bellaterra; Universitat de València; Universitat Autònoma de Barcelona, 2000. — V. 18, fasc. 2. — P. 319—332. — ISSN 2174-6486. — doi:10.5565/rev/ensciencias.4049.
- ↑ Maskelyne, N (6 juliol 1775). “An Account of Observations made on the Mountain Schehallien for finding its Attraction”. Phil. Trans. [англ.] (65): 500—542.
- ↑ Coulomb, C.A (1784). “Recherches théoriques et expérimentales sur la force de torsion et sur l’élasticité des fils de metal”. Histoire de l’Académie Royale des Sciences: 229—269.
- ↑ 1 2 3 4 5 6 Cavendish, H (1 gener 1798). “Experiments to Determine the Density of the Earth. By Henry Cavendish, Esq. F. R. S. and A. S.”. Phil. Trans. R. Soc. Lond. 88: 469—526. DOI:10.1098/rstl.1798.0022.
- ↑ 1 2 Голин, Филонович, 1989, с. 255.
- ↑ 1 2 3 Poynting, 1894, p. 42.
- ↑ 1 2 3 Jungnickel, Christa. Cavendish : [англ.]. — Philadelphia, Pa : American Philosophical Society, 1996. — ISBN 9780871692207.
- ↑ Feynman, Richard. The Feynman lectures on physics (англ.). — NY: Basic Books, 2010. — ISBN 0465072984.
- ↑ Holton, Gerald. Introducción a los conceptos y teorías de las ciencias físicas : [англ.]. — Barcelona : Reverte, 1993. — ISBN 8429143238.
- ↑ 1 2 Cornu, A.; Baille, J.-B. (1873). “Détermination nouvelle de la constante de l’attraction et de la densité moyenne de la Terre”. Comptes Rendus. 15 (76): 954—958.
- ↑ 1 2 Голин, Филонович, 1989, с. 258.
- ↑ 2 439 000 гранов; один английский (тройский) гран равен 64,79891 мг.
- ↑ Голин, Филонович, 1989, с. 256.
- ↑ Голин, Филонович, 1989, с. 260.
- ↑ 1 2 3 Falconer, 1999, p. 475.
- ↑ 1 2 Clotfelter, 1987.
- ↑ Clotfelter, 1987, p. 212.
- ↑ Falconer, 1999, p. 476.
- ↑ Andrew Mark Allen. Gravitational Torsion Pendulum (англ.) (5 ноября 2011). Дата обращения: 21 января 2022.
- ↑ 1 2 3 Poynting, 1894, p. 41.
- ↑ 1 2 Chen and Cook, 2005, p. 87.
- ↑ Chen and Cook, 2005, p. 210.
- ↑ Chen and Cook, 2005, p. 209.
- ↑ Poynting, 1894, p. 49.
- ↑ Poynting, 1894, p. 50.
- ↑ 1 2 Poynting, 1894, p. 51.
- ↑ Baily, F (1843). “Experiments with the Torsion Rod for Determining the Mean Density of the Earth by Francis Baily”. Mem. Roy. Astronom. Soc. 14: 1—129 i i-ccxlvii.
- ↑ Раус, Э. Дж. Динамика системы твёрдых тел / Под ред. Ю. А. Архангельского и В. Г. Дёмина. — М.: Наука, 1983. — Т. 1. — С. 417. — 464 с. — ISBN КАЕ070720-53.
- ↑ 1 2 Раус, 1983, с. 423.
- ↑ Capderou, Michel. Handbook of satellite orbits : from Kepler to GPS. — Cham : Springer, 2014. — ISBN 9783319034157.
- ↑ Background to Boys’ experiment to determine G (англ.). Department of Physics. University of Oxford (2011). Дата обращения: 30-octubre-2014.
- ↑ Boys, C.V. (1895). “On the Newtonian Constant of Gravitation”. Philos. Trans. Roy. Soc. (A186): 1—72.
- ↑ Poynting, John Henry (1910), Gravitation Constant and Mean Density of the Earth, Encyclopædia Britannica, 11th Ed., vol. 12, The Encyclopædia Britannica Co., pp. 385–389, <http://books.google.cat/books?id=DgTALFa3sa4C&pg=PA385>. Проверено 23 января 2022..
- ↑ Heyl, P.R (1930). “A redetermination of the constant of gravitation”. J. Res. Nat. Bur. Stds. 29: 1—31.
- ↑ Heyl, P.R (1942). “A new determination of the constant of gravitation”. J. Res. Nat. Bur. Stds. 29: 1—31.
- ↑ Luther, G.G. (1982). “Redetermination of the Newtonian gravitational constant G”. Phys. Rev. Lett. 48 (121): 121—3.
- ↑ Hawking, Stephen. Three hundred years of gravitation. — Cambridge Cambridgeshire New York : Cambridge University Press, 1987. — ISBN 0521343127.
- ↑ Новые измерения гравитационной постоянной ещё сильнее запутывают ситуацию // Элементы, Игорь Иванов, 13.09.13.
- ↑ Закон всемирного тяготения действует и в миллимасштабе • Антон Бирюков • Новости науки на «Элементах» • Физика
- ↑ Грушинский, Сажина, 1972, с. 10.
- ↑ 1 2 3 4 Chen and Cook, 2005, p. 215.
- ↑ Baily, 1843, p. ccxivii, Table VII.
- ↑ Baily, 1843, p. 79.
- ↑ 1 2 Poynting, 1894, p. 55.
- ↑ Poynting, 1894, p. 58.
- ↑ Poynting, 1894, p. 63.
- ↑ Poynting, 1894, p. 68.
- ↑ Boys, 1895.
- ↑ Heyl, 1930.
- ↑ 1 2 3 Chen and Cook, 2005, p. 228.
- ↑ Heyl, Chrzanowski, 1942.
- ↑ Luther, Towler, 1982.
- ↑ PhysicsCentral, 2000.
- ↑ 2018 CODATA RECOMMENDED VALUES OF THE FUNDAMENTAL CONSTANTS OF PHYSICS AND CHEMISTRY (англ.). NIST (2019). Дата обращения: 24 февраля 2022.
Литература[править | править код]
- Статьи
- The Laws of Gravitation. Онлайн-копия статьи Кавендиша 1798 года и другие ранние измерения гравитационной постоянной.
- Boys, C. Vernon (1894). “On the Newtonian constant of gravitation”. Nature. 50 (1292): 330—4. Bibcode:1894Natur..50..330.. DOI:10.1038/050330a0. Дата обращения 2013-12-30.
- Clotfelter, B.E (1987). “The Cavendish experiment as Cavendish knew it”. Am. J. Phys (55): 210—213.
- Falconer, Isobel (1999). “Henry Cavendish: the man and the measurement”. Measurement Science and Technology. 10 (6): 470—477. Bibcode:1999MeScT..10..470F. DOI:10.1088/0957-0233/10/6/310.
- Hodges, Laurent The Michell-Cavendish Experiment, faculty website, Iowa State Univ. Дата обращения: 30 декабря 2013. Discusses Michell’s contributions, and whether Cavendish determined G.
- Lally, Sean P. (1999). “Henry Cavendish and the Density of the Earth”. The Physics Teacher. 37 (1): 34—37. Bibcode:1999PhTea..37…34L. DOI:10.1119/1.880145.
- Boys C. V. On the Newtonian Constant of Gravitation // Philos. Trans. Roy. Soc.. — 1895.
- Paul R. Heyl. A Redetermination of the Constant of Gravitation // Bureau of Standards Journal of Research. — 1930.
- Paul R. Heyl, Peter Chrzanowski. A New Determination of the Constant of Gravitation // Journal of Research of the National Bureau of Standards. — 1942.
- Gabriel G. Luther, William R. Towler. Redetermination of the Newtonian Gravitational Constant G // Physical Review Letters. — 1982. — Т. 48, вып. 3. — С. 121–123. — doi:10.1103/PhysRevLett.48.121.
- Clive C. Speake. Newton’s constant and the twenty-first century laboratory // Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences. — 2005. — Т. 363, вып. 1834. — С. 2265–2287. — doi:10.1098/rsta.2005.1643.
- Книги
- Грушинский Н. П., Гравитационная разведка. — 2-е.. — М.: Недра, 1972. — 388 с.
- Francis Baily. Experiments with the Torsion Rod for Determining the Mean Density of the Earth. — Royal Astronomical Society, 1843. — 120 с.
- Кавендиш Г. Опыты по определению плотности Земли // Классики физической науки / Голин Г. М., Филонович С. Р.. — М.: Высшая школа, 1989. — С. 253—268. — 576 с. — ISBN 5060000583.
- Chen, Y. T. Gravitational experiments in the laboratory. — New York : Cambridge University Press, 2005. — ISBN 9780521675536.
- Shamos, Morris. Great experiments in physics : firsthand accounts from Galileo to Einstein. — New York : Dover Publications, 1987. — ISBN 9780486139623.
- Jungnickel, Christa. Cavendish. — Philadelphia, Pa : American Philosophical Society, 1996. — ISBN 0871692201.
- Poynting, John Henry. The Mean Density of the Earth. — 1894. Обзор гравитационных измерений с 1740 года.
- Chen, Y. T. Gravitational experiments in the laboratory / Y. T. Chen, Alan Cook. — New York : Cambridge University Press, 2005. — ISBN 9780521675536.
Ссылки[править | править код]
- Angel Franco Garcia. La experiencia de Cavendish (исп.) (2010). Дата обращения: 23 января 2022.
- John W. Dooley. Sideways Gravity in the Basement: Norman Scheinberg’s Cavendish Experiment (англ.) (1 июля 2005). Архивировано из оригинала 5 июля 2008 года. Самодельный эксперимент Кавендиша, показывающий расчёт результатов и необходимые меры предосторожности для устранения ошибок из-за электростатических зарядов и ветра
- Big ‘G’ (англ.). https://www.physicscentral.com/. PhysicsCentral (2000). Дата обращения: 23 января 2022. Эксперимент в университете Вашингтона для измерения «G» с использованием варианта метода Кавендиша
Гравитационная постоянная (также известная как «универсальная гравитационная постоянная», «ньютоновская константа тяготения» или «гравитационная постоянная Кавендиша»), обозначенная буквой GG или малой греческой буквой γγ, является эмпирической физической константой, участвующей в вычислении гравитационных эффектов.
В законе Ньютона она представляет собой коэффициент пропорциональности, связывающий гравитационную силу между двумя телами с результирующей их масс и обратным квадратом их расстояния:
F=γmMR2,F=gamma frac{mM}{{{R}^{2}}},
где γγ – коэффициент пропорциональности, который называют гравитационной постоянной.
В уравнениях поля Эйнштейна она количественно определяет связь между геометрией пространства-времени и тензором энергии-импульса.
Физический смысл γ
Физический смысл γγ нетрудно установить. Для этого в выражении закона притяжения положим m1=m2=1m_1 = m_2 = 1 кг, r=1r = 1 м.
Тогда F=γF = γ, то есть гравитационная постоянная численно равна силе взаимодействия двух материальных точек с массами 1 кг, находящихся на расстоянии 1 м.
Оценка величины γγ на основе предположений о средней плотности Земли показала, что гравитационное притяжение между телами обычных размеров, то есть в лабораторных условиях, очень мало.
Это свидетельствует о том, что для определения γγ нужны достаточно точные и сложные эксперименты.
Опыт Кавендиша
Впервые экспериментально доказал справедливость закона гравитационного притяжения в земных условиях, а также определил гравитационную постоянную γγ английский ученый Г. Кавендиш (1731 – 1810). Для определения были использованы крутильные весы. Основная часть весов – однородный стержень-коромысло длиной ll, подвешенный на тонкой упругой нити аа:
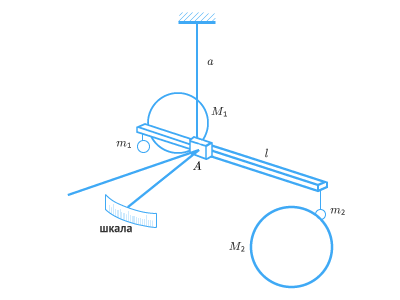
На концах стержня прикрепляли два одинаковых свинцовых шарика, массы которых m1m1 = m2m2 = 730г. С разных сторон этих шариков размещали две другие крупные свинцовые пули, массы которых M1M1 = M2M2 = 158 кг. Вследствие гравитационного взаимодействия между шарами коромысло начинает поворачиваться вокруг оси, проходящей через нить подвеса, на некоторый угол φ. Поскольку длина l стержня значительно больше расстояния между центрами масс шаров m1m1 и M1M1, m2m2 и M2M2, то гравитационным взаимодействием между шарами m1m1 и M2M2, m2m2 и M1M1 можно пренебречь.
Закручивания нити подвеса происходит до тех пор, пока момент пары сил гравитационного взаимодействий не уравновесится моментом упругой силы закручивания нити Μ = kφ.
Угол φφ определяли по отклонению отраженного луча от зеркала А. Модуль кручения kk определили в результате наблюдений за свободными колебаниями коромысла. Чтобы конвекционные потоки воздуха не влияли на результаты измерений, Г. Кавендиш разместил экспериментальную установку в закрытом ящике, который находился в закрытой комнате. Наблюдения и измерения проводились из другого помещения с помощью телескопа. Опыт Кавендиша не раз повторялся в разных вариантах.
Опыт Жолли
Точное значение γγ определено методом, который предложил немецкий физик Ф. Жолли (1809 – 1884). На одном из плеч рычажных весов подвешивали две чаши, между которыми располагали тяжелое свинцовое тело правильной геометрической формы:
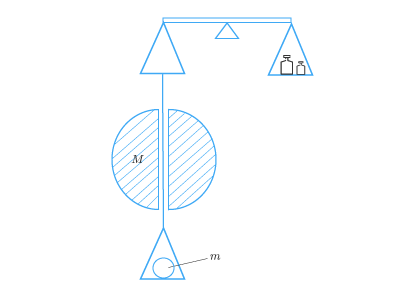
Когда на верхнюю чашу положить тело массой mm, то на него действует сила:
F1=mg+FF1 = mg + F,
где FF – сила гравитационного притяжения между телами массами mm и ММ. Если положить тело массой m в нижнюю чашку, то на него будет действовать сила F2=mg−FF2 = mg – F. Силы F1F1 и F2F2 определяют с помощью грузиков, которые нужны для уравновешивания весов. На основе этих измерений находят γγ:
γ=F1−F22Mmr2gamma =frac{{{F}_{1}}-{{F}_{2}}}{2Mm}{{r}^{2}}
где rr – расстояние между центрами масс mm и ММ.
По современным данным, гравитационная постоянная γγ = 6.67408 · 10-11 м3 кг-1 с-2
Поскольку значение гравитационной постоянной мало, то гравитационное притяжение может быть значительным для тел достаточно больших масс. В результате действия сил гравитационного притяжения осуществляется движение всех небесных тел.
Знание гравитационной постоянной дало возможность определить массу Луны, Солнца и других небесных тел.
Тест по теме «Гравитационная постоянная»
В современной формулировке закона всемирного тяготения присутствует коэффициент , называющийся гравитационной постоянной и стоящий перед формулой особняком. Интересно, что Ньютон, открывший закон притяжения, не использовал явную форму константы, численно она была определена больше века спустя со дня смерти учёного.

Содержание
- Что такое и чему равна гравитационная постоянная
- В чём измеряется гравитационная постоянная
- Как найти гравитационную постоянную – история открытия
- Работы Ньютона
- Как была экспериментально определена гравитационная постоянная – эксперимент Кавендиша
- Измерение гравитационной постоянной
- Современная история изменений гравитационной постоянной
Что такое и чему равна гравитационная постоянная
Формула закона всемирного тяготения, известная по курсу школьной механики:

G – коэффициент пропорциональности или гравитационная постоянная;
m1, m2 – массы двух тел, испытывающих взаимное притяжение;
r – расстояние между ними.
Коэффициент пропорциональности G обозначает силу, с которой притягивается пара килограммовых объектов, расположенных друг от друга на метровом расстоянии. Значение константы обычно принимается равным:

Столь маленькое число объясняет, почему несмотря на постоянное действие гравитации люди, находящиеся рядом, не чувствуют силу тяготения – она проявляется на объектах огромных масс, имеющих высокие порядки, например, массе планет, Солнца, других звёзд.

В чём измеряется гравитационная постоянная
Несмотря на то, что гравитационная постоянная численно равна силе, её единицы измерения не ньютоны. Размерность коэффициента может показаться страшной – 
, но её возникновение легко объясняется.
Согласно Международной системе единиц (системе интернациональной или СИ), сила измеряется в ньютонах, причём

то есть 1 ньютон – сила, изменяющая скорость килограммового объекта на 1 м/с за одну секунду.
После открытия закона тяготения определено: пара килограммовых тел притягивается друг к другу силой со значением, зависящим обратно пропорционально от квадрата расстояния между объектами.
То есть единица измерения гравитационной силы –

и размерность не совпадает с привычной ![]() . Требуется коэффициент, который должен уравнять единицы измерения привычной силы и силы гравитационного взаимодействия.
. Требуется коэффициент, который должен уравнять единицы измерения привычной силы и силы гравитационного взаимодействия.
Проведём математические вычисления самостоятельно.
Нужно уравнять ![]()
и  .
.
Для этого ![]() нужно разделить на 1с2 и 1кг, а также умножить на м3, получим:
нужно разделить на 1с2 и 1кг, а также умножить на м3, получим:

Получилась требуемая размерность.
Следовательно, постоянная имеет размерность ![]() .
.
Как найти гравитационную постоянную – история открытия
Коэффициент G – универсальная константа, измерение которой осуществляется экспериментальным путём. Доподлинно неизвестно, кто открыл значение гравитационной постоянной, первое употребление в «Трактате по механике» Пуассона датируется 1811 годом.
Работы Ньютона
При публикации закона тяготения в трактате Ньютона отсутствовало явное обозначение константы, характеризующее гравитацию и её действие. Коэффициент не появлялся в работах по физике вплоть до конца восемнадцатого века, его точное значение не было вычислено.

Вместо известной сегодня постоянной присутствовал гравитационный параметр:
![]()
M – масса объекта, причём, масса планеты или звезды, так как гравитационный параметр нашёл широкое распространение в астрофизике.
Сегодня для объектов Солнечной системы значение параметра рассчитано точнее, чем гравитационная постоянная G и масса по отдельности, так как она не требует серьёзных экспериментов, вычисляется на основании астрономических наблюдений.
Например:
- для Земли
 ;
; - Луны
 ;
; - Солнца
 .
.
Подробнее о использовании закона всемирного тяготения в астрономии вы можете прочитать в нашей статье.
Как была экспериментально определена гравитационная постоянная – эксперимент Кавендиша
Естествоиспытатель Джон Митчел придумал эксперимент для определения массы Земли при помощи крутильных весов, однако не реализовал его. После его смерти идея опыта и аппаратура перешли к английскому физику и химику Генри Кавендишу, который, усовершенствовав прибор, провёл ряд экспериментов и осуществил задумку своего предшественника.

Главенствующая роль в опытах отводилась установке. На метровой нити из меди подвешивалось коромысло длиной 1,8 метра, на его концах устанавливалась пара свинцовых шариков диаметром 5 сантиметров, массой 775 грамм. Чуть выше крепилась поворотная ферма, причём тщательно соблюдалось требование совпадения оси вращения фермы с медной нитью. На концах поворотной штанги находилось по одному большому свинцовому шару диаметром 20 сантиметров, массой 49,5 килограмм. Чтобы избежать влияния конвекционных воздушных потоков, вся установка накрывалась плотным деревянным кожухом. Вследствие взаимодействия лёгкие шарики притягивались к тяжёлым, закручивая нить и отклоняя коромысло. Угол отклонения фиксировался двумя телескопами, а сила упругости нити приравнивалась гравитационному взаимодействию шаров.

Величина определённой силы притяжения составляла 0,17 микроньютона. Если сравнивать это значение с весом маленького шара, то оно меньше последнего примерно в 45 миллионов раз.
В результате своего эксперимента Генри Кавендиш рассчитал среднюю плотность Земли, причём его эксперимент был точным – погрешность измеренного значения в сравнении с современным значением составляет всего 0,7%. Именно Кавендишу приписывают открытие значения гравитационной постоянной, однако он никогда не задавался подобной целью при проведении своих опытов. Очевидно, величина константы определена на основании результатов его эксперимента, но кто сделал это первым, неизвестно.

Измерение гравитационной постоянной
Значение константы, полученное по измеренной Кавендишем плотности, по разным источникам разнится. Британская энциклопедия называет число, равное ![]() , с каковым некоторые современные физики. Леон Нил Купер утверждает, что экспериментально полученное число равно
, с каковым некоторые современные физики. Леон Нил Купер утверждает, что экспериментально полученное число равно  , а Олег Павлович Спиридонов в сборнике постоянных приводит значение
, а Олег Павлович Спиридонов в сборнике постоянных приводит значение ![]() .
.
Коэффициент пропорциональности определяли после Генри Кавендиша, причём зачастую его установку модернизировали новыми материалами. Например, в 1872 году Корню и Байль для измерения гравитационной постоянной использовали платиновые маленькие шарики и стеклянные, наполненные ртутью, большие. Результаты опыта показали значение
 с относительной погрешностью 5*10-3.
с относительной погрешностью 5*10-3.
Современная история изменений гравитационной постоянной
Гравитационная постоянная – десятичная дробь, её значение постоянно уточняется, причём измерение коэффициента G происходит путём усовершенствования прибора Митчела и улучшения методов наблюдения. Например, в 2018 году учёные из России и Китая проводили опыты на установках разной конструкции. В первой группе применялся метод «time of swing» (TOS), где коэффициент пропорциональности зависит от колебательной частоты весов. Во второй – метод «angular acceleration feedback» (AAF), где угловое ускорение независимо вращающихся коромысел шаров измеряется системой управления с обратной связью, при этом нить поддерживается незакрученной.

По результатам команды первый метод продемонстрировал значение гравитационной постоянной ![]() , второй метод –
, второй метод – ![]() . Относительная погрешность составила 11,6*10-6
. Относительная погрешность составила 11,6*10-6
Комитет по данным для науки и техники (CODATA) рекомендовал на 2020 год значение коэффициента пропорциональности, равное:

Таким образом, гравитационная постоянная всё время уточняется, требуя новые, более точные способы измерения и вычисления.
Сила, которая удерживает нас на поверхности планеты – сила притяжения – не вызывает, на первый взгляд, никаких вопросов: всю свою жизнь мы живем в поле ее действия. Но что это за сила, откуда она берется, как именной действует и чем переносится – для ответов на эти вопросы стоит углубиться в тему более подробно.
Телеграмм-канал Космос нас ждет – больше космоса и красоты. Подписывайтесь!
Закон всемирного тяготения
История открытия
В поместье родителей Исаака Ньютона был прекрасный яблоневый сад. И молодой английский физик любил размышлять, гуляя по нему.
Когда в очередную такую прогулку, ученый увидел, как падает с ветки яблоко (не ему на голову), то у него возник закономерный вопрос: почему яблоко упало именно вниз? Почему не улетело прочь от Земли? Значит, на яблоко, со стороны планеты действует сила, что его притянула.
Этот эпизод произошел в 1666 году. Исааку Ньютону было 23 года.
Тогда получалось, что Луна также подвержена этой силе, ведь она не «улетает» от Земли и вращается вокруг нее. И все остальные предметы на планете тоже «держаться» только благодаря этой силе притяжения.
И только спустя 21 год после прогулки в яблоневом саду, Исаак Ньютон получил вывод формулы для силы, что удерживает Луну и планеты на орбите, а людей на Земле. Свои труды Исаак Ньютон опубликовал в «Математических началах натуральной философии» в 1687.
Запись и формулировка закона
Формулировка Ньютона дошла до наших дней и осталась в первозданном виде:
Из закона всемирного тяготения следует, что между всеми телами, обладающими массой, есть сила притяжения.
Как «представить» гравитацию?
Для наглядного представления, как же именно работает закон всемирного тяготения, представим пространство как резиновую простыню. Она легко прогибается под тяжелыми предметами, если их на нее положить.
Возьмем большой и тяжелый шар для боулинга и положим его на простыню – это наше Солнце. Вокруг него образовалась «воронка». Если теперь рядом с «Солнцем» рассыпать много маленьких шариков – они все скатятся к нему. Так притягиваются планеты к Солнцу и не улетают в свободный полет в космос. Аналогично и Луна около Земли – спутник попал в «гравитационную воронку» нашей планеты и не может из нее выбраться.
Гравитационная постоянная
В формуле закона всемирного тяготения присутствует постоянный коэффициент G – гравитационная постоянная или гравитационная константа. Это фундаментальная величина в современной классической физике, которая является неизменной. Еще она носит название — постоянная Ньютона, хотя в публикациях ученого она не фигурировала.
Чему равна гравитационная постоянная
Значение этого параметра постоянно уточняется, так как гравитационная константа представляет собой десятичную бесконечную дробь.
Современные установки и компьютеры, позволяют измерить значение очень точно. По последним измерения гравитационная постоянная численно равна
Гравитационная постоянная показывает с какой силой притягиваются два тела массой по 1 кг на расстоянии 1 метр.
Именно из-за маленького значения гравитационной постоянной, объясняется тот факт, что мы не ощущаем силу притяжения между предметами. Значение силы становится существенной только при больших массах – звезд и планет.
В чем измеряется гравитационная постоянная.
Если расписать размерность силы – ньютон в Международной системе единиц
то закон всемирного тяготения запишется следующим образом
Сокращая килограммы и выражая G, получим
Эксперимент Генри Кавендиша
Опыт Генри Кавендиша состоялся в 1798 году.
Экспериментальная установка Кавендиша состояла из двух коромысел. На одном коромысле на концах находились массивные шары, на другом маленькие. Масса шаров отличалась почти в 64 раза, размер в 4 раза. Из-за такой большой разницы масс притяжение шаров должно было быть заметно.
Малые шары были подвешены на длинной нити и по повороту коромысла от первоначального положения, можно было определить силу притяжения шаров.
Правда, опыт Кавендиша был нацелен на определение средней плотности Земли, что он и сделал с погрешностью всего лишь в 0,7%. Однако, результаты его эксперимента легли в основу вычисления гравитационной постоянной.
Гравитационный параметр
Вычисление гравитационной постоянной было затруднено, так как все вычисления основывались на движения планет, а сила тяготения, действующая на них со стороны Солнца, зависит от массы самой планеты.В работах Ньютона так же не было упоминания именно гравитационной константы, зато появился гравитационный параметр.
Даже сейчас значение гравитационной постоянной варьируется, а во времена первых открытии найти его было сложно, как и отдельно массы планет. Поэтому гравитационный параметр был более распространен и вычислен для многих планет Солнечной системы.
Ускорение свободного падения
В условиях нашей планеты, мы привыкли оперировать понятие силы тяжести – силы, что действует на объект со стороны планеты.
Сила тяжести выводится из закона всемирного притяжения путем замены величин, не зависящих от массы тела, на одну величину – ускорение свободного падения.
Таким образом, вместо использования многих значений: массы планеты, ее радиуса и гравитационной константы, можно использовать одно.
Чем отличается вес и масса
Эти два понятия перепутались в повседневной жизни и часто заменяют одно другое. Но вес и масса – это две совершенно разных величины.
Масса – это то, сколько килограммов «есть» в теле. Это его характеристика, которая зависит только от свойств самого объекта.
А вес – это сила, с которой объект давит на опору. На горизонтальных поверхностях он равен силе тяжести, на наклонных чуть меньше, но тоже зависит от силы тяжести.
Именно из-за маленькой силы притяжения, космонавты на Луне могли так высоко подпрыгивать, ведь их вес стал значительно меньше, а их масса осталась неизменной.
Открытие планет
По видимой траектории планет и их отклонений от теоретических траекторий, стало возможно расширение Солнечной системы.
Так, в 1781 году была открыта седьмая планета – Уран. Но, ее предсказанный путь вокруг Солнца не совпадал с наблюдаемым. И был сделан вывод, что на Уран гравитацией действует еще один объект за пределами его орбиты. И в 1846 был обнаружен Нептун.
Но и восьмая планета двигалась не в соответствии с теоретическими выводами. Спустя 100 лет, в 1930 году был открыт Плутон, получивший гордое название Девятой планеты, но лишившийся его из-за небольшой массы.
Гравитон — мифическая частица
Гравитация является одним из фундаментальных взаимодействий в современной физике. Вместе с электромагнитным взаимодействием, гравитация описывает весь наш видимый мир. Но в отличие от электромагнитного (его переносчиком является фотон), гравитация не имеет частицы, которая бы являлась переносчиком этого взаимодействия.
Пытаясь «уравнять» эти взаимодействия, ученые предположили, что частица, которая переносит гравитацию может существовать и назвали ее «гравитон».
Однако, экспериментального доказательства ее существования нет.
Предположительно, гравитон не должен обладать массой, электрическим и другими зарядами. Но для того, чтобы выполнять роль переносчика гравитации должен обладать энергией и двигаться со скоростью света.
Таким образом, гравитация, которая формирует галактики и звездные системы таит в себе еще много загадок. Сформулированный в 1687 году закон Ньютона прекрасно описывает движение планет и взаимодействие между телами, но не дает объяснения, так что же такое гравитация и как она «работает».
Сравнительная таблица планет Солнечной системы
«Коэффициент в сравнении с Земным g» показывает, во сколько раз будет отличатся вес на каждой планете. Например, на Марсе наш вес будет составлять только 38% от Земного, а на Юпитере в 2,54 раза больше.
Если Вам понравилось статья:














