Как найти гравитационный радиус черной дыры

Гравитацио́нный ра́диус (или ра́диус Шва́рцшильда) представляет собой характерный радиус, определённый для любого физического тела, обладающего массой: это радиус сферы, на которой находился бы горизонт событий, создаваемый этой массой (с точки зрения ОТО), если бы она была распределена сферически симметрично, была бы неподвижной (в частности, не вращалась, но радиальные движения допустимы) и целиком лежала бы внутри этой сферы. Введён в научный обиход немецким учёным Карлом Шварцшильдом в 1916 году.

Величина[править | править код]

Гравитационный радиус пропорционален массе тела M и равен ${displaystyle r_{g}=2GM/c^{2},}$ где G — гравитационная постоянная, с — скорость света в вакууме. Это выражение можно переписать как r_g ≈ 1,48·10⁻²⁷ · (M / 1 кг) м. Для астрофизиков удобной является запись r_g ≈ 2,95 · (M / M_⊙) км, где M_⊙ — масса Солнца.

При переходе к планковскому масштабу $ell _{P}={sqrt {(G/c^{3}),hbar }}$ ≈ 10⁻³⁵ м, удобной является запись в форме ${displaystyle r_{g}=2,(G/c^{3}),M,c,}$ .

Свойства[править | править код]

По величине гравитационный радиус совпадает с радиусом сферически-симметричного тела, для которого в классической механике вторая космическая скорость на поверхности была бы равна скорости света. Данный факт не случаен, он является следствием того, что классическая механика и ньютоновская теория тяготения содержатся в общей теории относительности как её предельный случай^[1]. На важность этой величины впервые обратил внимание Джон Мичелл в своём письме к Генри Кавендишу, опубликованном в 1784 году. В рамках общей теории относительности гравитационный радиус (в других координатах) впервые вычислил в 1916 году Карл Шварцшильд (см. метрика Шварцшильда)^[2].

Гравитационный радиус обычных астрофизических объектов ничтожно мал по сравнению с их действительным размером: так, для Земли r_g ≈ 0,887 см, для Солнца r_g ≈ 2,95 км. Исключение составляют нейтронные звёзды и гипотетические бозонные и кварковые звёзды. Например, для типичной нейтронной звезды радиус Шварцшильда составляет около 1/3 от её собственного радиуса. Это обусловливает важность эффектов общей теории относительности при изучении таких объектов. Гравитационный радиус объекта с массой наблюдаемой вселенной был бы равен примерно 10 миллиардам световых лет^[3].

С достаточно массивными звёздами (как показывает расчёт, с массой больше двух-трёх солнечных масс) в конце их эволюции может происходить процесс, называемый релятивистским гравитационным коллапсом: если, исчерпав ядерное «горючее», звезда не взрывается и не теряет массу, то, испытывая релятивистский гравитационный коллапс, она может сжаться до размеров гравитационного радиуса. При гравитационном коллапсе звезды до сферы $r_{g}$ наружу не может выходить никакое излучение, никакие частицы. С точки зрения внешнего наблюдателя, находящегося далеко от звезды, с приближением размеров звезды к $r_{g}$ собственное время частиц звезды неограниченно замедляет темп своего течения. Поэтому для такого наблюдателя радиус коллапсирующей звезды приближается к гравитационному радиусу асимптотически, никогда не становясь равным ему. Но можно, однако, указать момент, начиная с которого внешний наблюдатель уже не будет видеть звезду и не сможет узнать какую-либо информацию относительно неё. Так что с этого момента вся информация, содержащаяся в звезде, фактически будет потеряна для внешнего наблюдателя^[4].

Физическое тело, испытавшее гравитационный коллапс и достигшее гравитационного радиуса, называется чёрной дырой. Сфера радиуса r_g совпадает с горизонтом событий невращающейся чёрной дыры. Для вращающейся чёрной дыры горизонт событий имеет форму эллипсоида, и гравитационный радиус даёт оценку его размеров. Радиус Шварцшильда для сверхмассивной чёрной дыры в центре нашей Галактики равен примерно 16 миллионам километров^[5].

Шварцшильдовский радиус объекта, имеющего спутники, во многих случаях может быть измерен с гораздо более высокой точностью, чем масса этого объекта. Этот несколько парадоксальный факт связан с тем, что при переходе от измеренных периода обращения спутника T и большой полуоси его орбиты a (эти величины можно измерить с очень высокой точностью) к массе центрального тела M необходимо разделить гравитационный параметр объекта μ = GM = 4π²a³/T² на гравитационную постоянную G, которая известна с гораздо худшей точностью (примерно 1 к 7000 на 2018 год), чем точность большинства других фундаментальных констант. В то же время шварцшильдовский радиус равен, с точностью до коэффициента 2/с², гравитационному параметру объекта:

${displaystyle r_{g}={frac {2GM}{c^{2}}}={frac {2mu }{c^{2}}} ,}$

причём скорость света c в настоящее время является по определению абсолютно точным переходным коэффициентом, поэтому относительные погрешности измерения гравитационного параметра и гравитационного радиуса равны друг другу.

Примеры[править | править код]

Так, например, упомянутый выше шварцшильдовский радиус Солнца равен:^[6]

${displaystyle r_{godot }={frac {2GM_{odot }}{c^{2}}}={frac {2mu _{odot }}{c^{2}}}=2{,}953,250,077(2) {text{км}}}$

с относительной погрешностью 8·10⁻¹¹, тогда как масса Солнца 1,988 744(93)·10³⁰ кг известна лишь с относительной погрешностью 4,7·10⁻⁵.

Аналогично, шварцшильдовский радиус Земли равен:^[6]

${displaystyle r_{goplus }={frac {2GM_{oplus }}{c^{2}}}={frac {2mu _{oplus }}{c^{2}}}=8{,}870,056,078(18) {text{мм}}}$

с относительной погрешностью 2·10⁻⁹, тогда как масса Земли 5,973 236(28)·10²⁴ кг известна лишь с относительной погрешностью 4,7·10⁻⁵.

Примечания[править | править код]

↑ Гинзбург В. Л. О физике и астрофизике. — М.: Наука, 1980. — С. 112.
↑ Стюарт, 2018, с. 358.
↑ Michel Marie Deza, Elena Deza. Encyclopedia of Distances. — Springer Science & Business Media, 2012. — 644 с. — ISBN 9783642309588. Архивная копия от 24 декабря 2016 на Wayback Machine
↑

В течение коллапса объект испустил бы только ограниченное число фотонов прежде, чем пересечь горизонт событий. Этих фотонов было бы совершенно недостаточно, чтобы передать нам всю информацию относительно коллапсирующего объекта. Это означает, что в квантовой теории не существует никакого способа, которым внешний наблюдатель мог бы определить состояние такого объекта.
↑ Открыт объект у горизонта событий чёрной дыры Млечного Пути. «Мембрана (портал)» (4 сентября 2008). Дата обращения: 12 декабря 2008. Архивировано 17 февраля 2012 года.
↑ ¹ ² Каршенбойм С. Г. Уточнение значений фундаментальных физических констант: основа новых «квантовых» единиц СИ // Физика элементарных частиц и атомного ядра. — 2018. — Т. 49, вып. 2. — С. 409—475. Архивировано 30 мая 2018 года.

Литература[править | править код]

Мизнер Ч., Торн К., Уилер Дж. Гравитация. — М.: Мир, 1977. — Т. 1—3.
Шапиро С. Л., Тьюколски С. А. Чёрные дыры, белые карлики и нейтронные звезды / Пер. с англ. под ред. Я. А. Смородинского. — М.: Мир, 1985. — Т. 1—2. — 656 с.
Иэн Стюарт. Математика космоса. Как современная наука расшифровывает Вселенную = Stewart Ian. Calculating the Cosmos: How Mathematics Unveils the Universe. — Альпина Паблишер, 2018. — 542 p. — ISBN 978-5-91671-814-0.

Ссылки[править | править код]

Schaffer, Simon. John Mitchell and Black Holes (англ.) // Journal for the History of Astronomy. — 1979. — Vol. 10. — P. 42—43. — doi:10.1177/002182867901000104. — Bibcode: 1979JHA….10…42S.

Источник

From Wikipedia, the free encyclopedia

The Schwarzschild radius or the gravitational radius is a physical parameter in the Schwarzschild solution to Einstein’s field equations that corresponds to the radius defining the event horizon of a Schwarzschild black hole. It is a characteristic radius associated with any quantity of mass. The Schwarzschild radius was named after the German astronomer Karl Schwarzschild, who calculated this exact solution for the theory of general relativity in 1916.

The Schwarzschild radius is given as

${displaystyle r_{text{s}}={frac {2GM}{c^{2}}},}$

where G is the gravitational constant, M is the object mass, and c is the speed of light.^{[note 1]}^[1]^[2]

History[edit]

In 1916, Karl Schwarzschild obtained the exact solution^[3]^[4] to Einstein’s field equations for the gravitational field outside a non-rotating, spherically symmetric body with mass (see Schwarzschild metric). The solution contained terms of the form ${displaystyle 1-{r_{text{s}}}/r}$ and ${displaystyle {frac {1}{1-{r_{text{s}}}/r}}}$ , which becomes singular at and ${displaystyle r=r_{text{s}}}$ respectively. The ${displaystyle r_{text{s}}}$ has come to be known as the Schwarzschild radius. The physical significance of these singularities was debated for decades. It was found that the one at ${displaystyle r=r_{text{s}}}$ is a coordinate singularity, meaning that it is an artifact of the particular system of coordinates that was used; while the one at is a spacetime singularity and cannot be removed.^[5] The Schwarzschild radius is nonetheless a physically relevant quantity, as noted above and below.

This expression had previously been calculated, using Newtonian mechanics, as the radius of a spherically symmetric body at which the escape velocity was equal to the speed of light. It had been identified in the 18th century by John Michell^[6] and Pierre-Simon Laplace.^[7]

Parameters[edit]

The Schwarzschild radius of an object is proportional to its mass. Accordingly, the Sun has a Schwarzschild radius of approximately 3.0 km (1.9 mi), whereas Earth’s is only about 9 mm (0.35 in) and the Moon’s is about 0.1 mm (0.0039 in).^[8]^{[disputed – discuss]}

Object’s Schwarzschild radius

Object	Mass	Schwarzschild radius ${textstyle {frac {2GM}{c^{2}}}}$	Actual radius	Schwarzschild density ${textstyle {frac {3c^{6}}{32pi G^{3}M^{2}}}}$ or ${textstyle {frac {3c^{2}}{8pi Gr^{2}}}}$
Milky Way	1.6×10⁴² kg	2.4×10¹⁵ m (0.25 ly)	5×10²⁰ m (52900 ly)	0.000029 kg/m³
Phoenix A (largest known black hole)	1.99×10⁴¹ kg	2.95×10¹⁴ m (~1975 AU)		0.0018 kg/m³
Ton 618	1.3×10⁴¹ kg	1.9×10¹⁴ m (~1300 AU)		0.0045 kg/m³
SMBH in NGC 4889	4.2×10⁴⁰ kg	6.2×10¹³ m (~410 AU)		0.042 kg/m³
SMBH in Messier 87^[9]	1.3×10⁴⁰ kg	1.9×10¹³ m (~130 AU)		0.44 kg/m³
SMBH in Andromeda Galaxy^[10]	3.4×10³⁸ kg	5.0×10¹¹ m (3.3 AU)		640 kg/m³
Sagittarius A* (SMBH in Milky Way)^[11]	8.262×10³⁶ kg	1.227×10¹⁰ m (0.08 AU)		1.0678×10⁶ kg/m³
SMBH in NGC 4395^[12]	7.1568×10³⁵ kg	1.062×10⁹ m (1.53 R_⊙)		1.4230×10⁸ kg/m³
Potential intermediate black hole in HCN-0.009-0.044^[13]	6.3616×10³⁴ kg	9.44×10⁸ m (14.8 R_🜨)		1.8011×10¹⁰ kg/m³
Resulting intermediate black hole from GW190521 merger^[14]	2.823×10³² kg	4.189×10⁵ m (0.066 R_🜨)		9.125×10¹⁴ kg/m³
Sun	1.99×10³⁰ kg	2.95×10³ m	7.0×10⁸ m	1.84×10¹⁹ kg/m³
Jupiter	1.90×10²⁷ kg	2.82 m	7.0×10⁷ m	2.02×10²⁵ kg/m³
Saturn	5.683×10²⁶ kg	8.42×10⁻¹ m	6.03×10⁷ m	2.27×10²⁶ kg/m³
Neptune	1.024×10²⁶ kg	1.52×10⁻¹ m	2.47×10⁷ m	6.97×10²⁷ kg/m³
Uranus	8.681×10²⁵ kg	1.29×10⁻¹ m	2.56×10⁷ m	9.68×10²⁷ kg/m³
Earth	5.97×10²⁴ kg	8.87×10⁻³ m	6.37×10⁶ m	2.04×10³⁰ kg/m³
Venus	4.867×10²⁴ kg	7.21×10⁻³ m	6.05×10⁶ m	3.10×10³⁰ kg/m³
Mars	6.39×10²³ kg	9.47×10⁻⁴ m	3.39×10⁶ m	1.80×10³² kg/m³
Mercury	3.285×10²³ kg	4.87×10⁻⁴ m	2.44×10⁶ m	6.79×10³² kg/m³
Moon	7.35×10²² kg	1.09×10⁻⁴ m	1.74×10⁶ m	1.35×10³⁴ kg/m³
Human	70 kg	1.04×10⁻²⁵ m	~5×10⁻¹ m	1.49×10⁷⁶ kg/m³
Planck mass	2.18×10⁻⁸ kg	3.23×10⁻³⁵ m (2 l_P)		1.54×10⁹⁵ kg/m³

Derivation[edit]

Black hole classification by Schwarzschild radius[edit]

Black hole classifications

Class	Approx. mass	Approx. radius
Supermassive black hole	10⁵–10¹⁰ M_Sun	0.001–400 AU
Intermediate-mass black hole	10³ M_Sun	10³ km ≈ R_Earth
Stellar black hole	10 M_Sun	30 km
Micro black hole	up to M_Moon	up to 0.1 mm

Any object whose radius is smaller than its Schwarzschild radius is called a black hole. The surface at the Schwarzschild radius acts as an event horizon in a non-rotating body (a rotating black hole operates slightly differently). Neither light nor particles can escape through this surface from the region inside, hence the name “black hole”.

Black holes can be classified based on their Schwarzschild radius, or equivalently, by their density, where density is defined as mass of a black hole divided by the volume of its Schwarzschild sphere. As the Schwarzschild radius is linearly related to mass, while the enclosed volume corresponds to the third power of the radius, small black holes are therefore much more dense than large ones. The volume enclosed in the event horizon of the most massive black holes has an average density lower than main sequence stars.

Supermassive black hole[edit]

A supermassive black hole (SMBH) is the largest type of black hole, though there are few official criteria on how such an object is considered so, on the order of hundreds of thousands to billions of solar masses. (Supermassive black holes up to 21 billion (2.1 × 10¹⁰) M_☉ have been detected, such as NGC 4889.)^[15] Unlike stellar mass black holes, supermassive black holes have comparatively low average densities. (Note that a (non-rotating) black hole is a spherical region in space that surrounds the singularity at its center; it is not the singularity itself.) With that in mind, the average density of a supermassive black hole can be less than the density of water.

The Schwarzschild radius of a body is proportional to its mass and therefore to its volume, assuming that the body has a constant mass-density.^[16] In contrast, the physical radius of the body is proportional to the cube root of its volume. Therefore, as the body accumulates matter at a given fixed density (in this example, 997 kg/m³, the density of water), its Schwarzschild radius will increase more quickly than its physical radius. When a body of this density has grown to around 136 million solar masses (1.36 × 10⁸ M_☉), its physical radius would be overtaken by its Schwarzschild radius, and thus it would form a supermassive black hole.

It is thought that supermassive black holes like these do not form immediately from the singular collapse of a cluster of stars. Instead they may begin life as smaller, stellar-sized black holes and grow larger by the accretion of matter, or even of other black holes.^{[citation needed]}

The Schwarzschild radius of the supermassive black hole at the Galactic Center of the Milky Way is approximately 12 million kilometres.^[11] Its mass is about 4.1 million M_☉.

Stellar black hole[edit]

Stellar black holes have much greater average densities than supermassive black holes. If one accumulates matter at nuclear density (the density of the nucleus of an atom, about 10¹⁸ kg/m³; neutron stars also reach this density), such an accumulation would fall within its own Schwarzschild radius at about 3 M_☉ and thus would be a stellar black hole.

Micro black hole[edit]

A small mass has an extremely small Schwarzschild radius. A mass similar to Mount Everest^[17]^{[note 2]} has a Schwarzschild radius much smaller than a nanometre.^{[note 3]} Its average density at that size would be so high that no known mechanism could form such extremely compact objects. Such black holes might possibly be formed in an early stage of the evolution of the universe, just after the Big Bang, when densities were extremely high. Therefore, these hypothetical miniature black holes are called primordial black holes.

Other uses[edit]

In gravitational time dilation[edit]

Gravitational time dilation near a large, slowly rotating, nearly spherical body, such as the Earth or Sun can be reasonably approximated as follows:^[18]

${displaystyle {frac {t_{r}}{t}}={sqrt {1-{frac {r_{mathrm {s} }}{r}}}}}$

where:

t_r is the elapsed time for an observer at radial coordinate r within the gravitational field;
t is the elapsed time for an observer distant from the massive object (and therefore outside of the gravitational field);
r is the radial coordinate of the observer (which is analogous to the classical distance from the center of the object);
r_s is the Schwarzschild radius.

Compton wavelength intersection[edit]

The Schwarzschild radius ( ${displaystyle 2GM/c^{2}}$ ) and the Compton wavelength () corresponding to a given mass are similar when the mass is around one Planck mass (), when both are of the same order as the Planck length ( ${textstyle {sqrt {hbar G/c^{3}}}}$ ).

Calculating the maximum volume and radius possible given a density before a black hole forms[edit]

The Schwarzschild radius equation can be manipulated to yield an expression that gives the largest possible radius from an input density that doesn’t form a black hole. Taking the input density as ρ,

${displaystyle r_{text{s}}={sqrt {frac {3c^{2}}{8pi Grho }}}.}$

For example, the density of water is 1000 kg/m³. This means the largest amount of water you can have without forming a black hole would have a radius of 400 920 754 km (about 2.67 AU).

Notes[edit]

^ In geometrized unit systems, G and c are both taken to be unity, which reduces this equation to ${displaystyle r_{text{s}}=2M}$ .
^ Using these values,^[17] one can calculate a mass estimate of 6.3715×10¹⁴ kg.
^ One can calculate the Schwarzschild radius: 2 × 6.6738×10⁻¹¹ m³⋅kg⁻¹⋅s⁻² × 6.3715×10¹⁴ kg / (299792458 m⋅s⁻¹)² = 9.46×10⁻¹³ m = 9.46×10⁻⁴ nm.

References[edit]

^ Kutner, Marc (2003). Astronomy: A Physical Perspective. Cambridge University Press. p. 148. ISBN 9780521529273.
^ Guidry, Mike (2019-01-03). Modern General Relativity: Black Holes, Gravitational Waves, and Cosmology. Cambridge University Press. p. 92. ISBN 978-1-107-19789-3.
^ K. Schwarzschild, “Über das Gravitationsfeld eines Massenpunktes nach der Einsteinschen Theorie”, Sitzungsberichte der Deutschen Akademie der Wissenschaften zu Berlin, Klasse fur Mathematik, Physik, und Technik (1916) pp 189.
^ K. Schwarzschild, “Über das Gravitationsfeld einer Kugel aus inkompressibler Flussigkeit nach der Einsteinschen Theorie”, Sitzungsberichte der Deutschen Akademie der Wissenschaften zu Berlin, Klasse fur Mathematik, Physik, und Technik (1916) pp 424.
^ Wald, Robert (1984). General Relativity. The University of Chicago Press. pp. 152–153. ISBN 978-0-226-87033-5.
^ Schaffer, Simon (1979). “John Michell and Black Holes”. Journal for the History of Astronomy. 10: 42–43. Bibcode:1979JHA….10…42S. doi:10.1177/002182867901000104. S2CID 123958527. Retrieved 4 June 2018.
^ Colin Montgomery, Wayne Orchiston and Ian Whittingham, “Michell, Laplace and the origin of the Black Hole Concept” Archived 2014-05-02 at the Wayback Machine, Journal of Astronomical History and Heritage, 12(2), 90–96 (2009).
^ Deza, Michel Marie; Deza, Elena (Oct 28, 2012). Encyclopedia of Distances (2nd ed.). Heidelberg: Springer Science & Business Media. p. 452. doi:10.1007/978-3-642-30958-8. ISBN 978-3-642-30958-8. Retrieved 8 December 2014.
^ Event Horizon Telescope Collaboration (2019). “First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole”. Astrophysical Journal Letters. 875 (1): L1. arXiv:1906.11238. Bibcode:2019ApJ…875L…1E. doi:10.3847/2041-8213/AB0EC7.
6.5(7)×10⁹ M_☉ = 1.29(14)×10⁴⁰ kg.
^ Bender, Ralf; Kormendy, John; Bower, Gary; et al. (2005). “HST STIS Spectroscopy of the Triple Nucleus of M31: Two Nested Disks in Keplerian Rotation around a Supermassive Black Hole”. Astrophysical Journal. 631 (1): 280–300. arXiv:astro-ph/0509839. Bibcode:2005ApJ…631..280B. doi:10.1086/432434. S2CID 53415285.
1.7(6)×10⁸ M_☉ = 0.34(12)×10³⁹ kg.
^ ^a ^b Ghez, A. M.; et al. (December 2008). “Measuring Distance and Properties of the Milky Way’s Central Supermassive Black Hole with Stellar Orbits”. Astrophysical Journal. 689 (2): 1044–1062. arXiv:0808.2870. Bibcode:2008ApJ…689.1044G. doi:10.1086/592738. S2CID 18335611.
^ Peterson, Bradley M.; Bentz, Misty C.; Desroches, Louis-Benoit; Filippenko, Alexei V.; Ho, Luis C.; Kaspi, Shai; Laor, Ari; Maoz, Dan; Moran, Edward C.; Pogge, Richard W.; Quillen, Alice C. (2005-10-20). “Multiwavelength Monitoring of the Dwarf Seyfert 1 Galaxy NGC 4395. I. A Reverberation-Based Measurement of the Black Hole Mass”. The Astrophysical Journal. 632 (2): 799–808. arXiv:astro-ph/0506665. Bibcode:2005ApJ…632..799P. doi:10.1086/444494. hdl:1811/48314. ISSN 0004-637X. S2CID 13886279.
^ Sciences, National Institutes of Natural. “Hiding black hole found”. phys.org. Retrieved 2022-06-15.
^ Abbott, R.; Abbott, T. D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R. X.; Adya, V. B.; Affeldt, C.; Agathos, M.; Agatsuma, K. (2020-09-02). “Properties and Astrophysical Implications of the 150 M_⊙ Binary Black Hole Merger GW190521″. The Astrophysical Journal. 900 (1): L13. arXiv:2009.01190. Bibcode:2020ApJ…900L..13A. doi:10.3847/2041-8213/aba493. ISSN 2041-8213. S2CID 221447444.
^ McConnell, Nicholas J. (2011-12-08). “Two ten-billion-solar-mass black holes at the centres of giant elliptical galaxies”. Nature. 480 (7376): 215–218. arXiv:1112.1078. Bibcode:2011Natur.480..215M. doi:10.1038/nature10636. PMID 22158244. S2CID 4408896.
^ Robert H. Sanders (2013). Revealing the Heart of the Galaxy: The Milky Way and its Black Hole. Cambridge University Press. p. 36. ISBN 978-1-107-51274-0.
^ ^a ^b “How does the mass of one mole of M&M’s compare to the mass of Mount Everest?” (PDF). School of Science and Technology, Singapore. March 2003. Archived from the original (PDF) on 10 December 2014. Retrieved 8 December 2014. If Mount Everest is assumed* to be a cone of height 8850 m and radius 5000 m, then its volume can be calculated using the following equation:
volume = πr²h/3 […] Mount Everest is composed of granite, which has a density of 2750 kg⋅m⁻³.
^ Keeton, Keeton (2014). Principles of Astrophysics: Using Gravity and Stellar Physics to Explore the Cosmos (illustrated ed.). Springer. p. 208. ISBN 978-1-4614-9236-8. Extract of page 208

Источник

Сегодня о черных дырах слышали практически все. О них пишут фантастические произведения, снимают художественные и научно-популярные фильмы и даже используют это выражение в переносном смысле, как символ места, где что-нибудь безвозвратно исчезает. И это, в общем, верно.

Но почему исчезает и почему безвозвратно? Для ответа на вопрос нам понадобится одно из ключевых понятий теории черных дыр – понятие радиуса Шварцшильда. Это- критический размер для любого объекта, обладающего массой, нужно только втиснуть данную массу в этот размер, и она окажется наглухо отделена от внешнего мира горизонтом событий.

Как сделать черную дыру

Получить простейшую черную дыру нетрудно – мысленно, конечно. Нужно взять звезду (или любое другое тело – например, планету или булыжник) и сжимать, уменьшая ее радиус при сохранении массы. Представим себя на такой звезде или планете: при сжатии она уплотняется, расстояние между всеми частицами ее вещества сокращается, следовательно, возрастает сила притяжения между ними – в полном соответствии с законом всемирного тяготения. Нас тоже станет прижимать к поверхности – ведь все частицы звезды приближаются и к нам.

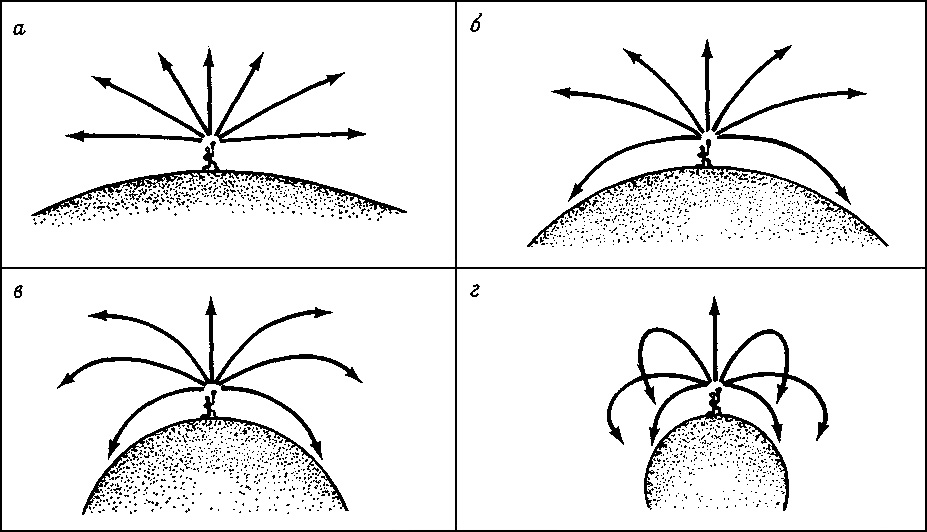
Покинуть злосчастное небесное тело будет все труднее, а через некоторое время мы не сможем не только улететь с него, но и послать сигнал SOS – если дождемся момента, когда вторая космическая скорость (скорость убегания) на поверхности не достигнет скорости света. Произойдет это при достижении звездой некоторого критического размера.

Немного вычислений

Расчет радиуса Шварцшильда (гравитационного радиуса) для любого тела очень прост. Нужно взять формулу для расчета второй космической скорости v₂ =√(2GM/r)_, где v₂ – скорость убегания, M – масса, r – радиус, G – гравитационная постоянная, коэффициент пропорциональности, установленный экспериментальным путем. Значение его постоянно уточняется; сейчас оно принято равным 6,67408 × 10^-11 м³ кг^-1 с^-2.

Пусть v=c. Производим необходимую замену в уравнении и получаем: r_g=2GM/c², где r_g – гравитационный радиус.

В правой части уравнения имеем две константы – гравитационную постоянную и скорость света. Так что радиус Шварцшильда – это величина, зависящая только от массы тела и прямо пропорциональная ей.

Произведя несложные вычисления, легко узнать, чему равен радиус Шварцшильда, например, для Земли: 8,86 мм. Втисните массу планеты в шарик диаметром чуть более полутора сантиметров – и вы получите черную дыру. Для Юпитера гравитационный радиус составит 2,82 м, для Солнца – 2,95 км. Играть можно с чем угодно, единственное ограничение на условия нахождения радиуса Шварцшильда – это минимальная возможная масса черной дыры 2,176 × 10^-8 кг (планковская масса).

Черные дыры обязаны быть

Идея о том, что должны существовать объекты с таким соотношением массы и радиуса, что даже свет не может вырваться из этой гравитационной «ловушки», довольно стара. Восходит она к концу XVIII века, к работам Дж. Митчелла и П. Лапласа и ныне представляет интерес, скорее, для истории науки. А современное понимание сущности черных дыр берет начало в 1916 году, когда немецкий физик и астроном Карл Шварцшильд впервые применил общую теорию относительности для решения астрофизической задачи.

Требовалось описать гравитационное поле одиночного сферического невращающегося тела в вакууме. Решением задачи стала так называемая метрика Шварцшильда, в которой присутствует уже знакомый нам параметр, равный 2GM/c²– гравитационный радиус (ученый обозначил его как r_S).

Вблизи опасной черты

Расчеты Шварцшильда показывают, что, если размеры объекта много больше этой критической для массы M величины, то структура пространства-времени не слишком искажается его гравитацией: собственно, в этом случае можно пользоваться ньютоновским описанием тяготения и пренебречь поправками ОТО. Последние становятся существенны при r → r_S. Например, замедление времени и связанный с ним эффект гравитационного красного смещения. Тяготение искривляет пространство-время таким образом, что для удаленного наблюдателя время вблизи гравитирующего тела замедляется, в связи с чем уменьшается частота электромагнитных колебаний. Наблюдая сжимающуюся звезду, мы зафиксируем ее быстрое «покраснение» (вклад в данный эффект вносит еще и доплеровский сдвиг, поскольку поверхность звезды от нас будет удаляться).

Что такое радиус Шварцшильда и горизонт событий

Как только радиус звезды достигнет значения r_S, время на ее поверхности замрет, и частота излучения будет равна нулю. Никакой сигнал не выходит из-под поверхности шварцшильдовского радиуса – горизонта событий, – будучи заморожен гравитацией. Иными словами, события (точки пространства-времени в понимании ОТО) по разные стороны сферы Шварцшильда никаким образом не могут быть соединены, и внешний наблюдатель лишен возможности узнать что-либо о событиях внутри.

Итак, радиус Шварцшильда – это параметр поверхности, на которой располагался бы горизонт событий, создаваемый массой сферически-симметричного невращающегося тела, если бы эта масса целиком была заключена внутри данной сферы.

Проскочив горизонт событий, сжимающееся тело не остановится – коллапс после этого рубежа станет необратимым, и оно рухнет в гравитационную “могилу” сингулярности. Мы действительно получили черную дыру.

Интересно ведет себя свет вблизи горизонта событий: в сильно искривленном пространстве лучи его оказываются пойманы на круговые орбиты. Совокупность таких неустойчивых хаотических орбит образует фотонную сферу.

Все сложнее

Шварцшильдовская черная дыра – это простейший случай, вряд ли реализуемый во Вселенной, поскольку трудно найти невращающееся космическое тело, и при образовании реальных черных дыр угловой момент должен сохраняться. Вращающаяся черная дыра может постепенно терять энергию, приближаясь к шварцшильдовскому состоянию. Скорость вращения ее будет стремиться к нулю, но не достигнет его.

Расчеты радиуса черной дыры Шварцшильда сделаны в рамках ОТО и являются классическими. Однако, мы не будем касаться эффектов, налагаемых на современные модели черных дыр квантовой механикой, так как одно перечисление их увело бы нас далеко от темы.

Сделаем только одно замечание: классическая теория утверждает, что прямое наблюдение горизонта событий невозможно. Впрочем, в истории науки часто считавшееся невозможным успешно осуществлялось, и в этом смысле теоретические исследования квантовомеханических явлений в черных дырах наверняка принесут еще много неожиданного и интересного. В рамках же классики физика черных дыр – это пример прекрасно разработанной, красивой теории, а основой ее исторически является работа Шварцшильда.

Источник

Гравитационным радиусом обладает любое тело — от Земли до массивной черной дыры

Гравитационный радиус (иначе радиус Шварцшильда) – характеристика любого массивного физического тела. Если представить тело в форме симметричного не вращающегося сверхплотного шара, то гравитационный радиус описывает вокруг него сферу, на которой располагался бы горизонт событий. Гравитационный радиус определяет поле, которое было названо полем Шварцшильда, в честь немецкого астронома, первым нашедшего решения уравнений Эйнштейна для данного случая.

Отличие теории тяготения Ньютона от ОТО

Общая теория относительности, описанная Альбертом Эйнштейном, несколько иначе рассчитывает тяготение массивных объектов. Таким образом, если измерить данную характеристику, находясь на поверхности Земли (предполагая ее симметричность и отсутствие вращения), то согласно ОТО, сила тяготения будет несколько больше, нежели с точки зрения Ньютоновской теории. За данным различием скрывается математический аппарат упомянутых теорий, однако в масштабах Земли это различие в измерении пренебрежительно мало.

Материалы по теме

Представим, что планета постепенно начала сжиматься. В таком случае при сжатии в два раза, сила тяготения Ньютона возрастет в четыре раза. Сила тяготения, описываемая ОТО – несколько быстрее. В результате, сила тяготения возрастает до бесконечности. Правда, в теории Ньютона для этого планету придется сжать практически в точку, в то время как в ОТО радиус такого тела будет значительно больше. Этот радиус и называется гравитационным.

Если продолжить сжимать тело и далее, то его радиус будет меньше, чем его гравитационный радиус. Подобную ситуацию можно пронаблюдать на примере черной дыры, гравитационный радиус которой создает горизонт событий, в то время как, предположительно, само тело черной дыры значительно меньше.

Следствия решения Шварцшильда

Из всего написанного выше следует, что гравитационный радиус создает горизонт событий, где сила тяготения стремится к бесконечности, – это некоторая граница массивного тела, перейдя которую, свет и любая материя не способны уже вновь выбраться «наружу».

Пространство-время, искаженное Землей

Радиус Шварцшильда не только предполагает наличие горизонта событий, но также и изменение самого пространства-времени. Как мы уже упоминали ранее, около горизонта событий сила тяготения значительно возрастает, что согласно теории Эйнштейна, искривляет пространство-время.

Солнце, радиусом 700 тысяч километров имеет гравитационный радиус всего 2,95 километра, а Земля с радиусом 6400 км — всего 0,884 см. Таким образом, благодаря силам гравитации, на поверхности Земли время течет медленней, например, чем на GPS спутнике, с разницей в 38 микросекунд в день.

Очевидно, что радиус Шварцшильда не используется для прикладных физических вычислений, а актуален лишь в области астрофизики и космологии. Его эффекты учитывают при изучении природы таких тел как нейтронные звезды, так как их гравитационный радиус составляет около трети от физического, черных дыр или коллапсирующих звезд.

Источник

Всем известно, что черная дыра – это нечто экстремальное и непостижимое. Некоторые даже читали Стивена Хокинга и знают, что на подлете к ней время останавливается, пространство растягивается в бесконечность, гравитация разрывает материю в клочья, и вообще, на горизонте событий перестает работать даже общая теория относительности. Очень немногие даже дочитали том “Теория поля” Ландау-Лившица до конца. Но и они не могут ответить на, казалось бы, простой вопрос: “Что же происходит в ближайшей окрестности черной дыры?”.

Но давайте попробуем смоделировать подлет к черной дыре с непривычной точки зрения современных представлений в предположении: условия на подлете к горизонту черной дыры близки к классическим. Ниже будет показано, что такое возможно при определенных параметрах черной дыры.

Упрямым ортодоксам далее можно не читать, а сразу оставлять уничижительные комментарии.

Для начала оценим, чему равно ускорение свободного падения на черную дыру у самого ее горизонта?

Поскольку я исхожу из предположения, что на горизонте черной дыры условия близки к классическим, то считаю возможным пользоваться классической небесной механикой для оценки физических процессов. Конечно, классический подход будет не точным, но для оценки порядка величин вполне сгодится.

Итак, что мы знаем о черной дыре? То, что ее радиус, радиус Шварцшильда (или “горизонт событий”) имеет величину порядка

где G – гравитационная постоянная, M – масса черной дыры, c – скорость света.

Известно также, что фотон, оказавшийся на таком расстоянии от центра черной дыры и летящий по касательной к горизонту событий, будет двигаться по круговой орбите. А значит будет испытывать центростремительное ускорение порядка

где c – скорость света, G – гравитационная постоянная, M – масса черной дыры, R – радиус черной дыры

Это и есть величина ускорения свободного падения на так называемом горизонте событий черной дыры.

Если подставить в эту формулу значения постоянных:

то получим для ускорения свободного падения величину порядка:

Из этой формулы следует, что увеличивая массу черной дыры, мы уменьшаем ускорение свободного падения на горизонте событий рассматриваемой черной дыры. Что мешает нам сделать эту массу равной порядка 10 в 43 степени килограмм, когда ускорение свободного падения на горизонте будет примерно равно земному?

Рассмотрим галактические масштабы. Масса нашей родной галактики Млечный путь примерно в триллион раз больше массы нашего Солнца и имеет массу порядка 42-43 в килограммах. То есть, по крайней мере, уже в галактических масштабах мы можем надеяться найти черную дыру, подвластную описанию в рамках классической небесной механики.

Итак, допустим, мы подлетаем к черной дыре с массой 43-го порядка в килограммах. Ускорение свободного падения на ее горизонте будет порядка земного g. Теперь попробуем построить график напряженности гравитационного поля вокруг и внутри этой черной дыры. Для простоты предположим, что черная дыра представляет из себя шар, имеющий более-менее равномерную плотность. В этом случае радиус черной дыры:

А средняя плотность вещества такой черной дыры:

Это значение, конечно, очень далеко от средней плотности галактик. Действительно, плотность галактики Млечный путь оценивается значением около -25, что на 20 порядков меньше, чем требуется для того, чтобы наша галактика стала галактической черной дырой. Очевидно, для этого придется рассматривать еще большие масштабы, а именно: галактические скопления. И тут можно вспомнить про такие гипотетические объекты как Великий Аттрактор. Но это тема для другой статьи.

А пока построим график напряженности гравитационного поля (ускорения свободного падения) для рассмотренной черной дыры галактического масштаба. В классическом приближении:

Снаружи черной дыры:

Внутри черной дыры:

Ниже представлен график этой функции на логарифмической шкале. И Вы увидите всплеск напряженности гравитационного поля на горизонте этой черной дыры:

А теперь будем увеличивать массу черной дыры. Радиус черной дыры при этом пропорционален ее массе. Поскольку плотность пропорциональна массе и обратно пропорциональна кубу радиуса, плотность черной дыры будет уменьшаться в квадратичном отношении к росту ее массы. То есть при увеличении массы и, соответственно, увеличении радиуса черной дыры на 10-15 порядков, ее плотность уменьшится на 20-30 порядков. И это уже приближается к плотности межгалактического пространства.

Вот тут и мы приближаемся к параметрам, когда реальная физическая система со средней плотностью порядка плотности межгалактического пространства может оказаться черной дырой.

Радиус наблюдаемой вселенной оценивается в 10 миллиардов световых лет. 1 световой год равен примерно 10 в 16 степени метров, что как раз соответствует радиусу рассмотренной черной дыры. Получается, что радиус наблюдаемой вселенной на 10 порядков больше рассмотренного, и плотность, достаточная для формирования черной дыры в масштабах наблюдаемой вселенной, будет порядка 10 в минус 25 степени килограмм на метр кубический.

Эта оценка довольно близка к современной оценке критической плотности Вселенной (см. здесь):

Здесь H – постоянная Хаббла, G – гравитационная постоянная

На этом полуслове, пожалуй, пора закончить эту статью.

Источник

Величина[править | править код]