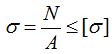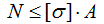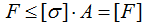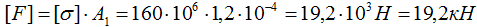Как найти грузоподъемность в задаче - Сайт, где вы сможете решить свои вопросы

Задачи на грузоподъемность (задачи на грузоперевозки) — частный случай задач на работу. Грузоподъемность машины — это ее производительность труда. Вместо времени работы — количество рейсов (если груз перевозит одна машина), либо количество машин.

Эти величины связаны одной из формул:

Оформляются задачи на грузоподъемность аналогично задачам на работу по плану — с помощью таблицы. И решаются аналогично — через систему уравнений.

Рассмотрим примеры задач на грузоперевозки.

1) Для перевозки 30 тонн груза машине надо было сделать несколько рейсов. Но груз пришлось перевозить на машине, имеющей грузоподъемность на 2 тонны больше, чем планировалось. Из-за этого для перевозки груза понадобилось на 4 рейса меньше. Найти грузоподъемность машины, перевезшей груз.

Решение:

Пусть по плану машина должна была иметь грузоподъемность x тонн и перевезти груз за y рейсов.

	Грузоподъемность	Количество рейсов	Объем работы
по плану	x	y	30
фактически	(x+2) — ?	y-4	30

Составим и решим систему уравнений:

$[left{ begin{array}{l}xy = 30\(x + 2)(y - 4) = 30end{array} right.]$

Раскроем скобки во втором уравнении. Заметим, что xy=30, поэтому во втором уравнении заменяем xy на 30 и упрощаем:

$[left{ begin{array}{l}xy = 30\xy - 4x + 2y - 8 = 30end{array} right. Rightarrow left{ begin{array}{l}xy = 30\30 - 4x + 2y - 8 = 30end{array} right.]$

После упрощения второе уравнение стало линейным. Выразим из него y через x:

$[begin{array}{l} - 4x + 2y - 8 = 0, Rightarrow 2y = 4x + 8, Rightarrow y = 2x + 4\end{array}]$

Подставим полученное выражение в первое уравнение:

$[x(2x + 4) = 30, Rightarrow 2{x^2} + 4x = 30, Rightarrow {x^2} + 2x - 15 = 0.]$

Корни этого уравнения

$[{x_1} = 3,{x_2} = - 5.]$

Второй корень — посторонний (так как грузоподъемность не может быть отрицательным числом). Грузоподъемность машины, перевезшей груз, равна 3+2=5 тонн.

Ответ: 5 тонн.

2) Для перевозки 60 тонн груза было заказано определенное количество грузовиков. Из-за поломки двух из них на каждую машину пришлось грузить на 1 тонну больше, чем планировалось. Сколько машин должно было работать на перевозке груза.

Решение:

Пусть по плану на каждую машину должны были погрузить x тонн и груз должны были перевозить y машин.

Грузоподъемность

Количество

машин

Объем

работы

по плану

y-?

фактически

x+1

y-2

Составим и решим систему уравнений:

$[left{ begin{array}{l}xy = 60\(x + 1)(y - 2) = 60end{array} right.]$

$[left{ begin{array}{l}xy = 60\xy - 2x + y - 2 = 60end{array} right. Rightarrow left{ begin{array}{l}xy = 60\60 - 2x + y - 2 = 60end{array} right.]$

Из второго уравнения выражаем y через x:

Полученное выражение подставляем в первое уравнение:

$[x(2x + 2) = 60, Rightarrow 2{x^2} + 2x = 60, Rightarrow {x^2} + x - 30 = 0]$

$[{x_1} = 5,{x_2} = - 6.]$

Второй корень не подходит по смыслу задачи. На перевозке груза должно было работать y машин, y=2x+2=2∙5+2=12.

Ответ: 12 машин.

Источник

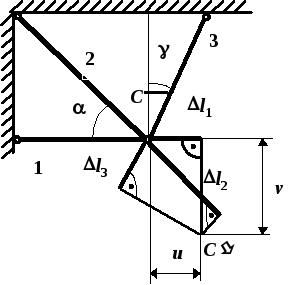
Имеется шарнирно-стержневая система,
состоящая из трех деформируемых стержней,
загруженная силой

(рис. 1.15). Заданы: геометрические
характеристики системы (,
,
);
площади поперечных сечений стержней
,
,
;
материал конструкции 
пластичный. Требуется^⁴:

Рис. 1.15. Схема
конструкции

В задаче № 6

определить грузоподъемность
системы тремя способами:

расчетом по упругой стадии деформаций;
расчетом по упругопластической стадии;
расчетом по предельному пластическому
состоянию;

2*) определить остаточные напряжения в
стержнях системы при полной разгрузке
из положения предельного равновесия.

Решение

Определение грузоподъемности системы
расчетом

по упругой стадии деформаций

Найдем степень статической неопределимости
системы. В данной конструкции имеем три
неизвестные продольные силы в стержнях.
Число уравнений статики, которые можно
составить для системы сил, сходящихся
в одной точке, равно двум. Таким образом,
число неизвестных больше числа уравнений
равновесия на единицу, и система является
один раз статически неопределимой.
Можно определить степень статической
неопределимости и по-другому. Шарнир

(модель которого 
точка) для неподвижного закрепления на
плоскости требует наложения двух
линейных связей. Такими необходимыми
связями являются любые два стержня из
имеющихся трех стержней системы.
Следовательно, оставшийся третий
стержень становится лишней кинематической
связью (лишним стержнем), а система
является один раз статически неопределимой.

Рис. 1.16. План
перемещений при расчете по упругой
стадии

Для раскрытия статической
неопределимости требуется составить
уравнения статики, одно (по числу лишних
связей) кинематическое соотношение
(условие совместности деформаций) и
физические уравнения. Рекомендуем
начинать решение задачи с записи условия
совместности деформаций, построив
предполагаемый план перемещений. Для
составления уравнений равновесия строим
план сил, направления усилий на котором
должны быть согласованы с планом
перемещений.

1. Уравнение совместности деформаций.
Построим предполагаемый план перемещений
(рис. 1.16). Величины двух абсолютных
деформаций задаем произвольно (например,
считаем, что стержни 2 и 3 удлиняются, и
откладываем произвольные отрезки

и

вдоль стержней). На пересечении траекторий
поворота концов двух стержней
(перпендикуляров к направлениям стержней)
получаем новое положение шарнира

– точку С на
рис. 1.16. Опустив из этой точки
перпендикуляр на направление оси стержня
1, найдем величину его абсолютной
деформации
.

Разложим полное перемещение шарнира

– отрезок
– на составляющие

и
.
Найдем абсолютные деформации стержней,
выразив их через

и
,
используя их геометрическую связь:

Исключив из этих выражений

и
,
получим искомое соотношение между
абсолютными деформациями

Допускается составлять уравнение
совместности деформаций приближенно,
измеряя отношения между абсолютными
деформациями по построенному в масштабе
плану перемещений. Для приближенного
определения связи между абсолютными
деформациями представим эту связь в
виде

Неизвестные параметры данной зависимости

и

определим из двух планов перемещений.
При построении первого плана перемещений
предположим, что
.
Измерим деформации первого
и
третьего
стержней.
Тогда

Построив второй план перемещений в
предположении, что
,
найдем отношение деформаций первого
и
второго
стержней и получим

2. Уравнения равновесия. Составим их на
основании плана сил. Нарисуем план сил,
вырезав узел

и заменив отброшенные части стержней
внутренними усилиями, причем направления
усилий покажем в соответствии с планом
перемещений растягивающими (рис. 1.17).
Запишем два независимых уравнения
статики. Для данной системы таковыми
являются:

;

Рис. 1.17. План сил
в упругой

стадии работы

3. Физические соотношения. Поскольку
расчет ведется по упругой стадии
деформаций, то материал конструкции
подчиняется закону Гука (1.3) и для каждого
стержня записываем физические уравнения:

; ; .

Полученную систему уравнений решаем
относительно усилий
,
,
.
Например, при
,

это решение имеет вид

,,.

Найденное решение показывает, что усилие
в первом стержне

отрицательно, т. е. стержень не растянут,
как мы предполагали, а сжат. Полученные
положительные знаки

и

подтверждают предположение о том, что
эти стержни растянуты.

Для проверки прочности конструкции
определим напряжения в стержнях системы:

;

При расчете по упругой стадии деформации
считаем, что предельное состояние
конструкции наступит тогда, когда
потечет один, наиболее напряженный,
стержень. Поскольку пластичный материал
имеет одинаковые пределы текучести при
сжатии и растяжении, то знак напряжения
не имеет значения и первым потечет
стержень, в сечении которого возникают
наибольшие по модулю напряжения. В
данном случае это третий стержень. Из
условия его текучести находим предельную
нагрузку:

, ;

а из условия прочности 
допускаемую нагрузку на конструкцию:

, .

Отметим, что при расчете по упругой
стадии деформаций нагрузка и напряжения
на всем участке деформирования связаны
прямой пропорциональной зависимостью,
а потому коэффициенты запаса по
напряжениям и по нагрузке равны между
собой.

Определение предельной грузоподъемности
системы

расчетом по упругопластической стадии

Рис. 1.18. Диаграмма
Прандтля

Проследим за дальнейшим развитием
процесса нагружения – деформирования
системы после того, как напряжения в
третьем стержне достигли предела
текучести. Примем, что материал конструкции
работает в соответствии с идеализированной
диаграммой упругопластического тела
– диаграммой Прандтля (рис. 1.18). При
продолжении роста нагрузки напряжения
в третьем стержне будут оставаться
постоянными и равными
.
При работе конструкции в упругопластической
стадии напряжения в остальных стержнях
будут расти в соответствии с упругим
законом, но при изменившихся параметрах
линейной зависимости от нагрузки. Эти
изменения связаны с перераспределением
нагрузки только на упругие стержни,
обеспечивающие неизменяемость системы
в этой стадии ее работы.

Поскольку усилие в стержне 3 уже известно,
задача становится статически определимой
и усилия в стержнях 1 и 2 находим из
уравнений равновесия узла

(план сил на рис. 1.19):

; ;

; .

Решение этой системы уравнений при
,
:

, .

Зависимости напряжений от нагрузки на
данной стадии работы системы:

, .

Рис. 1.19. План сил

в упругопластической
стадии работы

Предельное пластическое состояние
конструкции достигается тогда, когда
напряжения в одном из упругих стержней
1 и 2 достигнут предела текучести и
конструкция превратится в механизм.
Определим, какой из стержней потечет
первым, приравняв напряжения в стержнях
пределу текучести и найдя, при каком
значении нагрузки стержни потекут:

,
;

, .

Видно, что нагрузка, при которой
,
меньше и первый стержень потечет раньше
второго. Нагрузка, при которой будут
течь два стержня (3 и 1), и есть предельная
нагрузка для всей конструкции

Заметим, что в предельном состоянии
напряжения в первом и третьем стержнях
достигли предела текучести. При этом
первый стержень потек вслед за третьим,
хотя к концу упругой стадии напряжения
в нем были меньше, чем во втором стержне.
Зависимость между напряжениями и
нагрузкой с начала деформирования в
упругопластической стадии уже не
является линейной, а потому одинаковым
коэффициентам запаса по нагрузке и по
напряжениям в наиболее напряженном
упругом стержне будут соответствовать
различные значения допускаемой нагрузки.
Так, в нашем случае допускаемая нагрузка
с коэффициентом запаса

по напряжениям определяется из условия

; ; .

Если же исходить из коэффициента запаса

по нагрузке, то

; ; .

Очевидно, что расчет по допускаемой
нагрузке приводит к повышенному запасу
прочности в отдельных стержнях системы,
а расчет по допускаемым напряжениям не
обеспечивает заданного коэффициента
запаса по нагрузке. Поэтому значение
допускаемой нагрузки принимаем из
условия прочности по нагрузке:
.

Следует отметить, что современными
строительными нормами проектирования
предусматривается раздельное применение
коэффициентов надежности по нагрузке
и по материалу. Условие прочности в этом
случае приняло бы вид

где

и

 коэффициенты
надежности (запаса) по нагрузке и по
материалу соответственно.

Определение предельной грузоподъемности
системы

расчетом по предельному пластическому
состоянию

Заданная система имеет три деформируемых
стержня, один из которых является лишним,
так как система один раз статически
неопределима. В предельном состоянии,
когда конструкция превращается в
механизм, должны потечь два стержня
(один лишний и один необходимый). В
рассмотренных ранее способах решения
этой задачи рассматривался порядок
перехода материала стержней в пластическую
стадию работы, было выяснено, какой
стержень потечет первым, какой – вторым.
При этом конструкция сначала работает
в упругой стадии (материал всех стержней
подчиняется закону Гука), затем переходит
в упругопластическую стадию работы.
Решение вопроса о предельной нагрузке
на конструкцию, при которой последняя
переходит в механизм, может быть получено
и без рассмотрения упругой и
упругопластической стадий работы
конструкции. Для этого достаточно
исследовать равновесие системы в момент
перехода в предельное пластическое
состояние, т. е. в так называемое предельное
равновесие. Сложность состоит в том,
что конкретный механизм перехода системы
в предельное пластическое состояние
заранее неизвестен. Поэтому приходится
рассматривать все кинематически
возможные варианты перехода к предельному
равновесию и для каждого из них вычислять
предельную нагрузку. Фактически будет
иметь место тот вариант предельного
состояния, которому соответствует
минимальное значение предельной
нагрузки.

В данной задаче возможны три варианта
предельного равновесия конструкции:
1) текут стержни 1 и 3; 2) текут стержни 2 и
3 и, наконец, 3) текут стержни 2 и 1.

Рис. 1.20. Вариант
1 предельного пластического состояния:

а
– план перемещений;

б
– план сил

В качестве примера рассмотрим два
варианта предельного пластического
состояния в нашей задаче. Согласно
первому варианту допустим, что напряжения
в стержнях 1 и 3 равны
,
а стержень 2 работает упруго. Для
определения направления усилий в
стержнях 1 и 3 построим план перемещений,
используя те же правила построения
плана перемещений, которые описаны при
решении задач № 3 и 5. Поскольку упругие
деформации стержня 2 много меньше
пластических деформаций стержней 1 и
3, то при построении плана перемещений
стержень 2 можно считать абсолютно
жестким. Под действием нагрузки жесткий
стержень 2 повернется вокруг шарнира
А, и этот поворот вызовет укорочение
стержня 1 на l₁
и удлинение стержня 3 на l₃
(рис. 1.20, а). Соответствующий
плану перемещений план сил для первого
варианта перехода в предельное состояние
показан на рис. 1.20, б.

Чтобы неизвестное усилие N₂
не входило в уравнение, в качестве
условия предельного равновесия выберем
уравнение “сумма моментов относительно
шарнира

равна нулю” (см. рис. 1.20, б):

Из этого уравнения при
,

найдем
.

Во втором варианте предельного
пластического состояния напряжения в
стержнях 2 и 3 равны _т,
а первый стержень работает в упругой
стадии. Планы сил и перемещений показаны
на рис. 1.21. Запишем уравнение предельного
равновесия для узла С (такое уравнение
равновесие, в которое не входит неизвестное
усилие N₁):

; .

Рис. 1.21. Вариант
2 предельного пластического состояния:

а
– план перемещений;

б
– план сил

Отсюда
.

Аналогично можно определить предельную
нагрузку для третьего варианта, в котором
пластически деформироваться будут
стержни 1 и 2. Фактической предельной
нагрузкой будет минимальное значение
из трех полученных. В нашей задаче это

(первый вариант предельного состояния),
что совпадает со значением, найденным
ранее расчетом по упругопластической
стадии.

Надо отметить, что число кинематически
возможных вариантов предельного
состояния может уменьшиться, если ось
какого-либо стержня совпадает с линией
действия нагрузки (в этом случае поворота
этого стержня не происходит и механизма
не образуется).

Допускаемое значение нагрузки определяем
как отношение предельного значения
нагрузки к коэффициенту запаса прочности
n.

IV. Определение остаточных напряжений

Процесс нагружения
конструкции в упругой и упругопластической
стадиях, рассмотренный в пп. I и II, можно
отобразить на диаграмме в осях

(рис. 1. 22). Характерные точки этой
диаграммы получены по соответствующим
зависимостям

для трех стержней конструкции.

Рассмотрим процесс
полной разгрузки системы из положения
предельного равновесия (на диаграмме
это соответствует вертикальной прямой
с абсциссой
).
Процесс разгрузки можно трактовать как
наложение на существующие напряжения
напряжений от отрицательного приращения
нагрузки. Закон изменения последних
определяется упругим решением задачи
до тех пор, пока величина напряжения в
одном из стержней не достигнет
,
поэтому линии разгрузки каждого стержня
будут направлены параллельно линиям
упругого нагружения (левый участок
диаграммы). Если одно из напряжений при
разгрузке достигнет величины
(как
это имеет место в нашем случае), то законы
изменения напряжений станут соответствовать
упругопластической стадии, а их графики
будут параллельны соответствующим
линиям нагружения (правый участок
диаграммы).

Зависимости

можно записать, пользуясь уравнением
прямой с известным угловым коэффициентом,
проходящей через заданную точку:

где


угловой коэффициент прямой линии
нагружения, параллельной рассматриваемой
линии разгрузки;

и


начальные параметры (напряжение и
нагрузка в начале участка). В нашем
случае
,

для стержней 1 и 3, а для стержня 2
.

Запишем эти
зависимости непосредственно после
начала разгрузки:

Напряжение
,
как легко вычислить, достигнет значения

при снижении нагрузки до
.
При этом напряжения в остальных стержнях
будут
,
.

Пользуясь найденными
значениями как начальными параметрами,
запишем зависимости для напряжений на
втором участке разгрузки, проходящей
в упругопластической стадии:

При полной разгрузке
()
получаем следующие значения остаточных
напряжений:
,
,
.
В заключение следует проверить равновесие
узла

при полученных значениях остаточных
напряжений.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

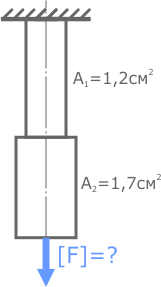
Пример решения задачи на расчет грузоподъемности стального ступенчатого стержня по условию прочности при продольном нагружении.

Задача

Рассчитать по условию прочности величину грузоподъемности [F] прямого ступенчатого стального стержня.

Другие примеры решений >
Помощь с решением задач >

Площади поперечного сечения указаны на расчетной схеме.
Допустимые напряжения [σ]=160МПа.

Решение

Расчет грузоподъемности сводится к определению величины максимально допустимой внешней силы F, которую может выдержать стержень, оставаясь прочным.

В данном случае имеет место продольное нагружение, потому для расчетов используем условие прочности при растяжении-сжатии:

где σ — напряжения в элементе, которые не должны превышать допустимых значений [σ],
N – внутренняя продольная сила,
А – площадь поперечного сечения элемента.

Перепишем эту формулу относительно внутренней силы N:

Так как стержень содержит только один силовой участок то по всей его длине N=F, поэтому:

Площадь поперечного сечения по длине стержня не постоянна, следовательно, допустимая сила для разных размеров сечения тоже будет отличаться.

Наша задача найти значение внешней силы, которая не нарушит прочность абсолютно всех сечений стержня.

Очевидно, что наименее прочным является фрагмент стержня с меньшей площадью поперечного сечения A₁<A₂ (принцип «где тонко там и рвется»). По ней и будем вести расчет:

Таким образом для обеспечения заданной прочности продольная растягивающая сила, приложенная к стержню не должна превышать значения [F]=19,2кН.

Другие примеры решения задач >

Сохранить или поделиться с друзьями

Вы находитесь тут:

На нашем сайте Вы можете получить решение задач и онлайн помощь

Подробнее

Источник

Две автомашины перевезли 21 т груза, сделав по 6 рейсов каждая. Узнай грузоподъемность каждой машины, если первая машина перевозила каждый раз на 500 кг груза меньше второй.

reshalka.com

ГДЗ учебник по математике 4 класс Дорофеев. Часть 2 страница 97. Номер №4

Решение

1) 6 * 500 = 3000 (кг) = на 3 (т) − груза больше перевезла вторая машина, чем первая;
2) 21 + 3 = 24 (т) − перевезли бы обе машины, если бы грузоподъемность у них была как у второй машины;
3) 6 + 6 = 12 (рейсов) − всего сделали машины;
4) 24 : 12 = 2 (т) − грузоподъемность второй машины;
5) 2 т − 500 кг = 2000 кг − 500 кг = 1500 (кг) = 1 т 500 кг − грузоподъемность первой машины.
Ответ: 1 т 500 кг и 2 т.

Источник

Методика решения текстовых задач на производительность и грузоперевозки.

Существует несколько способов решения текстовых задач:

арифметический способ – это способ решения текстовой задачи с помощью чисел и знаков арифметических действий сложения, вычитания, умножения и деления, то есть с помощью нескольких действий над числами, связанных между собой;

алгебраический способ – это способ решения текстовой задачи с помощью введения переменных и составления соответствующего уравнения или неравенства, или системы уравнений или неравенств;

геометрический способ – это способ решения текстовой задачи с помощью применения геометрических знаний;

схематический способ – это способ решения текстовой задачи с помощью схем;

графический способ – это способ решения текстовой задачи с помощью графиков в прямоугольной системе координат.

Текстовые задачи на производительность и грузоперевозки

Текстовые задачи на производительность и грузоперевозки наряду с задачами на движение являются одними из наиболее популярных видов задач на экзаменах разного уровня. Как в задачах на движение, в которых присутствуют элементы v –скорость, t –время и S – расстояние, так и в задачах на производительность и грузоперевозки есть аналогичные элементы.

В задачах на производительность существуют:

р – производительность, аналог скорости, то есть количество работы, производимой в единицу времени;

t – время работы;

А – объём работы, аналог расстояния.

Все три элемента связаны друг с другом формулой: объём работы А равен произведению производительности p на время t.

А = p · t

В задачах на грузоперевозки:

в роли скорости v выступает грузоподъёмность m, это есть масса груза, перевозимая одним транспортным средством;

в роли времени t выступает количество транспортных единиц n перевозчиков (машин, тележек, цистерн и т.д.);

в роли расстояния выступает общая масса M перевозимого груза.

Эти элементы связаны между собой формулой

М = m · n

Как правило, в этих задачах предполагается, что в ходе выполнения работы и перевозки грузов производительность и грузоподъёмность неизменны, то есть остаются постоянными. В силу аналогичности текстовых задач на движение, производительность и грузоподъёмность все способы и приёмы решения задач на движение применимы и к решению задач на производительность и грузоподъёмность.

Выбор переменной в текстовых задачах на производительность и грузоперевозки

Если в условии задачи не указаны единицы измерения работы, то весь объём работы и объём перевозимого груза удобнее обозначить за единицу, тогда производительность и грузоподъёмность будет измеряться в доле объёма работы и объёма груза в единицу времени.

Полезно также помнить, что производительность совместного труда нескольких участников и грузоподъёмность нескольких перевозящих средств равны сумме производительностей и сумме грузоподъёмностей соответственно.

Для успешного решения текстовых задач на производительность и грузоперевозки алгебраическим способом обычно за переменную принимают производительность или грузоподъёмность, но иногда удобнее обозначать переменной время. Сориентироваться в выборе переменной помогает главный вопрос задачи.

Полезно также помнить, что, если в условии описано много различных взаимосвязей между неизвестными величинами, то лучше все неизвестные обозначить буквами и опираясь на них составить по условию задачи несколько уравнений. В этом случае не должна пугать громоздкость составленных математических моделей. Обычно с помощью несложных преобразований уравнения хорошо упрощаются, а их количество сокращается.

Примеры решения текстовых задач на производительность и грузоперевозки

ЗАДАЧА 1. В Простоквашино Дядя Фёдор, кот Матроскин, Шарик и почтальон Печкин решили покрасить забор. Если красить забор будут Дядя Фёдор, кот Матроскин и почтальон Печкин, то они покрасят его за 1 час. Кот Матроскин, Шарик и почтальон Печкин смогут выкрасить забор за 1 час 15 минут, а Дядя Фёдор и Шарик справятся с работой за 1 час 40 минут. За сколько минут смогут выкрасить забор все четыре героя из Простоквашино?

Р Е Ш Е Н И Е :

Решим задачу геометрическим способом. Так как в условии задачи не указаны единицы измерения работы, то логично объём работы покраски забора обозначить за 1 единицу. Тогда производительность работы:

Известно, что общая производительность каждого вида работы равна сумме производительностей каждого участника работы. Смоделируем условия задачи на геометрических фигурах:

– производительность Дяди Фёдора,

–производительность кота Матроскина,

–производительность почтальона Печкина,

–производительность Шарика.

+ + =1/60 (ед./мин) –производительность 1/60 работы в минуту совместного труда Дяди Фёдора, кота Матроскина и почтальона Печкина.

+ + =1/75 (ед./мин) –производительность 1/75 единицы работы в минуту совместного труда кота Матроскина, Шарика и почтальона Печкина.

+ =1/100 (ед./мин) –производительность 1/100 единицы работы в минуту совместного труда Дяди Фёдора и Шарика.

Несложно заметить, что во всех трёх строках встречается по два прямоугольника каждого из четырёх цветов, следовательно, сложив соответственно левые и правые части, получаем, что удвоенная сумма всех четырёх производительностей равна

Чтобы найти производительность всех четверых участников их совместной работы, надо обе части полученного равенства поделить на два.

Чтобы ответить на главный вопрос задачи и найти время работы всех четверых участников, надо работу 1 единицу разделить на полученную производительность 1/50 (ед./мин).

Таким образом, все четыре героя из Простоквашино смогут выкрасить забор за 50 минут.

О Т В Е Т: 50 минут.

ЗАДАЧА 2. Первая труба наполняет резервуар на 5 минут дольше, чем вторая. Обе трубы вместе наполнят этот резервуар за 6 минут. За сколько минут наполняет этот резервуар первая труба?

Р Е Ш Е Н И Е:

Решим задачу алгебраическим способом. Главный вопрос задачи – это время, за которое первая труба заполняет резервуар. Тогда логично будет обозначить эту величину за переменную t (мин). Тогда второй трубе на наполнение резервуара понадобится (t – 5) (мин). Так как в условии задачи не даны единицы измерения объёма резервуара, то примем этот объём за 1 единицу.

Тогда можно выразить производительность работы первой и второй труб. Производительность их совместной работы равна сумме производительностей каждой трубы, значит:

По условию задачи сказано, что вместе две трубы наполняют резервуар за 6 минут. Следовательно, их производительность равна 1 /6 резервуара в минуту. Получили уравнение

Приведём дроби к общему знаменателю и перенесём всё в левую часть, имеем

Решая квадратное уравнение –t2 + 17t – 30 = 0, умножим обе части уравнения на –1. Получаем t2 – 17t + 30 = 0. Корнями этого уравнения являются t1 = 15 и t2 = 2.

По смыслу задачи время работы первой трубы должно быть больше 5, так как по условию задачи первая труба наполняет резервуар на 5 минут дольше, чем вторая.

Значит, значение t = 2 является посторонним решением.

Таким образом, первая труба наполняет резервуар за 15 минут. Мы ответили на главный вопрос задачи.

О Т В Е Т: 15 минут.

ЗАДАЧА 3. Три самосвала разной грузоподъёмности возят груз. Он будет вывезен полностью, если все они сделают по 8 рейсов. Груз также будет вывезен, если первый самосвал сделает 4 рейса, второй – 2 рейса, третий – 16 рейсов. Если первый и третий совершат соответственно 6 и 12 рейсов, то сколько рейсов нужно сделать второму, чтобы весь груз был вывезен?

Р Е Ш Е Н И Е:

Решим задачу алгебраическим способом с помощью системы уравнений. В условии задачи нет единиц измерения массы груза, следовательно, весь груз примем за 1 единицу.

Введём переменные:

х – доля груза, который помещается на первый самосвал;

у – доля груза, который помещается на второй самосвал;

z – доля груза, который помещается на третий самосвал;

k – количество рейсов, которое нужно сделать второму самосвалу, чтобы весь груз был вывезен.

По условию задачи груз будет вывезен полностью, если все самосвалы сделают по 8 рейсов, значит, составим уравнение

8x + 8y + 8z = 1.

Так же по условию задачи груз будет вывезен, если первый самосвал сделает 4 рейса, второй –2 рейса, третий – 16 рейсов, значит, получим ещё одно уравнение:

4x + 2y + 16z = 1.

А еще по условию задачи, если первый и третий совершат соответственно 6 и 12 рейсов, то k рейсов нужно сделать второму, чтобы весь груз был вывезен, тогда получим уравнение:

6x + ky + 12z = 1.

Рассмотрим систему трёх уравнений с четырьмя неизвестными:

Обнулим коэффициенты при х у второго и третьего уравнений. Для этого из удвоенных слагаемых второго уравнения вычтем соответствующие слагаемые первого уравнения, а затем из слагаемых третьего уравнения вычтем соответствующие слагаемые первого уравнения, умноженные на 0,75. Получаем новую систему уравнений:

Теперь аналогично обнулим коэффициенты при z во втором и третьем уравнениях. Для этого из коэффициентов второго уравнения вычтем учетверённые соответствующие коэффициенты третьего уравнения. Получаем новое уравнение:

(20 – 4k)y = 0.

Так как по смыслу задачи грузоподъёмность второго самосвала у не может равняться 0, то решением полученного уравнения будет k = 5.

Мы ответили на главный вопрос задачи: для вывоза всего груза второй самосвал должен сделать 5 рейсов.

О Т В Е Т: 5 рейсов.

Примеры решения текстовых задач на производительность

ЗАДАЧА 1. Три поросёнка Ниф-Ниф, Наф-Наф и Нуф-Нуф решили своими руками сделать игрушки для новогодней ёлки. Ниф-Ниф изготовлял 5 игрушек в час, а Наф-Наф 8 игрушек в час. Ниф-Ниф и Наф-Наф начали работу одновременно, а Нуф-Нуф –на полчаса позже. Через некоторое время Нуф-Нуф догнал по количеству изготовленных игрушек Ниф-Нифа, а ещё через полтора часа после этого догнал и Наф-Нафа. Определите производительность труда Нуф-Нуфа.

Р Е Ш Е Н И Е:

Решим задачу алгебраическим способом.

Введём переменные:

р – производительность труда Нуф-Нуфа игрушек в час.

t – время в часах, через которое Нуф-Нуф догнал по количеству изготовленных игрушек Ниф-Нифа.

По условию задачи Нуф-Нуф начал работать на полчаса позже, значит, он проработал до этого момента (t –0,5) часов. Так как Нуф-Нуф догнал по количеству изготовленных игрушек Ниф-Нифа, значит, можно составить уравнение:

p(t – 0,5) = 5t.

По условию задачи через полтора часа Нуф-Нуф догнал по количеству игрушек и Наф-Нафа. Значит, за время работы Нуф-Нуф сделал p(t +1) игрушек, а Наф-Наф 8(t + 1,5) игрушек. Мы получили второе уравнение:

p(t +1) = 8(t + 1,5).

По условию задачи надо найти значение переменной р. Следовательно, из каждого полученного уравнения выразим переменную t через переменную р. Из первого уравнения имеем:

Из второго уравнения получим

Левые части выражений равны, следовательно, и правые части тоже равны. Мы получили пропорциональное уравнение с одной переменной р, а именно:

Известно, что в верной пропорции произведение крайних членов равно произведению средних членов. Значит, получим уравнение:

0,5р(р – 8) = (12 – р)(р – 5).

Раскрыв скобки, перенесём всё в левую часть уравнения и приведём подобные члены. Получаем квадратное уравнение

1,5р2 – 21р + 60 = 0.

Обе части уравнения умножим на две третьих. Имеем квадратное уравнение:

р2 –14р + 40 = 0; с корнями р1 = 4 и р2 = 10.

По условию задачи Нуф-Нуф начал работать позже и догнал по количеству изготовленных игрушек своих друзей, следовательно, его производительность должна быть больше производительности и Ниф-Нифа, и Наф-Нафа. Значит, по смыслу задачи значение р должно быть больше 8-ми. Получили, что р = 4 является посторонним решением, а значение р = 10даёт ответ на главный вопрос задачи: производительность труда Нуф-Нуфа 10 игрушек в час.

О Т В Е Т: 10 игрушек в час.

ЗАДАЧА 2. В бассейн проведены две труб – подающая и отводящая, причём через первую бассейн наполняется на 2 часа дольше, чем через вторую опорожняется. При заполненном на одну треть бассейне были открыты обе трубы, и бассейн оказался пустым через 8 часов. За сколько часов, действуя отдельно, первая труба наполняет бассейн?

Р Е Ш Е Н И Е:

Решим задачу алгебраическим способом.

Введём переменные.

Главный вопрос задачи заключается в определении количества часов, за которое первая труба, действуя отдельно, наполняет бассейн. Значит:

t – время работы первой трубы для заполнения бассейна в часах;

t – 2 – время слива воды из бассейна через вторую трубу в часах, так как по условию задачи через первую бассейн наполняется на 2 часа дольше, чем через вторую опорожняется.

В условии задачи отсутствуют единицы измерения объёма бассейна, значит, весь объём бассейна примем за 1 единицу. При заполненном на одну треть бассейне были открыты обе трубы, и бассейн оказался пустым через 8 часов. Следовательно, 2/3 бассейна заполняется

Выразим объём бассейна через производительность подающей трубы, а именно, как одна третья бассейна плюс её производительность 1 делённая на t и умноженная на время работы трубы 8 часов

Объём бассейна через производительность отводящей трубы выразится как её производительность 1 деленная на (t – 2) и умноженная на время работы 8 часов

Приведём дроби к общему знаменателю и упростим числитель.

Тогда получим уравнение

Известно, что дробь равна 0, если числитель равен 0. Решая квадратное уравнение

t2 – 2t – 48 = 0,

Получаем корни t1 = – 6 и t2 = 8. По смыслу задачи значение времени t должно быть неотрицательной величиной, значит, корень t = – 6 является посторонним решением. А корень t = 8 даёт ответ на главный вопрос задачи: первая труба заполняет бассейн за 8 часов.

О Т В Е Т: 8 часов.

ЗАДАЧА 3. Одновременно зажжены две свечи одинаковой длины, но разной толщины. Одна сгорает за 5 часов, а другая – за 4 часа. Через сколько минут были погашены одновременно две свечи, если от первой свечи остался огарок в 4 раза длиннее, чем от второй?

Р Е Ш Е Н И Е:

Решим задачу алгебраическим способом.

Введём переменную. Так как главным вопросом является количество минут одновременного горения свечек, то логично за переменную t часов обозначить это время.

t – количество минут одновременного горения свечек в часах.

По условию задачи две свечи одинаковой длины, причём их длина не выражена в единицах измерения, значит, примем длину свечей за 1 единицу. Также в условии сказано, что свечи разной толщины и одна из них сгорает за 5 часов, а другая – за 4 часа. Следовательно,

Выразим длину огарков после горения свечей в течение t часов.

По условию задачи от первой свечи остался огарок в 4 раза длиннее, чем от второй. Значит, составим уравнение

Раскрыв скобки и проведя алгебраические преобразования, получаем корень уравнения

Мы ответили на главный вопрос задачи: через 3,75 часа огарок первой свечи будет в 4 раза длиннее огарка второй свечи. Выразим результат времени в минутах, для этого 3,75 умножим на 60 минут. Получаем 225 минут.

О Т В Е Т: 225 минут.

Пример решения текстовых задач на грузоперевозки

ЗАДАЧА. Три автомашины перевозят зерно, загружаясь в каждом рейсе полностью. За один рейс первая и вторая машины перевозят вместе 6 тонн зерна, а первая и третья вместе за два рейса перевозят столько же зерна, сколько вторая за 3 рейса. Какое количество зерна перевозит за один рейс вторая машина, если известно, что некоторое количество зерна вторая и третья перевозят вместе, совершая в 3 раза меньше рейсов, чем потребовалось бы третьей машине для перевозки того же количества зерна.

Р Е Ш Е Н И Е:

Решим задачу алгебраическим способом.

Введём переменные. Так как главным вопросом задачи является определение количества зерна, которое перевозит за один рейс вторая машина, то логично обозначить за х тонн зерна за один рейс грузоподъёмность второй машины.

x – грузоподъёмность второй машины за один рейс в тоннах.

По условию задачи за один рейс первая и вторая машины перевозят вместе 6 тонн зерна, значит,

(6 – х) – грузоподъёмность первой машины за один рейс в тоннах.

у – грузоподъёмность третьей машины в тоннах.

По условию задачи первая и третья машины вместе за два рейса перевозят столько же зерна, сколько вторая за 3 рейса. Тогда можем составить уравнение

2(6 – х + у) = 3х.

По условию задачи некоторое количество зерна вторая и третья машины перевозят вместе, совершая в 3 раза меньше рейсов, чем потребовалось бы третьей машине для перевозки того же количества зерна. Тогда можем составить уравнение

х + у = 3у.

Так как главным вопросом задачи является значение переменной х, то из второго уравнения выразим у через х.

Имеем у = 0,5х. Подставим полученное выражение в первое уравнение вместо у. Получаем уравнение с одной переменной

2(6 – 0,5х) = 3х.

Раскрыв скобки, решим уравнение 12 – х = 3х. Нетрудно вычислить его корень х = 3. Мы ответили на главный вопрос задачи 3 тонны зерна перевозит за один рейс вторая машина.

О Т В Е Т: 3 тонны.

Литература:

1. Г.Н. Тимофеев Математика для поступающих в вузы. Учебное пособие. Текстовые задачи. – Йошкар-Ола: Мар. гос. ун-т, 2006 г.

2. В. Булынин Применение графических методов при решении текстовых задач. – Еженедельная учебно-методическая газета «Математика», №14, 2005 г.

3. Н.И. Попов, А.Н. Марасанов Задачи на составление уравнений. Учебное пособие. Йошкар-Ола: Мар. гос. ун-т, 2003 г.

4. http://festival.1september.ru/articles/310281/ Н.А. Зарипова Программа элективного курса “Текстовые задачи”.

5. http://festival.1september.ru/articles/415044/ Н.А. Зарипова Методика решения задач группы vts. Материалы к проведению элективного курса “Решение текстовых задач”

Источник

В задаче № 6

Решение

ГДЗ учебник по математике 4 класс Дорофеев. Часть 2 страница 97. Номер №4

Решение

Вам также может понравиться

Как мне найти искупление

Как найти площадь треугольника зная координаты точек

Как найти объем молекулы зная ее массу

Добавить комментарий Отменить ответ