Решение уравнений – навык, который необходим каждому нацеленному на успешную сдачу ЕГЭ и ОГЭ школьнику. Он поможет решить задания №4, 12 и 14 из профильного уровня математики.
Одна из их разновидностей уравнений – степенные уравнения, которые иногда также называют показательными. Основная отличительная особенность – наличие степеней и переменной (х) не в основании степени, а в самом показателе. Как это выглядит:
$$ a^{f(x)}=b^{g(x)}; $$
Где (a) и (b) – некоторые числа, а (f(x)) и (g(x)) – какие-то выражения, зависящие от (x). Не бойтесь – это самый общий вид показательных уравнений. Реальные примеры выглядят как-то так:
$$2^x=8;$$
$$ 2^x=2^{2x+1};$$
$$3^{x^2}=2^{x^2-2x+3};$$
Внимательно посмотрите на приведенные уравнения. В каждом из них присутствует, так называемая, показательная (степенная) функция. При решении необходимо помнить об основных свойствах степени, а также использовать особые правила, помогающие вычислить значение (х). Познакомиться с понятием степени и ее свойствами можно тут и тут.
И вам понадобится умение решать обыкновенные линейные и квадратные уравнения, те, что вы проходили в 7-8 классе. Вот такие:
$$ 7x+2=16;$$
$$x^2-4x+5=0;$$
И так, любое уравнение, в котором вы увидите показательную (степенную) функцию, называется показательным уравнением.
Ура! Теперь знаем, как выглядят показательные уравнения, но толку от этого не очень много. Было бы неплохо научиться их решать. Отличная новость – на наш взгляд показательные уравнения одни из самых простых типов уравнений, по сравнению с логарифмическими, тригонометрическими или иррациональными.
Простейшие показательные уравнения
Давайте начнем с самых простых типов уравнений и разберем сразу несколько примеров:
Пример 1
$$ 2^x=8;$$
Что такое решить уравнение? Это значит, что нужно найти такое число, которое при подстановке в исходное уравнение вместо (х) даст верное равенство. В нашем примере нужно найти такое число, в которое нужно возвести двойку, чтобы получить восемь. Ну это просто:
$$ 2^3=2*2*2=8; $$
Значит, если (х=3), то мы получим верное равенство, а значит мы решили уравнение.
Решим что-нибудь по-сложнее.
Пример 2
$$ 3^{4x-1}=frac{1}{9};$$
Такое уравнение выглядит сложнее. Попробуем преобразовать правую часть уравнения:
$$frac{1}{9}=frac{1}{3^2}=3^{-2};$$
Мы применили свойство отрицательной степени по формуле:
$$ a^{-n}=frac{1}{a^n};$$
Теперь наше уравнение будет выглядеть так:
$$ 3^{4x-1}=3^{-2};$$
Заметим, что слева и справа у нас стоят показательные функции, и там, и там основания одинаковые и равны (3), только вот степени разные – слева степень ((4х-1)), а справа ((-2)). Логично предположить, что если степени у такой конструкции будут равны, при условии, что основания одинаковые, то мы получим верное равенство. Так и поступим:
$$ 4x-1=-2;$$
Такое мы решать умеем, ведь это обыкновенное линейное уравнение.
$$4х=-2+1;$$
$$4x=-1;$$
$$x=-frac{1}{4}.$$
Поздравляю, мы нашли корень нашего показательного уравнения.
Пример 3
$$125^x=25;$$
Попробуем поступить так, как в предыдущем примере – преобразуем левую и правую часть, чтобы слева и справа была показательная функция с одинаковым основанием. Как это сделать? Обращаем внимание, что (125=5*5*5=5^3), а (25=5*5=5^2), подставим:
$$ (5^3)^x=5^2;$$
Воспользуемся одним из свойств степеней ((a^n)^m=a^{n*m}):
$$ 5^{3*x}=5^2;$$
И опять мы получили две показательные функции, у которых одинаковые основания и для того, чтобы равенство выполнялось, необходимо приравнять из степени:
$$ 3*x=2;$$
$$ x=frac{2}{3};$$
И еще один пример:
Пример 4
$$2^x=-4;$$
Те, кто хорошо знает свойства степеней, знают, что показательная функция не может быть отрицательной. Действительно, попробуйте возводить (2) в различную степень, вы никогда не сможете получить отрицательное число.
Внимание! Показательная функция не может быть отрицательной, поэтому, когда вы встречаете примеры на подобии примера 4, то знайте, что такого быть не может. Здесь корней нет, потому что показательная функция всегда положительна.
Теперь давайте разработаем общий метод решения показательных уравнений. И научимся решать более сложные примеры.
Общий метод решения показательных уравнений
Пусть у нас есть вот такой пример:
$$ a^x=b;$$
Где (a,b) какие-то положительные числа. ((a>0, ; b>0)).
Согласно разобранным выше примерам, логично предположить, что для того, чтобы решить данное уравнение, нужно его преобразовать к виду, где слева и справа стоят показательные функции с одинаковым основанием. Так и поступим.
Слева у нас уже стоит (a^x), с этим ничего делать не будем, а вот справа у нас стоит загадочное число (b), которое нужно попытаться представить в виде (b=a^m). Тогда уравнение принимает вид:
$$ a^x=a^m;$$
Раз основания одинаковые, то мы можем просто приравнять степени:
$$x=m.$$
Вот и весь алгоритм решения. Просто нужно преобразовать исходное уравнение таким образом, чтобы слева и справа стояли показательные функции с одинаковыми основаниями, тогда приравниваем степени и вуаля – сложное показательное уравнение решено. Осталось только разобраться, как так преобразовывать. Опять разберем на примерах:
Пример 5
$$2^x=16;$$
Замечаем, что (16=2*2*2*2=2^4) это степень двойки:
$$2^x=2^4$$
Основания одинаковые, значит можно приравнять степени:
$$x=4.$$
Пример 6
$$5^{-x}=125 Rightarrow 5^{-x}=5*5*5 Rightarrow 5^{-x}=5^3 Rightarrow –x=3 Rightarrow x=-3.$$
Пример 7
$$9^{4x}=81 Rightarrow (3*3)^{4x}=3*3*3*3 Rightarrow(3^2)^{4x}=3^4 Rightarrow 3^{8x}=3^4 Rightarrow 8x=4 Rightarrow x=frac{1}{2}.$$
Здесь мы заметили, что (9=3^2) и (81=3^4) являются степенями (3).
Все здорово, но проблема в том, что такая схема решения показательных уравнений работает не всегда. Что делать, если привести к одинаковому основанию не получается. Например:
Пример 8
$$ 3^x=2;$$
(3) и (2) привести к одинаковому основанию затруднительно. Но тем не менее мы должны это сделать. Воспользуемся следующей схемой преобразований: пусть есть некоторое положительное число (b>0), тогда его можно представить в виде степени любого, нужного вам, положительного числа не равного единице (a>0, ; a neq 1):
$$ b=a^{log_{a}(b)};$$
Эта очень важная формула, рекомендуем ее выучить. Вернемся к нашему примеру и по формуле представим (2) в виде (3) в какой-то степени, где (a=3), а (b=2):
$$ 2=3^{log_{3}(2)};$$
Подставим данное преобразование в наш пример:
$$3^x=3^{log_{3}(2)};$$
Получили равенство двух показательных функций с одинаковым основанием, значит можем приравнять их степени:
$$x=log_{3}(2).$$
Так в ответ и запишем. Никакой ошибки здесь нет, дело в том, что такие логарифмы можно посчитать только на калькуляторе, поэтому на ЕГЭ или в контрольной работе вы просто оставляете ответ в таком виде.
Кто забыл, что такое логарифм, можно посмотреть здесь.
Рассмотрим еще несколько аналогичных примеров.
Пример 9
$$ 7^{2x}=5;$$
$$ 7^{2x}=7^{log_{7}(5)};$$
$$2x=log_{7}(5);$$
$$x=frac{1}{2}*log_{7}(5).$$
Те, кто хорошо знает свойства логарифмов, могут поиграться с последней формулой и получить ответ в разном виде:
$$ x=frac{1}{2}*log_{7}(5)=log_{7}(5^{frac{1}{2}})=log_{7}(sqrt{5});$$
Все эти варианты ответа верные, их можно смело писать в ответ.
И так, мы с вами научились решать любые показательные уравнения вот такого вида: (a^x=b), где (a>0; ; b>0).
Но это еще далеко не все. Часто вы будете встречать показательные уравнения гораздо более сложного типа. В ЕГЭ по профильной математике это номер 15 из 2й части. Но бояться тут не нужно, все на первый взгляд сложные уравнения при помощи обычно не самых сложных преобразований сводятся к уравнениям типа (a^x=b), где (a>0; ; b>0). Рассмотрим типы сложных уравнений, которые могут попасться:
Решение показательных уравнений при помощи замены
Рассмотрим уравнение:
Пример 10
$$ 9^x-5*3^x+6=0;$$
Самое первое, что вы должны всегда делать, это пытаться привести все имеющиеся показательные функции к одинаковому основанию.
Здесь это сделать легко, замечаем, что (9=3^2), тогда (9^x=(3^2)^x=3^{2x}=(3^x)^2). Здесь мы воспользовались свойством степеней: ((a^n)^m=a^{n*m}). Подставим:
$$(3^x)^2-5*3^x+6=0;$$
Обратим внимание, что во всем уравнении все (х) «входят» в одинаковую функцию – (3^x). Сделаем замену (t=3^x, ; t>0), так как показательная функция всегда положительна.
$$t^2-5t+6=0;$$
Квадратное уравнение, которое решается через дискриминант:
$$D=5^2-4*6=25-24=1; Rightarrow t_{1}=frac{5+sqrt{1}}{2}=3; Rightarrow t_{2}=frac{5-sqrt{1}}{2}=2;$$
Оба корня больше нуля, значит оба нам подходят. Сделаем обратную замену и уравнение сводится к решению двух простых показательных уравнений:
$$ 3^x=3;$$
$$3^x=3^1;$$
$$x=1.$$
И второй корень:
$$ 3^x=2;$$
$$3^x=3^{log_{3}(2)};$$
$$x=log_{3}(2).$$
Ответ: (x_{1}=1; ; x_{2}=log_{3}(2).)
И еще один пример на замену:
Пример 11
$$3^{4x^2-6x+3}-10*3^{2x^2-3x+1}+3=0;$$
Воспользуемся нашим правилом, что все нужно приводить к одинаковому основанию – а стоп, тут и так у всех показательных функций основание (3). Давайте еще внимательно посмотрим на наш пример, очень похоже на то, что он тоже делается через замену. Но у нас тут нет одинаковых показательных функций, основания то одинаковые, а вот степени отличаются. Преобразуем первое слагаемое. Если быть внимательным, то можно заметить, что в первой степени можно разбить свободный член (3=2+1) и вынести общий множитель (2):
$$ 3^{4x^2-6x+3}=3^{4x^2-6x+2+1}=3^{2(2x^2-3x+1)+1}=3^{2*(2x^2-3x+1)}*3^1=3*(3^{2x^2-3x+1})^2;$$
Подставим в исходное уравнение:
$$3*(3^{2x^2-3x+1})^2-10*3^{2x^2-3x+1}+3=0;$$
Теперь показательные функции одинаковы и можно сделать замену:
$$t=3^{2x^2-3x+1}; ; t>0;$$
$$3*t^2-10t+3=0;$$
$$D=100-36=64; Rightarrow t_{1}=3; t_{2}=frac{1}{3};$$
Обратная замена, и наше уравнение сводится к простейшему:
$$ 3^{2x^2-3x+1}=3;$$
$$ 2x^2-3x+1=1;$$
$$x(2x-3)=0;$$
$$x=0; ; x=frac{3}{2}.$$
И второе значение (t):
$$3^{2x^2-3x+1}=frac{1}{3};$$
$$3^{2x^2-3x+1}=3^{-1};$$
$$2x^2-3x+1=-1;$$
$$2x^2-3x+2=0;$$
$$D=9-16=-7<0;$$
Раз дискриминант получился меньше нуля, то вторая ветка решений нам корней не дает.
Ответ: (x_{1}=0; ; x_{2}=frac{3}{2}.)
Однородные показательные уравнения
Иногда встречаются такие показательные уравнения, в которых не сразу видно, как сделать одинаковые функции, а именно одинаковые основания, чтобы произвести замену. Посмотрим на такой пример:
Пример 12
$$ 7^{x+1}+3*7^{x}=3^{x+2}+3^{x};$$
Тут у нас две показательные функции с основаниями (7) и (3), и как сделать из них одинаковые основания непонятно. Этот пример решается при помощи деления. Давайте поделим все наша уравнение на (3^x):
$$ 7^{x+1}+3*7^{x}=3^{x+2}+3^{x} ; ; :3^x$$
$$ frac{7^{x+1}}{3^x}+frac{3*7^{x}}{3^x}=frac{3^{x+2}}{3^x}+frac{3^{x}}{3^x};$$
Здесь нам придется воспользоваться свойствами степеней:
$$frac{a^n}{a^m}=a^{n-m};$$
$$ a^n*a^m=a^{n+m};$$
$$ frac{a^n}{b^n}=(frac{a}{b})^n;$$
Разберем каждое слагаемое:
$$ frac{7^{x+1}}{3^x}=frac{7*7^x}{3^x}=7*frac{7^x}{3^x}=7*(frac{7}{3})^x;$$
$$ frac{3*7^{x}}{3^x}=3*frac{7^x}{3^x}=3*(frac{7}{3})^x;$$
$$ frac{3^{x+2}}{3^x}=3^2*frac{3^x}{3^x}=3^2*1=9;$$
$$ frac{3^{x}}{3^x}=1;$$
Теперь подставим получившееся преобразования в исходное уравнение:
$$ 7*(frac{7}{3})^x+3*(frac{7}{3})^x=9+1;$$
Теперь видно, что в нашем уравнении есть одинаковая функция, которую можно убрать в замену (t=(frac{7}{3})^x):
$$7t+3t=10;$$
$$10t=10;$$
$$t=1;$$
Сделаем обратную замену:
$$(frac{7}{3})^x=1;$$
Вспоминаем, что (1=(frac{7}{3})^0):
$$(frac{7}{3})^x=(frac{7}{3})^0;$$
$$x=0.$$
Ответ: (x=0).
И последний пример на замену:
Пример 13
$$2^{x+2}+0,5^{-x-1}+4*2^{x+1}=28;$$
Первым делом нужно сделать так, чтобы все показательные функции были с одинаковым основанием и в идеале с одинаковой степенью. Для этого нам понадобятся формулы для степеней:
$$ a^n*a^m=a^{n+m};$$
$$a^{-n}=frac{1}{a^n};$$
$${(a^n)}^m=a^{n*m};$$
Разберем каждое слагаемое нашего уравнения:
$$2^{x+2}=2^x*2^2=4*2^x;$$
Все десятичные дроби всегда разумно представить в виде обыкновенных дробей. И будьте внимательны – отрицательная степень не имеет никакого отношения к знаку показательной функции!
$$0,5^{-x-1}=0,5^{-(x+1)}={(frac{1}{2})}^{-(x+1)}={(2^{-1})}^{-(x+1)}=2^{x+1}=2^x*2^1=2*2^x;$$
И последнее слагаемое со степенью:
$$ 4*2^{x+1}=4*2^x*2^1=8*2^x;$$
Подставим все наши преобразования в исходное уравнение:
$$4*2^x+2*2^x+8*2^x=28;$$
Теперь можно сделать замену (t=2^x) или можно обойтись без замены, просто приведя подобные слагаемые (вынести общий множитель (2^x)):
$$2^x*(4+2+8)=28;$$
$$14*2^x=28;$$
$$2^x=frac{28}{14}=2;$$
$$2^x=2^1;$$
$$x=1.$$
Ответ: (x=1.)
Особенно стоит подчеркнуть прием, который мы использовали при решении 13-го примера.
Всегда старайтесь избавляться от десятичных дробей. Переводите их в обыкновенные дроби.
И другой тип степенных уравнений, где обычно не нужно делать замену, а необходимо отлично знать все свойства степеней, некоторые из них мы уже обсудили выше. Все про свойства степеней можно посмотреть тут
Пример 14
$$2^{x+1}*5^x=10^{x+1}*5^{x+2};$$
Вот такое уравнение, в котором у нас, во-первых, показательных функции перемножаются, а еще хуже то, что у них у всех разные основания. Катастрофа, а не пример. Но ничего, все не так страшно, как кажется. Внимательно посмотрите на основания: у нас есть в основании (2), (5) и (10). Очевидно, что (10=2*5). Воспользуемся этим и подставим в наше уравнение:
$$2^{x+1}*5^x=(2*5)^{x+1}*5^{x+2};$$
Воспользуемся формулой ((a*b)^n=a^n*b^n):
$$ 2^{x+1}*5^x=2^{x+1}*5^{x+1}*5^{x+2};$$
И перекинем все показательные функции с основанием (2) влево, а с основанием (5) вправо:
$$frac{2^{x+1}}{2^{x+1}}=frac{5^{x+1}*5^{x+2}}{5^x};$$
Сокращаем и воспользуемся формулами (a^n*a^m=a^{n+m}) и (frac{a^n}{a^m}=a^{n-m}):
$$1=frac{5^{x+1+x+2}}{5^x};$$
$$1=frac{5^{2x+3}}{5^x};$$
$$1=5^{2x+3-x};$$
$$1=5^{x+3};$$
$$5^0=5^{x+3};$$
$$x+3=0;$$
$$x=-3.$$
Ответ: (x=-3).
Самая главная идея при решении показательных уравнений – это любыми доступными способами свести все имеющиеся степенные функции к одинаковому основанию. А еще лучше и к одинаковой степени. Вот почему необходимо знать все свойства степеней, без этого решить уравнения будет проблематично.
Как же понять, где какие преобразования использовать? Не бойтесь, это придет с опытом, чем больше примеров решите, тем увереннее будете себя чувствовать на контрольных в школе или на ЕГЭ по профильной математике. Сначала потренируйтесь на простых примерах и постепенно повышайте уровень сложности. Успехов в изучении математики!
Приветствую вас дорогие учащиеся!
Рекомендуем подписаться на канал на youtube нашего сайта TutoMath.ru, чтобы быть в курсе всех новых видео уроков.
Для начала вспомним основные формулы степеней и их свойства.
Произведение числа a само на себя происходит n раз, это выражение мы можем записать как a•a•…•a=an
1. a0 = 1 (a ≠ 0)
2. a1 = a
3. an • am = an + m
4. (an)m = anm
5. anbn = (ab)n
6. a-n= 1/an
7. an/am= an — m
Степенные или показательные уравнения – это уравнения в которых переменные находятся в степенях (или показателях), а основанием является число.
Примеры показательных уравнений:
6x=36
В данном примере число 6 является основанием оно всегда стоит внизу, а переменная x степенью или показателем.
Приведем еще примеры показательных уравнений.
2x*5=10
16x — 4x — 6=0
Теперь разберем как решаются показательные уравнения?
Возьмем простое уравнение:
2х = 23
Такой пример можно решить даже в уме. Видно, что x=3. Ведь чтобы левая и правая часть были равны нужно вместо x поставить число 3.
А теперь посмотрим как нужно это решение оформить:
2х = 23
х = 3
Для того, чтобы решить такое уравнение, мы убрали одинаковые основания (то есть двойки) и записали то что осталось, это степени. Получили искомый ответ.
Теперь подведем итоги нашего решения.
Алгоритм решения показательного уравнения:
1. Нужно проверить одинаковые ли основания у уравнения справа и слева. Если основания не одинаковые ищем варианты для решения данного примера.
2. После того как основания станут одинаковыми, приравниваем степени и решаем полученное новое уравнение.
Теперь прорешаем несколько примеров:
Начнем с простого.
2х+2 = 24
Основания в левой и правой части равны числу 2, значит мы можем основание отбросить и приравнять их степени.
x+2=4 Получилось простейшее уравнение.
x=4 — 2
x=2
Ответ: x=2
В следующем примере видно, что основания разные это 3 и 9.
33х — 9х+8 = 0
Для начала переносим девятку в правую сторону, получаем:
33х = 9х+8
Теперь нужно сделать одинаковые основания. Мы знаем что 9=32 . Воспользуемся формулой степеней (an)m = anm.
33х = (32)х+8
Получим 9х+8 =(32)х+8 =3 2х+16
33х = 3 2х+16 теперь видно что в левой и правой стороне основания одинаковые и равные тройке, значит мы их можем отбросить и приравнять степени.
3x=2x+16 получили простейшее уравнение
3x — 2x=16
x=16
Ответ: x=16.
Смотрим следующий пример:
22х+4 — 10•4х = 24
В первую очередь смотрим на основания, основания разные два и четыре. А нам нужно, чтобы были — одинаковые. Преобразовываем четверку по формуле (an)m = anm.
4х = (22)х = 22х
И еще используем одну формулу an • am = an + m:
22х+4 = 22х•24
Добавляем в уравнение:
22х•24 — 10•22х = 24
Мы привели пример к одинаковым основаниям. Но нам мешают другие числа 10 и 24. Что с ними делать? Если приглядеться видно, что в левой части у нас повторяется 22х ,вот и ответ — 22х мы можем вынести за скобки:
22х(24 — 10) = 24
Посчитаем выражение в скобках:
24 — 10 = 16 — 10 = 6
6•22х = 24
Все уравнение делим на 6:
22х = 4
Представим 4=22:
22х = 22 основания одинаковые, отбрасываем их и приравниваем степени.
2х = 2 получилось простейшее уравнение. Делим его на 2 получаем
х = 1
Ответ: х = 1.
Решим уравнение:
9х – 12*3х +27= 0
Преобразуем:
9х = (32)х = 32х
Получаем уравнение:
32х — 12•3х +27 = 0
Основания у нас одинаковы равны трем.В данном примере видно, что у первой тройки степень в два раза (2x) больше, чем у второй (просто x). В таком случаем можно решить методом замены. Число с наименьшей степенью заменяем:
3х = t
Тогда 32х = (3х)2 = t2
Заменяем в уравнении все степени с иксами на t:
t2 — 12t+27 = 0
Получаем квадратное уравнение. Решаем через дискриминант, получаем:
D=144-108=36
t1 = 9
t2 = 3
Возвращаемся к переменной x.
Берем t1:
t1 = 9 = 3х
Стало быть,
3х = 9
3х = 32
х1 = 2
Один корень нашли. Ищем второй, из t2:
t2 = 3 = 3х
3х = 31
х2 = 1
Ответ: х1 = 2; х2 = 1.
На сайте Вы можете в разделе ПОМОГИТЕ РЕШИТЬ задавать интересующие вопросы мы Вам обязательно ответим.
Вступайте в группу ВКОНТАКТЕ
Как решать
показательные уравнения?
Решение уравнений – навык, который необходим каждому нацеленному на успешную сдачу ЕГЭ и ОГЭ школьнику. Это поможет решить задания №5, 13 и 15 из профильного уровня математики.
Одна из их разновидностей – степенные уравнения, которые иногда также называют показательными. Основная отличительная особенность – наличие переменной (х) не в основании степени, а в самом показателе. Как это выглядит:
Не бойтесь – это самый общий вид показательных уравнений. Реальные примеры выглядят как-то так:
Внимательно посмотрите на приведенные уравнения. В каждом из них присутствует, так называемая, показательная (степенная) функция. При решении необходимо помнить об основных свойствах степени, а также использовать особые правила, помогающие вычислить значение (х). Познакомиться с понятием степени и ее свойствами можно тут и тут.
И вам понадобится умение решать обыкновенные линейные и квадратные уравнения, те, что вы проходили в 7-8 классе. Вот такие:
И так, любое уравнение, в котором вы увидите показательную (степенную) функцию, называется показательным уравнением. Кроме самой показательной функции в уравнении могут быть любые другие математические конструкции – тригонометрические функции, логарифмы, корни, дроби и т.д. Если вы видите степень, значит перед вам показательное уравнение.
Ура! Теперь знаем, как выглядят показательные уравнения, но толку от этого не очень много. Было бы неплохо научиться их решать. Отличная новость – на наш взгляд показательные уравнения одни из самых простых типов уравнений, по сравнению с логарифмическими, тригонометрическими или иррациональными.
Простейшие показательные уравнения
Давайте начнем с самых простых типов уравнений и разберем сразу несколько примеров:
Что такое решить уравнение? Это значит, что нужно найти такое число, которое при подстановке в исходное уравнение вместо (х) даст верное равенство. В нашем примере нужно найти такое число, в которое нужно возвести двойку, чтобы получить восемь. Ну это просто:
Значит, если (х=3), то мы получим верное равенство, а значит мы решили уравнение.
Решим что-нибудь посложнее.
Такое уравнение выглядит сложнее. Попробуем преобразовать правую часть уравнения:
Мы применили свойство отрицательной степени по формуле:
Теперь наше уравнение будет выглядеть так:
Заметим, что слева и справа у нас стоят показательные функции, и там, и там основания одинаковые и равны (3), только вот степени разные – слева степень ((4х-1)), а справа ((-2)). Логично предположить, что если степени у такой конструкции будут равны, при условии, что основания одинаковые, то мы получим верное равенство. Так и поступим:
Такое мы решать умеем, ведь это обыкновенное линейное уравнение.
Поздравляю, мы нашли корень нашего показательного уравнения.
Попробуем поступить так, как в предыдущем примере – преобразуем левую и правую часть, чтобы слева и справа была показательная функция с одинаковым основанием. Как это сделать? Обращаем внимание, что (125=5*5*5=5^3), а (25=5*5=5^2), подставим:
Воспользуемся одним из свойств степеней ((a^n)^m=a^):
И опять мы получили две показательные функции, у которых одинаковые основания и для того, чтобы равенство выполнялось, необходимо приравнять из степени:
И еще один пример:
Те, кто хорошо знает свойства степеней, знают, что показательная функция не может быть отрицательной. Действительно, попробуйте возводить (2) в различную степень, вы никогда не сможете получить отрицательное число.
Внимание! Показательная функция не может быть отрицательной, поэтому, когда вы встречаете примеры на подобии примера 4, то знайте, что такого быть не может. Здесь корней нет, потому что показательная функция всегда положительна.
Теперь давайте разработаем общий метод решения показательных уравнений. И научимся решать более сложные примеры.
Общий метод решения показательных уравнений
Пусть у нас есть вот такой пример:
Где (a,b) какие-то положительные числа. ((a>0, ; b>0).
Согласно разобранным выше примерам, логично предположить, что для того, чтобы решить данное уравнение, нужно его преобразовать к виду, где слева и справа стоят показательные функции с одинаковым основанием. Так и поступим.
Слева у нас уже стоит (a^x), с этим ничего делать не будем, а вот справа у нас стоит загадочное число (b), которое нужно попытаться представить в виде (b=a^m). Тогда уравнение принимает вид:
Раз основания одинаковые, то мы можем просто приравнять степени:
Вот и весь алгоритм решения. Просто нужно преобразовать исходное уравнение таким образом, чтобы слева и справа стояли показательные функции с одинаковыми основаниями, тогда приравниваем степени и вуаля – сложное показательное уравнение решено. Осталось только разобраться, как так преобразовывать. Опять разберем на примерах:
Замечаем, что (16=2*2*2*2=2^4) это степень двойки:
Основания одинаковые, значит можно приравнять степени:
$$x=4.$$
Пример 6 $$5^<-x>=125 Rightarrow 5^<-x>=5*5*5 Rightarrow 5^<-x>=5^3 Rightarrow –x=3 Rightarrow x=-3.$$
Пример 7 $$9^<4x>=81 Rightarrow (3*3)^<4x>=3*3*3*3 Rightarrow(3^2)^<4x>=3^4 Rightarrow 3^<8x>=3^4 Rightarrow 8x=4 Rightarrow x=frac<1><2>.$$
Здесь мы заметили, что (9=3^2) и (81=3^4) являются степенями (3).
Все здорово, но проблема в том, что такая схема решения показательных уравнений работает не всегда. Что делать, если привести к одинаковому основанию не получается. Например:
(3) и (2) привести к одинаковому основанию затруднительно. Но тем не менее мы должны это сделать. Воспользуемся следующей схемой преобразований: пусть есть некоторое положительное число (b>0), тогда его можно представить в виде степени любого, нужного вам, положительного числа не равного единице (a>0, ; a neq 1):
Эта очень важная формула, рекомендуем ее выучить. Вернемся к нашему примеру и по формуле представим (2) в виде (3) в какой-то степени, где (a=3), а (b=2):
Подставим данное преобразование в наш пример:
Получили равенство двух показательных функций с одинаковым основанием, значит можем приравнять их степени:
Так в ответ и запишем. Никакой ошибки здесь нет, дело в том, что такие логарифмы можно посчитать только на калькуляторе, поэтому на ЕГЭ или в контрольной работе вы просто оставляете ответ в таком виде.
Кто забыл, что такое логарифм, можно посмотреть здесь.
Рассмотрим еще несколько аналогичных примеров.
Те, кто хорошо знает свойства логарифмов, могут поиграться с последней формулой и получить ответ в разном виде:
Все эти варианты ответа верные, их можно смело писать в ответ.
И так, мы с вами научились решать любые показательные уравнения вот такого вида: (a^x=b), где (a>0; ; b>0).
Но это еще далеко не все. Часто вы будете встречать показательные уравнения гораздо более сложного типа. В ЕГЭ по профильной математике это номер 15 из 2й части. Но бояться тут не нужно, все на первый взгляд сложные уравнения при помощи обычно не самых сложных преобразований сводятся к уравнениям типа (a^x=b), где (a>0; ; b>0). Рассмотрим типы сложных уравнений, которые могут попасться:
Решение показательных уравнений при помощи замены
Самое первое, что вы должны всегда делать, это пытаться привести все имеющиеся показательные функции к одинаковому основанию.
Здесь это сделать легко, замечаем, что (9=3^2), тогда (9^x=(3^2)^x=3^<2x>=(3^x)^2). Здесь мы воспользовались свойством степеней: ((a^n)^m=a^). Подставим:
Обратим внимание, что во всем уравнении все (х) «входят» в одинаковую функцию – (3^x). Сделаем замену (t=3^x, ; t>0), так как показательная функция всегда положительна.
Квадратное уравнение, которое решается через дискриминант:
Оба корня больше нуля, значит оба нам подходят. Сделаем обратную замену и уравнение сводится к решению двух простых показательных уравнений:
И второй корень:
И еще один пример на замену:
Воспользуемся нашим правилом, что все нужно приводить к одинаковому основанию – а стоп, тут и так у всех показательных функций основание (3). Давайте еще внимательно посмотрим на наш пример, очень похоже на то, что он тоже делается через замену. Но у нас тут нет одинаковых показательных функций, основания то одинаковые, а вот степени отличаются. Но если быть внимательным, то можно заметить, что в первой степени можно разбить свободный член (3=2+1) и вынести общий множитель (2):
Подставим в исходное уравнение:
Теперь показательные функции одинаковы и можно сделать замену:
Обратная замена, и наше уравнение сводится к простейшему:
И второе значение (t):
Тут у нас две показательные функции с основаниями (7) и (3), и как сделать из них одинаковые основания непонятно. Этот пример решается при помощи деления. Давайте поделим все наша уравнение на (3^x):
Здесь нам придется воспользоваться свойствами степеней:
Разберем каждое слагаемое:
Теперь подставим получившееся преобразования в исходное уравнение:
Теперь видно, что в нашем уравнении есть одинаковая функция, которую можно убрать в замену (t=(frac<7><3>)^x):
Сделаем обратную замену:
И последний пример на замену:
Первым делом нужно сделать так, чтобы все показательные функции были с одинаковым основанием и в идеале с одинаковой степенью. Для этого нам понадобятся формулы для степеней:
Разберем каждое слагаемое нашего уравнения:
Все десятичные дроби всегда разумно представить в виде обыкновенных дробей. И будьте внимательны – отрицательная степень не имеет никакого отношения к знаку показательной функции!
И последнее слагаемое со степенью:
Подставим все наши преобразования в исходное уравнение:
Теперь можно сделать замену (t=2^x) или можно обойтись без замены, просто приведя подобные слагаемые (вынести общий множитель (2^x)):
Особенно стоит подчеркнуть прием, который мы использовали при решении 13-го примера. Всегда старайтесь избавляться от десятичных дробей. Переводите их в обыкновенные дроби.
И другой тип степенных уравнений, где обычно не нужно делать замену, а необходимо отлично знать все свойства степеней, некоторые из них мы уже обсудили выше. Все про свойства степеней можно посмотреть тут
Вот такое уравнение, в котором у нас, во-первых, показательных функции перемножаются, а еще хуже то, что у них у всех разные основания. Катастрофа, а не пример. Но ничего, все не так страшно, как кажется. Внимательно посмотрите на основания: у нас есть в основании (2), (5) и (10). Очевидно, что (10=2*5). Воспользуемся этим и подставим в наше уравнение:
Воспользуемся формулой ((a*b)^n=a^n*b^n):
И перекинем все показательные функции с основанием (2) влево, а с основанием (5) вправо:
Сокращаем и воспользуемся формулами (a^n*a^m=a^) и (frac=a^):
Самая главная идея при решении показательных уравнений – это любыми доступными способами свести все имеющиеся степенные функции к одинаковому основанию. А еще лучше и к одинаковой степени. Вот почему необходимо знать все свойства степеней, без этого решить уравнения будет проблематично.
Как же понять, где какие преобразования использовать? Не бойтесь, это придет с опытом, чем больше примеров решите, тем увереннее будете себя чувствовать на контрольных в школе или на ЕГЭ по профильной математике. Сначала потренируйтесь на простых примерах и постепенно повышайте уровень сложности. Успехов в изучении математики!
Степенные или показательные уравнения.
Для начала вспомним основные формулы степеней и их свойства.
Произведение числа a само на себя происходит n раз, это выражение мы можем записать как a•a•…•a=a n
3. a n • a m = a n + m
5. a n b n = (ab) n
7. a n /a m = a n — m
Степенные или показательные уравнения – это уравнения в которых переменные находятся в степенях (или показателях), а основанием является число.
Примеры показательных уравнений:
В данном примере число 6 является основанием оно всегда стоит внизу, а переменная x степенью или показателем.
Приведем еще примеры показательных уравнений.
2 x *5=10
16 x — 4 x — 6=0
Теперь разберем как решаются показательные уравнения?
Возьмем простое уравнение:
Такой пример можно решить даже в уме. Видно, что x=3. Ведь чтобы левая и правая часть были равны нужно вместо x поставить число 3.
А теперь посмотрим как нужно это решение оформить:
Для того, чтобы решить такое уравнение, мы убрали одинаковые основания (то есть двойки) и записали то что осталось, это степени. Получили искомый ответ.
Теперь подведем итоги нашего решения.
Алгоритм решения показательного уравнения:
1. Нужно проверить одинаковые ли основания у уравнения справа и слева. Если основания не одинаковые ищем варианты для решения данного примера.
2. После того как основания станут одинаковыми, приравниваем степени и решаем полученное новое уравнение.
Теперь прорешаем несколько примеров:
Начнем с простого.
Основания в левой и правой части равны числу 2, значит мы можем основание отбросить и приравнять их степени.
x+2=4 Получилось простейшее уравнение.
x=4 — 2
x=2
Ответ: x=2
В следующем примере видно, что основания разные это 3 и 9.
Для начала переносим девятку в правую сторону, получаем:
Теперь нужно сделать одинаковые основания. Мы знаем что 9=3 2 . Воспользуемся формулой степеней (a n ) m = a nm .
Получим 9 х+8 =(3 2 ) х+8 =3 2х+16
3 3х = 3 2х+16 теперь видно что в левой и правой стороне основания одинаковые и равные тройке, значит мы их можем отбросить и приравнять степени.
3x=2x+16 получили простейшее уравнение
3x — 2x=16
x=16
Ответ: x=16.
Смотрим следующий пример:
2 2х+4 — 10•4 х = 2 4
В первую очередь смотрим на основания, основания разные два и четыре. А нам нужно, чтобы были — одинаковые. Преобразовываем четверку по формуле (a n ) m = a nm .
4 х = (2 2 ) х = 2 2х
И еще используем одну формулу a n • a m = a n + m :
2 2х+4 = 2 2х •2 4
Добавляем в уравнение:
2 2х •2 4 — 10•2 2х = 24
Мы привели пример к одинаковым основаниям. Но нам мешают другие числа 10 и 24. Что с ними делать? Если приглядеться видно, что в левой части у нас повторяется 2 2х ,вот и ответ — 2 2х мы можем вынести за скобки:
2 2х (2 4 — 10) = 24
Посчитаем выражение в скобках:
2 4 — 10 = 16 — 10 = 6
Все уравнение делим на 6:
Представим 4=2 2 :
2 2х = 2 2 основания одинаковые, отбрасываем их и приравниваем степени.
2х = 2 получилось простейшее уравнение. Делим его на 2 получаем
х = 1
Ответ: х = 1.
9 х – 12*3 х +27= 0
Преобразуем:
9 х = (3 2 ) х = 3 2х
Получаем уравнение:
3 2х — 12•3 х +27 = 0
Основания у нас одинаковы равны трем.В данном примере видно, что у первой тройки степень в два раза (2x) больше, чем у второй (просто x). В таком случаем можно решить методом замены. Число с наименьшей степенью заменяем:
Тогда 3 2х = (3 х ) 2 = t 2
Заменяем в уравнении все степени с иксами на t:
t 2 — 12t+27 = 0
Получаем квадратное уравнение. Решаем через дискриминант, получаем:
D=144-108=36
t1 = 9
t2 = 3
Возвращаемся к переменной x.
3 х = 9
3 х = 3 2
х1 = 2
Один корень нашли. Ищем второй, из t2:
t2 = 3 = 3 х
3 х = 3 1
х2 = 1
Ответ: х1 = 2; х2 = 1.
На сайте Вы можете в разделе ПОМОГИТЕ РЕШИТЬ задавать интересующие вопросы мы Вам обязательно ответим.
Показательные уравнения

О чем эта статья:
6 класс, 7 класс
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение показательного уравнения
Показательными называются уравнения с показательной функцией f(x) = a х . Другими словами, неизвестная переменная в них может содержаться как в основании степени, так и в ее показателе. Простейшее уравнение такого вида: a х = b, где a > 0, a ≠ 1.
Конечно, далеко не все задачи выглядят так просто, некоторые из них включают тригонометрические, логарифмические и другие конструкции. Но для решения даже простых показательных уравнений нужно вспомнить из курса алгебры за 6–7 класс следующие темы:
Если что-то успело забыться, советуем повторить эти темы перед тем, как читать дальнейший материал.
С точки зрения геометрии показательной функцией называют такую: y = a x , где a > 0 и a ≠ 1. У нее есть одно важное для решения показательных уравнений свойство — это монотонность. При a > 1 такая функция непрерывно возрастает, а при a
Иногда в результате решения будет получаться несколько вариантов ответа, и в таком случае мы должны выбрать тот корень, при котором показательная функция больше нуля.
Свойства степеней
Мы недаром просили повторить свойства степенной функции — на них будет основано решение большей части примеров. Держите небольшую шпаргалку по формулам, которые помогут упрощать сложные показательные уравнения.
[spoiler title=”источники:”]
http://tutomath.ru/uroki/stepennye-pokazatelnye-uravneniya.html
http://skysmart.ru/articles/mathematic/pokazatelnye-uravneniya
[/spoiler]
На этапе подготовки к заключительному тестированию учащимся старших классов необходимо подтянуть знания по теме «Показательные уравнения». Опыт прошлых лет свидетельствует о том, что подобные задания вызывают у школьников определенные затруднения. Поэтому старшеклассникам, независимо от уровня их подготовки, необходимо тщательно усвоить теорию, запомнить формулы и понять принцип решения таких уравнений. Научившись справляться с данным видом задач, выпускники смогут рассчитывать на высокие баллы при сдаче ЕГЭ по математике.
Готовьтесь к экзаменационному тестированию вместе со «Школково»!
При повторении пройденных материалов многие учащиеся сталкиваются с проблемой поиска нужных для решения уравнений формул. Школьный учебник не всегда находится под рукой, а отбор необходимой информации по теме в Интернете занимает долгое время.
Образовательный портал «Школково» предлагает ученикам воспользоваться нашей базой знаний. Мы реализуем совершенно новый метод подготовки к итоговому тестированию. Занимаясь на нашем сайте, вы сможете выявить пробелы в знаниях и уделить внимание именно тем заданиям, которые вызывают наибольшие затруднения.
Преподаватели «Школково» собрали, систематизировали и изложили весь необходимый для успешной сдачи ЕГЭ материал в максимально простой и доступной форме.
Основные определения и формулы представлены в разделе «Теоретическая справка».
Для лучшего усвоения материала рекомендуем попрактиковаться в выполнении заданий. Внимательно просмотрите представленные на данной странице примеры показательных уравнений с решением, чтобы понять алгоритм вычисления. После этого приступайте к выполнению задач в разделе «Каталоги». Вы можете начать с самых легких заданий или сразу перейти к решению сложных показательных уравнений с несколькими неизвестными или иррациональным уравнениям со знаком корня. База упражнений на нашем сайте постоянно дополняется и обновляется.
Те примеры с показателями, которые вызвали у вас затруднения, можно добавить в «Избранное». Так вы можете быстро найти их и обсудить решение с преподавателем.
Чтобы успешно сдать ЕГЭ, занимайтесь на портале «Школково» каждый день!
Решение простейших показательных уравнений
На чтение 3 мин. Просмотров 11.7k.
Решение показательных уравнений — это материал 10-11 класса. Какие же уравнения называются показательными?
Уравнения, содержащие переменную в показателе степени, называются показательными уравнениями.
Простейшие показательные уравнения
Простейшие показательные уравнения — это уравнения вида: ax=ay. Отсюда следует равенство: х=у. В самом деле, степени с одинаковыми основаниями могут быть равными только в том случае, если равны показатели этих степеней.
Ниже вы найдете примеры решения показательных уравнений.
Уравнение 1
Решить уравнение:
5x=125. Представим число 125 в виде степени числа 5:
5x=53; Степени равны, их основания равны, значит, и показатели степеней будут равны:
x=3.
Уравнение 2
4x=32. Представим левую и правую части в виде степеней с основанием 2:
(22)x=25; используем формулу возведения степени в степень: (ax)y=axy
22x=25;
2x=5 |:2
x=2,5.
Уравнение 3
32x-1=81. Число 81 представим в виде степени числа 3:
32x-1=34; приравняем показатели степеней с одинаковыми основаниями:
2x-1=4; решаем простейшее линейное уравнение:
2x=4+1;
2x=5 |:2;
x=2,5.
Уравнение 4
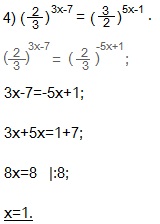
К правой части применяем формулу: (a/b)-x=(b/a)x. Получим равенство степеней с одинаковыми основаниями.
Приравниваем показатели степеней и находим х из полученного линейного уравнения.
Уравнение 5
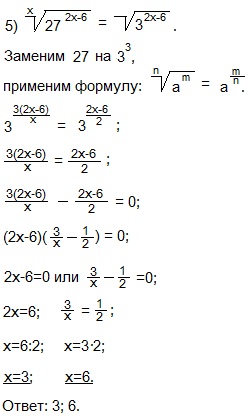
Приравняем показатели степеней с одинаковыми основаниями.
Переносим степень из правой части уравнения в левую.
Вынесли общий множитель (2х-6) за скобки. Произведение двух или нескольких множителей равно нулю, если один из множителей равен нулю, а другие при этом значении не теряют смысла. Содержимое каждой из скобок приравниваем к нулю и решаем простейшие уравнения.
Уравнение 6
7∙5x-5x+1=2∙53.
Показатели степеней складываются, если степени перемножаются ( ax∙ay=ax+y ), поэтому:
7∙5x-5x∙51=2∙53;
5x(7-5)=2∙53; вынесли общий множитель за скобки.
5x∙2=2∙53 |:2
5x=53; отсюда следует:
x=3.
Уравнение 7
3x+2+4∙3x+1=21. Применим формулу: ax+y=ax∙ay (При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели складывают):
3x∙32+4∙3x∙31=21; вынесем общий множитель за скобки:
3x(9+12)=21;
3x∙21=21 |:21
3x=1; число 1 можно представлять в виде нулевой степени с любым основанием.
3x=30;
x=0.
Уравнение 8
51+2x+52x+3=650. Решаем аналогично.
51∙52x+52x∙53=650;
52x(5+125)=650;
52x∙130=650 |:130
52x=5; приравняем показатели равных степеней с основаниями 5.
2x=1 |:2
x=0,5.
Методы решения показательных уравнений достаточно известны и мы подробно объяснили, как их применять при решении показательных уравнений на примерах.
( 9 оценок, среднее 4.56 из 5 )
