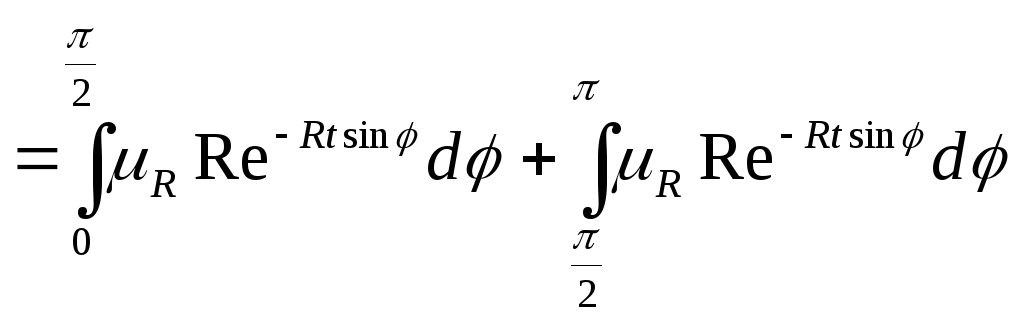Изолированные особые точки функций и полюсы
Классификация особых точек
Важное место в изучении и применении теории функций комплексного переменного занимает исследование их поведения в особых точках, где нарушается аналитичность функции. В частности, это точки, где функция не определена.
Исследование функции в особой точке определяется поведением ее в окрестности этой точки, т.е. исследованием
. Очевидно, имеют место три возможности:
а) не существует;
б) существует и равен конечному числу;
в) равен бесконечности.
Исследование пределов функции в комплексной области — задача более сложная, чем в действительной области, так как, согласно определению, переменная стремится к
по любому направлению. Вычисление пределов в точках аналитичности не представляет интереса, так как в этих случаях
.
Будем рассматривать , где
— особая точка.
Пример 4.1. Исследовать существование в случаях a)
; б)
.
Решение
a) В действительной области не существует, так как не равны односторонние пределы
, но существует предел второй функции:
.
б) В комплексной области, очевидно, не существует, так как он не существует в частном случае
.
Но для второй функции полученного выше результата не достаточно, так как рассмотрены только два направления на плоскости — по действительной положительной и действительной отрицательной полуосям.
Рассмотрим еще какое-нибудь направление, например по мнимой оси, т.е.
Сравнивая этот результат с полученным выше , заключаем, что в комплексной области
не существует.
Аналогично можно показать, что не существует , хотя
для случаев
и
(по действительной и мнимой осям).
Эти простые примеры показывают, что исследование функции в особой точке с помощью может представлять большие сложности. Но, с другой стороны, в примере 3.36 при вычислении пределов функции в особых точках было использовано разложение функции в ряд.
Представление функции в виде ряда как один из способов ее аналитического задания, может быть использовано для исследования функции, в частности, в особых точках.
Будем рассматривать изолированные особые точки функций, т.е. особые точки, для каждой из которых существует такая ее окрестность, в которой нет других особых точек функции.
В частности, конечная особая точка является изолированной особой точкой функции
, если существует число
, такое, что в круге
эта точка- единственная особая точка
, а в проколотой окрестности, т.е. в
функция
аналитическая.
Бесконечно удаленная особая точка является изолированной особой точкой функции
, если существует число
, такое, что в области
эта точка — единственная особая точка
, а в кольце
функция
— аналитическая.
Согласно теореме Лорана, функция, аналитическая в кольце, в частности, в проколотой окрестности особой точки, может быть представлена рядом Лорана. Это позволяет свести исследование функции в изолированной особой точке к исследованию соответствующего ряда. Особенности рядов как представления аналитических функций можно заметить, проанализировав некоторые примеры предыдущих лекций.
Пример 4.2. Исследовать поведение и вид ряда Лорана в окрестности особой точки функций:
а) ; б)
; в)
.
Решение
Эти простые примеры показывают, что поведение функции в особой точке связано с видом главной части ряда Лорана: трем отмеченным выше случаям нахождения предела функции в точке соответствуют три различных случая вида главной части ряда Лорана в окрестности точки. В примере 4.2 исследовалась конечная особая точка. Такой же результат можно получить, рассматривая точку
, например, для функций
и
.
Типы особых точек функции
В зависимости от трех случаев поведения функции в особой точке (исследования ) особые точки функций делят на три типа — производится классификация особых точек. В качестве определения типа особых точек можно выбрать либо поведение функции в особой точке, либо вид ряда Лорана. Выберем первый подход.
Изолированная особая точка функции
называется:
– устранимой особой точкой, если существует и конечен (4.1);
– полюсом, если (4.2);
– существенно особой точкой, если не существует (4.3).
Замечание 4.1. Если в случае устранимой особой точки положить
, то
будет аналитической в
и точку
можно считать правильной, т.е. не особой. В этом случае говорят, что в точке
устранена особенность.
Пример 4.3. Определить тип особой точки для функций
.
Решение
На основании результатов решения примеров 4.1, 4.2 заключаем, что является устранимой особой точкой функции
; полюсом для
при любом
; существенно особой точкой для функций
и
.
Пример 4.4. Определить тип особой точки для функций
и
.
Решение
Рассмотрим . Для удобства введем обозначение
. Для функции
получим
(см. пример 4.2), поэтому
является полюсом функции
. Для функции
точка
является существенно особой, так как
не существует (см. пример 4.1).
Пример 4.5. Найти все конечные особые точки функций: а) б)
и определить их тип.
Решение
Особыми точками дробей являются особые точки числителя, особые точки знаменателя и нули знаменателя.
а) Так как числитель и знаменатель функции — функции аналитические, то ее особыми точками являются только нули знаменателя, т.е. корни уравнения
. Это четыре точки
, или в алгебраической форме:
. Заметим, что точки расположены в вершинах квадрата, вписанного в окружность радиуса
с центром в начале координат, и справедливы равенства
.
Очевидно, все точки изолированные и являются полюсами, так как для любой точки
.
б) Особыми точками функции являются нули знаменателя, т.е. точки, для которых
или
, а также
— особая точка знаменателя. Точки
являются полюсами, так как
. Точка
— неизолированная особая точка функции, так как в любой ее окрестности
(
— любое число,
), кроме этой точки, расположено бесконечное множество особых точек вида
. Точку
в таком случае называют предельной точкой полюсов
, так как
.
Теоремы Сохоцкого и Пикара
Для исследования поведения функции в существенно особой точке имеют место следующие две теоремы.
Теорема 4.1 (Сохоцкого). Если — существенно особая точка функции
, то для любого
существует последовательность
, сходящаяся к точке
, такая, что
.
Теорема 4.2 (Пикара). В любой окрестности существенно особой точки функция принимает любое значение (причем бесконечное число раз) кроме, быть может, одного.
Пример 4.6. Исследовать поведение следующих функций в существенно особых точках, проиллюстрировать теоремы Сохоцкого и Пикара:
a) ; б)
.
Решение
В примерах 4.3 и 4.4 показано, что точки и
являются существенно особыми точками соответствующих функций. Исследуем пределы функций.
а) Для иллюстрации теоремы Сохоцкого выбираем и
. Используя результат примера 4.1, имеем
, если
, и
, если
, то есть
для последовательности
, такой, что
и
, и
для последовательности
, такой, что
и
.
Аналогично исследуем функцию . Для числа
выбираем
, где
и тогда
, а для
выбираем
, где
и тогда
.
Справедливость теоремы Пикара для этих функций следует из рассмотрения уравнений , которые, как известно, имеют бесконечное множество решений для любого
.
Например, для функции имеем
. Отсюда получаем
или
.
В частности, функция в любой окрестности точки
принимает значение
бесконечное множество раз: в точках
(рис. 4.1).
б) Точка является существенно особой точкой функции
(пример 4.4). Обозначив
, можно повторить рассуждения предыдущего пункта для функции
и точки
.
Ряд Лорана в окрестности особой точки
В предыдущем разделе на примере простых функций (см. пример 4.2) было высказано предположение, что вид ряда Лорана в окрестности особой точки зависит от типа особой точки и потому задача исследования функции в особой точке может быть сведена к исследованию соответствующего ряда Лорана . Подтверждением этого предположения в общем случае является доказательство соответствующих утверждений.
Утверждение 4.1
1. Для того чтобы особая точка функции была ее устранимой особой точкой, необходимо и достаточно, чтобы в разложении функции в ряд Лорана в окрестности этой точки отсутствовала главная часть. Это означает, что если — устранимая особая точка, то ряд Лорана функции
имеет вид
(4.4)
для — конечной точки
, и (для
)
(4.5)
2. Для того чтобы особая точка функции была полюсом, необходимо и достаточно, чтобы главная часть ряда Лорана функции в окрестности этой точки содержала конечное число членов. Ряд Лорана функции в случае
полюса имеет вид
(4.6)
если , и (если
)
(4.7)
3. Для того чтобы особая точка функции была ее существенно особой точкой, необходимо и достаточно, чтобы главная часть ряда Лорана функции в окрестности этой точки содержала бесконечное число членов. Ряд Лорана функции в случае
— существенно особой точки имеет вид
(4.8)
если , и (если
)
(4.9)
Замечания 4.2
1. Номер старшего члена главной части ряда Лорана функции в ее разложении в окрестности полюса называется порядком полюса.
Так, точка является полюсом порядка
функции
, если в разложении (4.6)
при
. Точка
является полюсом порядка
функции
, если в разложении (4.7)
при
.
2. Главная часть ряда Лорана в случае полюса порядка и записывается следующим образом:
а) в случае в виде
, или
, или, подробнее:
(4.10)
б) в случае в виде
, или
(см. (4.7)), или, подробнее:
(4.11)
3. Главная часть ряда Лорана в случае существенно особой точки записывается так:
а) в случае в виде
, или
(см.(4.8)), или, подробнее:
(4.12)
б) в случае в виде
или
(см.(4.9)), или, подробнее:
(4.13)
Пример 4.7. Определить тип особых точек функций: а) ; б)
.
Решение
Особыми точками функций являются . Чтобы определить тип особой точки, используем разложения функций в окрестности каждой точки, полученные в примерах 3.31 , 3.33 , 3.34.
a) . В главной части разложения — один член ряда:
, здесь
, все
для
. Следовательно, в точке
— полюс первого порядка, т.е. простой полюс функции
.
Аналогично из разложения получим такой же результат: точка
— простой полюс функции
.
Разложение . Функции в окрестности
не содержит главной части — разложение имеет вид (4.5). Следовательно, точка
— устранимая особая точка функции
.
б) Из разложения следует, что
— простой полюс функции
.
Из разложения , где
и все
для
, получаем, что
— полюс второго порядка функции
.
Разложение в окрестности
и не содержит положительных степеней, в чем можно убедиться, проанализировав разложения элементарных дробей (см. пример 3.34). Поэтому
— устранимая особая точка функции
.
Пример 4.8. Определить тип конечных особых точек для функций:
а) ; б)
.
Решение
а) Используем разложения функций по степеням
Убеждаемся, что для всех указанных функций точка является существенно особой точкой, так как в разложениях главная часть содержит бесконечное число членов, т.е. имеется бесконечное число членов с отрицательными степенями (см. п.1 утверждения 4.1).
б) Запишем разложения функций по степеням
Для первой функции при в разложении отсутствует главная часть — совокупность членов с отрицательными степенями. Следовательно, согласно п.1 утверждения 4.1, точка
для
является устранимой особой точкой.
При главная часть разложения содержит конечное число членов, поэтому точка
для
является полюсом (см. п.2 утверждения 4.1). Кроме того, так как при
в разложении старшая отрицательная степень равна
, то, согласно п. 1 замечаний 4.2, заключаем, что
для
при
является полюсом порядка
. Рассуждая аналогично, получаем, что
является полюсом первого порядка — простым полюсом для функции
.
Сравнивая разложения функций по степеням в окрестности
(формулы (4.4),(4.6),(4.8) при
) и
(формулы (4.5), (4.7), (4.9)), можно сделать следующее заключение.
Утверждение 4.2
1. Чтобы была устранимой особой точкой функции
, необходимо и достаточно, чтобы точка
была устранимой (или не особой) для
.
2. Чтобы была полюсом порядка
функции
, необходимо и достаточно, чтобы точка
была полюсом порядка
функции
.
3. Чтобы была существенно особой точкой функции
, необходимо и достаточно, чтобы точка
была существенно особой точкой функции
.
Замечание 4.3. Как и в случае конечной особой точки , в которой функция не определена, но
(см. утверждение 3.5) , так и для
в случае
, устранимую особую точку
можно считать нулем функции
. Порядок нуля можно определить как порядок нуля функции
в точке
.
Пример 4.9. Исследовать точку для функций: a)
; б)
; в)
.
Решение
Правила определения порядка полюса
Используя формулу (4.6) разложения функции в ряд в окрестности полюса, можно получить практически удобные правила определения порядка полюса, не требующие записи разложений в ряд в каждом конкретном случае.
Пусть — полюс порядка
функции
. Разложение (4.6), где главная часть имеет вид (4.10) , преобразуем следующим образом:
или
,
где — функция, аналитическая в точке
, как сумма степенного ряда, записанного в скобках, и
.
Далее рассмотрим функцию , то есть
или
, где
— аналитическая в точке
и
. Из этого, согласно утверждению 3.5, следует, что
является нулем порядка
функции
. Можно доказать и обратное утверждение.
А именно, если функция представлена в виде , где
— функция, аналитическая в точке
, и
, то
— полюс порядка
функции
, а также, если
— нуль порядка
функции
, то для функции
эта точка является полюсом порядка
.
Кроме того, рассмотрим частное , где точка
является нулем порядка
для функции
и нулем порядка
для функции
, то есть
. При
получаем
, из чего, с учетом приведенных выше рассуждений, находим, что
— полюс порядка
. Заметим, что при
точка
— устранимая особая точка; случай
рассмотрен ранее. Результаты приведенных рассуждений запишем в виде утверждения.
Утверждение 4.3
1. Для того чтобы точка была полюсом порядка
функции
, необходимо и достаточно, чтобы ее можно было записать в виде
(4.14)
2. Для того чтобы точка была полюсом порядка
функции
, необходимо и достаточно, чтобы она была нулем порядка
функции
(связь нулей с полюсами).
3. Если точка является нулем порядка
функции
и нулем порядка
функции
, то она — полюс порядка
для
.
Пример 4.10. Определить порядок полюсов функций из примеров: а) 4.7 ; б) 4.8.
Решение
Замечания 4.4
1. Так как конечными особыми точками рациональной дроби являются только нули знаменателя, то это либо полюсы, либо устранимые особые точки функции.
2. Такое же заключение можно сделать и для функции вида , где
— аналитическая функция. При этом, используя определение устранимой особой точки (4.1) и правила определения порядка нуля и полюса (утверждения 3.5 и 4.3), можно сделать следующие выводы относительно особой точки
— нуля порядка
знаменателя:
а) — полюс порядка
функции
, если
;
б) — полюс порядка
, если
— нуль порядка
функции
и
;
в) — устранимая особая точка функции
, если
— нуль порядка
функции
;
г) — нуль порядка
функции
, если
— нуль порядка
функции
и
; при этом полагаем
.
▼ Примеры нахождения особых точек и определения их типа
Пример 4.11. Найти конечные особые точки следующих функций и определить их тип:
а) ; б)
.
Решение
Конечными особыми точками этих рациональных дробей являются нули знаменателя. Чтобы для каждой их этих точек определить, является ли она полюсом или устранимой особой точкой, нужно, согласно определению, найти предел функции в этой точке. В случае полюса, т.е. когда , далее следует определить его порядок. Для этого используется утверждение 4.3.
Можно поступить иначе — согласно замечанию 4.4. Для этого нужно найти и нули числителя.
а) Особые точки функции . Для точки
можно применить формулу (4.14) и из
, где
и
, получить, что эта точка — полюс второго порядка. Для точки
формула (4.14) не применима, так как из
имеем
. Поступаем далее согласно замечанию 4.4. Раскладываем на множители числитель и записываем функцию
Получаем, что — полюс второго порядка для
.
б) Особые точки функции — корни уравнения , то есть
или
. Все эти точки:
— простые нули знаменателя, и так как числитель в этих точках не обращается в нуль, то они — простые полюсы функции
.
Пример 4.12. Найти конечные особые точки следующих функций и определить их тип:
а) ; б)
.
Решение
Пример 4.13. Найти конечные особые точки функций и определить их тип:
а) ; б)
.
Решение
Конечными особыми точками этих функций вида , где
— аналитическая функция, являются только нули знаменателя.
а) Особые точки функции: . Точки
и
— простые полюсы, так как числитель в этих точках не обращается в нуль и функцию можно представить в виде
— точка
или
. В точках
числитель обращается в нуль. Очевидно, это простые нули числителя, и поэтому его можно записать в виде
— точка
или
. Тогда для функции
получаем
Так как для
или
, то эти точки — устранимые особые точки функции
.
б) Особые точки функции: . Точки
и
— простые полюсы.
Для точек и
проводим рассуждения, как в предыдущем пункте, и находим, что они — устранимые особые точки
.
Пример 4.14. Определить тип особой точки для следующих функций: а)
; б)
.
Решение. В точке и числитель, и знаменатель каждой из функций обращается в нуль. Определим порядок нуля в каждом случае и используем п.3 утверждения 4.4.
а) Из разложений по степеням функций
находим, что — нуль второго порядка для числителя
и нуль пятого порядка для знаменателя
. Следовательно,
— полюс третьего порядка для функции
.
б) Используя правила определения порядка нуля, в частности, как и в предыдущем пункте, раскладывая функции в ряды по степеням , находим, что
является
для числителя и
для знаменателя. Следовательно,
-полюс пятого порядка для
.
Пример 4.15. Найти конечные особые точки следующих функций и определить их тип:
а) ; б)
.
Решение
Пример 4.16. Определить тип особой точки для следующих функций:
а) ; б)
; в)
; г)
.
Решение
Точка является нулем и знаменателя, и числителя для каждой из функций. Определим порядок нуля в каждом случае, используя правило определения порядка нуля (утверждение 3.5), в частности, раскладывая соответствующую функцию по степеням
.
а) Из разложений
находим, что является
для числителя и
— для знаменателя, поэтому она — устранимая особая точка. Так как
то, полагая , можно считать, что
— нуль для
, причем
(см. замечания 4.4).
б) Из разложений
и
находим, что является
для числителя и
— для знаменателя. Поэтому
— полюс третьего порядка для
.
в) Как и в предыдущих пунктах, находим, что является
для числителя и
— для знаменателя. Поэтому
— простой полюс для
.
г) Точка является простым нулем числителя, нулем второго порядка для знаменателя. Следовательно, это простой полюс для
.
Определение порядка полюса в бесконечно удаленной точке
Рассмотрим бесконечно удаленную точку. Тип особой точки можно определить, вычисляя или раскладывая функцию в ряд Лорана (см. примеры 4.4, 4.7). Можно свести задачу к исследованию конечной точки
(см. утверждение 4.2 и пример 4.9). В двух последних случаях определяется и порядок полюса.
Практически удобное правило определения порядка полюса можно получить, используя п. 2 утверждения 4.2 и правила определения порядка полюса в конечной точке (утверждение 4.3). Действительно, пусть
для функции
, тогда
для
и можно записать
(см. (4.14)). Поэтому, обозначив
, для
получим
(4.15)
Представление функции в виде (4.15) является необходимым и достаточным условием полюса порядка функции
в точке
.
Замечание 4.5. Используя формулу (4.15), нетрудно убедиться, что если для
и
для
, то
— полюс порядка
для функции
.
Пример 4.17. Определить тип особой точки для функций: а)
; б)
.
Решение
Так как в обоих случаях, то
для данных функций — полюс. Определим порядок полюса.
а) Точка является полюсом третьего порядка, в чем можно убедиться любым из следующих способов.
Первый способ. Разложение функции по степеням имеет вид
, все
, и по определению (см. формулы (4.7), (4.11)) заключаем, что
.
Второй способ. Обозначим , получим функцию
, для которой
. Поэтому, согласно п. 2 утверждения 4.2, точка
для
.
Третий способ. Запишем функцию в виде и, так как функция
— удовлетворяет условиям формулы (4.15), получим, что
для
.
б) Разложение функции в ряд по степеням представляет некоторые трудности. Используем другие способы.
Первый способ. Обозначим , получим
, или
.
Поэтому является
для
и, следовательно,
для
.
Второй способ. Представим функцию в виде или
, где
, и, согласно формуле (4.15),
для
.
Третий способ. Используем замечание 4.5. Можно определить порядок полюса для дроби
, зная соответствующие порядки полюсов числителя и знаменателя. Здесь, очевидно,
для числителя и
— для знаменателя (см. формулы (4.7), (4.11)). Поэтому
для
.
Пример 4.18. Определить порядок полюса в точке для следующих функций: а)
; б)
.
Решение
Определение типа особых точек для суммы, разности, произведения и частного функций
Пусть — особая точка функций
и
и тип особой точки для каждой из функций известен. Требуется определить тип особой точки для функций
. Рассмотрим следующие случаи.
Первый случай. Пусть точка го является полюсом порядка для функции
и полюсом порядка
для функции
.
а) При исследовании суммы воспользуемся формулой (4.14) (п.1 утверждения 4.3) и запишем слагаемые в виде
, где
.
При для суммы
получаем
или
, где
. Если
, то
для функции
. Однако для функций
может выполняться условие
и’ следовательно,
. В этом случае формула (4.14) не применима и точка
не будет полюсом порядка
для
. В соответствии с п.3 утверждения 4.3 порядок полюса будет меньше, чем
, и равен
в случае
, где
— порядок нуля функции
. Если
, то
— устранимая особая точка для
.
Таким образом, при сложении функций порядок полюса в точке может оказаться равным или меньше, чем наибольший из порядков слагаемых.
б) Для исследования произведения воспользуемся формулой связи нулей с полюсами (п.2 утверждения 4.3) и рассмотрим вспомогательные функции
. Для первой из этих функций
, для второй соответственно
. а поэтому для
она будет
. Согласно п.2 утверждения 4.3,
является
для
.
в) Аналогичные рассуждения для частного приводят к результату: при
точка
является
для
.
Второй случай. Пусть точка является полюсом, устранимой особой точкой или не особой для
и существенно особой для
. Так как
не существует, то по свойству пределов он не существует для каждой из рассматриваемых комбинаций
. Следовательно, для каждой из них
— существенно особая точка. Заметим, что для функции
эта точка является либо существенно особой точкой, либо не является изолированной особой точкой. Последнее проиллюстрировано в примере 4.5 для функции
.
Третий случай. Пусть — полюс порядка
для
и устранимая особая точка для
. Разложения этих функций в ряд в окрестности
имеют вид (4.6) и (4.4) соответственно.
а) При сложении рядов в общей области сходимости получится ряд, главную часть которого будет составлять главная часть ряда функции . Следовательно, для
точка
— полюс порядка
.
б) Аналогичные рассуждения приводят к заключению, что такой же результат получится и для , если
.
Если и
для функции
, то из равенства
заключаем, что
.
в) Для частного при условии
из равенства
заключаем, что
для
.
Если и
для
, то, используя условие кратного нуля, из равенства
заключаем, что является
для
, где
— порядок полюса функции
— порядок нуля функции
в точке
.
Подводя итог, запишем следующее утверждение.
Утверждение 4.4
1. Пусть точка является
для функции
и
для функции
. Тогда:
а) для она будет
, а при
— устранимой особой точкой;
б) для она является
;
в) для она будет
.
2. Пусть — существенно особая точка для функции
и устранимая особая точка или полюс для функции
. Тогда
— существенно особая точка для
.
3. Пусть точка является
для функции
и устранимой особой точкой для функции
. Тогда:
а) для она будет
;
б) для она является
, если
, и
, если
и
— порядок нуля
в точке
;
в) для она будет
, если
, и
, если
и
— порядок нуля
в точке
;
4. Если точка для
, то она существенно особая точка для сложной функции
. В этом можно убедиться, рассматривая ряды для
и
в окрестности
.
Пример 4.19. Определить тип особой точки для функции
, если
, где
, а функция
определяется следующим образом:
а) ; б)
; в)
.
Решение
Пример 4.20. Найти особые точки функции . Определить их тип.
Решение
Особыми точками функции являются особые точки первого слагаемого , особая точка второго слагаемого
входит в это множество. Точки
являются простыми нулями знаменателя и поэтому простыми полюсами первой функции; для второго слагаемого эти точки не являются особыми. Поэтому точки
-простые полюсы
(см. п. 3 “а” утверждения 4.4).
Точка — простой полюс и для первого, и для второго слагаемого. Для
— это или простой полюс, или устранимая особая точка (см. п.1 “а” утверждения 4.4). Преобразуем разность в дробь:
. Точка
является нулем второго порядка и для числителя, и для знаменателя. Следовательно, это — устранимая особая точка, в чем можно убедиться, используя определение, т.е. находя
. Действительно,
Точка для данной функции является неизолированной особой точкой, так как в любой ее окрестности
содержится бесконечное множество особых точек вида
. Эта точка- предельная точка полюсов. Заметим, что для знаменателя первого слагаемого функции она — существенно особая точка.
Пример 4.21. Найти особые точки следующих функций, определить их тип:
а) ; б)
.
Решение
Обозначим — первое слагаемое,
— второе слагаемое функции
, т.е. имеем
.
а) Для точка
является существенно особой точкой, так как это существенно особая точка для
множителя этой функции. Поэтому она — существенно особая точка для
(п. 2 утверждения 4.4).
Точки — полюсы второго порядка функции
, так как ее можно записать в виде
, где
, а для знаменателя эти точки — нули второго порядка . Так как для
эти точки не особые, то
— полюсы второго порядка для
(п. 3 утверждения 4.4).
С помощью аналогичных рассуждений получаем, что — простой полюс для
.
Особыми точками являются корни уравнения
, то есть
. Все они — простые нули знаменателя- функции
, а потому — простые полюсы для
. Так как эти точки не являются особыми для
, то для
— это простые полюсы.
Точка — неизолированная особая точка
.
б) Точка — полюс дроби
является существенно особой точкой для
(п.4 утверждения 4.4), поэтому она — существенно особая точка для
и, следовательно, для
.
Точка — простой полюс для
, так как можно записать
. Поскольку
не является особой точкой для
, то она — простой полюс для
.
Точка — устранимая особая точка для
, так как она — простой нуль и для числителя, и для знаменателя дроби
. Так как
не является особой точкой для
, то она — устранимая особая точка для
.
Особыми точками являются простые нули знаменателя — корни уравнения
, или
, то есть
. Все точки
, или
являются простыми полюсами для и, следовательно, простыми полюсами для
.
Точка — неизолированная особая точка
.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Напомним определение. Точка называется особой точкой аналитической функции
, если в ней аналитичность ее нарушается.
Определение 2. Точка называется изолированной особой точкой функции
, если существует окрестность
этой точки с исключенной точкой
, в которой
аналитична, кроме самой точки
.
Существует три типа изолированных особых точек. Приведем их определения.
Определение 3. Точка называется устранимой особой точкой
, если разложение ее в ряд Лорана в окрестности этой точки не содержит главной части.
Определение 4. Точка называется полюсом кратности N функции, если в разложении ее в ряд Лорана в окрестности точки
главная часть содержит конечное число членов, причем младшим отличным от нуля коэффициентом является
.
Определение 5. Точка называется существенно особой точкой функции
, если главная часть ее разложения в ряд Лорана в окрестности этой точки содержит бесконечное число членов.
Приведем критерии типа изолированных особых точек.
1) для того, чтобы точка была устранимой особой точкой функции
, необходимо и достаточно, чтобы
.
2) для того, чтобы точка была полюсом кратности N функции
, необходимо и достаточно, чтобы
,
.
3) для того, чтобы точка была существенно особой точкой функции
, необходимо и достаточно, чтобы
.
Полезна следующая теорема. Для того, чтобы точка была полюсом порядка N функции
, нужно, чтобы она была нулем N – го порядка функции
(связь между нулями и полюсами).
Пример 1. Для функции особой точкой является
. Имеем
–
есть устранимая особая точка.
Пример 2. Для функции
является особой точкой. Так как
– это полюс. Так как для функции
т.
является нулем пятого порядка, то
– полюс пятого порядка функции
.
Пример 3. Для функции
является особой точкой. Разложение
в ряд Лорана:

Пример 4. Найти все особые точки функции 
Решение. Особыми точками являются точка и точки, в которых знаменатель обращается в нуль. Имеем
, откуда



функция
имеет простые полюса. Точка
не является изолированной особой точкой, так как она является пределом полюсов:
: это означает, что любая окрестность точки
содержит бесконечное число особых точек
.
Задачи для самостоятельного решения
У нижеследующих функций найти нули и определить их порядки:
132. . 133.
. 134.
. 135.
. 136.
.
137. .
Найти порядок нуля для следующих функций:
138. 
. 140.

141. .
Определить характер особой точки для следующих функций:
142. . 143.


Найти особые точки и определить их характер у следующих функций:
145. . 146.
. 147.
. 148.
. 149.
.
150. 
. 152.

.
| < Предыдущая | Следующая > |
|---|
Особые точки функций комплексного переменного
Опр.
Особой точкой функции
называется точка в которой
не определена или не дифференцируема.
Опр.
Особая точка называется изолированной,
если
такая ее окрестность, в которой нет
других особых точек.
Утв. Если
–
изолированная особая точка
,
то в окрестности
,
раскладывается в ряд Лорана.
Классификация
особых точек
Опр1.
Особая точка называется устранимой,
если в ряде Лорана в окрестности этой
точки отсутствует главная часть.
Опр2.
Изолированная особая точка называется
полюсом, если главная часть ряда Лорана
в окрестности этой точки имеет конечное
число членов:
Число N
называется кратностью (порядком полюса).
Утв.
Если
– полюс
,
то
.
Док-во:
Опр3.
Изолированная особая точка называется
существенно особой, если главная часть
разложения в ряд Лорана в окрестности
этой точки содержит бесконечное число
членов.
Лекция 8
Связь между нулем
и полюсом
Утв1.
имеет в точке
нуль порядка n
имеет в точке
полюс порядка n.
Док-во: {}
Утв2.
имеет существенно особую точку в точке
имеет в
неизолированную особую точку ИЛИ
существенно особую точку.
Пример.
;
;
;
;
Таким образом,
получаем не изолированную особую точку.
Утв3.
Если
,
,
,
то
имеет при:
1)mn
устранимую особую точку,
2)m>n
полюс порядка n-m.
Док-во: {для
2}

;
Теорема Сохоцкого.
Если
-существенно
особая точка функции
,
то
.
Док-во:
1)
а)
-сходится
при
сходится при
б) Предположим
противное:
ограничена в
окрестности точки
.
в)
при
(т.е.
ограничена в окрестности
).
г)В круге
ограничена, как непрерывная функция в
замкнутой области.
д) Из б), в), г)
следует
ограничена на всей комплексной плоскости.
е)
ограничена на С,
аналитическая, по теореме Ляувилля
противоречие.
2)
а)
имеет
не изолированную особую точку.
б)
-изолированная
особая точка
имеет изолированную
особую точку в
имеет существенно особую точку
по Утв2
имеет существенно особую точку в
по
1)
Теорема доказана.
Особые точки в
бесконечности
Утв.
Если
-изолированная
особая точка
,
то
Док-во:
Пусть
.
Раскладываем
в окрестности нуля:
.
Вычеты
Опр.
-изолированная
особая точка.
называется вычетом, где
– коэффициент при -1 степени в разложении
ряда Лорана:
Основная теорема
о вычетах.
Если G
– односвязная область, Г – замкнутый
контур, Г ограничевает G,
G
содержит конечное число изолированных
особых точек
функции
,
то
.
Док-во:
Г
G
.
.
.
Окружит каждую
особую точку
окружностью
так, чтобы внутри
не было других особых точек, и чтобы
и
не пересекались(ij).
.
Вычисление
вычетов
1.
Утв.
Если
– устранимая особая точка
,
то
(Т.к.
главная часть ряда Лорана не содержит
ни одного члена
)
2.
а) Утв.
Если
-простой
полюс
(полюс
кратности 1), то
.
Док-во:
Пример.
,
имеет простой полюс.
б) Утв.
Если
,
,
,
,
то
.
Док-во:
-полюс
I
порядка
3.
Утв.
Если
-полюс
порядка n
,
то
.
Док-во:
Переходим к
и делим на
:
Пример1.
;
Пример2.
Лекция 9
Опр.
– изолированная особая точка
,
,
где Г- замкнутый контур.
Утв.
Если
,
то
.
Док-во:
1)
.
2) С: {}
,
при
3)
4)
Теорема.
Если
-изолированная
особая точка, кроме
имеется конечное число особых точек,
то
Док-во:
Возьмем замкнутый
контур С, охватывающий все особые точки,
кроме
;
;
;
Логарифмический
вычет.
Опр.
Логарифмическим вычетом называется:
,
если С – замкнутый контур,
– аналитическая внутри С и на нем за
исключением конечного числа особых
точек, все особые точки лежат внутри С,
все особые точки – полюсы.
Утв1.
Если
,
–
нуль кратности
фунции
,
то
.
Док-во:
Для функции
–
полюс I
порядка.
.
Утв2.
Если
-полюс
кратности n
функции
,
то
.
Док-во:
.
Принцип аргумента.
Теорема.
Логарифмический вычет функции
относительно контура С равен приращению
аргумента
при обходе контура С, деленному на
,
равно разности между числом нулей М и
числом полюсов N
функции
в облости D,
ограниченной контуром С:
Д
Z
W
z w
C
1)
2) Внутри С
будет иметь конечное число нулей, т.к.
она аналитическая в замкнутой области.
В силу Утв1 и Утв2 :
3)
Теорема Руше.
ЕСЛИ G
– односвязная область, С – замкнутый
контур, ограничивающий G,
и
аналитические в G
и на С,
на
С,
на
С,
–
сумма кратностей всех лежащих в G
нулей функции
,
–
сумма кратностей всех лежащих в G
нулей функции
+
,
ТО
.
Док-во:
1)
2
3)
w
Вектор из начала
координат в точку, при такой конфигурации
образа С, ни одного оборота не совершит.
.
4)
Пример.
Найти количество нулей, которые имеет
функция
в круге
.
,
при
:
имеет нуль кратности
5
w
имеет 5 нулей.
Утв.
Если
,
то
имеет n
корней.
Док-во:
С:
имеет
нуль кратности n,
т.о.
имеет n
нулей.
Теорема.
Если
,
аналитическая в G
,
то
– аналитическая.
Док-во:
1)
-
аналогично
доказываем
-
Из пунктов 1) и 2)
следует, что для F
выполнены условия Коши-Римана,
следовательно F
аналитическая.
Лекция 10
Вычисление
несобственных интегралов с помощью
вычетов
Теорема.
Если
при x=z,
-изолированная
особая точка f(z),
имеет в
нуль не ниже II
порядка,
не имеет особых точек на действительной
оси,
имеет конечное число особых точек, то
,
где
распространяется
на особые точки, лежащие выше действительной
оси.
Док-во:
Возьмем круг такого
радиуса, чтобы на нем и вне его не было
особых точек, кроме бесконечности.
Y
R
-R R x
.
Пример.
Найти интеграл:.
,
;
Операционное
исчисление
Опр.
Функция
называется оригиналом, если:
1)
определена при
,
и
являются
кусочно-непрерывными на любом конечном
интервале,
2) при
3).
Утв.
Если
-многочлен
степени n,
то
.
Док-во:
,
по
правилу Лопиталя
;
.
Опр.
называется изображением, соответствующим
оригиналу f(t),
если F(p)
– интеграл Лапласа:
;
.
Теорема.
Если f(t)
оригинал, то
–
изображение
,
1)
сходится
в полуплоскости
,
2)
является
в полуплоскости
аналитической функцией от p.
Док-во:
1)
,
таким образом F(p)
сходится.
2) Аналитичность
следует из теоремы, доказанной в
предыдущей лекции.
След. Если F(p)
– изображение некоторого оригинала,
то
Зам. Если
,
то F(p)
сходится равномерно.
Свойства
преобразования Лапласа:
-
Линейность
-
Однородность.
.
Док-во для 2:
Теорема о
дифференцировании оригинала.
Если f(t)
– оригинал,
-оригинал,
F(p)-изображение
f(t),
,
то
.
Док-во:
.
Следствие.
Если
-оригиналы,
то
.
Док-во:
далее по индукции.
Теорема о
дифференцировании изображения.
Если
,
то
.
Теорема об
интегрировании оригинала.
Если
,
то
.
Док-во:
1) Докажем, что
-оригинал.
а)
кусочная гладкость – по свойству
интеграла.
б)
,
t>0
–очевидно.
в)
2)
.
.
Лекция 11
Теорема об
интегрировании изображения
Если f(t)
– оригинал,
–
оригинал, то
.
Док-во:
.
,
.
Теорема о
запаздывание
Если
-оригинал,
,
то
.
Док-во:
.
Теорема смещения
Если
,
то
.
Таблица соответствий
1.
.
2.
3.
4.
5.
6.
.
7.
.
8.
9.
10.
11.
12.
13.
14.
15.
Опр.
Сверткой функций f
и g
называется
Утв.
Если
,
g(t)
– оригиналы, то f*g(t)
– оригинал.
Док-во:
Пункты 1) и 2) в
определении оригинала очевидно выполнены.
Докажем выполнение пункта 3).
,
,
где
Теорема о свертках.
Если f(t),
g(t)
– оригиналы,
,
,
то
.
Док-во:
.
Лемма Жордана
Лемма1.
Если f(z)
– аналитическая в верхней полуплоскости,
за исключением, быть может, конечного
числа точек,
–
полуокружность в верхней полуплоскости
.
Док-во:


Лекция12
Лемма2.
Если f(z)
– аналитическая в левой полуплоскости,
,
то
.
Док-во:
.
Лемма3.
Если f(z)
аналитическая,
,
то
.
y
R
x
Док-во:
-
Докажем, что
.
.
2)Если
аналогично.
3)
по Лемме 2.
4) Из пунктов
1), 2), 3) следует
.
Лемма4.
Если f(z)
аналитическая
,
то
Докозательство
следует из Леммы3.
Теорема об
интеграле Фурье.
Если f(t)
кусочно непрерывна и кусочно дифференцируема
на R,
то
(сходится
абсолютно).
Теорема обращения
преобразования Лапласа.
Если f(t)
– оригинал,
,
то
.
Док-во:
;
;
;
Теорема разложения.
,
для
выполнены условия леммы Жордана, то
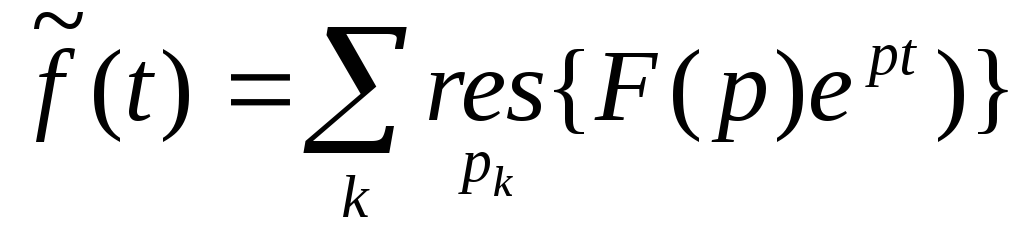
Док-во:

Пример.
;
;
.
Лекция13
Соседние файлы в папке Лекции и семинары
- #
- #

Особые точки функций комплексной переменной.
Правильная точка.
Пусть функция 







Если 


Теорема. Для того чтобы 



Доказательство. Необходимость. Если 




Достаточность. Пусть функция 



Так как функция 















Рекомендуемые материалы
Следствие. Разложение функции в ряд Лорана в окрестности правильной точки представляет собой ряд Тейлора и не содержит членов с отрицательными степенями.
Следствие.Теорема Лиувилля. Любая целая, ограниченная во всей расширенной плоскости функция, есть константа.
Доказательство. Целая функция содержит только положительные степени в ее разложении в ряд Лорана (




Полюсы
Пусть не существует конечного предела 




Связь полюсов и нулей.
Точка 


Теорема. Для того чтобы точка 


Доказательство. Необходимость. Пусть 





Тогда функция 








Достаточность. Пусть 





Тогда 





Примеры.
1. 




2. 



Будем считать 
Точка 


Точка 



Пример. 



Теорема. Для того чтобы точка 


Доказательство. Необходимость. Пусть точка 













Достаточность доказать самостоятельно (доказательство аналогично).
Теорема. Для того чтобы точка 




Доказательство. Необходимость. Если точка 








Достаточность. Пусть 





Существенно особая точка.
Если вообще не существует 


Теорема. Разложение функции в ряд Лорана в окрестности существенно особой точки конечной плоскости 

Доказательство. Если разложение в ряд Лорана в окрестности особой точки конечной плоскости 


Теорема Сохоцкого. Каково бы ни было число А, конечное или бесконечное, существует такая последовательность 


Доказательство. 1) Пусть A – конечное число. Предположим, что не существует последовательности, о которой идет речь в теореме. Тогда значения функции отделены от A, т.е. 

Из предыдущей оценки следует, что в 






a) Пусть 







b) Пусть 

Тогда 


2) Пусть 







Классификация особой точки 

Если разложение функции 


1. Не содержит отрицательных степеней, то 

2. Содержит конечное число отрицательных степеней, то 

3. Содержит бесконечное количество членов с отрицательными степенями, то 

Это следует из доказанных выше теорем.
Классификация бесконечно удаленной особой точки 

Разложение в ряд Лорана в окрестности точки 


Если разложение в ряд Лорана в окрестности точки 

1 Не содержит положительных степеней, то 

2 Содержит конечное число положительных степеней, то 

3 Содержит бесконечное количество членов с положительными степенями, то 

Примеры.
Люди также интересуются этой лекцией: 33. Феномен «Монд» .
1 




2 






3 





4. 


В разложении старшая положительная степень – первая, поэтому 



Классификация особых точек. Связь между нулем и полюсом функции
Как уже знаем, особой точкой функции 
Особая точка 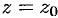


Если 

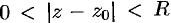

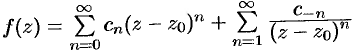
При этом возможны следующие случаи:
1) Ряд Лорана не содержит главной части, т. е. в ряде нет членов с отрицательными показателями. В этом случае точка 

2) Разложение Лорана содержит в своей главной части конечное число членов, т. е. в ряде есть конечное число членов с отрицательными показателями. В этом случае точка 

3) Разложение Лорана содержит в своей главной части бесконечное множество членов, т. е. в ряде есть бесконечно много членов с отрицательными показателями. В этом случае точка 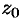

Укажем особенности поведения аналитической функции 
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
- Решение задач по высшей математике
Другие темы по высшей математике возможно вам они будут полезны: