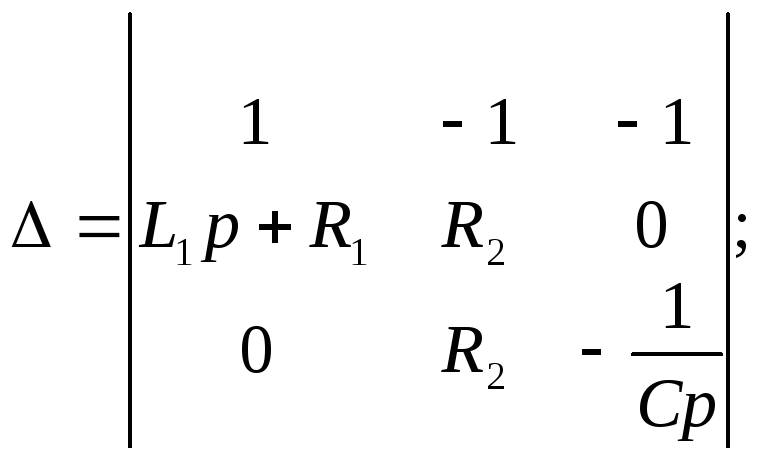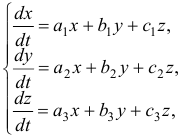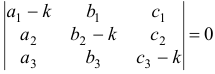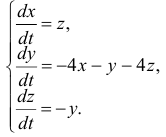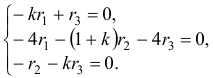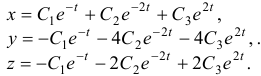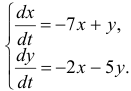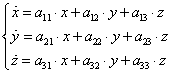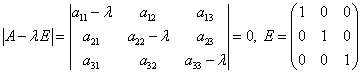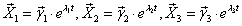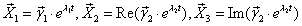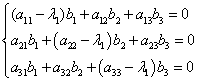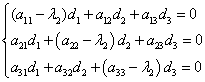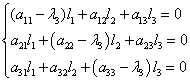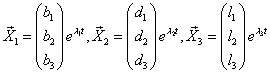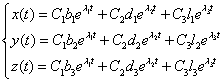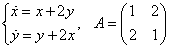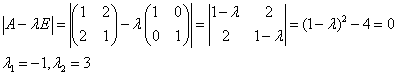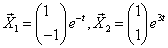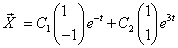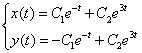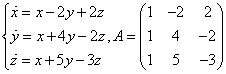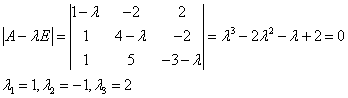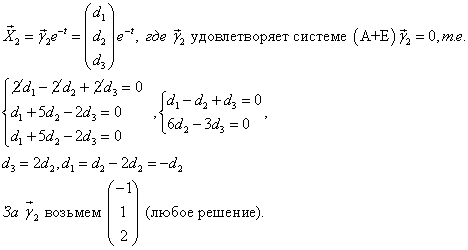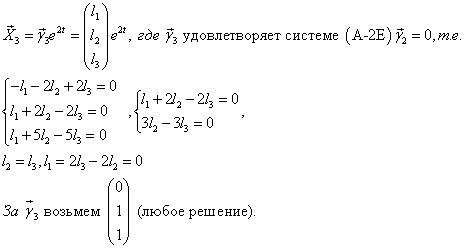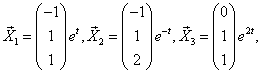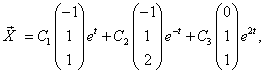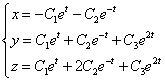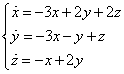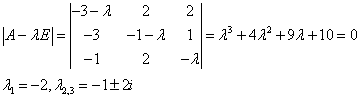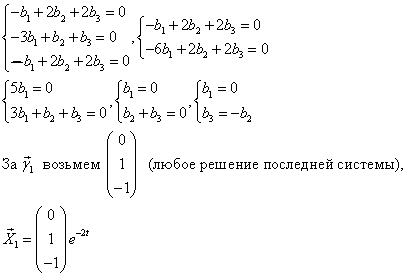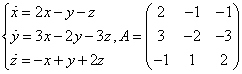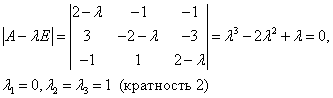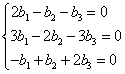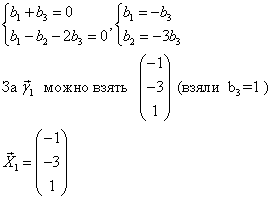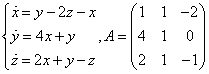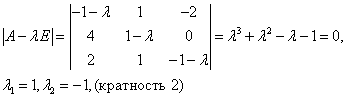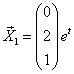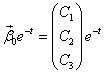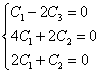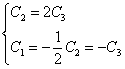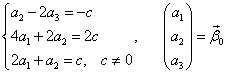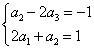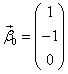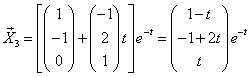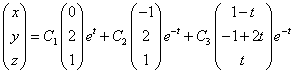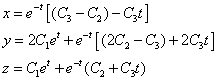Как найти характеристическое уравнение для системы
Характеристическое уравнение составляется для цепи после коммутации. Оно может быть получено следующими способами:
- непосредственно на основе дифференциального уравнения вида (2) (см. лекцию №24), т.е. путем исключения из системы уравнений, описывающих электромагнитное состояние цепи на основании первого и второго законов Кирхгофа, всех неизвестных величин, кроме одной, относительно которой и записывается уравнение (2);
- путем использования выражения для входного сопротивления цепи на синусоидальном токе;
- на основе выражения главного определителя.
Согласно первому способу в предыдущей лекции было получено дифференциальное уравнение относительно напряжения 
Следует отметить, что, поскольку линейная цепь охвачена единым переходным процессом, корни характеристического уравнения являются общими для всех свободных составляющих напряжений и токов ветвей схемы, параметры которых входят в характеристическое уравнение. Поэтому по первому способу составления характеристического уравнения в качестве переменной, относительно которой оно записывается, может быть выбрана любая.
Применение второго и третьего способов составления характеристического уравнения рассмотрим на примере цепи рис. 1.
Составление характеристического уравнения по методу входного сопротивления заключается в следующем:
записывается входное сопротивление цепи на переменном токе;
j w заменяется на оператор р;
полученное выражение приравнивается к нулю.
совпадает с характеристическим.
Следует подчеркнуть, что входное сопротивление может быть записано относительно места разрыва любой ветви схемы. При этом активный двухполюсник заменяется пассивным по аналогии с методом эквивалентного генератора. Данный способ составления характеристического уравнения предполагает отсутствие в схеме магнитосвязанных ветвей; при наличии таковых необходимо осуществить их предварительное развязывание.
Для цепи на рис. 1 относительно зажимов источника
.
Заменив j w на р и приравняв полученное выражение к нулю, запишем
При составлении характеристического уравнения на основе выражения главного определителя число алгебраических уравнений, на базе которых он записывается, равно числу неизвестных свободных составляющих токов. Алгебраизация исходной системы интегро-дифференциальных уравнений, составленных, например, на основании законов Кирхгофа или по методу контурных токов, осуществляется заменой символов дифференцирования и интегрирования соответственно на умножение и деление на оператор р. Характеристическое уравнение получается путем приравнивания записанного определителя к нулю. Поскольку выражение для главного определителя не зависит от правых частей системы неоднородных уравнений, его составление можно производить на основе системы уравнений, записанных для полных токов.
Для цепи на рис. 1 алгебраизованная система уравнений на основе метода контурных токов имеет вид
Отсюда выражение для главного определителя этой системы
.
Приравняв D к нулю, получим результат, аналогичный (1).
Общая методика расчета переходных процессов классическим методом
В общем случае методика расчета переходных процессов классическим методом включает следующие этапы:
- Запись выражения для искомой переменной в виде
- Нахождение принужденной составляющей общего решения на основании расчета установившегося режима послекоммутационной цепи.
- Составление характеристического уравнения и определение его корней (для цепей, описываемых дифференциальными уравнениями первого порядка, вместо корней можно находить постоянную времени t – см. лекцию №26). Запись выражения свободной составляющей в форме, определяемой типом найденных корней.
- Подстановка полученных выражений принужденной и свободной составляющих в соотношение (2).
- Определение начальных условий и на их основе – постоянных интегрирования.
Примеры расчета переходных процессов классическим методом
1. Переходные процессы в R-L цепи при ее подключении к источнику напряжения
Такие процессы имеют место, например, при подключении к источнику питания электромагнитов, трансформаторов, электрических двигателей и т.п.
Рассмотрим два случая:
а)
б) .
Согласно рассмотренной методике для тока в цепи на рис. 2 можно записать
Тогда для первого случая принужденная составляющая тока
,
откуда и постоянная времени .
Подставляя (4) и (5) в соотношение (3), запишем
.
В соответствии с первым законом коммутации . Тогда
,
откуда .
Таким образом, ток в цепи в переходном процессе описывается уравнением
,
а напряжение на катушке индуктивности – выражением
.
Качественный вид кривых и , соответствующих полученным решениям, представлен на рис. 3.
При втором типе источника принужденная составляющая рассчитывается с использованием символического метода:
,
где .
.
Выражение свободной составляющей не зависит от типа источника напряжения. Следовательно,
.
Поскольку , то
.
Таким образом, окончательно получаем
Анализ полученного выражения (6) показывает:
- При начальной фазе напряжения постоянная интегрирования А=0. Таким образом, в этом случае коммутация не повлечет за собой переходного процесса, и в цепи сразу возникнет установившийся режим.
- При свободная составляющая максимальна по модулю. В этом случае ток переходного процесса достигает своей наибольшей величины.
Если значительна по величине, то за полпериода свободная составляющая существенно не уменьшается. В этом случае максимальная величина тока переходного процесса может существенно превышать амплитуду тока установившегося режима. Как видно из рис. 4, где
, максимум тока имеет место примерно через . В пределе при .
Таким образом, для линейной цепи максимальное значение тока переходного режима не может превышать удвоенной амплитуды принужденного тока: .
Аналогично для линейной цепи с конденсатором: если в момент коммутации принужденное напряжение равно своему амплитудному значению и постоянная времени цепи достаточно велика, то примерно через половину периода напряжение на конденсаторе достигает своего максимального значения , которое не может превышать удвоенной амплитуды принужденного напряжения: .
2. Переходные процессы при отключении катушки индуктивности от источника питания
При размыкании ключа в цепи на рис. 5 принужденная составляющая тока через катушку индуктивности .
,
откуда и .
В соответствии с первым законом коммутации
.
Таким образом, выражение для тока в переходном режиме
и напряжение на катушке индуктивности
Анализ (7) показывает, что при размыкании цепей, содержащих индуктивные элементы, могут возникать большие перенапряжения, которые без принятия специальных мер могут вывести аппаратуру из строя. Действительно, при модуль напряжения на катушке индуктивности в момент коммутации будет во много раз превышать напряжение источника: . При отсутствии гасящего резистора R указанное напряжение прикладывается к размыкающимся контактам ключа, в результате чего между ними возникает дуга.
3. Заряд и разряд конденсатора
При переводе ключа в положение 1 (см. рис. 6) начинается процесс заряда конденсатора:
.
Принужденная составляющая напряжения на конденсаторе .
Из характеристического уравнения
определяется корень . Отсюда постоянная времени .
.
При t=0 напряжение на конденсаторе равно (в общем случае к моменту коммутации конденсатор может быть заряженным, т.е. ). Тогда и
.
Соответственно для зарядного тока можно записать
.
В зависимости от величины : 1 – ; 2 – ; 3 – ; 4 – – возможны четыре вида кривых переходного процесса, которые иллюстрирует рис. 7.
При разряде конденсатора на резистор (ключ на рис.6 переводится в положение 2) . Постоянная времени .
Тогда, принимая, что к моменту коммутации конденсатор был заряжен до напряжения (в частном случае ), для напряжения на нем в переходном режиме можно записать
.
Соответственно разрядный ток
Как видно из (8), во избежание значительных бросков разрядного тока величина должна быть достаточно большой.
В заключение отметим, что процессы заряда и разряда конденсатора используются в генераторах пилообразного напряжения, широко применяемых в автоматике. Для этого ключ в схеме на рис. 6 заменяется на электронный.
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
- Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
- Теоретические основы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.1. К.М.Поливанов. Линейные электрические цепи с сосредоточенными постоянными. –М.: Энергия- 1972. –240с.
- Составить характеристическое уравнение для цепи на рис. 1, используя выражение входного сопротивления относительно места разрыва ветви с резистором .
- Может ли в одной части линейной цепи протекать колебательный переходный процесс, а в другой – апериодический?
- Для чего в схеме на рис. 5 служит цепочка, состоящая из диода и резистора R?
- Почему можно разрывать ветвь с конденсатором и нельзя – ветвь с индуктивным элементом?
- Почему корни характеристического уравнения не зависят от того, относительно какой переменной было записано дифференциальное уравнение?
- Для цепи на рис. 8 составить характеристическое уравнение и определить, при каких значениях переходный процесс в ней будет носить апериодический характер, если .
Ответ: .
Определить в цепи на рис. 9, если , , , .
Ответ: .
Решение систем дифференциальных уравнений с помощью характеристического уравнения
Пусть дана однородная система
где — постоянные. Будем искать частные решения системы в виде , где и — неопределенные коэффициенты, которые следует найти. Уравнение
называется характеристическим уравнением системы. Отыскав корни этого уравнения, и поочередно подставляя их в исходную систему, определим коэффициенты .
Пример №1
Найти общее решение системы
Решение:
Система в данном случае имеет вид:
Характеристическое уравнение имеет корни . Для Решением этой системы будут, например, числа (здесь выбрано произвольно). Следовательно, . Для Решая эту систему, получим тогда .
Наконец, для Здесь можно положить и будем иметь .
Общее решение данной системы дифференциальных уравнений таково:
Пример №2
Решение:
Чаще системы дифференциальных уравнений записывают в виде: Составим характеристическое уравнение и найдем его корни . Так как эти корни комплексные, система уравнений будет иметь комплексные коэффициенты и даст комплексные значения для чисел и . В этом случае, учитывая возможность произвольного выбора и , целесообразно сразу положить и, записав функцию или, что то же самое, , найти функцию , используя первое уравнение системы: . Для этого найдем или . Подставляя и в первое уравнение системы, получим . Общим решением системы будет и .
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Возможно вам будут полезны эти страницы:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Портал ТОЭ
6.2 Классический метод расчёта переходных процессов
Анализ переходного процесса в линейной цепи с сосредоточенными параметрами R , L , C (рис. 6.2 ) сводится к решению линейных неоднородных уравнений, выражающих законы Кирхгофа.
где i ( t ) – переходный ток.
Дифференцированием приводим это уравнение к неоднородному дифференциальному уравнению 2-го порядка:
Порядок дифференциального уравнения определяется числом накопителей энергии в цепи.
Решение дифференциального уравнения:
где i пр ( t ) – частное решение неоднородного уравнения, принуждённая составляющая, ток в установившемся режиме, когда переходный процесс закончен (при t = ∞ );
i св ( t ) – общее решение однородного уравнения, свободная составляющая, ток во время переходного процесса, возникающий вследствие изменения электрических и магнитных полей.
Таким образом здесь используется метод наложения. Физически существует только i ( t ) , а разложение его на i пр и i св является математическим приёмом, облегчающим расчёт переходного процесса.
Расчёт принуждённой составляющей сводится к расчёту по известным методам установившегося значения искомой величины в схеме после коммутации.
Для расчёта свободной составляющей следует найти корни характеристического уравнения p k и n постоянных интегрирования A k .
Если характеристическое уравнение
имеет n различных корней p k ( k = 1 , 2 , … ,n ) , то
Корню p k кратности m k ≥ 1 соответствует слагаемое свободной составляющей вида
Чтобы определить постоянные интегрирования A k , необходимо знать значения искомой величины и всех её производных до ( n − 1) порядка включительно в момент времени t = 0+ . Для их определения используются законы коммутации.
Составление характеристического уравнения
-
Составляем уравнение электрического состояния цепи для свободного режима (т.е. при устранении вынужденной (принуждающей) силы). Это соответствует схеме с исключёнными источниками – источники ЭДС закорачиваются, ветви с источниками тока размыкаются.
Например для рис. 6.3 :
где Z вх ( p ) – входное сопротивление схемы относительно двух зажимов, получающихся в результате размыкания любой ветви схемы;
Y вх ( p ) – входная проводимость схемы относительно произвольной пары узлов схемы.
Корни характеристического уравнения – собственные частоты цепи, т.к. они определяют характер свободных процессов.
Степень характеристического уравнения может быть определена по электрической схеме без составления уравнения: она равна числу основных независимых начальных условий в послекоммутационной схеме после максимального её упрощения и не зависит от числа ЭДС в схеме.
Упрощение заключается в том, что последовательно и параллельно соединённые реактивные элементы должны быть заменены эквивалентными.
Рассмотрим схему на рис. 6.4 . Три реактивных элемента в упрощённой схеме определяют три независимых начальных условия, т.е. порядок характеристического уравнения равен трём.
Свободный процесс происходит в цепи, освобождённой от источников энергии, поэтому свободные токи не могут протекать сколь угодно долго в цепи, где есть активные элементы. Свободные токи должны затухать, в связи с этим действительные части корней p k характеристического уравнения должны быть отрицательными.
-
Так, при наличии одного корня p = − a
[spoiler title=”источники:”]
http://lfirmal.com/reshenie-sistem-differentsialnyih-uravnenij-s-pomoschyu-harakteristicheskogo-uravneniya/
http://toeportal.ru/lections/toe/6.2
[/spoiler]
Число алгебраических
уравнений равно числу неизвестных
свободных токов. Положим, что р известно
(в действительности оно пока не найдено
и будет определено в дальнейшем) и решим
систему (8.8) относительно
.Получим:
где — определитель системы. В рассмотренном
примере
Определитель 1получим из выражения для определителя
Л путем замены первого столбца правой
частью уравнений (8.8):
определитель 2получим из выражения дляпутем замены второго столбца правой
частью системы (8.8), и т. д.
Так как в правой
части системы (8.8) находятся нули, то в
каждом определителе 1,2и3один из столбцов будет состоять из
нулей.
Известно, что если
в определителе один из столбцов состоит
из нулей, то этот определитель равен
нулю. Следовательно, 1=0;2=0;3=0.
Из физических
соображений ясно, что каждый из свободных
токов не может быть равен нулю, ибо в
этом случае не будут выполнены законы
Коммутации. Однако из предыдущего
следует, что
Свободные токи
могут быть не равны нулю в том случае,
если определитель системы
= 0.
(8.9)
При этом каждый
из токов представляет собой неопределенность
раскрыв которую
можно получить действительное
значение каждого свободного тока.
Раскрытием
неопределенностей заниматься не будем,
а воспользуемся тем существенным
для дальнейшего выводом, что определитель
алгебраизированной
системы уравнений должен равняться
нулю.
Уравнение = 0 называют характеристическим уравнением.
Единственным неизвестным в нем
является р.
Пример 75. Используя
уравнение (8.8), составить характеристическое
уравнение для схемы рис. 8.4, а и найти
его корни.
Решение.
или
Если дробь равна
нулю, то равен нулю ее числитель.
Следовательно,
(8.10)
Корни квадратного
уравнения
В начале § 8.11
говорилось о том, что решение для
свободного тока берется в виде Аеpt.
Если характеристическое уравнение
имеет не один корень, а несколько,
напримерn, то для каждого свободного
тока нужно взять
Пример 76. Найти
корни характеристического уравнения
схемы рис. 8.4, а при трех значениях С:1) С=1 мкФ, 2) С =10 мкФ, 3) С ==100 мкФ, R2=100
Ом; L1=l Гн.
Решение. При С = 1
мкФ
При
При
§ 8.13. Составление
характеристического уравнения путем
использования выражения для входного
сопротивления цепи на переменном
токе. Характеристическое уравнение для
определения р часто составляют более
простым способом, чем обсуждавшийся в
предыдущем параграфе. С этой целью
составляют выражение входного
сопротивления двухполюсника на
переменном токе [обозначим его Z(j)],
заменяют в немjна р[получаютZ(p)] и приравниваютZ(p)нулю.
Уравнение Z (р) =
0совпадает с характеристическим.
Такой способ составления характеристического
уравнения предполагает, что в схеме
отсутствуют магнитносвязанные ветви.
Если же магнитная связь между ветвями
имеется, то предварительно следует
осуществить развязывание
магнитносвязанных ветвей.
В § 8.41 показано,
что число р можно представить в виде
j, где
– комплексная угловая частота;Z
(р)есть сопротивление цепи на
комплексной частоте. Сопротивление
цепи для синусоидального тока частотой
а, т. е.Z (j),есть частный случайZ(p),когда
=.
Входное сопротивление
на комплексной частоте по отношению к
некоторой k-й ветви
,
где(р) — определитель
системы уравнений, составленных по
методу контурных токов;k(р)—алгебраическое
дополнение.
Корни уравнения
Zk(р) = 0совпадают с
корнями уравнения(р)=0.
Следует иметь в
виду, что во избежание потери корня
(корней) нельзя сокращать (р)
иk(р) на общий
множитель, если он имеется.
И последнее
замечание: при составлении Z (р)следует учитывать внутреннее сопротивление
источника питания.
Характеристическое
уравнение можно составлять также, приняв
за основу при. его составлении не метод
контурных токов, а метод узловых
потенциалов. В этом случае следует
приравнять нулю определитель матрицы
узловых проводи-мостей, полагая при
составлении матрицы один из узлов схемы
заземленным.
Пример 77. Для схемы
рис. 8.4, а входное сопротивление
относительно зажимов аb при переменном
токе
Заменим в нем j’o
на р и приравняем его нулю:
Отсюда
или
(8.10`)
Уравнение (8.10′)
совпадает с уравнением (8.10), составленным
иным путем. Уравнение (8.10′) получено
путем использования выражения для
входного сопротивления первой ветви
схемы рис. 8.4, а относительно зажимов
аb. Точно такое же уравнение можно
получить, если записать выражение для
входного сопротивления любой другой
ветви.
Соседние файлы в папке Новая папка
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Пусть дана однородная система
где 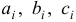
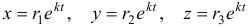
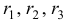
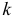
называется характеристическим уравнением системы. Отыскав корни этого уравнения, и поочередно подставляя их в исходную систему, определим коэффициенты 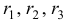
Пример №1
Найти общее решение системы
Решение:
Система в данном случае имеет вид:
Характеристическое уравнение 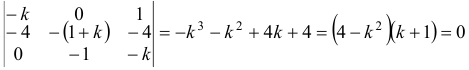
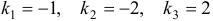
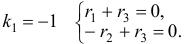
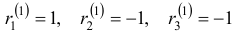
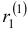
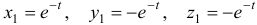
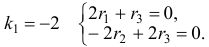
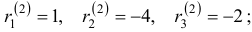
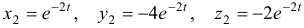
Наконец, для 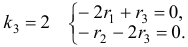
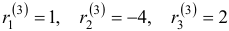
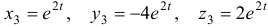
Общее решение данной системы дифференциальных уравнений таково:
Пример №2
Решить систему
Решение:
Чаще системы дифференциальных уравнений записывают в виде: 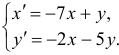
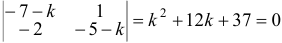
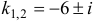
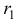
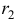
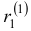
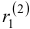
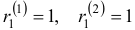
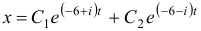
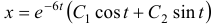
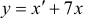
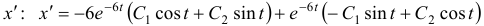
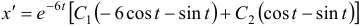
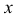
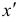
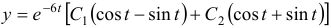
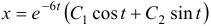
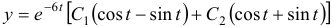
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
Алгоритм решения линейных систем дифференциальных уравнений третьего порядка.
Для более глубокого понимания происходящего в этой статье можно ознакомиться с краткой теоретической справкой.
Рассмотрим однородную систему дифференциальных уравнений третьего порядка
Здесь x(t), y(t), z(t) – искомые функции на промежутке (a, b), aij (i, j =1, 2, 3) – вещественные числа.
Запишем исходную систему в матричном виде
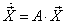
где
Решение исходной системы будем искать в виде
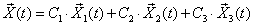
где 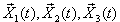
Чтобы найти фундаментальную систему решений, нужно решить так называемое характеристическое уравнение
Это уравнение является алгебраическим уравнением третьего порядка, следовательно оно имеет 3 корня. При этом возможны следующие случаи:
1. Корни (собственные значения) 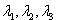
2. Среди корней (собственных значений) есть комплексно-сопряженные, пусть
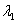
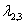
3. Корни (собственные значения) действительны. Один из корней кратный.
Чтобы разобраться, как действовать в каждом из этих случаев, нам понадобятся:
Теорема 1.
Пусть 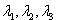
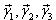
образуют фундаментальную систему решений исходной системы.
Замечание
.
Пусть 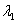
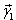
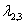
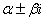
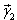
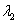
(Re – действительная часть, Im – мнимая)
образуют фундаментальную систему решений исходной системы. (Т.е. 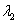
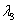
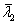
Теорема 3.
Пусть – корень характеристического уравнения кратности 2. Тогда исходная система имеет 2 линейно независимых решения вида
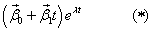
где 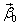
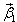
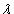
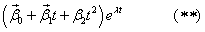
Векторы 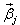
Чтобы лучше понять метод нахождения решений вида (*) и (**), смотри разобранные типичные примеры ниже.
Теперь рассмотрим более подробно каждый из вышеописанных случаев.
1. Алгоритм решения однородных систем дифференциальных уравнений третьего порядка в случае различных действительных корней характеристического уравнения.
Дана система
1) Составляем характеристическое уравнение
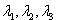
2)Строим 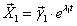
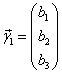
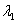
3)Строим 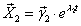
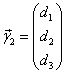
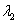
4)Строим 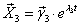
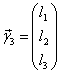
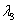
5)
составляют фундаментальную систему решений. Далее записываем общее решение исходной системы в виде
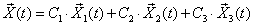
здесь C1, C2, C3 – произвольные постоянные,
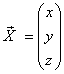
или в координатном виде
Расмотрим несколько примеров:
Пример 1.
1)Составляем и решаем характеристическое уравнение:
2) Находим
3)Находим
4)Вектор-функции
образуют фундаментальную систему. Общее решение имеет вид
или в координатной записи
Пример 2.
1)Составляем и решаем характеристическое уравнение:
2) Находим
3)Находим
4)Находим
5)Вектор-функции
образуют фундаментальную систему. Общее решение имеет вид
или в координатной записи
2. Алгоритм решения однородных систем дифференциальных уравнений третьего порядка в случае комплексно-сопряженных корней характеристического уравнения.
1) Составляем и решаем характеристическое уравнение
– действительный корень,
2)Строим , где
3) Строим
(т.е. и
рассматриваем вместе), где
Здесь Re – действительная часть
Im – мнимая часть
4) составляют фундаментальную систему решений. Далее записываем общее решение исходной системы:
, где
С1, С2,С3 произвольные постоянные.
Пример 1.
1) Составляем и решаем характеристическое уравнение
2)Строим
3) Строим
, где
2) Сошлемся на Теорему 3, из которой следует, что существуют два линейно независимых решения вида
,
где ,
– постоянные векторы. Их возьмем за
.
3) – фундаментальная система решений. Далее записываем общее решение исходной системы:
Рассмотрим случай б):
1) Сошлемся на Теорему 3, из которой следует, что существует три линейно независимых решения вида
,
где ,
,
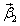
.
2) – фундаментальная система решений. Далее записываем общее решение исходной системы.
Чтобы лучше понять как находить решения вида (*), рассмотрим несколько типичных примеров.
Пример 1.
Составляем и решаем характеристическое уравнение:
Имеем случай а)
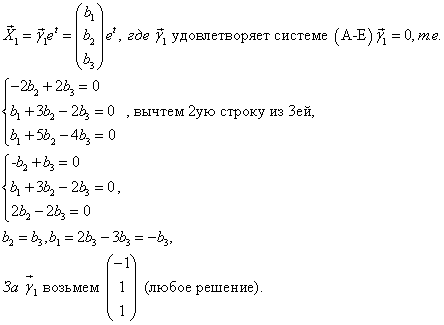
1) Строим
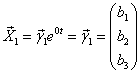
Из второго уравнения вычитаем первое:
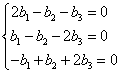
2) = 1 (кратность 2)
Этому корню по Т.3 должно соответствовать два линейно независимых решения вида .
Попробуем найти все линейно незваисимые решения, у которых , т.е. решения вида
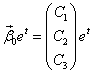
Такой вектор будет решением тогда и только тогда, когда – собственный вектор, соответствующий
=1, т.е.
, или
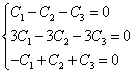
Система свелась к одному уравнению. Следовательно, имеется два свободных неизвестных, например, и
. Дадим им сначала значения 1, 0; потом значения 0, 1. Получим такие решения:
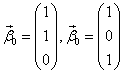
Следовательно, 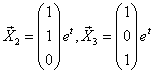
3) – фундаментальная система решений. Осталось записать общее решение исходной системы:
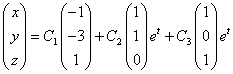
Пример 2.
Составляем и решаем характеристическое уравнение:
Имеем случай а).
1) Строим
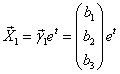
| где | , т.е. |
За возьмем
.Тогда
2) =-1 (кратности 2).
Этому корню по Т.3 соответствуют два линейно независимых решения вида .
Попробуем найти линейно независимые решения, у которых , т.е. решения вида
Но тогда будет собственным вектором, соответствующим
=-1, т.е.
, т.е.
Третья строка аналогична второй, отбрасываем ее.
Пусть C3=1, тогда
| [ | нашли, когда искали | Х2] |
Второе уравнение последней системы запишем так:
Этому матричному уравнению соответствует система линейных уравнений:
Вычеркнем третью строку (она подобна второй). Система совместна (имеет решение) при любом с. Пусть с=1.
Выпишем какое-нибудь частное решение последней системы.
a3=0, a2=-1, a1=1 т.е.
Тогда
3) – фундаментальная система решений. Выпишем общее решение исходной системы:
или
Уравнений с постоянными коэффициентами.
При рассмотрении систем дифференциальных уравнений ограничимся случаем системы трех уравнений (n = 3). Все нижесказанное справедливо для систем произвольного порядка.
Определение. Нормальная система дифференциальных уравнений c постоянными коэффициентами называется Линейной однородной, если ее можно записать в виде:

Решения системы (2) обладают следующими свойствами:
1) Если Y, Z, U – Решения системы, то Cy, Cz, Cu , Где C = Const – Тоже являются решениями этой системы.
2) Если Y1, Z1, U1 И Y2, Z2, U2 – решения системы, то Y1 + Y2, Z1 + Z2, U1 + U2 – тоже являются решениями системы.
Решения системы ищутся в виде:
Подставляя эти значения в систему (2) и перенеся все члены в одну сторону и сократив на Ekx, получаем:
Для того, чтобы полученная система имела ненулевое решение необходимо и достаточно, чтобы определитель системы был равен нулю, т. е.:
В результате вычисления определителя получаем уравнение третьей степени относительно K. Это уравнение называется Характеристическим уравнением И имеет три корня K1, K2, K3. Каждому из этих корней соответствует ненулевое решение системы (2):
Линейная комбинация этих решений с произвольными коэффициентами будет решением системы (2):
Пример. Найти общее решение системы уравнений:
Составим характеристическое уравнение:
Решим систему уравнений:
Для K1:
Полагая (принимается любое значение), получаем:
Для K2:
Полагая (принимается любое значение), получаем:
Общее решение системы:
Этот пример может быть решен другим способом:
Продифференцируем первое уравнение:
Подставим в это выражение производную У¢ =2X + 2Y из второго уравнения.
Подставим сюда У, выраженное из первого уравнения:
Обозначив , получаем решение системы:
Пример. Найти решение системы уравнений
Эта система дифференциальных уравнений не относится к рассмотренному выше типу, т. к. не является однородным (в уравнение входит независимая переменная Х).
Для решения продифференцируем первое уравнение по Х. Получаем:
Заменяя значение Z’ из второго уравнения получаем: .
С учетом первого уравнения, получаем:
Решаем полученное дифференциальное уравнение второго порядка.
Общее решение однородного уравнения:
Теперь находим частное решение неоднородного дифференциального уравнения по формуле
Общее решение неоднородного уравнения:
Подставив полученное значение в первое уравнение системы, получаем:
Пример. Найти решение системы уравнений:
Составим характеристическое уравнение:
1) K = -1.
Если принять g = 1, то решения в этом случае получаем:
2) K2 = -2.
Если принять g = 1, то получаем:
3) K3 = 3.
Если принять g = 3, то получаем:
Общее решение имеет вид:
Элементы теории устойчивости.
Теория устойчивости решений дифференциальных уравнений является одним из разделов Качественной теории дифференциальных уравнений, которая посвящена не нахождению какого – либо решения уравнения, а изучению характера поведения этого решения при изменении начальных условий или аргумента.
Этот метод особенно важен, т. к. позволяет делать вывод о характере решения без непосредственного нахождения этого решения. Т. е. даже в тех случаях, когда решение дифференциального уравнения вообще не может быть найдено аналитически.
Пусть имеется некоторое явление, описанное системой дифференциальных уравнений:
(1)
И начальные условия:
Для конкретного явления начальные условия определяются опытным путем и поэтому неточны.
Теорема. (о непрерывной зависимости решения от начальных условий)
Если правая часть дифференциального уравнения Непрерывна и по переменной у имеет ограниченную частную производную
на области прямоугольника, ограниченного
, то решение
, удовлетворяющее начальным условиям
, непрерывно зависит от начальных данных, т. е. для любого
, при котором если
то
при условии, что
где
Эта теорема справедлива как для одного дифференциального уравнения, так и для системы уравнений.
Определение. Если – решение системы дифференциальных уравнений, то это решение называется Устойчивым по Ляпунову, если для любого
, такое, что для любого решения
той же системы, начальные условия которого удовлетворяют неравенствам
Справедливы неравенства
(Ляпунов Александр Михайлович (1857 – 1918) академик Петерб. АН)
Т. е. можно сказать, что решение j(t) устойчиво по Ляпунову, если близкие к нему по начальным условиям решения остаются близкими и при T ³ T0.
Если , то решение j(t) называется Асимптотически устойчивым.
Исследование на устойчивость по Ляпунову произвольного решения системы
Можно свести к исследованию на устойчивость равного нулю решения некоторой другой системы, которая получена из данной заменой неизвестных функций:
Тогда:
(2)
Система (2) имеет тривиальное (равное нулю) решение
Теорема. Решение системы (1) устойчиво по Ляпунову тогда и только тогда, когда устойчиво по Ляпунову тривиальное решение системы (2).
Это тривиальное решение называется Положением равновесия Или Точкой покоя.
Определение. Точка покоя Системы (2) устойчива по Ляпунову, если для любого
такое, что из неравенства
Следует
.
Теорема. (Теорема Ляпунова). Пусть задана система
Имеющая тривиальное решение .
Пусть существует дифференцируемая функция , удовлетворяющая условиям:
1) ³0 и V = 0 только при у1 = у2 = … = уN =0, т. е. функция V Имеет минимум в начале координат.
2) Полная производная функции V Вдоль фазовой траектории (т. е. вдоль решения Yi(T) системы (1)) удовлетворяет условию:
при
Тогда точка покоя устойчива по Ляпунову.
Если ввести дополнительное требование, чтобы вне сколь угодно малой окрестности начала координат выполнялось условие
Где B – постоянная величина, то точка покоя асимптотически устойчива.
Функция V называется Функцией Ляпунова.
Классификация точек покоя.
Рассмотрим систему двух линейных дифференциальных уравнений с постоянными коэффициентами
Характеристическое уравнение этой системы имеет вид:
Рассмотрим следующие возможные случаи:
1) Корни характеристического уравнения действительные, отрицательные и различные.
Точка покоя будет устойчива. Такая точка покоя называется Устойчивым узлом.
2) Корни характеристического уравнения действительны и
или
.
В этом случае точка покоя также будет устойчива.
3) Хотя бы один из корней положителен.
В этом случае точка покоя Неустойчива, и такую точку называют Неустойчивым седлом.
4) Оба корня характеристического уравнения положительны .
В этом случае точка покоя Неустойчива, и такую точку называют Неустойчивым узлом.
Если полученного решения 
дает траекторию движения в системе координат XOY.
Возможны следующие случаи:

a a
Устойчивый узел. Неустойчивый узел. Седло.
5) Корни характеристического уравнения комплексные .
Если Р = 0, т. е. корни чисто мнимые, то точка покоя (0, 0) устойчива по Ляпунову.
Такая точка покоя называется Центром.
Если P< 0, то точка покоя устойчива и называется Устойчивым фокусом.
Если P > 0, то точка покоя неустойчива и называется Неустойчивым фокусом.
Уравнения математической физики.
Уравнения в частных производных.
Определение. Дифференциальным уравнением в частных производных Называется уравнение относительно неизвестной функции нескольких переменных, ее аргументов и ее частных производных различных порядков.
Порядком Дифференциального уравнения в частных производных называется порядок старшей производной, входящей в это уравнение. Решением Уравнения будет некоторая функция , которая обращает уравнение в тождество.
| < Предыдущая | Следующая > |
|---|