Макеты страниц
Характеристика кольца.
Пусть 




ОПРЕДЕЛЕНИЕ. Говорят, что кольцо 



Поскольку всякое поле 



Примеры. 1. Пусть 


2. Пусть 




3. Пусть 



4. Пусть 





ТЕОРЕМА 1.7. Характеристикой области целостности является либо нуль, либо простое число.
Доказательство. Пусть 




Если 



Предположим теперь, что 

Следовательно,

Так как 





ТЕОРЕМА 1.8. Пусть 


Доказательство. Пусть а — любой ненулевой элемент кольца 









У этого термина существуют и другие значения, см. Кольцо.
Кольцо́ (также ассоциативное кольцо) в общей алгебре — алгебраическая структура, в которой определены операция обратимого сложения и операция умножения, по свойствам похожие на соответствующие операции над числами. Простейшими примерами колец являются совокупности чисел (целых, вещественных, комплексных), совокупности числовых функций, определённых на заданном множестве. Во всех случаях имеется множество, похожее на совокупности чисел в том смысле, что его элементы можно складывать и умножать, причём эти операции ведут себя естественным образом[1].
Понятие кольца[2] было введено для изучения общих свойств операций умножения и сложения, их внутренней связи между собой, безотносительно природы элементов, над которыми операции производятся.
Кольца являются основным объектом изучения теории колец — крупного раздела общей алгебры, в котором разработаны инструментальные средства, нашедшие широкое применение в алгебраической геометрии, алгебраической теории чисел, алгебраической 
История[править | править код]
Бурное развитие алгебры как науки началось в XIX веке. Одной из главных задач теории чисел в 1860—1870-е годы было построение теории делимости в общих полях алгебраических чисел.
Решение этой задачи было опубликовано Рихардом Дедекиндом («X Дополнение к лекциям по теории чисел Дирихле», 1871 год). В этой работе было впервые рассмотрено понятие кольца целых числового поля, в этом контексте были определены понятия модуля и идеала[3].
Определение[править | править код]
Кольцо — множество 



— коммутативность сложения;
— ассоциативность сложения;
— существование нейтрального элемента относительно сложения;
— существование противоположного элемента относительно сложения;
— ассоциативность умножения;
— дистрибутивность.
Иными словами, кольцо — универсальная алгебра 




Кольца могут обладать следующими дополнительными свойствами:
Иногда под кольцом понимают только кольца с единицей[4] (то есть требуют, чтобы 
Вместо символа 

Простейшие свойства[править | править код]
Непосредственно из аксиом кольца можно вывести следующие свойства:
Основные понятия[править | править код]
Виды элементов кольца[править | править код]
Пусть в кольце есть элементы, отличные от нуля (кольцо не является тривиальным[⇨]). Тогда левый делитель нуля — ненулевой элемент 




рассмотрим кольцо непрерывных функций на интервале 








Нильпотентный элемент — элемент 



Идемпотентный элемент 

в кольце матриц 
Если 







Подкольцо[править | править код]
Подмножество 






По определению, подкольцо непусто, поскольку содержит нулевой элемент. Нуль и единица кольца являются нулем и единицей любого его подкольца[11].
Подкольцо наследует свойство коммутативности[12].
Пересечение любого множества подколец является подкольцом. Наименьшее подкольцо, содержащее подмножество 




Подкольцо кольца с единицей 


Идеалы[править | править код]
Определение и роль идеала кольца сходны с определением нормальной подгруппы в теории групп[14].
Непустое подмножество 

Из первого свойства следует и замкнутость 

Аналогично определяется правый идеал, замкнутый относительно умножения на элемент кольца справа.
Двусторонний идеал (или просто идеал) кольца 
Также идеал кольца 

Если 







Идеал кольца, не совпадающий со всем кольцом, называется простым, если факторкольцо по этому идеалу не имеет делителей нуля. Идеал кольца, не совпадающий со всем кольцом и не содержащийся ни в каком большем идеале, не равном кольцу, называется максимальным[17].
Гомоморфизм[править | править код]
Гомоморфизм колец (кольцевой гомоморфизм) — отображение, сохраняющее операции сложения и умножения. А именно, гомоморфизм из кольца 


,
.
В случае колец с единицей иногда требуют также условия 
Гомоморфизм колец называется изоморфизмом, если существует обратный гомоморфизм колец. Любой биективный гомоморфизм колец является изоморфизмом. Автоморфизм — гомоморфизм из кольца в себя, который является изоморфизмом. Пример: тождественное отображение кольца на себя является автоморфизмом[20].
Если 






Факторкольцо[править | править код]
Определение факторкольца по идеалу аналогично определению факторгруппы. Более точно, факторкольцо кольца 



,
.
Аналогично случаю групп, существует канонический гомоморфизм 


Аналогично теореме о гомоморфизме групп существует теорема о гомоморфизме колец:
пусть 


Некоторые особые классы колец[править | править код]
- Кольцо с единицей
, в котором каждый ненулевой элемент обратим, называется телом[23].
- Коммутативное тело называется полем[24]; иначе говоря, поле — коммутативное кольцо с единицей, не имеющее нетривиальных идеалов[8][25].
- Коммутативное кольцо без делителей нуля называется областью целостности (или целостным кольцом)[26]. Любое поле является областью целостности, но обратное неверно[27].
- Целостное кольцо
, не являющееся полем, называется евклидовым, если на кольце задана норма
такая, что:
- для любых ненулевых
верно, что
;
- для любых ненулевых
существуют
такие, что
и
или
[26].
- для любых ненулевых
- Целостное кольцо, в котором всякий идеал является главным, называется кольцом главных идеалов; всякие евклидово кольцо и всякое поле являются кольцами главных идеалов[12].
- Кольцо, элементами которого являются числа, а операциями — сложение и умножение чисел, называют числовым кольцом, например, множество чётных чисел является числовым кольцом, но не будет кольцом никакая система отрицательных чисел, так как их произведение положительное[28].
Примеры[править | править код]
— тривиальное кольцо, состоящее из одного нуля. Это единственное кольцо, в котором ноль является мультипликативной единицей[5]. Этот тривиальный пример полезно считать кольцом с точки зрения теории категорий, так как при этом в категориях колец возникает терминальный объект.
— целые числа (с обычным сложением и умножением). Это важнейший пример кольца, так как любое кольцо можно рассматривать как алгебру над
. Также это начальный объект в категории Ring колец с единицей.[29][30]
— конечное кольцо вычетов по модулю натурального числа n. Это классические примеры колец из теории чисел. Кольцо вычетов является полем тогда и только тогда, когда число n простое.[31] Соответствующие поля являются отправной точкой для построения теории конечных полей. Кольца вычетов также важны при исследовании структуры конечнопорождённых абелевых групп, их также можно использовать для построения p-адических чисел.
— кольцо рациональных чисел, являющееся полем. Это простейшее поле характеристики 0. Оно является основным объектом исследования в теории чисел. Пополнение его по различным неэквивалентным нормам даёт поля вещественных чисел
и p-адических чисел
где p — произвольное простое число[32].
- Для произвольного коммутативного кольца
можно построить кольцо многочленов от n переменных
с коэффициентами в
[11] В частности,
Кольцо многочленов с целыми коэффициентами является универсальным кольцом многочленов, в том смысле что все кольца многочленов выражаются через тензорное произведение:
- Кольцо подмножеств множества
— кольцо, элементами которого являются подмножества в
. Операция сложения есть симметрическая разность, а умножение — пересечение множеств:
- Аксиомы кольца легко проверяются. Нулевым элементом является пустое множество, единичным — всё
Все элементы кольца являются идемпотентами, то есть
Любой элемент является своим обратным по сложению:
Кольцо подмножеств важно в теории булевых алгебр и теории меры, в частности в построении теории вероятностей[5].
Конструкции[править | править код]
Прямое произведение[править | править код]
Произведение 




Сходная конструкция существует для произведения произвольного семейства колец (сложение и умножение задаются покомпонентно)[33].
Пусть 

сюръективно, а его ядро — 
Кольцо эндоморфизмов[править | править код]
Множество эндоморфизмов абелевой группы 






Поле частных и кольцо частных[править | править код]
Для целостного кольца 


тогда и только тогда, когда
,
с обычными операциями: 

Не вполне очевидно, что заданное отношение действительно является отношением эквивалентности: для доказательства приходится воспользоваться целостностью кольца. Существует обобщение данной конструкции на произвольные коммутативные кольца: мультипликативно замкнутая система 



тогда и только тогда, когда существует
, такое что
.
Также эту конструкцию называют локализацией кольца (так как в алгебраической геометрии она позволяет исследовать локальные свойства многообразия в отдельной его точке). Пример: кольцо десятичных дробей — локализация кольца целых чисел по мультипликативной системе

Существует естественное отображение 



Категорное описание[править | править код]
Кольца вместе с гомоморфизмами колец образуют категорию, обычно обозначаемую 


Можно дать следующее категорное определение кольца: ассоциативное кольцо с единицей — моноид в категории абелевых групп (абелевы группы образуют моноидальную категорию относительно операции тензорного произведения). Действие кольца R на абелевой группе (кольца, рассматриваемого как моноид по умножению) превращает абелеву группу в R-модуль. Понятие модуля обобщает понятие векторного пространства: грубо говоря, модуль — «векторное пространство над кольцом».[29][30]
Специальные классы колец[править | править код]
- Артиново кольцо
- Дедекиндово кольцо
- Дистрибутивное кольцо
- Дифференциальное кольцо
- Кольцо главных идеалов
- Евклидово кольцо
- Кольцо Безу
- Кольцо Ли
- Конечное кольцо
- Локальное кольцо
- Нётерово кольцо
- Область целостности
- Область главных идеалов
- Первичное кольцо
- Полулокальное кольцо
- Полупервичное кольцо
- Полупростое кольцо
- Полуцепное кольцо
- Простое кольцо
- Факториальное кольцо
- Цепное кольцо
Обобщения — неассоциативное кольцо, полукольцо, почтикольцо.
Структуры над кольцами[править | править код]
- Алгебра над кольцом
- Бимодуль над кольцом
- Модуль над кольцом
Примечания[править | править код]
- ↑ Винберг, 2011, с. 17—19.
- ↑ Бельский А., Садовский Л. Кольца // Квант. — 1974. — № 2. Архивировано 1 сентября 2004 года.
- ↑ Erich Reck. Dedekind’s Contributions to the Foundations of Mathematics // The Stanford Encyclopedia of Philosophy / Edward N. Zalta. — 2012-01-01. Архивировано 2 декабря 2013 года.
- ↑ Атья, Макдональд, 1972, с. 9.
- ↑ 1 2 3 4 Винберг, 2011, с. 18—19.
- ↑ Курош, 1968, с. 273—275.
- ↑ 1 2 Ван дер Варден, 1975, с. 51—53.
- ↑ 1 2 Атья, Макдональд, 1972, с. 11.
- ↑ Ван дер Варден, 1975, с. 359.
- ↑ Винберг, 2011, с. 407.
- ↑ 1 2 3 Куликов, 1979, с. 110—111.
- ↑ 1 2 Винберг, 2011, с. 21.
- ↑ Куликов, 1979, с. 437.
- ↑ Ван дер Варден, 1975, с. 64.
- ↑ 1 2 Фейс, 1977, с. 153.
- ↑ Куликов, 1979, с. 430—431.
- ↑ Винберг, 2011, с. 406.
- ↑ 1 2 Фейс, 1979, с. 10.
- ↑ Винберг, 2011, с. 388.
- ↑ Куликов, 1979, с. 107—108.
- ↑ Куликов, 1979, с. 432.
- ↑ Винберг, 2011, с. 387—390.
- ↑ Винберг, 2011, с. 523.
- ↑ Фейс, 1977, с. 152.
- ↑ Куликов, 1979, с. 430.
- ↑ 1 2 Винберг, 2011, с. 118.
- ↑ Атья, Макдональд, 1972.
- ↑ Курош, 1968, с. 266.
- ↑ 1 2 Фейс, 1977.
- ↑ 1 2 Фейс, 1979.
- ↑ Винберг, 2011, с. 28—34.
- ↑ Ван дер Варден, 1975, с. 509—512.
- ↑ Ван дер Варден, 1975, с. 33.
- ↑ Ван дер Варден, 1975, с. 173.
- ↑ Ван дер Варден, 1975, с. 450—452.
- ↑ Курош, 1968, с. 305—311.
Литература[править | править код]
- М. Атья, И. Макдональд. Введение в коммутативную алгебру. — М.: Мир, 1972. — 160 с.
- Бельский А., Садовский Л. Кольца. // Квант № 2, 1974.
- Ван дер Варден Б. Л. Алгебра. — М.: Мир, 1975. — 623 с.
- Винберг Э. Б. Курс алгебры. – Новое издание, перераб. и доп.. — М.: МЦНМО, 2011. — 592 с.
- Глейзер Г. И. История математики в школе: IX-X класс. Пособие для учителей – Новое издание, перераб. и доп.. — М.: Просвещение, 1983. — 351 с.
- Математика XIX века. Математическая логика. Алгебра. Теория чисел. Теория вероятностей / Колмогоров А. Н., Юшкевич А. П. (ред.). — М.: Наука, 1978. — 255 с.
- Куликов Л. Я. Алгебра и теория чисел: Учеб. пособие для педагогических институтов. — М.: Высш. школа, 1979. — 559 с.
- Курош А. Г. Курс высшей алгебры.. — М.: Наука, 1968. — 431 с.
- Фейс К. Алгебра. Кольца, модули, категории. — М.: Мир, 1977. — Т. 1. — 688 с.
- Фейс К. Алгебра. Кольца, модули, категории. — М.: Мир, 1979. — Т. 2. — 464 с.
- Херстейн И. Некоммутативные кольца. — М.: Мир, 1972. — 190 с.
Характеристика
кольца
с 1 — целое положительное число

для которого выполняется
и никакое другое положительное число,
меньшее

этим свойством не обладает. Если такого
нет, то говорят, что кольцо имеет
характеристику 0.
Примеры.
-
Кольцо
имеет характеристику 0, так как
;
кольцо
также имеет характеристику 0. -
Кольцо
,
то есть множество классов вычетов по
,
имеет характеристику
.
Действительно
.
В частности, кольцо
,
то есть множество классов вычетов по
модулю 3:
,
так как
,
то есть характеристика
равна 3.
Лемма.
Если характеристика кольца
равна

то для любого

Теорема.
Характеристика любого кольца без
делителей 0 (в частности, поля) либо 0,
либо простое число.
Действительно,
если нет делителей 0, то есть нет таких
чисел

что

то из определения характеристики
следует, что либо

либо
— простое, так как в противном случае
и, следовательно,

то есть имеются делители 0. Теорема
доказана.
Следствие.
— множество классов вычетов по

где
— не простое, имеет делители 0. Например,
имеет делители 0:

12. Простой идеал. Необходимое и достаточное условие того, что идеал кольца — простой Простой идеал
Простой
идеал
в кольце
— идеал, в котором из
следует, что либо

либо

либо оба.
Единичный
идеал
— всегда простой, так как это само кольцо

В
кольце целых чисел
идеал
прост при простом
Так, например,
— прост, так как
содержит числа кратные 3. Идеал
— не прост, так как
— не простое. Например,

Теорема.
Идеал
кольца
является простым тогда и только тогда,
когда кольцо классов вычетов
не содержит делителей нуля.
Доказательство.
Кольцо
классов вычетов
не имеет делителей 0 в том и только в том
случае, если из

где

следует, что

либо

либо оба, но тогда: либо

либо

либо оба, что равносильно по определению
тому, что идеал
— простой. Теорема доказана.
13. Поле классов вычетов. Минимальное поле. Примеры Поле классов вычетов
Теорема.
(Следствие из предыдущей.) Кольцо классов
вычетов кольца целых чисел
по модулю
является полем тогда и только тогда,
когда
— простое число.
Примеры.
-
.
Если
,
то
.
Если
,
то
,
так как
.
Все ненулевые элементы имеют
противоположные, делителей нуля нет,
то есть
— поле. -
:
— есть делители 0, так как 4 — не простое.
,
то есть
— не поле.
Минимальное
поле — поле, не имеющее подполей,
отличных от него самого.
Примеры.
-
Поле рациональных чисел
— минимально. -
Поля классов вычетов кольца целых чисел
по простым модулям:
— минимальные.
14. Евклидово кольцо. Свойства (8 свойств). Примеры Евклидово кольцо
Евклидово
кольцо
— кольцо
без делителей 0, в котором каждому
ненулевому элементу
сопоставляется целое неотрицательное
число

называемое нормой элемента

со следующими свойствами:
-
.
-
,
причём либо
,
либо
,
либо оба (возможность деления с остатком).
Примеры.
-
Кольцо
— евклидово кольцо с нормой
.
Действительно,
не имеет делителей нуля, а введённая
норма удовлетворяет условиям 1 и 2
определения:
1)

если
— целое, 2) деление с остатком введено.
-
Кольцо
целых гауссовых чисел
— евклидово кольцо с нормой.
Действительно:
-
,
если
,
то
и
-
Можно ввести деление с остатком.
Например:
|
|
|
|
|
|
|
|
То есть

Остаток:

-
Кольцо многочленов от одной переменной
с коэффициентами в поле
— евклидово кольцо с нормой
равной степени многочлена
.
Действительно:
-
Пусть
,
,
тогда
-
Алгоритм деления многочлена на многочлен
известен.
Пусть
— любое кольцо без делителей 0. Говорят,
что
делит
(то есть
делится на
без остатка), если
такой, что

Запись:

Ясно,
что

то есть если элемент кратен
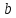
то он кратен и

Простой
необратимый элемент
евклидового кольца — необратимый
элемент евклидового кольца, который
допускает лишь тривиальное разложение,
то есть из равенства
следует, что или

или
обратимы. Например, в случае:
— тривиальные делители числа
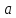
и

Любое
число
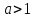
у которого существует нетривиальное
разложение на множители, называется
составным.
Пример.
В кольце
простые элементы:

Причём сомножитель этих чисел:
— обратим. Составные:

(
Пусть 
Определение 1. Рассмотрим гомоморфизм колец 







Замечание 1. Так как 


Замечание 2. Каждое поле 

Определение 2. Поле, не имеющее собственного подполя, называется простым6).
Предложение 1. Поле 



Предложение 2. В каждом поле 
Предложение 3. Характеристика поля 




Определение
Пусть 










Характеристика кольца 

Примеры
Свойства
- Если кольцо
с единицей и без делителей нуля имеет положительную характеристику
, то
— простое число. Следовательно, характеристика любого поля
есть либо
, либо простое число
. В первом случае поле
содержит в качестве подполя поле изоморфное полю рациональных чисел
, во втором случае поле
содержит в качестве подполя поле изоморфное
. В обоих случаях это подполе называется простым полем (содержащимся в
).
- Характеристикой конечного поля является простое число. Заметим, что из того, что характеристика поля конечна, не следует, что поле конечно. Примерами таких полей являются поле рациональных функций над
и алгебраическое замыкание поля
.
- Если
— коммутативное кольцо простой характеристики
, то
для всех
,
.
Литература
- Лидл Р., Нидеррайтер Г. Конечные поля: В 2-х т. Т. 1. Пер. с англ. — М.: Мир, 1988.
- Кострикин А. И. Введение в алгебру. — М.: Наука, 1977.
- Глухов М. М., Елизаров В. П., Нечаев А. А. Алгебра: Учебник. В 2-х т. Т. 2. — М.: Гелиос АРВ, 2003.
























![R[x_1,x_2,dots,x_n]](https://wikimedia.org/api/rest_v1/media/math/render/svg/7de1d5767a8f5ee8e1b21bad9b0a1b973342f0d3)
![R[x][y]=R[x,y].](https://wikimedia.org/api/rest_v1/media/math/render/svg/634dbdfb9abac4cc6d44e11c3b5aafc4a37c73d6)
![R[x_1,dots,x_n] = R otimes left(Z[x_1,dots,x_n]right).](https://wikimedia.org/api/rest_v1/media/math/render/svg/7578a64a6b1b1ca956a10f00edd7d510f42ce683)















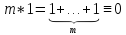


 ;
;
 ,
, ,
, .
. .
. ,
, ,
, ,
,

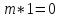















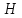
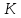
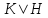
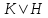




 .
. ,
, .
. ,
, ,
, .
.
 :
: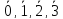
 ,
,





 .
. ,
, ,
,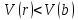 ,
,
 .
.
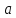


 .
. ,
, ,
,


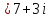


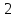
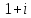



 .
. ,
, ,
,













 с единицей и без делителей нуля имеет положительную характеристику
с единицей и без делителей нуля имеет положительную характеристику  есть либо
есть либо  . В первом случае поле
. В первом случае поле  , во втором случае поле
, во втором случае поле  . В обоих случаях это подполе называется простым полем (содержащимся в
. В обоих случаях это подполе называется простым полем (содержащимся в  для всех
для всех  ,
,  .
.