К ним относятся
-
наибольшее и наименьшее значение СВ,
-
мода – значение СВ, которому отвечает
максимальное значение плотности
распределения, -
медиана – значение ВС, которое делит
площадь фигуры, ограниченной графиком
плотности распределения, пополам, -
математическое ожидание – среднее
значение ВС для всех элементов выборки, -
дисперсия и среднее квадратичное
отклонение – характеристики разброса
значений СВ, -
коэффициент асимметрии – характеристика
несимметричности графика плотности
распределения СВ, -
коэффициент эксцесса – характеристика
«остроты» графика плотности распределения
СВ.
Приведем расчетные формулы. В них
–
число элементов выборки,
– номер элемента выборки,
,
–
значение СВ для-го
элемента выборки,
–
математическое ожидание
,
–
дисперсия
,
–
среднее квадратичное отклонение
,
–
коэффициент асимметрии
,
–
коэффициент эксцесса
.
7 Расчет необходимого объема выборки для получения достоверных суждений о генеральной совокупности
Степень достоверности суждений о
генеральной совокупности на основе
наблюдений за ограниченной выборкой
будем характеризовать возможной ошибкой
в оценке среднего значения СВ для всей
генеральной совокупности по ее среднему
значению для выборки. Допускаемую про
этом возможную ошибку оценивают следующим
образом.
-
Задаются объемом выборки
,
находят для ее элементов значения СВ
и рассчитывают математическое ожидание
и среднее квадратичное отклонение. -
Задаются желаемой вероятностью
достоверности оценки (т.н. доверительной
вероятностью)
,
например,.
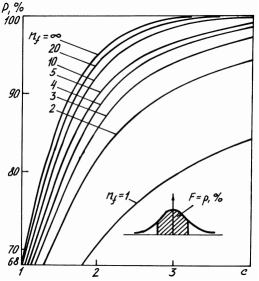
-
По рисунку 5, приняв
, определяют значение т.н. коэффициента
Стьюдента.
-
Рассчитывают доверительные границы
погрешности
,
с которой среднее значение СВ, рассчитанное
для выборки, характеризует среднее
значение этой СВ для всей генеральной
совокупности
.
Если величина ошибки представляется
слишком большой, необходимо увеличить
объем выборки и провести расчет повторно.
Рисунок 5 – Определение коэффициента
Стьюдента
8 Оценка различия двух выборок
Чтобы убедиться, что две выборки
действительно различны с точки зрения
значений одной и той же СВ, можно
использовать три критерия:
-
Крамера-Уэлча, если элементы этих
выборок не связаны между собой, -
Вилкоксона-Манна-Уитни, если есть
возможность попарно сравнивать между
собой элементы этих выборок, -
«хи-квадрат», если СВ измеряется не в
непрерывной, а в порядковой шкале
(например, балльной)
При этом объемы выборок должны быть не
менее 10.
Проверка по критерию Крамера-Уэлча.
-
Для выборок
и
с объемами
и
вычисляются
математические ожидания и средние
квадратичные отклонения/
-
Вычисляется значение коэффициента
по формуле
.
-
Задаются значением доверительной
вероятности
и по рисунку 5 находят значение
коэффициента Стьюдентапри
.
-
Если
,
то делается вывод, «выборкии
различны с доверительной вероятностью
».
Проверка по критерию Вилкоксона-Манна-Уитни.
-
Для каждого элемента первой выборки
подсчитывается коэффициент, равный
количеству элементов второй выборки,
у которых значение СВ больше, чем у
данного элемента первой выборки. К
этому коэффициенту добавляется число,
равное половинному количеству элементов
второй выборки, у которых значение СВ
совпадает со значением СВ для данного
элемента первой выборки. Рассчитанные
таким образом коэффициенты для всех
элементов первой выборки суммируются.
Их сумму обозначим через
.
-
Рассчитывается коэффициент
по формуле

-
Задаются значением доверительной
вероятности
и по рисунку 5 находят значение
коэффициента Стьюдентапри
.
-
Если
,
то делается вывод, «выборкии
различны с доверительной вероятностью
».
Проверка по критерию «хи-квадрат».
Пусть СВ измеряется в порядковой шкале
с
различными
баллами. Количества объектов в выборкахи
,
значения СВ для которых равны-му
баллу, обозначим черезсоответственно. Требуется, чтобы было
и
.
Тогда
-
Вычисляется коэффициент
по формуле

-
Задаются значением доверительной
вероятности
и по таблице 3 находят значение
коэффициента.
-
Если
,
то делается вывод, «выборкии
различны с доверительной вероятностью
».
Таблица 3 – Критические значения критерия
«хи-квадрат»
|
L |
Доверительная |
||||||||||||
|
0,5% |
1% |
2,50% |
5% |
10% |
25% |
50% |
75% |
90% |
95% |
97,5% |
99% |
99,5% |
|
|
2 |
0,00004 |
0,00016 |
0,00098 |
0,00393 |
0,02 |
0,10 |
0,45 |
1,32 |
2,71 |
3,84 |
5,02 |
6,63 |
7,88 |
|
3 |
0,01003 |
0,0201 |
0,05064 |
0,10259 |
0,21 |
0,58 |
1,39 |
2,77 |
4,61 |
5,99 |
7,38 |
9,21 |
10,60 |
|
4 |
0,07172 |
0,11483 |
0,2158 |
0,35185 |
0,58 |
1,21 |
2,37 |
4,11 |
6,25 |
7,81 |
9,35 |
11,34 |
12,84 |
|
5 |
0,20699 |
0,29711 |
0,48442 |
0,71072 |
1,06 |
1,92 |
3,36 |
5,39 |
7,78 |
9,49 |
11,14 |
13,28 |
14,86 |
|
6,00 |
0,41 |
0,55 |
0,83 |
1,15 |
1,61 |
2,67 |
4,35 |
6,63 |
9,24 |
11,07 |
12,83 |
15,09 |
16,75 |
|
7,00 |
0,68 |
0,87 |
1,24 |
1,64 |
2,20 |
3,45 |
5,35 |
7,84 |
10,64 |
12,59 |
14,45 |
16,81 |
18,55 |
|
8,00 |
0,99 |
1,24 |
1,69 |
2,17 |
2,83 |
4,25 |
6,35 |
9,04 |
12,02 |
14,07 |
16,01 |
18,48 |
20,28 |
|
9,00 |
1,34 |
1,65 |
2,18 |
2,73 |
3,49 |
5,07 |
7,34 |
10,22 |
13,36 |
15,51 |
17,53 |
20,09 |
21,95 |
|
10,00 |
1,73 |
2,09 |
2,70 |
3,33 |
4,17 |
5,90 |
8,34 |
11,39 |
14,68 |
16,92 |
19,02 |
21,67 |
23,59 |
|
11,00 |
2,16 |
2,56 |
3,25 |
3,94 |
4,87 |
6,74 |
9,34 |
12,55 |
15,99 |
18,31 |
20,48 |
23,21 |
25,19 |
|
12,00 |
2,60 |
3,05 |
3,82 |
4,57 |
5,58 |
7,58 |
10,34 |
13,70 |
17,28 |
19,68 |
21,92 |
24,72 |
26,76 |
|
13,00 |
3,07 |
3,57 |
4,40 |
5,23 |
6,30 |
8,44 |
11,34 |
14,85 |
18,55 |
21,03 |
23,34 |
26,22 |
28,30 |
|
14,00 |
3,57 |
4,11 |
5,01 |
5,89 |
7,04 |
9,30 |
12,34 |
15,98 |
19,81 |
22,36 |
24,74 |
27,69 |
29,82 |
|
15,00 |
4,07 |
4,66 |
5,63 |
6,57 |
7,79 |
10,17 |
13,34 |
17,12 |
21,06 |
23,68 |
26,12 |
29,14 |
31,32 |
|
16,00 |
4,60 |
5,23 |
6,26 |
7,26 |
8,55 |
11,04 |
14,34 |
18,25 |
22,31 |
25,00 |
27,49 |
30,58 |
32,80 |
|
17,00 |
5,14 |
5,81 |
6,91 |
7,96 |
9,31 |
11,91 |
15,34 |
19,37 |
23,54 |
26,30 |
28,85 |
32,00 |
34,27 |
|
18,00 |
5,70 |
6,41 |
7,56 |
8,67 |
10,09 |
12,79 |
16,34 |
20,49 |
24,77 |
27,59 |
30,19 |
33,41 |
35,72 |
|
19,00 |
6,26 |
7,01 |
8,23 |
9,39 |
10,86 |
13,68 |
17,34 |
21,60 |
25,99 |
28,87 |
31,53 |
34,81 |
37,16 |
|
20,00 |
6,84 |
7,63 |
8,91 |
10,12 |
11,65 |
14,56 |
18,34 |
22,72 |
27,20 |
30,14 |
32,85 |
36,19 |
38,58 |
|
21,00 |
7,43 |
8,26 |
9,59 |
10,85 |
12,44 |
15,45 |
19,34 |
23,83 |
28,41 |
31,41 |
34,17 |
37,57 |
40,00 |
|
22,00 |
8,03 |
8,90 |
10,28 |
11,59 |
13,24 |
16,34 |
20,34 |
24,93 |
29,62 |
32,67 |
35,48 |
38,93 |
41,40 |
|
23,00 |
8,64 |
9,54 |
10,98 |
12,34 |
14,04 |
17,24 |
21,34 |
26,04 |
30,81 |
33,92 |
36,78 |
40,29 |
42,80 |
|
24,00 |
9,26 |
10,20 |
11,69 |
13,09 |
14,85 |
18,14 |
22,34 |
27,14 |
32,01 |
35,17 |
38,08 |
41,64 |
44,18 |
|
25,00 |
9,89 |
10,86 |
12,40 |
13,85 |
15,66 |
19,04 |
23,34 |
28,24 |
33,20 |
36,42 |
39,36 |
42,98 |
45,56 |
|
26,00 |
10,52 |
11,52 |
13,12 |
14,61 |
16,47 |
19,94 |
24,34 |
29,34 |
34,38 |
37,65 |
40,65 |
44,31 |
46,93 |
|
27,00 |
11,16 |
12,20 |
13,84 |
15,38 |
17,29 |
20,84 |
25,34 |
30,43 |
35,56 |
38,89 |
41,92 |
45,64 |
48,29 |
|
28,00 |
11,81 |
12,88 |
14,57 |
16,15 |
18,11 |
21,75 |
26,34 |
31,53 |
36,74 |
40,11 |
43,19 |
46,96 |
49,64 |
|
29,00 |
12,46 |
13,56 |
15,31 |
16,93 |
18,94 |
22,66 |
27,34 |
32,62 |
37,92 |
41,34 |
44,46 |
48,28 |
50,99 |
|
30,00 |
13,12 |
14,26 |
16,05 |
17,71 |
19,77 |
23,57 |
28,34 |
33,71 |
39,09 |
42,56 |
45,72 |
49,59 |
52,34 |
Проверка по критерию Фишера (для
двухуровневых шкал).
Критерий применяется в случаях, когда
выборки анализируются на предмет наличия
в их элементах некоторого признака.
Обозначим через
количество
элементов, обладающих этим признаком,
и общее количество элементов в каждой
из сравниваемых выборок.
1. Вычисляется коэффициент Фишера по
формуле
.
2. Если
,
делается вывод, что выборки различны с
доверительной вероятностью 0,95.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Числовые характеристики выборки (случайной величины)
В.С. Иванов (1990) в книге «Основы математической статистики» пишет: «Вариационные ряды и графики эмпирических распределений дают наглядное представление о том, как варьирует признак в выборочной совокупности. Но они недостаточны для полной характеристики выборки, поскольку содержат много деталей, охватить которые невозможно без обобщающих числовых характеристик. Числовые характеристики выборки дают количественное представление об эмпирических данных и позволяют сравнивать их между собой».
Наибольшее практическое значение имеют характеристики положения, рассеивания и асимметрии (табл.1).
Таблица 1 — Название и обозначение числовых характеристик выборки (случайной величины)
|
Числовые характеристики случайной величины |
||
| Положения | Вариативности | Формы распределения |
| Среднее арифметическое (М) | Размах вариации (R) | Коэффициент асимметрии (As) |
| Мода (Мо) | Дисперсия (S2) | Коэффициент эксцесса (Ex) |
| Медиана (Ме) | Стандартное отклонение (S) | — |
|
Коэффициент вариации (V%) |
Характеристики положения
Среднее арифметическое (М) – одна из основных характеристик выборки. Этот показатель характеризуется тем, что сумма отклонений от него выборочных значений (с учетом знака) равна нулю.
Для вычисления среднего арифметического сумму всех значений признака делим на объем выборки.
Пример: xi : 20, 15, 15, 20, 30, среднее арифметическое равно 20. При этом сумма отклонений вариант от среднего арифметического равна нулю: сумма отклонений= 0 +(-5) + (-5) + 0 + 10 = 0.
М=(20+15+15+20+30)/5=20
Следует заметить, что среднее арифметическое измеряется в тех же единицах, что и признак. Например, если масса человека измеряется в кг, то и среднее арифметическое измеряется в кг.
Среднее арифметическое, вычисленное на основе выборочных данных, то есть данных, полученных на выборке, называется выборочным средним арифметическим. Оно обозначается как М. Среднее арифметическое генеральной совокупности называется генеральным средним. Оно обозначается буквой мю (μ).
Мода (Мо) – характеристика положения. Представляет собой значение признака, встречающееся в выборке наиболее часто.
В качестве примера рассмотрим выборку: xi :3; 3; 3; 5; 5; 3; 4; 6; 7; 5; 3.
В выборке цифра «3» встречается 5 раз, поэтому Мо = 3.
Медиана (Ме)- характеристика положения, представляет собой такое значение признака, при котором одна половина значений меньше ее, а другая – больше.
В качестве примера рассмотрим выборку: xi :3; 3; 3; 5; 5; 3; 4; 6; 7; 5; 3.
Чтобы легко было определить медиану расположим варианты па возрастанию.
xi :3; 3; 3; 3; 3; 4; 5; 5; 5; 6; 7. Варианта со значением «4» стоит в середине этой выборки. Это и есть медиана.
Характеристики варативности
Средние значения не дают полной информации о вариации признака, поэтому наряду со средними значениями вычисляют характеристики вариативности.
К этим характеристикам относятся:
- размах вариации (R);
- дисперсия (S2)
- стандартное отклонение (S)
- коэффициент вариации (V%)
Размах вариации
Размах вариации (R) вычисляется как разность между максимальным и минимальным значением признака:
R= Xmax-Xmin.
Размах вариации измеряется в тех же единицах, что и признак. Информативность этого показателя невелика, так как эмпирические распределения результатов могут иметь одинаковый размах варьирования, а их форма будет очень отличаться.
Дисперсия
Дисперсия (S2) – средний квадрат отклонений значений признака от среднего арифметического. Если признак измеряется в метрах, то дисперсия – в м2. Это является недостатком, поэтому наиболее часто в публикациях приводится не дисперсия, а стандартное отклонение (S). Этот показатель также называется среднеквадратическим отклонением или СКО. Стандартное отклонение представляет собой корень квадратный из дисперсии. Чем больше стандартное отклонение, тем больше варьирует признак.
Коэффициент вариации
Коэффициент вариации (V%). Чтобы сопоставить вариативность признаков, измеренных в различных единицах, используется относительный показатель (V%), который называется коэффициентом вариации.
Коэффициент вариации рассчитывается следующим образом. Стандартное отклонение делится на среднее арифметическое и умножается на 100%.
V%=100% (S /M)
Например, если среднее арифметическое роста спортсменок равно М=170 см, а стандартное отклонение S=5 см, тогда коэффициент вариации равен: V%= 100% (5/170)=2,94.
Коэффициент вариации часто используют для оценки однородности выборки. Если V<10% – выборка однородна, то есть, получена из одной генеральной совокупности.
Характеристики формы распределения
Коэффициент асимметрии (As) характеризует “скошенность“ эмпирического распределения. Если коэффициент асимметрии равен нулю – распределение симметричное. Если больше нуля – скошено влево, если меньше нуля – вправо.
Коэффициент эксцесса (Ex) определяет характер эмпирического распределения: остро- или плосковершинный.
Литература
- Высшая математика и математическая статистика: учебное пособие для вузов / Под общ. ред. Г. И. Попова. – М. Физическая культура, 2007.– 368 с.
- Гласс Дж., Стэнли Дж. Статистические методы в педагогике и психологии. М.: Прогресс. 1976.- 495 с.
- Катранов А.Г. Компьютерная обработка данных экспериментальных исследований: Учебное пособие/ А. Г. Катранов, А. В. Самсонова; СПб ГУФК им. П.Ф. Лесгафта. – СПб.: изд-во СПб ГУФК им. П.Ф. Лесгафта, 2005. – 131 с.
- Основы математической статистики: Учебное пособие для ин-тов физ. культ / Под ред. В.С. Иванова.– М.: Физкультура и спорт, 1990. 176 с.
Лекция 7
Числовые характеристики выборки
1.6.1. Выборочное среднее. Выборочная дисперсия.
Выборочное среднее квадратическое отклонение
В теории вероятностей определили числовые характеристики для случайных величин, с помощью которых можно сравнивать однотипные случайные величины. Аналогично можно определить ряд числовых характеристик и для выборки. Поскольку эти характеристики вычисляются по статистическим данным (по данным, полученным в результате наблюдений), их называют статистическими характеристиками.
Пусть дано статистическое распределение выборки объема :
где – число вариантов.
Определение. Выборочным средним называется среднее арифметическое всех значений выборки:
.
Выборочное среднее можно записать и так: ,
где – частость.
В случае интервального статистического ряда в качестве берут середины интервалов, а – соответствующие им частоты.
Определение. Выборочной дисперсией называется среднее арифметическое квадратов отклонений значений выборки от выборочного среднего :
или .
Выборочное среднее квадратическое выборки определяется формулой:
.
Особенность состоит в том, что оно измеряется в тех же единицах, что и данные выборки.
Если объем выборки мал (), то пользуются исправленной выборочной дисперсией:
.
Величина называется исправленным средним квадратическим отклонением.
1.6.2. Выборочные начальные и центральные моменты.
Асимметрия. Эксцесс.
Приведем краткий обзор характеристик, которые наряду с уже рассмотренными применяются для анализа статистических рядов и являются аналогами соответствующих числовых характеристик случайной величины.
Среднее выборочное и выборочная дисперсия являются частным случаем более общего понятия – момента статистического ряда.
Определение. Начальным выборочным моментом порядка называется среднее арифметическое – х степеней всех значений выборки:
или .
Из определения следует, что начальный выборочный момент первого порядка: .
Определение. Центральным выборочным моментом порядка называется среднее арифметическое – х степеней отклонений наблюдаемых значений выборки от выборочного среднего :
или .
Из определения следует, что центральный выборочный момент второго порядка :
.
Определение. Выборочным коэффициентом асимметрии называется число , определяемое формулой: .
Выборочный коэффициент асимметрии служит для характеристики асимметрии полигона вариационного ряда. Если полигон асимметричен, то одна из ветвей его, начиная с вершины, имеет более пологий «спуск», чем другая.
Если , то более пологий «спуск» полигона наблюдается слева; если – справа. В первом случае асимметрию называют левосторонней, а во втором – правосторонней.
Определение. Выборочным коэффициентом эксцесса или коэффициентом крутости называется число , определяемое формулой :
.
Выборочный коэффициент эксцесса служит для сравнения на «крутость» выборочного распределения с нормальным распределением.
Коэффициент эксцесса для случайной величины, распределенной по нормальному закону, равен нулю.
Поэтому за стандартное значение выборочного коэффициента эксцесса принимают .
Если , то полигон имеет более пологую вершину по сравнению с нормальной кривой; если , то полигон более крутой по сравнению с нормальной кривой.
1.7. Вычисление числовых характеристик выборки
Таблица 6
– середины интервалов; – частоты; – объем выборки;
с помощью суммы находим ;
с помощью суммы находим и ;
с помощью суммы находим ;
с помощью суммы находим .
1.7.1. Упрощенный способ вычисления
статистических характеристик вариационных рядов
При больших значениях вариантов и соответствующих им частот вычисление выборочного среднего, дисперсии и выборочных моментов по приведенным ниже формулам приводит к громоздким вычислениям.
В этом случае используют условные варианты , определяемые по формулам: , где числа и выбираются произвольно.
Чтобы упростить вычисления в качестве выбирают вариант, который имеет наибольшую частоту или находится в середине ряда. Число называется «ложным нулем». В качестве выбирают число равное длине интервала ( в случае интервального ряда) или наибольший общий делитель разностей .
Для вычисления числовых характеристик выборки составляем табл. 7.
Таблица 7.
Контроль:
С помощью сумм, полученных в нижней строке таблицы, находим условные моменты:
, ,
, .
Числовые характеристики выборки вычисляем по формулам:
; ; ;
; ,
где и находим по формулам:
,
.
Исследование выборки: числовые характеристики, графики
Исследование выборки – базовая тема при изучении математической статистики, с нее начинаются любые курсы МС. Нужно научиться находить объем выборки, числовые характеристики (выборочное среднее, дисперсию, исправленную дисперсию, среднее квадратическое отклонение, коэффициент вариации и т.п.). При этом для выборок большого объема часто требуется перейти к интервальному представлению (правильно рассчитав число интервалов и их длину, обычно по формуле Стерджеса). Это все относится к первичной обработке статистической выборки.
Помимо проведения вычислений (чаще всего с помощью Excel) нужно уметь графически представлять выборку: строить полигон, гистограмму, кумуляту, огиву и другие графики и диаграммы.
В этом разделе мы рассмотрим решения задач на исследование выборки, нахождение ее характеристик и построение соответствующих графиков. Изучайте!
Примеры решений онлайн
Полезная страница? Сохрани или расскажи друзьям
Простой вариационный ряд
Задача 1. Дан следующий вариационный ряд
1 2 3 4 5 6 7 8 9 10
1 1 2 2 4 4 4 5 5 5
Требуется
1) Построить полигон распределения
2) Вычислить выборочную среднюю, дисперсию, моду, медиану.
3) Построить выборочную функцию распределения
4) Найти несмещенные оценки математического ожидания и дисперсии.
Задача 2. Из изучаемой налоговыми органами обширной группы населения было случайным образом было отобрано 10 человек и собраны сведения об их доходах за истёкший год в тысячах рублей: х1, х2,….х10, найти выборочное среднее, выборочную дисперсию, исправленную выборочную дисперсию. Считая распределения доходов в группе нормальным и используя в качестве его параметров выборочное среднее и исправленную выборочную дисперсию, определить какой процент группы имеет годовой доход, превышающий а тысяч рублей
Задача 3. Из генеральной совокупности извлечена выборка объема n. Найти выборочную среднюю, выборочную дисперсию, выборочное среднее квадратическое отклонение, исправленную выборочную дисперсию, коэффициент вариации, моду и медиану.
10,5 11 11,5 12 12,5 13 13,5
2 18 40 25 6 5 4
Задача 4. Дана выборка. Требуется:
а) Построить статистический ряд распределения частот и полигон частот;
б) Вариационный ряд;
в) Найти оценки математического ожидания и дисперсии;
г) Найти выборочные моду, медиану, коэффициент вариации, коэффициент асимметрии.
10,20,20,5,15,20,5,10,20,5.
Задача 5. Найти методом произведений: 1) выборочную дисперсию, 2) выборочное среднее квадратическое отклонение по данному статистическому распределению выборки (в первой строке указаны выборочные варианты $x_i$, а во второй строке – соответствующие частоты $n_i$).
Задача 6. При определении удельного расхода корундового шлифовального круга при шлифовке стальных деталей (отношение изношенного объема круга в мм3 к объему сошлифованного металла в мм3) были получены следующие результаты:
Провести статистическую обработку результатов испытаний.
Интервальный ряд
Задача 7. Проведено выборочное обследование магазинов города. Имеются следующие данные о величине товарооборота для 50 магазинов города (xi – товарооборот, млн. руб.; ni – число магазинов).
xi 25-75 75-125 125-175 175-225 225-275 275-325
ni 12 15 9 7 4 3
Найти
а) среднее, среднее квадратическое отклонение S и коэффициент V;
б) построить гистограмму и полигон частот.
Задача 8. Ряд распределения заработной платы рабочих механического цеха приведен в таблице. Требуется вычислить коэффициент вариации $V$, приняв $i=1$.
Заработная плата (руб.) 212-214 214-216 216-218 218-220 220-222
Число рабочих 7 12 12 9 5
Задача 9. Требуется для решения:
– Построить интервальный ряд распределения, для каждого интервала подсчитать локальные, а также накопленные частоты, построить вариационный ряд.
– Построить полигон и гистограмму.
– определить выборочную среднюю, а также низшую и высшую частные средние ,моду и медиану, дисперсию и среднее квадратическое отклонение, коэффициент вариации.
– проверить при уровне значимости 0,05 гипотезу о нормальном законе распределения соответствующего признака с помощью критериев согласия Пирсона, и Смирнова.
-найти точечные и интервальные оценки генеральной средней и среднего квадратичного отклонения (при доверительной вероятности Р=0,95.
– найти ошибки выборочных оценок.
– произвести анализ всех вычисленных статистических параметров.
Задание: произвести обработку данных по среднегодовому удою молока по 11-70 хозяйствам, 80 хозяйств.
Задача 10. Для исследования доходов населения города, составляющего 20000 чел. по схеме бесповторной выборки было отобрано некоторое количество жителей. Получено следующее распределение жителей по месячному доходу (см. таблицу вариантов).
Построить гистограмму, полигон и кумуляту относительных частот.
Найти вероятность того, что истинный средний доход отличается от среднего дохода по выборке не более, чем на 45 у.е. (по абсолютной величине).
Определить границы, в которых заключен доход с вероятностью 0,99.
Найти объем выборки, при котором, гарантируется вероятность тех же границ, равная 0,9973.
Другие задания
Задача 11. Как изменится выборочное среднее, мода, медиана и выборочная дисперсия, если каждый член выборки уменьшить в 5 раз?
Нужно решить задачи на исследование выборки?
Полезные ссылки
- Статистические таблицы и формулы
- Решение задач по математической статистике на заказ
- Ссылки на учебники по математической статистике
- Решенные контрольные по математической статистике