Как найти хиксианский спрос

Функция
компенсированного спроса
– функция,
которая
выражает
индивидуальный
спрос
на
товары
через
цены
определенного
уровня
полезности

В теории
потребителя спрос
Хикса отражает
те
наборы, которые потребитель выберет
при заданных ценах и уровне полезности,
решая задачу
минимизации своих расходов.
Назван по имени английского экономиста Хикса.
Также называюткомпенсированным
спросом.

Если
требуется узнать, как меняется объем
спроса на товар по мере изменения его
цены без учета эффекта дохода (только
под воздействием эффекта замены), то
следует построить кривую спроса по
Хиксу.

В
этом случае предполагается, что в
результате компенсации (положительной
или отрицательной) бюджета потребителя
изменение цены товара не меняет его
благосостояния: (U = const).
Поэтому бюджетная линия, меняя наклон
при изменении цены, все время касается
исходной кривой безразличия.

Графически
функцию хиксианского спроса можно
изобразить через связь между количеством
спрашиваемого блага и ценой на это
благо, предполагая, что все другие цены
и полезность не меняются. 

Кривая
компенсированного спроса показывает
взаимосвязь между ценой

блага
и количеством этого блага, которое
покупается потребителем при данной
цене,

при
условии, что цены других благ и полезность
остаются постоянными.

Свойства:

При
условии непрерывности функции
полезности и
задания её в нуле таким образом, что,
спрос Хиксаобладает
следующими свойствами:

1. Однородность
   нулевой степени по ценам p:
   для всех ,,
   так как наборx,
   минимизирующий сумму ,
   также минимизирует суммупри
   том же бюджетном ограничении.

2. Ограничение удовлетворяется
   как равенство:.
   Это следует из непрерывности функции
   полезности, так как можно тратить меньше
   на некое δe и уменьшать значение
   полезности на δu, пока оно не станет
   равным в точности.

3. Если
   предпочтения выпуклы,
   то—выпуклое
   множество.

4. Если
   предпочтения строго
   выпуклые, тосостоит
   из одного элемента (является функцией
   компенсированного спроса).

5. Имеет
   место закон
   компенсированного спроса:

Удобство
подхода Хикса заключается в том, что
минимизируемая функция
расходов имеет
линейный вид.

Если
предпочтения потребителя
являются непрерывными и
функция полезности задана в нуле так,
что ,
то спрос по Хиксу является
решением задачи
максимизации полезности при
ценах и
доходе ,
где e(•) —функция
расходов. При
этом .

По
Хиксу реальный доход
измеряется полезностью приобретаемого
набора товаров. Если после изменения
цен потребитель может купить на весь
свой доход набор, имеющий такую же
полезность, что и прежний набор, то его
благосостояние, т.е. реальный доход, не
изменяется. При выделении эффекта
замещения по Хиксу влияние дохода
элиминируется тем, что вспомогательная
бюджетная линия (на которой находится
вспомогательный набор, разделяющий
эффект замещения и эффект дохода)
касается кривой безразличия, на которой
находится первоначальный набор.

Компенсированный
спрос по Хиксу есть функция товара при
постоянной цене товара и
фиксированной полезности набора,
приобретаемого потребителем .

2.Отличия
функций компенсированного и
некомпенсированного спроса

Различают
два типа функций спроса: некомпенсированный
(маршаллианский) спрос и компенсированный
(хиксианский) спрос. Известно, что
изменение цен порождает как эффект
замещения, так и эффект дохода.
Маршаллианская и хиксианская функции
спроса различаются “отношением”
к этим двум эффектам.

В отличие от функции спроса Маршалла (Marshalliandemand function) в функции спроса Хикса изменение цены товара будет иметь лишь один эффект, а именно
эффект замещения (substitution), поскольку уровень полезности считается постоянным. 

Маршаллианские
функции спроса хорошо известны из
макроэкономической теории. Они получаются
в результате максимизации потребителем
функции полезности с учетом бюджетного
ограничения. 

Маршаллианский
спрос определяется следующей формулой

C(M)_i=Ci(P₁,P₂,…,P_N,Y),
i=
1,…,N.

Таким
образом, спрос на каждое благо – это
функция от цен всех благ и от дохода.
Кривая спроса изображается графически
обычно, чтобы установить связь между
количеством спрашиваемого блага и ценой
на это благо, предполагая, что все другие
цены и доход не меняются. Этот спрос
некомпенсированный, т.к. не рассматриваются
никакие компенсации, выплаченные для
снятия эффекта дохода. Движение вдоль
кривой маршаллианского спроса, таким
образом, представляет собой комбинацию
эффектов дохода и замещения при изменении
цены.

Хиксианская
функция спроса является результатом
решения другой задачи:

Функция
хиксианского спроса имеет следующий
вид:

C(H)_i=H_i(P₁,P₂,…,P_N,U^F).

Таким
образом, спрос на i-тый товар – это функция
от цены на все блага и от требуемого
уровня полезности.

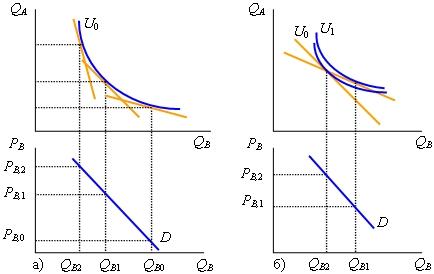
Графически
функцию хиксианского спроса можно
изобразить через связь между количеством
спрашиваемого блага и ценой на это
благо, предполагая, что все другие цены
и полезность не меняются.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

В теории потребителя спрос Хикса отражает те наборы, которые потребитель выберет при заданных ценах и уровне полезности, решая задачу минимизации своих расходов. Назван по имени английского экономиста Хикса. Также называют компенсированным спросом.

Математическая запись[править | править код]

где h(p,u) — спрос Хикса при ценах p и значении функции полезности .

В случае когда известна функция расходов и она непрерывна в точке , компенсированный спрос может быть найден по лемме Шепарда и выглядит следующим образом:

Двойственность в теории потребления[править | править код]

Удобство подхода Хикса заключается в том, что минимизируемая функция расходов имеет линейный вид, но переменные для функции маршалловского спроса (p, w), легче наблюдать на практике.

Если предпочтения потребителя являются непрерывными и функция полезности задана в нуле так, что , то спрос по Хиксу является решением задачи максимизации полезности при ценах и доходе , где e(•) — функция расходов. При этом .

Обратное тоже имеет место, но при других условиях. Если предпочтения являются локально ненасыщаемыми, то маршалловский спрос является решением задачи минимизации расходов и .

Свойства[править | править код]

При условии непрерывности функции полезности и задания её в нуле таким образом, что , спрос Хикса обладает следующими свойствами:

1. Однородность нулевой степени по ценам p: для всех , , так как набор x, минимизирующий сумму , также минимизирует сумму при том же бюджетном ограничении.
2. Ограничение удовлетворяется как равенство: . Это следует из непрерывности функции полезности, так как можно тратить меньше на некое δe и уменьшать значение полезности на δu, пока оно не станет равным в точности .
3. Если предпочтения выпуклы, то  — выпуклое множество.
4. Если предпочтения строго выпуклые, то состоит из одного элемента (является функцией компенсированного спроса).
5. Имеет место закон компенсированного спроса:

См. также[править | править код]

• Задача потребителя
• Маршалловский спрос

Литература[править | править код]

• Фридман А. А. Лекции по курсу микроэкономики продвинутого уровня. — М.: Издательский дом ГУ ВШЭ, 2007. — С. 71. — ISBN 978-5-7598-0335-5..

From Wikipedia, the free encyclopedia

In microeconomics, a consumer’s Hicksian demand function or compensated demand function for a good is his quantity demanded as part of the solution to minimizing his expenditure on all goods while delivering a fixed level of utility. Essentially, a Hicksian demand function shows how an economic agent would react to the change in the price of a good, if the agent’s income was compensated to guarantee the agent the same utility previous to the change in the price of the good—the agent will remain on the same indifference curve before and after the change in the price of the good. The function is named after John Hicks.

Mathematically,^[1]

.

where h(p,u) is the Hicksian demand function, or commodity bundle demanded, at price vector p and utility level . Here p is a vector of prices, and x is a vector of quantities demanded, so the sum of all p_ix_i is total expenditure on all goods. (Note that if there is more than one vector of quantities that minimizes expenditure for the given utility, we have a Hicksian demand correspondence rather than a function.)

Hicksian demand functions are useful for isolating the effect of relative prices on quantities demanded of goods, in contrast to Marshallian demand functions, which combine that with the effect of the real income of the consumer being reduced by a price increase, as explained below.

Relationship to other functions[edit]

Hicksian demand functions are often convenient for mathematical manipulation because they do not require income or wealth to be represented. Additionally, the function to be minimized is linear in the , which gives a simpler optimization problem. However, Marshallian demand functions of the form that describe demand given prices p and income are easier to observe directly. The two are related by

where is the expenditure function (the function that gives the minimum wealth required to get to a given utility level), and by

where is the indirect utility function (which gives the utility level of having a given wealth under a fixed price regime). Their derivatives are more fundamentally related by the Slutsky equation.

Whereas Marshallian demand comes from the Utility Maximization Problem, Hicksian Demand comes from the Expenditure Minimization Problem. The two problems are mathematical duals, and hence the Duality Theorem provides a method of proving the relationships described above.

The Hicksian demand function is intimately related to the expenditure function. If the consumer’s utility function is locally nonsatiated and strictly convex, then
by Shephard’s lemma it is true that

Hicksian demand and compensated price changes[edit]

Marshallian demand curves show the effect of price changes on quantity demanded. As the price of a good rises, ordinarily, the quantity of that good demanded will fall, but not in every case. The price rise has both a substitution effect and an income effect. The substitution effect is the change in quantity demanded due to a price change that alters the slope of the budget constraint but leaves the consumer on the same indifference curve (i.e., at the same level of utility). The substitution effect always is to buy less of that good. The income effect is the change in quantity demanded due to the effect of the price change on the consumer’s total buying power. Since for the Marshallian demand function the consumer’s nominal income is held constant, when a price rises his real income falls and he is poorer. If the good in question is a normal good and its price rises, the income effect from the fall in purchasing power reinforces the substitution effect. If the good is an inferior good, the income effect will offset in some degree to the substitution effect. If the good is a Giffen good, the income effect is so strong that the Marshallian quantity demanded rises when the price rises.

The Hicksian demand function isolates the substitution effect by supposing the consumer is compensated with exactly enough extra income after the price rise to purchase some bundle on the same indifference curve.^[2] If the Hicksian demand function is steeper than the Marshallian demand, the good is a normal good; otherwise, the good is inferior. Hicksian demand always slopes down.

Mathematical properties[edit]

If the consumer’s utility function is continuous and represents a locally nonsatiated preference relation, then the Hicksian demand correspondence satisfies the following properties:

i. Homogeneity of degree zero in p: For all , . This is because the same x that minimizes also minimizes subject to the same constraint.^[3]

ii. No excess demand: The constraint holds with strict equality, . This follows from continuity of the utility function. Informally, they could simply spend less until utility was exactly .

See also[edit]

• Marshallian demand function
• Convex preferences
• Expenditure minimization problem
• Slutsky equation
• Duality (optimization)

References[edit]

• Mas-Colell, Andreu; Whinston, Michael & Green, Jerry (1995). Microeconomic Theory. Oxford: Oxford University Press. ISBN 0-19-507340-1.

Рассмотрим вопрос о том, какие денежные средства требуются потребителю при данных ценах на достижение заданного уровня благосостояния и какие потребительский наборы обеспечивают минимальное значение потребительских расходов. Ответы на эти вопросы можно получить с помощью следующей задачи:
ph Ч> min hex
h У x.

В этой задаче требование к минимально допустимому уровню благосостояния задается потребительским набором x. В верхнем лебеговском множестве набора x, L+(x) = { y el | y ^ x }, ищется самый дешевый (в ценах p) набор. На основе этой задачи приходим к понятию хикси- анского спроса.
Определение 25:
Отображение
h(p, x) = argmin ph
hИL+(x)
называется спросом по Хиксу (хиксианским спросом) . В случае если данное отображение является однозначным, h(p, x) называется функцией спроса по Хиксу .
Таким образом, хиксианский спрос при заданных p и x – это самый дешевый потребительский набор при заданных ценах p, среди всех наборов, которые не хуже, чем x, в то время как обычный (маршаллианский) спрос – это наилучший с точки зрения предпочтений индивидуума набор в бюджетном множестве. На Рис. 3.2 в случае двух благ иллюстрируется разница в понятиях маршаллианского и хиксианского спросов.
хиксианский спрос

i
Х2 бюджетная прямая i ^ кривая безразличия

маршаллианский спрос
Рис. 3.2. Маршаллианский и хиксианский спрос
Если предпочтения представимы функцией полезности u : X ^ R, отображение хиксианского спроса может быть найдено как решение параметрического семейства задач математического программирования:
ph ^ min
heX (H)
u(h) Z u(x),
каждая из которых обычно называется двойственной (взаимной) к соответствующей задаче потребителя (задаче поиска маршаллианского спроса).
Следующая теорема устанавливает основные свойства отображения (функции) хиксианского спроса.

Теорема 25 (свойства хиксианского спроса):
Пусть p e R++, предпочтения потребителя являются непрерывными. Тогда
решение двойственной задачи потребителя существует, т. е. h(p, x) = 0 Vx e X;
если предпочтения потребителя выпуклы, то h(p, x) – выпуклое множество;
если предпочтения потребителя строго выпуклы, то h(p, x) – непрерывная функция;
отображение h(p, x) однородно нулевой степени по p, т. е. h(Ap, x) = h(p, x) (A > 0);
если x’ ~ x”, то h(p, x’) = h(p, x”);
для каждого h e h(p, x) справедливо h ~ x. J
Доказательство: Доказательство в общих чертах идет по схеме доказательства Теоремы 23 и оставляется читателю в качестве упражнения. ж
Обсудим, как и в случае с маршаллианским спросом, необходимые и достаточные условия оптимума задачи минимизации расходов (поиска хиксианского спроса)
ph ^ min
hZ0 (H’)
u(h) Z u(x),
Здесь предполагается, что X = R+, т. е. h Z 0 – условие того, что h – допустимый набор, и что функция полезности u(-) определена на более широком, чем X = R+, открытом множестве (например, R1), и является дифференцируемой.
Условия КунаЧ Таккера для задачи (H’) в точке h имеют вид
(1) – p + AVu(h) < 0; (2) (-p + AVu(h))h = 0;
(3) A(u(h) – u(x)) = 0; (4) A Z 0.
Если набор h, допустимый в задаче (H’), удовлетворяет этим условиям при некотором множителе Лагранжа A, и функция полезности квазивогнута (предпочтения выпуклы), то по обратной теореме КунаЧ Таккера h является решением этой задачи. Действительно, поскольку целевая функция ph линейна, то она вогнута; ограничение же задается квазивогнутой функцией u(h) – u(x) .
С другой стороны, если h – решение рассматриваемой задачи, то (при выполнении условий регулярности) найдется множитель Лагранжа A, такой что для (h, A) выполнены условия КунаЧ Таккера. Предположение Vu(h) = 0 обеспечивает выполнение условий регулярности в форме КунаЧ Таккера.
Таким образом, приведенные условия являются необходимыми и достаточными условиями того, чтобы набор h (h x) являлся решением задачи минимизации расходов.
Для внутреннего набора h e int X в более общей задаче (H) условия КунаЧТаккера принимают более простой вид:
– p + AVu(h) < 0;
A(u(h) – u(x)) = 0; (3) A Z 0.
Заметим попутно, что, как несложно увидеть, если x = x(p, R) – решение задачи потребителя при ценах p e R++ и доходе R > 0, и A – множитель Лагранжа, отвечающий этому решению, такой что A > 0, то множитель Лагранжа в соответствующей задаче поиска хик-сианского спроса A должен быть равен ^. (О взаимосвязи двух задач речь пойдет ниже в Теореме 27.)
Используя условия КунаЧ Таккера, найдем теперь функцию хиксианского спроса для случая, рассматривавшегося нами в Примере 11.?
3.1. Модель поведения потребителя: основные понятия и свойства 76
Пример 14 (продолжение Примера 11):
Для функции полезности u(x) = yfx + a^fx2 хиксианский спрос является решением следующей задачи:
pihi + p2h2 ^ min
/h + ^v/h2 ^ u(x).
Функция Лагранжа для этой задачи имеет вид:
L(h, Л) = -pihi – p2h2 + A(v/hi + afh2 – u(x)).
Предположим, что решение является внутренним, т. е. hi > 0, h2 > 0. При этом из условий КунаЧ Таккера получим
-pi +Лш = 0, -Р2 +Ла27h2 = 0.
Несложно заметить, что из этих двух равенств следует Л > 0, а, значит, yfhi + afh2 = u(x). Отсюда имеем ^^hL = pi или h2 = (ap^j hi. Так как /hi + a/h2 = u(x), то /hi +
a2pi/^ = u(x) или h^ = )2, откуда, h2 = (Pf+g-)2.
Читатель может проверить, что невнутренние наборы, удовлетворяющие ограничению задачи, дают более высокое значение расходов, чем найденный набор, т. е. найденный набор является оптимумом, причем единственным. (что, впрочем очевидно, так как решение задачи минимизации расходов при строго вогнутой функции полезности (строго выпуклых предпочтениях) единственно, а условия Куна-Таккера в данном случае являются не только необходимыми, но и достаточными. Таким образом, хиксианский спрос равен
w ii P2u(x) 2 / apiu(x) h(p, x) 11 11
Р2 + a2pi) p2 + a2pi
Проиллюстрируем теперь свойства функции хиксианского спроса, доказанные в Теореме 25. То, что хиксианский спрос однороден нулевой степени по ценам очевидно. Действи-тельно,
, . . . tp2u(x) 2 / atpiu(x)
h(tp, x) 11 11
tp2 + a2tpiJ ‘ tp2 + a2tpi
2
p2u(x) 2 f apiu(x)
t0h(p, x).
P2 + a2pi) ‘2 + a2pi
Проверим, что u(h(p, x)) = u(x). Подставив хиксианский спрос в функцию полезности, мы получим:
u(h(p, x)) = Уhi(p, x) + aJh2(p, x)
/ p2u(x) / apiu(x) p2u(x) apiu(x)
= W( )2 + aW( Ч)2 = + a = u(x). Д
у ‘2 + a2pi у ‘2 + a2pi ‘2 + a2pi ‘2 + a2pi
Аналогом непрямой функции полезности в двойственной задаче потребителя является функция расходов .

Определение 26:
Функция e(p, x) = ph, где h e h(p, x) – хиксианский спрос приданных p и x, называется функцией расходов (затрат).
Другими словами, функция расходов e(p, x) – значение целевой функции двойственной задачи в точке оптимума при данных p и x. Согласно определению, для каждого достижимого уровня полезности функция расходов указывает минимальный уровень расходов (дохода), обеспечивающий такой уровень полезности.
Теорема 26 (свойства функции расходов):
Пусть выполнены предположения Теоремы 25. Тогда
функция e(p, x) однородна первой степени по ценам: e(Ap, x) = Ae(p, x) (A > 0);
функция e(p, x) не убывает по ценам: e(p’, x) ^ e(p, x) при p Z p’;
функция e(p, x) – вогнутая функция цен p;
функция e(p, x) непрерывна;
x ^ y тогда и только тогда, когда e(p, x) Z e(p, y); J
Доказательство: (i) Первый пункт утверждения следует из того, что решения двойственной задачи при векторе цен p и векторе цен Ap совпадают.
Пусть p’ Z p, p’ = p, he h(p, x) и h’ e h(p’, x). Тогда ph’ Z ph = e(p, x). С другой стороны, e(p’, x) = p’h’ Z ph’. (Заметим, что если h’ > 0, то e(p’, x) > e(p, x).)
Мы должны показать, что для двух произвольных векторов p1 и p2 при 0 ^ a ^ 1 выполняется e(ap1+(1-a)p2, x) Z ae(p1, x)+(1-a)e(p2, x). Пусть h – решение двойственной задачи при ценах pa = ap1 + (1-a)p2, т. е. h e h(pa, x). Отметим, pah = e(pa, x). Допустимое множество { he X | h x } не зависит от p, поэтому потребительский набор h допустим в двойственной задаче как при ценах p1 , так и при ценах p2 . Из определения функции расходов и допустимости h имеем e(p1, x) ^ p1h и e(p2, x) ^ p2h. Отсюда
ae(p1, x) + (1 – a)e(p2, x) < pah = e(pa, x).
Доказательство непрерывности оставляем читателю в качестве упражнения. Заметим только, что непрерывность функции расходов по ценам следует из того, что она является вогнутой (как функция цен) и определена на открытом множестве (а любая вогнутая функция непрерывна во внутренности своей области определения).
(v^) Докажем, что из x ^ y следует e(p, x) Z e(p, y). Так как x ^ y, то все потребительские наборы, допустимые в двойственной задаче при наборе параметров (p, x), являются допустимыми в этой задаче при наборе параметров (p, y). В том числе, допустимыми являются и наборы, принадлежащие h(p, x), а это и означает что e(p, x) Z e(p, y).
(v^) Докажем, что из e(p, x) Z e(p, y) следует x ^ y. Предположим противное, то есть y У x. При этом e(p, y) = e(p, x) и, значит, h(p, y) С h(p, x). Возьмем h e h(p, y). В силу непрерывности предпочтений и того, что X – выпуклое множество и 0 X, существует такое число a < 1, что ah x .В этом случае p ж (ah) = ae(p, y) < e(p, x), что противоречит определению e(p, x). ж
На основании пункта (v) можно говорить о функции e(p, x), как о функции полезности, которая представляет исходные предпочтения. Это свойство – одно из самых важных свойств функции расходов и является ключевым при обсуждении вопроса о восстановлении предпочтений по наблюдаемой функции спроса (см. параграф 3.C).
Проиллюстрируем теперь нахождение функции расходов.
Пример 15 (продолжение Примера 11):
Найдем функцию расходов e(p, x), соответствующую функции полезности u(x) = -^/х? + й/ж2. Как было показано выше, функция хиксианского спроса для рассматриваемого потре- ,2 / ДД Д,/Дч 2ч
бителя равна h(p,x) = ^(pp+al^) , (pf+U2*!) ) ‘ Из определения функции расходов имеем:
/ p2u(x) 2 / apiu(x) 2
e(p, x) = pihi(p, x)+ p2^2(p, x) = pi жЧ^ + p2 жЧ^ =
VP2 + a2pi/ VP2 + a2pi/
= / u(x) ^ (pi(p2)2 + a2p2(pi)2) = ( U(x)2 ) (pip2 + a2pi)pip2 = Vp2 + a2pi / Vp2 + a2pi /
u(x) ^2(pip2 + a2pi)pip2 = pip2 (u(x))2
p2 + a2pi / p2 + a2pi
На примере данной функции проиллюстрируем выполнение свойств, доказанных в Теореме 26.
Покажем, что полученная функция однородна первой степени по ценам.
e = tpitp2(u(x))2 = tpip2(u(x))2 = te(p, x).
tp2 + a2 tpi p2 + a2pi
Проверим свойство неубывания по ценам. Отметим, что
( ) = pip2(u(x))2 = (u(x))2
e(p, x)= p2 + a2pi = pi + p2 .
pi p2
Действительно при росте при росте pi величина ^ убывает, что в свою очередь влечет рост значения дроби (U(x))2 , и, тем самым, рост функции расходов.
Pi + Р2
Проверим теперь вогнутость функции расходов по ценам. Матрица вторых частных про-
изводных для функции расходов e(p, x) = pip2+u (2x)) равна
(X “
p2+ a2pi
u(x)) 2a 2 pip2(u(x)
(p2+ a2pi)3 (p2+ a2pi)3
2a2pip2(u(x))2 2a2p2(u(x))2
У (p2 +a2pi)3 (p2+a2 pi)3
H
( 2a2p2(u(x))2 2a2pip2(u(x))2′
Несложно заметить, что первый главный последовательный минор отрицателен, а второй равен 0. Значит, главные последовательные миноры чередуют свой знак, начиная с первого, который отрицателен. Таким образом, матрица H отрицательно полуопределена и, соответственно, функция e(p, x) вогнута.
Наконец проверим, что x y ^ e(p, x) Z e(p, y). Действительно, в силу положительности цен имеем: e(p, x) Z e(p, y) ^ pfйxf Z ^ (u(x))2 Z (u(y))2. Так как u(x) =
/Xi + a/x2 и, тем самым, неотрицательна, то условие (u(x))2 Z (u(y))2 эквивалентно условию u(x) Z u(y). То есть, e(p, x) Z e(p, y) ^ u(x) Z u(y). Откуда по определению функции полезности имеем, что e(p, x) Z e(p, y) ^ x ^ y. Д
Рассмотрим теперь вопрос о взаимосвязи прямой и двойственной задач потребителя. Следующая теорема, называемая теоремой взаимности (двойственности), устанавливает условия совпадения решений прямой и двойственной задач потребителя.
Теорема 27 (теорема взаимности /двойственности/):
Пусть X = R++ и p ? R++, а предпочтения потребителя непрерывны. Тогда
если предпочтения локально ненасыщаемы, то x ? x(p, R) влечёт x ? h(p, x);
для любого h ? h(p, x), где x ? X, выполнено h ? x(p, e(p, x)) = x(p, ph). J

Доказательство: (i) Предположим противное. Пусть x ? h(p, x), т. е. в двойственной задаче существует потребительский набор h’ ^ x такой, что px > ph’. Из локальной ненасыщаемости предпочтений следует, что существует набор h”, такой что h” У h’ ^ x, и при этом px > ph”. А это противоречит оптимальности x в прямой задаче потребителя.
(ii) Случай h = 0 очевиден, поэтому будем исходить из того, что h = 0 (и, следовательно, ph > 0). Набор h допустим в прямой задаче потребителя при ценах p и доходе ph. Предположим, что он не является решением этой задачи. Тогда существует потребительский набор x = ph ? B(p, ph)) такой, что x’ У h .В силу непрерывности предпочтений найдется 0 < a < 1 такое, что ax’ h. Набор ax’ стоит дешевле h в ценах p, а это противоречит оптимальности h в двойственной задаче потребителя. ж
Следующая теорема является следствием предыдущей и устанавливает другие связи между характеристиками прямой и взаимной задачи потребителя.
Теорема 28 (соотношения двойственности, следствие Теоремы 27):
Пусть выполнены все предположения Теоремы 27 (включая локальную ненасыщаемость предпочтений). Тогда верны следующие тождества:
для любого x ? x(p, R) выполнено e(p, x) = R;
для любого x ? x(p, R) выполнено x(p, R) = h(p, x);
v(p,e(p, x)) = u(x);
^p^fo x)) = x). J
Доказательство: (i) Теорема 27 показывает, что для любого x ? x(p, R) выполнено x ? h(p, x). Отсюда, по определению функции расходов, e(p, x) = px. В силу локальной ненасыщаемости предпочтений px = R.
То, что для любого x ? x(p, R) выполнено x(p, R) = h(p, x), является тривиальным следствием пунктов (i) и (iv).
Пусть h ? h(p, x) при некотором x ? X. Согласно пункту (vi) Теоремы 25 при непрерывности предпочтений должно выполняться u(h) = u(x). Кроме того, по доказанной теореме двойственности h ? x(p, e(p, x)), т. е. набор h оптимален в прямой задаче при ценах p и доходе e(p, x). Таким образом, по определению непрямой функции полезности v(p, e(p, x)) = u(h), откуда v(p, e(p, x)) = u(x).
Включение h(p, x) С x(p,e(p, x)) доказано в теореме двойственности. Докажем обратное включение. Пусть x ? x(p, e(p, x)). Из пункта (i) Теоремы 27 следует, что x ? h(p, x), а из пункта (i) доказываемой теоремы – что e(p, x) = e(p, x). Из пункта (v) Теоремы 26 следует, что x ~ x. Таким образом, h(p, x) = h(p, x), и поэтому x ? h(p, x). ж
Проиллюстрируем полезность установленных соотношений двойственности. Пусть, решив задачу потребителя, мы нашли функцию спроса и непрямую функцию полезности. Как демонстрируют следующие примеры, этой информации достаточно для того, чтобы найти функцию хиксианского спроса и функцию расходов, не решая соответствующую двойственную задачу.
Пример 16:
Как показано в Примерaх 11 и 13, функции полезности u(x) = у/ХТ + ay/x2 соответствует маршаллианская функция спроса
( Rp2 a2Rpi
x(p, R) ж
pi’2 + a2(pi)2′ (P2)2 + a2pi’2
и непрямая функция полезности v(p, R) = JPl) . Из соотношения v(p,e(p, x)) = u(x), имеем ^Je(p’x)j(pp+a Pl) = u(x). Отсюда несложно выразить расходы через полезность: e(p, x) =

p2+a2pi Х С учетом этого легко наити хиксианскии спрос:
Р1Р2(u(x))2 I / P2u(x) / apiu(x)
h(p, x) = x(p,e(p, x)) =x . 2 , . 2 , ,, . 2
у P2 + a2pi / V P2 + fl2Pv P2 + a2Pi,
Эти формулы совпадают с теми, которые получены в Примерах 15 и 14. Д
Пример 17:
Для гомотетичных предпочтении (однородной функции полезности) непрямая функция полезности и спрос имеют следующий вид: v(p, R) = a(p)R и x(p, R) = Rx(p, 1) (см. Примеры 10 и 12). Используя соотношения двойственности, несложно увидеть, что функция расходов и хиксианская функция спроса имеют вид
e(p,x)=, h(p,x)=x(p,e(p,x)) = x(p,1)- Д

Рис. 3.3. Толстая кривая безразличия
Рассмотрим теперь пример, когда хиксианский и маршаллианский спрос не совпадают. Для построения этого примера достаточно рассмотреть предпочтения, не обладающие свойством локальной ненасыщаемости. В качестве таковых, рассмотрим предпочтения, порождающие лтолстую кривую безразличия (такие кривые безразличия появятся, например, если взять в качестве функции полезности целую часть какой-нибудь лнормальной функции полезности). Хиксианский спрос всегда будет лежать (случай двух благ) на левой границе лтолстой кривой безразличия. На Рис. 3.3 эта граница изображена темной линией. Маршаллианский же спрос может лежать внутри лтолстой кривой безразличия. (Найдите его на приведенном рисунке!)
В этом параграфе мы рассмотрели прямую и двойственную задачи потребителя, изучили их свойства и рассмотрели некоторые основные соотношения связывающие эти задачи. В следующем параграфе мы продолжим рассмотрение основных свойств данных задач, используя аппарат дифференциального исчисления.

Спрос потребителя по набору товаров, который минимизирует их расходы, обеспечивая при этом фиксированный уровень полезности.

В микроэкономике, соответствие спроса потребителя – это спрос потребителя на набор товаров, который сводит к минимуму их расходы, обеспечивая при этом фиксированный уровень полезности. Если соответствие на самом деле является функцией , оно упоминается как функция спроса Хикса или функция компенсированного спроса . Функция названа в честь Джона Хикса.

Математически

h (p, u ¯) = arg ⁡ min x ∑ ipixi { displaystyle h (p, { bar {u}}) = arg min _ {x} sum _ {i} p_ {i} x_ {i}}

subjecttou (x) ≥ u ¯ { displaystyle { rm {subject ~ to}} u (x) geq { bar {u}}}.

где h (p, u) – функция спроса по Хиксу или спрос на набор товаров при векторе цен p и уровне полезности u ¯ { displaystyle { bar {u }}}. Здесь p – вектор цен, а x – вектор объемов спроса, так что сумма всех p ixiявляется общими расходами на товары x.

Содержание

• 1 Связь с другими функциями
• 2 Спрос по Хиксу и компенсируемые изменения цен
• 3 Математические свойства
• 4 См. Также
• 5 Ссылки

Связь с другими функциями

Функции спроса Хикса часто удобны для математических манипуляций, поскольку они не требуют представления дохода или богатства. Кроме того, минимизируемая функция является линейной в x i { displaystyle x_ {i}}, что дает более простую задачу оптимизации. Однако функции спроса по Маршаллу вида x (p, w) { displaystyle x (p, w)}, которые описывают спрос с учетом цен p и дохода w { displaystyle w}легче наблюдать напрямую. Эти два тривиально связаны следующим образом:

час (p, u) = x (p, e (p, u)), { displaystyle h (p, u) = x (p, e (p, u)), }

где e (p, u) { displaystyle e (p, u)}– это функция расходов (функция, которая дает минимальное требуемое богатство чтобы достичь заданного уровня полезности), и

h (p, v (p, w)) = x (p, w), { displaystyle h (p, v (p, w)) = x ( p, w), }

где v (p, w) { displaystyle v (p, w)}– это функция косвенной полезности (которая дает уровень полезности данного богатства при режиме фиксированных цен). Их производные более фундаментально связаны между собой уравнением Слуцкого.

В то время как маршаллианский спрос возникает из проблемы максимизации полезности, спрос Хикса возникает из проблемы минимизации расходов. Эти две проблемы являются математически двойственными, и, следовательно, теорема двойственности обеспечивает метод доказательства отношений, описанных выше.

Функция спроса Хикса тесно связана с функцией расходов. Если функция полезности потребителя u (x) { displaystyle u (x)}локально не насыщена и строго выпуклая, то h (p, u) = ∇ pe (p, u). { displaystyle h (p, u) = nabla _ {p} e (p, u).}

Спрос по Хиксу и компенсированные изменения цен

Нисходящие маршаллианские кривые спроса показывают влияние изменений цен по требуемому количеству. По мере того, как цена на товар растет, вероятно, количество этого спроса будет падать, при этом богатство и другие цены останутся неизменными. Однако этот эффект изменения цен на объемы спроса обусловлен как эффектом дохода, так и эффектом замещения. Эффект замещения – это изменение объема спроса из-за изменения цены, которое изменяет наклон бюджетного ограничения, но оставляет потребителя на той же кривой безразличия (т. Е. На том же уровне полезности). Благодаря этому эффекту потребитель постулируется. заменить на добро, которое становится сравнительно менее дорогим. Если рассматриваемый товар является нормальным товаром, то эффект дохода от повышения покупательной способности в результате падения цен усиливает эффект замещения. Если товар является неполноценным товаром, то эффект дохода в некоторой степени компенсирует эффект замещения.

Функция спроса Хикса также имеет нисходящий наклон, но изолирует эффект замещения, предполагая, что потребитель получает компенсацию ровно настолько, чтобы купить какой-то пакет на той же кривой безразличия. Спрос Хикса иллюстрирует новую потребительскую корзину потребителя после изменения цены, при этом он получает компенсацию, позволяющую потребителю быть таким же счастливым, как и раньше (оставаться на том же уровне полезности). Если функция спроса Хикса «круче», чем маршаллианский спрос, товар является нормальным товаром; в противном случае хорошее низкое.

Математические свойства

Если функция полезности потребителя u (x) { displaystyle u (x)}является непрерывной и представляет локально ненасыщенное отношение предпочтения, то соответствие спроса Хикса h (p, u) { displaystyle h (p, u)}удовлетворяет следующим свойствам:

я. Однородность нулевой степени в p: для всех a>0 { displaystyle a>0}, h (ap, u) = h (p, u) { displaystyle h (ap, u) = h (p, u)}. Это потому, что тот же x, который минимизирует ∑ ipixi { displaystyle sum _ {i} p_ {i} x_ {i}}, также минимизирует ∑ iapixi { displaystyle sum _ {i} ap_ {i} x_ {i}}с тем же ограничением.

ii. Отсутствие избыточного спроса: ограничение u (hx) ≥ u ¯ { displaystyle u (hx) geq { bar {u}}}выполняется со строгим равенством, u (x) = u ¯ { displaystyle u (x) = { bar {u}}}. Это следует из непрерывности функции полезности. Неформально они могут просто тратить меньше, пока полезность не станет точно u ¯ { displaystyle { bar {u}}}.

См. также

• Маршаллианская функция спроса
• Выпуклые предпочтения
• Задача минимизации расходов
• Уравнение Слуцкого

Re ferences

• Мас-Колелл, Андреу ; Уинстон, Майкл и Грин, Джерри (1995). Микроэкономическая теория. Оксфорд: Издательство Оксфордского университета. ISBN 0-19-507340-1.