Парабола: определение, свойства, построение
Параболой называется геометрическое место точек плоскости, равноудаленных от заданной точки и заданной прямой
, не проходящей через заданную точку. Это геометрическое определение выражает директориальное свойство параболы.
Директориальное свойство параболы
Точка называется фокусом параболы, прямая
— директрисой параболы, середина
перпендикуляра, опущенного из фокуса на директрису, — вершиной параболы, расстояние
от фокуса до директрисы — параметром параболы, а расстояние
от вершины параболы до её фокуса — фокусным расстоянием (рис.3.45,а). Прямая, перпендикулярная директрисе и проходящая через фокус, называется осью параболы (фокальной осью параболы). Отрезок
, соединяющий произвольную точку
параболы с её фокусом, называется фокальным радиусом точки
. Отрезок, соединяющий две точки параболы, называется хордой параболы.
Для произвольной точки параболы отношение расстояния до фокуса к расстоянию до директрисы равно единице. Сравнивая директориальные свойства эллипса, гиперболы и параболы, заключаем, что эксцентриситет параболы по определению равен единице .
Геометрическое определение параболы, выражающее её директориальное свойство, эквивалентно её аналитическому определению — линии, задаваемой каноническим уравнением параболы:
(3.51)
Действительно, введем прямоугольную систему координат (рис.3.45,б). Вершину параболы примем за начало системы координат; прямую, проходящую через фокус перпендикулярно директрисе, примем за ось абсцисс (положительное направление на ней от точки
к точке
); прямую, перпендикулярную оси абсцисс и проходящую через вершину параболы, примем за ось ординат (направление на оси ординат выбирается так, чтобы прямоугольная система координат
оказалась правой).
Составим уравнение параболы, используя её геометрическое определение, выражающее директориальное свойство параболы. В выбранной системе координат определяем координаты фокуса и уравнение директрисы
. Для произвольной точки
, принадлежащей параболе, имеем:
где — ортогональная проекция точки
на директрису. Записываем это уравнение в координатной форме:
Возводим обе части уравнения в квадрат: . Приводя подобные члены, получаем каноническое уравнение параболы
т.е. выбранная система координат является канонической.
Проводя рассуждения в обратном порядке, можно показать, что все точки, координаты которых удовлетворяют уравнению (3.51), и только они, принадлежат геометрическому месту точек, называемому параболой. Таким образом, аналитическое определение параболы эквивалентно его геометрическому определению, выражающему директориальное свойство параболы.
Уравнение параболы в полярной системе координат
Уравнение параболы в полярной системе координат (рис.3.45,в) имеет вид
где
— параметр параболы, а
— её эксцентриситет.
В самом деле, в качестве полюса полярной системы координат выберем фокус параболы, а в качестве полярной оси — луч с началом в точке
, перпендикулярный директрисе и не пересекающий её (рис.3.45,в). Тогда для произвольной точки
, принадлежащей параболе, согласно геометрическому определению (директориальному свойству) параболы, имеем
. Поскольку
, получаем уравнение параболы в координатной форме:
что и требовалось доказать. Заметим, что в полярных координатах уравнения эллипса, гиперболы и параболы совпадают, но описывают разные линии, поскольку отличаются эксцентриситетами ( для эллипса,
для параболы,
для гиперболы).
Геометрический смысл параметра в уравнении параболы
Поясним геометрический смысл параметра в каноническом уравнении параболы. Подставляя в уравнение (3.51)
, получаем
, т.е.
. Следовательно, параметр
— это половина длины хорды параболы, проходящей через её фокус перпендикулярно оси параболы.
Фокальным параметром параболы, так же как для эллипса и для гиперболы, называется половина длины хорды, проходящей через её фокус перпендикулярно фокальной оси (см. рис.3.45,в). Из уравнения параболы в полярных координатах при получаем
, т.е. параметр параболы совпадает с её фокальным параметром.
Замечания 3.11.
1. Параметр параболы характеризует её форму. Чем больше
, тем шире ветви параболы, чем ближе
к нулю, тем ветви параболы уже (рис.3.46).
2. Уравнение (при
) определяет параболу, которая расположена слева от оси ординат (рис. 3.47,a). Это уравнение сводится к каноническому при помощи изменения направления оси абсцисс (3.37). На рис. 3.47,a изображены заданная система координат
и каноническая
.
3. Уравнение определяет параболу с вершиной
, ось которой параллельна оси абсцисс (рис.3.47,6). Это уравнение сводится к каноническому при помощи параллельного переноса (3.36).
Уравнение , также определяет параболу с вершиной
, ось которой параллельна оси ординат (рис.3.47,в). Это уравнение сводится к каноническому при помощи параллельного переноса (3.36) и переименования координатных осей (3.38). На рис. 3.47,б,в изображены заданные системы координат
и канонические системы координат
.
4. График квадратного трехчлена является параболой с вершиной в точке
, ось которой параллельна оси ординат, ветви параболы направлены вверх (при
) или вниз (при
). Действительно, выделяя полный квадрат, получаем уравнение
которое приводится к каноническому виду , где
, при помощи замены
и
.
Знак выбирается совпадающим со знаком старшего коэффициента . Эта замена соответствует композиции: параллельного переноса (3.36) с
и
, переименования координатных осей (3.38), а в случае
еще и изменения направления координатной оси (3.37). На рис.3.48,а,б изображены заданные системы координат
и канонические системы координат
для случаев
и
соответственно.
5. Ось абсцисс канонической системы координат является осью симметрии параболы, поскольку замена переменной на
не изменяет уравнения (3.51). Другими словами, координаты точки
, принадлежащей параболе, и координаты точки
, симметричной точке
относительно оси абсцисс, удовлетворяют уравнению (3.S1). Оси канонической системы координат называются главными осями параболы.
Пример 3.22. Изобразить параболу в канонической системе координат
. Найти фокальный параметр, координаты фокуса и уравнение директрисы.
Решение. Строим параболу, учитывая её симметрию относительно оси абсцисс (рис.3.49). При необходимости определяем координаты некоторых точек параболы. Например, подставляя в уравнение параболы, получаем
. Следовательно, точки с координатами
принадлежат параболе.
Сравнивая заданное уравнение с каноническим (3.S1), определяем фокальный параметр: . Координаты фокуса
, т.е.
. Составляем уравнение директрисы
, т.е.
.
Общие свойства эллипса, гиперболы, параболы
1. Директориальное свойство может быть использовано как единое определение эллипса, гиперболы, параболы (см. рис.3.50): геометрическое место точек плоскости, для каждой из которых отношение расстояния до заданной точки (фокуса) к расстоянию до заданной прямой
(директрисы), не проходящей через заданную точку, постоянно и равно эксцентриситету
, называется:
а) эллипсом, если ;
б) гиперболой, если ;
в) параболой, если .
2. Эллипс, гипербола, парабола получаются в сечениях кругового конуса плоскостями и поэтому называются коническими сечениями. Это свойство также может служить геометрическим определением эллипса, гиперболы, параболы.
3. К числу общих свойств эллипса, гиперболы и параболы можно отнести биссекториальное свойство их касательных. Под касательной к линии в некоторой её точке понимается предельное положение секущей
, когда точка
, оставаясь на рассматриваемой линии, стремится к точке
. Прямая, перпендикулярная касательной к линии и проходящая через точку касания, называется нормалью к этой линии.
Биссекториальное свойство касательных (и нормалей) к эллипсу, гиперболе и параболе формулируется следующим образом: касательная (нормаль) к эллипсу или к гиперболе образует равные углы с фокальными радиусами точки касания (рис.3.51,а,б); касательная (нормаль) к параболе образует равные углы с фокальным радиусом точки касания и перпендикуляром, опущенным из нее на директрису (рис.3.51,в). Другими словами, касательная к эллипсу в точке является биссектрисой внешнего угла треугольника
(а нормаль — биссектрисой внутреннего угла
треугольника); касательная к гиперболе является биссектрисой внутреннего угла треугольника
(а нормаль — биссектрисой внешнего угла); касательная к параболе является биссектрисой внутреннего угла треугольника
(а нормаль — биссектрисой внешнего угла). Биссекториальное свойство касательной к параболе можно сформулировать так же, как для эллипса и гиперболы, если считать, что у параболы имеется второй фокус в бесконечно удаленной точке.
4. Из биссекториальных свойств следуют оптические свойства эллипса, гиперболы и параболы, поясняющие физический смысл термина “фокус”. Представим себе поверхности, образованные вращением эллипса, гиперболы или параболы вокруг фокальной оси. Если на эти поверхности нанести отражающее покрытие, то получаются эллиптическое, гиперболическое и параболическое зеркала. Согласно закону оптики, угол падения луча света на зеркало равен углу отражения, т.е. падающий и отраженный лучи образуют равные углы с нормалью к поверхности, причем оба луча и ось вращения находятся в одной плоскости. Отсюда получаем следующие свойства:
– если источник света находится в одном из фокусов эллиптического зеркала, то лучи света, отразившись от зеркала, собираются в другом фокусе (рис.3.52,а);
– если источник света находится в одном из фокусов гиперболического зеркала, то лучи света, отразившись от зеркала, расходятся так, как если бы они исходили из другого фокуса (рис.3.52,б);
– если источник света находится в фокусе параболического зеркала, то лучи света, отразившись от зеркала, идут параллельно фокальной оси (рис.3.52,в).
5. Диаметральное свойство эллипса, гиперболы и параболы можно сформулировать следующим образом:
– середины параллельных хорд эллипса (гиперболы) лежат на одной прямой, проходящей через центр эллипса (гиперболы);
– середины параллельных хорд параболы лежат на прямой, коллинеарной оси симметрии параболы.
Геометрическое место середин всех параллельных хорд эллипса (гиперболы, параболы) называют диаметром эллипса (гиперболы, параболы), сопряженным к этим хордам.
Это определение диаметра в узком смысле (см. пример 2.8). Ранее было дано определение диаметра в широком смысле, где диаметром эллипса, гиперболы, параболы, а также других линий второго порядка называется прямая, содержащая середины всех параллельных хорд. В узком смысле диаметром эллипса является любая хорда, проходящая через его центр (рис.3.53,а); диаметром гиперболы является любая прямая, проходящая через центр гиперболы (за исключением асимптот), либо часть такой прямой (рис.3.53,6); диаметром параболы является любой луч, исходящий из некоторой точки параболы и коллинеарный оси симметрии (рис.3.53,в).
Два диаметра, каждый их которых делит пополам все хорды, параллельные другому диаметру, называются сопряженными. На рис.3.53 полужирными линиями изображены сопряженные диаметры эллипса, гиперболы, параболы.
Касательную к эллипсу (гиперболе, параболе) в точке можно определить как предельное положение параллельных секущих
, когда точки
и
, оставаясь на рассматриваемой линии, стремятся к точке
. Из этого определения следует, что касательная, параллельная хордам, проходит через конец диаметра, сопряженного к этим хордам.
6. Эллипс, гипербола и парабола имеют, кроме приведенных выше, многочисленные геометрические свойства и физические приложения. Например, рис.3.50 может служить иллюстрацией траекторий движения космических объектов, находящихся в окрестности центра притяжения.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Задача 28997 4.3.116) Найти длину хорды, соединяющей.
Условие
![]()
4.3.116) Найти длину хорды, соединяющей точки пересечения двух парабол, имееющих общую вершину в начале координат, а фокусы
в точках (2; 0) и (0; 2).
Решение
![]()
Каноническое уравнение параболы, симметричной относительно оси Ох и имеющей фокус на оси Ох имеет вид:
y^2=2p_(1)x
F_(1)(p_(1)/2;0)
Каноническое уравнение параболы, симметричной относительно оси Оy и имеющей фокус на оси Оy имеет вид:
x^2=2p_(2)y
F_(2)(0; p_(2)/2)
Так по условию
F_(1)(p_(2)/2;0)=(2;0) ⇒ p_(1)/2=2 ⇒ p_(1)=4
F_(2)(0; p_(2)/2)=(0;2) ⇒ p_(2)/2=2 ⇒ p_(2)=4
Уравнения парабол имеют вид:
y^2=8x и x^2=8y
Находим точки пересечения парабол, решаем систему уравнений:
и подставляем в первое уравнение:
(x^2/8)^2=8x;
x^4/64=8x
x^4=512x
x^4-512x=0
x*(x^3-512)=0
x_(1)=0 или x^3-512=0 ⇒ x_(2)=8
y_(1)=0 ; y_(2)=(x^2_(2))/8=8
Расстояние между точками O(0;0) и А (8;8)
OA=sqrt((8-0)^2+(8-0)^2)=sqrt(64+64)=8sqrt(2)
О т в е т. 8 sqrt(2) 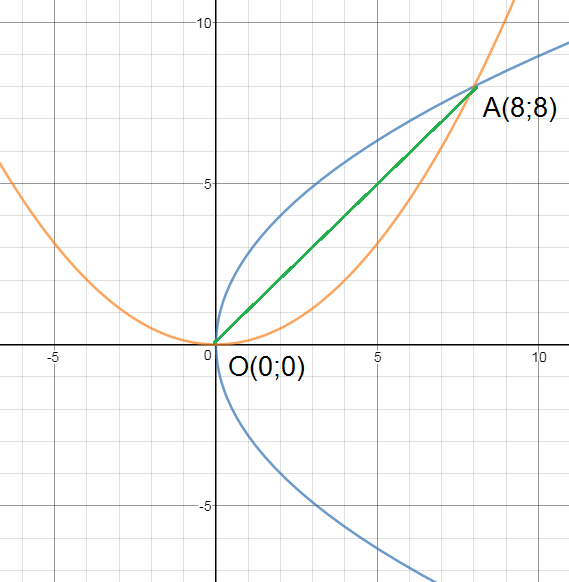
Задачи для самостоятельного решения. 1 Составить уравнение хорды окружности х2+у2 = 49, делящейся в точке А(1;2) пополам
1 Составить уравнение хорды окружности х 2 +у 2 = 49, делящейся в точке А(1;2) пополам.
Ответ.х + 2у -5 = 0.
2. Определить координаты центров и радиусы окружностей:
Ответ: а) а = 4, b=-3, r= 5; б) а = -5, b = 2, r=0. Уравнение определяет точку;
в) а =2, b=-7, r 2 =-1. Уравнение не имеет геометрического смысла (мнимая, окружность).
3. Найти угол между радиусами окружности
х 2 +у 2 +4х-6у=0, проведенными в точки пересечения ее с осью Оу.
Ответ: tgφ=-2,4.
4. Составить уравнение окружности, проходящей через точки А(1; 2), В(0;-1), С(-3; 0).
Ответ: (х+1) 2 +(у -1) 2 =5.
5. Составить уравнение окружности, проходящей через точки А (7; 7) и В(-2; 4), зная, что ее центр лежит на прямой
Ответ: (х– З) 2 +(у-4) 2 =25.
6. Составить уравнение общей хорды окружностей х 2 +у 2 =16 и (х -5) 2 + у 2 = 9.
Ответ: х=3,2.
7. Составить уравнение прямой, проходящей через левый фокус и нижнюю вершину эллипса 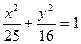 .
.
Ответ: 4х+3у+12= 0.
8. На прямой х+5=0 найти точку, одинаково удаленную от левого фокуса и верхней вершины эллипса 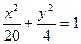 .
.
Ответ: М(—5; 7).
9. Пользуясь определением эллипса, составить его уравнение, зная, что точки F1 (0; 0) и F2 (1; 1) являются фокусами эллипса, а длина большой оси равна 2.
Ответ: Зх 2 + Зу 2 – 2ху – 2х – 2у – 1 == 0.
10. Составить уравнение геометрического места точек, расстояния которых от точки А (0; 1) з два раза меньше расстояния до прямой у—4=0.
Ответ: 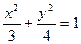 .
.
Занятие 16. Кривые второго порядка: гипербола, парабола
Гипербола.
Гиперболой называется геометрическое место точек, абсолютная величина разности расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная (её обозначают через 2а), причем эта постоянная меньше расстояния между фокусами. Поместив фокусы гиперболы в точках F1(с; 0) и F2(-с;0), получаем уравнение гиперболы в виде 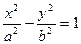 ,
,
 где b 2 =c 2 –a 2 ;
где b 2 =c 2 –a 2 ;
это простейшее (каноническое) уравнение гиперболы. Гипербола состоит из двух ветвей и расположена симметрично относительно осей координат. Точки А1(а;0) и А2(-а;0) называются вершинами гиперболы.
Отрезок А1А2=2а называют вещественной осью гиперболы, а отрезок В1В2=2b – мнимой осью (рис. 15).
Прямая называется асимптотой гиперболы, если расстояние точки гиперболы М (х;у) от этой прямой стремится к нулю при х→+∞ или х→-∞. Гипербола имеет две асимптоты, уравнения которых 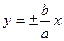 .Для построения асимптот гиперболы строят осевой прямоугольник гиперболы со сторонами х=а,
.Для построения асимптот гиперболы строят осевой прямоугольник гиперболы со сторонами х=а,
х = – а, у=b, у=-b. Прямые, проходящие через противоположные вершины этого прямоугольника, являются асимптотами гиперболы. На чертеже указано взаимное расположение гиперболы и ее асимптот. Отношение ε 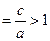 называется эксцентриситетом гиперболы.
называется эксцентриситетом гиперболы.
Если а=b, то уравнение гиперболы принимает вид
Такая гипербола называется равнобочной.
 (или
(или 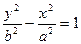 )
)
также является уравнением гиперболы, но вещественной осью этой гиперболы служит отрезок оси Оу длины 2b.
Две гиперболы  и
и 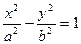 имеют одни и те же полуоси и одни и те же асимптоты; но вещественная ось одной служит мнимой осью другой, и наоборот. Такие две гиперболы называются сопряженными.
имеют одни и те же полуоси и одни и те же асимптоты; но вещественная ось одной служит мнимой осью другой, и наоборот. Такие две гиперболы называются сопряженными.
Пример 16.1.Эксцентриситет гиперболы равен 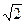 . Составить простейшее уравнение гиперболы, проходящей через точку М(
. Составить простейшее уравнение гиперболы, проходящей через точку М( 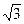 ;
; 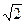 ).
).
Решение. По определению эксцентриситета можем написать равенство 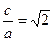 , или с 2 =2а 2 . Но с 2 = а 2 + b 2 , следовательно, а 2 + b 2 = 2а 2 , или а 2 = b 2 , т. е. гипербола равнобочная.
, или с 2 =2а 2 . Но с 2 = а 2 + b 2 , следовательно, а 2 + b 2 = 2а 2 , или а 2 = b 2 , т. е. гипербола равнобочная.
Другое равенство имеем из условия нахождения точки М на гиперболе, т. е. 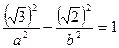 , или
, или 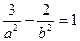 . Поскольку а 2 =b 2 , получим
. Поскольку а 2 =b 2 , получим 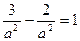 , т.е. а 2 =1.
, т.е. а 2 =1.
Таким образом, уравнение искомой гиперболы имеет вид х 2 – у 2 =1.
Парабола.
Параболой называется геометрическое место точек, равноудаленных от данной точки, называемой фокусом, и данной прямой, называемой директрисой. Если директрисой параболы  является прямая
является прямая 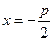 , а фокусом – точка
, а фокусом – точка 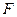 (
( 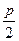 ,0), то уравнение параболы имеет вид
,0), то уравнение параболы имеет вид

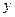
 =
= 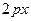 . (16.1)
. (16.1)
Эта парабола расположена симметрично относительно оси абсцисс (рис.6, где р 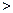 0).
0).
Уравнение 
 (16.2)
(16.2) 
является уравнение параболы, симметричной относительно оси ординат. При p>0 параболы (16.1) и (16.2) обращены в положительную сторону соответствующей оси, а при p
Решение. Поскольку известны длина хорды и расстояние ее от вершины, то, следовательно , известны координаты конца этой хорды-точки М, лежащей на параболе. Уравнение параболы имеет вид 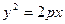 ; пологая в нем
; пологая в нем  ,
, 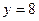 , находим
, находим 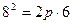 ,откуда
,откуда  .
.
Таким образом, уравнение искомой параболы 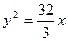 .
.
Пример 16.3. Составить уравнение параболы с вершиной в начале координат, симметричной относительно оси Оу и отсекающей на биссектрисе  и
и 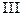 координатных углов хорду длиной
координатных углов хорду длиной  .
.
Решение. Искомое уравнение параболы  , уравнение биссектрисы
, уравнение биссектрисы  . Следовательно, точками пересечения параболы с биссектрисой будут О(0;0) и М(2р;2p).
. Следовательно, точками пересечения параболы с биссектрисой будут О(0;0) и М(2р;2p).
Длина хорды определяется как расстояние между двумя точками 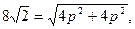 откуда
откуда 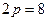 .Следовательно , уравнение искомой параболы имеет вид
.Следовательно , уравнение искомой параболы имеет вид  .
.
Как посчитать хорду окружности
Онлайн калькулятор
Хорда круга – отрезок соединяющий две точки, лежащие на окружности.
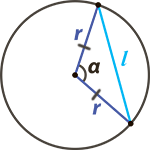
Чтобы посчитать длину хорды вам необходимо знать, чему равен радиус (r) окружности и угол (α) между двумя радиусами, образующими вместе с хордой равнобедренный треугольник (см. рис.)
Как посчитать длину хорды (градусы)
Чему равна длина хорды окружности если её радиус ,
а
Как посчитать длину хорды (радианы)
Чему равна длина хорды окружности если её радиус ,
а
Теория
Чему равна длина хорды (l) окружности если известны её радиус (r) и центральный угол (α), опирающийся на данную хорду?
Формула
Пример
Если радиус круга равен 4 см, а ∠α = 90°, то длина хорды примерно равна 5.65 см.
[spoiler title=”источники:”]
http://lektsii.org/3-113924.html
http://poschitat.online/horda
[/spoiler]
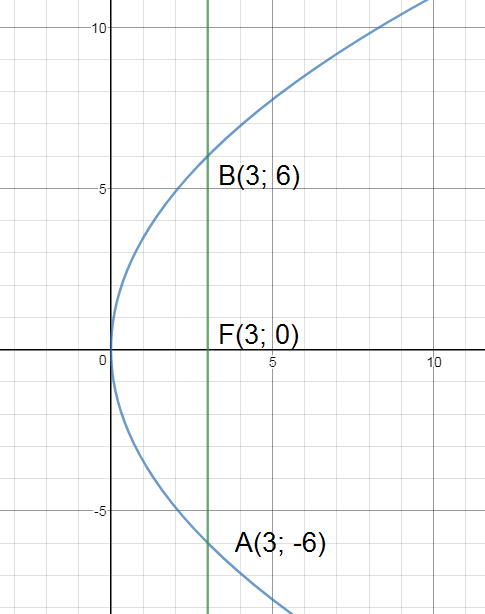
Задача 28996 4.3.114) Через фокус параболы у^2 = 12х…
Условие
![]()
4.3.114) Через фокус параболы у^2 = 12х проведена хорда, перпендикулярная к ее оси. Найти длину хорды.
математика ВУЗ
6207
Решение
![]()
★
Каноническое уравнение параболы имеет вид:
y^2=2px ( p > 0)
F(p/2;0) – фокус параболы.
у^2 = 12х
2p=12
p=6
F(3;0)
х=3 – прямая, проходящая через фокус перпендикулярно оси параболы.
Находим точки пересечения прямой x=3 и параболы y^2=12x
y^2=12*3
y^2=36
y_(1)=-6 или y_(2)=6
Прямая x=3 пересекает параболу в точках
A(3:-6) и В (3;6)
d=AB=|y_(2) – y_(1)| = |6 – ( – 6)| =12
О т в е т. 12.
Написать комментарий
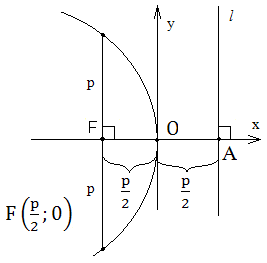
Определение.
Параболой называется множество точек
плоскости, каждая из которых находится
на одинаковом расстоянии от данной
точки F,
называемой фокусом, и данной прямой l,
не проходящей через фокус, называемой
директрисой.
Для
вывода уравнения параболы за ось Ox
примем прямую, проходящую через фокус
F
перпендикулярно директрисе l.
За положительное направление оси абсцисс
возьмём направление от директрисы к
фокусу. За начало координат возьмем
точку O,
которая делит пополам отрезок от
директрисы до фокуса. Длину этого отрезка
обозначим через P
и назовем фокальным параметром параболы.
Тогда
фокус F
имеет координаты ![]()
,
а точка A
оси Ox,
через которую проходит директриса l,
имеет
координаты ![]()
.
Возьмем произвольную точку M(x,y)
параболы и соединим ее с фокусом F,
а затем опустим перпендикуляр MN
на директрису l.
При этом длину отрезка MN
обозначим через r
и назовем фокальным радиусом точки M,
а длину отрезка MN
обозначим d.
Тогда по определению параболы имеем:
![]()
.

Замечание:
По аналогии с эллипсом и гиперболой
число ![]()
,
назовем директрисой параболы. Так как
r=d,
то для параболы ![]()
.

Теорема.
Пусть прямоугольная декартова система
координат Oxy
выбрана указанным выше способом. Тогда
в этой системе координат парабола имеет
каноническое уравнение: ![]()
.
Доказательство.
Пусть
M(x;y)
– произвольная точка параболы, ![]()
– фокус, ![]()
или ![]()
– уравнение директрисы. Тогда имеем:
![]()
; ![]()
– расстояние от точки M(x,y)
до прямой l,
причем x≥0.
![]()
.
![]()
.
Теорема
доказана.
§19. Исследование уравнения параболы
Пусть
парабола задана каноническим уравнением:
(1)
1. Ось и вершина
Так
как уравнение (1) содержит переменную
во второй степени, то оно не изменится
при замене
на ![]()
,
следовательно, парабола симметрична
относительно оси абсцисс Ox.
Других
осей симметрии и центра симметрии у
параболы нет.
С
осью Ox
парабола пересекается в начале координат,
так как при ![]()
имеем и ![]()
.
Определение.
Ось симметрии параболы называется ее
осью, точка пересечения параболы с осью
называется ее вершиной.
2. Расположение относительно оси и директрисы
Так
как ![]()
(расстояние), то из (1) имеем:
.
Следовательно, парабола расположена
относительно оси Oy,
а следовательно, и относительно и
директрисы по ту же сторону, что и фокус.
Если ![]()
,
то ![]()
.
Следовательно, при неограниченном
удалении от вершины парабола неограниченно
удаляется от оси.
3. Фокальная хорда
Определение.
Фокальной называется хорда, проходящая
через фокус параболы перпендикулярно
ее оси.

Покажем,
что ее длина равна удвоенному фокальному
параметру:

![]()
4. Другие виды уравнения параболы
1)
![]()
.
2)
![]()
.

3)
![]()
.

4)
![]()
.

5)
![]()
.

Oˡ(x0;y0)
– вершина параболы.
§20. Уравнения эллипса, гиперболы и параболы в полярных координатах
Теорема
1.
Эллипс, отличный от окружности, гипербола
и парабола являются множествами точек
плоскости, для которых отношение
расстояния до данной точки F
к расстоянию до данной прямой l
есть величина постоянная.
Замечания.
1)
Для эллипса и гиперболы теорема 1
непосредственно следует из теоремы о
директрисах, причем F
– один из фокусов, l
– ближайшая к этому фокусу директриса.
Для параболы теорема 1 следует из ее
определения, где F
– фокус параболы, l
– ее директриса;
2)
Указанное отношение расстояний есть
эксцентриситет линии;
3)
Окружность не имеет директрис, так как
Ɛ=0
и ![]()
.
Теорема
2.
Эллипс, гипербола, парабола, эксцентриситетами
Ɛ
имеют в некоторой полярной системе
координат уравнение:
![]()
.
(1)
Доказательство.
Примем
за полюс фокус F
соответствующей линии, полярную ось
проведем через фокус F
перпендикулярно соответствующей
директрисе l
в направлении от l
к F.
Пусть
M
– произвольная точка линии, M0
– точка линии, для которой ![]()
;
обозначим FM0
через p
– фокальный параметр точки M0.
![]()
;

Согласно
теореме 1 имеем:

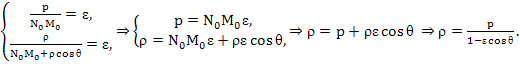
Замечания.
1)
Для параболы Ɛ=1,
p
– фокальный параметр, тогда парабола
имеет полярное уравнение
.
2)
Для эллипса и гиперболы – уравнениям
![]()
и (2)
![]()
,
(3)
получаем:
![]()
.
Например,
для уравнения (2) имеем: ![]()
=p
– фокальный параметр, тогда для точки
M0
эллипса имеем:

![]()
.
Для
окружности Ɛ=0
и ее полярное уравнение принимает вид:
![]()
,
где p
– радиус окружности, ![]()
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Через фокус параболы у2 = 10х проведена хорда, перпендикулярная к ее оси. Определить длину этой хорды.
![]()
Harry
214k15 золотых знаков117 серебряных знаков229 бронзовых знаков
задан 25 янв 2017 в 9:37
![]()
2
Читайте, что такое парабола.
Для параболы в каноническом виде  фокус находится в точке
фокус находится в точке  . Значения y при
. Значения y при  , само собой, равны
, само собой, равны  . Расстояние между этими точками, думаю, и сами найдете? 🙂
. Расстояние между этими точками, думаю, и сами найдете? 🙂
ответ дан 25 янв 2017 в 9:44
![]()
HarryHarry
214k15 золотых знаков117 серебряных знаков229 бронзовых знаков
0
