Как найти хорошую задачу

Первая стадия системы «Найди время» — выбор Главного, важнейшей задачи на день. Далее вам нужно применить особую тактику, чтобы сохранять прицельную (как у лазерного устройства) сосредоточенность на этой задаче. Мы предложим вам целое меню ухищрений, позволяющих победить всевозможные отвлечения в мире, где все постоянно находятся «на связи». На протяжении дня вы будете подпитываться энергией, чтобы не выпускать из-под контроля время и внимание. И наконец, вы будете заниматься осмыслением, то есть обдумывать прошедший день, сделав несколько простых заметок.

Начинайте каждый день с выбора точки фокусировки

Первый шаг в системе «Найди время» — решить, для чего вам нужно это время. Каждый день вы будете выбирать одно действие для того, чтобы сделать его главным и застолбить в своём календаре. Это может быть важная рабочая задача, например завершение презентации. Или домашнее занятие — скажем, приготовление ужина либо посадка растений в саду.

Ваше Главное вполне может оказаться чем-то таким, что вы не обязательно должны сделать, а просто хотите сделать, например поиграть с детьми или почитать книгу. При этом оно зачастую включает в себя несколько этапов. Например, завершение презентации — это написание выводов, оформление слайдов и репетиция выступления. Сделав Главным «завершение презентации», вы обещаете себе выполнить все ступени процесса.

Конечно, Главное не единственное ваше занятие за день, но основное. Вопросом «Что станет для меня главным в этот день?» вы побуждаете себя проводить время за делами, которые важны для вас, а не тратить его, реагируя на приоритеты других людей. Выбирая Главное, вы тем самым начинаете мыслить активно и позитивно.

Мы поможем вам в этом и поделимся своими любимыми тактическими приёмами для ежедневного выбора Главного и высвобождения времени на его реализацию. Кроме того, вам потребуется изменить своё отношение к отвлекающим факторам, которые могут встретиться на вашем пути. […]

Мы хотим, чтобы каждый день вы начинали с размышлений о том, что — как вы надеетесь — станет в нём самым ярким пятном.

Заранее представьте, как под вечер вас кто-нибудь спросит: «Что у тебя сегодня было самое главное?» Что из событий минувшего дня вы вспомните? Часы, посвященные какому занятию, или радость от какого достижения вам захочется заново пережить? Это и есть ваше Главное.

Имейте в виду: это Главное не обязательно съедает день без остатка. Большинство из нас всё-таки не может совсем уж игнорировать входящие письма или отказаться выполнять поручения шефа. Однако выбор Главного даёт вам шанс самому решить, как организовать своё время, а не позволять технологиям, офисным установкам по умолчанию, а также другим людям формировать вашу повестку дня. Пусть Движение Занятых пропагандирует ежедневное стремление к максимально возможной производительности — мы-то знаем: разумнее сосредоточиться на собственных приоритетах, пусть и в ущерб некоторым текущим делам из списка.

Ваше Главное наделяет каждый день фокусной точкой. Исследования выявили: ваше восприятие жизни в первую очередь определяется вовсе не тем, что происходит с вами. На самом деле вы создаёте собственную реальность, выбирая, на что обращать внимание. При всей кажущейся очевидности это очень важный вывод. Вы способны перекраивать время, выбирая, на чем сконцентрироваться. И ваше ежедневное Главное — объект этой концентрации. […]

Критерии выбора Главного

Выбор Главного начинается с вопроса, который вы сами себе задаёте: «Что я хочу сегодня сделать Главным?» Ответить не всегда просто, особенно если вы лишь недавно начали использовать систему «Найди время». Иногда перед вашим мысленным взором возникает сразу много важных задач. Одна воодушевляет («Испечь торт ко дню рождения Н»), другая грозит дедлайном («Закончить набор слайдов»), а третья вызывает чуть ли не отвращение («Поставить крысоловки в гараже»). Как же принять решение? При выборе Главного мы руководствуемся одним из трех критериев.

Срочность

Первый критерий — срочность. Что сегодня нужно сделать как можно скорее?

Случалось ли вам часами копаться в письмах и сидеть на совещаниях, а в конце дня вдруг сообразить, что вы так и не сумели выкроить время на одну-единственную вещь, которая действительно не терпит отлагательств? Нам вот случалось. И очень часто. Всякий раз, когда такое происходит, мы чувствуем себя очень скверно. Ах, эти запоздалые сожаления!

Если над вами висит нечто такое, что сегодня позарез необходимо сделать, пусть оно и станет вашим Главным. Такие срочные дела частенько можно отыскать в обычном списке на день, в почте, календаре. Ищите значимые проекты, для которых существенную роль играет срок исполнения и которые при этом имеют, так сказать, средние размеры (то есть требуют все-таки не десяти минут — но и не десяти часов).

Ваше срочное Главное может быть, например, таким:

• Сформулировать коммерческое предложение и отправить заказчику, который рассчитывает получить его до конца недели.
• Попросить владельцев свободных площадок и поставщиков питания выслать вам свои условия — для мероприятия, которое вы организуете на работе.
• Успеть приготовить ужин до прихода друзей.
• Помочь дочери доделать большой школьный проект, который она должна сдать завтра.
• Отредактировать отпускные фотографии и выложить их для ваших родственников, которые очень хотят их увидеть.

Удовлетворённость

При применении второго критерия задайте себе вопрос: «Какое Главное принесёт мне наибольшее удовлетворение в конце дня?»

Первая стратегия позволяет определить, что вам нужно сделать. А вторая побуждает сфокусироваться на том, что вы хотите сделать.

Опять же, можете начать со списка дел. На сей раз сосредотачивайтесь не на сроках и приоритетах. Используйте иной подход.

Подумайте о том, какую степень удовлетворения принесёт вам каждое из возможных Главных.

Оно не должно относиться к разряду срочных. Изучите те проекты, за которые вы давно хотели взяться, только никак не находили времени. Возможно, вы обладаете каким-нибудь навыком, который хотите применить на практике. А может, это проект-хобби, которым вы хотите втихомолку заняться, прежде чем поведать о нём миру. Для таких проектов, несмотря на их «несрочность», проволочки чрезвычайно губительны.

Правильный выбор Главного поможет вам разорвать порочный круг под названием «Когда-нибудь я за это возьмусь». Вот несколько примеров Главного, Которое Приносит Удовлетворение:

• Завершите составление бизнес-плана нового проекта, который вас воодушевляет. Поделитесь им с несколькими доверенными коллегами.
• Изучите места, где вы могли бы провести с семьёй ближайший отпуск.
• Начерно набросайте кусок очередной главы вашего романа — 1 500 слов. […]

Радость

Третий критерий — радость. Задайтесь вопросом: «Когда я вечером буду вспоминать сегодняшние события, какое из них больше всего меня порадует?»

Не каждый час нужно оптимизировать и отлаживать так, чтобы выжимать из него максимум эффективности. Одна из целей нашей системы — увести вас от несбыточного идеала предельно чётко распланированных дней к жизни, в которой больше радости и меньше недовольства неприятными делами. А значит, стоит делать некоторые вещи просто потому, что вам нравится их делать.

Другим ваше Радостное Главное может иной раз показаться напрасной тратой времени: скажем, если речь идёт о том, чтобы посидеть дома с книгой, или побросать с приятелем в парке фрисби, или поразгадывать кроссворд. Но мы так не считаем. Вы зря теряете время лишь в том случае, если не относитесь к его проведению сознательно и целенаправленно.

Радость можно получать от Главного всевозможных видов. Вот некоторые примеры:

• Отправиться на новоселье к друзьям.
• Подобрать аккорды к новой песне.
• Пообедать с коллегой — мастерским рассказчиком забавных историй.
• Сходить с ребёнком на детскую площадку.

Прислушивайтесь к интуиции

Какую же из приведённых стратегий использовать в тот или иной день? Нам кажется, что при выборе Главного лучше всего довериться интуиции. Она-то и поможет определить, какое Главное для вас сегодня оптимально — срочное, удовлетворяющее или радостное.

При этом полезно учесть, сколько времени займёт то или иное дело. Мы советуем выбирать Главное, на которое уйдёт 60–90 минут. Если дело требует меньше часа, вы не успеете настроиться на нужную волну. А после полутора часов сосредоточенных занятий большинству требуется перерыв. Итак, 60–90 минут — золотая середина. За это время можно успеть сделать нечто осмысленное и важное, не перекраивая кардинально своё расписание. Мы убеждены: применяя тактики, описанные в этой главе и на других страницах книги, вы сумеете выделить по 60–90 минут на ваше Главное.

В самом начале процесс выбора может показаться вам странным или сложным. Не переживайте — это совершенно нормально. Постепенно вы освоитесь, и выбор будет даваться всё легче и легче. И помните: совсем уж провалить процесс овладения нашей системой просто невозможно. К тому же она предназначена для ежедневного пользования: что не получилось сегодня, скорее всего, получится завтра.

Конечно же, ваше Главное не какая-то волшебная палочка. Само по себе решение, на что потратить основные усилия в тот или иной день, ещё не гарантирует удачного результата. Но осознанная целеустремлённость — важнейший шаг на пути к высвобождению дополнительного времени. Выбор Главного подразумевает фокусировку на приоритетах. Благодаря ей вы сумеете сберечь время и энергию для действительно важных дел, а не на то, чтобы постоянно отвлекаться на чужие приманки и откликаться на чужие требования.

---

Читайте об остальных трёх шагах системы и практических способах внедрения их в повседневную жизнь в книге «Найди время».

Купить книгу

Читайте также 🧐

• 6 советов, как найти свободное время
• Как найти время на спорт, когда ваш график забит до отказа
• Как организовать свой день: методики гениев продуктивности

В курсе математики обязательно встречаются разного рода уравнения и задачи, но у многих они вызывают затруднения. Все дело в том, что необходимо отработать и автоматизировать эти процессы. Как научиться решать задачи по математике, понимать их, вы узнаете в данной статье.

Простейшие задачи

Начнем с самого легкого. Чтобы получить правильный ответ на задачу, необходимо понять ее суть, поэтому тренироваться необходимо на простейших примерах для младшей школы. Как научиться решать задачи по математике, мы опишем вам в данном разделе на конкретных примерах.

Пример 1: Ваня и Дима ловили вместе рыбу, но у Димы клевало плохо. Какой улов у ребят? Дима поймал на 18 рыб меньше, чем весь улов, у одного из ребят на 14 рыб меньше, чем у другого.

Данный пример взят из курса математики за четвертый класс. Чтобы решить задачу, необходимо понять ее суть, точный вопрос, что в итоге необходимо найти. Этот пример решается в два простых действия:

18-14=4 (рыбы) – поймал Дима;

18+4=22 (рыбы) – поймали ребята.

Теперь можно смело записывать ответ. Вспоминаем главный вопрос. Какой общий улов? Ответ: 22 рыбы.

Пример 2:

Летят воробей и орел, известно, что воробей за два часа пролетел четырнадцать километров, а орел за три часа пролетел 210 километров. Во сколько раз скорость орла больше.

Обратим внимание на то, что в этом примере два вопроса, записывая итог, не забываем указывать два ответа.

Переходим к решению. В этой задаче необходимо знать формулу: S=V*T. Она, наверняка, известна многим.

Решение:

14/2=7 (км/ч) – скорость воробья;

210/3=70 (км/ч) – скорость орла;

70/7=10 – во столько раз скорость орла превосходит скорость воробья;

70-7=63 (км/ч) – на сколько скорость воробья меньше скорости орла.

Записываем ответ: в 10 раз скорость орла превосходит скорость воробья; на 63 км/ч орел быстрей воробья.

Более сложный уровень

Как научиться решать задачи по математике, используя таблицы? Все очень просто! Как правило, таблицы используются для упрощения и систематизации условия. Чтобы понять суть данного метода, разберем пример.

Перед вами книжный шкаф с двумя полками, на первой книг в три раза больше, чем на второй. Если с первой полки убрать восемь книг, а на вторую поставить 32, то их станет поровну. Ответьте на вопрос: сколько книг было первоначально на каждой полке?

Как научиться решать текстовые задачи по математике, сейчас все наглядно покажем. Для упрощения восприятия условия составим таблицу.

Условие

	1 полка	2 полка
Было	3х	х
Стало	3х-8	х+32

Теперь можем составить уравнение:

3х-8=х+32;

3х-х=32+8;

2х=40;

х=20 (книг) – было на второй полке;

20*3=60 (книг) – было на первой полке.

Ответ:60;20.

Вот наглядный пример решения задачи на составление уравнения с использованием вспомогательной таблицы. Она значительно упрощает восприятие.

Логика

В курсе математики встречаются и более сложные задания. Как научиться решать логические задачи по математике, мы рассмотрим в данном разделе. Для начала вчитываемся в условие, оно состоит из нескольких пунктов:

1. Перед нами лист с числами от 1 до 2009.
2. Мы вычеркнули все нечетные числа.
3. Из оставшихся вычеркнули числа, стоящие на нечетных местах.
4. Последнее действие выполняли до тех пор, пока не осталось одно число.

Вопрос: какое число осталось не зачеркнутым?

Как быстро научиться решать задачи по математике на логику? Для начала не спешим писать все эти числа и вычеркивать по одному, поверьте, это очень долгое и глупое занятие. Задачу данного типа несложно решить и в несколько действий. Предлагаем вместе поразмыслить над решением.

Ход решения

Давайте предположим, какие числа останутся после первого действия. Если исключить все нечетные, то остаются: 2, 4, 6, 8, … , 2008. Заметим, что все они кратны двум.

Убираем числа на нечетных местах. Что у нас остается? 4, 8, 12, … , 2008. Замечаем, что все они кратны четырем (то есть делятся без остатка на четыре).

Далее убираем числа на нечетных местах. Мы в итоге имеем числовой ряд: 8, 16, 24, … , 2008. Наверное, вы уже догадались, что все они кратны восьми.

Нетрудно догадаться о наших последующих действиях. Далее оставляем числа кратные 16, затем 32, далее 64, 128, 256.

Когда мы дошли до чисел, кратных 512, то у нас остаются всего три числа: 512, 1024, 1536. Следующим этапом оставляем число, кратное 1024, оно в нашем списке одно: 1024.

Как видите, задача решается элементарно, без особых усилий и массы потраченного времени.

Олимпиада

В школе существует такое понятие, как олимпиада. Туда попадают дети с особыми навыками. Как научиться решать олимпиадные задачи по математике, и что они собой представляют, рассмотрим далее.

Начать стоит с более низкого уровня, далее его усложняя. Отработать навыки решения олимпиадных задач предлагаем на примерах.

Олимпиада, 5 класс. Пример.

На нашей ферме живет девять свиней, они за три дня съедают двадцать семь мешков корма. Сосед фермер попросил оставить пять своих свиней на пять дней. Сколько же нужно корма пяти свиньям на пять дней?

Олимпиада, 6 класс. Пример.

Большой орел пролетает три метра за одну секунду, а орленок один метр за полсекунды. Они одновременно стартовали с одной вершины на другую. Сколько взрослому орлу придется ждать своего детеныша, если расстояние между вершинами 240 метров?

Решения

В прошлом разделе мы рассмотрели две простых олимпиадных задачи за пятый и шестой класс. Как научиться решать задачи по математике олимпиадного уровня, предлагаем рассмотреть прямо сейчас.

Начнем с пятого класса. Что нужно нам для начала? Узнать сколько мешков съедают девять поросят за один день, для этого сделаем простейшее вычисление: 27:3=9. Мы нашли количество мешков для девяти поросят на один день.

Теперь вычисляем сколько необходимо мешков одному поросенку на один день: 9:9=1. Вспоминаем, что говорилось в условии, сосед оставил пять свиней на пять дней, следовательно, нам необходимо 5*5=25 (мешков корма). Ответ: 25 мешков.

Решение задачи за шестой класс:

240:3=80 секунд летел взрослый орел;

орленок за 1 секунду пролетает два метра, следовательно: 80*2=160 метров пролетит орленок за 80 секунд;

240-180=80 метров останется пролететь орленку, когда взрослый орел уже приземлился на скалу;

80:2=40 секунд еще потребуется орленку, чтобы долететь до взрослого орла.

Ответ: 40 секунд.

Какие задачи хорошо подходят для научных исследований?

Какое число нужно вставить в последний треугольник?

Учёные решают задачи; такая у них работа. Но какие задачи будут многообещающими темами для проведения исследований? Для ответа на этот вопрос я написала книгу “Затерянные в математике”, где рассмотрела задачи, связанные с основами физики.

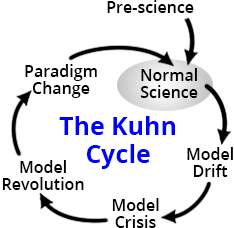
Первую, грубую классификацию исследовательских задач можно организовать, используя цикл развития научных теорий Томаса Куна. Цикл Куна состоит из фазы «обычной науки», за которой следует «кризис», ведущий к смене парадигмы, после которой начинается новая фаза «обычной науки». Это невероятное упрощение реальности, но для последующих рассуждений подходит.

Обычные задачи

В течение фазы обычной науки вопросы для исследований обычно можно сформулировать как «Как бы нам это измерить?» (для экспериментаторов) и «Как бы нам это подсчитать?» (для теоретиков).

В основах физики таких «обычных проблем» полно. У экспериментаторов много проблем, потому что все легко решаемые задачи уже были решены, и сложность измерения чего-то нового постоянно растёт. Проблемы у теоретиков происходят из того, что предсказания в физике не вываливаются сами по себе из гипотез. Часто требуется пройти много этапов аргументации и проделать множество длительных вычислений, чтобы прийти к численным последствиям теоретических предположений.

Хорошим примером обычной задачи в основах физики будет холодная тёмная материя. Гипотеза достаточно проста: в космосе есть холодное и тёмное нечто, что ведёт себя, как жидкость, и слабо взаимодействует само с собой и с другой материей. Но это само по себе не особенно полезное предсказание. Хорошей исследовательской задачей была бы следующая: «Как холодная тёмная материя влияет на температурные флуктуации реликтового излучения?» А потом следует экспериментальный вопрос: «Как нам это измерить?»

Другие задачи такого типа в основах физики – это: «Какой вклад гравитация вносит в магнитный момент мюона?» и «Каков фон рассеяния фотонов в Большом адронном коллайдере?»

Ответы на такие обычные задачи расширяют наше понимание существующих теорий. Эти расчёты можно сделать в рамках имеющихся у нас платформ, но они могут оказаться довольно сложными.

Приведённые в предыдущих параграфах в качестве примеров задачи решены, или, по крайней мере, мы знаем, как их решать, хотя всегда можно затребовать повышения точности. Но в этой категории имеются и нерешённые задачи.

К примеру, квантовая теория сильного ядерного взаимодействия, должна предсказывать массы частиц, состоящих из нескольких кварков – нейтронов, протонов, других подобных (но нестабильных) составных частиц. Но такие подсчёты чертовски сложны. Сегодня они осуществляются при помощи сложных компьютерных программ – расчётов решёток – и всё равно их предсказания оказываются не такими уж хорошими. Связанный с этим вопрос – как ведёт себя ядерная материя в ядрах нейтронных звёзд.

Это просто случайно выбранные примеры множества открытых вопросов физики, представляющие собой «нормальные задачи», на которые, как считается, можно найти ответ в рамках уже известных нам теорий – но, думаю, они хорошо иллюстрируют данную тему.

Если выйти за рамки основ, то у нас есть нормальные задачи вроде предсказания солнечных циклов и солнечной погоды – они сложны из-за крайней нелинейности и частичной турбулентности системы, но мы не ожидаем, что они вступят в конфликт с существующими теориями. Есть ещё высокотемпературная сверхпроводимость, хорошо изученное, но теоретически недостаточно понятное явление, поскольку в таких материалах недостаёт квазичастиц. И так далее.

Такие вот задачи мы изучаем, когда всё идёт по плану. Но есть ещё задачи, которые в принципе могут менять парадигмы, задачи, сообщающие о наличие «кризиса» в терминологии Куна.

Кризисные задачи

Очевидные кризисные задачи – это наблюдения, которые нельзя объяснить на основе известных теорий.

Я не считаю большую часть наблюдений, связанных с тёмной материей и тёмной энергией, кризисными. Большую часть этих данных можно объяснить достаточно хорошо, просто добавив два новых компонента в энергетический бюджет Вселенной. Вы, конечно, будете жаловаться, что это не даст нам микроскопического описания, но данных для микроскопических структур у нас нет, поэтому и сформулировать задачу пока не получается.

Но некоторые наблюдения тёмной материи относятся к «кризисным». Необъяснимые корреляции, закономерности в галактиках, которые тяжёло объяснить при помощи холодной тёмной материи, например, зависимость Талли — Фишера, или странная способность тёмной материи отслеживать распределение материи. Для этих наблюдений пока нет удовлетворительного объяснения на основе известных теорий. Модификация гравитации успешно объясняет некоторые из них, но порождает другие проблемы. Вот вам и кризис! И это хороший кризис, смею заметить, поскольку у нас есть данные, которые улучшаются с каждым днём.

Это не единственная хорошая кризисная проблема наблюдений, которая существует в основах физики. Одна из старейших, но всё ещё живых и здравствующих – магнитный момент мюона. У нас есть давнее несоответствие теоретических предсказаний и измерений, которое до сих пор не разрешено. Многие теоретики считают это признаком того, что его нельзя объяснить в рамках Стандартной Модели, и поэтому требуется новая, улучшенная теория.

Существует ещё парочка подобных проблем, и довольно настырных. К примеру, эксперимент DAMA. В этом эксперименте учёные ищут тёмную материю. Они принимают сигнал от неизвестного источника с годовой модуляцией, и следят за ним уже более десяти лет. Сигнал точно есть, но если это окажется тёмная материя, то результат вступит в конфликт с другими экспериментальными результатами. В итоге, DAMA что-то видит, но никто не знает, что именно.

Ещё есть озадачивающие результаты наблюдений эксперимента LSND за нейтринными осцилляциями, не согласующиеся ни с какими другими комбинациями параметров. А ещё есть странное расхождение в результатах измерений радиуса протона с использованием двух разных методов, а также ещё одна похожая история со временем жизни нейтрона. Также недавно появились противоречия в измерении параметра Хаббла с использованием разных методов, и об этом, возможно, не стоит, а возможно, что и стоит беспокоиться.

Конечно, у каждой из этих аномалий в данных может существовать «обычное» объяснение. Это может быть систематической ошибкой измерения или ошибкой в вычислениях или упущенный ингредиент, вносящий свой вклад. Но возможно, возможно, это что-то большее.

Это один из типов «кризисных проблем» – конфликт между теорией и наблюдениями. Но кроме этих, существуют кризисные проблемы совершенно другого рода, расположенные на стороне разработки теорий. Это проблемы внутренней непротиворечивости.

Проблема внутренней непротиворечивости появляется, когда ваша теория предсказывает конфликтующие, двусмысленные или бессмысленные наблюдения. Типичным примером этого могут служить вероятности, становящиеся больше единицы, что не совпадает с интерпретацией вероятности. Именно из-за этой проблемы физики были уверены, что БАК продемонстрирует нам новую физику. Они не знали, будет ли это Хиггс, и это могло быть что-то ещё – например, неожиданное изменение слабого ядерного взаимодействия – но это оказался Хиггс. Восстановление внутренней непротиворечивости привело к успешному предсказанию.

Исторически, изучение проблем с непротиворечивостью привело ко множеству поразительных прорывов.

Примером такой проблемы может служить “ультрафиолетовая катастрофа”, в которой источник тепла должен был бы излучать бесконечное количество света на малых длинах волн. Это явно не соответствует осмысленной физической теории, в которой наблюдаемые величины должны быть конечными. (Отметьте, что этот конфликт возникает с предположением. Математически в бесконечности нет ничего плохого). Планк решил эту проблему, и решение в итоге привело к разработке квантовой механики.

Ещё одна знаменитая проблема с непротиворечивостью связана с тем, что ньютонова механика оказалась несовместимой с симметрией пространства-времени электродинамики. Эйнштейн разрешил это разногласие и получил специальную теорию относительности. Дирак позже разрешил противоречие между квантовой механикой и СТО, что привело к созданию квантовой теории поля. Эйнштейн устранил дополнительные противоречия между СТО и ньютоновой гравитацией, и получил ОТО.

Все эти проблемы были хорошо определены и конкретизированы.

Но большая часть сегодняшних теоретических проблем в основах физики не относятся к этому типу. Да, было бы неплохо, если бы три взаимодействия Стандартной Модели можно было бы объединить в одно. Было бы неплохо, но это не обязательно для непротиворечивости. Да, было бы неплохо, если бы Вселенная была суперсимметричной. Было бы неплохо, но это не обязательно для непротиворечивости. Да, было бы неплохо, если бы мы смогли объяснить, почему масса Хиггса технически неестественна. Но в том, что масса Хиггса такая, какая она есть, противоречий нет.

Хорошо описан тот факт, что Эйнштейн, а ещё больше и Дирак, вдохновлялись красотой своих теорий. Особенно Дирак любил восхвалять использование математической элегантности при разработке теорий. Но их личная мотивация интересует нас постольку, поскольку. Заглядывая назад, мы понимаем, что они добились успеха, потому что изначально взялись за хорошие задачи.

В основах физики сегодня существует мало реальных теоретических проблем, но они есть. Одна из них – отсутствие квантования гравитации. Математически не получается просто сгрести в одну кучу Стандартную Модель и ОТО, а как это сделать правильно, нам неизвестно.

Ещё одна серьёзная проблема со Стандартной моделью – это полюс Ландау в одной из констант связи. Это значит, что сила одного из взаимодействий становится бесконечной. Это не физический результат, точно так же, как ультрафиолетовая катастрофа, поэтому тут что-то должно произойти. Этой проблеме посвящено мало внимания, поскольку большая часть теоретиков считают, что стандартная модель объединяется задолго до достижения полюса Ландау, из-за чего экстраполяция становится избыточной.

Есть ещё случаи, в которых непонятно, с задачей какого рода мы имеем дело. Один из них — расходимость разложения по малым возмущениям [non-convergence of the perturbative expansion]. Возможно, вопрос только в улучшении математического аппарата, или, возможно, мы совсем неверно понимаем квантовую теорию поля. Тот же случай с теоремой Хаага. Также мне сложно классифицировать проблему измерения в квантовой механике. Апелляция к макроскопическим процессам в аксиомах теории несовместима с идеалами редукционистов, но, опять-таки, это не фундаментальная проблема, а концептуальное беспокойство. Так что по поводу этого вопроса я в затруднении.

Однако урок, которому нас учит история кризисных проблем, ясен: проблемы – это многообещающие темы для исследований, если они действительно представляют собой проблемы. То есть, вы должны суметь сформулировать математическое противоречие. Если же проблема просто состоит в том, что вам не нравится определённый аспект теории, то вы, скорее всего, просто потратите своё время.

Найти эффективное решение

Каждый из нас так или иначе постоянно сталкивается с различными задачами и проблемами. Это могут быть проблемы личного и делового характера, нерешенные вопросы, которые с течением времени превращаются в проблемы, личная ответственность за принятие того или иного решения.

Не всегда и у всех получается находить наилучший выход из создавшейся ситуации. Чаще всего для того, чтобы найти эффективное решение, не хватает опыта, мудрости, времени или знаний. Существует множество различных техник нахождения решений, и главная задача состоит в том, какая их техник подходит конкретно вам или конкретной ситуации.

Не так давно появились утверждения о том, что проблем не существуют. Есть только задачи, которые нужно решить. Проблемы существуют только в наших головах. На этот счет есть много мнений, и в принципе, каждый волен думать по-своему. Но так как слово “решение” в большей степени соответствует слову “задача”, давайте постараемся рассматривать свои проблемы как задачи, так их будет проще решить. Мы же все в школе учились решать задачи: с одним неизвестным, с двумя неизвестными, были даже такие, когда исходных данных для ее решения казалось совсем мало.

Вот так и в жизни, когда находишься на первый взгляд в неразрешимой ситуации, сначала кажется, что справиться в одиночку практически невозможно, но начиная распутывать клубок вопросов, становится понятно, что решение найдено и найдено верно.

Как же сделать так, чтобы в любых ситуациях мы действовали по одному и тому же алгоритму, который ранее доказал свою эффективность? Ответ банально простой – создавать свою личную систему принятия решений, и оттачивать мастерство поиска эффективных решений до автоматизма.

“Если мы поймем, что любая проблема или задача имеет решение, то наши мысли будут фокусироваться не нашем отношении к ней, а на том, что сделать, чтобы на одну задачу или проблему стало меньше.”

“Безвыходность положения заключается чаще всего не в отсутствии выхода из него, а в неспособности его найти.”

“Все наши трудности в большей степени связаны с тем, что мы думаем о них, а не с истинным положением вещей. Поэтому проблема заключается не в том, что именно произошло, а в том, как мы реагируем на произошедшее.”

“Парадоксы и закономерности нашей жизни и бизнеса таковы, что за отсутствие проблем, приходится платить… отсутствием успехов!”

Мудрые мысли, афоризмы, порой как отголоски из далеких миров и веков, часто бывают хорошими помощниками и советчиками в разнообразных ситуациях. Это уже чей-то пережитый опыт. Но мы привычно хотим наступать на свои, а не на чужие грабли, поэтому ценность советов чаще всего оцениваем уже после того как…

Давайте посмотрим, как находят решение задач и проблем те, кто уже умеет это делать. Заметьте, что перед нами сейчас стоит важная задача: научиться находить самое эффективное решение.

Техники поиска эффективного решения

1. Убедитесь, что вы решаете ту задачу, которую нужно. Важно на забывать: “Главное внимание – главным вещам”.

2. На второе место я поставлю способность задавать себе нужные вопросы. Вспомните, иногда чей-то вопрос способен в корне изменить отношение к проблеме и взглянуть на нее под другим углом зрения. Вопросы нужны и для того, чтобы проанализировать имеющуюся ситуацию, понять, от чего нужно отталкиваться и какими ресурсами мы обладаем.

Способностью задавать вопросы обладают коучи. Коучем называют такого человека, который профессионально решает чужие задачи. В своей практике коучи используют технику, при которой они искусственно создают ситуацию, в которой человек должен найти свое собственное правильное и эффективное решение. То решение, которое он с большим желанием и удовольствием реализует.

Брайан Трейси утверждает, что успешные люди тратят 25 % всего времени, отведенного на  решения задачи. Действительно, наша неспособность определить истинную причину возникновения ситуации привет к тому, что эта проблема может повторяться снова и снова в разных вариациях.

3. Эффективным средством в поиске наиболее эффективного решения может стать обычный мозговой штурм, проведенный в кругу коллег, сотрудников, друзей, членов семьи. В таких случаях говорят: “Одна голова хорошо, а две лучше.” Более того, в такой среде часто возникают идеальные и креативные способы решения задачи. Имея на руках несколько вариантов, главной задачей будет выбрать наилучшее из них. Нелишним в этом случае будет знание о том, как правильно сделать выбор.

4. Эффективным считают метод “Шести думающих шляп”, изобретенным Эдвардом де Боно для оценки провокационных и необычных идей, инновационных предложений и ситуаций.

Учитывая, что коллективное мнение часто представляет собой борьбу разных мнений, метод “Шести думающих шляп” побуждает участников думать параллельно. Для этого участники одевают шляпы разных цветов, и смотрят на задачу в ракурсе соответствующего цвета шляпы. Сначала озвучивается предложение, а затем каждый участник по очереди одевает шляпы:

Белая шляпа – шляпа информации. В белой шляпе можно попросить предоставить дополнительную информацию, цифры, факты, которые помогут оценить ситуацию.

Красная шляпа – шляпа эмоций. Можно описать эмоции, которые вызывает данное предложение.

Желтая шляпа – шляпа оптимизма. Даже если идея кажется плохой, нужно найти в ней положительные стороны.

Черная шляпа – шляпа пессимизма. Даже если идея отличная, надо найти в ней недостатки и угрозы.

Зеленая шляпа – шляпа роста и возможностей. Каждый может предложить способ улучшения идеи для того, чтобы она работала лучше.

Голубая шляпа – шляпа процесса. Одевая шляпу голубого цвета люди включаются в процесс размышления над ним. Цель: выяснить, насколько эффективен данный метод оценки предложения.

С помощью метода “Шести думающих шляп” в корпорациях решают проблемы текучки кадров или обмена электронного документооборота.

5. Найти максимальное количество информации по данному вопросу. В этом случае также появится необходимость выбора из имеющегося арсенала и адаптации чьего-то эффективного решения под конкретную ситуацию. Старайтесь читать хорошую бизнес-литературу, накапливайте знания. Читайте больше, анализируйте прочитанное, запоминайте информацию.

6. Самый любимый и быстрой поиск нужного и эффективного решения – подбросить монетку. Это на случай, когда хороших вариантов так много, что определиться становится трудно.

Встретила по этому поводу перевод стихотворения Питера Хейна:

Коль ты в плену сомнений мук,

В них заперт, словно в клетке.

Мудрей всего, не смейся друг, –

Подбросить вверх монетку.

Лишь в воздух устремиться грош,

Лишь станет мир короче.

Ты неожиданно поймешь,

Чего ты втайне хочешь.

7. Хорошо бы услышать свою интуицию. Иногда, в экстремальных ситуациях, подсознание способно предложить наилучший выход. Доверяя своей интуиции надо помнить о вероятности ошибок.

8. Случайно наткнулась на технику “Лощади”, который, считаю, имеет право на жизнь в некоторых случаях. Когда не остается сил, а решение еще не найдено, ложитесь спать. “Утро вечера мудренее” – говорили наши бабушки. Только перед сном мысленно подумайте о задаче и скажите: “Пусть об этом подумает лошадь”.

Таким образом вы отпускаете проблему, и если навязчивая задача будет беспокоить, говорите себе, что теперь это не ваша задача, что теперь об этом думает Лошадь. Сняв таким образом напряжение и поверив в то, что ответ найдется у Лошади, автор метода советует поблагодарить Лошадь, когда ответ придет вам в голову или вложит в уста другого человека.

9. Техника стакана воды по Методу Сильвы. С помощью этого метода можно задействовать скрытые способности сознания. Это по сути – самовнушение, и оно стимулирует творческие способности нашего мозга за счет использования обоих полушарий.

Перед тем, как лечь спать, наполните стакан чистой водой и выпейте половину. Затем закройте глаза и направьте взгляд слегка вверх. Произнесите мысленно: “Это все, что мне нужно сделать, чтобы найти решение проблемы, о которой я думаю”. После этого отпустите проблему и перестаньте о ней думать – вы передали ее на рассмотрение своему сознанию.

Проснувшись утром, выпейте вторую половину воды и проделайте те же действия, что и перед сном. Люди, использующие этот метода, считают, что решение приходит либо ночью во сне, либо в виде какой-то случайной подсказки. Этот метод очень похож на технику “Лошади”, вероятно, в поисках эффективного решения люди изобрели много подобных способов на тот случай, когда идея совершенно не приходила в голову.

10. А теперь, когда единственное решение все-таки найдено, его можно проверить на соответствие критериям “Каким должно быть эффективное решение”.

• Наше решение является обоснованным.
• Наше решение является реальным, у нас есть все ресурсы для его осуществления.
• Наше решение можно разложить на простые составляющие.
• Наше решение своевременно. Его исполнение все еще актуально.
• Наше решение является гибким. Его можно адаптировать под изменившиеся условия.
• Наше решение должно принести максимальную выгоду.
• Наше решение предусматривает контроль над его исполнением.

Друзья, никто из нас не застрахован от принятия неверных решений. Это нужно понимать и постараться избавиться от этого страха. Единственный разумный способ справиться с проблемами и задачами – как можно быстрее создать импульс движения. Не пускать все на самотек, а начать действовать. В процессе движения обязательно появляются средства и пути решения проблемы, обычно скрытые от нас.

Может быть стоит поучиться и узнать, как найти эффективное решение сегодня, чтобы завтра не ошибиться.

Смотрите один из способов принятия решения от Константина Коптелова.

[message type="warning"

]"Успевайте больше за меньшее время вместе с 

«Копилкой Эффективных Советов»

[/message]

Просмотры: 748

Ни один человек не умеет с рождения решать математические задачи. Но этому можно и нужно научиться. Чтобы быстро и правильно решать задачи, нужно знать и выполнять несколько важных условий. В этой статье мы расскажем об этих “секретных ингредиентах”, которые позволят ребенку постичь таинство быстрого решения математических задач. 

Математика — это нестрашно

Многие дошкольники боятся математики как страшного чудовища, которое мучает непонятными условиями и решениями. Эти страхи навязаны взрослыми, упрекающими своё чадо в нежелании заниматься или ругающими за неверные ответы. Первая задача взрослых — не напугать предметом, а показать,  что математика — это нестрашно.

Чтобы “царица наук” приносила только положительные эмоции, каждый день постарайтесь обращать внимание ребёнка на самые простые признаки этого предмета. Математика окружает нас везде: мы считаем  в магазине деньги, смотрим номера домов на улице, вычисляем время, которое нам нужно для поездки, и многое-многое другое. В время прогулки с малышом предложите решить вместе весёлую задачку: узнать, сколько шагов до ближайшего дерева или качели. Также обратите внимание ребёнка на пользу математики в решении самых обычных дел. 

Если ваш малыш не проявляет интерес к математике и его больше интересуют гуманитарные науки, не стоит огорчаться и принуждать к занятиям. Начните давать посильные задачи: например, пересчитать гостей и принести нужное количество вилок на стол, или определить, в какой тарелке больше фруктов. После выполнения задания обязательно похвалите ребёнка и отметьте, что он отлично справился с задачей. Так малыш поймет важность и необходимость математических знаний.

Как решить задачу

Прозвенел первый звонок, и теперь ваш малыш настоящий школьник! Математика — один из самых главных уроков, на котором ребёнка будут ждать цифры, числа, фигуры, примеры и, конечно, задачи. Ведь именно в процессе решения любых математических задач ребёнок развивает логическое мышление, воображение, память, внимание и самоконтроль. 

Умение быстро решать задачи для 1 класса по математике — очень важный навык. Освоив его, ребёнок будет легче понимать задачи и в старших классах, поэтому стоит запастись терпением и помочь малышу хорошо разобраться в этом вопросе,  чтобы потом он решал задачи по математике самостоятельно. Согласитесь, лучше приложить немного больше усилий в 1 классе, чтобы потом не делать с ребёнком математику все школьные годы?

Учимся решать задачи

Алгоритм решения задач

Решать задачи ребёнку придётся всю школьную жизнь, и не только математические, но и по физике, химии, биологии. Именно поэтому с начальных классов стоит усвоить алгоритм решения, который применим к абсолютно любой задаче:

1. Читаем условие задачи
   Первый раз ребёнок читает условие задачи вслух, затем ему нужно ещё раз прочитать задачу внимательно и не торопясь. Чтобы проверить понимание, попросите малыша пересказать условие задачи. Если он что-то забыл, спокойно задайте наводящий вопрос. Очень важно, чтобы у ребёнка не возникало затруднений в представлении объектов задачи.  Если малыш не понимает какие-то слова в условии, обязательно расскажите и подробно объясните. Дайте ребёнку возможность прочитать условие столько раз, сколько нужно, не ругайтесь и не нервничайте, а лучше похвалите и подбодрите в этом старании.

   

2. Представляем задачу
   Разобравшись с условием и усвоив все объекты в задаче, переходите к её схематическому представлению. Это можно сделать в виде рисунка или схемы,  используя игрушки и реальные предметы. Например, если речь идёт о вазе с конфетами, можно взять несколько карамелек и разложить их по стаканам. Задачи на движение можно нарисовать схематично: домик, велосипед, дорогу и рядом изобразить знаки вопроса. Чем лучше и нагляднее будет нарисована задача, тем проще будет представить, какие действия нужно сделать для её решения. Возможно, уже в ходе создания рисунка ребёнок сможет решить задачу.
   Детям в начале школьной жизни ещё очень сложно представлять задачу только в уме, абстрактно. Малышам гораздо легче и проще решать задачи, когда можно увидеть все объекты на рисунке или потрогать и переложить их. С возрастом ребёнок научится “видеть” задачу в голове, но сначала ему нужно понять, как это делается.

   

3. Решение задачи
   Теперь можно переходить к решению. “Увидев” задачу, малыш уже может понять, какие действия нужно совершить, чтобы получить ответ. Если ребёнок не смог сразу найти решение, не нервничайте, а начните задавать наводящие вопросы, обращайте внимание на детали и обязательно хвалите. Малыш старается решить, а это уже большое дело! Не концентрируйтесь на текстовом условии, а используйте любые способы: инсценировка задачи, наглядное представление из подручных предметов, схема или рисунок.
   Если в задаче нужно выполнить несколько действий, помогите малышу разложить задачу на несколько простых шагов. Такой способ поможет ребёнку увидеть закономерность и последовательность действий. 

   

4. Записываем решение
   Когда малыш уже полностью понял задачу, увидел все действия, которые нужно совершить, только после этого приступайте к записи решения. Подробно записывайте и проговаривайте вслух всё, что фиксируется в тетради. Это поможет ребёнку быстрее запомнить последовательность записи решения. 
   Если решение состоит из нескольких действий, то после вычислений ребёнку нужно обязательно записывать, что обозначает каждое число,  чтобы в итоге не перепутать огурцы с грибами. 

   

5. Ответ
   Как только все вычисления сделаны и записаны, нужно сформулировать и зафиксировать на бумаге ответ. Для этого возвращаемся к условию задачи. Попросите малыша прочитать вопрос в задаче, а потом развернуто дать ответ. Например, если вопрос звучит так: “Сколько яблок съел Дима?”, ребёнку нужно ответить не просто “6 яблок”, а подробно — “Дима съел 6 яблок”, а потом записать этот развернутый ответ в тетрадь. Таким образом видно, что принцип формирования ответа заключается в вопросе, но без использования числительного. Конечно, первокласснику можно объяснить проще: “Вместо слова “сколько” говорим число и получаем развёрнутый ответ”. 

   

6. Проверка
   Задача решена! Похвалите ребёнка за все старания и усилия, ведь он смог решить математическую задачу, но не забывайте о проверке решения. Выполняя проверку, ребёнок учится очень важным навыкам — контролю и самоконтролю.
   Не пугайте малыша, что теперь нужно ещё раз что-то решать, просто  заинтересованно спросите: “Как ты думаешь, это правильный ответ? Давай проверим!”.

Выполнять проверку можно несколькими способами:

а) Сверка ответа
Самый простой способ — это посмотреть ответ в конце учебника. Но такой способ не всегда хорош и полезен, потому старайтесь пользоваться им нечасто.

б) Прикидка ответа
Прочитав условие задачи, ребёнок прикидывает, в каких пределах должен получиться ответ. Например, решая задачу, где нужно сложить 10 яблок и 15 груш, малыш задаётся вопросом: может ли получиться ответ меньше 10? В этом способе есть свои преимущества, но он менее точный.

в) Решение задачи другим способом
Такой способ хорош для более сложных задач, когда ребёнок уже достаточно хорошо ориентируется в действиях и умеет представлять условие. Однако к этому способу не стоит обращаться в самом начале обучения решению задач.

г) Подстановка результата в условие задачи
Именно так стоит обучать ребёнка проверке решения. Способ подходит для самых лёгких и первых задач по математике 1 класса. 

Со временем вы можете показать малышу разные способы проверки решения задач, но не используйте все способы сразу. Это может только запутать первоклассника.

‍

Учимся решать задачи до 20

Очень важно, чтобы ребёнок четко усвоил алгоритм решения задач. Для этого старайтесь решать по одной задаче, не смешивая их с примерами или выполнением домашнего задания по другим предметам. Дайте малышу отдохнуть после решения, тогда новая информация хорошо усвоится и не забудется. 

На нашем сайте в разделе Решаем задачи и примеры вы найдёте не только задачи и примеры по математике для 1 класса, но и для других классов начальной школы и даже для дошкольников. Ребёнок может выполнять задания для 1 класса как самостоятельно, так и вместе с вами. Кроме этого, малыш может оттачивать математические навыки в тренировке Математик,  которая обновляется каждый день. 

Решаем и составляем задачи 1 класс

Задачи в два действия 2 класс

Задачи на умножение и деление 3 класс

Задачи на движение 4 класс

Также рекомендуем вам нашу статью “Математические головоломки с ответами”. Занимайтесь математикой в игровой форме!

Ольга Шадрина,
практикующий педагог-дефектолог, автор упражнений и обучающих материалов IQsha.ru