Кроме линии регрессии, есть другой способ изучения той же зависимости — УСЛОВНОЕ СРЕДНЕЕ, то есть среднее при выполнении некоторого условия. Это среднее арифметическое значений результативного признака Y ПРИ УСЛОВИИ, что соответствующие значения факторного признака X попадают в заданный интервал.
Вот пример условного среднего: средний вес людей, у которых рост окажется в диапазоне от 160 до 170 см. Мы выбираем людей ростом от 160 до 170 см, измеряем их вес и находим среднее значение веса только по этой группе. Здесь рост — это факторный признак Х, а вес — это результативный признак Y. Мы получили средний «игрек», а условие определяли по «иксу».
На новом листе добавим интервалы группировки по X: нижние и верхние границы, а также среднее значение. Интервалы группировки выбираем точно так же, как описано в первой работе. Ссылка для скачивания пособия по первой работе приводится в конце данного выпуска.
В нашем примере возьмём 10 интервалов по 100 единиц, чтобы охватить диапазон значений от 1000 до 2000.
Для нахождения условного среднего можно использовать функцию
SUMIF
СУММЕСЛИ.
Функция позволяет вычислить сумму при выполнении заданного условия. Формат функции следующий:
SUMIF (range, criteria, [sum_range])
СУММЕСЛИ (диапазон; критерий; [диапазон_суммирования])
range — диапазон — диапазон ячеек;
criteria — критерий — условие;
sum_range — диапазон_суммирования — диапазон ячеек для суммирования. Если диапазон не указан, то суммируются значения из диапазона, указанного в первом аргументе.
Для определения средних значений фактора Х в каждом интервале группировки используем только два первых аргумента функции.
Рассмотрим примеры условных сумм — см. формулы.
Условные суммы
Первая формула вычисляет сумму значений фактора, не превышающих верхнюю границу первого интервала. Сюда попадут все значения из первого интервала, а также все точки, которые окажутся левее этого интервала.
Вторая формула определяет сумму значений фактора, попадающих во второй интервал.
В третьей формуле мы фиксируем номера строк для диапазона исходных данных с помощью символа $. Это позволит нам скопировать формулу и заполнить весь столбец.
Для упрощения расчётов мы определяем разность сумм значений, не превышающих верхние границы интервалов. В этом случае формулы получаются немного короче и понятнее. Мы уже использовали подобный приём в первой работе, когда определяли частоту попадания в интервал. Мы находили относительные частоты как разность соседних значений накопленной частоты.
Функция SUMIF
При вычислении среднего арифметического нужно поделить сумму значений на их количество.
Для определения количества элементов используем функцию
COUNTIF
СЧЕТЕСЛИ.
Формула для расчета условного среднего фактора Х получается довольно громоздкой — см. формулы.
Расчёт условного среднего
Изучите формулы и найдите следующие элементы:
— диапазон ячеек от А2 до А121 на листе 04;
— верхняя граница первого интервала на листе 05;
— верхняя граница второго интервала на листе 05.
Чтобы не запутаться, проведём наши расчёты по частям. Сначала найдём суммы и количества значений Х, не превышающих верхней границы. Затем определим разности соседних ячеек. Затем проведём деление и в результате получим среднее значение Х в каждом интервале группировки.
Вычисление условного среднего значения результативного признака Y немного сложнее. Здесь проверяется условие попадания факторного признака Х в интервал группировки, а сумма считается по столбцу результативного признака Y. Для этого используется третий аргумент функции SUMIF — см. формулу.
Условное среднее Y (X)
Для копирования формулы фиксируем номера строк с помощью знака $.
Вычисление условного среднего
После вычислений наносим линию условного среднего на диаграмму разброса. Для этого нам потребуется ломаная линия с маркерами точек.
Строим диаграмму разброса, как описано выше.
Выбираем второй ряд данных:
Select Data — Select Data Source — Add
Выбрать данные — Выбор источника данных — Добавить.
Добавляем новые данные для графика. В качестве значений x берём условные средние «иксы», а в качестве y — условные средние «игреки». На графике появляются новые точки.
Изменяем тип диаграммы: щёлкаем правой кнопкой по графику и выбираем комбинированный график:
Change Chart Type — Combo
Изменить тип диаграммы — Комбинированная.
Для исходных данных оставляем диаграмму разброса:
Scatter
Точечная.
Для условного среднего выбираем ломаную линию:
Scatter with Straight Lines
Точечная с прямыми отрезками и маркерами.
Для использовани единого масштаба на графиках снимаем выбор пункта:
Secondary Axis
Вспомогательная ось.
Если на графике будет две вертикальных оси, то будет свой масштаб для каждого набора данных. Такие графики будет невозможно сравнивать. Нам нужен общий, единый масштаб.
Комбинация графиков
В процессе настройки графиков можно видеть, как меняется изображение. При выборе данных для графиков мы не указывали названия рядов, поэтому они названы по умолчанию Series1 и Series2. Пока на графике не так много данных, это не доставляет неудобств. В следующей работе всё-таки придётся задать имена для каждого набора данных, чтобы легче было работать с несколькими графиками.
Как и раньше, настраиваем масштаб, заголовки, цвета. График готов.
Условное среднее на диаграмме разброса
7.3.1. Уравнение линейной регрессии Y на X
Это и есть та самая оптимальная прямая 
, которая проходит максимально близко к точкам. Обычно её
находят методом наименьших квадратов, и мы
пойдём знакомым путём. Заполним расчётную таблицу:
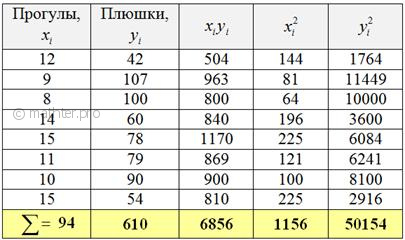
Коэффициенты «а» и «бэ» функции 
найдём из решения системы:
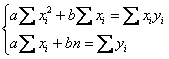, в нашей
задаче:
Сократим оба уравнения на 2, всё попроще будет:
Систему выгоднее решить по формулам
Крамера:
, значит,
система имеет единственное решение.
И проверка forever, подставим полученные значения 
в левую часть каждого уравнения исходной
системы:
– в результате получены соответствующие правые части, значит, система решена верно.
Таким образом, искомое уравнение регрессии:
и на самом деле «игрек» правильнее записать с чертой:
– по той
причине, что для различных «икс» мы будем получать средние (среднеожидаемые) значения «игрек». Но дабы избежать
«накладок» с обозначениями, да и просто для чистоты я буду часто записывать голый «игрек».
Полученное уравнение показывает, что с увеличением количества прогулов («икс») на 1 единицу суммарная успеваемость
падает в среднем на 6,0485 – примерно на 6 баллов. Об этом нам рассказал коэффициент «а». И ещё раз обращаю
внимание на тот факт, что найденная функция возвращает нам средние или
среднеожидаемые значения «игрек» для различных значений «икс».
А почему это регрессия именно «
на 
» и о происхождении самого термина «регрессия» я
рассказал чуть ранее, в параграфе эмпирические линии регрессии. Если кратко, то
полученные с помощью уравнения средние значения успеваемости («игреки») регрессивно возвращают нас к первопричине –
количеству прогулов. Вообще, регрессия – не слишком позитивное слово, но какое уж есть.
Линию регрессии изобразим на том же чертеже, вместе с диаграммой рассеяния. Для того чтобы построить прямую,
достаточно знать две точки, выберем пару удобных значений «икс» и вычислим соответствующие «игреки»:
Отметим найденные точки на чертеже (малиновый цвет) и проведём линию регрессии:
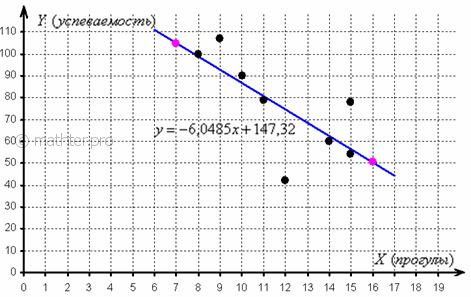
Говорят, что уравнение регрессии аппроксимирует (приближает) эмпирические данные (точки), и с помощью
него можно интерполировать (оценивать) неизвестные промежуточные значения, так при количестве прогулов 
среднеожидаемая успеваемость
ориентировочно составит 
балла.
И, конечно, осуществимо прогнозирование, так при 
среднеожидаемая успеваемость составит 
баллов. Единственное, нежелательно
брать «иксы», которые расположены слишком далеко от эмпирических точек, поскольку прогноз, скорее всего, не будет
соответствовать действительности. Например, при 
соответствующее значение 
может вообще оказаться невозможным, ибо у успеваемости есть
свой фиксированный «потолок». И, разумеется, «икс» или «игрек» в нашей задаче не могут быть отрицательными.
Второй вопрос касается тесноты зависимости. Очевидно, что чем ближе расположены эмпирические
точки к прямой, тем теснее линейная корреляционная зависимость – тем уравнение регрессии достовернее отражает ситуацию, и тем
качественнее полученная модель. И наоборот, если многие точки разбросаны вдали от прямой, то признак 
зависит от 
вовсе не линейно (если вообще зависит) и
линейная функция плохо отражает реальную картину. Прояснить данный вопрос нам поможет:
7.3.2. Линейный коэффициент корреляции
7.3. Модель пАрной линейной регрессиих
| Оглавление |
Среднее арифметическое
Онлайн калькулятор поможет найти среднее арифметическое чисел. Среднее арифметическое множества чисел (ряда чисел) — число, равное сумме всех чисел множества, делённой на их количество.
Программа вычисляет среднее арифметическое элементов массива, среднее арифметическое натуральных чисел, целых чисел, набора дробных чисел.
Формула которая используется для расчета среднего арифметического значения:
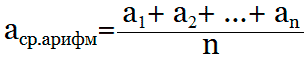
Приведём примеры нахождения среднего арифметического ряда чисел:
Среднее арифметическое двух чисел: (2+5)/2=3.5;
Среднее арифметическое трёх чисел: (2+5+7)/3=4.66667;
Среднее арифметическое 4 чисел: (2+5+7+2)/4=4;
Найти выборочное среднее (математические ожидание):
Среднее арифметическое 5 чисел: (2+5+7+2+3)/5=3.8;
Среднее арифметическое 6 чисел: (2+5+7+2+3+4)/6=3.833;
Среднее арифметическое 7 чисел: (2+5+7+2+3+4+8)/7=4.42857;
Среднее арифметическое 8 чисел: (2+5+7+2+3+4+8+5)/8=4.5;
Среднее арифметическое 10 чисел: (2+5+7+2+3+4+8+5+9+1)/10=4.6;
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»
Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»
Смотрите также
Содержание
- Решение задач по эконометрике
- Корреляционно-регрессионный метод анализа
- Непараметрические показатели связи
- Гетероскедастичность случайной составляющей
- Автокорреляция
- Эконометрические методы проведения экспертных исследований
- Классификация эконометрических моделей и методов
- Введение
- I. Основная часть
- Параметрическая идентификация парной линейной эконометрической модели
- Критерий Фишера
- Параметрическая идентификация парной нелинейной регрессии
- Прогнозирование спроса на продукцию предприятия. Использование в MS Excel функции «Тенденция»
Решение задач по эконометрике
Корреляционно-регрессионный метод анализа
- Уравнение парной линейной регрессии (см. также уравнение парной линейной регрессии матричным методом);
При регрессионном анализе необходимо найти уравнение линейной парной регрессии. Исходные данные представляют собой значения X (признак-фактор) и значения Y (признак-результат).
Для этого указывается количество строк . Второй вариант ввода данных — вставить их из Excel (X — первый столбец,Y — второй столбец). Пример. Для зависимой переменной, если указан процент (например, 105%), то значение рассчитывается от среднего значения X. - Уравнение нелинейной регрессии: экспоненциальная y = a*e bx ,степенная y = a x b , равносторонняя гипербола y = b/x + a , логарифмическая y = b ln(x) + a , показательная y = a*b x . Если необходимо найти полиномиальное уравнение второго порядка (парабола), то можно воспользоваться сервисом Аналитическое выравнивание;
Далее выбирается вид регрессии, зависимая переменная и уровень значимости α. - Дисперсионный анализ. Разложение дисперсий для анализа влияния анализируемого признака (см. также Однофакторный дисперсионный анализ);
- Уравнение множественной регрессии. Дополнительно с помощью другого онлайн-калькулятора Матрица парных коэффициентов корреляции находятся уравнения множественной регрессии в стандартизованном и натуральном масштабе.
- Расчет коэффициента детерминации;
- Метод статистических уравнений зависимостей;
- Система одновременных уравнений:
. Необходимое и достаточное условия идентификации.
Непараметрические показатели связи
Гетероскедастичность случайной составляющей
Автокорреляция
- Автокорреляция уровней временного ряда. Проверка на автокорреляцию с построением коррелограммы;
Эконометрические методы проведения экспертных исследований
- Метод средних оценок.
- Метод медиан рангов.
- Коэффициент конкордации.
- Коэффициент контингенции.
- Критерий Манна-Уитни
- Методом дисперсионного анализа проверить нулевую гипотезу о влиянии фактора на качество объекта.
Полученное решение оформляется в формате Word . Сразу после решения следует ссылка на скачивание шаблона в Excel, что дает возможность проверить все полученные показатели. Если в задании требуется решение в Excel , то можно воспользоваться статистическими функциями в Excel.
Источник
Классификация эконометрических моделей и методов
| Доступные действия |
|
- Прокомментировать файл
МОСКОВСКИЙ ГУМАНИТАРНО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
Кафедра общегуманитарных дисциплин
Специальность: Бухгалтерский учет, анализ и аудит.
Учебная дисциплина: «Эконометрика»
студентки 3 курса группа ББ-341
факультет экономики и управления
Тимофеевой Татьяны Евгеньевны
Снастин Александр Анатольевич
I. Основная часть
Параметрическая идентификация парной линейной эконометрической модели
Параметрическая идентификация парной нелинейной регрессии
Прогнозирование спроса на продукцию предприятия. Использование в MS Excel функции «Тенденция»
Введение
Классификация эконометрических моделей и методов.
Эконометрика — это наука, лежащая на стыке между статистикой и математикой, она разрабатывает экономические модели для цели параметрической идентификации, прогнозирования (анализа временных рядов).
Классификация эконометрических моделей и методов.
Эконометрические модели (ЭМ)
| Эконометрические модели параметрической идентификации | Эконометрические модели для цели прогнозирования | Система эконометрических моделей |
(установление параметров (есть ли тренд) (комплексная модели) оценка)
y — зависимая переменная (отклик), прибыль, например. x — независимая переменная (регрессор), какова численность персонала, например. На основании наблюдений оцениваются a и b (определение параметров моделей или регрессионные коэффициенты).
| № п/п | y | x |
| 1 | 11 | 1 |
| 2 | 13 | 2 |
| 3 | 14 | 3 |
| 4 | 12 | 4 |
| 5 | 17 | 5 |
| 6 | 16,7 | 6 |
| 7 | 17,8 | 7 |
На основании наблюдений оценивается a и b (определение параметров моделей или регрессионные коэффициенты).
Параметрическая идентификация занимается оценкой эконометрических моделей, в которых имеется один или несколько x и один y. Для целей установления влияния одних параметров работы предприятия на другие.
Если x в первой степени и нет корней, ни степеней, нет 1/x, то модель линейная.
y=ax b — степенная функция;
y=ab x — показательная функция;
y=a1/x — парабола односторонняя.
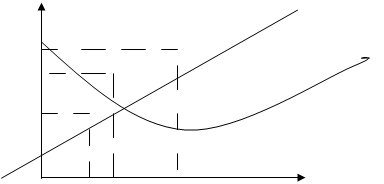Y -прибыль — линейная модель
Выбираем наиболее надежную модель. После построения по одним и тем же эксперт данным одной линейной и нескольких нелинейных моделей над каждой из полученных моделей производим две проверки.
1 — на надежность модели или статистическую значимость. Fкр — или критерий Фишера. Табличное F и расчетное F. Если Fp > Fтабл. — то модель статистически значима.
2 — Отобрав из моделей все значимые модели, среди них находим самую точную, у которой минимальная средняя ошибка аппроксимации.
Эконометрические модели для прогнозов исследуют поведение одного параметра работы предприятия во времени.
I. Основная часть
Параметрическая идентификация парной линейной эконометрической модели
По семи областям региона известны значения двух признаков за 2007г.
Расходы на покупку продовольственных товаров в общих расходах,%, у
среднедневная заработная плата одного работающего, руб., х
1 68,8 45,1 2 61,2 59 3 59,9 57,2 4 56,7 61,8 5 55 58,8 6 54,3 47,2 7 49,3 55,2
(ŷ — у) 2
(y-ŷ) /y 1 68,80 45,10 3102,88 2034,01 61,33 11,8286862 55,87562 0,108648 2 61, 20 59,00 3610,80 3481,00 56,46 2,0326612 22,46760 0,077451 3 59,90 57, 20 3426,28 3271,84 57,09 0,6331612 7,89610 0,046912 4 56,70 61,80 3504,06 3819,24 55,48 5,7874612 1,48840 0,021517 5 55,00 58,80 3234,00 3457,44 56,53 1,8379612 2,34090 0,027820 6 54,30 47, 20 2562,96 2227,84 60,59 7,3131612 39,56410 0,115840 7 49,30 55, 20 2721,36 3047,04 57,79 0,0091612 72,08010 0,172210 Итого 405, 20 384,30 22162,34 21338,41 405,27 29,4422535 201,7128 0,570398 Средн. з 57,89 54,90 3166,05 3048,34 57,90 4, 2060362 28,81612 0,081485
y x yx x 2
Исходные данные x и y могут быть двух типов:
а) рассматриваем одно предприятие, то наблюдения берутся через равностоящие промежутки времени (1 в квартал);
б) если каждое наблюдение — это отдельное предприятие, то данные берутся на одну и ту же дату, например, на 01.01.07
у — расходы на продовольственные товары в процентах; траты, например, на еду.
yx-yx
(Гаусс) x² — (x) ²
х — среднедневная заработная плата, в руб.
у = а + b х — линейная парная регрессионная ЭМ.
=-0.35 a=y — b x =76,88
b = (3166,049-57,88571*54,9) / (3048,344-54,9) = — 0,35
а = 57,88571 — ( — 0,35) *54,9 = 77,10071
ŷ (игрек с крышечкой) = 76,88-0,35х -это модельное значение y, которое получается путем подстановки в y = a + b x, конкретное значение a и b коэффициенты, а также x из конкретной строчки.
Критерий Фишера
Σ (ŷ -y) 2 m
n — количество наблюдений;
m — количество регрессоров (x1)
Допустим, 0,7. Fкрит не может быть меньше единицы, поэтому, если мы получим значение П
2,95 2,79 2,61 2,40
Когда m=1, выбираем 1 столбец.
k2=n-m=7-1=6 — т.е.6-я строка — берем табличное значение Фишера
Влияние х на у — умеренное и отрицательное
ŷ — модельное значение.
| F расч. = | 28,648: 1 | = 0,92 |
| 200,50: 5 |
А = 1/7 * 398,15 * 100% = 8,1% Fтабл
Нарушается данная модель, поэтому данное уравнение статистически не значимо.
Так как расчетное значение меньше табличного — незначимая модель.
1 Σ (y — ŷ) *100%
N y
A= 1/7*0,563494* 100% = 8,04991% 8,0%
Считаем, что модель точная, если средняя ошибка аппроксимации менее 10%.
Параметрическая идентификация парной нелинейной регрессии
Модель у = а * х b — степенная функция
Чтобы применить известную формулу, необходимо логарифмировать нелинейную модель.
log у = log a + b log x
Y=C+b*X -линейная модель.
yx-Y*X
x²- (x) ²
C=Y-b*X
С = 1,7605 — ( — 0,298) * 1,7370 = 2,278
Возврат к исходной модели
Ŷ=10 с *x b =10 2.278 *x -0.298
| №п/п | У | X | Y | X | Y*X | У | I (y-ŷ) /yI | |
| 1 | 68,80 | 45,10 | 1,8376 | 1,6542 | 3,039758 | 2,736378 | 60,9614643 | 0,113932 |
| 2 | 61, 20 | 59,00 | 1,7868 | 1,7709 | 3,164244 | 3,136087 | 56,2711901 | 0,080536 |
| 3 | 59,90 | 57, 20 | 1,7774 | 1,7574 | 3,123603 | 3,088455 | 56,7931534 | 0,051867 |
| 4 | 56,70 | 61,80 | 1,7536 | 1,7910 | 3,140698 | 3, 207681 | 55,4990353 | 0,021181 |
| 5 | 55,00 | 58,80 | 1,7404 | 1,7694 | 3,079464 | 3,130776 | 56,3281590 | 0,024148 |
| 6 | 54,30 | 47, 20 | 1,7348 | 1,6739 | 2,903882 | 2,801941 | 60,1402577 | 0,107555 |
| 7 | 49,30 | 55, 20 | 1,6928 | 1,7419 | 2,948688 | 3,034216 | 57,3987130 | 0,164274 |
| Итого | 405, 20 | 384,30 | 12,3234 | 12,1587 | 21,40034 | 21,13553 | 403,391973 | 0,563493 |
| Средняя | 57,88571 | 54,90 | 1,760486 | 1,736957 | 3,057191 | 3,019362 | 57,62742 | 0,080499 |
Входим в EXCEL через «Пуск»-программы. Заносим данные в таблицу. В «Сервис» — «Анализ данных» — «Регрессия» — ОК
Если в меню «Сервис» отсутствует строка «Анализ данных», то ее необходимо установить через «Сервис» — «Настройки» — «Пакет анализа данных»
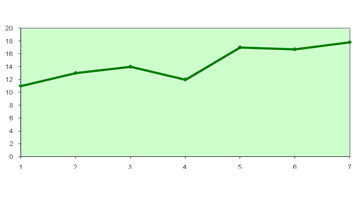
Прогнозирование спроса на продукцию предприятия. Использование в MS Excel функции «Тенденция»
A — спрос на товар. B — время, дни
B
1 11 1 2 14 2 3 13 3 4 15 4 5 17 5 6 17,9
6
Шаг 1. Подготовка исходных данных
Шаг 2. Продлеваем временную ось, ставим на 6,7 вперед; имеем право прогнозировать на 1/3 от данных.
Шаг 3. Выделим диапазон A6: A7 под будущий прогноз.
Шаг 4. Вставка функция
Полный алфавитный перечень Тенденция
Известные значения x (курсор В1: В5)
Выделяем с 1 по 5
| Новый x | В6: В7 |
| Известный y | А1: А5 |
| Const | 1 |
| Ок |
Шаг 5. ставим курсор в строку формул за последнюю скобку
Вставка диаграмма нестандартны гладкие графики
диапазон у готово.
Если каждое последующее значение нашего временной оси будет отличаться не на несколько процентов, а в несколько раз, тогда нужно использовать не функцию «Тенденция», а функцию «Рост».
Источник
Корреляционная таблица
Пример 1 . По данной корреляционной таблице построить прямые регрессии с X на Y и с Y на X . Найти соответствующие коэффициенты регрессии и коэффициент корреляции между X и Y .
| y/x | 15 | 20 | 25 | 30 | 35 | 40 |
| 100 | 2 | 2 | ||||
| 120 | 4 | 3 | 10 | 3 | ||
| 140 | 2 | 50 | 7 | 10 | ||
| 160 | 1 | 4 | 3 | |||
| 180 | 1 | 1 |
Решение:
Уравнение линейной регрессии с y на x будем искать по формуле
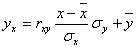
а уравнение регрессии с x на y, использовав формулу:
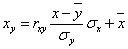
где x x , y – выборочные средние величин x и y, σx, σy – выборочные среднеквадратические отклонения.
Находим выборочные средние:
x = (15(1 + 1) + 20(2 + 4 + 1) + 25(4 + 50) + 30(3 + 7 + 3) + 35(2 + 10 + 10) + 40(2 + 3))/103 = 27.961
y = (100(2 + 2) + 120(4 + 3 + 10 + 3) + 140(2 + 50 + 7 + 10) + 160(1 + 4 + 3) + 180(1 + 1))/103 = 136.893
Выборочные дисперсии:
σ 2 x = (15 2 (1 + 1) + 20 2 (2 + 4 + 1) + 25 2 (4 + 50) + 30 2 (3 + 7 + 3) + 35 2 (2 + 10 + 10) + 40 2 (2 + 3))/103 – 27.961 2 = 30.31
σ 2 y = (100 2 (2 + 2) + 120 2 (4 + 3 + 10 + 3) + 140 2 (2 + 50 + 7 + 10) + 160 2 (1 + 4 + 3) + 180 2 (1 + 1))/103 – 136.893 2 = 192.29
Откуда получаем среднеквадратические отклонения:
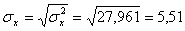и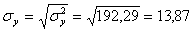 
Определим коэффициент корреляции:
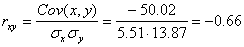
где ковариация равна:
Cov(x,y) = (35•100•2 + 40•100•2 + 25•120•4 + 30•120•3 + 35•120•10 + 40•120•3 + 20•140•2 + 25•140•50 + 30•140•7 + 35•140•10 + 15•160•1 + 20•160•4 + 30•160•3 + 15•180•1 + 20•180•1)/103 – 27.961 • 136.893 = -50.02
Запишем уравнение линий регрессии y(x):
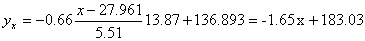
и уравнение x(y):
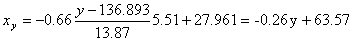
Построим найденные уравнения регрессии на чертеже, из которого сделаем следующие вывод:
1) обе линии проходят через точку с координатами (27.961; 136.893)
2) все точки расположены близко к линиям регрессии.
Пример 2 . По данным корреляционной таблицы найти условные средние y и x . Оценить тесноту линейной связи между признаками x и y и составить уравнения линейной регрессии y по x и x по y . Сделать чертеж, нанеся его на него условные средние и найденные прямые регрессии. Оценить силу связи между признаками с помощью корреляционного отношения.
Корреляционная таблица:
| X / Y | 2 | 4 | 6 | 8 | 10 |
| 1 | 5 | 4 | 2 | 0 | 0 |
| 2 | 0 | 6 | 3 | 3 | 0 |
| 3 | 0 | 0 | 1 | 2 | 3 |
| 5 | 0 | 0 | 0 | 0 | 1 |
Уравнение линейной регрессии с y на x имеет вид:
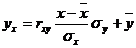
Уравнение линейной регрессии с x на y имеет вид:
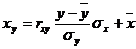
найдем необходимые числовые характеристики.
Выборочные средние:
x = (2(5) + 4(4 + 6) + 6(2 + 3 + 1) + 8(3 + 2) + 10(3 + 1) + )/30 = 5.53
y = (2(5) + 4(4 + 6) + 6(2 + 3 + 1) + 8(3 + 2) + 10(3 + 1) + )/30 = 1.93
Дисперсии:
σ 2 x = (2 2 (5) + 4 2 (4 + 6) + 6 2 (2 + 3 + 1) + 8 2 (3 + 2) + 10 2 (3 + 1))/30 – 5.53 2 = 6.58
σ 2 y = (1 2 (5 + 4 + 2) + 2 2 (6 + 3 + 3) + 3 2 (1 + 2 + 3) + 5 2 (1))/30 – 1.93 2 = 0.86
Откуда получаем среднеквадратические отклонения:
σx = 2.57 и σy = 0.93
и ковариация:
Cov(x,y) = (2•1•5 + 4•1•4 + 6•1•2 + 4•2•6 + 6•2•3 + 8•2•3 + 6•3•1 + 8•3•2 + 10•3•3 + 10•5•1)/30 – 5.53 • 1.93 = 1.84
Определим коэффициент корреляции:
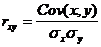
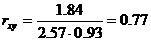
Запишем уравнения линий регрессии y(x):
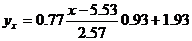
и вычисляя, получаем:
yx = 0.28 x + 0.39
Запишем уравнения линий регрессии x(y):
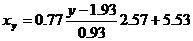
и вычисляя, получаем:
xy = 2.13 y + 1.42
Если построить точки, определяемые таблицей и линии регрессии, увидим, что обе линии проходят через точку с координатами (5.53; 1.93) и точки расположены близко к линиям регрессии.
Значимость коэффициента корреляции.
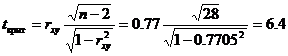
По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=30-m-1 = 28 находим tкрит:
tкрит (n-m-1;α/2) = (28;0.025) = 2.048
где m = 1 – количество объясняющих переменных.
Если tнабл > tкритич, то полученное значение коэффициента корреляции признается значимым (нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается).
Поскольку tнабл > tкрит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически – значим.
Пример 3 . Распределение 50 предприятий пищевой промышленности по степени автоматизации производства Х (%) и росту производительности труда Y (%) представлено в таблице. Необходимо:
1. Вычислить групповые средние i и j x y, построить эмпирические линии регрессии.
2. Предполагая, что между переменными Х и Y существует линейная корреляционная зависимость:
а) найти уравнения прямых регрессии, построить их графики на одном чертеже с эмпирическими линиями регрессии и дать экономическую интерпретацию полученных уравнений;
б) вычислить коэффициент корреляции; на уровне значимости α= 0,05 оценить его значимость и сделать вывод о тесноте и направлении связи между переменными Х и Y;
в) используя соответствующее уравнение регрессии, оценить рост производительности труда при степени автоматизации производства 43%.
Скачать решение
Пример . По корреляционной таблице рассчитать ковариацию и коэффициент корреляции, построить прямые регрессии.
Пример 4 . Найти выборочное уравнение прямой Y регрессии Y на X по данной корреляционной таблице.
Решение находим с помощью калькулятора.
Скачать
Пример №4
Пример 5 . С целью анализа взаимного влияния прибыли предприятия и его издержек выборочно были проведены наблюдения за этими показателями в течение ряда месяцев: X – величина месячной прибыли в тыс. руб., Y – месячные издержки в процентах к объему продаж.
Результаты выборки сгруппированы и представлены в виде корреляционной таблицы, где указаны значения признаков X и Y и количество месяцев, за которые наблюдались соответствующие пары значений названных признаков.
Решение.
Пример №5
Пример №6
Пример №7
Пример 6 . Данные наблюдений над двумерной случайной величиной (X, Y) представлены в корреляционной таблице. Методом наименьших квадратов найти выборочное уравнение прямой регрессии Y на X. Построить график уравнения регрессии и показать точки (x;y)б рассчитанные по таблице данных.
Решение.
Скачать решение
Пример 7 . Дана корреляционная таблица для величин X и Y, X- срок службы колеса вагона в годах, а Y – усредненное значение износа по толщине обода колеса в миллиметрах. Определить коэффициент корреляции и уравнения регрессий.
| X / Y | 0 | 2 | 7 | 12 | 17 | 22 | 27 | 32 | 37 | 42 |
| 0 | 3 | 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 25 | 108 | 44 | 8 | 2 | 0 | 0 | 0 | 0 | 0 |
| 2 | 30 | 50 | 60 | 21 | 5 | 5 | 0 | 0 | 0 | 0 |
| 3 | 1 | 11 | 33 | 32 | 13 | 2 | 3 | 1 | 0 | 0 |
| 4 | 0 | 5 | 5 | 13 | 13 | 7 | 2 | 0 | 0 | 0 |
| 5 | 0 | 0 | 1 | 2 | 12 | 6 | 3 | 2 | 1 | 0 |
| 6 | 0 | 1 | 0 | 1 | 0 | 0 | 2 | 1 | 0 | 1 |
| 7 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
Решение.
Скачать решение
Пример 8 . По заданной корреляционной таблице определить групповые средние количественных признаков X и Y. Построить эмпирические и теоретические линии регрессии. Предполагая, что между переменными X и Y существует линейная зависимость:
- Вычислить выборочный коэффициент корреляции и проанализировать степень тесноты и направления связи между переменными.
- Определить линии регрессии и построить их графики.
Скачать
Уравнение прямой линии регрессии игрек на икс имеет вид
Запрошуємо усіх хто любить цікаві задачі та головоломки відвідати групу! Зараз діє акція – підтримай студента! Знижки на роботи + безкоштовні консультації.
Контакты
Администратор, решение задач
Роман
Tel. +380685083397
[email protected]
skype, facebook:
roman.yukhym
Решение задач
Андрей
facebook:
dniprovets25
Задача №1 Построение уравнения регрессии
Имеются следующие данные разных стран об индексе розничных цен на продукты питания (х) и об индексе промышленного производства (у).
| Индекс розничных цен на продукты питания (х) | Индекс промышленного производства (у) | |
|---|---|---|
| 1 | 100 | 70 |
| 2 | 105 | 79 |
| 3 | 108 | 85 |
| 4 | 113 | 84 |
| 5 | 118 | 85 |
| 6 | 118 | 85 |
| 7 | 110 | 96 |
| 8 | 115 | 99 |
| 9 | 119 | 100 |
| 10 | 118 | 98 |
| 11 | 120 | 99 |
| 12 | 124 | 102 |
| 13 | 129 | 105 |
| 14 | 132 | 112 |
Требуется:
1. Для характеристики зависимости у от х рассчитать параметры следующих функций:
В) равносторонней гиперболы.
2. Для каждой модели рассчитать показатели: тесноты связи и среднюю ошибку аппроксимации.
3. Оценить статистическую значимость параметров регрессии и корреляции.
4. Выполнить прогноз значения индекса промышленного производства у при прогнозном значении индекса розничных цен на продукты питания х=138.
Решение:
1. Для расчёта параметров линейной регрессии
Решаем систему нормальных уравнений относительно a и b:
Построим таблицу расчётных данных, как показано в таблице 1.
Таблица 1 Расчетные данные для оценки линейной регрессии
| № п/п | х | у | ху | x 2 | y 2 | ||
|---|---|---|---|---|---|---|---|
| 1 | 100 | 70 | 7000 | 10000 | 4900 | 74,26340 | 0,060906 |
| 2 | 105 | 79 | 8295 | 11025 | 6241 | 79,92527 | 0,011712 |
| 3 | 108 | 85 | 9180 | 11664 | 7225 | 83,32238 | 0,019737 |
| 4 | 113 | 84 | 9492 | 12769 | 7056 | 88,98425 | 0,059336 |
| 5 | 118 | 85 | 10030 | 13924 | 7225 | 94,64611 | 0,113484 |
| 6 | 118 | 85 | 10030 | 13924 | 7225 | 94,64611 | 0,113484 |
| 7 | 110 | 96 | 10560 | 12100 | 9216 | 85,58713 | 0,108467 |
| 8 | 115 | 99 | 11385 | 13225 | 9801 | 91,24900 | 0,078293 |
| 9 | 119 | 100 | 11900 | 14161 | 10000 | 95,77849 | 0,042215 |
| 10 | 118 | 98 | 11564 | 13924 | 9604 | 94,64611 | 0,034223 |
| 11 | 120 | 99 | 11880 | 14400 | 9801 | 96,91086 | 0,021102 |
| 12 | 124 | 102 | 12648 | 15376 | 10404 | 101,4404 | 0,005487 |
| 13 | 129 | 105 | 13545 | 16641 | 11025 | 107,1022 | 0,020021 |
| 14 | 132 | 112 | 14784 | 17424 | 12544 | 110,4993 | 0,013399 |
| Итого: | 1629 | 1299 | 152293 | 190557 | 122267 | 1299,001 | 0,701866 |
| Среднее значение: | 116,3571 | 92,78571 | 10878,07 | 13611,21 | 8733,357 | х | х |
| 8,4988 | 11,1431 | х | х | х | х | х | |
| 72,23 | 124,17 | х | х | х | х | х |
Среднее значение определим по формуле:
Cреднее квадратическое отклонение рассчитаем по формуле:
и занесём полученный результат в таблицу 1.
Возведя в квадрат полученное значение получим дисперсию:
Параметры уравнения можно определить также и по формулам:
Таким образом, уравнение регрессии:
Следовательно, с увеличением индекса розничных цен на продукты питания на 1, индекс промышленного производства увеличивается в среднем на 1,13.
Рассчитаем линейный коэффициент парной корреляции:
Связь прямая, достаточно тесная.
Определим коэффициент детерминации:
Вариация результата на 74,59% объясняется вариацией фактора х.
Подставляя в уравнение регрессии фактические значения х, определим теоретические (расчётные) значения .
,
следовательно, параметры уравнения определены правильно.
Рассчитаем среднюю ошибку аппроксимации – среднее отклонение расчётных значений от фактических:
В среднем расчётные значения отклоняются от фактических на 5,01%.
Оценку качества уравнения регрессии проведём с помощью F-теста.
F-тест состоит в проверке гипотезы Н0 о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического Fфакт и критического (табличного) Fтабл значений F-критерия Фишера.
Fфакт определяется по формуле:
где n – число единиц совокупности;
m – число параметров при переменных х.
Таким образом, Н0 – гипотеза о случайной природе оцениваемых характеристик отклоняется и признаётся их статистическая значимость и надёжность.
Полученные оценки уравнения регрессии позволяют использовать его для прогноза.
Если прогнозное значение индекса розничных цен на продукты питания х = 138, тогда прогнозное значение индекса промышленного производства составит:
2. Степенная регрессия имеет вид:
Для определения параметров производят логарифмирование степенной функции:
Для определения параметров логарифмической функции строят систему нормальных уравнений по способу наименьших квадратов:
Построим таблицу расчётных данных, как показано в таблице 2.
Таблица 2 Расчетные данные для оценки степенной регрессии
| №п/п | х | у | lg x | lg y | lg x*lg y | (lg x) 2 | (lg y) 2 |
|---|---|---|---|---|---|---|---|
| 1 | 100 | 70 | 2,000000 | 1,845098 | 3,690196 | 4,000000 | 3,404387 |
| 2 | 105 | 79 | 2,021189 | 1,897627 | 3,835464 | 4,085206 | 3,600989 |
| 3 | 108 | 85 | 2,033424 | 1,929419 | 3,923326 | 4,134812 | 3,722657 |
| 4 | 113 | 84 | 2,053078 | 1,924279 | 3,950696 | 4,215131 | 3,702851 |
| 5 | 118 | 85 | 2,071882 | 1,929419 | 3,997528 | 4,292695 | 3,722657 |
| 6 | 118 | 85 | 2,071882 | 1,929419 | 3,997528 | 4,292695 | 3,722657 |
| 7 | 110 | 96 | 2,041393 | 1,982271 | 4,046594 | 4,167284 | 3,929399 |
| 8 | 115 | 99 | 2,060698 | 1,995635 | 4,112401 | 4,246476 | 3,982560 |
| 9 | 119 | 100 | 2,075547 | 2,000000 | 4,151094 | 4,307895 | 4,000000 |
| 10 | 118 | 98 | 2,071882 | 1,991226 | 4,125585 | 4,292695 | 3,964981 |
| 11 | 120 | 99 | 2,079181 | 1,995635 | 4,149287 | 4,322995 | 3,982560 |
| 12 | 124 | 102 | 2,093422 | 2,008600 | 4,204847 | 4,382414 | 4,034475 |
| 13 | 129 | 105 | 2,110590 | 2,021189 | 4,265901 | 4,454589 | 4,085206 |
| 14 | 132 | 112 | 2,120574 | 2,049218 | 4,345518 | 4,496834 | 4,199295 |
| Итого | 1629 | 1299 | 28,90474 | 27,49904 | 56,79597 | 59,69172 | 54,05467 |
| Среднее значение | 116,3571 | 92,78571 | 2,064624 | 1,964217 | 4,056855 | 4,263694 | 3,861048 |
| 8,4988 | 11,1431 | 0,031945 | 0,053853 | х | х | х | |
| 72,23 | 124,17 | 0,001021 | 0,0029 | х | х | х |
Продолжение таблицы 2 Расчетные данные для оценки степенной регрессии
| №п/п | х | у | ||||
|---|---|---|---|---|---|---|
| 1 | 100 | 70 | 74,16448 | 17,34292 | 0,059493 | 519,1886 |
| 2 | 105 | 79 | 79,62057 | 0,385112 | 0,007855 | 190,0458 |
| 3 | 108 | 85 | 82,95180 | 4,195133 | 0,024096 | 60,61728 |
| 4 | 113 | 84 | 88,59768 | 21,13866 | 0,054734 | 77,1887 |
| 5 | 118 | 85 | 94,35840 | 87,57961 | 0,110099 | 60,61728 |
| 6 | 118 | 85 | 94,35840 | 87,57961 | 0,110099 | 60,61728 |
| 7 | 110 | 96 | 85,19619 | 116,7223 | 0,11254 | 10,33166 |
| 8 | 115 | 99 | 90,88834 | 65,79901 | 0,081936 | 38,6174 |
| 9 | 119 | 100 | 95,52408 | 20,03384 | 0,044759 | 52,04598 |
| 10 | 118 | 98 | 94,35840 | 13,26127 | 0,037159 | 27,18882 |
| 11 | 120 | 99 | 96,69423 | 5,316563 | 0,023291 | 38,6174 |
| 12 | 124 | 102 | 101,4191 | 0,337467 | 0,005695 | 84,90314 |
| 13 | 129 | 105 | 107,4232 | 5,872099 | 0,023078 | 149,1889 |
| 14 | 132 | 112 | 111,0772 | 0,85163 | 0,00824 | 369,1889 |
| Итого | 1629 | 1299 | 1296,632 | 446,4152 | 0,703074 | 1738,357 |
| Среднее значение | 116,3571 | 92,78571 | х | х | х | х |
| 8,4988 | 11,1431 | х | х | х | х | |
| 72,23 | 124,17 | х | х | х | х |
Решая систему нормальных уравнений, определяем параметры логарифмической функции.
Получим линейное уравнение:
Выполнив его потенцирование, получим:
Подставляя в данное уравнение фактические значения х, получаем теоретические значения результата . По ним рассчитаем показатели: тесноты связи – индекс корреляции и среднюю ошибку аппроксимации.
Связь достаточно тесная.
В среднем расчётные значения отклоняются от фактических на 5,02%.
Таким образом, Н0 – гипотеза о случайной природе оцениваемых характеристик отклоняется и признаётся их статистическая значимость и надёжность.
Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение индекса розничных цен на продукты питания х = 138, тогда прогнозное значение индекса промышленного производства составит:
3. Уравнение равносторонней гиперболы
Для определения параметров этого уравнения используется система нормальных уравнений:
Произведем замену переменных
и получим следующую систему нормальных уравнений:
Решая систему нормальных уравнений, определяем параметры гиперболы.
Составим таблицу расчётных данных, как показано в таблице 3.
Таблица 3 Расчетные данные для оценки гиперболической зависимости
| №п/п | х | у | z | yz | ||
|---|---|---|---|---|---|---|
| 1 | 100 | 70 | 0,010000000 | 0,700000 | 0,0001000 | 4900 |
| 2 | 105 | 79 | 0,009523810 | 0,752381 | 0,0000907 | 6241 |
| 3 | 108 | 85 | 0,009259259 | 0,787037 | 0,0000857 | 7225 |
| 4 | 113 | 84 | 0,008849558 | 0,743363 | 0,0000783 | 7056 |
| 5 | 118 | 85 | 0,008474576 | 0,720339 | 0,0000718 | 7225 |
| 6 | 118 | 85 | 0,008474576 | 0,720339 | 0,0000718 | 7225 |
| 7 | 110 | 96 | 0,009090909 | 0,872727 | 0,0000826 | 9216 |
| 8 | 115 | 99 | 0,008695652 | 0,860870 | 0,0000756 | 9801 |
| 9 | 119 | 100 | 0,008403361 | 0,840336 | 0,0000706 | 10000 |
| 10 | 118 | 98 | 0,008474576 | 0,830508 | 0,0000718 | 9604 |
| 11 | 120 | 99 | 0,008333333 | 0,825000 | 0,0000694 | 9801 |
| 12 | 124 | 102 | 0,008064516 | 0,822581 | 0,0000650 | 10404 |
| 13 | 129 | 105 | 0,007751938 | 0,813953 | 0,0000601 | 11025 |
| 14 | 132 | 112 | 0,007575758 | 0,848485 | 0,0000574 | 12544 |
| Итого: | 1629 | 1299 | 0,120971823 | 11,13792 | 0,0010510 | 122267 |
| Среднее значение: | 116,3571 | 92,78571 | 0,008640844 | 0,795566 | 0,0000751 | 8733,357 |
| 8,4988 | 11,1431 | 0,000640820 | х | х | х | |
| 72,23 | 124,17 | 0,000000411 | х | х | х |
Продолжение таблицы 3 Расчетные данные для оценки гиперболической зависимости
| №п/п | х | у | ||||
|---|---|---|---|---|---|---|
| 1 | 100 | 70 | 72,3262 | 0,033231 | 5,411206 | 519,1886 |
| 2 | 105 | 79 | 79,49405 | 0,006254 | 0,244083 | 190,0458 |
| 3 | 108 | 85 | 83,47619 | 0,017927 | 2,322012 | 60,61728 |
| 4 | 113 | 84 | 89,64321 | 0,067181 | 31,84585 | 77,1887 |
| 5 | 118 | 85 | 95,28761 | 0,121031 | 105,8349 | 60,61728 |
| 6 | 118 | 85 | 95,28761 | 0,121031 | 105,8349 | 60,61728 |
| 7 | 110 | 96 | 86,01027 | 0,10406 | 99,79465 | 10,33166 |
| 8 | 115 | 99 | 91,95987 | 0,071112 | 49,56344 | 38,6174 |
| 9 | 119 | 100 | 96,35957 | 0,036404 | 13,25272 | 52,04598 |
| 10 | 118 | 98 | 95,28761 | 0,027677 | 7,357059 | 27,18882 |
| 11 | 120 | 99 | 97,41367 | 0,016024 | 2,516453 | 38,6174 |
| 12 | 124 | 102 | 101,46 | 0,005294 | 0,291565 | 84,90314 |
| 13 | 129 | 105 | 106,1651 | 0,011096 | 1,357478 | 149,1889 |
| 14 | 132 | 112 | 108,8171 | 0,028419 | 10,1311 | 369,1889 |
| Итого: | 1629 | 1299 | 1298,988 | 0,666742 | 435,7575 | 1738,357 |
| Среднее значение: | 116,3571 | 92,78571 | х | х | х | х |
| 8,4988 | 11,1431 | х | х | х | х | |
| 72,23 | 124,17 | х | х | х | х |
Значения параметров регрессии a и b составили:
Связь достаточно тесная.
В среднем расчётные значения отклоняются от фактических на 4,76%.
Таким образом, Н0 – гипотеза о случайной природе оцениваемых характеристик отклоняется и признаётся их статистическая значимость и надёжность.
Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение индекса розничных цен на продукты питания х = 138, тогда прогнозное значение индекса промышленного производства составит:
По уравнению равносторонней гиперболы получена наибольшая оценка тесноты связи по сравнению с линейной и степенной регрессиями. Средняя ошибка аппроксимации остаётся на допустимом уровне.
[spoiler title=”источники:”]
http://yukhym.com/ru/sluchajnye-velichiny/postroenie-uravneniya-pryamoj-regressii-y-na-x.html
http://ecson.ru/economics/econometrics/zadacha-1.postroenie-regressii-raschyot-korrelyatsii-oshibki-approximatsii-otsenka-znachimosti-i-prognoz.html
[/spoiler]
