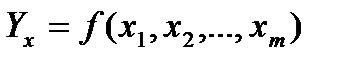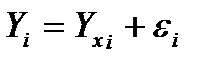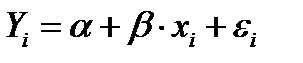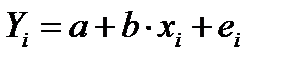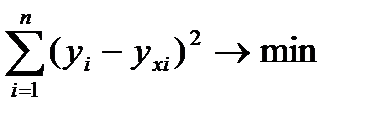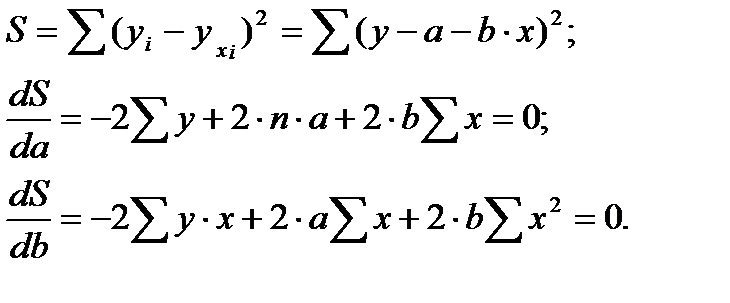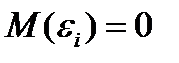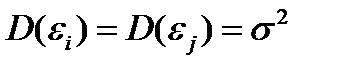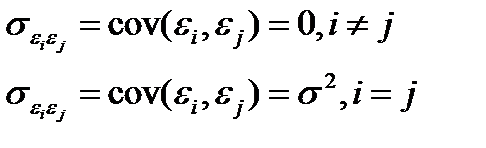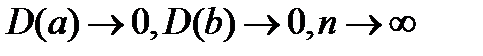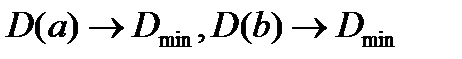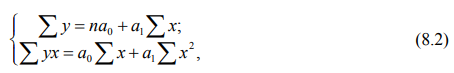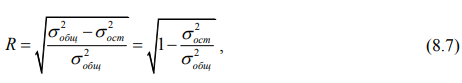Как найти игрек теоретическое

На основе найденных
коэффициентов уравнения регрессии
можно определить теоретическое значение
на­блюдаемой величины y.
Вычислим теоретическое
значе­ние у в ячейке С2, заменяя x
на А2 по формуле, получен­ной в результате
регрессионного анализа (рисунки 3.7,
3.8):

= – 0.0536*А2^2 + 2,2607*А2 + 4,9.

Затем необходимо скопировать
значение ячейки С2 на весь столбец С,
используя контекстное меню или панель
инструментов.

Рисунок
3.7
– Нахождение теоретических значений

Рисунок
3.8
– Нахождение ошибки и карманов

На следующем шаге вычисляется
ошибка модели в ячейке D2
по формуле = С2 – В2 и также копируется на
весь столбец.

После этого следует проверить
модель на адек­ватность, для чего
используют различные методы. Одна из
методик – построение гистограммы
распределения ос­татков модели. Для
этого нужно найти на интервале ми­нимальное
и максимальное его значение с помощью
функций МАКС() и МИН().

После нахождения минимального
и максимально­го значения весь диапазон
изменения остатков разбива­ют на
несколько равных поддиапазонов (от 4 до
20) и рассчитывают число попаданий ошибки
(остатков) в каждый поддиапазон.

Для этого все границы
интервалов записывают в отдельную
строку или столбец (рисунок 3.8).

Для построения диаграммы
распределения остат­ков выберем
команду Сервис, Анализ
данных (если этой
опции не будет, необходимо выбрать
команду Над­стройки…
и в появившемся
диалоговом окне отметить флажком опцию
Пакет анализа). В
появившемся диало­говом окне Анализ
данных в разделе
Инструменты ана­лиза
выбрать опцию
Гистограмма.

В появившемся диалоговом
окне Гистограмма в
по­ле Входной интервал
выберем интервал, в
котором нахо­дится диапазон ошибок
(D2:D7),
в поле Интервал
кар­манов – диапазон
значений отрезков поддиапазонов. Отметим
флажками Интервальный
процент и
Вывод гра­фика (рисунок
3.9).

Результаты построения приведены на
рисунке 3.10.

По полученным результатам
необходимо сделать выводы и провести
анализ полученных данных.

Рисунок 3.9 –
Построение гистограммы распределения
остатков модели

Рисунок 3.10 –
Гистограмма распределения остатков

4 Варианты заданий для лабораторных работ

4.1 Часть I

1	Определить зависимость механических свойств латуни ЛН65-5 от степени деформации. Исходный материал – проволока мягкая диаметром от 0,25 мм и более. Спрогнозировать относительное удлинение , % и предел прочности при растяжении в, кгс/мм2, при 80% деформации.
Предел прочности	42	45	50	55	59	62	65	69	72	75	79	82	85	87	88
Относительное удлинение	35	30	20	17	10	8	6	5	5	4	4	4	4	2	2
Степень деформации, %	0	5	10	15	20	25	30	35	40	45	50	55	60	65	70
2	Определить зависимость механических свойств латуни ЛН65-5 от степени деформации. Исходный материал – трубки манометрические с толщиной стенки 2 мм. Спрогнозировать относительное удлинение , % и предел прочности при растяжении в, кгс/мм2, при 70% деформации.
Предел прочности	32	38	40	43	49	53	55	59	60	63	65	67	67	67
Относительное удлинение	65	55	43	35	28	20	15	12	9	7	6	5	4	4
Степень деформации, %	0	5	10	15	20	25	30	35	40	45	50	55	60	65
3	Определить зависимость механических свойств латуни ЛН65-5 от степени деформации. Исходный материал – ленты мягкие толщиной 1,6 мм. Спрогнозировать относительное удлинение , % и предел прочности при растяжении в, кгс/мм2, при 75% деформации.
Предел прочности	30	35	37	40	43	47	49	50	52	53	55	58	59	60
Относительное удлинение	65	55	43	35	29	22	18	12	10	9	7	6	5	5
Степень деформации, %	0	5	10	15	20	25	30	35	40	45	50	55	60	65
4	Определить зависимость механических свойств латуни ЛО90-1 от температуры отжига. Продолжительность отжига 1 ч. Исходный материал – полосы толщиной 3 мм, деформированные на 60%. Спрогнозировать относительное удлинение , % и предел прочности при растяжении в, кгс/мм2, при 800С.
Предел прочности	63	65	63	60	50	38	32	30	28	27
Относительное удлинение	7	7	7	10	18	35	45	55	59	57
Температура отжига, С	0	100	200	300	350	400	450	500	600	700
5	Определить зависимость механических свойств латуни ЛО70-1 от температуры отжига. Продолжительность отжига 1 ч. Исходный материал – трубы конденсаторные, деформированные на 50%. Спрогнозировать относительное удлинение , % и предел прочности при растяжении в, кгс/мм2, при 700С.
Предел прочности	79	80	81	78	70	50	42	40	38	36
Относительное удлинение	4	5	6	24	42	50	60	65	67	72
Температура отжига, С	0	100	200	250	300	350	400	450	500	600
6	Определить зависимость изменения механических свойств латуни ЛО70-1 при высоких температурах. Исходный материал – прутки диаметром 25 мм, деформированные на 35%. Спрогнозировать относительное удлинение , % и предел прочности при растяжении в, кгс/мм2, при 800С.
Предел прочности	52	50	47	45	35	26	16	10	4	2
Относительное удлинение	12	6	8	11	15	23	36	45	32	26
Температура отжига, С	150	200	250	300	350	400	450	500	600	700
7	Определить зависимость изменения механических свойств латуни ЛО60-1 при высоких температурах. Спрогнозировать относительное удлинение , % и предел прочности при растяжении в, кгс/мм2, при 800С.
Предел прочности	46	43	35	28	19	12	8	6	4	2	1	1
Относительное удлинение	21	23	25	25	24	22	20	17	12	18	25	36
Температура отжига, С	50	100	200	250	300	350	400	450	500	600	650	700
8	Определить зависимость изменения механических свойств латуни ЛО60-1 при высоких температурах. Спрогнозировать относительное удлинение , % и предел прочности при растяжении в, кгс/мм2, при 800С.
Предел прочности	44	42	34	30	25	20	12	7	5	2	1	1
Относительное удлинение	33	32	25	20	11	9	16	20	22	29	30	33
Температура отжига, С	50	100	200	250	300	350	400	450	500	600	650	700
9	Определить зависимость изменения механических свойств латуни ЛО60-1 содержащей 0,4% Ni, при высоких температурах. Спрогнозировать относительное удлинение , % и предел прочности при растяжении в, кгс/мм2, при 800С.
Предел прочности	42	41	37	29	24	19	13	9	6	4	3	2	1
Относительное удлинение	27	29	30	32	28	26	22	21	25	35	46	52	59
Температура отжига, С	50	100	200	250	300	350	400	450	500	550	600	650	700
10	Определить зависимость механических свойств латуни ЛС59-1 от температуры отжига (58,5% Cu, 1,2% Pb, остальное Zn). Продолжительность отжига 1 ч. Исходный материал – прутки диаметром 5 мм, деформированные на 15%. Спрогнозировать относительное удлинение , % и предел прочности при растяжении в, кгс/мм2, при 800С.
Предел прочности	65	64	63	61	55	52	48	47	46	46	45	44	44
Относительное удлинение	36	38	44	47	51	57	63	66	68	69	68	66	64
Температура отжига, С	0	100	200	250	300	350	400	450	500	550	600	650	700
11	Определить зависимость механических свойств литых оловянных бронз от содержания олова. Спрогнозировать относительное удлинение , % и предел прочности при растяжении в, кгс/мм2, при 15% Sn (по массе).
Предел прочности	21	23	28	31	37	39	38	37	37
Относительное удлинение	50	48	46	42	40	32	23	11	3
Sn, % (по массе)	0	2	4	6	8	10	11	12	14
12	Определить зависимость механических свойств бронзы Бр.ОФ7,5-0,4 от температуры отжига. Продолжительность отжига 2 ч. Исходный материал – полосы, деформированные на 20%. Спрогнозировать относительное удлинение , % и предел прочности при растяжении в, кгс/мм2, при 750С.
Предел прочности	80	81	80	70	65	61	50	48	46	42
Относительное удлинение	5	5	9	20	40	55	61	69	73	79
Температура отжига, С	0	100	200	300	333	366	400	500	600	700
13	Определить зависимость механических свойств бронзы Бр.ОФ6,5-0,4 от температуры отжига. Продолжительность отжига 1 ч. Исходный материал – прутки твердые диаметром 4 мм. Спрогнозировать относительное удлинение , % и предел прочности при растяжении в, кгс/мм2, при 800С.
Предел прочности	86	85	81	70	60	52	50	46	41	39
Относительное удлинение	2	3	4	11	20	40	55	62	62	60
Температура отжига, С	0	100	200	300	333	366	400	500	600	700
14	Определить зависимость механических свойств бронзы Бр.ОФ6,5-0,4, при высоких температурах. Спрогнозировать относительное удлинение , % и предел прочности при растяжении в, кгс/мм2, при 750С.
Предел прочности	30	35	34	32	30	23	15	10
Относительное удлинение	33	35	32	27	22	10	5	4
Температура, С	100	200	300	350	400	500	600	700
15	Определить зависимость механических свойств бронзы Бр.ОФ4-0,5 (наклеп 60%) от температуры отжига. Спрогнозировать относительное удлинение , % и предел прочности при растяжении в, кгс/мм2, при 750С.
Предел прочности	67	66	65	60	46	36	35	33	31
Относительное удлинение	5	4	5	12	31	49	51	52	53
Температура отжига, С	0	100	200	300	350	400	500	600	700
16	Определить зависимость механических свойств бронзы Бр.ОЦ4-3 от температуры отжига. Продолжительность отжига 1 ч. Исходный материал – полосы твердые толщиной 4 мм. Спрогнозировать относительное удлинение , % и предел прочности при растяжении в, кгс/мм2, при 800С.
Предел прочности	84	81	60	45	40	39	36	34
Относительное удлинение	1	2	10	19	32	40	39	34
Температура отжига, С	100	200	300	350	400	500	600	700
17	Определить зависимость механических свойств алюминиевых бронз от химического состава. Исходный материал – литье в кокиль. Спрогнозировать относительное удлинение , % и предел прочности при растяжении в, кгс/мм2, при 12% Al.
Предел прочности	20	22	25	26	28	30	33	38	40	48	57	59
Относительное удлинение	80	79	75	72	70	65	63	61	60	50	30	10
Al, % (по массе)	0	1	2	3	4	5	6	7	8	9	10	11
18	Определить зависимость механических свойств алюминиевых бронз от химического состава. Исходный материал – полосы, деформированные на 40% и отожженные при 650С, 30 мин. Спрогнозировать относительное удлинение , % и предел прочности при растяжении в, кгс/мм2, при 12% Al.
Предел прочности	20	22	24	28	35	40	45	47	48	51	57	59
Относительное удлинение	52	53	60	63	69	68	60	52	43	20	10	5
Al, % (по массе)	0	1	2	3	4	5	6	7	8	9	10	11
19	Определить зависимость изменения механических свойств бронзы Бр.АЖМц10-3-1,5 при высоких температурах. Спрогнозировать относительное удлинение , % и предел прочности при растяжении в, кгс/мм2, при 900С.
Предел прочности	60	61	59	50	41	35	24	12	8	5	4	3
Относительное удлинение	21	20	19	15	20	30	41	40	29	41	50	62
Температура, С	0	100	200	300	350	400	500	600	650	700	750	800
20	Определить зависимость механических свойств бериллиевой бронзы Бр.Б2 от температуры испытания. Исходный материал – полоса горячекатаная толщиной 10 мм. Спрогнозировать относительное удлинение , % и предел прочности при растяжении в, кгс/мм2, при 800С.
Предел прочности	64	64	60	57	55	52	39	24	16	12	10	9
Относительное удлинение	30	31	30	20	19	20	40	55	75	95	103	105
Температура, С	0	100	200	300	350	400	500	550	600	650	700	750
21	Определить зависимость механических свойств бронзы Бр.КМц3-1 от температуры отжига. Продолжительность отжига 1 ч. Исходный материал – полосы мягкие, деформированные на 50%. Спрогнозировать относительное удлинение , % и предел прочности при растяжении в, кгс/мм2, при 800С.
Предел прочности	80	80	80	77	69	58	40	32	29	26	25	24
Относительное удлинение	3	3	3	5	15	30	43	46	50	53	55	57
Температура отжига, С	0	100	200	300	350	400	500	550	600	650	700	750
22	Определить зависимость изменения механических свойств бронзы Бр.КМц3-1 при высоких температурах. Выдержка при испытании 1 ч. Исходный материал – прутки диаметром 25 мм. Спрогнозировать относительное удлинение , % и предел прочности при растяжении в, кгс/мм2, при 800С.
Предел прочности	18	17	15	17	17	18	17	10	9	5	3	2
Относительное удлинение	70	65	56	50	45	40	45	65	82	100	104	104
Температура, С	0	100	200	300	350	400	500	550	600	650	700	750
23	Определить зависимость механических свойств бронзы Бр.КН1-3 от температуры отжига. Продолжительность отжига 1 ч. Исходный материал – полосы мягкие толщиной 2 мм, деформированные на 70%. Спрогнозировать относительное удлинение , % и предел прочности при растяжении в, кгс/мм2, при 800С.
Предел прочности	60	61	62	65	68	70	50	45	42	38	37
Относительное удлинение	2	2	4	5	6	8	15	18	20	25	29
Температура отжига, С	0	100	200	300	350	400	500	550	600	700	750
24	Определить зависимость твердости бронзы HV, кгс/мм2, от температуры отпуска. Исходный материал – пруток закаленный [175]. Спрогнозировать твердость при 700С.
Cu ÷ 0,19% Zr	44	45	46	48	51	56	70	85	75	68	64
Cu ÷ 0,003% Zr	35	36	38	40	41	43	45	49	49	48	46
Температура отжига, С	0	100	200	300	350	400	450	500	550	600	650
25	Определить зависимость твердости HV, кгс/мм2, закаленной и деформированной циркониевой бронзы от температуры отпуска. Исходный материал – проволока, деформированная на 90%. Спрогнозировать твердость при 700С.
Cu ÷ 0,19% Zr	130	130	135	151	152	151	145	134	120	99	85
Cu ÷ 0,003% Zr	110	110	110	110	86	52	51	51	51	51	51
Температура отжига, С	0	100	200	300	350	400	450	500	550	600	650
26	Определить зависимость изменения механических свойств мельхиора МН19 при высоких температурах. Исходный материал – прутки диаметром 25 мм, величиной зерна 0,035 мм, деформированные на 20%. Выдержка при температуре испытания 1 ч. Спрогнозировать относительное удлинение , %, с предел прочности при растяжении в, кгс/мм2, при 1000С.
Предел прочности	45	43	40	38	32	25	22	17	12	7	6	4	3
Относительное удлинение	30	29	28	25	22	17	16	17	19	22	25	28	32
Температура, С	0	100	200	300	400	500	550	600	650	700	750	800	900
27	Определить зависимость механических свойств сплава МН10 (10,25% Ni, 1% Fe, 0,87% Mn, остальное – медь) от температуры отжига. Продолжительность отжига 2 ч. Исходный материал – полоса, деформированная на 50%. Спрогнозировать относительное удлинение , %, и предел прочности при растяжении в, кгс/мм2, при 1000С.
Предел прочности	51	51	52	52	51	49	45	37	34	32	31	30	30
Относительное удлинение	5	6	7	9	12	20	25	35	38	39	38	37	35
Температура отжига, С	0	100	200	300	400	500	550	600	650	700	750	800	900
28	Определить изменение механических свойств сплава МН10 (10,25% Ni, 1% Fe, 0,87% Mn, остальное – медь) при высоких температурах. Исходное состояние – полоса горячекатаная. Спрогнозировать относительное удлинение , %, и предел прочности при растяжении в, кгс/мм2, при 1000С.
Предел прочности	31	29	28	26	23	20	18	16	12	9	7	6	4
Относительное удлинение	23	22	21	19	17	15	12	11	10	12	13	17	22
Температура, С	0	100	200	300	400	500	550	600	650	700	750	800	900
29	Определить изменение механических свойств сплава ТБ (МН16) от температуры отжига. Исходный материал – проволока твердая диаметром 1,5 мм. Спрогнозировать относительное удлинение , %, и предел прочности при растяжении в, кгс/мм2, при 800С.
Предел прочности	75	75	74	70	60	50	38	32	31	31	31
Относительное удлинение	0	1	2	3	5	11	20	25	26	26	26
Температура отжига, С	0	100	200	300	400	450	500	600	650	700	750
30	Определить изменение механических свойств мельхиора (32,8% Ni, 0,99% Fe, 1,3% Mn, остальное – медь) от температуры отжига. Продолжительность отжига 1 ч. Исходный материал – полосы толщиной 2 мм, деформированные на 50%. Спрогнозировать относительное удлинение , %, и предел прочности при растяжении в, кгс/мм2, при 800С.
Предел прочности	68	69	70	70	69	67	64	59	50	48	47	46
Относительное удлинение	4	4	4	4	5	9	12	20	30	35	37	36
Температура отжига, С	0	100	200	300	400	450	500	550	600	650	700	750

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Рис. 15.1. Виды мотивации

Показателями эффективности мотивации являются результаты деятельности сотрудников и организации, а также характеристики, определяющие отношение к труду (усилие, старание, настойчивость, внимательность, добросовестность, контактность).

 

Рис. 15.2. Взаимосвязи мотивационных процессов

Методы мотивации

Работники мотивируются посредством методов мотивации или их совокупности. Методы мотивации подразделяются следующим образом:

2. Методы психологического поощрения. Удовлетворение работой, большая ответственность, безопасность. Не требуют дополнительных затрат и не приводят к насыщению.

3. Целевой метод. Посредством целей внимание и усилия сосредоточиваются на определенных направлениях. Цели могут выступать в качестве нормативов, с которыми сопоставляются результаты; могут влиять на структуру и процедуры организационных систем; часто отражают глубинные мотивы и особенности как работников, так и организации.

4. Метод устранения отрицательных стимулов. Устранение несправедливости, фаворитизма и пр.

5. Метод проектирования работ, обогащения труда. Проектирование работ – это формальная и неформальная спецификация относящихся к работе действий индивида, включая как структурные, так и межличностные аспекты работы, с учетом потребностей и запросов организации и индивида. Если работа или задание изменяются в связи с новой технологией, структурной реорганизацией, инициативой работника, указанием руководства или процессом управления по целям, то речь идет о перепроектировании работы. Основная цель перепроектирования состоит в повышении мотивации людей и роста эффективности путем изменения работы. Перепроектирование работы связано с ее расширением и обогащением труда. Расширить работу – это значит дать работнику больше работы того же типа. Обогащение труда предполагает более содержательную работу.

6. Метод соучастия (партисипативности) или вовлечения работников в управление. Этот метод означает: голос при решении проблемы; консультации, поиски согласия; согласие с окончательным решением; целенаправленные, систематизированные попытки выявить и использовать индивидуальную и коллективную мудрость; действенное делегирование прав; совместное принятие решений; совместное выявление проблем и соответствующих действий; возможность создать надлежащие условия и установки; механизм для улучшения сотрудничества работников и администрации. Этот метод направлен на раскрепощение творческой активности работника, создание простора для индивидуальных достижений талантливых работников и обеспечивает необходимое интегрирование одиночных усилий в единое коллективное действие.

7. Метод косвенных усилий. Проведение конференций и совещаний, обучение, наблюдения на рабочем месте и т. д. Помимо главной цели эти мероприятия выступают и в качестве инструментов мотивации.

8. Дисциплинарный метод. Выговоры, предупреждения, замечания об ошибочных действиях, лишение привилегий. Дисциплинарный метод часто дает меньший эффект, чем от него ожидается. Наказанный работник в будущем будет стараться избежать наказания, а не работать лучше.

Использование вышеперечисленных методов мотивации нужно осуществлять разумно, определяя, для каких групп работников какой метод более применим.

Классификация и описание теорий мотивации

Существуют различные классификации теорий мотивации. Х. Шольц разделяет их на три главных направления: 1) теории, в основе которых лежит специфическая картина работника – человека; 2) внутриличностные теории (общеупотребительное название – содержательные теории); 3) процессуальные теории. Первая группа рассматривает определенный образ работника, его потребности и мотивы, вторая анализирует структуру потребностей и их проявление; третья изучает влияние на мотивацию различных факторов среды.

Далее будет рассмотрен ряд мотивационных теорий, их положительные и отрицательные стороны и приемлемость для российских условий.

1. Теории, в основе которых лежит специфическая картина работника – человека

Теории «Икс» и «Игрек» Д. Макгрегора

Дуглас Макгрегор (1960) в своей книге «Человеческий фактор предприятий» изложил «теорию Икс». Он предположил, что основные потребности людей, удовлетворяемые посредством работы, – это потребности, имеющие отношение к экономике и безопасности. Из-за существования в людях антипатии к работе большинство из них нужно принуждать, контролировать, направлять, угрожать им наказанием, чтобы заставить приложить адекватные усилия для достижения целей организации.

Средний человек предпочитает, чтобы им руководили, желает избежать ответственности, имеет мало амбиций, нуждается прежде всего в чувстве безопасности и уверенности в будущем.

Работники рассматривают работу саму по себе как неизбежное зло, с которым нужно смириться и которое нужно терпеть для того, чтобы иметь возможность делать необходимые покупки и откладывать средства на старость. Выбирая, люди стремятся найти работу с минимальными затратами труда и дискомфорта и при этом максимизировать материальную выгоду. Сделав свой выбор, они работают лишь настолько, чтобы не быть уволенными, но не более того; они будут избегать тяжелой работы, если смогут. Они будут реагировать на внешние воздействия, которые необходимы, чтобы преодолеть присущие работникам тенденции к ленивости, праздности и инерции.

Школы менеджмента до 1940-х гг. поддерживали эти утверждения относительно обыкновенного наемного работника. Большая часть работы во время разработки теории – на ферме или на фабрике – была неприятной. И принимая во внимание стандарты жизни в то время, возможно, большая часть людей видела экономическую необходимость в собственном принуждении к работе.

Макгрегор сделал следующее наблюдение: те, кто управлял организациями на основе предположений «теории Икс», создавали основу для подтверждения этих предположений. Если управляющий пытается регулировать поведение работника, ограничивая его физически и морально обременительными заданиями, трудовая мотивация работника будет вращаться вокруг максимизации материальной выгоды, минимизации дискомфорта от работы и использования любого возможного преимущества. Поступая таким образом, работник, конечно, вызывает более строгий контроль со стороны того, кто его организует. Начинается новый виток спирали.

В соответствии с точкой зрения Макгрегора в современном мире «теория Игрек» более предпочтительна, чем «теория Икс».

Цель теорий Икс и Игрек – выявить потребности людей, удовлетворяемых посредством работы, сопоставить цели работников с целями организации. В чистом виде ни один ни другой вариант, предложенные Макгрегором, не существует. Согласно рекомендации Макгрегора теории Икс и Игрек необходимо использовать, учитывая конкретное состояние уровня сознания и мотивации работников. Менеджеры должны стремиться развивать работников, если они недостаточно мотивированы от состояния Икс к состоянию Игрек, или от состояния «экономического человека» к «человеку социальному». В целом во взглядах современных специалистов и менеджеров на работника преобладают установки теории Игрек.

Теория человеческих отношений

Элтон Мэйо, возглавлявший с 1926 по 1947 г. факультет промышленных исследований в Гарварде, провел ряд исследований в цехах Западной электрической компании в районе Хауторн около Чикаго.

Один из экспериментов заключался в следующем. Две равные по численности бригады рабочих были размещены в две похожие комнаты и обе группы выполняли один и тот же вид работы. Уровень освещения был увеличен только в одной комнате, но производительность возросла в обеих. Это исследование получило название «хауторнский эксперимент» и заложило краеугольный камень в развитие теории организации и управления. Э. Мэйо изложил свои взгляды, выходящие далеко за пределы экспериментов, в книге «Социальные проблемы индустриальной культуры». Таким образом зародилась теория человеческих отношений, которая дала импульс для дальнейшего развития различных теорий гуманизации труда.

Исследования Мэйо серьезно повлияли на управленческую мысль. В частности, результаты этих исследований подтвердили первенство экономических мотивов в управлении рабочим поведением. Несмотря на то что никто не сомневался в важности иметь работу, для того чтобы обеспечивать материальный комфорт, полученные данные также отмечали важность социальных потребностей, которые влияют на рабочее поведение. Факты, основывающиеся на исследованиях, доказывают, что люди, как только предоставляется возможность, начинают спонтанно развивать неформальные организационные структуры, которые обеспечивают удовлетворение потребностей в привязанности и принадлежности. Эти структуры развивают вновь появившиеся нормы приемлемого поведения, несмотря на официальные правила. Управляющие считают рациональным принимать эти структуры или хотя бы распознавать их, чем пытаться их преодолеть. Это не значит, что неформальные организации являются неизбежным злом для управляющих. Часто, наоборот, неформальная организация дополняет формальную организацию в обслуживании конструктивных задач – к примеру, снижая абсентеизм, обеспечивая лидерство и изучая и аккумулируя багаж знаний и навыков для того, чтобы работать более эффективно. Хотя экономические потребности объясняют, почему люди идут на работу, социальные потребности показывают, что происходит после того, как люди устроились на работу.

Теория человеческих отношений получила широкое распространение и практическое использование, однако в настоящее время она подвергается критике. Ее упрекают в том, что она преувеличивает значение удовлетворенности трудом в мотивации работников, уделяет чрезмерное внимание социальным потребностям, которые не всегда совпадают с целями организации. Кроме того, вопреки одному из главных тезисов теории человеческих отношений доказано, что в определенных условиях повышению производительности может способствовать неудовлетворенность трудом.

Тем не менее многие идеи теории человеческих отношений широко используются в наши дни. Эта теория оказала большое влияние на практику коллективной мотивации.

Теория Z

Теория Z была разработана профессором Калифорнийского университета Вильямом Оучи в 80-е гг.

В. Оучи классифицирует американское управление на два типа – А и Z. Организации типа А основаны на индивидуализме и конкуренции. Организации типа Z предполагают, что мотивация работников исходит из ценностей предприятия как одной большой семьи. Организации типа Z более адаптивны, органичны, характеризуются более высоким уровнем сотрудничества и производительности. Согласно его теории у работников необходимо развивать отношения доверия и солидарности, преданности коллективу и общим целям, удовлетворенности трудом. Главным мотиватором выступает построенная по клановому принципу корпорация. Теория Z исходит из того, что лучшая координация индивидуальных усилий приводит к более высокой производительности. Главное внимание теория уделяет коллективной мотивации и раскрепощению инициативы работника.

Теории мотивации, в основе которых лежит специфическая картина работника, служат важным ориентиром практической деятельности в области мотивации труда. Более глубоко трудовая мотивация исследуется в содержательных и процессуальных теориях.

2. Содержательные теории

Цель содержательных теорий – установить потребности работников и определить, как и в каких пропорциях применять внутреннее и внешнее вознаграждения.

Теория иерархии потребностей Абрахама Маслоу

Смотрите также

• Кадры решают все – или немного теории кадровых агенств
• Выпускники профессиональных учебных заведений на региональном рынке труда – исследовательская работа

Словарные статьи

• Заработная плата, цена и прибыль
• Кадры
• Безработица
• Пособие по безработице

Смотрите также

• Государство и право
• Инвестиции
• Недвижимость
• Производство и промышленность
• Товары и услуги
• Экономика

Словари и справочники

• Бизнес-словари
• Экономические словари
• Глоссарий по дисциплине “Мировая экономика”
• Глоссарий по менеджменту
• Глоссарий по налоговой системе
• Глоссарий по экономическому анализу
• Коммерческие ценные бумаги
• Краткий словарь маркетолога
• Недвижимость. Терминология с украинским
• Рекламный словарь
• Рынок ценных бумаг
• Терминологический словарь менеджера
• Словарь терминов по курсу «Ценообразование»
• Словарь экономических терминов

Дуглас Макгрегор был великим руководителем. Компетентный, остроумный и проницательный, он пользовался огромным уважением у своих подчиненных и верил, что люди от природы полны энтузиазма, ответственны и нравственны. Он верил в это так сильно, что в 1960 году написал книгу, которая навсегда изменила теорию управления, в те времена опиравшуюся на представление о том, что люди по природе ленивы и работают только тогда, когда их заставляют. Макгрегор умер в 1964 году, внеся существенный вклад в теорию и практику управления, и его творческое наследие еще долго будет оставаться предметом исследований. Даже через полвека после ее выхода в свет журналисты и ученые ссылаются на эту регулярно переиздаваемую книгу! Если вы руководите людьми, но до сих пор не читали книгу Макгрегора – вам стоит поторопиться.

“Теория X”

Как вы думаете, какой из методов управления людьми является самым эффективным? Согласно “теории X”, люди по своей природе ленивы и работают только по принуждению. В свое время “теория X” была самым распространенным подходом к управлению, однако сегодня она кажется устаревшей – по трем причинам:

1. Она опирается на устаревшие парадигмы. Иерархические модели по образцу армии или церкви не применимы в современном бизнесе. Например, сегодня члены рабочих групп часто не подчинены одному-единственному боссу, а решают проблемы нескольких подразделений сразу.

2. Она чересчур абстрактная. “Теория X” не принимает во внимание политические, социальные и экономические условия деятельности отдельно взятой компании.

3. Она исходит из неверных предпосылок о природе человека. Например, эта теория предполагает, что люди могут работать только по принуждению. Однако любое принуждение имеет свои пределы. Часто люди работают гораздо лучше под воздействием убеждения или интереса к совместной работе.

“Теория X” придерживается пессимистического взгляда на природу человека. Согласно ей, отношения между руководителями и подчиненными основаны на обоюдной враждебности. Руководители, следующие этой теории, считают, что работники не способны мыслить и действовать самостоятельно. По этой причине такие руководители ради общего блага компании стремятся тщательно контролировать деятельность своих подчиненных, предполагая, что люди не желают добровольно брать на себя ответственность, поскольку их интересует только зарплата. Им кажется, что подчиненные не видят общую картину дел или не заботятся об успехе компании в целом. Иначе говоря, руководители, придерживающиеся “теории X”, считают, что подчиненные работают только тогда, когда за ними кто-то постоянно следит.

“Теория X” основана на трех предпосылках:

1. Люди не хотят работать. Человек испытывает врожденное отвращение к труду и старается от него уклониться. Нормы выработки, выполнение целевых показателей и табельные часы – это реакция руководителей на природную склонность людей отлынивать от дела.

2. Принуждение неизбежно. Компания не достигнет поставленных целей без принуждения и запугивания своих сотрудников. Их единственный стимул к работе – наказание, а не поощрение. Повышение по службе, премии и льготы лишь увеличивают запросы человека, а не пробуждают желание упорно трудиться.

3. Люди стараются уклониться от ответственности. Все, что они хотят от жизни – это спокойная работа с регулярной зарплатой.

В чем ошибочность “теории Х”

В компаниях, работающих по принципам “теории X”, царит атмосфера подозрительности, которая угнетает естественное стремление людей к совершенству. Прежде всего их отпугивает то, что начальство сводит к минимуму возможности для творческого самовыражения. Когда работник подозревает, что ему грозит увольнение, он начинает думать исключительно о самосохранении и крайне неохотно идет на риск – из опасения, что начальники не одобрят его действий и даже накажут за них.

Чтобы сотрудники не боялись рисковать и активнее выдвигали инновационные предложения, они прежде всего должны чувствовать себя в безопасности. Иными словами, они просто хотели бы, чтобы их уважали, хвалили и ценили. Многие люди испытывают потребность ощущать себя частью коллектива, чтобы вместе с другими гордиться достигнутым. Тем не менее руководители, верящие в “теорию X”, считают, что любое объединение сотрудников является угрозой, так как может воспрепятствовать успешной работе компании. Поэтому вместо того, чтобы поощрять коллективное взаимодействие, такие руководители всячески стараются посеять вражду между сотрудниками.

Часто менеджеры не могут понять, почему высокая зарплата, медицинские пособия, хорошие отпускные, оплата больничных и щедрые пенсионные отчисления практически никак не мотивируют подчиненных. Дело в том, что всех этих мер недостаточно. Прежде всего человек хотел бы знать, что делает важную и осмысленную работу. Он желает ощущать, что с его мнением считаются. Поэтому как только он понимает, что компания не ценит то, чем он занимается, им овладевает безразличие, он начинает относиться к своему делу формально и при выполнении работы прежде всего стремится не дать повод к увольнению.

“Теория Y”

Если “теория X” ошибочна, то какова ее альтернатива? Совершенно иной подход к управлению людьми предлагает “теория Y”: начальники должны уважать подчиненных и давать им возможность действовать самостоятельно, чтобы пробуждать в них стремление следовать нравственным принципам и соблюдать дисциплину. Согласно “теории Y”, если персонал не проявляет интереса к работе и не выполняет распоряжений, то винить в этом следует не сотрудников, а плохое руководство. “Теория Y” исходит из следующих постулатов:

• Люди не испытывают врожденной неприязни к работе. При определенных условиях работники получают удовольствие от того, чем занимаются.
• Сотрудников не обязательно держать в страхе. Должным образом мотивированные сотрудники будут работать без понуканий и прилагать активные усилия для решения задач, стоящих перед компанией.
• Ощущение успеха доставляет людям удовольствие. Достигнутые успехи укрепляют уверенность в своих силах, и в результате сотрудники еще активнее стремятся достичь поставленных перед ними целей.
• Люди хотят заниматься ответственной работой. Это неправда, что человек по природе ленив и безответствен. На самом деле он, наоборот, ищет любую возможность, чтобы выполнить ответственную работу.
• В человеке от природы заложена способность к творчеству. Большинство людей способно творчески решать стоящие перед ними проблемы.
• Люди умны и сообразительны. Часто руководители сильно недооценивают интеллектуальные способности своих подчиненных.

“Теория X” утверждает, что внутреннюю политику компании должно определять ее руководство, ни о чем не советуясь с персоналом. Согласно же “теории Y”, руководство должно принимать во внимание как нужды компании в целом, так и потребности ее сотрудников, которые, в свою очередь, желали бы приносить пользу своей организации.

Различия между двумя теориями

В компаниях, руководство которыми основано на “теории Х”, важное значение придается формальной иерархии. Рассмотрим пример с контролем качества работы. Когда контролер из ОТК, проверяя продукцию одного из подразделений, обнаруживает проблему, он сообщает о ней своему непосредственному руководителю. Последний передает эту информацию заместителю начальника отдела, который извещает руководителя подразделения, а тот вызывает к себе заместителя по производству, чтобы сообщить ему неприятную новость. Заместитель возвращается к себе и вызывает работников, имевших непосредственное отношение к проблеме. Поскольку эти работники не подозревали, что контролер проверял их продукцию, они сразу попадают в ситуацию конфронтации.

В компании, работающей в соответствии с “теорией Y”, контролер из ОТК в первую очередь извещает о найденной проблеме самих работников, которые сразу же приступают к ее решению. Как и в первом случае, контролер отчитывается перед вышестоящими начальниками, но к тому времени, когда его отчет достигает верхней ступени иерархии, проблема оказывается решена. Работники при этом понимают, что руководство не собирается их наказывать или шпионить за ними, и высоко оценивают этот честный подход.

В итоге укрепляется атмосфера взаимного уважения, а не подозрительности.

“Теория Y” на практике

Директор одной средней школы оказался исключительно талантливым руководителем. По итогам стандартных тестов ученики этой школы неизменно показывают превосходные результаты, а их родители поддерживают хорошие отношения с учителями. Не удивительно, что инспектор из министерства образования решает использовать таланты директора на административной должности в школьном округе. Проведя собеседование с десятком кандидатов, совет округа дает рекомендацию именно этому директору.

Директору предлагают значительную прибавку к зарплате и солидную должность. Единственная проблема состоит в том, что он не хочет переходить на новую работу. Ему нравится быть директором школы и наблюдать, как подростки взрослеют, приобретают знания и навыки общения. Все подчиненные преданы ему и готовы на многое ради своего начальника. Директор выражает свое несогласие инспектору из министерства, но тот не желает уступать. Он считает, что округ только выиграет от этого перехода, а сам директор будет доволен своим решением, как только освоится в новой для себя роли.

Через два года инспектор будет все так же удовлетворен работой экс-директора, зато последний будет чувствовать себя несчастным и мечтать о возвращении в свою старую школу. Это пример наихудшего проявления “теории X”: ради общего блага в одностороннем порядке принимается решение, совершенно не учитывающее интересы конкретного человека. Директор в данной ситуации не мог отказаться от новой должности, не поставив под угрозу свои карьерные перспективы.

Если бы школьный округ управлялся в соответствии с “теорией Y”, то директор школы и инспектор из министерства открыто обсудили бы свои друг с другом свои потребности. Инспектор попросил бы директора принять во внимание всю важность предлагаемой должности и предложил бы ему свою помощь и поддержку в начальный период. Кроме этого, он рассказал бы директору, как тот мог бы использовать новые возможности для обогащения своего опыта и выработки управленческих навыков. В свою очередь, директор наверняка бы понял, что лучше воспользоваться шансом на обогащение опыта и согласиться, нежели принять предложение, затаив в сердце обиду. “Теория Y” предполагает, что даже если руководитель ради общего блага вынужден прибегнуть к принуждению, взаимоприемлемое решение все равно должно быть найдено.

“Теория Y” и власть

“Теорию Y” можно применять даже в такой организации, как армия, где, казалось бы, должна безраздельно властвовать “теория Х”. Военные обязаны беспрекословно выполнять приказы своих командиров. Офицер, посылающий солдат в сражение, не беспокоится о том, способствует ли участие в этом сражении их личностному росту. Американский генерал Джордж Паттон, например, просто посмеялся бы над мнением о том, что на войне нужно принимать во внимание желания и потребности солдат.

Тем не менее отдавать приказы и управлять – разные вещи. Офицер понимает, что сражение будет проиграно, если его солдаты не приложат все усилия для выполнения боевой задачи. Это значит, что он не управляет солдатами, а, скорее, зависит от них. Генерал Паттон тоже зависел от своих подчиненных, передававших его приказы по цепочке вниз. Армейские командиры, как и руководители обычных компаний, способны контролировать своих людей не больше, чем погоду. Они должны полностью доверять подчиненным, но все равно отдавать приказы. Доверие и командование не исключают друг друга.

В рамках “теории Y” руководители не только могут, но и должны действовать решительно, ибо в конечном итоге именно они отвечают за решение стоящих перед ними проблем. При возникновении критической ситуации подчиненные будут ждать от них указаний о том, какие действия предпринимать. Это не значит, что в кризис “теория Y” становится неактуальной. Даже в критической ситуации руководитель должен относиться к людям вежливо и беспристрастно, не подвергая сомнению их мотивы. Тем не менее он должен действовать твердо и при необходимости даже увольнять сотрудников – особенно тех, менталитет которых соответствует “теории Х”.

Видимость и реальность

У жестких авторитарных руководителей, которые, казалось бы, лишены даже элементарной вежливости, часто бывают преданные и мотивированные подчиненные. Если некий начальник отдела имеет привычку кричать на подчиненных, сквернословить и угрожать им дисциплинарными мерами, можно подумать, что этот стиль руководства –

иллюстрация “теории Х”. Тем не менее подчиненные этого начальника работают не хуже, а иногда и лучше сотрудников других отделов, и при этом производят вид удовлетворенных своей работой, профессионально состоявшихся людей.

Дело в том, что этот внешне грубый начальник искренне интересуется жизнью своих сотрудников. Ему небезразличны их семейные проблемы, он всегда готов помочь людям, попавшим в трудную ситуацию, и время от времени приглашает сотрудников на обед, чтобы показать, как он их ценит. Этот начальник упорно отстаивает интересы подчиненных в конфликтах с вышестоящим начальством и даже готов пожертвовать ради них своей должностью. Сотрудники, которые знают, что могут полагаться на своих начальников, верят в собственные силы и готовы работать с высокой эффективностью.

Источник : hr-academy.ru

“

ТЕМА 1. Парная линейная регрессия.

Аналитический метод выбора функциональной зависимости сводится к попытке выяснения содержательного смысла зависимости изучаемого показателя от объясняющего фактора и последующего выбора на этой основе соответствующей функциональной зависимости.

Временной (динамический) ряд (time-seriesdata) — выборка, в которой важны не только сами наблюдаемые значения, но и порядок их следования друг за другом. Чаще всего данные представляют собой наблюдения одной и той же величины в последовательные моменты времени.

Выборочная остаточная дисперсия — статистика, которая является несмещенной оценкой теоретической остаточной дисперсии σ 2 и определяется формулой

Выборочный коэффициент парной корреляции определяется по формуле

где — выборочные дисперсии x и y , соответственно.

Геометрический метод выбора функциональной зависимости сводится к следующему. На координатной плоскости Oxy наносятся точки (x_i,y_i), i=1. n, соответствующие выборке. Полученное графическое изображение называется полем корреляции (диаграммой рассеяния).

Достоверным событием называется некоторое событие, которое обязательно происходит в условиях данного эксперимента.

Задача эконометрического моделирования: На основании экспериментальных данных определить (оценить) объясненную часть зависимой переменной и, рассматривая случайную составляющую как случайную величину, получить оценки параметров ее распределения.

Коэффициент детерминации определяется по формуле:

Величина коэффициента детерминации представляет собой долю вариации зависимой переменной, обусловленную вариацией объясняющей переменной.

Метод наименьших квадратов (МНК). Согласно методу наименьших квадратов значения параметров функции (будем обозначать их через a,b) выбираются таким образом, чтобы сумма квадратов отклонений выборочных значений y_i от значений была минимальной

где минимум ищется по параметрам a, b, которые входят в зависимость .

Модель линейной парной регрессии — y=α+βx+ε.

Объясняющие переменные (факторы) — переменные (факторы) от которых зависят зависимые (объесняемые) переменные.

Основная задача эконометрического моделирования — построение по выборке эмпирической модели, выборочной парной регрессии , являющейся оценкой теоретической регрессии (функции f(x) ):, здесь — эмпирическая (выборочная) регрессия, описывающая усредненную по x зависимость между изучаемым показателем и объясняющим фактором.

Основные этапы эконометрического моделирования и анализа:

• Постановочный — формируется цель исследования (анализ экономического объекта, прогноз его показателей, имитация развития, выработка управленческих решений), теоретическое обоснование выбора переменных;
• Априорный — анализ сущности изучаемого объекта, формирование и формализация имеющейся информации;
• Параметризация — выбор вида модели (вида функции f(X)), анализ взаимосвязей и спецификация модели;
• Информационный — сбор необходимой статистической информации — наблюдаемых значений переменных;
• Идентификация модели — статистический анализ модели и оценка ее параметров;
• Верификация модели — проверка адекватности, статистической значимости модели.

Оценка теоретическое регрессии линейной парной регрессии строится в виде: =a+bx, где a, b являются оценками параметров α, β теоретической регрессии.

Оценками неизвестных параметров регрессии по методу наименьших квадратов (оценками МНК) называются значения параметров a и b, которые минимизируют сумму квадратов отклонений выборочных значений у_i от значений .

Пространственная выборка (cross-sectional data) — набор экономических показателей, полученных в некоторый момент времени (или в относительно небольшом промежутке времени), т. е. набор независимых выборочных данных из некоторой генеральной совокупности (так как практически независимость случайных величин проверить трудно, то обычно за независимые принимаются величины, не связанные причинно);

Спецификация модели — формулировка исходных предпосылок и ограничений, выбор структуры уравнения модели, представление в математической форме обнаруженных взаимосвязей и соотношений, установление состава объясняющих переменных.

Средняя ошибка аппроксимации регрессии по формуле определяется по формуле:

Значение этой ошибки в пределах 5-7% свидетельствует о хорошем соответствии модели эмпирическим данным.

Статическая (стохастическая, вероятностная) зависимость — форма связи между переменными величинами, когда каждому значению одной переменной соответствует не какое-то определенное значение другой переменной, а множество возможных значений (более точно — некоторое условное распределение) другой переменной.

Теорема Гаусса-Маркова . Если регрессионная модель y=α+βx+ε удовлетворяет условиям Гаусса-Маркова, то оценки МНК a и b имеют наименьшую дисперсию в классе всех линейных несмещенных оценок.

Теоретическое уравнение регрессии — E_X(y)=f(X), где f(X) — теоретическая функция регрессии.

Уравнение регрессионной модели — y= E_X(y)+ε

• Величины ε_i являются случайными.
• Математическое ожидание возмущений равно нулю: E(ε_i)=0.
• Возмущения ε_i и ε_j некоррелированы: E(ε_iε_j)=0, i ≠ j.
• Дисперсия возмущения ε_i постоянна для каждого i: D(ε_i)=σ 2 . Это условие называется условием гомоскедастичности. Нарушение этого условия называется гетероскедастичностью.
• Величины ε_i взаимно независимы со значениями объясняющих переменных.
  Здесь, во всех условиях i=1,2. n.

Эконометрика — это раздел математики, занимающийся разработкой и применением статистических методов для измерений взаимосвязей между экономическими переменными.

Эконометрическая модель — y=f(X)+ε, y — зависимая переменная, X=(x₁,x₂. x_k) — объясняющие переменные, f(X) — объясненная часть, ε — случайная составляющая (возмущение или ошибка).

Эмпирическое уравнение регрессии (модельная функция регрессии) — y=f(X,B).

Эмпирический метод выбора функциональной зависимости состоит в следующем. Выбирается некоторая параметрическая функциональная зависимость f(x).

ТЕМА 2. Множественная линейная регрессия.

Выборочная остаточная дисперсия — статистика, вычисляемая по правилу , где n — число наблюдений, k — число факторов модели.

Выборочный коэффициент частной корреляции (частный коэффициент корреляции) между зависимыми переменными x_i и x_j используется для оценки взаимосвязи этих переменных, «очищенной» от влияния других факторов (см. § 2.4).

Качественный признак — признак, имеющий несколько значений.

Классическая нормальная линейная модель множественной регрессии

Модель множественной линейной регрессии Y=Xβ+ε, удовлетворяющая условиям Гаусса-Маркова, называется классической нормальной линейной моделью множественной регрессии , в предположении, что ε — нормально распределенный случайный вектор.

Коэффициент детерминации (множественный) является мерой адекватности регрессионной модели и определяется по формуле , где — сумма квадратов отклонений, обусловленная регрессией, — остаточная сумма квадратов, представляет собой общую сумму квадратов отклонений зависимой переменной от средней.

Коэффициент эластичности (частный коэффициент эластичности) используют для сравнения влияния на зависимую переменную различных объясняющих переменных. Он показывает, на сколько процентов изменится в среднем y при увеличении только переменной x_i на 1% и неизменных значениях остальных переменных.

Ловушкой фиктивных переменных называют ситуацию, когда сумма фиктивных переменных тождественно равна константе.

Модель множественной линейной регрессии имеет вид y_i=α+β₁x_i1+. +β_kx_ik+ε, , что в матричной форме может быть записано Y=Xβ+ε, где , x_ij — i-е наблюдение объясняющей переменной x_j, n — объем выборки,k — число факторов.

Под мультиколлинеарностью понимается высокая взаимная коррелированность объясняющих переменных. Мультиколлинеарность может проявляться в двух формах: функциональной и стохастической.

Оценками неизвестных параметров α, β₁, β₂. β_k линейной множественной регрессии по методу наименьших квадратов (оценками МНК) называются значения параметров a,b₁,b₂. b_k, минимизирующие сумму квадратов отклонений выборочных значений у_i от расчетных значений (см. §2.2).

Правило введения фиктивных переменных: если качественный признак имеет p альтернативных значений (градаций), то число бинарных фиктивных переменных должно быть равно p-1.

Регрессионные уравнения с переменной структурой — модели, в которых качественные признаки существенно влияют на структуру линейных связей между переменными.

Скорректированный (исправленный) коэффициент детерминации определяется формулой: .

Стандартизованный коэффициент регрессии , используют для сравнения влияния на зависимую переменную различных объясняющих переменных. Он показывает, на сколько величин s_y изменится в среднем зависимая переменная y при увеличении только i-ой переменной на .

Стандартная ошибка m_a коэффициента a вычисляется по правилу , где — первый элемент, стоящий на главной диагонали матрицы (X T X) -1 .

Стандартная ошибка коэффициента b_i вычисляется по правилу .

Стохастическая (неполная, несовершенная) форма мультиколлинеарности имеет место в случае, когда хотя бы между двумя объясняющими переменными имеется достаточно высокая степень корреляции.

Если выполнены условия Гаусса-Маркова, то оценки метода наименьших квадратов параметров модели линейной множественной регрессии являются наиболее эффективными (в смысле минимума дисперсии линейных комбинаций оценок параметров) в классе линейных несмещенных оценок.

Фиктивная (искусственная) переменная — переменная, описывающая количественным образом различные состояния качественного признака.

Функциональная (полная, совершенная) форма мультиколлинеарности — форма мультиколлинеарности, при которой, по крайней мере, между двумя объясняющими переменными существует линейная зависимость.

Эконометрическая модель множественной регрессии — y=f(x₁,x₂. x_k)+ε, где f(x₁,x₂. x_k) — неизвестная функциональная зависимость (теоретическая регрессия); ε — случайное слагаемое (возмущение), представляющее собой совокупное действие не включенных в модель факторов, ошибки измерения.

Эмпирическая (выборочная) множественная линейная регрессия имеет вид: , где a,b₁,b₂. b_k являются оценками параметров α, β₁, β₂,. β_k теоретической регрессии.

Эмпирическая (выборочная) регрессия — оценка теоретической регрессии (функции f(x₁,x₂. x_k)), описывающая усредненную зависимость между изучаемым показателем и факторами.

ТЕМА 3. Гетероскедастичность и автокоррелированность остатков.

Под автокорреляцией (сериальной, последовательной корреляцией) понимается корреляция между наблюдаемыми показателями, упорядоченными определенным образом.

Автокорреляция первого порядка — тип автокорреляции, для которого наибольшее влияние на наблюдение оказывает результат предыдущего наблюдения.

Гетероскедастичности условие — условие непостоянства дисперсий возмущений.

Гомоскедастичности условие — условие постоянства дисперсий возмущений.

Классическая регрессионная модель

Модель множественной линейной регрессии Y=Xβ+ε, удовлетворяющая условиям Гаусса-Маркова, называется классической регрессионной моделью .

Коэффициент автокорреляции первого порядка — парный коэффициент корреляции между рядами e₁, e₂. e_n-1 и e₂, e₃. e_n, вычисляемый по формуле .

Лаговые переменные — факторы, влияние которых характеризуется определенным запаздыванием.

Модели с гетероскедастичностью — регрессионные модели, для которых дисперсии возмущений не одинаковы.

Модели с корреляцией ошибок — регрессионные модели, для которых наблюдаемые значения зависимой переменной коррелируют со значениями в предыдущие моменты времени, т.е. имеет место корреляция между различными возмущениями.

Обобщенная линейная модель множественной регрессии имеет вид Y=Xβ+ε, где переменые Y — вектор зависимых переменных размера (nx1), X — (nxk) матрица объясняющих переменных, β — (kx1) вектор параметров регрессии, ε — (nx1) вектор случайных возмущений, причем предполагаются выполненными условия:

1. Вектор возмущений ε=(ε₁. ε_n) является случайным вектором.
2. E(ε)=0_n (0_n — нулевой вектор размера n).
3. Σ_ε= E(εε T )=Ω, где Ω — положительно определнная матрица.
4. Величины ε_i взаимно независимы со значениями объясняющих переменных.
5. r(X)=k+1.

Обобщенный метод наименьших квадратов (ОМНК) — способ оценивания вектора коэффициентов регрессионного уравнения, при котором оценка зависит от матрицы ковариации ошибок.

Отрицательная автокорреляция имеет место, если r(ε_t-1,ε_t) Положительная автокорреляция имеет место, если r(ε_t-1,ε_t)>0.

Статистика Дарбина-Уотсона используется в тесте Дарбина-Уотсона для оценки корреляции остатков и вычисляется

В классе линейных несмещенных оценок вектора β для обобщенной регрессионной модели оценка имеет наименьшую матрицу ковариаций.

Тест Дарбина-Уотсона является критерием обнаружения автокорреляции первого порядка (см. §3.3.1).

Тест Голдфелда-Квандта позволяет определить наличие гетероскедастичности (см. §3.2.2).

Тест ранговой корреляции Спирмена позволяет определить наличие гетероскедастичности (см. §3.2.1).

ТЕМА 4. Нелинейные модели и их линеаризация.

Абсолютная ошибка аппроксимации используется для оценки качества нелинейной регрессии и вычисляется следующим образом:

Двойная логарифмическая модель — линейная модель, в которой и зависимая и объясняющая переменные заданы в логарифмической виде .

Индекс корреляции используется для оценки качества нелинейной регрессии и вычисляется следующим образом:

Коэффициент эластичности характеризует влияние фактора на зависимую переменную и вычисляется по формуле .

Линейно логарифмические (полулогарифмические) модели — нелинейные по объясняющим переменным, но линейные по оцениваемым параметрам модели, имеющие вид: .

Логарифмически линейная (логлинейная) модель — нелинейная модель вида lny= α+βx+ε.

Модель с квадратными корнями — нелинейная по объясняющим переменным, но линейная по оцениваемым параметрам модель, имеющая вид: .

Обратная (гиперболическая) модель — нелинейная по объясняющим переменным, но линейная по оцениваемым параметрам модель, имеющая вид: .

Показательная (экспоненциальная) модель — нелинейная модель вида y=αe βx ε.

Полиномиальная модель — нелинейная по объясняющим переменным, но линейная по оцениваемым параметрам модель, имеющая вид:

Среднее абсолютное отклонение используется для оценки качества нелинейной регрессии и вычисляется следующим образом:

Стандартная ошибка регрессии (среднее квадратическое отклонение) используется для оценки качества нелинейной регрессии и вычисляется следующим образом:

Степенная модель — нелинейная по объясняющим переменным, но линейная по оцениваемым параметрам модель, имеющая вид:

ТЕМА 5. Системы линейных уравнений.

Двухшаговый метод наименьших квадратов – метод построения оценок структурных коэффициентов, основанный на методе инструментальных переменных (см. §5.2).

Идентифицируемость – возможность определения структурных коэффициентов уравнения по коэффициентам приведенной формы.

Идентифицируемое уравнение – уравнение, все входящие структурные параметры которого идентифицируемы.

Идентифицируемый параметр – структурный параметр, который может быть однозначно оценен с помощью косвенного метода наименьших квадратов.

Инструментальные переменные – новые переменные, которые тесно коррелируют с исходными регрессорами и не коррелируют со случайными составляющими.

Косвенный метод наименьших квадратов – метод построения оценок структурных коэффициентов с помощью оценок коэффициентов приведенной формы (см. §5.1).

Лагированные переменные (эндогенные переменные с лагом) — эндогенные переменные, относящиеся к предыдущим моментам времени.

Метод инструментальных переменных – один из самых распространенных методов оценивания уравнений, в которых регрессоры коррелируют со случайными компонентами (см. §5.2).

Неидентифицируемый параметр – структурный параметр, значение которого нельзя определить, даже зная точные значения параметров приведенной формы.

Предопределенными переменными называют экзогенные переменные и эндогенные переменные с лагом.

Приведенная форма системы одновременных уравнений – разрешенная относительно эндогенных переменных система уравнений в структурной форме, в правых частях новых уравнений которой останутся только экзогенные переменные:

Порядковые условия – необходимые условия, используемые для проверки идентифицируемости структурных уравнений (см. §5.3).

Сверхидентифицируемый параметр – структурный параметр, которому косвенный метод наименьших квадратов дает несколько различных его оценок, то есть существует несколько значений структурного коэффициента, соответствующих найденным значениям приведенных коэффициентов.

Система линейных одновременных уравнений записывается таким образом, что в левых частях уравнений будут выделены эндогенные переменные, рассматриваемые как объясняемые переменные, в правой части будет представлена зависимость этих переменных от экзогенных переменных и оставшихся эндогенных.

Структурная форма системы линейных одновременных уравнений имеет вид

то есть, эндогенных переменных в такой системе столько же, сколько и уравнений, но в отдельном уравнении их может быть несколько. В каждом уравнении, взятом в отдельности, только одна переменная, помещенная в левую часть, может рассматриваться как объясняемая, а остальные эндогенные переменные в этом уравнении являются регрессорами, причем коррелирующими со случайным возмущением.

Структурные параметры – параметры системы линейных одновременных уравнений, записанной в структурной форме.

Трехшаговый метод наименьших квадратов – метод построения оценок структурных коэффициентов, сочетающий процедуру одновременного оценивания и метод инструментальных переменных (см. §5.2).

Экзогенные переменные — переменные, определяемые вне системы.

Эндогенные переменные — переменные, определяемые внутри системы.

ТЕМА 6. Временные ряды.

Авторегрессионная модель скользящей средней порядков p и q соответственно имеет вид

Авторегрессионная модель p-го порядка описывает изучаемый показатель в момент t в зависимости от его значений в предыдущие моменты y_t-1, y_t-2. y_t-p и имеет вид:

Авторегрессионные модели – модели, в которых в качестве лаговых переменных участвуют значения зависимых переменных.

Аддитивная модель временного ряда представляется в виде суммы компонент: y_t=u_t+s_t+v_t+ε_t.

Временной (динамический) ряд – последовательность наблюдений некоторого признака, упорядоченных в порядке возрастания моментов времени.

Выборочный коэффициент автокорреляции определяется по формуле

Гипотеза случайности значений ряда наблюдений – гипотеза о независимости и стационарности распределения наблюдений, образующих временной ряд.

Коррелограмма – график выборочной автокорреляционной функции .

Критерий «восходящих и нисходящих» серий – критерий, согласно которому проверяется гипотеза случайности (см. §6.2.2).

Критерий серий, основанный на медиане выборки – критерий, согласно которому проверяется гипотеза случайности (см. §6.2.1).

Лаговые переменные — переменные, влияние которых характеризуется некоторым запаздыванием.

Метод аналитического выравнивания используется для оценки тренда и периодической составляющей временного ряда (см. §6.3).

Методы сглаживания временного ряда используются для оценки тренда и периодической составляющей временного ряда и делятся на:

• сглаживание с помощью скользящей средней (см. §6.4);
• сглаживание с помощью простой скользящей средней (см. §6.4);
• сглаживание с помощью взвешенной скользящей средней (см. §6.4);
• сглаживание с помощью скользящей медианы (см. §6.4);
• экспоненциальное сглаживание (см. §6.5).

Модели с лагами (распределенными лагами) – динамическая модели, содержащие в качестве лаговых переменных только независимые (объясняющие) переменные.

Модель скользящей средней q-го порядка имеет вид:

Мультипликативная модель временного ряда представляется в виде произведения компонент: y_t=u_t× s_t× v_t× ε_t.

Сезонная компонента s_t уровней временного ряда – компонента уровней временного ряда, отражающая повторяемость экономических процессов в течение не слишком длительного периода.

Случайная компонента ε_t уровней временного ряда – компонента уровней временного ряда, отражающая влияние случайных, а также неучтенных факторов.

Стационарный временной ряд – временной ряд y_t, вероятностные свойства которого (закон распределения y_t и его числовые характеристики) не зависят от момента времени t.

Тренд u_t уровней временного ряда – плавно меняющаяся компонента уровней временного ряда, отражающая влияние долговременных, систематических факторов, основную тенденцию в формировании рассматриваемого показателя.

Уровни ряда – отдельные наблюдения y_t, t=1,2. n (где n – число наблюдений).

Циклическая компонента v_t уровней временного ряда – компонента уровней временного ряда, отражающая повторяемость экономических процессов в течение длительных периодов.

Тема 3. Линейная модель парной регрессии и метод наименьших квадратов

Аннотация.Данная тема раскрывает суть регрессионного анализа в эконометрике.

Ключевые слова.Модель регрессии, метод наименьших квадратов, остатки регрессии.

Методические рекомендации по изучению темы

· Тема содержит лекционную часть, где даются общие представления по теме.

· В качестве самостоятельной работы предлагается ознакомиться с решениями типовых задач, выполнить практические задания и ответить на вопросы для самоконтроля.

· Для проверки усвоения темы имеется тест для самоконтроля.

· Для подготовки к экзамену имеются контрольный тест.

Рекомендуемые информационные ресурсы:

2. Эконометрика: [Электронный ресурс] Учеб.пособие / А.И. Новиков. — 2-e изд., испр. и доп. — М.: ИНФРА-М, 2011. — 144 с.: с. (http://znanium.com/catalog.php?item=booksearch&code=%D1%8D%D0%BA%D0%BE%D0%BD%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D0%BA%D0%B0&page=1#none) С. 28-46.

3.Уткин, В. Б. Эконометрика [Электронный ресурс] : Учебник / В. Б. Уткин; Под ред. проф. В. Б. Уткина. — 2-е изд. — М.: Издательско-торговая корпорация «Дашков и К°», 2012. — 564 с.

(http://znanium.com/catalog.php?item=booksearch&code=%D1%8D%D0%BA%D0%BE%D0%BD%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D0%BA%D0%B0&page=4#none) С. 323-338.

4. Валентинов, В. А. Эконометрика [Электронный ресурс]: Практикум / В. А. Валентинов. — 3-е изд. — М.: Дашков и К, 2010. — 436 с.

(http://znanium.com/catalog.php?item=booksearch&code=%D1%8D%D0%BA%D0%BE%D0%BD%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D0%BA%D0%B0&page=3#none) С. 38-99.

5.Эконометрика. Практикум: [Электронный ресурс] Учебное пособие / С.А. Бородич. — М.: НИЦ ИНФРА-М; Мн.: Нов.знание, 2014. — 329 с. (http://znanium.com/catalog.php?item=booksearch&code=%D1%8D%D0%BA%D0%BE%D0%BD%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D0%BA%D0%B0&page=4#none) С. 82-99.

6. Электронныйкурс “Econometrics and Public Policy (Advanced)”, Princeton University, URL: https://blackboard.princeton.edu/webapps /portal/frameset.jsp?tab_group=courses&url=%2Fwebapps%2Fblackboard%2Fexecute%2FcourseMain%3Fcourse_id%3D_214206_1

Глоссарий

Множественная регрессия представляет собой модель, где теоретическое (среднее) значение зависимой переменной Y рассматривается как функция нескольких независимых переменных X₁, X₂. X_m.

Параметризация модели – выражение в математической форме взаимосвязи между переменными модели, формулирование исходных предпосылок и ограничений модели.

Парная регрессия представляет собой модель, где теоретическое (среднее) значение зависимой переменной Y рассматривается как функция одной независимой переменной X.

Спецификация модели — формулирование вида модели, исходя из соответствующей теории связи между переменными.

Цель регрессионного анализа – оценка функциональной зависимости между независимыми переменными X и условным математическим ожиданием зависимой переменной Y.

Вопросы для изучения:

1. Спецификация линейной модели парной регрессии.

2. Метод наименьших квадратов (МНК) – идентификация линейной модели парной регрессии.

3.Предпосылки МНК и свойства МНК-оценок.

Спецификация линейной модели парной регрессии.Основная цель регрессионного анализа – оценка функциональной зависимости между независимыми переменными X и условным математическим ожиданием зависимой переменной Y.Простая (парная) регрессия представляет собой модель, где теоретическое (среднее) значение зависимой переменной Y рассматривается как функция одной независимой переменной X: Множественная регрессия представляет собой модель, где теоретическое (среднее) значение зависимой переменной Y рассматривается как функция нескольких независимых переменных X1, X2. Xm:

Спецификация модели — формулирование вида модели, исходя из соответствующей теории связи между переменными.Определяется состав переменных и математическая функция для отражения связи между ними.

Спецификация линейной модели (уравнения) парной регрессии:

где Y_i — фактическое значение зависимой переменной Y;

Y_xi — теоретическое (среднее) значение зависимой переменной Y;

ε_i — случайная величина (остаток регрессии).

Теоретическое уравнение регрессии (гипотетически для генеральной совокупности):

где α – свободный коэффициент;

β — коэффициент регрессии;

ε_i – случайное отклонение (возмущение).

Случайное отклонение включает влияние не учтенных в модели факторов, случайных ошибок и особенностей измерения. Источники его присутствия в модели: спецификация модели, выборочный характер исходных данных, особенности измерения переменных.

Эмпирическое уравнение регрессии (для выборки наблюдений):

где а – эмпирическая (выборочная) оценка свободного коэффициента;

b — эмпирическая (выборочная) оценка коэффициента регрессии;

e_i – эмпирическая (выборочная) оценка теоретического случайного отклонения ε (остаток регрессии).

Метод наименьших квадратов (МНК).Суть метода наименьших квадратов (МНК) — оценки параметров таковы, что сумма квадратов отклонений фактических значений зависимой переменной Y_iот расчетных (теоретических) Y_x минимальна:

Предпосылки МНК и свойства МНК-оценок.Предпосылки МНК:

1. Математическое ожидание случайного отклонения εi равно нулю для всех наблюдений:

2. Дисперсия случайных отклонений εi постоянна. Выполнение предпосылки называется гомоскедатичностью, нарушение – гетероскедастичностью:

3.Случайные отклонения ε_i и ε_j являются независимыми друг от друга для i ≠ j. Выполнение данной предпосылки говорит об отсутствии автокорреляции, нарушение – о присутствии автокорреляции:

4.Случайное отклонение должно быть независимо от объясняющих переменных:

5.Модель линейна относительно параметров.

Если предпосылки МНК выполнены, то МНК-оценки регрессии обладают следующими свойствами:

1.Оценки являются несмещенными:

2. Оценки состоятельны, так как их дисперсия при увеличении выборки стремится к нулю:

3.Оценки эффективны, имеют наименьшую дисперсию по сравнению с другими оценками, линейными относительно зависимой переменной:

Вопросы и задания для самоконтроля

1. Что такое функция регрессии?

2. Чем регрессионная модель отличается от функции регрессии?

3. Каковы основные причины наличия в регрессионной модели случайного отклонения?

4. Как осуществляется спецификация модели?

5. В чем состоит различие между теоретическим и эмпирическим уравнениями регрессии?

6. В чем суть метода наименьших квадратов?

7. Каковы формулы расчета коэффициентов эмпирического парного линейного уравнения регрессии по МНК?

8. Каковы предпосылки МНК? Каковы последствия их выполнимости или невыполнимости?

9. Действительно ли оценки коэффициентов регрессии будут иметь нормальное распределение, если случайные отклонения распределены нормально?

10. Действительно ли в любой линейной регрессионной модели, построенной по МНК, сумма случайных отклонений равна нулю?

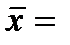
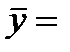
Задача 1. При исследовании корреляционной зависимости между ценой на нефть X и индексом нефтяных компаний Y получены следующие данные: 16,2; 4000; 4; 40.

Задание: построить линейное уравнение регрессии Y на X.

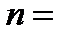
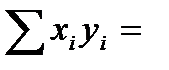
Задача 2. По выборке объема 10 получены следующие данные:

100; 200; 21000; 12000; 45000.

Задание: оценить с помощью МНК параметры линейного уравнения регрессии, найти выборочный коэффициент корреляции .

Методические основы корреляционно-регрессионного анализа

Понятие о корреляционно-регрессионном анализе

Убедившись при помощи аналитической группировки и расчета показателя эмпирического корреляционного отношения, что теснота связи между исследуемыми явлениями достаточно высока, можно и перейти к корреляционно-регрессионному анализу.

Экономические явления и процессы хозяйственной деятельности предприятий зависят от большого количества взаимодействующих и взаимообусловленных факторов.

В наиболее общем виде задача изучения взаимосвязей факторов состоит в количественной оценке их наличия и направления, а также характеристике силы и формы влияния одних факторов на другие. Для ее решения применяются две группы методов, одна из которых включает в себя методы корреляционного анализа, а другая – методы регрессионного анализа, объединенные в методы корреляционно-регрессионного анализа, что имеет под собой некоторые основания: наличие целого ряда общих вычислительных процедур, взаимодополнение при интерпретации результатов и др.

Задачи корреляционного анализа сводятся к измерению тесноты связи между варьирующими признаками и оценке факторов, оказывающих наибольшее влияние на результативный признак. К показателям, используемым для оценки тесноты связи, относятся эмпирическое корреляционное отношения, теоретическое корреляционное отношение, линейный коэффициент корреляции и т.п.

Задачи регрессионного анализа состоят в установлении формы зависимости между исследуемыми признаками (показателями), определении функции регрессии, использования уравнения регрессии для оценки неизвестных значений зависимой переменной. Найти уравнение регрессии –

значит по эмпирическим (фактическим) данным описать изменения взаимно коррелируемых величин.

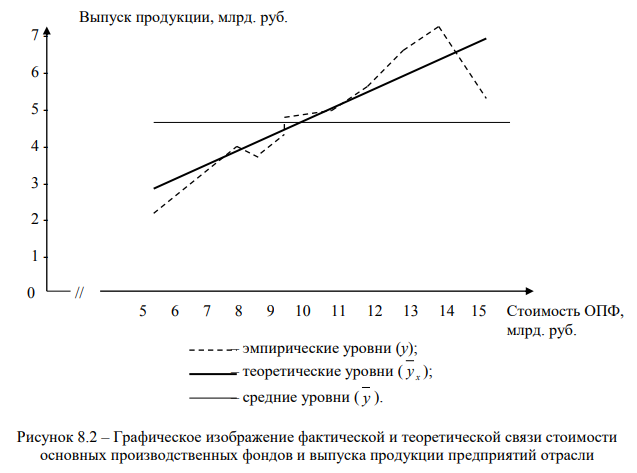
Уравнение регрессии должно определить, каким будет среднее значение результативного признака у при том или ином значении факторного признака х, если остальные факторы, влияющие на у и не связанные с х не учитывать, т.е. абстрагироваться от них. Уравнение регрессии называют теоретической линией регрессии, а рассчитанные по нему значения результативного признака – теоретическими. Теоретические значения результативного признака обычно обозначаются y _x (читается: «игрек, выровненный по икс») и рассматриваются как функция от х, т.е. y _x = f (x). Иногда для простоты записи вместо y _x пишут y’ или y.

Для аналитической связи между х и у используются следующие простые виды уравнений: y _x = a₀ + a₁x (прямая); y _x = a₀ + a₁x + a₂x 2 (парабола второго порядка); y _x = a₀ + a₁/x (гипербола); y _x = a₀ × a₁ x (показательная или экспоненциальная функция); y _x = a₀ + b × lg x (логарифмическая функция) и др.

Обычно зависимость, выраженную уравнением прямой, называют линейной (или прямолинейной), а все остальные – криволинейными (см. табл. 7.1). Кроме того, различают парную и множественную (многофакторную) корреляцию (см. там же), а, следовательно, и, парную и множественную регрессии.

Корреляционно-регрессионный анализ, в частности многофакторный корреляционный анализ, состоит из нескольких этапов.

На первом этапе определяются факторы, оказывающие воздействие на изучаемый показатель, и отбираются наиболее существенные. От того, насколько правильно сделан отбор факторов, зависит точность выводов по итогам анализа. При отборе факторов придерживаются требований, представленных на рис. 8.1.

Требования к отбору факторов при корреляционнорегрессионном анализе:

• учитываются причинно-следственные связи между показателями
• отбираются самые значимые факторы, оказывающие решающее воздействие на результативный показатель (факторы, которые имеют критерий надежности по Стьюденту меньше табличного, не рекомендуется принимать в расчет)
• все факторы должны быть количественно измеримы
• не рекомендуется включать в корреляционную модель взаимосвязанные факторы (если парный коэффициент корреляции между двумя факторами больше 0,85, то по правилам корреляционного анализа один из них необходимо исключить, иначе это приведет к искажению результатов анализа)
• нельзя включать в корреляционную модель факторы, связь которых с результативным показателем носит функциональный характер
• в корреляционную модель линейного типа не рекомендуется включать факторы, связь которых с результативным показателем имеет криволинейный характер

Рисунок 8.1 – Перечень основных требований, учитываемых при отборе факторов, при корреляционно-регрессионном анализе

На втором этапе собирается и оценивается исходная информация, необходимая для корреляционного анализа. Собранная исходная информация должна быть проверена на точность (достоверность), однородность и соответствие закону нормального распределения. Критерием однородности информации служит среднеквадратическое отклонение и коэффициент вариации. Если вариация выше 33%, то это говорит о неоднородности информации и ее необходимо исключить или отбросить нетипичные наблюдения.

На третьем этапе изучается характер и моделируется связь между факторами и результативным показателем, т.е. подбирается и обосновывается математическое уравнение, которое наиболее точно выражает сущность исследуемой зависимости. Для обоснования функции используются те же приемы, что и для установления наличия связи: аналитические группировки, линейные графики и др. Если связь всех факторных показателей с результативным носит прямолинейный характер, то для записи этих зависимостей можно использовать линейную функцию: y _x = a₀ + a₁x₁ + a₂x₂ +. + a_nx_n. Если связь между функцией и исследуемыми показателями носит криволинейный характер, то может быть использована степенная функция: y _x = b₀ × x₁ b1 × x₂ b2 × . × x_n bn .

На четвертом этапе проводится расчет основных показателей связи корреляционного анализа. Рассчитываются матрицы парных и частных коэффициентов корреляции уравнения множественной регрессии, а также показатели, с помощью которых оценивается надежность коэффициентов корреляции и уравнения связи: критерий Стьюдента, критерий Фишера, множественные коэффициенты корреляции и др.

На пятом этапе дается статистическая оценка результатов корреляционного анализа и практическое их применение. Для этого дается оценка коэффициентов регрессии, коэффициентов эластичности и бета-коэффициентов.

Одним из основных условий применения и ограничения корреляционно-регрессионного метода является наличие данных по достаточно большой совокупности явлений. Обычно считают, что число наблюдений должно быть не менее чем в 5-6, а лучше – не менее чем в 10 раз больше числа факторов.

Парная линейная регрессия

Парная линейная зависимость – наиболее часто используемая форма связи между двумя коррелируемыми признаками, выражаемая при парной корреляции уравнением прямой:

где y _x – выровненное среднее значение результативного признака;
х – значение факторного признака;
а0 и а1 – параметры уравнения;
а0 – значение у при х = 0;
а1 – коэффициент регрессии.

Коэффициент регрессии а1 показывает, на сколько (в абсолютном выражении) изменится результативный признак у при изменении факторного признака х на единицу.

Если а1 имеет положительный знак, то связь прямая, если отрицательный – связь обратная.

Параметры уравнения связи определяются способом (методом) наименьших квадратов (МНК) с помощью составленной и решенной системы двух уравнений с двумя неизвестными:

где n – число членов в каждом из двух сравниваемых рядов (число единиц совокупности);
Σx – сумма значений факторного признака;
Σx 2 – сумма квадратов значений факторного признака;
Σy – сумма значений результативного признака;
Σyx – сумма произведений значений факторного признака на значения результативного признака.

Для справки: суть метода наименьших квадратов заключается в следующем требовании: искомые теоретические значения результативного признака должны быть такими, при которых бы обеспечивалась минимальная сумма квадратов их отклонений от эмпирических значений.

Решив систему уравнений, получаем значения параметров уравнения связи, определяемые по формулам:

Если параметры уравнения определены правильно, то Σу = Σ y _x.

Пример построения уравнения парной линейной регрессии

По данным таблицы 8.1 необходимо построить линейное уравнение регрессии, характеризующее зависимость выпуска продукции десяти предприятий одной отрасли от стоимости их основных производственных фондов.

Номер предприятия	1	2	3	4	5	6	7	8	9	10
Стоимость ОПФ, млрд. руб.	12	8	10	6	9	15	11	13	14	10
Выпуск продукции, млрд. руб.	5,6	4,0	4,0	2,4	3,6	5,0	4,6	6,5	7,0	4,5

Данные, характеризующие десять предприятий одной отрасли

Для расчета параметров уравнения регрессии и выровненных по х значений у построим вспомогательную таблицу 8.2.

№ завода (n)	Стоимость ОПФ (х), млрд. руб.	Выпуск продукции (у), млрд. руб.	x 2	xу	y 2	y x = 0,167 + 0,421x
1	12	5,6	144	67,2	31,36	5,2
2	8	4	64	32	16	3,5
3	10	4	100	40	16	4,4
4	6	2,4	36	14,4	5,76	2,7
5	9	3,6	81	32,4	12,96	4
6	15	5	225	75	25	6,5
7	11	4,6	121	50,6	21,16	4,8
8	13	6,5	169	84,5	42,25	5,6
9	14	7	196	98	49	6,1
10	10	4,5	100	45	20,25	4,4
Всего	108	47,2	1236	539,1	239,74	47,2
В среднем на 1 завод	10,8	4,72	123,6	53,91	23,974	х

Данные, используемые для расчета параметров линейного уравнения связи стоимости основных производственных фондов и выпуска продукции десяти предприятий отрасли

По формуле 8.3 параметр уравнения прямой: a0 = 0,167.

По формуле 8.4 коэффициент регрессии: a1 = 0,421.

По формуле 8.1 линейное уравнение связи между стоимостью основных производственных фондов и выпуском продукции имеет вид: y _x = 0,167 + 0,421x

Коэффициент регрессии а1 = 0,421 показывает, что при увеличении стоимости основных производственных фондов на 1 млрд. руб. выпуск продукции в среднем увеличится на 0,421 млрд. руб.

Последовательно подставляя в полученное уравнение значения факторного признака х, находим выровненные значения результативного признака y _x, показывающие, каким теоретически должен быть средний размер выпущенной продукции при данном размере основных производственных фондов (при прочих равных условиях). Выровненные (теоретические) значения выпуска продукции приведены в последней графе таблицы 8.2.

Правильность расчета параметров уравнения подтверждает равенство Σу = Σ y _x (47,2 = 47,2).

На рис. 8.2 представлены эмпирические, теоретические и средние уровни выпуска продукции предприятий отрасли, отличающихся по стоимости основных производственных фондов.

Для экономической интерпретации линейных и нелинейных связей между двумя исследуемыми явлениями часто используют рассчитанные на основе уравнений регрессии коэффициенты эластичности.

Коэффициент эластичности показывает, на сколько процентов изменится в среднем результативный признак у при изменении факторного признака х на 1%.

Для линейной зависимости коэффициент эластичности (ε) определяется:

– для отдельной единицы совокупности по формуле:

– в целом для совокупности по формуле:

Пример расчета коэффициентов эластичности

По данным таблицы 8.2 необходимо найти коэффициенты эластичности для отдельных предприятий и в среднем по отрасли.

По формуле 8.5 коэффициент эластичности на первом предприятии равен: ε₁ = 0,97, т.е. 1% прироста стоимости основных производственных фондов обеспечивает прирост выпуска продукции на этом предприятии на 0,97%; …; на пятом предприятии – на 0,95%; …; на десятом предприятии – на 0,96%.

По формуле 8.6 коэффициент эластичности равен:

ε = 0,963. Это означает, что при увеличении стоимости основных производственных фондов в целом по предприятиям отрасли на 1%, выпуск продукции увеличится в среднем на 0,963%. Определение тесноты связи в корреляционно-регрессионном анализе основывается на правиле сложения дисперсий, как и в методе аналитической группировки. Но в отличие от него, где для оценки линии регрессии используют групповые средние результативного признака, в корреляционно-регрессионном анализе для этой цели используют теоретические значения результативного признака.

Наглядно представить и обосновать корреляционно-регрессионный анализ позволяет график.

На графике на рис. 8.2 проведены три линии: у – ломанная линия фактических данных; y _x – прямая наклонная линия теоретических значений у при абстрагировании от влияния всех факторов, кроме фактора х (переменная средняя); y – прямая горизонтальная линия, из среднего значения которой исключено влияние на у всех без исключения факторов (постоянная средняя).

Несовпадение линии переменной средней y _x с линией постоянной средней y поясняется влиянием факторного признака х, что, в свою очередь, свидетельствует о наличии между признаками у и х неполной, нефункциональной связи. Для определения тесноты этой связи необходимо рассчитать дисперсию отклонений у и y _x, то есть остаточную дисперсию, которая обусловлена влиянием всех факторов, кроме фактора х. Разница между общей и остаточной дисперсиями дает теоретическую (факторную) дисперсию, которая измеряет вариацию, обусловленную фактором х.

На сопоставлении этой разницы с общей дисперсией построен индекс корреляции или теоретическое корреляционное отношение (R), которое определяется по формулам:

где σ 2 _общ – общая дисперсия;
σ 2 _ост – остаточная дисперсия;
σ 2 _{y x} – факторная (теоретическая) дисперсия.

Факторную дисперсию по теоретическим значениям исчисляют по формуле:

Остаточную дисперсию определяют по формулам:

Коэффициент детерминации (R 2 ) характеризует ту часть вариации результативного признака у, которая соответствует линейному уравнению регрессии (т.е. обусловлена вариацией факторного признака) и исчисляется по формуле:

Индекс корреляции принимает значения от 0 до 1. Когда R = 0, то связи между вариацией признаков х и у нет. Остаточная дисперсия равняется общей, а теоретическая дисперсия равняется нулю. Все теоретические значения y _x совпадают со средними значениями y , линия y _x на графике совпадает с линией y , то есть принимает горизонтальное положение. При R = 1 теоретическая дисперсия равна общей, а остаточная равна нулю, фактические значения у совпадают с теоретическими y _x, следовательно, связь между исследуемыми признаками линейно-функциональная.

Индекс корреляции пригоден для измерения тесноты связи при любой ее форме. Он, как и эмпирическое корреляционное отношение, измеряет только тесноту связи и не показывает ее направление.

Для измерения тесноты связи и определения ее направления при линейной зависимости используется линейный коэффициент корреляции (r), определяемый по формулам:

Значение r колеблется в пределах от -1 до +1. Положительное значение r означает прямую связь между признаками, а отрицательное – обратную.

Оценка тесноты связи между признаками проводится по данным таблицы 8.3.

Сила связи	Значение r при наличии
прямой связи	обратной связи
Слабая	0,1-0,3	(-0,1)-(-0,3)
Средняя	0,3-0,7	(-0,3)-(-0,7)
Тесная	0,7-0,99	(-0,7)-(-0,99)

Качественная оценка связи между признаками

Проверка надежности (существенности) связи в корреляционно-регрессионном анализе осуществляют при помощи тех же самых критериев и процедур, что и в аналитической группировке.

Фактическое значение F-критерия определяют по формуле:

Степени свободы k1 и k2 зависят от числа параметров уравнения регрессии (m) и количества единиц исследуемой совокупности (n) и рассчитываются по формулам:

Надежность связи между признаками, т.е. надежность коэффициента детерминации R 2 проверяют при помощи таблицы по F-критерию для 5%-ного уровня значимости (см. табл. 7.10).

Для установления достоверности рассчитанного линейного коэффициента корреляции используют критерий Стьюдента, рассчитываемый по формуле

где μ_r – средняя ошибка коэффициента корреляции, рассчитываемая по формуле:

При достаточно большом числе наблюдений (n > 50) коэффициент корреляции можно считать достоверным, если он превышает свою ошибку в 3 и больше раз, а если он меньше 3, то связь между исследуемыми признаками у и х не доказана.

Пример расчета индекса корреляции (теоретического корреляционного отношения), коэффициента детерминации, линейного коэффициента корреляции и критериев Фишера и Стьюдента

По данным таблицы 8.2 необходимо оценить силу и направление связи между стоимостью основных производственных фондов предприятий и выпуском продукции, а также проверить надежность рассчитанного коэффициента детерминации и достоверность линейного коэффициента корреляции.

Для расчета индекса корреляции, используемого для оценки тесноты связи между результативным (выпуском продукции) и факторным (стоимостью ОПФ) признаками рассчитаем ряд вспомогательных показателей.

По формуле 8.9 по данным таблицы 7.15 факторная дисперсия равна: 1,238.

Общую дисперсию исчислим по данным таблицы 8.2, используя способ разности (формула 5.12): = 1,696 – 1,238 = 0,458.

Таким образом, по формулам 8.7 и 8.8 индекс корреляции равен: R = 0,854, что свидетельствует о тесной связи между выпуском продукции и стоимостью основных производственных фондов предприятий (см. табл. 5.10).

По формуле 8.12 коэффициент детерминации равен: 0,730. Это говорит о том, что в обследуемой совокупности предприятий 73,0% вариации выпуска продукции объясняется разным уровнем их оснащенности основными производственными фондами, т.е. вариация выпуска продукции на 73,0% обусловлена вариацией стоимости основных производственных фондов.

Для расчета линейного коэффициента корреляции, позволяющего оценить не только силу, но и направление связи между исследуемыми признаками, найдем ряд промежуточных показателей.

Преобразовав формулу 5.12 и используя данные таблицы 8.2, получим среднее квадратическое отклонение факторного признака: 2,638и среднее квадратическое отклонение результативного признака 1,302.

Таким образом, по формуле 8.13 (8.14) и данным таблицы 8.2 линейный коэффициент корреляции равен: 0,854, что подтверждает наличие тесной (сильной) прямой связи между стоимостью основных производственных фондов и выпуском продукции предприятий. Абсолютная величина линейного коэффициента корреляции практически совпадает с индексом корреляции (отклонение составляет 0,01).

Для оценки надежности связи между выпуском продукции и стоимостью основных производственных фондов предприятий найдем фактическое значение F-критерия.

Так как линейное уравнение имеет только два параметра, то по формуле 8.16 степень свободы k1 = 2 – 1 = 1, а потому, что обследованием было охвачено 10 предприятий по формуле 8.17 степень свободы k2 = 10 – 2 = 8.

По формуле 8.15 фактическое значение F-критерия равно: 19,68.

По данным таблицы 7.10 с вероятностью 0,95 критическое значение Fт = 5,32, что значительно меньше полученного фактического значения F-критерия. Это подтверждает надежность корреляционной связи между исследуемыми признаками.

Для установления достоверности рассчитанного линейного коэффициента корреляции найдем значение критерия Стьюдента. Для этого по формуле 8.19 исчислим среднюю ошибку коэффициента корреляции: 0,092.

По формуле 8.18 критерий Стьюдента равен: 9,27. Так как 9,27 > 3, то это дает основание считать, что рассчитанный линейный коэффициент корреляции достаточно точно характеризует тесноту связи между исследуемыми признаками.

Множественная регрессия

На практике на результативный признак, как правило, влияет не один, а несколько факторов.

Между факторами существуют сложные взаимосвязи, поэтому их влияние на результативный признак комплексное и его нельзя рассматривать как простую сумму изолированных влияний.

Многофакторный корреляционно-регрессионный анализ позволяет оценить степень влияния на исследуемый результативный показатель каждого из введенных в модель факторов при фиксированных на среднем уровне других факторах. При этом важным условием является отсутствие функциональной связи между факторами.

Математически задача корреляционно-регрессионного анализа сводится к поиску аналитического выражения, которое как можно лучше отражало бы связь факторных признаков с результативным признаком, т.е. к нахождению функции: y _x = f(x₁,x₂,x₃. x_n).

Множественная регрессия – это уравнение статистической связи результативного признака (зависимой переменной) с несколькими факторами (независимыми переменными).

Наиболее сложной проблемой является выбор формы связи, выражающейся аналитическим уравнением, на основе которого по существующим факторам определяются значения результативного признака – функции. Эта функция должна лучше других отражать реально существующие связи между исследуемым показателем и факторами. Эмпирическое обоснование типа функции при помощи графического анализа связей для многофакторных моделей практически непригодно.

Форму связи можно определить путем перебора функций разных типов, но это связано с большим количеством лишних расчетов. Принимая во внимание, что любую функцию нескольких переменных можно путем логарифмирования или замены переменных привести к линейному виду, уравнение множественной регрессии можно выразить в линейной форме:

Параметры уравнения находят методом наименьших квадратов.

Так, для расчета параметров уравнения линейной двухфакторной регрессии, представленного формулой:

где y _x – расчетные значения результативного признака-функции;
х₁ и х₂ – факторные признаки;
а₀, а₁ и а₂ — параметры уравнения, методом наименьших квадратов необходимо решить систему нормальных уравнений:

Каждый коэффициент уравнения (а₁, а₂, …, а_n) показывает степень влияния соответствующего фактора на результативный показатель при фиксированном положении остальных факторов, т.е., как изменится результативный показатель при изменении отдельного факторного показателя на единицу. Свободный член уравнения множественной регрессии экономического содержания не имеет.

Если, подставляя в уравнение регрессии значения х₁ и х₂, получаем соответствующие значения переменной средней, достаточно близко воссоздающие значения фактических уровней результативного признака, то выбор формы математического выражения корреляционной связи между тремя исследуемыми факторами сделан правильно.

Однако на основе коэффициентов регрессии нельзя судить, какой из факторных признаков больше влияет на результативный признак, поскольку коэффициенты регрессии между собой не сравнимы, ибо не сопоставимы по сути отражаемые ими явления, и они выражены разными единицами измерения.

С целью выявления сравнимой силы влияния отдельных факторов и резервов, заложенных в них, статистика рассчитывает частные коэффициенты эластичности, а также бета-коэффициенты.

Частные коэффициенты эластичности (ε_i) рассчитываются по формуле:

где а_i – коэффициент регрессии при i-ом факторе;

x _i – среднее значение i-го фактора;

y – среднее значение результативного фактора.

Бета-коэффициенты (β_i) рассчитываются по формуле:

где σ_xi – среднее квадратическое отклонение i-го фактора;
σ_y – среднее квадратическое отклонение результативного признака.

Частные коэффициенты эластичности показывают, на сколько процентов в среднем изменится результативный признак при изменении на 1% каждого фактора и при фиксированном положении других факторов.

Для определения факторов, имеющих наибольшие резервы улучшения исследуемого признака, с учетом степени вариации факторов, положенных в уравнение множественной регрессии, рассчитывают частные β-коэффициенты, показывающие на какую часть среднего квадратического отклонения изменяется результативный признак при изменении соответствующего факторного признака на величину его среднего квадратического отклонения.

Для характеристики тесноты связи при множественной линейной корреляции используют множественный коэффициент корреляции (R), рассчитываемый по формуле:

где r_yx1, r_yx2, r_x1x2 – парные коэффициенты линейной корреляции, позволяющие оценить влияние каждого фактора отдельно на результативный показатель, и определяемые по формулам:

Множественный коэффициент корреляции колеблется в пределах от 0 до + 1 и интерпретируется так же, как и теоретическое корреляционное отношение.

Совокупный коэффициент множественной детерминации показывает, какую часть общей корреляции составляют колебания под влиянием факторов х1, х2, …, хn, положенных в многофакторную модель для исследования.

На основе парных коэффициентов корреляции находятся частные коэффициенты корреляции первого порядка, показывающие связь каждого фактора с исследуемым показателем в условиях комплексного взаимодействия факторов, рассчитываемые по формулам

С целью более глубокого анализа взаимосвязи общественных явлений и их признаков увеличивают количество существенных факторов, включаемых в модель исследуемого показателя, и строят многофакторные уравнения регрессии. Их рассчитывают при помощи персональных компьютеров. Современнон программное обеспечение позволяет за относительно короткое время получить достаточно много вариантов уравнений. В ЭВМ вводятся значения зависимой переменной у и матрица независимых переменных х, принимается форма уравнения, например линейная. Ставится задача включить в уравнение k наиболее значимых х. В результате получим уравнение регрессии с k наиболее значимыми факторами. Аналогично можно выбрать наилучшую форму связи. Этот традиционный прием, называемый пошаговой регрессией, позволяет быстро и достаточно точно определиться с уравнением множественной регрессии.

Пример расчета параметров уравнения множественной регрессии, частных коэффициентов эластичности и бета-коэффициентов, множественного коэффициента корреляции и частных коэффициентов корреляции первого порядка

В таблице 8.4 представлены данные о производительности труда (выработке продукции на одного работающего), доле бракованной продукции в общем объеме ее производства и средней себестоимости 1 т продукции по двадцати пяти предприятиям, специализирующимся на выпуске кондитерских изделий (печенья в ассортименте).

Необходимо установить зависимость средней себестоимости 1 т продукции от двух факторов: выработки продукции на одного работающего и доли бракованной продукции в общем объеме ее производства. С целью выявления сравнимой силы влияния этих факторов, а также резервов повышения средней себестоимости 1 т продукции, заложенных в производительности труда и удельном весе брака, нужно рассчитать частные коэффициенты эластичности и бетакоэффициенты. Кроме того, следует оценить силу влияния обозначенных факторов, как по отдельности, так и вместе на заданный результативный признак, определить какую долю вариации средней себестоимости 1 т продукции обусловливают только выработка и только процент брака; охарактеризовать связь каждого фактора с исследуемым показателем в условиях комплексного взаимодействия факторов.

№ предприятия	Выработка продукции на одного работающего, т	Удельный вес брака, %	Средняя себестоимость 1 т продукции, руб.
n	х1	х2	у
1	2	3	4
1	14,6	4,2	2398
2	13,5	6,7	2546
3	21,6	5,5	2620
4	17,4	7,7	2514
5	44,8	1,2	1589
6	111,9	2,2	1011
7	20,1	8,4	2598
8	28,1	1,4	1864
9	22,3	4,2	2041
10	25,3	0,9	1986
11	56,0	1,3	1701
12	40,2	1,8	1736
13	40,6	3,3	1974
14	75,8	3,4	1721
15	27,6	1,1	2018
16	88,4	0,1	1300
17	16,6	4,1	2513
18	33,4	2,3	1952
19	17,0	9,3	2820
20	33,1	3,3	1964
21	30,1	3,5	1865
22	65,2	1,0	1752
23	22,6	5,2	2386
24	33,4	2,3	2043
25	19,7	2,7	2050

Данные, характеризующие работу предприятий одной отрасли хозяйственной деятельности кондитерских предприятий

Для расчета параметров уравнения линейной двухфакторной регрессии и теоретических значений результативного признака (средней себестоимости 1 т продукции) составим вспомогательную таблицу 8.5.

_x

n	х1	х2	у	у×х1	у×х2	х1 2	х2 2	y 2	х1×х2	y x
1	2	3	4	5	6	7	8	9	10	11
1	14,6	4,2	2398	35010,8	10071,6	213,16	17,6	5750404	61,32	2330
2	13,5	6,7	2546	34371,0	17058,2	182,25	44,9	6482116	90,45	2559
3	21,6	5,5	2620	56592,0	14410,0	466,56	30,3	6864400	118,80	2371
4	17,4	7,7	2514	43743,6	19357,8	302,76	59,3	6320196	133,98	2607
5	44,8	1,2	1589	71187,2	1906,8	2007,04	1,4	2524921	53,76	1756
6	111,9	2,2	1011	113130,9	2224,2	12521,61	4,8	1022121	246,18	1152
7	20,1	8,4	2598	52219,8	21823,2	404,01	70,6	6749604	168,84	2640
8	28,1	1,4	1864	52378,4	2609,6	789,61	2,0	3474496	39,34	1946
9	22,3	4,2	2041	45514,3	8572,2	497,29	17,6	4165681	93,66	2250
10	25,3	0,9	1986	50245,8	1787,4	640,09	0,8	3944196	22,77	1931
11	56,0	1,3	1701	95256,0	2211,3	3136,00	1,7	2893401	72,80	1649
12	40,2	1,8	1736	69787,2	3124,8	1616,04	3,2	3013696	72,36	1856
13	40,6	3,3	1974	80144,4	6514,2	1648,36	10,9	3896676	133,98	1983
14	75,8	3,4	1721	130451,8	5851,4	5745,64	11,6	2961841	257,72	1629
15	27,6	1,1	2018	55696,8	2219,8	761,76	1,2	4072324	30,36	1925
16	88,4	0,1	1300	114920,0	130,0	7814,56	0,0	1690000	8,84	1211
17	16,6	4,1	2513	41715,8	10303,3	275,56	16,8	6315169	68,06	2300
18	33,4	2,3	1952	65196,8	4489,6	1115,56	5,3	3810304	76,82	1970
19	17,0	9,3	2820	47940,0	26226,0	289,00	86,5	7952400	158,10	2751
20	33,1	3,3	1964	65008,4	6481,2	1095,61	10,9	3857296	109,23	2060
21	30,1	3,5	1865	56136,5	6527,5	906,01	12,3	3478225	105,35	2109
22	65,2	1,0	1752	114230,4	1752,0	4251,04	1,0	3069504	65,20	1528
23	22,6	5,2	2386	53923,6	12407,2	510,76	27,0	5692996	117,52	2335
24	33,4	2,3	2043	68236,2	4698,9	1115,56	5,3	4173849	76,82	1970
25	19,7	2,7	2050	40385,0	5535,0	388,09	7,3	4202500	53,19	2146
Всего	919,3	87,1	50962	1653422,7	198293,2	48693,93	450,3	108378316	2435,45	50962

Данные для расчета параметров уравнения линейной двухфакторной регрессии и теоретические значения результативного признака – функции y

В среднем на 1 предприятие х 36,8 3,5 2038 66136,9 7931,7 1947,76 18,01 4335133 97,42 2038

Подставим данные таблицы 8.5 в систему нормальных уравнений 8.22 и получим систему уравнений:

⌈ 50962 = 25 a₀ + 919,3 a₁ + 87,1 a₂ ;
〈 165322,7 = 919.3 a₀ + 48693.93 a₁ + 2435,45 a₂ ;
⌊ 198293,2 = 87,1 a₀ + 2435,45 a₁ + 450,3 a₂ .

Таким образом, уравнение связи, определяющее зависимость средней себестоимости 1 т продукции предприятий (результативного признака) от производительности труда их работников и удельного веса брака (двух факторных признаков), имеет вид (формула 8.21):

Подставляя в полученное уравнение значения х₁ и х₂, получаем соответствующие значения переменной средней (последняя графа таблицы 7.18), которые достаточно близко воссоздают значения фактических уровней себестоимости продукции. Это свидетельствует про правильный выбор формы математического выражения корреляционной связи между тремя исследуемыми факторами.

Значения параметров уравнения линейной двухфакторной регрессии показывают, что с увеличением выработки одного работника на 1 т, средняя себестоимость 1 т продукции снижается на 10,31 руб., а при увеличении процента брака на 1, средняя себестоимость 1 т продукции возрастает на 87,40 руб.

Вместе с тем полученные значения коэффициентов регрессии не позволяют сделать вывод о том, какой из двух факторных признаков оказывает большее влияние на результативный признак, поскольку между собой эти факторные признаки несравнимы.

По формуле 8.23 на основании данных таблицы 8.5 и полученных значений коэффициентов регрессии рассчитаем частные коэффициенты эластичности:

Анализ частных коэффициентов эластичности показывает, что в абсолютном выражении наибольшее влияние на среднюю себестоимость 1 т продукции оказывает выработка работников предприятий – фактор х1, с увеличением которой на 1% средняя себестоимость 1 т продукции снижается на 0,19%. При увеличении удельного веса бракованной продукции на 1% средняя себестоимость 1 т продукции повышается на 0,15%.

Для расчета β–коэффициентов необходимо рассчитать соответствующие средние квадратические отклонения.

Преобразовав формулу 5.12 и используя данные таблицы 8.5, получим средние квадратические отклонения факторных признаков, а также среднее квадратическое отклонение результативного признака:

Тогда по формуле 8.24 значения β–коэффициентов равны:

Анализ β-коэффициентов показывает, что на среднюю себестоимость продукции наибольшее влияние (а значит и наибольшие резервы ее снижения) из двух исследуемых факторов с учетом их вариации имеет фактор х1 – выработка работников, ибо ему соответствует большее по модулю значение β-коэффициента.

Для характеристики тесноты связи между себестоимостью 1 т продукции, выработкой работников и удельным весом бракованной продукции используется множественный коэффициент корреляции, для расчета которого предварительно нужно получить парные коэффициенты корреляции.

По формулам 8.26-8.28 на основе данных таблицы 8.5 и значений средних квадратических отклонений факторных и результативного признаков парные коэффициенты корреляции соответственно равны:

Высокие значения парных коэффициентов корреляции свидетельствуют о сильном влиянии (отдельно) выработки работников и уровня брака на среднюю себестоимость 1 т продукции.

Отметим, что отрицательное значение парного коэффициента корреляции между факторными признаками свидетельствует об обратной зависимости между выработкой и количеством бракованной продукции. Тот факт, что парный коэффициент корреляции между выработкой работников и уровнем бракованной продукции равный -0,519, по модулю меньше 0,85 (см. рис. 8.1), говорит о правильном включении этих факторов в одну корреляционную модель.

По формуле 8.25 множественный коэффициент корреляции равен: R_yx1x2 = 0,822. Он показывает, что между двумя факторными и результативным признаками существует тесная связь.

Совокупный коэффициент множественной детерминации (0,676) свидетельствует про то, что вариация средней себестоимости 1 т продукции на 67,6% обусловлена двумя факторами, введенными в корреляционную модель: изменением выработки работников и уровня брака. Это означает, что выбранные факторы существенно влияют на исследуемый показатель.

На основе парных коэффициентов корреляции по формулам 8.29 и 8.30 рассчитаем частные коэффициенты корреляции первого порядка, отражающие связь каждого фактора с исследуемым показателем (средней себестоимостью 1 т продукции) в условиях комплексного взаимодействия факторов: