Как найти их скорости в момент встреч

Задачи на движение навстречу друг другу (встречное движение) — один из трех основных видов задач на движение.

Если два объекта движутся навстречу друг другу, то они сближаются:

Чтобы найти скорость сближения двух объектов, движущихся навстречу друг другу, надо сложить их скорости:  

   

Скорость сближения больше, чем скорость каждого из них.

Скорость, время и расстояние связаны между собой формулой пути:

   

Рассмотрим некоторые задачи на встречное движение.

Задача 1

Два велосипедиста выехали навстречу друг другу. Скорость одного из низ 12 км/ч, а другого — 10 км/ч. Через 3 часа они встретились. Какое расстояние было между ними в начале пути?

Решение:

Условие задач на движение удобно оформлять в виде таблицы:

	v, км/ч	t, ч	s, км
I велосипедист	12	3	?
II велосипедист	10	3	?

1) 12+10=22 (км/ч) скорость сближения велосипедистов

2) 22∙3=66 (км) было между велосипедистами в начале пути.

Ответ: 66 км.

Задача 2

Два поезда идут навстречу друг другу. Скорость одного из них 50 км/ч, скорость другого —  60 км/ч. Сейчас между ними 440 км. Через сколько часов они встретятся?

Решение:

	v, км/ч	t, ч	s, км
I поезд	60	?	?
II поезд	50	?	?

1) 60+50=110 (км/ч) скорость сближения поездов

2) 440:110=4 (ч) время, через которое поезда встретятся.

Ответ: через 4 ч.

Задача 3.

Два пешехода находились на расстоянии 20 км друг от друга. Они вышли одновременно навстречу друг другу и встретились через 2 часа. Скорость одного пешехода 6 км/ч. Найти скорость другого пешехода.

	v, км/ч	t, ч	s, км
I пешеход	6	2	?
II пешеход	?	2	?

1) 20:2=10 (км/ч) скорость сближения пешеходов

2) 10-6=4 (км/ч) скорость другого пешехода.

Ответ: 4 км/ч.

Теперь, когда мы с вами научились описывать движение тел, применим паши знания для решения практических задач. Начнем с одной из самых важных и распространенных в природе и технике задач – задачи о встрече тел. Наверняка вы неоднократно слышали о стыковках космических аппаратов, видели, как встречные поезда одновременно подъезжают к промежуточной станции, выпущенная из лука стрела попадает в цель и т. п. Все эти ситуации можно представить как движение двух точечных тел навстречу друг другу. Задача заключается в том, чтобы определить, где произойдет их встреча и когда, т. е. через какое время после начала движения тел, она состоится.

Считается, что два тела встретились, если в некоторый момент времени их положения в пространстве совпали. Иначе говоря, в этот момент времени их координаты в какой-либо системе отсчета сравнялись. Поэтому для решения задачи нам понадобится ввести систему отсчета, в которой необходимо будет описать движение этих тел (в графическом или аналитическом виде). Только таким образом мы сможем грамотно решить данную задачу.

Рассмотрим простой пример. Пусть по прямолинейной дороге навстречу друг другу одновременно начинают двигаться пешеход и велосипедист. Расстояние между ними в момент начала движения составляет l = 20 м. При этом они движутся равномерно относительно дороги навстречу друг другу со скоростями, модули которых |v_п| = 1 м/с и |v_в| = 3 м/с соответственно. (Мы поставили знаки модуля у скоростей движущихся тел. Это связано с тем, что, пока не выбрана система отсчета. мы не можем сказать, у кого из них значение скорости будет положительным, а у кого – отрицательным. Другими словами, мы не можем определить, будут увеличиваться или уменьшаться их координаты в процессе движения.)

Ответим на два вопроса. Где произойдет встреча пешехода и велосипедиста? Когда (через какое время после начала движения) она состоится?

Рассмотрим каждый шаг решения задачи.

Шаг 1. Введем систему отсчета (рис. 20). В качестве тела отсчета выберем землю, а началом отсчета – место, где растет дерево, от которого начинает свое движение пешеход. Координатную ось направим вдоль дороги в направлении движения пешехода. В качестве единицы длины выберем 1 м. Будем считать пешехода и велосипедиста точечными телами. Координата каждого из тел будет численно равна расстоянию от дерева до этого тела в заданный момент времени. Часы (секундомер) включим в тот момент, когда начинается движение.

Шаг 2. Определим значение координа пешехода и велосипедиста в момент включения секундомера. Ясно, что начальная координата пешехода xп0 (читается «икс пэ нулевое») равна 0, а велосипедиста xв0 = 20 м.

Шаг 3. Найдем значения скоростей равномерного движения тел. Из рисунка видно, что в выбранной нами системе отсчета координата пешехода в процессе движения будет увеличиваться. Следовательно, значение скорости пешехода положительно: v_п = 1 м/с. Напротив, велосипедист в выбранной системе отсчета движется так, что его координата со временем уменьшается. Поэтому значение его скорости отрицательно: vв = -3 м/с.

После того как определены начальные координаты и значения скоростей движения тел, можно переходить к описанию их движения. Для этого у нас есть несколько способов. Начнем с графического.

Шаг 4 (графический). Построим систему координат, состоящую из оси времени t и оси координаты X. Отметим начальные координаты пешехода и велосипедиста (рис. 21).

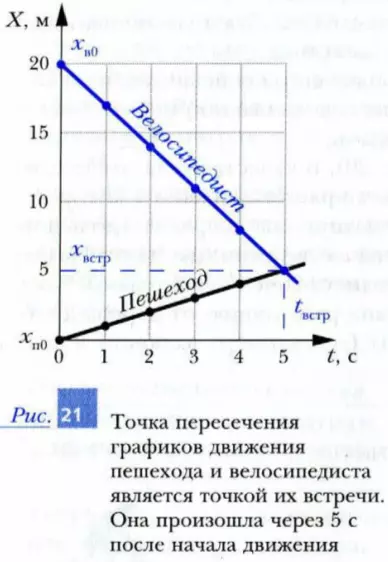
Шаг 5 (графический). Теперь от точки xп0 проведем прямую линию, описывающую зависимость координаты пешехода от времени. Поскольку по условию задачи координата пешехода за каждую секунду увеличиваются на 1 м, то это будет «поднимающаяся» прямая линия, проходящая через точки с координатами (1; 1), (2; 2), (3; 3), (4;4), (5; 5) и т.д.

График зависимости от времени координаты велосипедиста – это тоже прямая, но она исходит из точки x_в0 = 20 м, расположенной на оси координаты. Координата велосипедиста со временем уменьшается на 3 м за каждую секунду. Поэтому линия, описывающая зависимость этой координаты от времени, «опускается» за каждую секунду на 3 м, т. е. эта линия проходит через точки с координатами (0; 20), (1; 17), (2; 14), (3; 11), (4; 8), (5; 5) и т. д.

Из рис. 21 следует, что прямые, описывающие зависимости координат пешехода и велосипедиста от времени, пересекаются в точке (t_встр = 5 с, x_встр = 5 м). Это означает, что через 5 секунд после начала движения координаты пешехода и велосипедиста становятся равными: x_п = x_в = x_встр = 5 м. Иначе говоря, в этот момент времени положения тел в пространстве совпадут, и, таким образом, в момент t_встр = 5 с в точке с координатой x_встр = 5 м произойдет встречи пешехода и велосипедиста.

Итоги

Встречей двух тел считают совпадение их положений в пространстве (равенство их координат в одной и той же системе отсчета) в некоторый момент времени.

При графическом способе решения задачи о встрече движущихся тел необходимо: ввести систему отсчета; определить начальные координаты и значения скоростей тел; построить графики движения тел; найти точку пересечения этих графиков.

Вопросы

1. Приведите примеры встречи двух тел. Что означает в кинематике, что два тела встретились?
2. Перечислите шаги решения задачи «встреча».

Упражнения

1. Определите графическим способом время и место встречи двух равномерно движущихся навстречу друг другу школьников, если в момент включения часов: а) расстояние между ними l = 30 м, а модули их скоростей |v₁| = 3 м/с, |v₂| = 3 м/с; б) расстояние между ними l = 30 м, |v₁| = 1 м/с, |v₂| = 4 м/с.
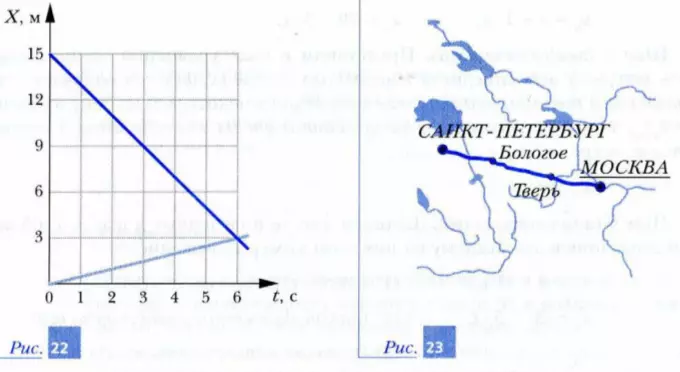
2. Сформулируйте условие задачи, решение которой дано на рис. 22.
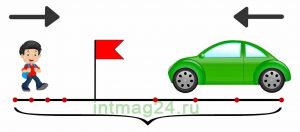
3. Определите место встречи (город) двух равномерно движущихся поездов, которые одновременно выезжают навстречу друг другу из Москвы (|v₁| = 100 км/ч) и Санкт-Петербурга (|v₂| = 50 км/ч) (рис. 23). Расстояние между Москвой и Санкт-Петербургом – 600 км.

Задачи на движение

Задачи на движение (скорость, время и расстояние) являются одной из основных типов задач по математике, которые должен уметь решать каждый школьник. В данной статье рассмотрены все типы задач на движение:
— простые задачи на скорость, время и расстояние;
— задачи на встречное и противоположное движение;
— задачи на движение в одном направлении (на сближение и удаление);
— решение задач на движение по реке.

Скорость, время и расстояние: определения, обозначения, формулы

скорость = расстояние: время — формула нахождения скорости;

время = расстояние: скорость — формула нахождения времени;

расстояние = скорость · время — формула нахождения расстояния.

Скорость – это расстояние, пройденное за единицу времени: за 1 секунду, за 1 минуту, за 1 час и так далее.
Пример обозначения: 7 км/ч (читается: семь километров в час).
Если весь путь проходится с одинаковой скоростью, то такое движение называется равномерным.

На сайте представлены калькуляторы онлайн, с помощью которых можно перевести скорость, время и расстояние в другие единицы измерения:

Примеры простых задач.

Задача 1.

Автомобиль проехал 180 км за 2 часа. Чему равна скорость автомобиля?
Решение: 180:2=90 (км/ч.)
Ответ: Скорость автомобиля равна 90 км/ч.

Задача 2.

Автобус проехал путь в 240 км со скоростью 80 км/ч. Сколько времени ехал автобус?
Решение: 240:80=3 (ч.)
Ответ: Автобус проехал 3 часа.

Задача 3.

Грузовик ехал 5 часов со скоростью 70 км/ч. Какое расстояние проехал грузовик за это время?
Решение: 70 · 3 = 350 (км)
Ответ: Грузовик за 5 часов проехал 350 км.

Задачи на встречное движение

В таких задачах два объекта движутся навстречу друг другу.
Задачи на встречное движение можно решать двумя способами:
1. Найти значения скорости, времени и расстояния для каждого объекта.
2. Найти скорость сближения объектов (как сумму их скоростей), общие время и расстояние. Скорость сближения — это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.

Задача 4.

Из двух пунктов навстречу друг другу одновременно выехали два поезда и встретились через 3 часа. Первый поезд ехал со скоростью 80 км/ч, а второй – со скоростью 70 км/ч. На каком расстоянии друг от друга находятся пункты?
Решение:
Первый способ. Найти расстояние, которое проехал каждый автобус, и сложить полученные данные:
80*3=240 (км) – проехал 1й автобус, 70*3=210 (км) – проехал 2й поезд,
240+210=450 (км) – проехали два поезда.
Второй способ. Найти скорость сближения поездов, то есть на сколько сокращалось расстояние между ними каждый час; а затем найти расстояние:
80+70=150 (км/ч), 150*3=450 (км).
Ответ: города находятся на расстоянии 450 км.

Задача 5.

Из двух городов навстречу друг другу одновременно выехали два автобуса. Первый автобус ехал со скоростью 80 км/ч, а второй – со скоростью 70 км/ч. Какое расстояние будет между ними через 2 часа, если расстояние между городами 450 км?
Решение:
Первый способ. Определить, сколько километров проехал каждый автобус и найти расстояние, которое осталось проехать:
80*2=160 (км)-проехал 1й автобус, 70*2=140 (км)-проехал 2й автобус,
160+140=300 (км)-проехали два автобуса, 450-300=150 (км)-осталось проехать.
Второй способ. Найти скорость сближения автобусов и умножить ее на время в пути.
80*70=150 (км/ч) – скорость сближения; 150*2=300 (км) – проехали два автобуса; 450-300=150 (км) – осталось проехать.
Ответ: Через 2часа расстояние между автобусами будет 150 км.

Задачи на движение в противоположных направлениях

В таких задачах два объекта движутся в противоположных направлениях, отдаляясь друг от друга. В таком типе задачи используется скорость удаления. Задачи на движение в противоположных направлениях также можно решить двумя способами:
1. Найти значения скорости, времени и расстояния для каждого объекта.
2. Найти скорость удаления объектов (как сумму их скоростей), общие время и расстояние. Скорость удаления — это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.

Задача 6.

Два автомобиля выехали одновременно из одного и того же пункта в противоположных направлениях. Скорость первого автомобиля 100 км/ч, скорость второго – 70 км/ч. Какое расстояние будет между автомобилями через 4 часа?
Решение:
Первый способ. Определить расстояние, которое проехал каждый автомобиль и найти сумму полученных результатов:
1) 100 · 4 = 400 (км) – проехал первый автомобиль
2) 70 · 4 = 280 (км) – проехал второй автомобиль
400 + 280 = 680 (км)
Второй способ. Найти скорость удаления, то есть значение увеличения расстояния между автомобилями за каждый час, а затем скорость удаления умножить на время в пути.
100 + 70= 170 км/ч – это скорость удаления автомобилей.
170 · 4 = 680 (км)
Ответ: Через 4 часа между автомобилями будет 680 км.

Задача 7.

Из двух населённых пунктов, расстояние между которыми 40 км, вышли в противоположных направлениях два туриста. Первый турист шёл со скоростью 4 км/ч, а второй — 5 км/ч. Какое расстояние между туристами будет через 5 часов?
Решение:
Первый способ. Определить сколько километров прошёл каждый из туристов за 5 часов, сложить полученные результаты, а затем к полученному расстоянию прибавить расстояние между населенными пунктами.
1) 4 · 5 = 20 (км) – прошёл первый турист;
2) 5 · 5 = 25 (км) – прошёл второй турист;
3) 20 + 25 = 45 (км);
4) 45 + 40 = 85 (км).
Второй способ. Найти скорость удаления пешеходов, затем найти пройденное расстояние, к полученному результату прибавить расстоянием между населёнными пунктами.
4 + 5 = 9 (км/ч);
9 · 5 = 45 (км);
45 + 40 = 85 (км);
Ответ: Через 5 часов расстояние между пешеходами будет 85 км.

Задачи на движение в одном направлении

В таких задачах два объекта движутся в одном направлении с разной скоростью, при этом они сближаются друг с другом или отдаляются друг от друга. Соответственно находится скорость сближения или скорость удаления объектов.

Формула нахождения скорости сближения или удаления двух объектов, которые движутся в одном направлении: из большей скорости вычесть меньшую.

Задача 8.

Из города выехал автомобиль со скоростью 40 км/ч. Через 4 часа вслед за ним выехал второй автомобиль со скоростью 60 км/ч. Через сколько часов второй автомобиль догонит первый?,
Решение:
Задачу можно решить с помощью уравнения.
В этом случае скорость первого автомобиля 40 км/час, время в пути на 4 часа больше, чем время второго автомобиля (или t+4). Скорость второго автомобиля 60 км/час, время в пути – t. Расстояние оба автомобиля проехали одинаковое. Поэтому можно составить уравнение: 40*(t+4)=60*t. Отсюда получаем t=8 (часов) – время в пути второго автомобиля, за которое он догонит первый.
Решение задачи без использования уравнения.
Так как на момент выезда второго автомобиля из города первый уже был в пути 4 часа, то за это время он успел удалиться от города на: 40 · 4 = 160 (км).
Второй автомобиль движется быстрее первого, значит, каждый час расстояние между автомобилями будет сокращаться на разность их скоростей: 60 — 40 = 20 (км/ч) – это скорость сближения.
Разделив расстояние между автомобилями на скорость их сближения, можно узнать, через сколько часов они встретятся: 160 : 20 = 8 (ч)
Ответ: Второй автомобиль догонит первый через 8 часов.

Задача 9.

Из двух посёлков между которыми 5 км, одновременно в одном направлении вышли два пешехода. Скорость пешехода, идущего впереди, 4 км/ч, а скорость пешехода, идущего позади 5 км/ч. Через сколько часов после выхода второй пешеход догонит первого?
Решение: Так как второй пешеход движется быстрее первого, то каждый час расстояние между ними будет сокращаться. Значит можно определить скорость сближения пешеходов: 5 — 4 = 1 (км/ч).
Оба пешехода вышли одновременно, значит расстояние между ними равно расстоянию между посёлками (5 км). Разделив расстояние между пешеходами на скорость их сближения, узнаем через сколько второй пешеход догонит первого: 5 : 1 = 5 (ч)
Ответ: Через 5 часов второй пешеход догонит первого.

Задача 10.

Два автомобиля выехали одновременно из одного и того же пункта в одном направлении. Скорость первого автомобиля 80 км/ч, а скорость второго – 40 км/ч.
1) Чему равна скорость удаления между автомобилями?
2) Какое расстояние будет между автомобилями через 3 часа?
3) Через сколько часов расстояние между ними будет 200 км?
Решение:
1) 80 — 40 = 40 (км/ч) — скорость удаления автомобилей друг от друга.
2) 40 · 3 = 120 (км) – расстояние между ними через 3 часа./
3) 200 : 40 = 5 (ч) – время, через которое расстояние между автомобилями станет 200 км.
Ответ:
1) Скорость удаления между автомобилями равна 40 км/ч.
2) Через 3 часа между автомобилями будет 120 км.
3) Через 5 часов между автомобилями будет расстояние в 200 км.

Задачи на движение по реке

Рассмотрим задачи, в которых речь идёт о движении объекта по реке. Скорость любого объекта в стоячей воде называют собственной скоростью этого объекта.

Чтобы узнать скорость объекта, который движется по течению реки, надо к собственной скорости объекта прибавить скорость течения реки. Чтобы узнать скорость объекта, который движется против течения реки, надо из собственной скорости объекта вычесть скорость течения реки.

Задача 11.

Лодка движется по реке. За сколько часов она преодолеет расстояние 120 км, если ее собственная скорость 27 км/ч, а скорость течения реки 3 км/ч?
Решение:
1) лодка движется по течению реки.
27 + 3 = 30 (км/ч) – скорость лодки по течению реки.
120 : 30 = 4 (ч) – проплывет путь.
2) лодка движется против течения реки.
27 — 3 = 24 (км/ч) — скорость лодки против течения реки
120 : 24 = 5 (ч) – проплывет путь.
Ответ:
1) При движении по течению реки лодка потратит 4 часа на путь.
2) При движении против течения реки лодка потратит 5 часов на путь.

Итак, для решения задач на движение:

Заключение.

Решая много задач по данной теме, ученик обязательно научится быстро ориентироваться в понятиях «скорость», «время» и «расстояние» и быстро решать задачи всех типов. Получить карточки с задачами разных видов можно по ссылке.

Источник

Движение навстречу друг другу

Задачи на движение навстречу друг другу (встречное движение) — один из трех основных видов задач на движение.

Если два объекта движутся навстречу друг другу, то они сближаются:

Чтобы найти скорость сближения двух объектов, движущихся навстречу друг другу, надо сложить их скорости:

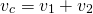
Скорость сближения больше, чем скорость каждого из них.

Скорость, время и расстояние связаны между собой формулой пути:

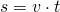
Рассмотрим некоторые задачи на встречное движение.

Два велосипедиста выехали навстречу друг другу. Скорость одного из низ 12 км/ч, а другого — 10 км/ч. Через 3 часа они встретились. Какое расстояние было между ними в начале пути?

Условие задач на движение удобно оформлять в виде таблицы:

1) 12+10=22 (км/ч) скорость сближения велосипедистов

2) 22∙3=66 (км) было между велосипедистами в начале пути.

Два поезда идут навстречу друг другу. Скорость одного из них 50 км/ч, скорость другого — 60 км/ч. Сейчас между ними 440 км. Через сколько часов они встретятся?

1) 60+50=110 (км/ч) скорость сближения поездов

2) 440:110=4 (ч) время, через которое поезда встретятся.

Два пешехода находились на расстоянии 20 км друг от друга. Они вышли одновременно навстречу друг другу и встретились через 2 часа. Скорость одного пешехода 6 км/ч. Найти скорость другого пешехода.

1) 20:2=10 (км/ч) скорость сближения пешеходов

2) 10-6=4 (км/ч) скорость другого пешехода.

Саетлана Михайловна, будьте добры, помогите с решением, пожалуйста. Два велосипедиста одновременно выехали навстречу друг другу из пункта А в пункт В, скорость первого 12 км/ч, второго 15 вм/ч, расстояние между пунктами равно 71 км, через какое время после (!) встречи, расстояние между велосипедистами будет 8 км?

1)12+15=27 (км/ч) скорость сближения велосипедистов
Когда велосипедисты встретятся, вместе они преодолеют все расстояние от пункта А до пункта В, что равно 71 км. Когда расстояние после их встречи станет равным 8 км, они проедут ещё дополнительно 8 км.
2)71+8=79 (км) расстояние, которое проехали 2 велосипедиста вместе с момента старта
3) 79:27=79/27=2 25/27 (часа) время, через которое расстояние между велосипедистами станет равным 8 км.

Насколько я поняла, требуется, чтобы все три объекта встретились в одной точке одновременно.
Примем расстояние между объектами 2 и 3 за s. Так как скорость объекта 3 в 3 раза больше скорости объекта 2, то за время до встречи объект пройдёт (3/4)s, а объект 2 — (1/4)s.
Так как в начальный момент движения расстояние от объекта 1 до объекта 3 в два раза меньше, чем до объекта 2, то расстояние от объекта 1 до объекта 3 составляет (1/3)s, а до объекта 2 — (2/3)s. Следовательно, объекту 1 следует двигаться в сторону объекта 2, чтобы попасть в точку в точку встречи.
Расстояние, которое нужно пройти объекту 1, можно найти как разность расстояний между объектами 1 и 2 в начальный момент времени и в момент встречи: (2/3)s — (1/4)s=(5/12)s.
Время в пути до встречи каждого из трёх объектов одинаково. Чтобы найти время, надо расстояние разделить на скорость. Время в пути объекта 2 равно ((1/4)s)/2, время в пути объекта 1 — ((5/12)s)/x, где x – скорость объекта 1. Из уравнения ((1/4)s)/2=((5/12)s)/x находим x=(10/3) км/ч.

Расстояние между поселком и городом 80 км. Из поселка в город выехал велосипедист со скоростью 15 км/ч. Одновременно из города в поселок выехал второй велосипедист со скоростью 12 км/ч. Какое расстояние будет между ними через 2 часа?

1) 15+12=27(км/ч) скорость сближения велосипедистов
2) 27∙2=54 (км) проехали велосипедисты вместе за 2 часа
3) 80-54=26 (км) такое расстояние будет между велосипедистами через 2 часа.

Пожалуйста помогите с задачей:расстояние между двумя пристанями равно 330 км. От этих пристаней одновременно навстречу друг другу отправились два катера. Скорость одного из них равна 24 км / ч что составляет 6 седьмых скорости второго. Какой будет расстояние между катерами через 4,5 часа после начала движения?

1) 26:(6/7)=24∙(7/6)=28 (км/ч) скорость первого катера
2) 28+24=52 (км/ч) скорость сближения катеров
3) 52∙4,5=234 (км) расстояние, которое прошли два катера навстречу друг другу за 4,5 часа
4) 330-234=96 (км) расстояние между катерами через 4,5 часа после начала движения.

Уважаемая Светлана! Прошу Вас пояснить, почему в задаче на сближение (прислала Карина 5 декабря 2018 г.)Вы, приняв расстояние между объектами 2 и 3 за единицу определили пути объектов как 14S и 34S пропорционально из скоростям (почему четверти. А расстояние между объектами 1, 2 и 3 Вы определяете как 1/3S и 2/3S (почему трети)и почему расстояние между объектами 1, 2 и 3 тоже приняли за S.
Большое спасибо. Жду с нетерпением Ваш комментарий!

С ДВУХ ПЕЩЕР,ЧТО НАХОДЯТСЯ НА РАССТОЯНИИ 12КМ, В ОДНОМ НАПРАВЛЕНИИ ВЫБЕЖАЛИ ДВА ТИГРА.СКОРОСТЬ ОДНОГО 12КМ/ЧАС, А ВТОРОГО — 22КМ/ЧАС. Через сколько времени первый тигр догонит второго?

1) 22-12=10(км/ч) скорость сближения тигров
2)12:10=1,2(ч) время, через которое второй тигр догонит первого.

Не указано в задаче, что тигры бегут навстречу друг другу. А если они бегут параллельно? Ведь это тоже в одном направлении!
Вы пересказали задачу или она так в учебнике сформулирована?

Я разобралась — бегут параллельно, но сближаются!

Татьяна, большие буквы в интернете означают крик.

Зачем же удалять мой вопрос к решению задачи? Модератор не понял логику. Прошу вернуть мой вопрос. Спасибо.

Наталья, Ваш вопрос не удаляла. Но для ответа просто не хватает времени.

как Это? навстречу друг другу параллельно?

Движение навстречу друг другу не на одной прямой, а по параллельным прямым.

Два поезда, расстояние между которыми 420 км, идут на встречу друг другу, один со скоростью 65 км/ч, другой — 75 км/ч. Какое расстояние будет между ними через 2 ч?

1)65+75=140 (км/ч) скорость сближения поездов
2)140∙2=280(км) столько прошли два поезда навстречу друг другу за 2 часа
3) 420-280=140(км) будет между поездами через 2 часа.

Примем весь путь за 1. Тогда второй пешеход в минуту проходит 1:45=1/45 пути, а вместе — 1:18=1/18 пути. Следовательно первый пешеход в минуту проходит 1/18-1/45=3/90=1/30 пути. 1:(1/30)=30 минут — время, за которое пройдёт расстояние между пунктами первый пешеход.

Большое спасибо за помощь! Я голову ломал целый день (((

Алексей, каждый раз, обдумывая задачу, мы шаг за шагом продвигаемся вперёд. И следующая задача может быть решена быстрее :).

Может Вы сможете помочь с уровнением.
4 1/2*16/45*(х:1 1/3)=1 1/2:4
просмотрел ни одно видео похожего уровнения не нашел. Ломаю голову второй день,удалёнка это кашмар для родителей.

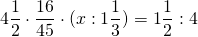
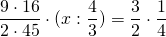
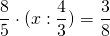
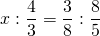
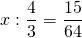
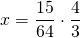
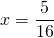
Успехов Вам, Алексей!

Светлана Михайловна, здравствуйте, помогите с задачей. Из двух пунктов на встречу друг другу, выехали два велосипедиста. Первый отправился со скоростью 15 км/ч. Через 4 часа выехал второй, со скоростью 17 км/ч. Через 7 часов они встретились. Определите расстояние между пунктами.

1) 15∙4=60(км) проехал первый велосипедист за 4 часа
2) 15+17=32(км/ч) скорость сближения велосипедистов
3) 32∙7=224 (км) проехали велосипедисты вместе до встречи
4) 60+224=284 (км) расстояние между пунктами

Светлана Михайловна, добрый день! Уже какой день голову ломаем. Нужно решить в двух действиях. Помогите, пожалуйста! Расстояние между городами 18 км. Из двух городов одновременно вышли два пешехода в одном направлении. Скорость первого 12 км/ч. Какая Скорость второго, если первый догнал его через 3 часа

Это задача на движение вдогонку.
1) 18:3=6(км/ч) скорость сближения пешеходов
2) 12-6=6(км/ч) скорость 2-го пешехода

Светлана МИхайловна, спасибо огромное!

Два велосипедиста из пунктов A и B отправились на встречу друг к другу. Скорость первого велосипедиста составляет 6 км/ч, что на 1,2 км/ч меньше скорости второго. Найдите расстояние между пунктами, если они встретились через 5 часов.помогите пожалуйста

6+1,2=7,2 (км/ч) скорость 2-го велосипедиста
6+7,2=13,2 (км/ч) скорость сближения
13,2∙5=66 (км) расстояние между пунктами.

Светлана Михайловна,пож-та,помогите решить задачу:
Расстояние между сёлами 90км.Навстречу друг другу выехали велосипедист и пешеход.Через 3 часа встретились.Если бы велосипедист выехал на 1ч15мин раньше пешехода, они встретились бы через 2ч.Какова скорость движения велосипедиста и пешехода?

Так как за 3 часа, двигаясь навстречу друг другу, велосипедист и пешеход преодолели 90 км, то их скорость сближения равна 90:3=30 км/ч. Пусть скорость пешехода равна x км/ч, тогда скорость велосипедиста — (30-x) км/ч. Известно, что если бы велосипедист выехал на 1ч15мин раньше пешехода, они встретились бы через 2ч. В этом случае время в пути велосипедиста рано 3 ч15 мин=3 ¼ ч= 13/4 ч, а пешехода — 2ч.
За это время велосипедист проехал 13/4 ∙ (30-x) км, пешеход — 2∙x км, а вместе — 90 км.
13/4 ∙ (30-x)+ 2x =90
x=6

Скорость пешехода 6 км/ч, велосипедиста — 30-6=24 км/ч.

Здравствуйте помогите пожалуйста. Расстояние между точками А и Б 180км. Это расстояние легковой автомобиль проезжает за 2часа (90км/час), а грузовой автомобиль за 3 часа (60 км/час). Из точки А в точку Б выехало грузовое авто, в это же время из точки Б в точку А выехал легковой автомобиль. Найдите расстояние до точки А когда эти два авто встретятся

90+60=150(км/ч) скорость сближения автомобилей
180:150=1,2(ч) через такое время автомобили встретятся
60∙1,2=72(км) расстояние, которое прошел до места встречи грузовой автомобиль, а значит, это расстояние от А до места встречи.

Два поезда одновременно выходят навстречу друг другу из пунктов А и В, расстояние между которыми равно 300 км. Поезд, вышедший из пункта А, может пройти это расстояние за 5 ч, другой — за 7,5 ч. Сколько времени пройдет до встречи поездов?

300:5=60(км/ч) скорость 1-го поезда
300:7,5=40(км/ч) скорость 2-го поезда
60+40=100(км/ч) скорость сближения
300:100=3(ч) — время, через которое поезда встретятся.

Помогите решить задачу.
2 велосипедиста выехали одновременно навстречу друг другу и через 3 ч встретились. Найди скорость каждого, если известно,что скорость первого на 4 км/ч больше скорсти второго,а вместе они проехали 108 км.

Из двух городов навстречу друг другу одновременно вышли два автомобиля. Скорость одного автомобиля 60,5 км/ч второго на 4 км/ч больше. Какое расстояние будет между автомобилями через 4 часа, если расстояние между городами 400 км?

60,5+4=64,5 км/ч скорость 2-го автомобиля
64,5+60,5=125 км/ч скорость сближения автомобилей
125∙4=500 км проехали автомобили за 4 часа.
500-400=100 км — такое расстояние между автомобилями через 4 часа после начала движения.

Здравствуйте! Помогите уже целый день не можем решить. Расстояние между точками А и В 280км. Две машины одновременно из этих точек вышли друг к другу и встретились через 2 часа. А пришла к пункту В на 1ч.10м. позже чем В на пункт А. Какова их скорость?

Пусть скорость одной машины x км/ч, другой — y км/ч. Так как за 2 часа они проехали вместе 280 км, то 2x+2y=280.
1й автомобиль на весь путь затратил на 1 час 10 мин= 1 1/6 ч=7/6 ч больше, чем другой, то 280/x-280/y=7/6. Остается решить систему уравнений.
x=60,y=80.

Светлана Михайловна помогите пожалуйста с решением задачи.
Два велосипедиста выехали одновременно из А и В навстречу друг другу.Скорость первого V1,а второго V2. При встрече оказалось,что второй проехал на а км больше первого. Найти длину пути.

Пусть 1-й велосипедист проехал до встречи x км, тогда 2-й — (x+a)км. Время в пути 1-го велосипедиста равно

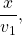
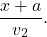
Так как они затратили на путь одинаковое время, то

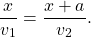
Отсюда xv2=xv1+av1, x(v2-v1)=av1,

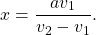
Весь путь равен x+(x+a)=2x+a=

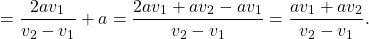
Здравствуйте.Помогите пожалуйста решить задачу.Расстояние между точками А и Б пешеход, вышедший из точки А проходит за 2 часа 24 минут, а пешеход, вышедший из точки Б, проходит за 3 часа. Если они начнут движение одновременно, через сколько минут они встретятся?

Примем весь путь за 1. Один пешеход проходит этот путь за 2 часа 24 минуты=144 минуты. Значит, за 1 минуту он проходит 1/144 часть пути. Второй пешеход проходит путь за 3 часа = 180 минут. За 1 минуту он преодолевает 1/180 пути. Поскольку пешеходы движутся навстречу друг другу, скорость их сближения равна

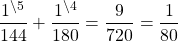
пути в минуту. Значит, до встречи они пройдут

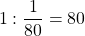
Одновременно на встречу друг к другу отправились из города Душанбе — автомобилист со скоростью 20 м/с, и из города Худжанд — велосипедист со скоростью 20 км/ч. Расстояние между городами 346 км. Какое расстояние будет между автомобилем и велосипедом через 2 часа?

1)20 м/с=20∙3,6=72 км/ч — скорость автомобиля
2)72+20=92(км/ч) скорость сближения автомобилиста и велосипедиста
2)92∙2=184 (км) — расстояние, которое проехали автомобилист и велосипедист вместе за 2 часа
3) 346-184=162 (км) таким будет расстояние между автомобилистом и велосипедистом через 2 часа после начала движения.

Пусть скорость первого автомобиля равна x км/ч, скорость второго — y км/ч.Если они начнут двигаться друг другу навстречу одновременно, то встретятся через 4 часа. Отсюда 4(x+y)=420.
Если первый автомобиль начнет движение на 4 часа и 12 минут раньше, то встретятся они через 2 часа после выезда другого.
4часа 12 минут=4 12/60 часа=4,2 ч. Отсюда 6,2x+2y=420.
Составляем и решаем систему из двух уравнений с двумя неизвестными.
x=50, y=55.
Ответ: 50 км/ч и 55 км/ч.
Но это уже алгебра 7 класса :).

Светлана Михайловна, помогите пожалуйста решить задачу:пешеход и велосипедист начали движение навстречу друг другу в 10 часов из двух пунктов между которыми 4 км. их встреча произошла в 10 ч 20 мин. на следующий день велосипедист выехал в 10 ч, а пешеход вышел в 10 ч.16 мин. поэтому в этот день они встретились в 10 ч 24 мин. найдите скорость пешехода

В первый день пешеход и велосипедист вместе преодолели 4 км за 20 минут =20/60=1/3 часа. Значит, скорость их сближения равна 4:1/3=12 км/ч.
Во второй день пешеход и велосипедист вместе ехали всего 10 ч 24 мин-10 ч 16 мин = 8 минут=8/60 часа. За это время они преодолели 12∙8/60=8/5=1,6 км.
Следовательно, велосипедист до начала движения пешехода проехал 4-1,6=2,4 км. Это расстояние он проехал за 10 ч 16 мин-10 ч = 16 минут = 16/60 часа. Отсюда, скорость велосипедиста
2,4:16/60=9 км/ч.
Скорость сближения пешехода и велосипедиста равна 12 км/ч, значит, скорость пешехода равна 12-9 = 3 км/ч.
Можно решить с помощью системы уравнений, но системы уравнений проходят в конце 7 класса.

Спасибо огромное. Все очень понятно!

Два пешехода одновременно отправились навстречу друг другу из пунктов, расположенных на расстоянии 36 км друг от друга. Скорость первого пешехода 5 км/ч, скорость второго пешехода 7 км/ч. Сколько километров прошел до встречи второй пешеход?

1)5+7=12(км/ч) скорость сближения пешеходов
2)36:12=3(ч) время с момента начала движения и до встречи
3)7∙3=21(км) прошёл до встречи второй пешеход.

Здравствуйте, Светлана Михайловна! Подскажите пожалуйста, как решить задачу, где из 2 городов выехали в одно время грузовик и легковой авто. Скорость авто v км/ч, а грузовика u км/ч. Найти надо расстояние между городами, если авто и грузовик вмтретились через t ч. Если v=70, u=40, t=2

Грузовик и авто едут навстречу друг другу, поэтому скорость сближения равна сумме их скоростей:v+u км/ч.
Они выехали одновременно и ехали до встречи t часов. Чтобы найти расстояние, надо скорость умножить на время: s=(v+u)t.
Если v=70, u=40, t=2, то s=(70+40)∙2=220 км.

По прямой дороге навстречу друг другу едут велосипедист и мопедист. Велосипидиста скорость 12 км/ч, мопедиста – 18 км/ч. Через сколько времени расстояние между ними будет 400метров, если в начале наблюдения расстояние между ними 2 км

12+18=30 км/ч — скорость сближения
400 м= 0,4 км
2-0,4=1,6 км — расстояние, на которое должно уменьшится данное расстояние
1,6:30=1,6/30=16/300=4/75 часа=(4/75)∙ 60 минут = 16/5 минуты= 3,2 минуты — через это время расстояние между объектами станет равным 400 метрам первый раз.

Можно сначала перевести километры в час в метры в минуту
30 км/ч = 30 ∙ 1000/60 м/мин=500 м/мин
2 км=2000 м
2000-400=1600 м
1600:500=3,2 минуты.

Добрый день! Помогите пожалуйста решить задачу! От двух пристаней, находящихся друг от друга на расстоянии 343км,вышли одновременно навстречу друг другу два парохода. Один пароход шёл со скоростью 26 км/ч. С какой скоростью шёл второй пароход, если они встретились через 8 часов?

343:8 = 42 7/8 (км/ч) скорость сближения пароходов.
42 7/8 — 26 = 16 7/8 = 16,875 (км/ч) скорость второго парохода.

Помогите пожалуйста разобраться с задачей.
Из двух поселков, между которыми 45 км, одновременно друг навстречу другу отправились два туриста, скорость одного была 4км/ч, второго 5км/ч. На каком расстоянии от каждого поселка будет их пункт встречи?

1)4+5=9(км/ч) скорость сближения туристов.
2)45:9=5(ч) через такое время после начала движения туристы встретятся
3)4∙5=20(км) пройдёт до места встречи один турист
4)5∙5=25(км) пройдёт другой турист.

Источник

Для начала следует перевести данные задачи в единую систему измерений. Либо в километры, либо в метры.

Я переведу в километры. Значит, расстояние между машинами – 0,07 км (исходя из того, что в одном километре 1000 метров, высчитываем, что 70 метров – это 70:1000=0,07км).

Далее высчитываем время, через которое произойдет столкновение.

Обозначив это время за х (для обоих машин время будет одинаковое), составим уравнение:

60х+80х=0,07

140х=0,07

х=0,07:140=0,0005

То есть столкновение произойдет через 0,0005 часа.

Теперь высчитаем точку этого столкновения.

Посчитаем, какое расстояние проедет за это время каждый из автомобилей.

Первый двигается со скоростью 60 км/ч, значит он пройдет расстояние 60*0,0005=0,03 километра (или 30 метров).

Теперь высчитываем расстояние второго автомобиля:

80*0,0005=0,04 километра (что равно 40 метрам).

Таким образом, до столкновения первый автомобиль проедет 30 метров, а второй – 40.