Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
на главную
Дискриминант
квадратного уравнения
Поддержать сайт
Мы уже разобрали,
как решать квадратные уравнения.
Теперь давайте более подробно рассмотрим, что называют
дискриминантом квадратного уравнения.
Вернемся к нашей формуле для нахожденя корней квадратного уравнения.
Запомните!
Выражение «b2 − 4ac», которое находится под корнем,
принято называть дискриминантом и обозначать буквой «D».
По-другому, через дискриминант формулу нахождения корней квадратного уравнения можно записать так:
x1;2 = , где «D = b2 − 4ac»
По одной из версий термин «Дискриминант» произошел от латинского discriminantis, что означает «отличающий» или «различающий».
В зависимости от знака «D» (дискриминанта)
квадратное уравнение может иметь два, один или ни одного корня. Рассмотрим все три случая.
I случай
D > 0
(дискриминант больше нуля)
2x2 + 5x −7 = 0
D = b2 − 4ac
D = 52 − 4 · 2 · (−7)
D = 25 + 56
D = 81
D > 0
x1;2 =
x1;2 =
x1;2 =
| x1 = |
x2 = |
| x1 = |
x2 = |
| x1 = 1 |
x2 = −3 |
| x1 = 1 |
x2 = −3 |
Ответ: x1 = 1;
x2 = −3
Вывод: когда «D > 0» в квадратном уравнении два корня.
II случай
D = 0
(дискриминант равен нулю)
16x2 − 8x + 1 = 0
D = b2 − 4ac
D = (−8)2 − 4 · 16 · 1
D = 64 − 64
D = 0
x1;2 =
x1;2 =
x1;2 =
x =
x =
Ответ: x =
Вывод: когда «D = 0» в квадратном уравнении один корень.
III случай
D < 0
(дискриминант меньше нуля)
9x2 − 6x + 2 = 0
D = b2 − 4ac
D = (−6)2 − 4 · 9 · 2
D = 36 − 72
D = −36
D < 0
x1;2 =
x1;2 =
Ответ: нет действительных корней
Вывод: когда «D < 0» в квадратном уравнении нет корней.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
Как решить квадратное уравнение
Квадратное уравнение 
Где 


Для решения квадратного уравнения общего вида, необходимо найти корни 
Дискриминант
Для того чтобы найти дискриминант, воспользуемся формулой 
D > 0
При условии, что дискриминант больше нуля, корня 2, вычисляются они по формуле:
D = 0
Если дискриминант равен нулю, корень один, вычисляется по формуле:
D < 0
Если дискриминант меньше нуля, делается вывод, что корней нет.
Пример 1
Например у нас следующие параметры:
a = 4;
b = 9;
c = 2.
Уравнение выглядит следующим образом:
Дискриминант больше нуля
Находим дискриминант по формуле:

Находим x1
Находим x2
Пример 2
Уравнение со следующими параметрами:
a = 3;
b = 6;
c = 3.
Уравнение выглядит следующим образом:
Дискриминант равен 0
Находим по формуле:

Находим X
Дискриминант меньше нуля
Если дискриминант меньше нуля, то искомые корни являются комплексными.
нет оценок
Категории
НаукаМатематикаАлгебра
Читайте также
- Найти X пропорционально
- Площадь ромба
- ГНОМ ГНОМ СКАЛА
- ДОМ ВОДА ДАЧА
- Периметр треугольника
- Объем шара
- Площадь треугольника по основанию и высоте
- Процентное отношение двух чисел
- Объем цилиндра
- Спряжение глагола “to obey” (Английский язык)
- Спряжение глагола “to transpose” (Английский язык)
- Спряжение глагола “to equate” (Английский язык)
Комментарии
Квадратными неравенствами называют неравенства, которые можно привести к виду (ax^2+bx+c) (⋁) (0), где (a),(b) и (с) – любые числа (причем (a≠0)), (x) – неизвестная переменная, а (⋁) – любой из знаков сравнения ((>),(<),(≤),(≥)).
Проще говоря, такие неравенства выглядят как квадратные уравнения, но со знаком сравнения вместо знака равно.
Примеры:
(x^2+2x-3>0)
(3x^2-x≥0)
((2x+5)(x-1)≤5)
Как решать квадратные неравенства?
Квадратные неравенства обычно решают методом интервалов. Ниже приведен алгоритм, как решать квадратные неравенства с дискриминантом больше нуля. Решение квадратных неравенств с дискриминантом равным нулю или меньше нуля – разобраны отдельно.
-
Приведите неравенство к виду (ax^2+bx+c⋁0).
Примеры:(x^2-6x-16<0) (-9x^2+x+8≤0)
-
Разложите выражение слева на множители. Для этого приравняйте его к нулю и решите получившееся уравнение, найдя корни (x_1) и (x_2). Затем запишите исходное выражение в виде (a(x-x_1 ) (x-x_2 )) Подробнее об этом можно почитать здесь.
(x^2-6x-16=0) (-9x^2+x+8=0)
(D=36-4 cdot 1 cdot (-16)=100=10^2) (D=1-4 cdot (-9) cdot 8=289)
(x_1=frac{6-10}{2}=-2) (x_1=frac{-1+17}{-18}=frac{16}{-18}=-frac{8}{9}) (x_2=frac{6+10}{2}=8) (x_2=frac{-1-17}{-18}=frac{-18}{-18}=1)
((x-8)(x+2)<0) (-9(x+frac{8}{9})(x-1)≤0) -
Начертите числовую ось и отметьте на ней найденные корни. Если неравенство строгое (со знаком (<) или (>)) то точки должны быть выколоты, если неравенство нестрогое (со знаком (≤) или (≥)), то точки должны быть закрашены.
-
Нанесенные корни разбивают числовую ось на несколько интервалов.
В первом справа интервале поставьте:
(-) знак плюс если перед скобками ничего не стоит или стоит положительное число
(-) знак минус если перед скобками стоит знак минус.
В следующих за ним интервалах поставьте чередующиеся знаки. -
Заштрихуйте подходящие интервалы, то есть числовые промежутки:
(-) со знаком «(+)», если в неравенстве стояло «(>0)» или «(≥0)»
(-) со знаком «(-)», если в неравенстве стояло «(<0)» или «(≤0)» -
Выпишите в ответ те интервалы, которые вы заштриховали.
Внимание! При строгих знаках неравенства ((<) или (>)) границы интервала НЕ ВХОДЯТ в решение, при этом в ответе сам интервал записывается в виде ((x_1;x_2)) – скобки круглые. При нестрогих знаках неравенства ((≤) или (≥)) – границы интервала ВХОДЯТ в решение, и ответ записывается в виде ([x_1;x_2]), с квадратными скобками на точках.Ответ: ((-2;8)) Ответ: ((-∞;frac{8}{9}]∪[1;∞))
Пример. Решите квадратное неравенство (frac{x^2}{5}+frac{2x}{3})(≥) (frac{8}{15})
Решение:
|
(frac{x^2}{5}+frac{2x}{3})(≥) (frac{8}{15}) |
Чтобы избавиться от дробей, умножим обе части неравенство на (15). |
|
|
(3x^2+10x≥8) |
Перенесем (8) влево. |
|
|
(3x^2+10x-8≥0) |
Вот мы и привели неравенство к виду (ax^2+bx+c⋁0). Запишем квадратное уравнение вида (ax^2+bx+c=0). |
|
|
(3x^2+10x-8=0) |
Решим полученное квадратное уравнение. |
|
|
(D=100+4⋅3⋅8=196=14^2) |
Когда корни найдены, запишем неравенство в разложенном на множители виде. |
|
|
(3(x+4)(x-frac{2}{3})≥0) |
Теперь начертим числовую ось, отметим на ней корни и расставим знаки на интервалах. |
|

|
Выпишем в ответ интересующие нас интервалы . Так как знак неравенства (≥), то нам нужны интервалы со знаком (+), при этом сами корни мы включаем в ответ (скобки на этих точках – квадратные). |
Ответ: (x∈(-∞;-4]∪[ frac{2}{3};∞))
Квадратные неравенства с отрицательным и равным нулю дискриминантом
Алгоритм выше работает, когда дискриминант больше нуля, то есть квадратный трехчлен имеет (2) корня. Что делать в остальных случаях? Например, таких:
|
(1) x^2+2x+9>0) |
(2) x^2+6x+9≤0) |
(3)-x^2-4x-4>0) |
(4) -x^2-64<0) |
|
(D=4-36=-32<0) |
(D=36-36=0) |
(D=16-16=0) |
(D=-4 cdot 64<0) |
Если (D<0), то квадратный трехчлен имеет постоянный знак, совпадающий со знаком коэффициента (a) (тем, что стоит перед (x^2)).
То есть, выражение:
(x^2+2x+9) – положительно при любых (x), т.к. (a=1>0)
(-x^2-64) – отрицательно при любых (x), т.к. (a=-1<0)
Если (D=0), то квадратный трехчлен при одном значении (x) равен нулю, а при всех остальных имеет постоянный знак, который совпадает со знаком коэффициента (a).
То есть, выражение:
(x^2+6x+9) – равно нулю при (x=-3) и положительно при всех остальных иксах, т.к. (a=1>0)
(-x^2-4x-4) – равно нулю при (x=-2) и отрицательно при всех остальных, т.к. (a=-1<0).
Как найти икс, при котором квадратный трехчлен равен нулю? Нужно решить соответствующее квадратное уравнение.
С учетом этой информации давайте решим квадратные неравенства:
|
1) (x^2+2x+9>0) |
Неравенство, можно сказать, задает нам вопрос: «при каких (x) выражение слева больше нуля?». Выше мы уже выяснили, что при любых. В ответе можно так и написать: «при любых (x)», но лучше туже самую мысль, выразить на языке математики. |
|
|
Ответ: (x∈(-∞;∞)) |
||
|
2) (x^2+6x+9≤0) |
Вопрос от неравенства: «при каких (x) выражение слева меньше или равно нулю?» Меньше нуля оно быть не может, а вот равно нулю – вполне. И чтобы выяснить при каком иске это произойдет, решим соответствующие квадратное уравнение. |
|
|
(x^2+6x+9=0) |
Давайте соберем наше выражение по формуле (a^2+2ab+b^2=(a+b)^2). |
|
|
((x+3)^2=0) |
Сейчас нам мешает только квадрат. Давайте вместе подумаем – какое число в квадрате равно нулю? Ноль! Значит, квадрат выражения равен нулю только если само выражение равно нулю. |
|
|
(x+3=0) |
Это число и будет ответом. |
|
|
Ответ: (-3) |
||
|
3)(-x^2-4x-4>0) |
Когда выражение слева больше нуля? Как выше уже было сказано выражение слева либо отрицательно, либо равно нулю, положительным оно быть не может. Значит ответ – никогда. Запишем «никогда» на языке математике, с помощью символа «пустое множество» – (∅). |
|
|
Ответ: (x∈∅) |
||
|
4) (-x^2-64<0) |
Когда выражение слева меньше нуля? Всегда. Значит неравенство выполняется при любых (x). |
|
|
Ответ: (x∈(-∞;∞)) |
Смотрите также:
Дробно-рациональные неравенства
Дискриминант квадратного уравнения
- Решение квадратных уравнений через дискриминант
Дискриминант квадратного уравнения — это выражение, находящееся под корнем в формуле нахождения корней квадратного уравнения. Дискриминант обозначается латинской буквой D.
| Вид уравнения | Формула корней | Формула дискриминанта |
|---|---|---|
| ax2 + bx + c = 0 |  |
b2 – 4ac |
| ax2 + 2kx + c = 0 |  |
k2 – ac |
| x2 + px + q = 0 |  |
 |
 |
p2 – 4q |
Все формулы нахождения корней квадратных уравнений можно записать короче с помощью дискриминанта:
| Вид уравнения | Формула |
|---|---|
| ax2 + bx + c = 0 |  , где D = b2 – 4ac , где D = b2 – 4ac |
| ax2 + 2kx + c = 0 |  , где D = k2 – ac , где D = k2 – ac |
| x2 + px + q = 0 |  , где D = , где D =  |
 , где D = p2 – 4q , где D = p2 – 4q |
Дискриминант позволяет определить, имеет ли уравнение корни и сколько их, не решая само уравнение:
- Если дискриминант больше нуля, то уравнение имеет два корня.
- Если дискриминант равен нулю, то уравнение имеет один корень.
- Если дискриминант меньше нуля, то уравнение не имеет корней.
Несмотря на то, что есть несколько формул дискриминанта, чаще всего используют первую:
D = b2 – 4ac,
так как она относится к формуле:

которая является универсальной формулой нахождения корней квадратного уравнения. Данная формула подходит даже для неполных квадратных уравнений.
Решение квадратных уравнений через дискриминант
Для решения квадратного уравнения по формуле можно сначала вычислить дискриминант и сравнить его с нулём. В зависимости от результата, либо искать корни по формуле, либо сделать вывод, что корней нет.
Пример 1. Решить уравнение:
3x2 – 4x + 2 = 0.
Определим, чему равны коэффициенты:
a = 3, b = -4, c = 2.
Найдём дискриминант:
D = b2 – 4ac = (-4)2 – 4 · 3 · 2 = 16 – 24 = -8,
D < 0.
Ответ: корней нет.
Пример 2.
x2 – 6x + 9 = 0.
Определим, чему равны коэффициенты:
a = 1, b = -6, c = 9.
Найдём дискриминант:
D = b2 – 4ac = (-6)2 – 4 · 1 · 9 = 36 – 36 = 0,
D = 0.
Уравнение имеет всего один корень:
Ответ: 3.
Пример 3.
x2 – 4x – 5 = 0.
Определим, чему равны коэффициенты:
a = 1, b = -4, c = -5
Найдём дискриминант:
D = b2 – 4ac = (-4)2 – 4 · 1 · (-5) = 16 + 20 = 36,
D > 0.
Уравнение имеет два корня:
x1 = (4 + 6) : 2 = 5,
x2 = (4 – 6) : 2 = -1.
Ответ: 5, -1.
На чтение 4 мин Просмотров 4.1к. Опубликовано 04.07.2019
Содержание
- I случай
D > 0
(дискриминант больше нуля) - II случай
D = 0
(дискриминант равен нулю) - III случай
D
(дискриминант меньше нуля) - Решение квадратных уравнений через дискриминант
Мы уже разобрали, как решать квадратные уравнения. Теперь давайте более подробно рассмотрим, что называют дискриминантом квадратного уравнения.
Вернемся к нашей формуле для нахожденя корней квадратного уравнения.
x1;2 =
Выражение « b 2 − 4ac », которое находится под корнем, принято называть дискриминантом и обозначать буквой « D ».
По-другому, через дискриминант формулу нахождения корней квадратного уравнения можно записать так:
x1;2 =
, где « D = b 2 − 4ac »
По одной из версий термин «Дискриминант» произошел от латинского discriminantis, что означает «отличающий» или «различающий».
В зависимости от знака « D » (дискриминанта) квадратное уравнение может иметь два, один или ни одного корня. Рассмотрим все три случая.
I случай
D > 0
(дискриминант больше нуля)
D —> , где « D = b 2 − 4ac »
—> —> D = b 2 − 4ac
D = 5 2 − 4 · 2 · (−7)
D = 25 + 56
D = 81
D > 0
x1;2 =
x1;2 =
x1;2 =
x2 =
−5 − 9
4
x1 =
4
4
x2 =
−14
4
x1 = 1
x2 = −3
2
4
x1 = 1
x2 = −3
1
2
Ответ: x1 = 1; x2 = −3
Вывод: когда « D > 0 » в квадратном уравнении два корня .
II случай
D = 0
(дискриминант равен нулю)
16x 2 − 8x + 1 = 0
D = b 2 − 4ac
D = (−8) 2 − 4 · 16 · 1
D = 64 − 64
D = 0
x1;2 =
x1;2 =
x1;2 =
x =
x =
Ответ: x =
Вывод: когда « D = 0 » в квадратном уравнении один корень .
III случай
D
(дискриминант меньше нуля)
D = b 2 − 4ac
D = (−6) 2 − 4 · 9 · 2
D = 36 − 72
D = −36
D
x1;2 =
x1;2 =
Ответ: нет действительных корней
Вывод: когда « D » в квадратном уравнении нет корней .
Рассмотрим решение квадратных уравнений, дискриминант которых отрицателен:
Пример 42.4. Решить уравнение: 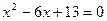
Решение. Найдем дискриминант: 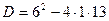
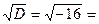
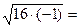
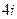
Тогда 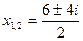

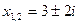
Ответ:
Видим, что если дискриминант квадратного уравнения отрицателен, то уравнение имеет решения на множестве комплексных чисел. В ответе получаются два сопряженных комплексных числа. Это очень важный результат: теперь мы знаем, что абсолютно любое квадратное уравнение имеет два корня на множестве комплексных чисел.
Подобное утверждение, известное под названием “основная теорема алгебры”, было доказано Гауссом в конце XVIII века: любое алгебраическое уравнение п-й степени имеет п комплексных корней (при этом некоторые корни являются кратными). Эти результаты подчеркивают ту исключительную роль, которую играют комплексные числа в теории алгебраических уравнений.
Дата добавления: 2014-12-27 ; Просмотров: 12919 ; Нарушение авторских прав? ;
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Дискриминант квадратного уравнения – это выражение, находящееся под корнем в формуле нахождения корней квадратного уравнения. Дискриминант обозначается латинской буквой D.
| Вид уравнения | Формула корней | Формула дискриминанта |
|---|---|---|
| ax 2 + bx + c = 0 |  |
b 2 — 4ac |
| ax 2 + 2kx + c = 0 |  |
k 2 — ac |
| x 2 + px + q = 0 |  |
 |
 |
p 2 — 4q |
Все формулы нахождения корней квадратных уравнений можно записать короче с помощью дискриминанта:
| Вид уравнения | Формула |
|---|---|
| ax 2 + bx + c = 0 |  , где D = b 2 — 4ac , где D = b 2 — 4ac |
| ax 2 + 2kx + c = 0 |  , где D = k 2 — ac , где D = k 2 — ac |
| x 2 + px + q = 0 |  , где D = , где D =  |
 , где D = p 2 — 4q , где D = p 2 — 4q |
Дискриминант позволяет определить, имеет ли уравнение корни и сколько их, не решая само уравнение:
- Если дискриминант больше нуля, то уравнение имеет два корня.
- Если дискриминант равен нулю, то уравнение имеет один корень.
- Если дискриминант меньше нуля, то уравнение не имеет корней.
Несмотря на то, что есть несколько формул дискриминанта, чаще всего используют первую:
так как она относится к формуле:
которая является универсальной формулой нахождения корней квадратного уравнения. Данная формула подходит даже для неполных квадратных уравнений.
Решение квадратных уравнений через дискриминант
Для решения квадратного уравнения по формуле можно сначала вычислить дискриминант и сравнить его с нулём. В зависимости от результата, либо искать корни по формуле, либо сделать вывод, что корней нет.
Пример 1. Решить уравнение:
Определим, чему равны коэффициенты:
D = b 2 — 4ac = (-4) 2 — 4 · 3 · 2 = 16 — 24 = -8, D 2 — 6x + 9 = 0
Определим, чему равны коэффициенты:
D = b 2 — 4ac = (-6) 2 — 4 · 1 · 9 = 36 — 36 = 0, D = 0
Уравнение имеет всего один корень:
Определим, чему равны коэффициенты:
D = b 2 — 4ac = (-4) 2 — 4 · 1 · (-5) = 16 + 20 = 36, D > 0

















